Effect of Gap Length and Partition Thickness on Thermal Boundary Layer in Thermal Convection
Abstract
1. Introduction
2. Numerical Method
2.1. Governing Equations
2.2. Lattice Boltzmann Method
2.3. Boundary and Initial Conditions
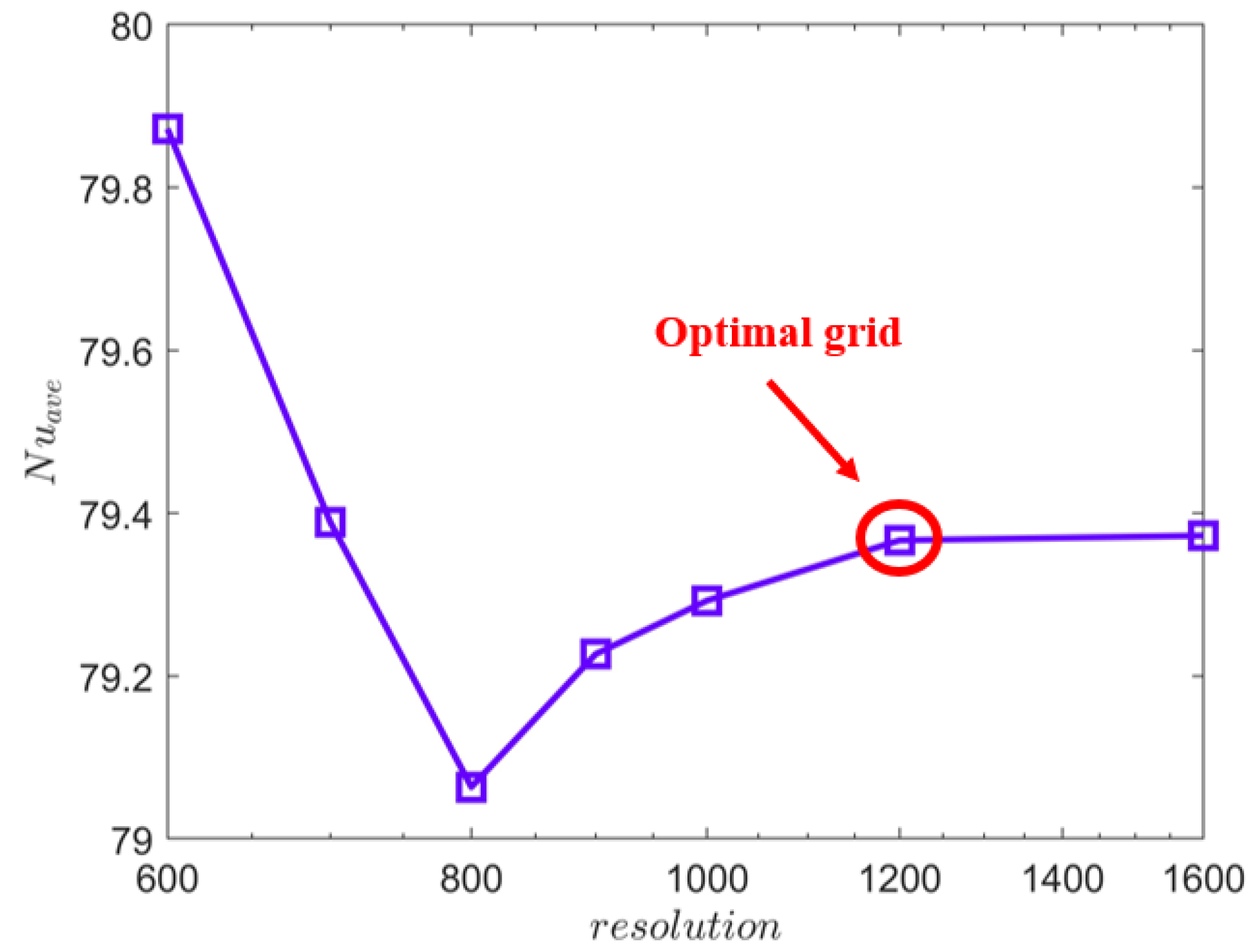
2.4. Grid Independence Test
2.5. Local Grid Refinement
3. Results and Discussion
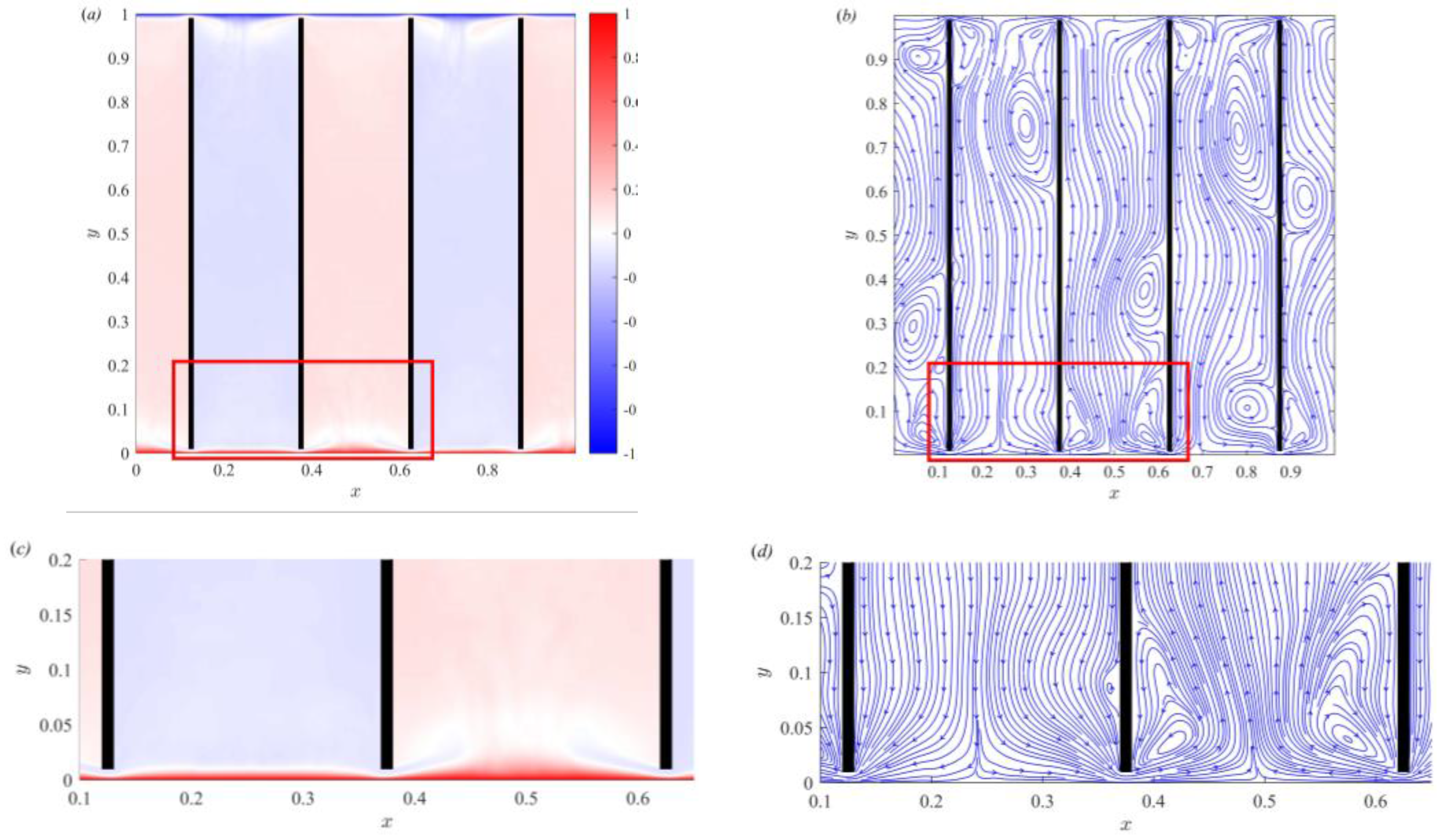
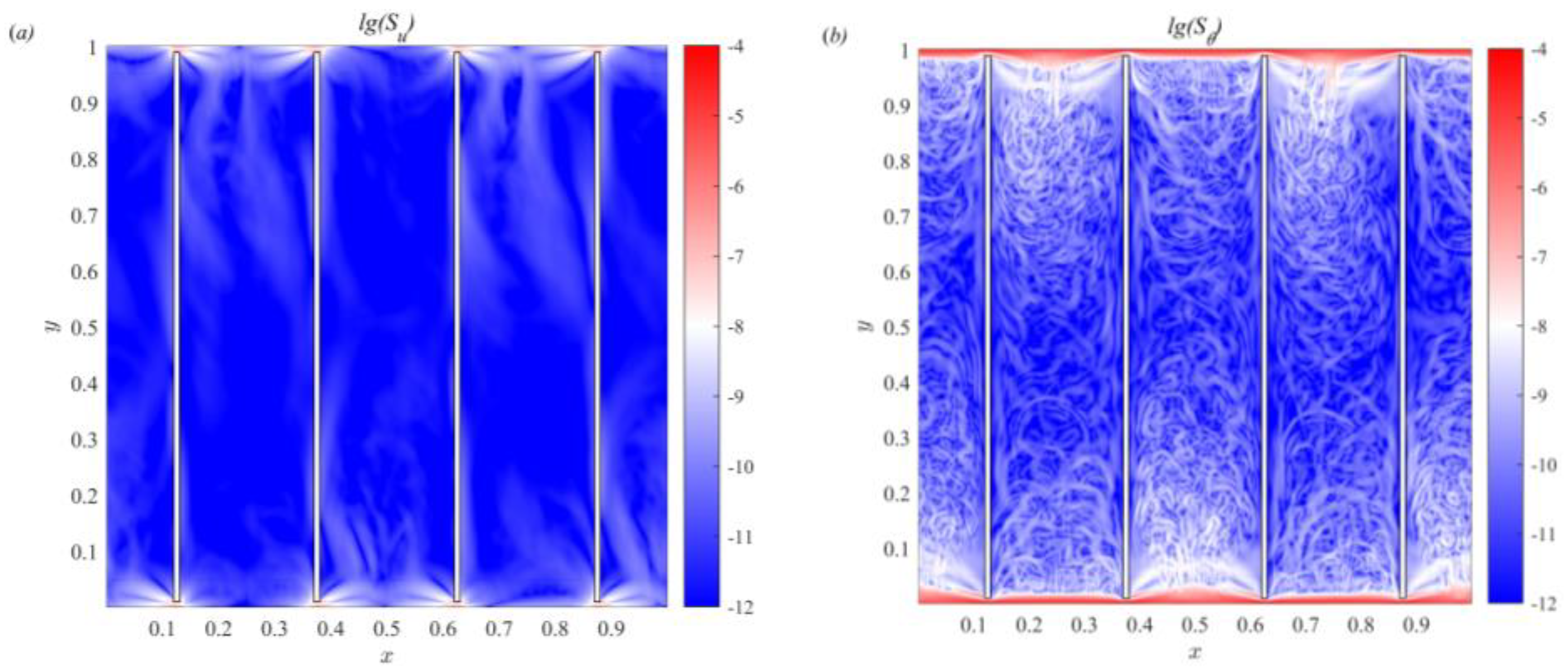
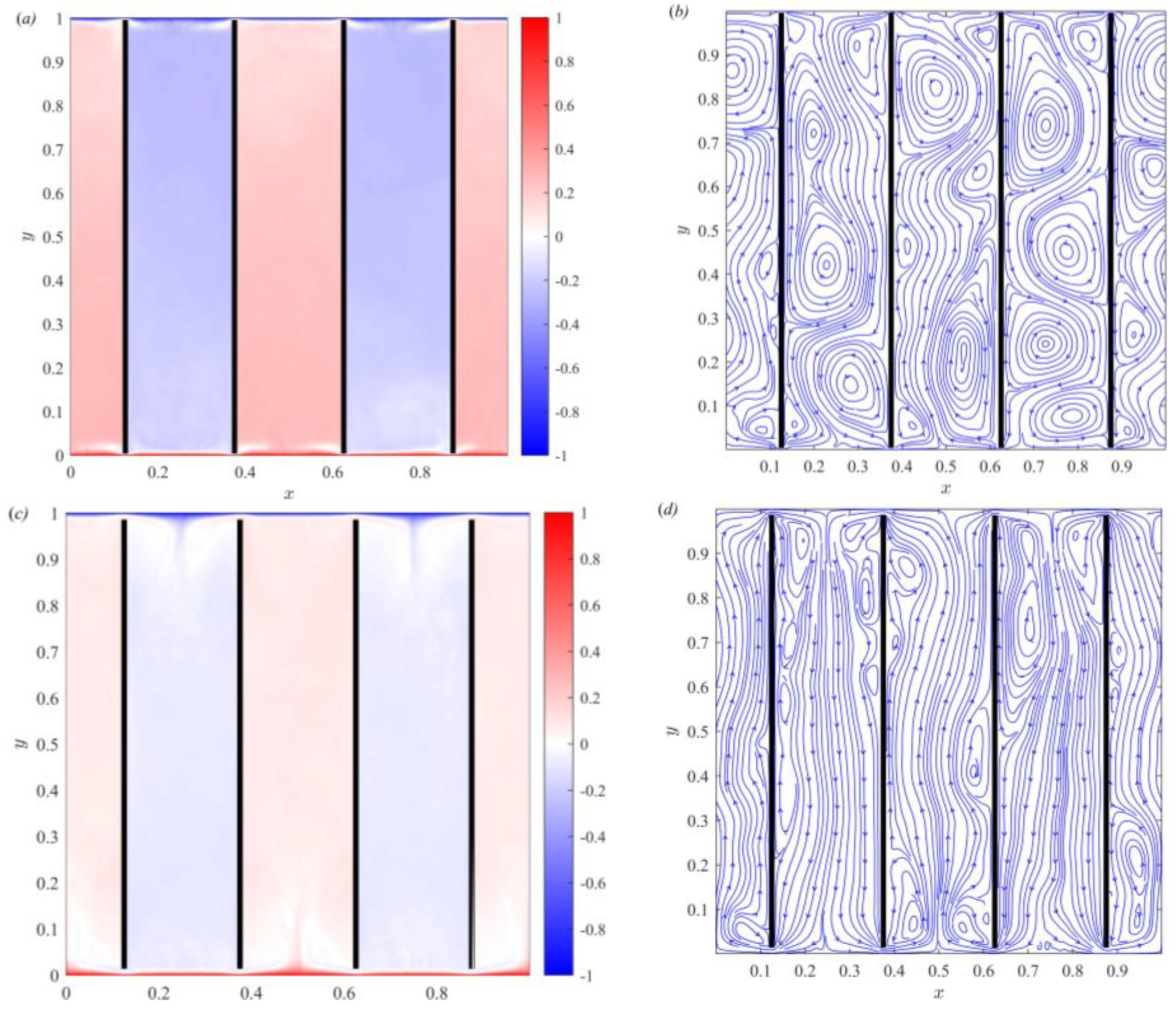
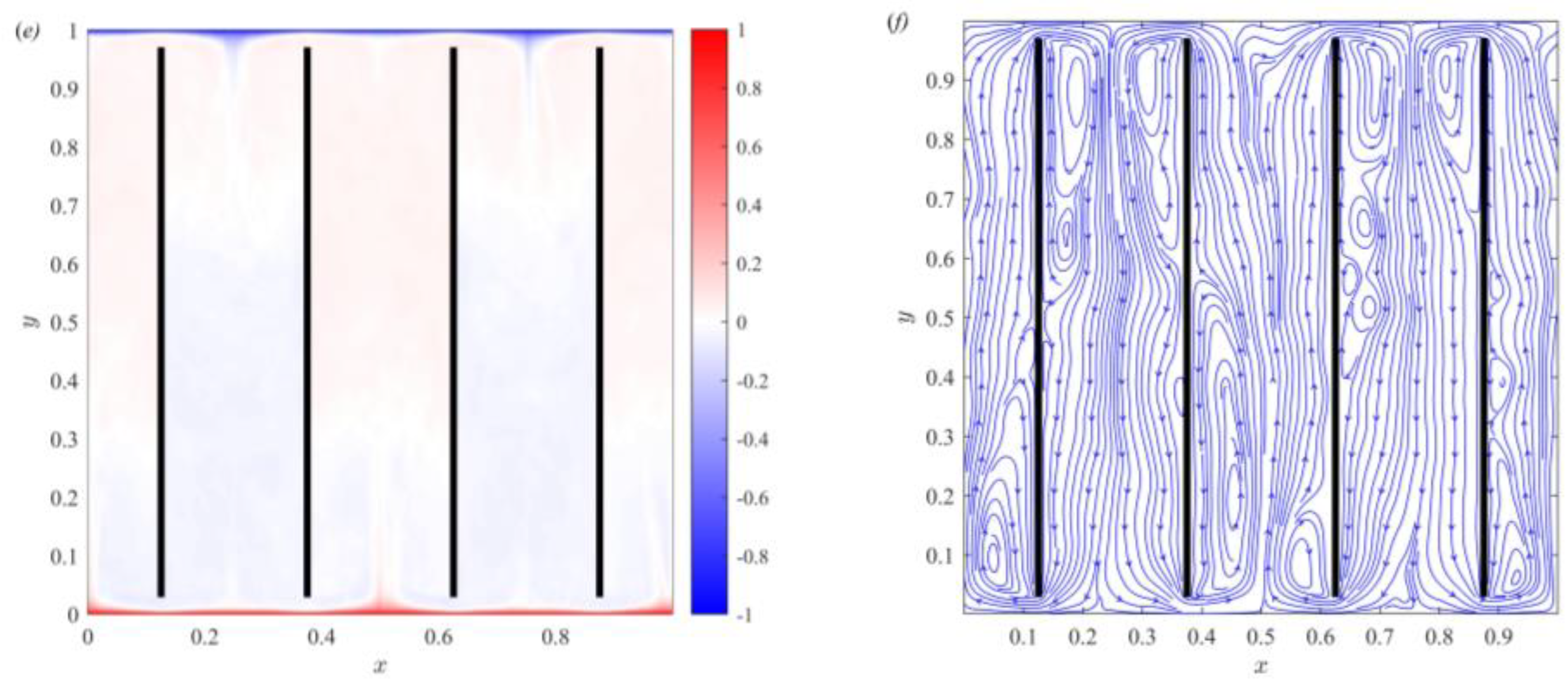
3.1. Temperature Field and Streamline Distribution of Partitioned Thermal Convection
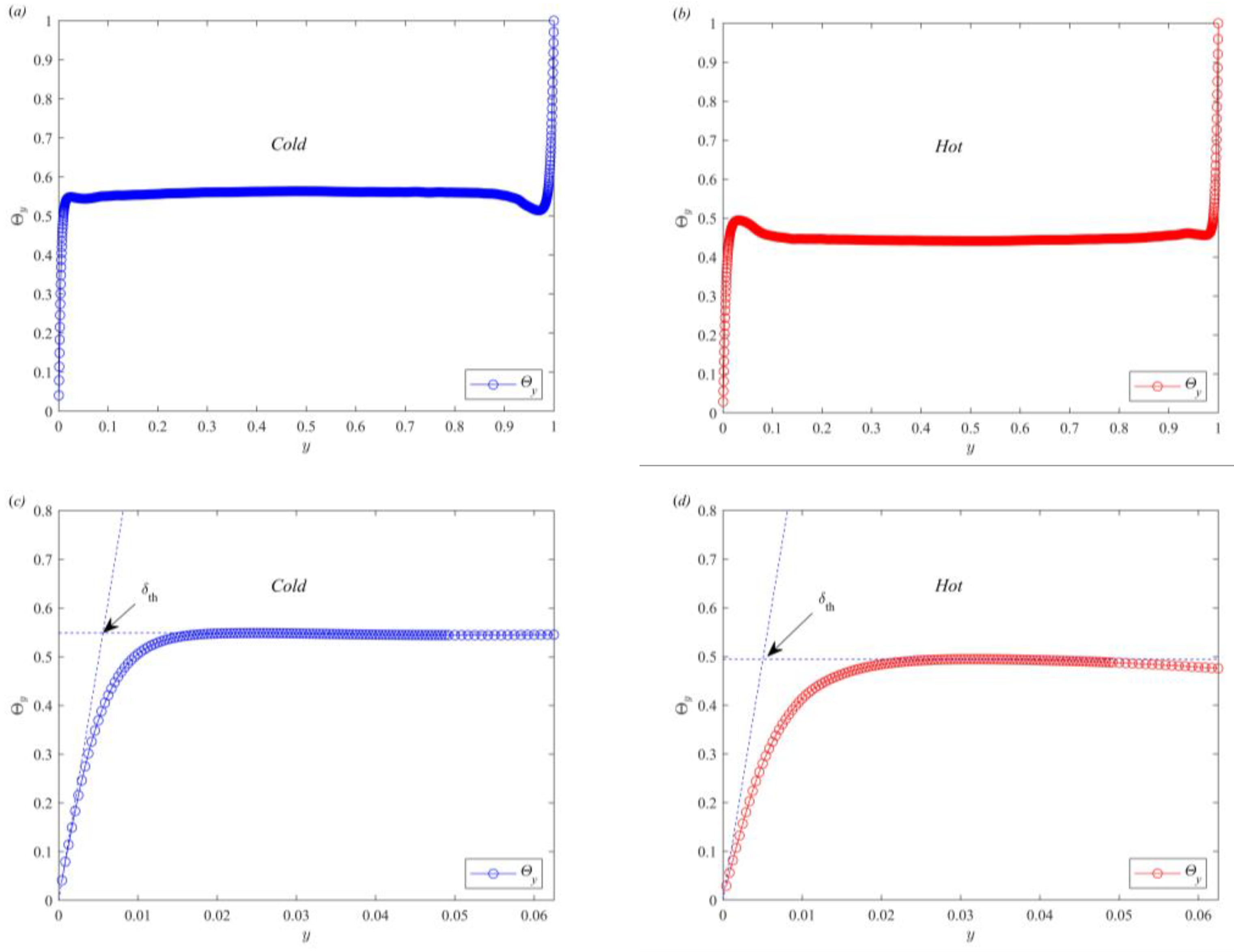
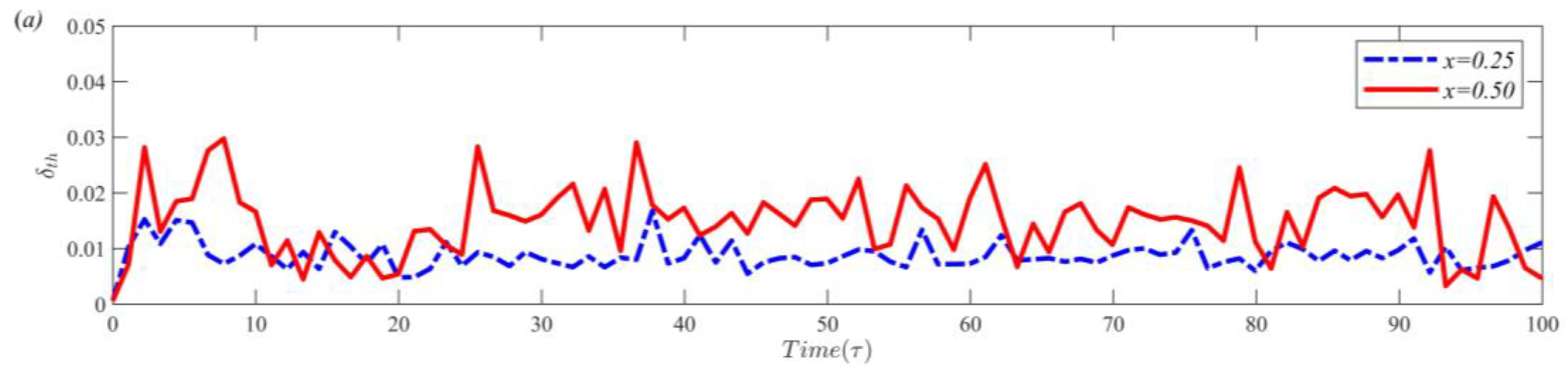
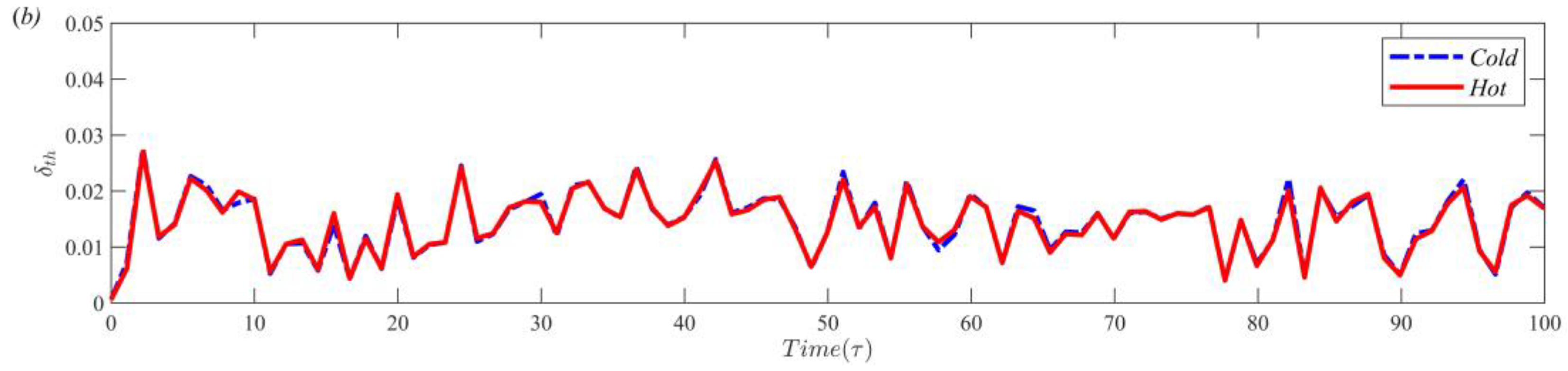
3.2. Thickness of Thermal Boundary Layer
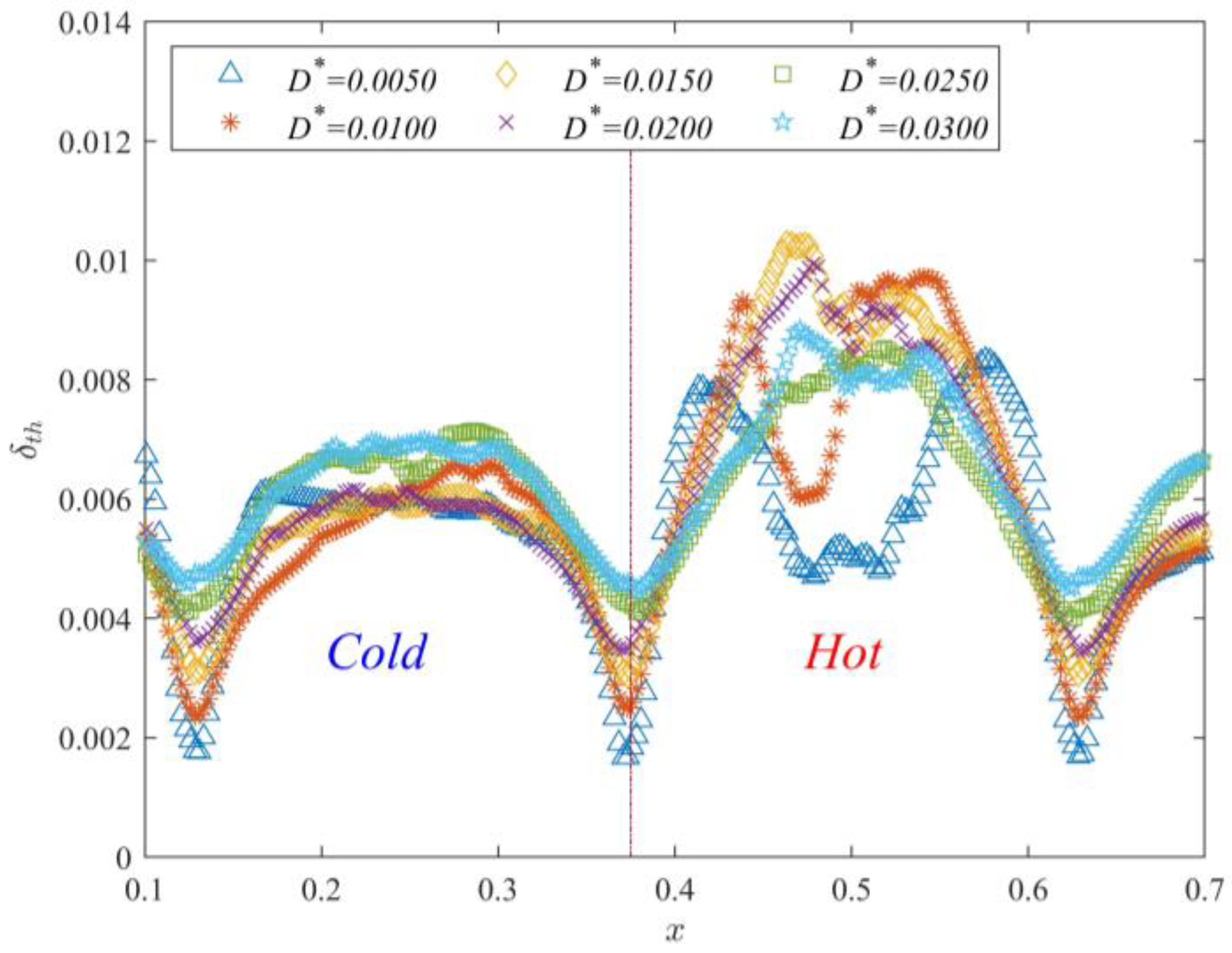
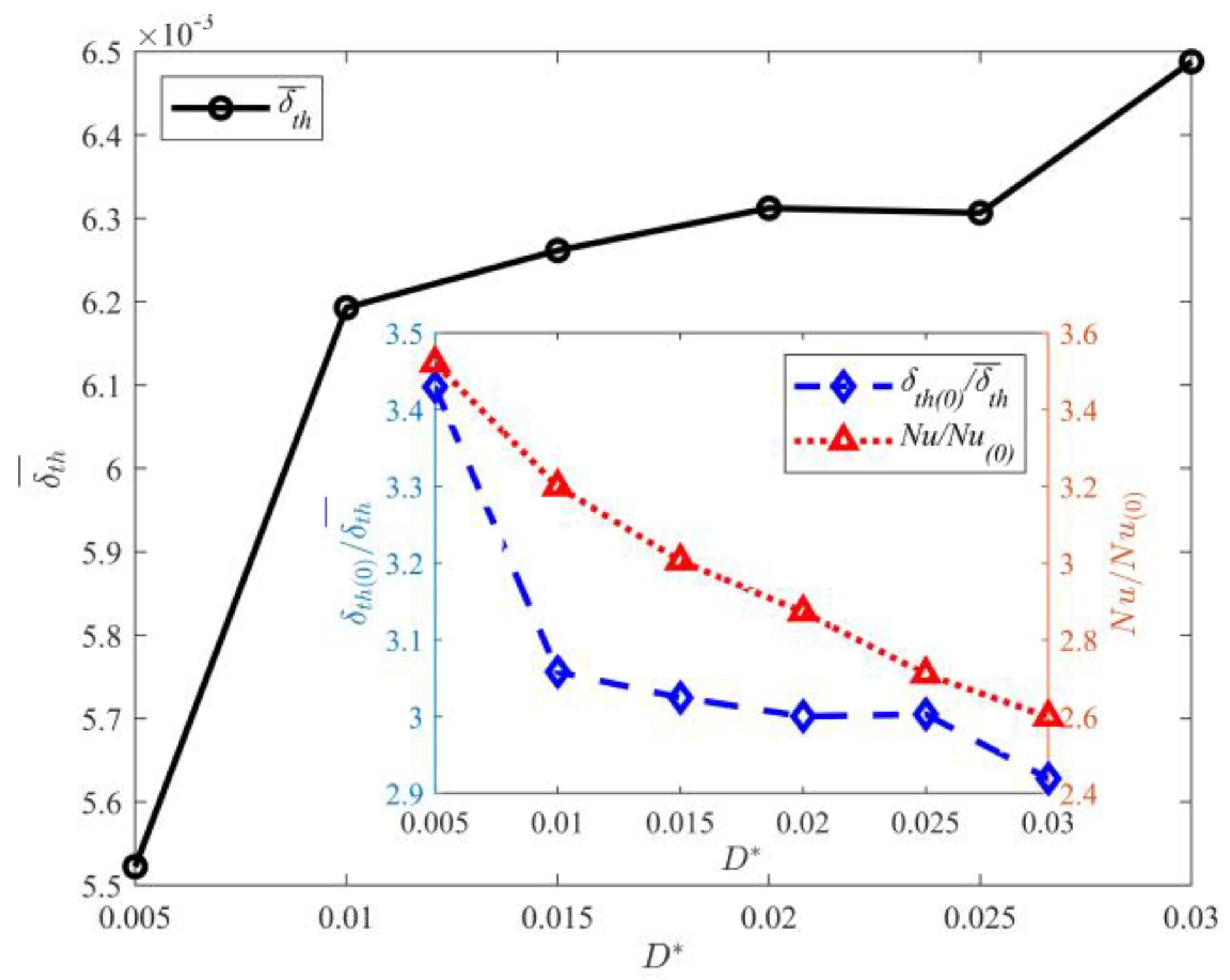
3.3. Effect of Gap Length on Thermal Boundary Layer
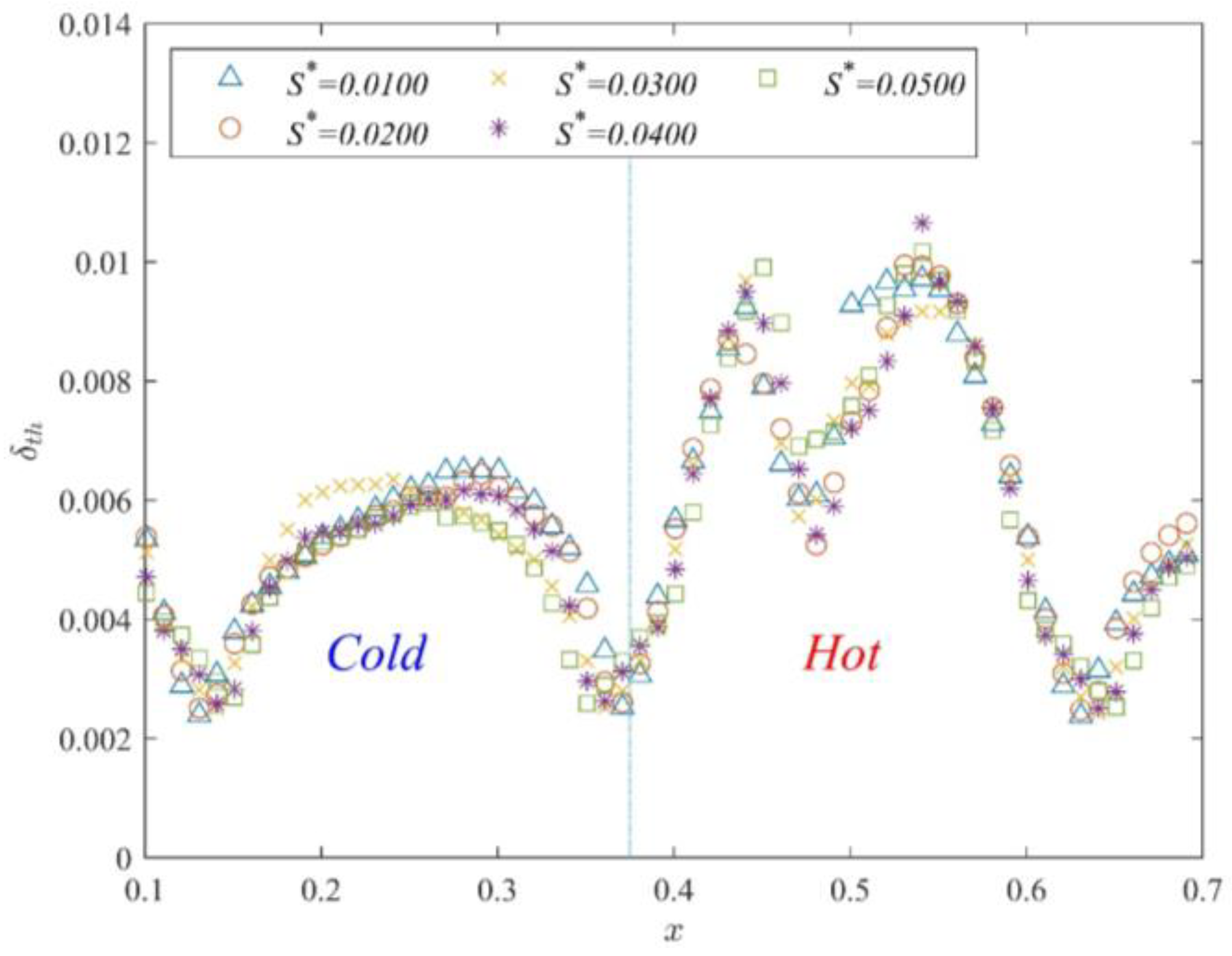
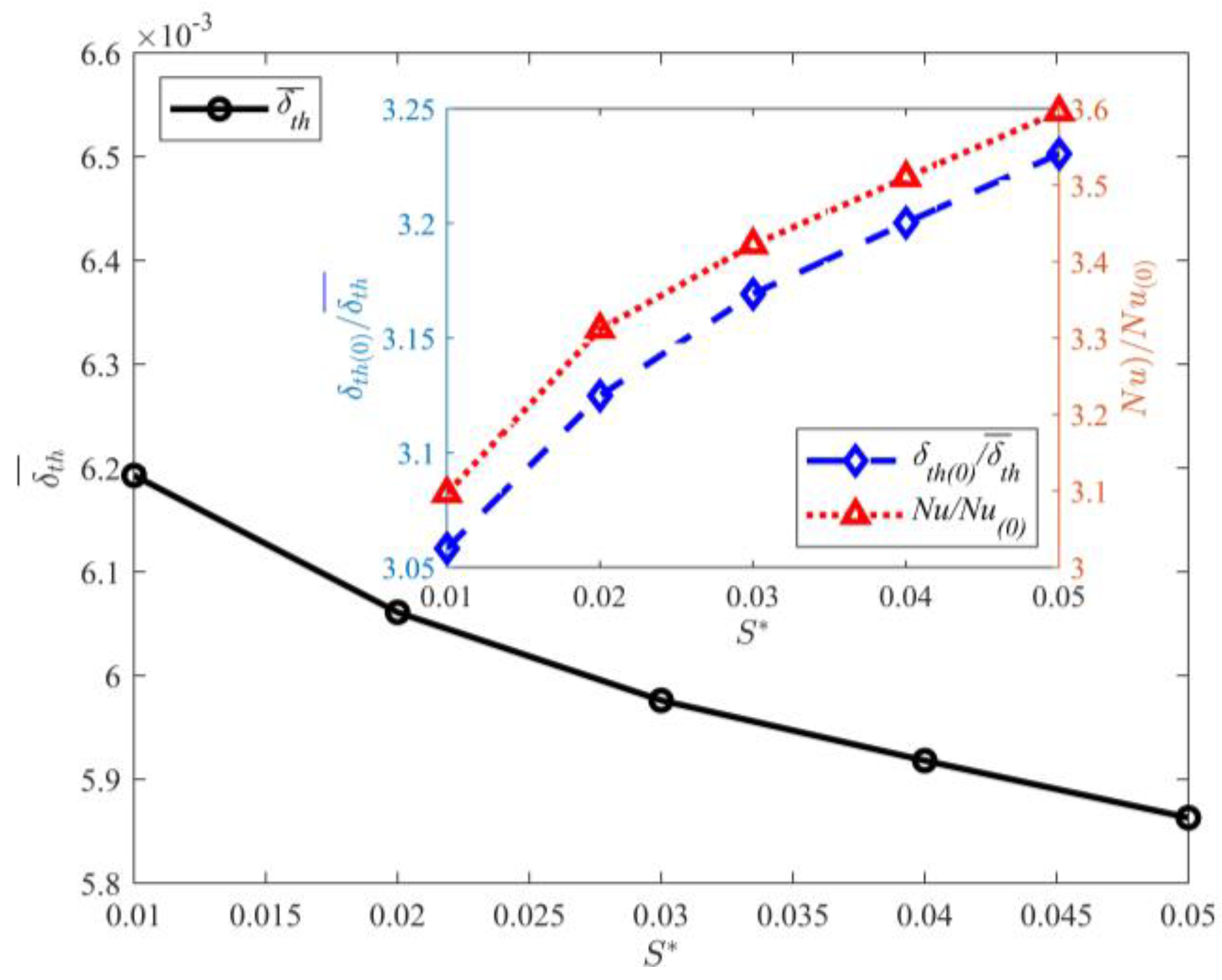
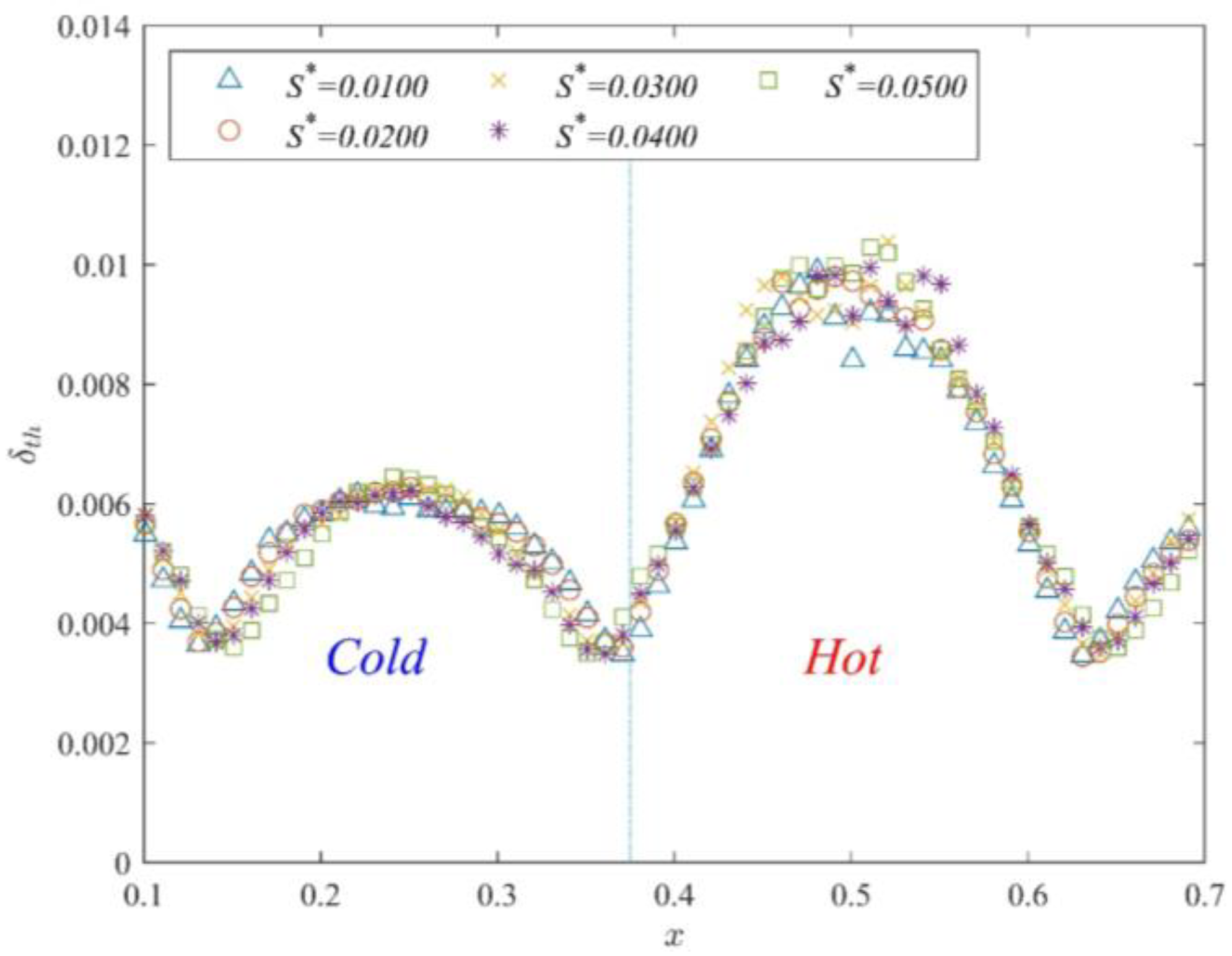
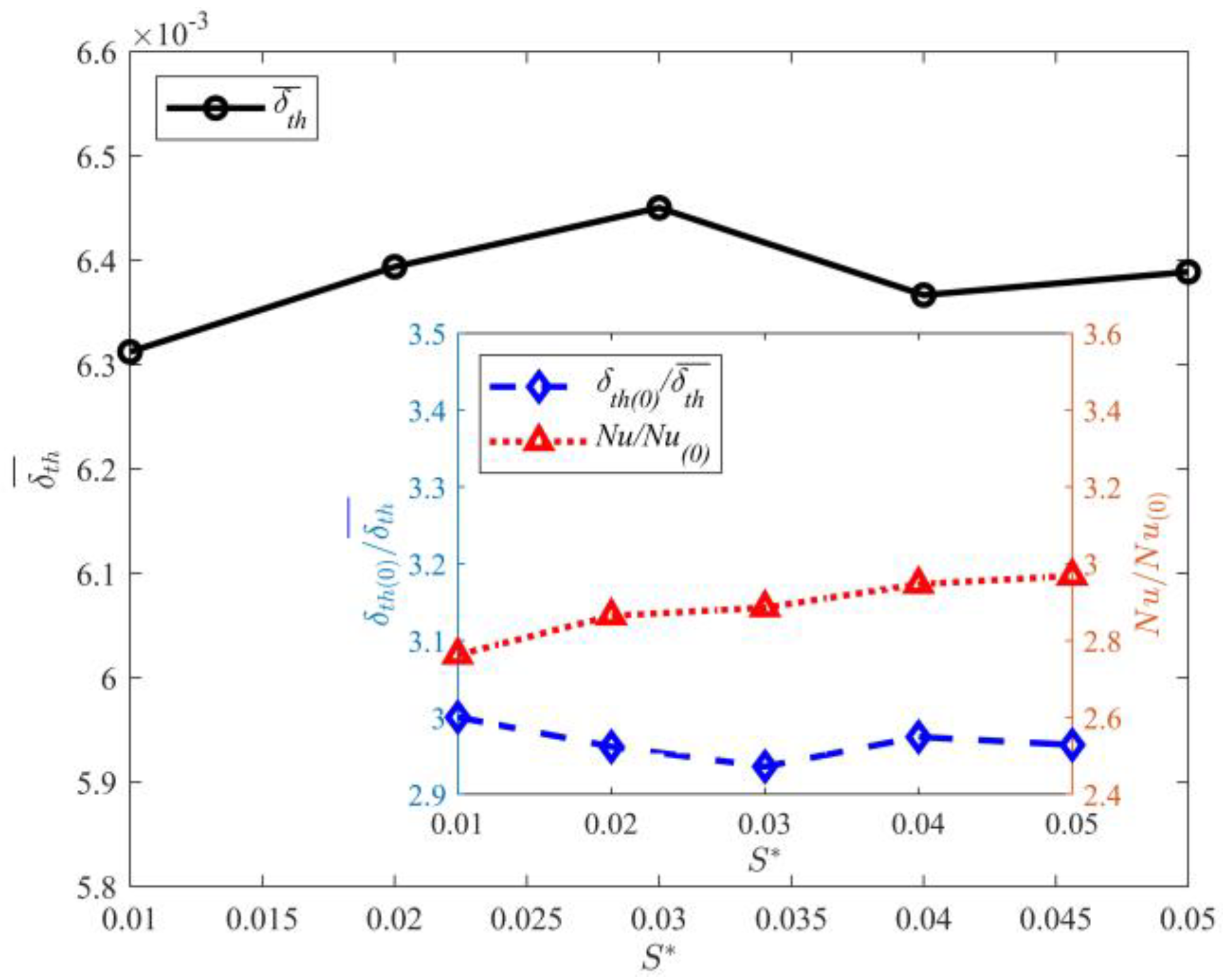
3.4. Effect of Partition Wall Thickness on Thermal Boundary Layer
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nu | Nusselt number |
| Ra | Rayleigh number |
| Pr | Prandtl number |
| κ | Thermal diffusivity |
| β | Thermal expansion |
| ν | Kinematic viscosity |
| g | Gravitational acceleration |
| ρ | Fluid density |
| p | Fluid pressure |
| Discrete space steps | |
| Discrete time steps | |
| Height of the computational domain | |
| Length of the computational domain | |
| Aspect ratio | |
| Partitioned walls of thickness | |
| Gap length between the cooling/heating plates and partitioned walls | |
| Width between two adjacent partitioned walls | |
| Particle position | |
| Discrete force term | |
| Weight coefficients | |
| Local temperature | |
| Temperature difference between the heating and cooling plates | |
| Non-dimensional temperature | |
| n | The Ratio of the coarse grid discrete steps to the fine grid discrete steps |
| < > | The Space average of the whole fluid domain |
| τ | Dimensionless time |
| Relaxation time for velocity field | |
| Relaxation time for temperature field | |
| Sound speed | |
| Discretized velocity vector | |
| Density distribution function of the velocity field | |
| Density distribution function of the temperature field | |
| Equilibrium distribution function of the velocity field | |
| Equilibrium distribution function of the temperature field | |
| Kinetic energy dissipation | |
| Thermal energy dissipation | |
| Thermal boundary layer thickness | |
| Average thickness of thermal boundary layer in time and space |
References
- Xu, A.; Chen, X.; Wang, F.; Xi, H.D. Correlation of internal flow structure with heat transfer efficiency in turbulent Rayleigh–Bénard convection. Phys. Fluids 2020, 32, 105112. [Google Scholar] [CrossRef]
- Liu, S.; Huisman, S.G. Heat transfer enhancement in Rayleigh-Bénard convection using a single passive barrier. Phys. Rev. Fluids 2020, 5, 123502. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, X.; Xia, Z.; Xi, H.D.; Zhou, Q.; Chen, S.Y. Stabilizing/destabilizing the large-scale circulation in turbulent Rayleigh-Bénard convection with sidewall temperature control. J. Fluid Mech. 2021, 915, A14. [Google Scholar] [CrossRef]
- Li, X.M.; He, J.D.; Tian, Y.; Hao, P.; Huang, S.D. Effects of Prandtl number in quasi-two-dimensional Rayleigh-Bénard convection. J. Fluid Mech. 2021, 915, A60. [Google Scholar] [CrossRef]
- Zhou, W.F.; Chen, J. Large-scale structures of turbulent Rayleigh-Bénard convection in a slim-box. Phys. Fluids 2021, 33, 65103. [Google Scholar] [CrossRef]
- He, X.; Chen, S.; Doolen, G.D. A novel thermal model for the lattice Boltzmann method in incompressible limit. J. Comput. Phys. 1998, 146, 282–300. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Scaling in thermal convection a unifying theory. J. Fluid Mech. 2000, 407, 27–56. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 2002, 66, 016305. [Google Scholar] [CrossRef]
- Ahlers, G.; Grossmann, S.; Lohse, D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection. Rev. Mod. Phys. 2009, 81, 503–537. [Google Scholar] [CrossRef]
- He, X.Z.; Funfschilling, D.; Bodenschatz, E.; Ahlers, G. Heat transport by turbulent Rayleigh–Bénard convection for Pr ≃ 0.8 and 4 × 1011 ≲ Ra ≲ 2 × 1014: Ultimate-state transition for aspect ratio Γ = 1.00. New J. Phys. 2012, 14, 063030. [Google Scholar] [CrossRef]
- Wang, B.F.; Zhou, Q.; Sun, C. Vibration-induced boundary-layer destabilization achieves massive heat-transport enhancement. Sci. Adv. 2020, 6, eaaz8239. [Google Scholar] [CrossRef]
- Ravichandran, S.; Wettlaufer, J.S. Melting driven by rotating Rayleigh–Bénard convection. J. Fluid Mech. 2021, 916, A28. [Google Scholar] [CrossRef]
- Ding, S.S.; Chong, K.L.; Shi, J.Q.; Ding, G.Y.; Lu, H.Y.; Zhong, J.Q. Inverse centrifugal effect induced by collective motion of vortices in rotating thermal convection. Nat. Commun. 2021, 12, 5585. [Google Scholar] [CrossRef] [PubMed]
- Wedi, M.; Moturi, V.M.; Funfschilling, D.; Weiss, S. Experimental evidence for the boundary zonal flow in rotating Rayleigh–Bénard convection. J. Fluid Mech. 2022, 939, A14. [Google Scholar] [CrossRef]
- Sajjadi, H.; Delouei, A.A.; Atashafrooz, M.; Sheikholeslami, M. Double MRT Lattice Boltzmann simulation of 3-D MHD natural convection in a cubic cavity with sinusoidal temperature distribution utilizing nanofluid. Int. J. Heat Mass Transf. 2018, 126, 489–503. [Google Scholar] [CrossRef]
- Sajjadi, H.; Delouei, A.A.; Sheikholeslami, M.; Atashafrooz, M. Simulation of three dimensional MHD natural convection using double MRT Lattice Boltzmann method. Phys. A Stat. Mech. Its Appl. 2019, 515, 474–496. [Google Scholar] [CrossRef]
- Liu, H.R.; Chong, K.L.; Yang, R.; Verzicco, R.; Lohse, D. Heat transfer in turbulent Rayleigh–Bénard convection through two immiscible fluid layers. J. Fluid Mech. 2022, 938, A31. [Google Scholar] [CrossRef]
- Bao, Y.; Chen, J.; Liu, B.F.; She, Z.S.; Zhou, Q. Enhanced heat transport in partitioned thermal convection. J. Fluid Mech. 2015, 784, R5. [Google Scholar] [CrossRef]
- Bao, Y.; Lin, Z.P. Effect of gap height on multiple enhancement of heat transfer and characteristics of temperature drift. Comput. Aided Eng. 2017, 26, 57–62. [Google Scholar]
- Lin, Z.P.; Bao, Y. Strong coupling between height of gaps and thickness of thermal boundary layer in partitioned convection system. Chin. Phys. B 2019, 28, 7094701. [Google Scholar] [CrossRef]
- Lin, Z.P.; Xu, S.Z.; Bao, Y. Characteristics of heat flow as well as process of heat conduction and transport in partitioned thermal convection. Acta Phys. Sin. 2020, 69, 014401. [Google Scholar] [CrossRef]
- Xu, S.Z.; Lin, Z.P.; Bao, Y. Remarkable enhancement of heat transfer efficiency in thin partitioned convection system. Chin. J. Hydrodyn. 2020, 35, 711–718. [Google Scholar]
- Babaei, M.R.; Sheikhzdeh, G.A.; Abbasian Arani, A.A. Numerical Investigation of Geometric Parameters Effects on Heat Transfer Enhancement in a Manifold Microchannel Heat Sink. Int. J. Eng. 2022, 35, 943–953. [Google Scholar]
- Van Erp, R.; Soleimanzadeh, R.; Nela, L.; Kampitsis, G.; Matioli, E. Co-designing electronics with microfluidics for more sustainable cooling. Nature 2020, 585, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Stevens, R.J.A.M.; Sugiyama, K.; Grossmann, S.; Lohse, D.; Xia, K.Q. Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 2010, 664, 297–312. [Google Scholar] [CrossRef]
- Zhou, Q.; Xia, K.Q. Advances and outlook in turbulent Rayleigh–Bénard convection. Adv. Mech. 2012, 42, 231–251. [Google Scholar]
- Guo, Z.L.; Shi, B.C.; Zheng, C.G. A coupled lattice BGK model for the Boussinesq equations. Int. J. Numer. 2002, 39, 325–342. [Google Scholar] [CrossRef]
- Xu, A.; Shi, L.; Zhao, T.S. Accelerated lattice Boltzmann simulation using GPU and OpenACC with data management. Int. J. Heat Mass Transf. 2017, 109, 577–588. [Google Scholar] [CrossRef]
- Xu, A.; Li, B.T. Multi-GPU thermal lattice Boltzmann simulations using OpenACC and MPI. Int. J. Heat Mass Transf. 2022. submitted. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Xu, Y.; Zhang, J.; Rahmani, A.; Sajadi, S.M.; Zarringhalam, M.; Toghraie, D. Numerical study of mixed convection of nanofluid inside an inlet/outlet inclined cavity under the effect of Brownian motion using Lattice Boltzmann Method (LBM). Int. Commun. Heat Mass Transf. 2021, 126, 105428. [Google Scholar] [CrossRef]
- Li, Z.; Yang, M.; Zhang, Y.W. Lattice Boltzmann method simulation of 3-D natural convection with double MRT model. Int. J. Heat Mass Transf. 2016, 94, 22–238. [Google Scholar] [CrossRef]
- Wei, Y.K.; Shen, P.P.; Wang, Z.D.; Liang, H.; Qian, Y.H. Time evolution features of entropy generation rate in turbulent Rayleigh-Bénard convection with mixed insulating and conducting boundary conditions. Entropy 2020, 22, 672. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Wang, Z.D.; Wei, Y.K.; Qian, Y.H. A bounce back-immersed boundary-lattice Boltzmann model for curved boundary. Appl. Math Model. 2020, 81, 428–440. [Google Scholar] [CrossRef]
- Chen, S.Y.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Wei, Y.K.; Li, Y.M.; Wang, Z.D.; Yang, H.; Zhu, Z.C.; Qian, Y.H.; Luo, K.H. Small-scale fluctuation and scaling law of mixing in three-dimensional rotating turbulent Rayleigh-Taylor instability. Phys. Rev. E 2022, 105, 015103. [Google Scholar] [CrossRef]
- Zhou, Q.; Sugiyama, K.; Stevens, R.J.A.M.; Grossmann, S.; Xia, K.Q. Horizontal structures of velocity and temperature boundary layers in two-dimensional numerical turbulent Rayleigh-Bénard convection. Phys. Fluids 2011, 23, 125104. [Google Scholar]
- Filippova, O.; Hänel, D. Grid refinement for lattice-BGK models. J. Comput. Phys. 1998, 147, 219–228. [Google Scholar] [CrossRef]
- Lin, C.L.; Lai, Y.G. Lattice Boltzmann method on composite grids. Phys. Rev. E 2000, 62, 2219–2225. [Google Scholar] [CrossRef]
- Guo, Z.L.; Shi, B.C.; Wang, N.C. A nonuniform lattice Boltzmann method based on domain decomposition. Chin. J. Comput. Phys. 2001, 18, 181–184. [Google Scholar]
- Dupuis, A.; Chopard, B. Theory and applications of an alternative lattice Boltzmann grid refinement algorithm. Phys. Rev. E 2003, 67, 066707. [Google Scholar] [CrossRef] [PubMed]
- Werne, J. Structure of hard-turbulent convection in two dimensions: Numerical evidence. Phys. Rev. E 1993, 48, 1020–1035. [Google Scholar] [CrossRef]
- Lui, S.L.; Xia, K.Q. Spatial structure of the thermal boundary layer in turbulent convection. Phys. Rev. E 1998, 57, 5494–5503. [Google Scholar] [CrossRef]
- Belmonte, A.; Tilgner, A.; Libchaber, A. Temperature and velocity boundary layers in turbulent convection. Phys. Rev. E 1994, 50, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xia, K.Q. Spatial variations of the mean and statistical quantities in the thermal boundary layers of turbulent convection. Eur. Phys. J. B 2003, 32, 127–136. [Google Scholar] [CrossRef]
- Huang, M.J.; Bao, Y. Characteristics of flow and thermal boundary layer in turbulent Rayleigh-Bénard convection. Acta Phys. Sin. 2016, 65, 204702. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Tong, H.; Wang, Z.; Yang, H.; Wei, Y.; Qian, Y. Effect of Gap Length and Partition Thickness on Thermal Boundary Layer in Thermal Convection. Entropy 2023, 25, 386. https://doi.org/10.3390/e25020386
Wang Z, Tong H, Wang Z, Yang H, Wei Y, Qian Y. Effect of Gap Length and Partition Thickness on Thermal Boundary Layer in Thermal Convection. Entropy. 2023; 25(2):386. https://doi.org/10.3390/e25020386
Chicago/Turabian StyleWang, Zhengyu, Huilin Tong, Zhengdao Wang, Hui Yang, Yikun Wei, and Yuehong Qian. 2023. "Effect of Gap Length and Partition Thickness on Thermal Boundary Layer in Thermal Convection" Entropy 25, no. 2: 386. https://doi.org/10.3390/e25020386
APA StyleWang, Z., Tong, H., Wang, Z., Yang, H., Wei, Y., & Qian, Y. (2023). Effect of Gap Length and Partition Thickness on Thermal Boundary Layer in Thermal Convection. Entropy, 25(2), 386. https://doi.org/10.3390/e25020386





