N-States Continuous Maxwell Demon
Abstract
1. Introduction
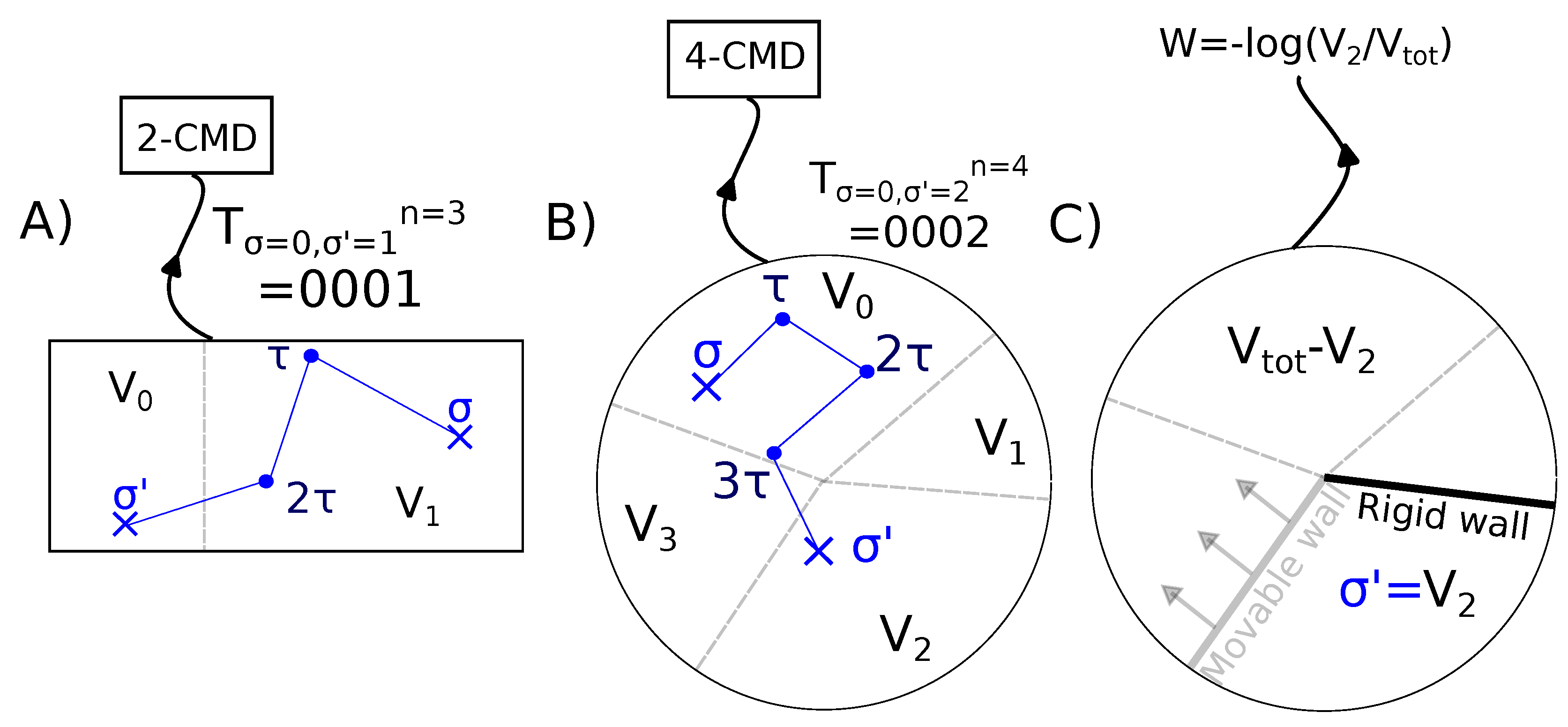
2. General Setting
2.1. Thermodynamic Work and Information-Content
2.2. Comparison with the Szilard Engine
3. Thermodynamic Power and Efficiency
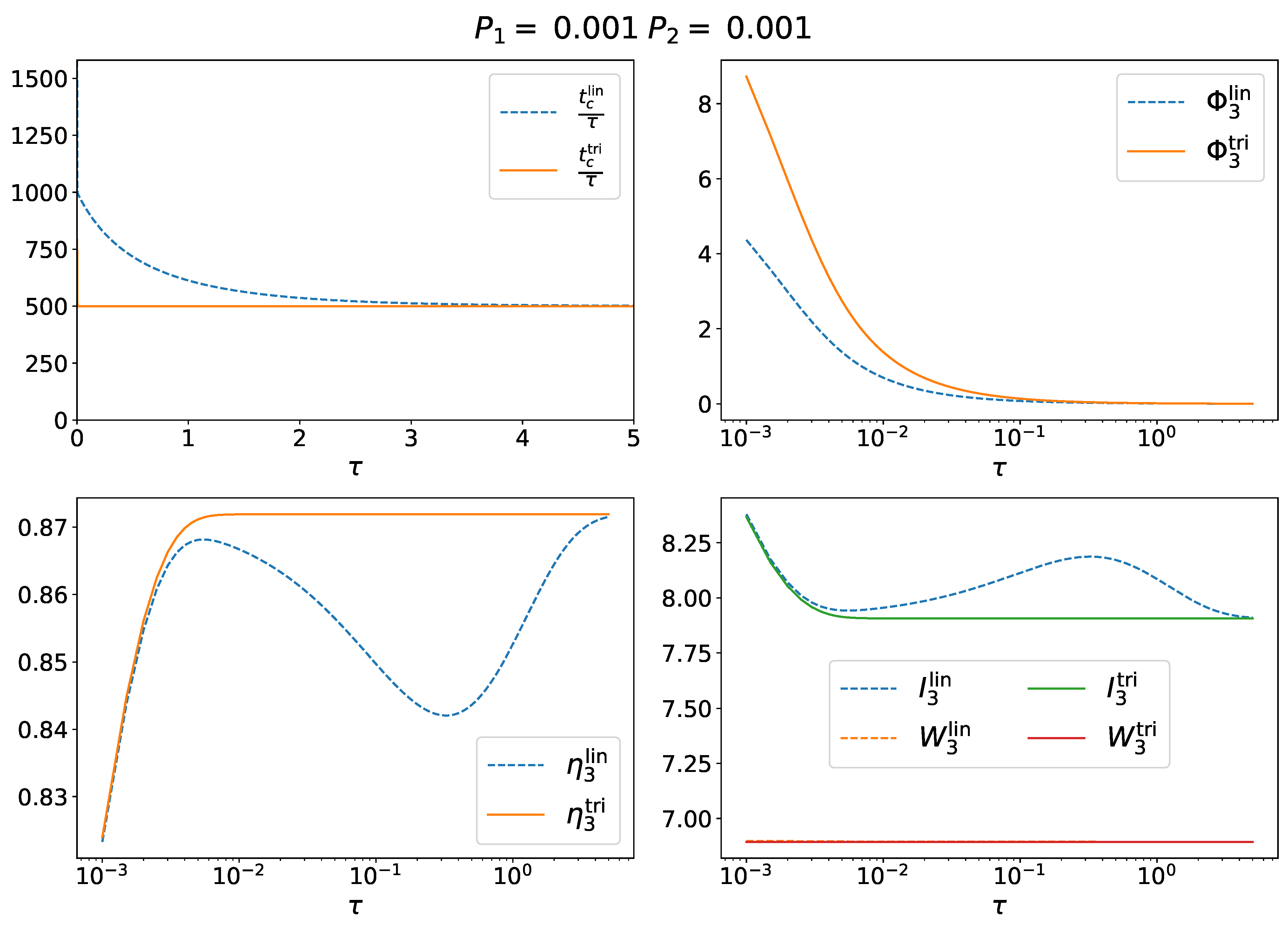
3.1. Average Cycle Length
3.2. Thermodynamic Power
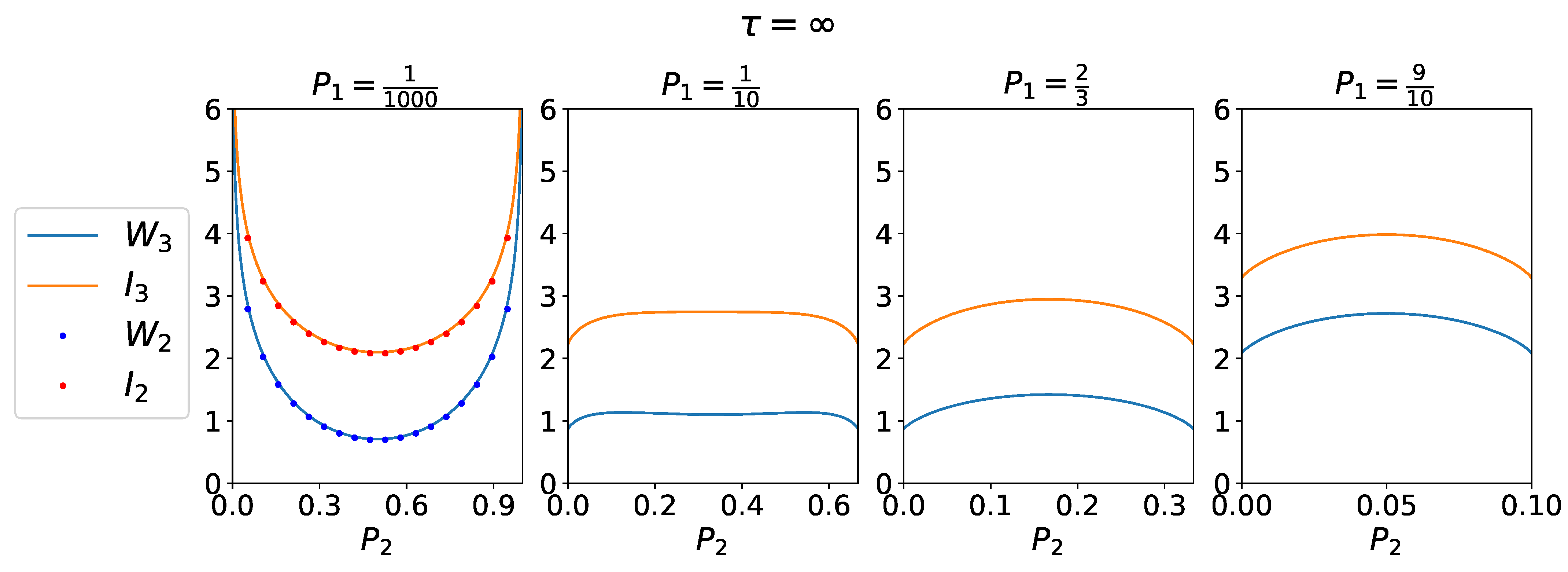
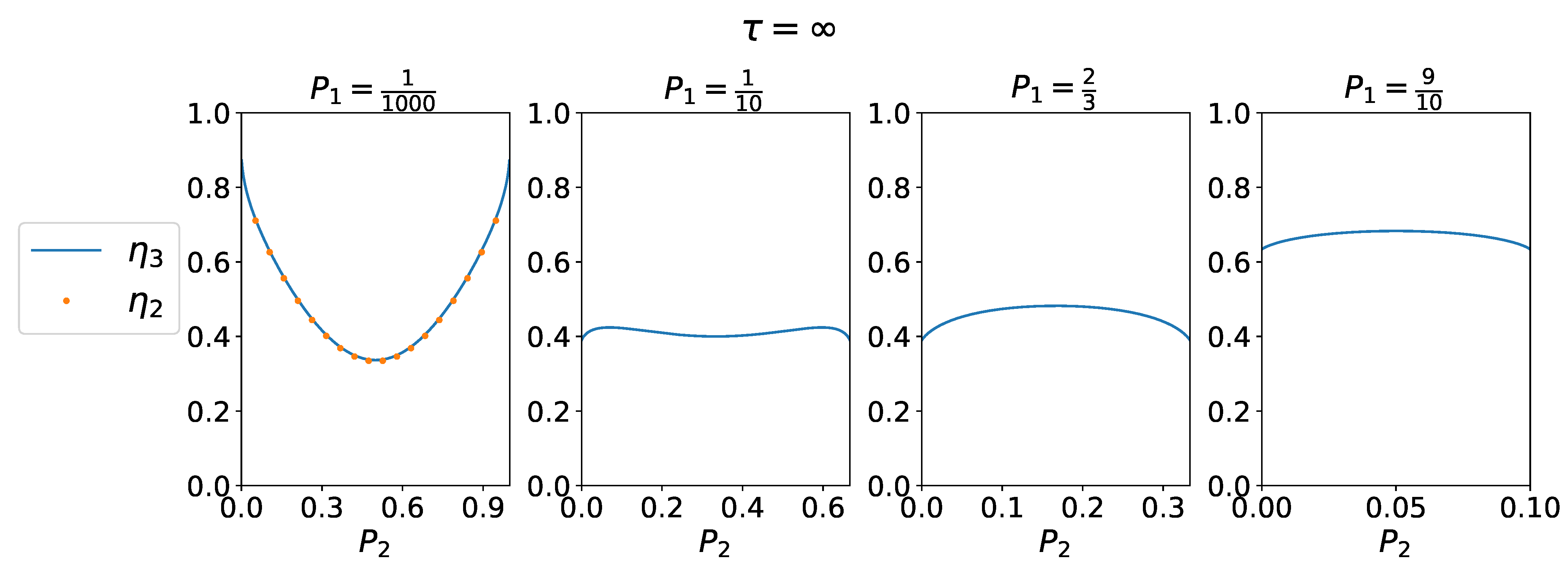
3.3. Information-to-Work Efficiency
4. Particular Cases
4.1. Case N = 2
4.2. Uniform Transition Rates
4.3. Case N = 3
- is the eigenvector associated to the eigenvalue 0 and it corresponds to the stationary probability. Since the detailed balance condition Equation (3) holds, the stationary probability is the Boltzmann distribution. Thus,where
- is the eigenvector associated to the second eigenvalue, which reads in the linear case, and in the triangular case. reads:
- is the eigenvector associated in both models to the eigenvalue . It reads:
4.4. Correlated Measurements in the 3-CMD
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leff, H.S.; Rex, A. Maxwell’s Demon. In Entropy, Information, Computing; Princeton University Press: Princeton, NJ, USA, 1990; pp. 160–172. [Google Scholar]
- Plenio, M.B.; Vitelli, V. The physics of forgetting: Landauer’s erasure principle and information theory. Contemp. Phys. 2001, 42, 25–60. [Google Scholar] [CrossRef]
- Ritort, F. The noisy and marvelous molecular world of biology. Inventions 2019, 4, 24. [Google Scholar] [CrossRef]
- Rex, A. Maxwell’s demon—A historical review. Entropy 2017, 19, 240. [Google Scholar] [CrossRef]
- Ciliberto, S. Experiments in stochastic thermodynamics: Short history and perspectives. Phys. Rev. X 2017, 7, 021051. [Google Scholar] [CrossRef]
- Barato, A.; Seifert, U. Unifying three perspectives on information processing in stochastic thermodynamics. Phys. Rev. Lett. 2014, 112, 090601. [Google Scholar] [CrossRef] [PubMed]
- Barato, A.C.; Seifert, U. Stochastic thermodynamics with information reservoirs. Phys. Rev. E 2014, 90, 042150. [Google Scholar] [CrossRef] [PubMed]
- Bérut, A.; Petrosyan, A.; Ciliberto, S. Detailed Jarzynski equality applied to a logically irreversible procedure. Europhys. Lett. 2013, 103, 60002. [Google Scholar] [CrossRef]
- Berut, A.; Petrosyan, A.; Ciliberto, S. Information and thermodynamics: Experimental verification of Landauer’s Erasure principle. J. Stat. Mech. Theory Exp. 2015, 2015, P06015. [Google Scholar] [CrossRef]
- Lutz, E.; Ciliberto, S. From Maxwells demon to Landauers eraser. Phys. Today 2015, 68, 30. [Google Scholar] [CrossRef]
- Szilard, L. Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Z. Phys. 1929, 53, 840–856. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Bennett, C.H. The thermodynamics of computation—A review. Int. J. Theor. Phys. 1982, 21, 905–940. [Google Scholar] [CrossRef]
- Sagawa, T.; Ueda, M. Information Thermodynamics: Maxwell’s Demon in Nonequilibrium Dynamics. In Nonequilibrium Statistical Physics of Small Systems: Fluctuation Relations and Beyond; Wiley Online Library: Hoboken, NJ, USA, 2013; pp. 181–211. [Google Scholar] [CrossRef]
- Parrondo, J.M.; Horowitz, J.M.; Sagawa, T. Thermodynamics of information. Nat. Phys. 2015, 11, 131–139. [Google Scholar] [CrossRef]
- Ribezzi-Crivellari, M.; Ritort, F. Large work extraction and the Landauer limit in a continuous Maxwell demon. Nat. Phys. 2019, 15, 660–664. [Google Scholar] [CrossRef]
- Ribezzi-Crivellari, M.; Ritort, F. Work extraction, information-content and the Landauer bound in the continuous Maxwell Demon. J. Stat. Mech. Theory Exp. 2019, 2019, 084013. [Google Scholar] [CrossRef]
- Garrahan, J.P.; Ritort, F. Generalized Continuous Maxwell Demons. arXiv 2021, arXiv:2104.12472. [Google Scholar]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing); Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Benichou, O.; Guérin, T.; Voituriez, R. Mean first-passage times in confined media: From Markovian to non-Markovian processes. J. Phys. A Math. Theor. 2015, 48, 163001. [Google Scholar] [CrossRef]
- Goupil, C.; Herbert, E. Adapted or Adaptable: How to Manage Entropy Production? Entropy 2019, 22, 29. [Google Scholar] [CrossRef]
- Van den Broeck, C.; Esposito, M. Ensemble and trajectory thermodynamics: A brief introduction. Phys. A Stat. Mech. Its Appl. 2015, 418, 6–16. [Google Scholar] [CrossRef]

| 0 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raux, P.; Ritort, F. N-States Continuous Maxwell Demon. Entropy 2023, 25, 321. https://doi.org/10.3390/e25020321
Raux P, Ritort F. N-States Continuous Maxwell Demon. Entropy. 2023; 25(2):321. https://doi.org/10.3390/e25020321
Chicago/Turabian StyleRaux, Paul, and Felix Ritort. 2023. "N-States Continuous Maxwell Demon" Entropy 25, no. 2: 321. https://doi.org/10.3390/e25020321
APA StyleRaux, P., & Ritort, F. (2023). N-States Continuous Maxwell Demon. Entropy, 25(2), 321. https://doi.org/10.3390/e25020321







