Harmonic Phasor Estimation Method Considering Dense Interharmonic Interference
Abstract
1. Introduction
2. Harmonic Phasor Estimation Model and Existing Problems
2.1. Harmonic Phasor Estimation Model
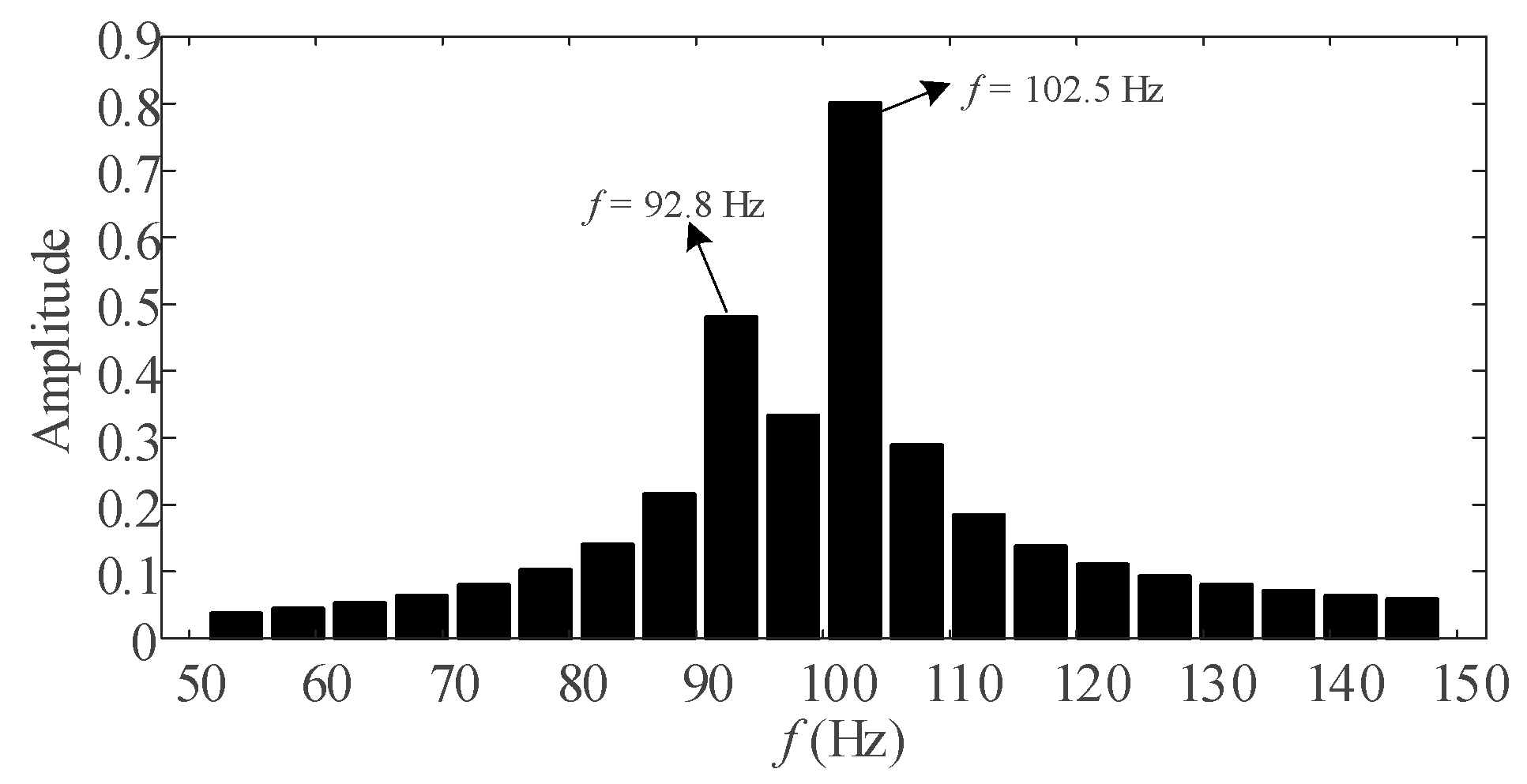
2.2. Interference of DIs on Harmonic Phasor Estimation
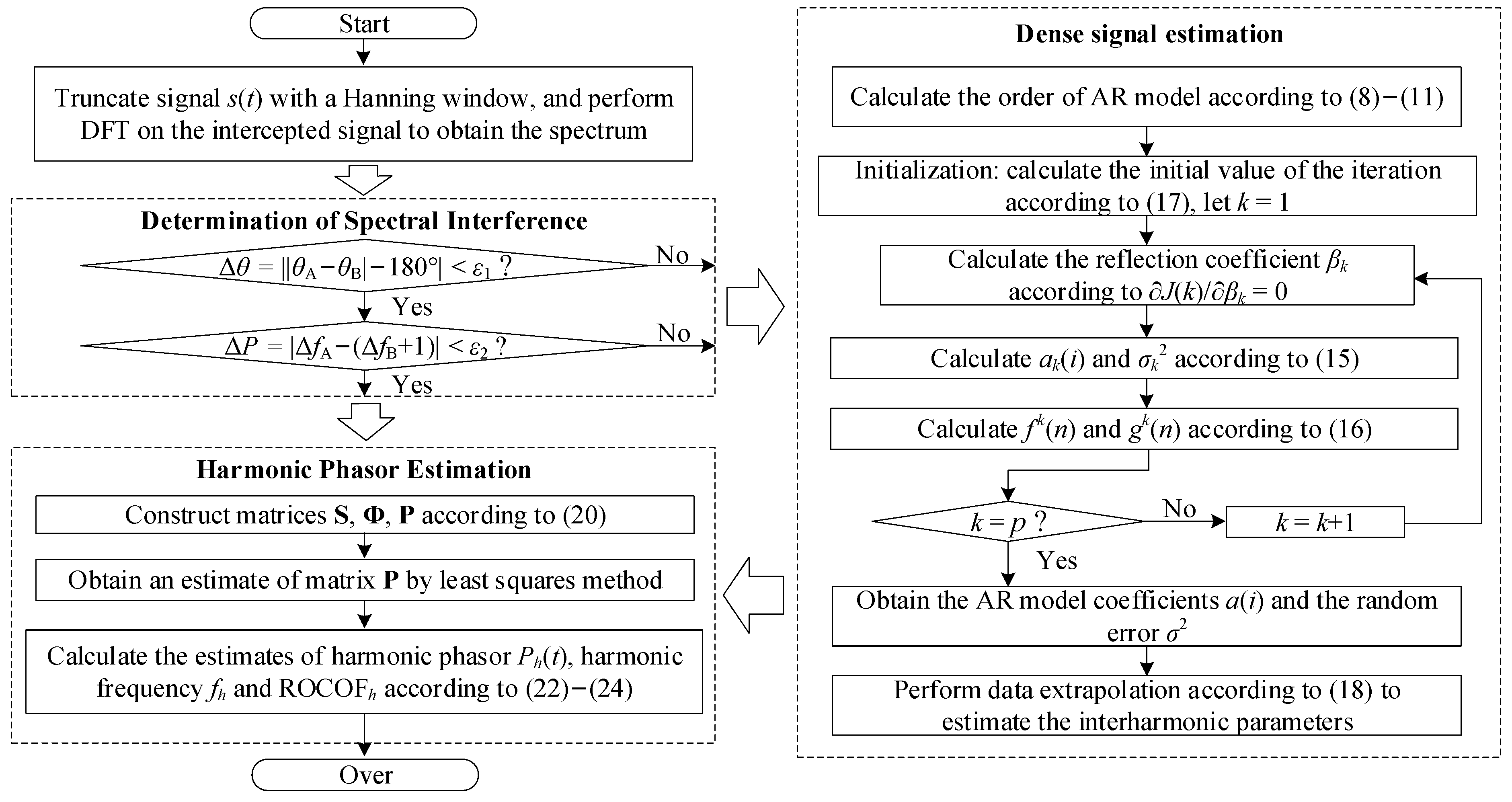
3. Proposed Method
3.1. Determination of Spectral Interference
3.2. Spectrum Refinement Algorithm
3.3. Harmonic Phasor Estimation
4. Simulation Analysis
4.1. Steady-State Test
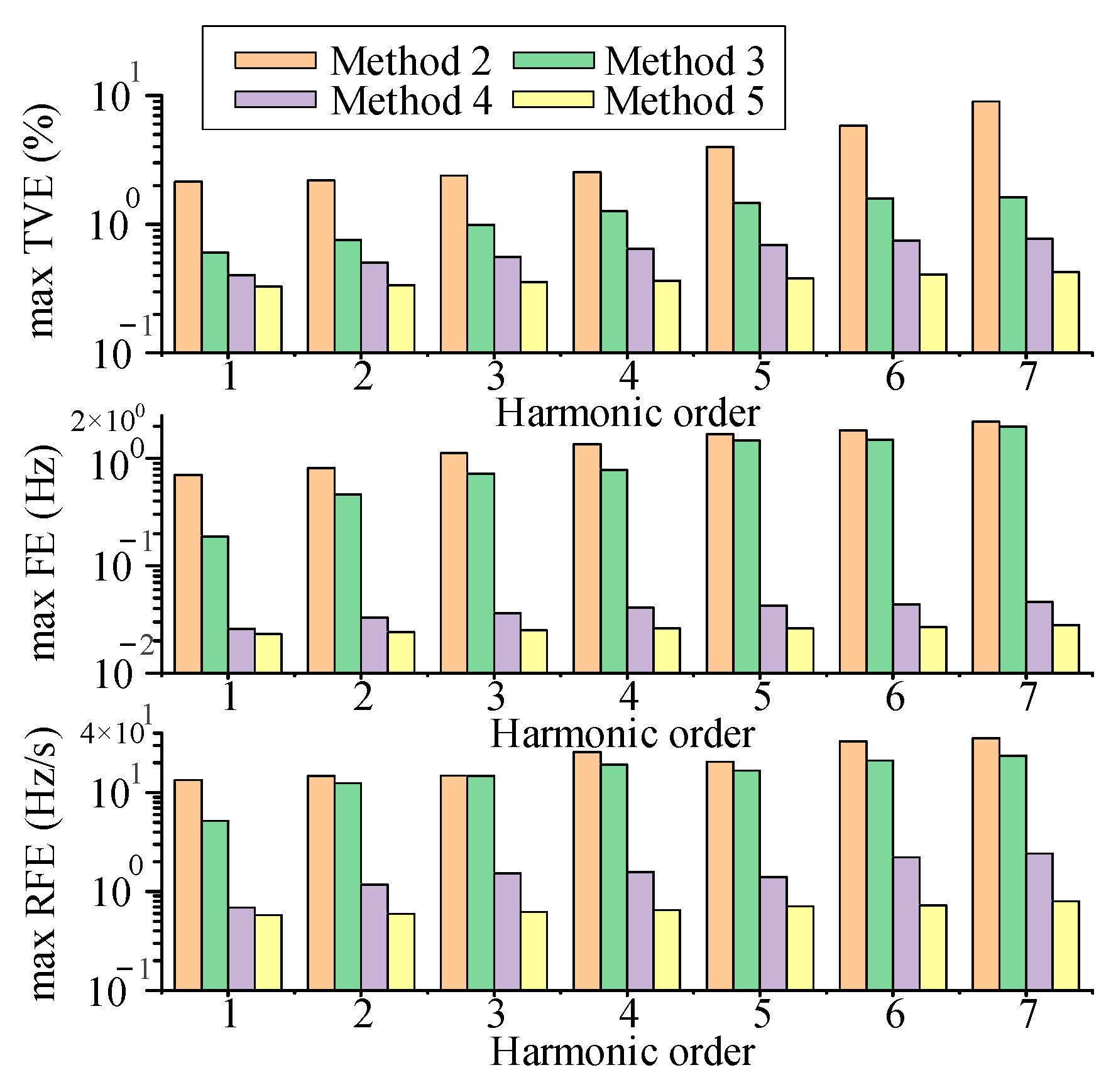
4.2. Dense Interharmonics Test
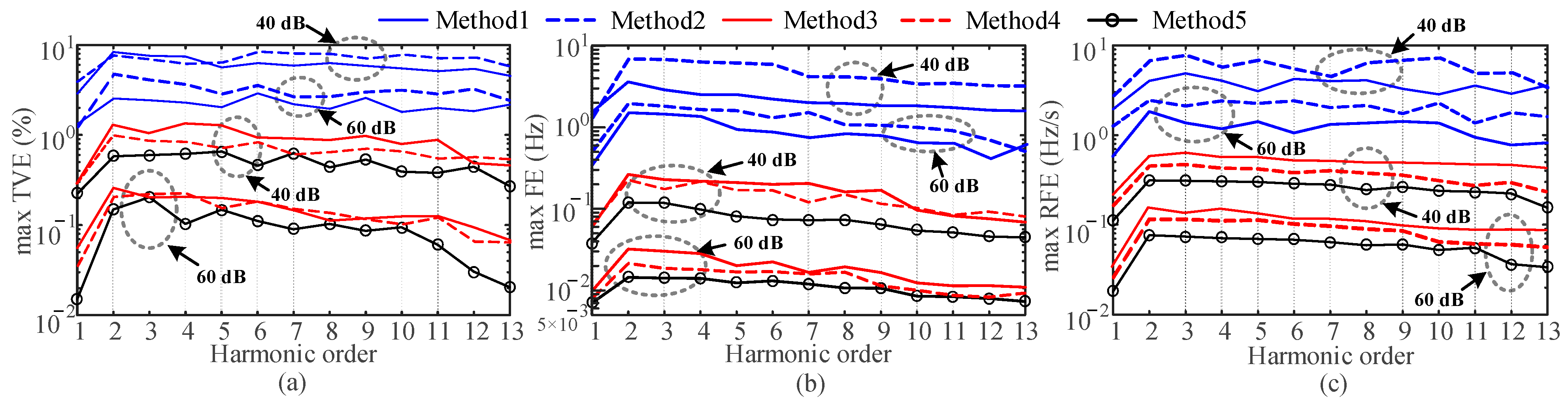
4.3. Wideband Noise Test
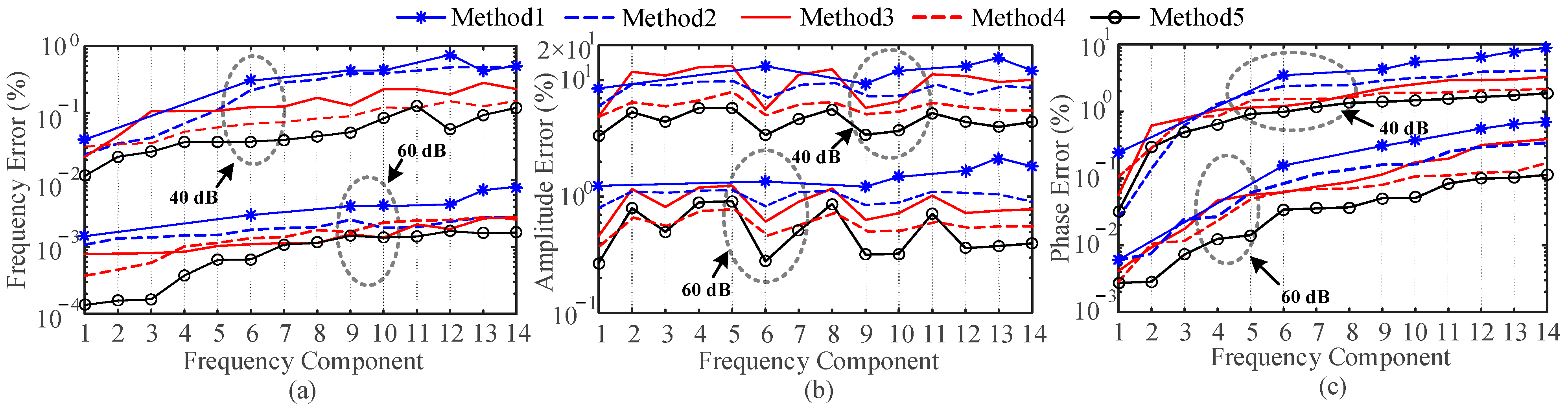
4.4. Frequency Deviation Test
4.5. Dynamic-State Test
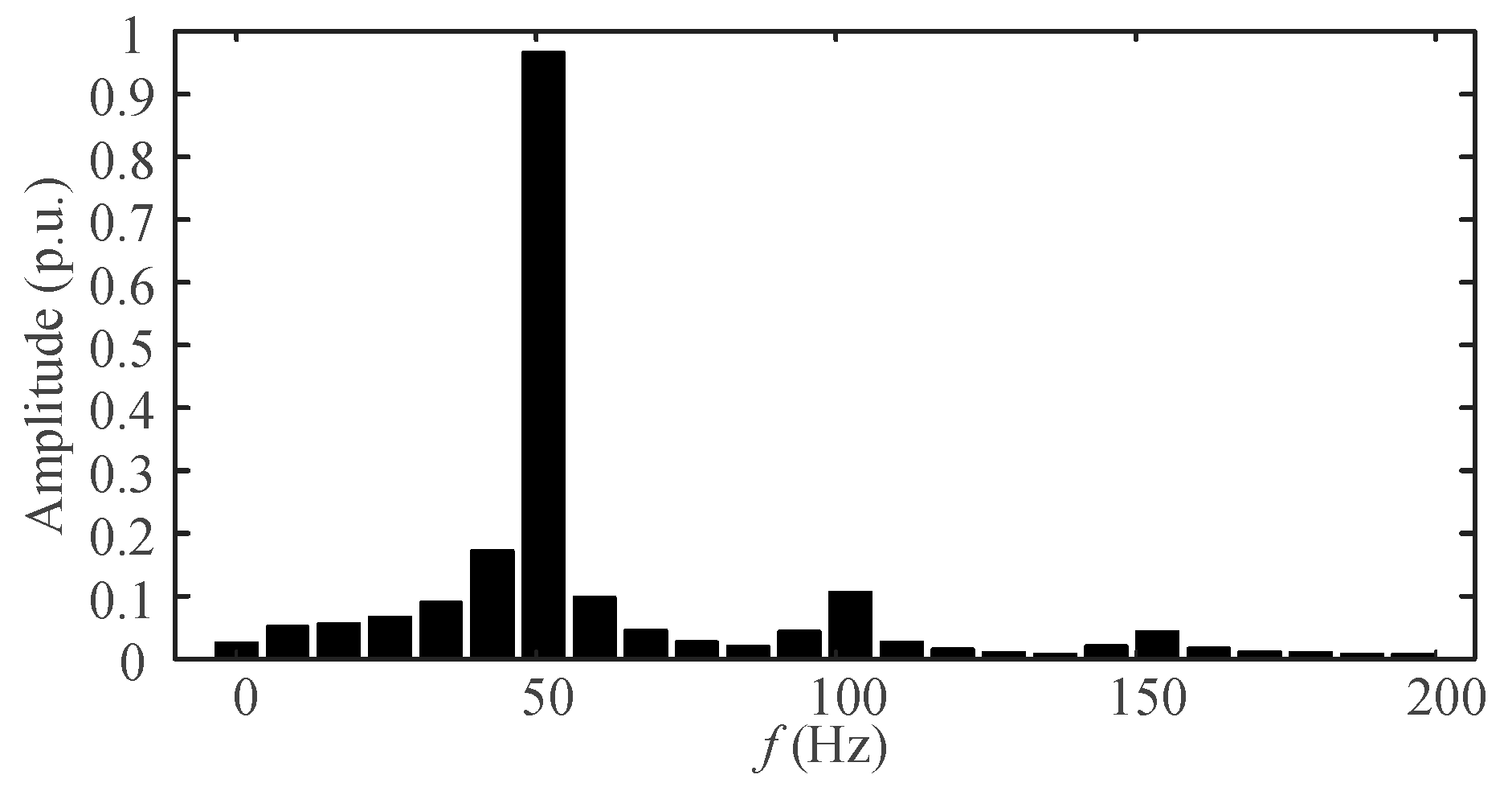
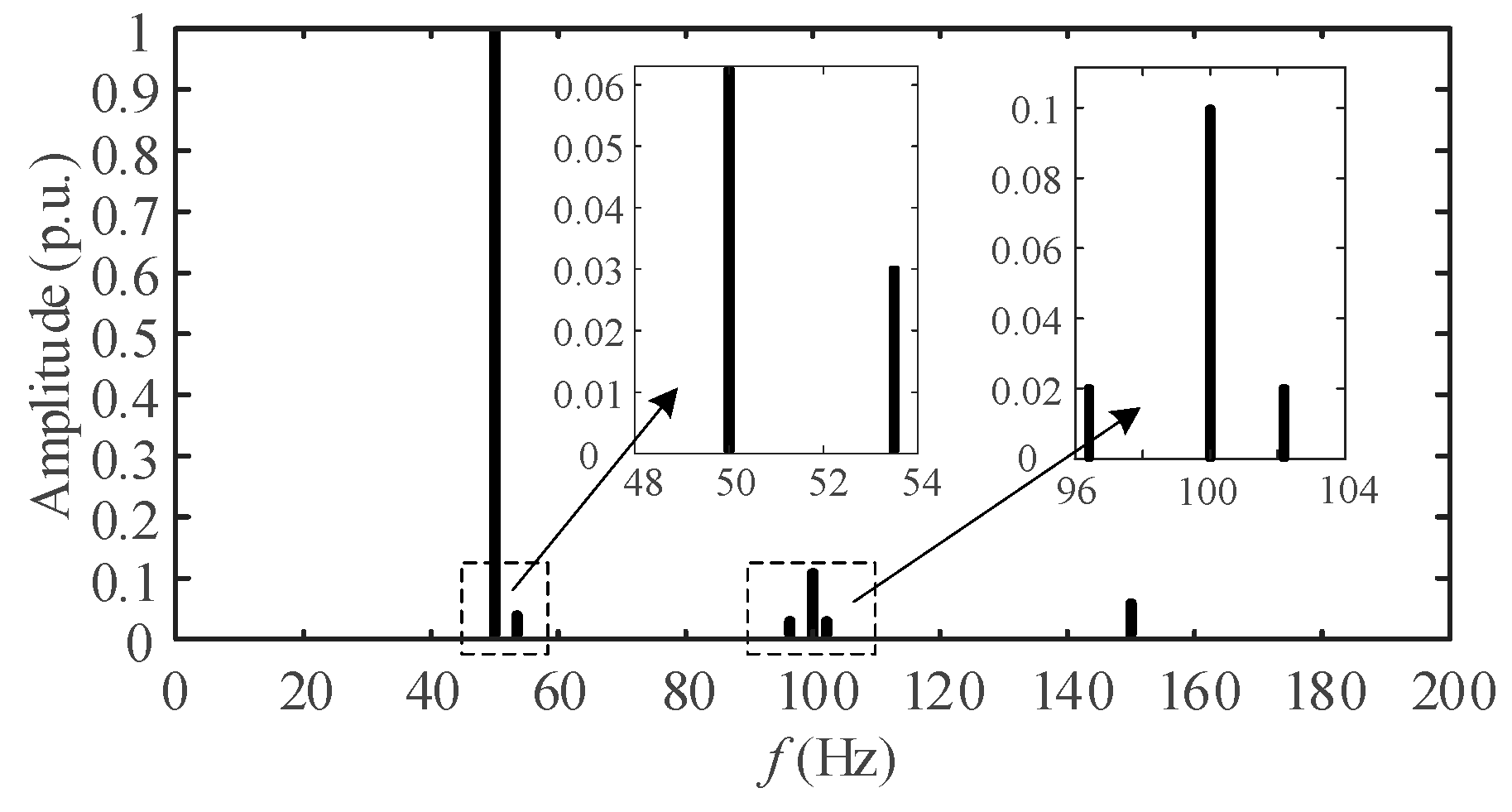
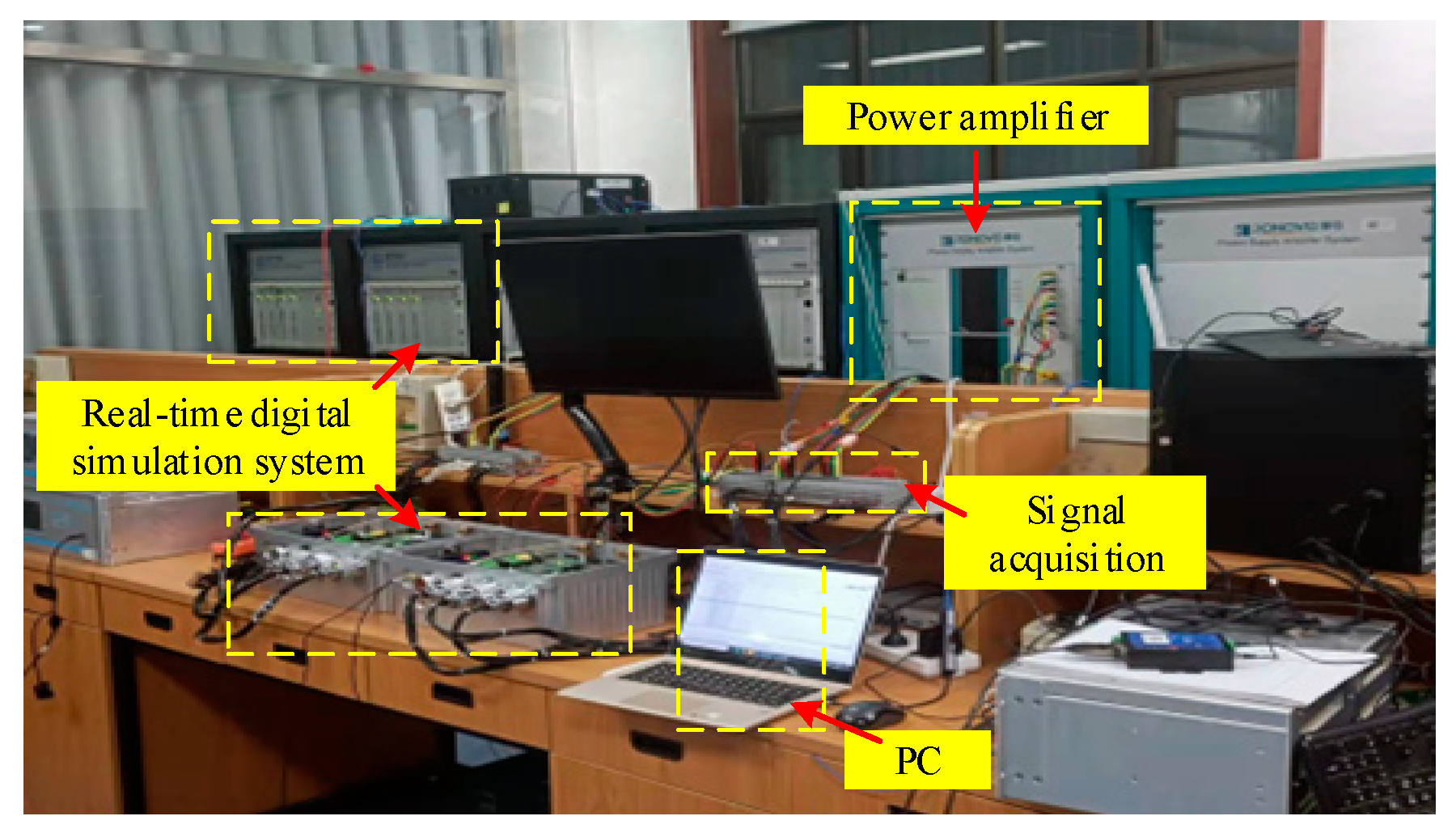
4.6. Experimental Signal Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Swamy, M.M. An Electronically Isolated 12-Pulse Autotransformer Rectification Scheme to Improve Input Power Factor and Lower Harmonic Distortion in Variable-Frequency Drives. IEEE Trans. Ind. Appl. 2015, 51, 3986–3994. [Google Scholar] [CrossRef]
- Sun, Y.; Xie, X.; Zhang, L.; Li, S. A Voltage Adaptive Dynamic Harmonic Model of Nonlinear Home Appliances. IEEE Trans. Ind. Electron. 2020, 67, 3607–3617. [Google Scholar] [CrossRef]
- Davis, E.J.; Emanuel, A.E. Harmonic pollution metering: Theoretical considerations. IEEE Trans. Power Deliv. 2000, 15, 19–23. [Google Scholar] [CrossRef]
- Yi, J.; Zhou, M.; Li, Z.; Li, J. A Novel Technique for Fundamental and Harmonic Parameter Estimation Using Nonergodic S-Transform. IEEE Trans. Instrum. Meas. 2019, 68, 3503–3513. [Google Scholar] [CrossRef]
- Feilat, E.A. Detection of Voltage Envelope Using Prony Analysis–Hilbert Transform Method. IEEE Trans. Power Deliv. 2006, 21, 2091–2093. [Google Scholar] [CrossRef]
- Jain, S.K.; Jain, P.; Singh, S.N. A Fast Harmonic Phasor Measurement Method for Smart Grid Applications. IEEE Trans. Smart Grid 2017, 8, 493–502. [Google Scholar] [CrossRef]
- Hasan, S.; Muttaqi, K.M.; Sutanto, D. Detection and Characterization of Time-variant Non-stationary Voltage Sag Waveforms Using Segmented Hilbert Huang Transform. IEEE Trans. Ind. Appl. 2020, 56, 4563–4574. [Google Scholar] [CrossRef]
- Chakir, M.; Kamwa, I.; Le Huy, H. Extended C37.118.1 PMU Algorithms for Joint Tracking of Fundamental and Harmonic Phasors in Stressed Power Systems and Microgrids. IEEE Trans. Power Deliv. 2014, 29, 1465–1480. [Google Scholar] [CrossRef]
- Bertocco, M.; Frigo, G.; Narduzzi, C.; Tramarin, F. Resolution Enhancement by Compressive Sensing in Power Quality and Phasor Measurement. IEEE Trans. Instrum. Meas. 2014, 63, 2358–2367. [Google Scholar] [CrossRef]
- Li, W.; Zhang, G.; Chen, M.; Zhong, H.; Geng, Y. Dynamic Harmonic Phasor Estimator Considering Frequency Deviation. IEEE Sens. J. 2021, 21, 24453–24461. [Google Scholar] [CrossRef]
- Lei, C.; Wei, Z.; Yu, Y.; Wang, Q.; Huang, S. In Improved Interpolated Dynamic DFT Synchrophasor Estimator Considering Second Harmonic Interferences. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference, Houston, TX, USA, 14–17 May 2018. [Google Scholar]
- Tosato, P.; Macii, D.; Luiso, M.; Brunelli, D.; Gallo, D.; Landi, C. A Tuned Lightweight Estimation Algorithm for Low-Cost Phasor Measurement Units. IEEE Trans. Instrum. Meas. 2018, 67, 1047–1057. [Google Scholar] [CrossRef]
- Belega, D.; Macii, D.; Petri, D. Fast Synchrophasor Estimation by Means of Frequency-Domain and Time-Domain Algorithms. IEEE Trans. Instrum. Meas. 2014, 63, 388–401. [Google Scholar] [CrossRef]
- de la O Serna, J.A. Dynamic Phasor Estimates for Power System Oscillations. IEEE Trans. Instrum. Meas. 2007, 56, 1648–1657. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; de la O Serna, J.A. Dynamic Harmonic Analysis Through Taylor–Fourier Transform. IEEE Trans. Instrum. Meas. 2011, 60, 804–813. [Google Scholar] [CrossRef]
- Bertocco, M.; Frigo, G.; Narduzzi, C.; Muscas, C.; Pegoraro, P.A. Compressive Sensing of a Taylor-Fourier Multifrequency Model for Synchrophasor Estimation. IEEE Trans. Instrum. Meas. 2015, 64, 3274–3283. [Google Scholar] [CrossRef]
- Frigo, G.; Giorgi, G.; Bertocco, M.; Narduzzi, C. In Multifunction phasor analysis for distribution networks. In Proceedings of the IEEE International Workshop on Applied Measurements for Power Systems, Aachen, Germany, 28–30 September 2016. [Google Scholar]
- Frigo, G.; Giorgi, G.; Narduzzi, C. In Efficient detection for multifrequency dynamic phasor analysis. In Proceedings of the 2016 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 28–30 September 2016. [Google Scholar]
- Narduzzi, C.; Bertocco, M.; Frigo, G.; Giorgi, G. Fast-TFM—Multifrequency Phasor Measurement for Distribution Networks. IEEE Trans. Instrum. Meas. 2018, 67, 1825–1835. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Wang, F.; Wang, Q.; Huang, S. An Interharmonic Phasor and Frequency Estimator for Subsynchronous Oscillation Identification and Monitoring. IEEE Trans. Instrum. Meas. 2019, 68, 1714–1723. [Google Scholar] [CrossRef]
- Bertocco, M.; Frigo, G.; Giorgi, G.; Narduzzi, C. In Frequency tracking for efficient phasor measurement based on a CSTFM model. In Proceedings of the 2015 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 23–25 September 2015. [Google Scholar]
- Chen, L.; Zhao, W.; Wang, Q.; Wang, F.; Huang, S. Dynamic Harmonic Synchrophasor Estimator Based on Sinc Interpolation Functions. IEEE Trans. Instrum. Meas. 2019, 68, 3054–3065. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Wang, F.; Huang, S. Harmonic Phasor Estimator for P-Class Phasor Measurement Units. IEEE Trans. Instrum. Meas. 2020, 69, 1556–1565. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Xie, X.; Zhao, D.; Huang, S. Harmonic Phasor Estimation Based on Frequency-Domain Sampling Theorem. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Sun, Z.; He, Z.; Zang, T.; Liu, Y. Multi-Interharmonic Spectrum Separation and Measurement Under Asynchronous Sampling Condition. IEEE Trans. Instrum. Meas. 2016, 65, 1902–1912. [Google Scholar] [CrossRef]
- Aiello, M.; Cataliotti, A.; Nuccio, S. A Chirp-Z Transform-Based Synchronizer for Power System Measurements. IEEE Trans. Instrum. Meas. 2005, 54, 1025–1032. [Google Scholar] [CrossRef]
- Lu, Z.; Ji, T.Y.; Tang, W.H.; Wu, Q.H. Optimal Harmonic Estimation Using A Particle Swarm Optimizer. IEEE Trans. Power Deliv. 2008, 23, 1166–1174. [Google Scholar] [CrossRef]
- Lin, H.C. Intelligent Neural Network-Based Fast Power System Harmonic Detection. IEEE Trans. Ind. Electron. 2007, 54, 43–52. [Google Scholar] [CrossRef]
- IEEE Std C37.118.1a-2014; IEEE Standard for Synchrophasor Measurements for Power Systems—Amendment 1: Modification of Selected Performance Requirements. IEEE: Piscatvie, NJ, USA, 2014.
- Jia, Q.; Yao, R.; Wang, N.; Meng, R. An Approach to Detect Harmonics/Inter-harmonics With Closing Frequencies Using Atomic Decomposition and Windowed Frequency Shifting Algorithm. Proc. Chin. Soc. Electr. Eng. 2014, 34, 4605–4612. [Google Scholar]
- Shu, Q.; Fan, Y.; Xu, F.; Wang, C.; He, J. A harmonic impedance estimation method based on AR model and Burg algorithm. Electr. Power Syst. Res. 2022, 202, 107568. [Google Scholar] [CrossRef]
- Shu, Q.; Wu, Y.; Xu, F.; Zheng, H. Estimate Utility Harmonic Impedance via the Correlation of Harmonic Measurements in Different Time Intervals. IEEE Trans. Power Deliv. 2020, 35, 2060–2067. [Google Scholar] [CrossRef]
- Fu, L.; Xiong, S.; Pan, C.; Bai, S.; He, Z.; Mai, R.; Li, X. A Multiple Frequency Taylor Model-Based Dynamic Synchrophasor Estimation Algorithm. IEEE Trans. Smart Grid 2019, 10, 6870–6882. [Google Scholar] [CrossRef]
- Liang, S.; Hu, Q.; Li, W.-J. A Survey of Harmonic Emissions of a Commercially Operated Wind Farm. IEEE Trans. Ind. Appl. 2012, 48, 1115–1123. [Google Scholar] [CrossRef]



| i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| fi (Hz) | 50 | 53.5 | 96.4 | 100 | 102.2 | 150 |
| ai (p.u.) | 1.00 | 0.03 | 0.02 | 0.10 | 0.02 | 0.05 |
| φi (rad) | 0.65 | 0.37 | 0.68 | 0.35 | 0.87 | 0.53 |
| Method | Actual | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| fi (Hz) | 50.00 | 48.83 | 50.33 | 50.02 | 49.99 | 50 |
| 53.50 | — | 55.16 | 52.71 | 53.46 | 53.4 | |
| 96.40 | — | 98.50 | 97.02 | 96.42 | 96.5 | |
| 100.00 | 102.54 | 99.58 | 100.15 | 99.97 | 100 | |
| 102.20 | — | 103.10 | 102.68 | 102.25 | 102.1 | |
| 150.00 | 151.37 | 149.45 | 150.07 | 149.95 | 150 | |
| ai (p.u.) | 1.00 | 0.899 | 0.980 | 1.001 | 0.998 | 1.00 |
| 0.03 | — | 0.039 | 0.036 | 0.029 | 0.03 | |
| 0.02 | — | 0.011 | 0.015 | 0.021 | 0.02 | |
| 0.10 | 0.082 | 0.096 | 0.098 | 0.101 | 0.10 | |
| 0.02 | — | 0.025 | 0.016 | 0.022 | 0.02 | |
| 0.05 | 0.055 | 0.046 | 0.053 | 0.048 | 0.05 | |
| φi (rad) | 0.65 | 1.40 | 0.67 | 0.65 | 0.65 | 0.65 |
| 0.37 | — | 0.33 | 0.42 | 0.40 | 0.39 | |
| 0.68 | — | 0.60 | 0.58 | 0.66 | 0.67 | |
| 0.35 | −1.14 | 0.32 | 0.35 | 0.35 | 0.35 | |
| 0.87 | — | 0.69 | 0.79 | 0.90 | 0.88 | |
| 0.53 | −0.67 | 0.51 | 0.54 | 0.53 | 0.53 |
| h | Max TVE (%) | Max FE (Hz) | Max RFE (Hz/s) | |||
|---|---|---|---|---|---|---|
| Method | Method | Method | ||||
| 4 | 5 | 4 | 5 | 4 | 5 | |
| 1 | 0.178 | 0.085 | 0.037 | 0.005 | 0.165 | 0.063 |
| 2 | 0.248 | 0.031 | 0.069 | 0.005 | 0.206 | 0.074 |
| 3 | 0.275 | 0.120 | 0.114 | 0.006 | 0.440 | 0.089 |
| 4 | 0.386 | 0.219 | 0.153 | 0.006 | 0.464 | 0.092 |
| 5 | 0.391 | 0.364 | 0.234 | 0.007 | 0.534 | 0.138 |
| 6 | 0.451 | 0.401 | 0.277 | 0.008 | 0.553 | 0.186 |
| 7 | 0.643 | 0.495 | 0.308 | 0.009 | 0.697 | 0.194 |
| 8 | 0.711 | 0.501 | 0.351 | 0.010 | 0.705 | 0.218 |
| 9 | 0.743 | 0.656 | 0.391 | 0.010 | 0.962 | 0.230 |
| 10 | 0.810 | 0.787 | 0.393 | 0.015 | 1.063 | 0.256 |
| 11 | 0.854 | 0.792 | 0.453 | 0.017 | 1.283 | 0.325 |
| 12 | 0.869 | 0.830 | 0.455 | 0.020 | 1.336 | 0.329 |
| 13 | 0.945 | 0.835 | 0.458 | 0.022 | 1.400 | 0.332 |
| h | Max TVE (%) | Max FE (Hz) | Max RFE (Hz/s) | |||
|---|---|---|---|---|---|---|
| Method | Method | Method | ||||
| 4 | 5 | 4 | 5 | 4 | 5 | |
| 1 | 0.057 | 0.048 | 0.048 | 0.013 | 19.578 | 0.732 |
| 2 | 0.061 | 0.134 | 0.133 | 0.017 | 18.685 | 0.955 |
| 3 | 0.357 | 0.234 | 0.136 | 0.020 | 15.033 | 1.514 |
| 4 | 0.292 | 0.271 | 0.163 | 0.036 | 13.749 | 1.773 |
| 5 | 0.412 | 0.391 | 0.180 | 0.048 | 12.453 | 1.820 |
| 6 | 0.917 | 0.391 | 0.288 | 0.054 | 10.036 | 1.991 |
| 7 | 1.081 | 0.569 | 0.360 | 0.055 | 5.778 | 2.540 |
| 8 | 1.086 | 0.774 | 0.363 | 0.061 | 2.693 | 2.769 |
| 9 | 1.106 | 0.969 | 0.414 | 0.061 | 5.769 | 2.794 |
| 10 | 1.163 | 0.913 | 0.496 | 0.063 | 10.003 | 3.158 |
| 11 | 1.291 | 1.030 | 0.523 | 0.067 | 13.573 | 3.818 |
| 12 | 1.301 | 1.055 | 0.563 | 0.077 | 16.157 | 3.958 |
| 13 | 1.396 | 1.108 | 0.593 | 0.097 | 19.233 | 4.605 |
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f (Hz) | 50 | 56 | 65 | 83 | 86 | 100 | 102 |
| A (V) | 100 | 2.5 | 3.0 | 1.0 | 2.0 | 10 | 3.0 |
| i | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| f (Hz) | 105 | 150 | 200 | 213 | 250 | 350 | 450 |
| A (V) | 2.5 | 10 | 10 | 3.0 | 10 | 10 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Zhou, R.; Ma, X.; Xu, R. Harmonic Phasor Estimation Method Considering Dense Interharmonic Interference. Entropy 2023, 25, 236. https://doi.org/10.3390/e25020236
Xiao X, Zhou R, Ma X, Xu R. Harmonic Phasor Estimation Method Considering Dense Interharmonic Interference. Entropy. 2023; 25(2):236. https://doi.org/10.3390/e25020236
Chicago/Turabian StyleXiao, Xianyong, Runze Zhou, Xiaoyang Ma, and Rui Xu. 2023. "Harmonic Phasor Estimation Method Considering Dense Interharmonic Interference" Entropy 25, no. 2: 236. https://doi.org/10.3390/e25020236
APA StyleXiao, X., Zhou, R., Ma, X., & Xu, R. (2023). Harmonic Phasor Estimation Method Considering Dense Interharmonic Interference. Entropy, 25(2), 236. https://doi.org/10.3390/e25020236






