Limiting Performance of the Ejector Refrigeration Cycle with Pure Working Fluids
Abstract
1. Introduction
2. Methodology
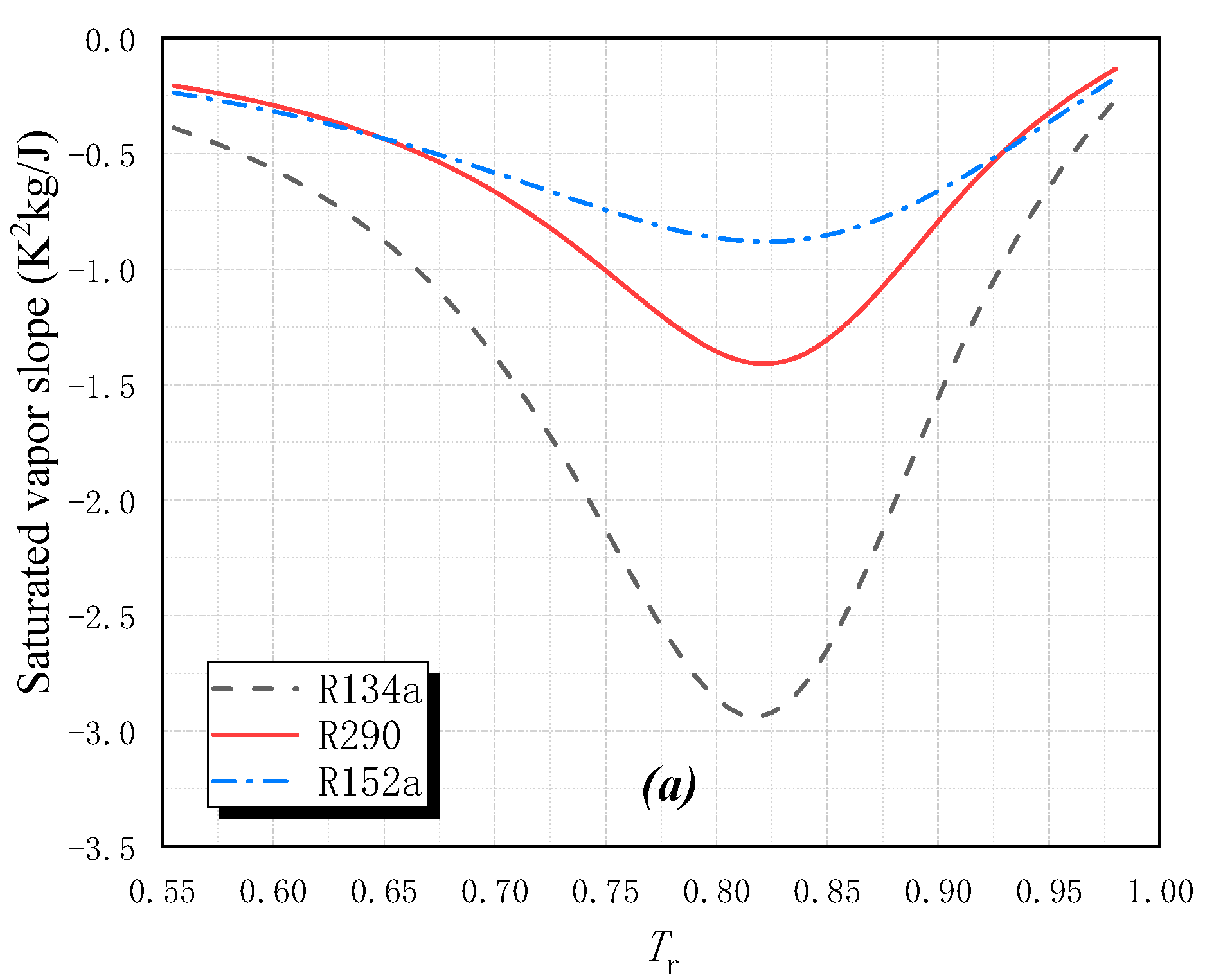
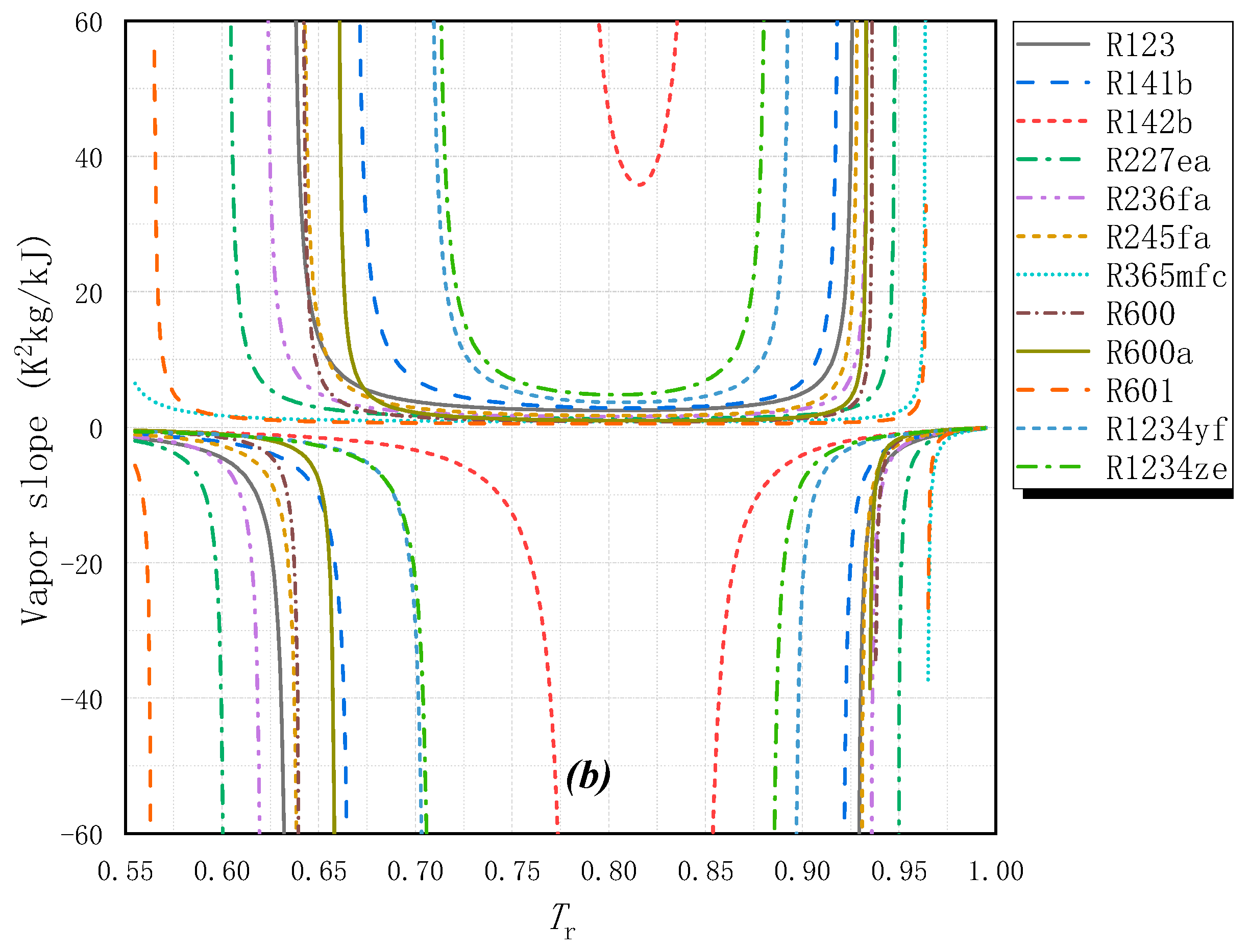
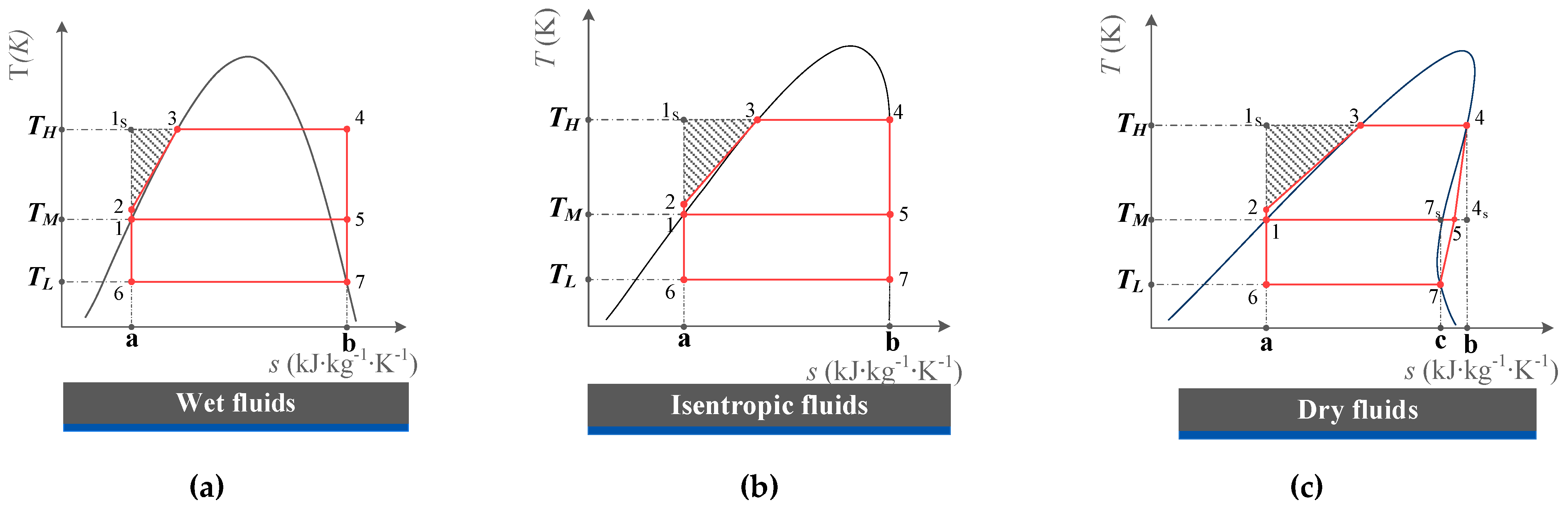
2.1. Fluid Classification and Fluid Slope
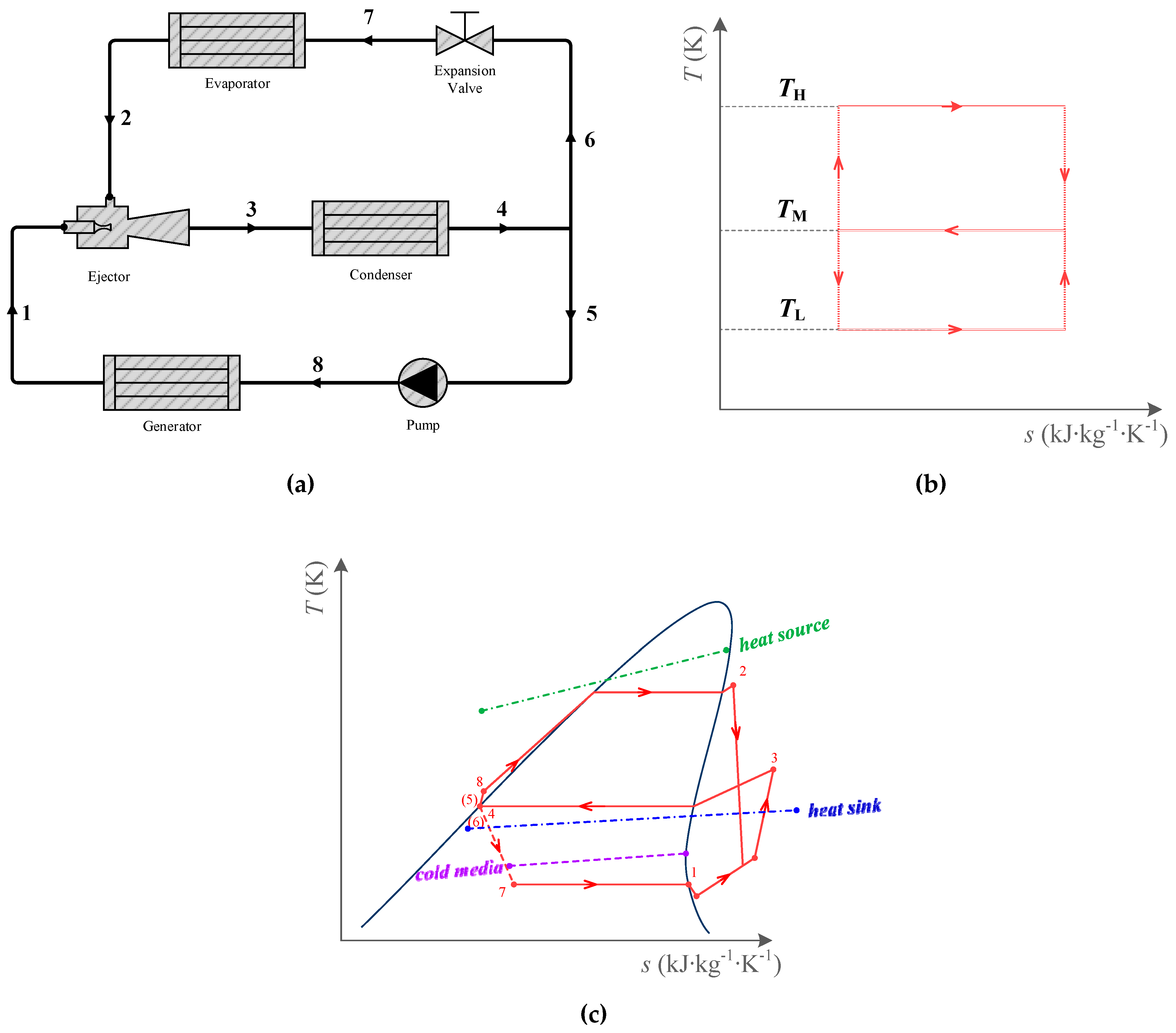
2.2. Limiting ERC
- (1)
- The heat exchange processes are idealized. The temperature of the heat source and heat sink is constant. In the generator, the highest temperature of the working fluid is equal to the heat source temperature. The condensing temperature is equal to the heat sink temperature, and the evaporating temperature is equal to the cold media temperature.
- (2)
- Irreversibility in other processes of the cycle is ignored, such as the compression process in the pump, and the expansion, mixing, and diffusion process in the ejector are all regarded as isentropic processes, etc.
2.3. Limiting COP
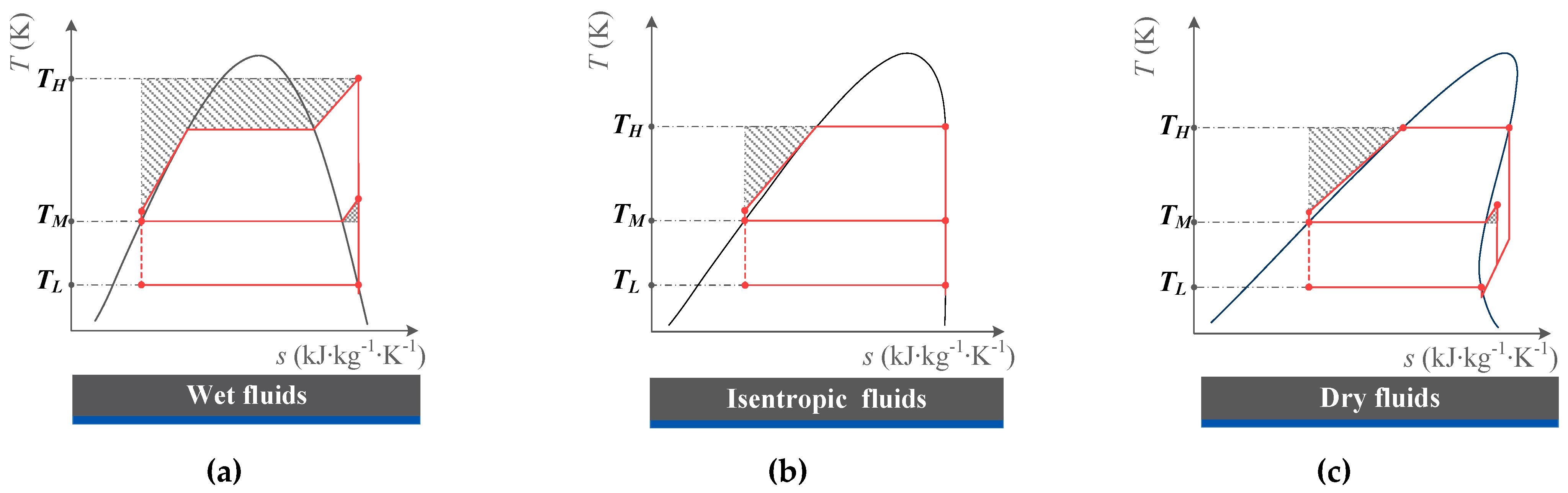
2.3.1. Wet Fluids and Isentropic Fluids
2.3.2. Dry Fluids
2.4. Limiting Thermodynamic Perfection
3. Results and Discussion
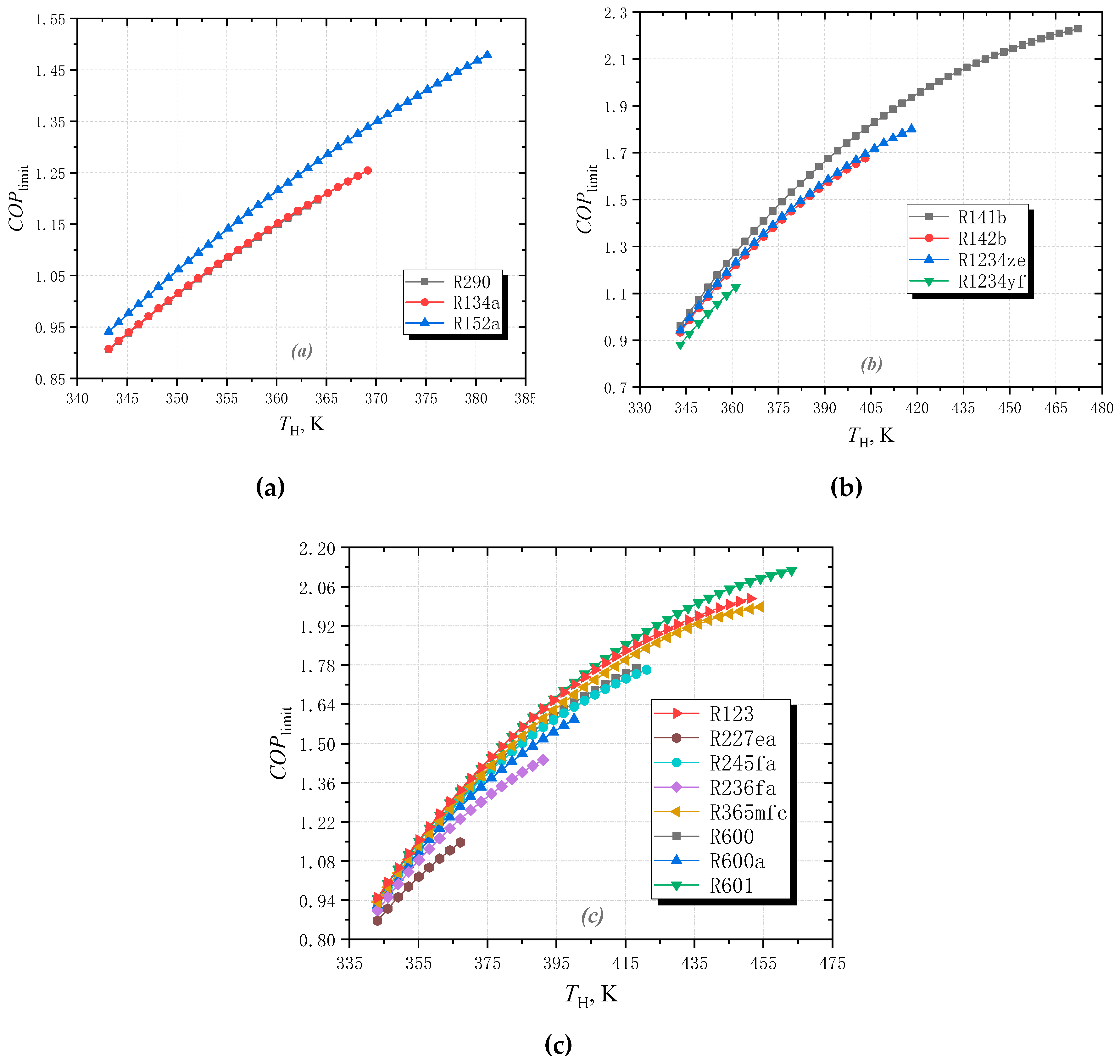
3.1. Effect of High Temperature
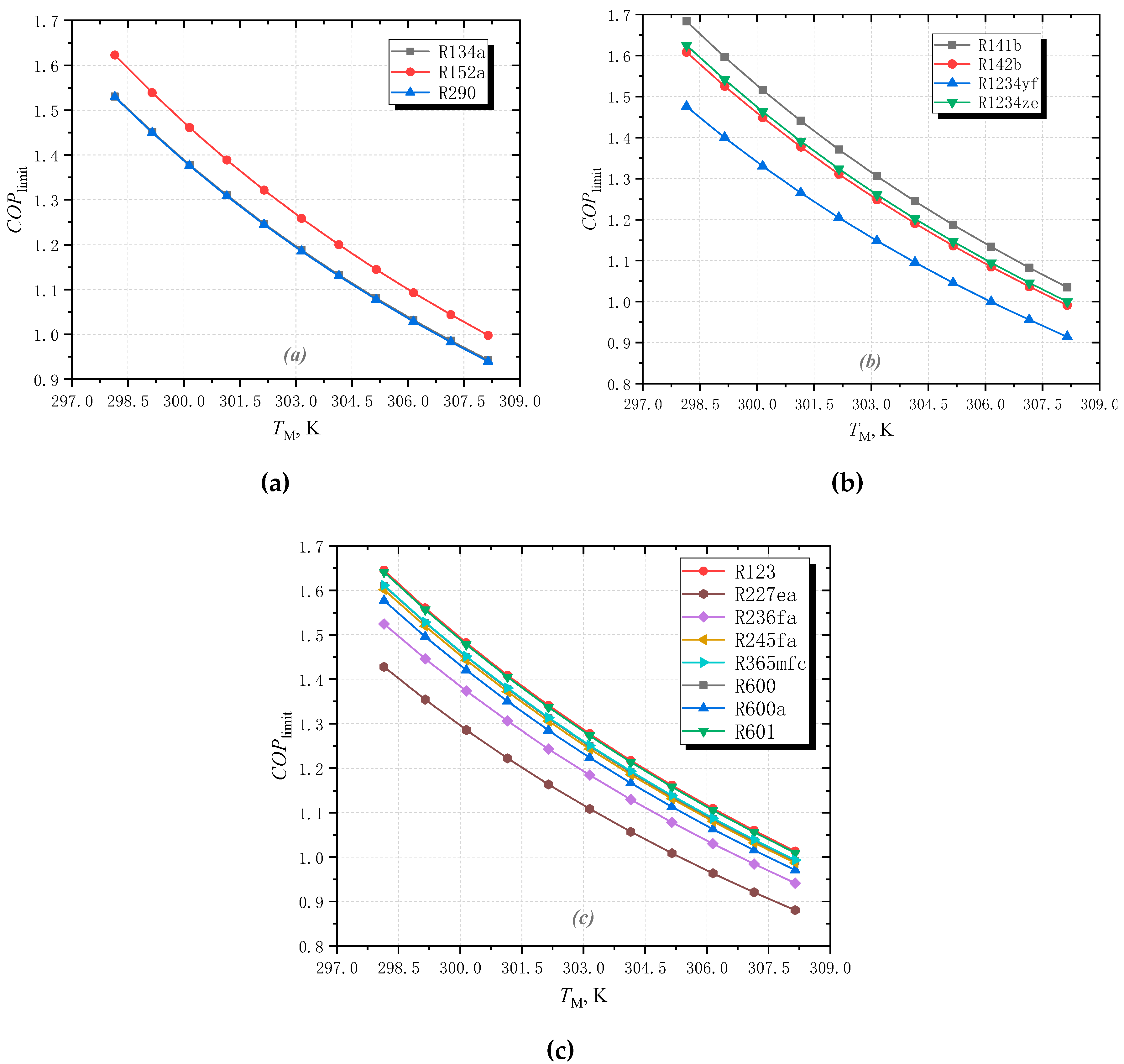
3.2. Effect of Middle Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| A | area |
| cp | specific heat capacity at constant pressure (kJ∙kg#x2212;1∙K#x2212;1) |
| COP | coefficient of performance |
| ERC | ejector refrigeration cycle |
| hL-V | specific heat of vaporization (kJ∙kg#x2212;1) |
| LERC | limiting ejector refrigeration cycle |
| mass flow rate (kg∙s#x2212;1) | |
| heat load (kW) | |
| s | specific entropy (kJ∙kg#x2212;1∙K#x2212;1) |
| T | temperature [K] |
| v | specific volume (m3∙kg#x2212;1) |
| αv | thermal expansion coefficient (1/K) |
| Greek letters | |
| β | slope of the oblique line |
| η | efficiency (%) |
| µ | entrainment ratio |
| ζ | relative heat loss ratio |
| ρ | density (kg/m3) |
| Subscripts | |
| bo | boiling |
| c | compression |
| co | condensation |
| cr | critical |
| ev | evaporation |
| ge | generation |
| H | high temperature in cycle |
| L | low temperature in cycle |
| limit | performance limit |
| LTP | limiting thermodynamic perfection |
| M | Middle temperature |
| p | pressure |
| r | reduced |
| s | saturated |
| V | saturated vapor |
| L | saturated liquid |
References
- Coulomb, D.; Dupont, J.-L.; Pichard, A. The Role of Refrigeration in the Global Economy—29 Informatory Note on Refrigeration Technologies; IIF-IIR: Paris, France, 2015; p. 32. [Google Scholar]
- Besagni, G.; Mereu, R.; Inzoli, F. Ejector Refrigeration: A Comprehensive Review. Renew. Sustain. Energy Rev. 2016, 53, 373–407. [Google Scholar] [CrossRef]
- Tashtoush, B.M.; Moh’d A, A.N.; Khasawneh, M.A. A comprehensive review of ejector design, performance, and applications. Appl. Energy 2019, 240, 138–172. [Google Scholar] [CrossRef]
- Elbel, S.; Hrnjak, P. Ejector Refrigeration: An Overview of Historical and Present Developments with an Emphasis on Air-Conditioning Applications; Purdue Universit: West Lafayette, IN, USA, 2008; p. 9. [Google Scholar]
- Yapıcı, R.; Yetişen, C.C. Experimental Study on Ejector Refrigeration System Powered by Low Grade Heat. Energy Convers. Manag. 2007, 48, 1560–1568. [Google Scholar] [CrossRef]
- Dorantès, R.; Lallemand, A. Influence de la nature des fluides, purs ou en mélanges non-azéotropiques, sur les performances d’une machine de climatisation à éjecto-compresseur. Int. J. Refrig. 1995, 18, 21–30. [Google Scholar] [CrossRef]
- Al-Khalidy, N. An Experimental Study of an Ejector Cycle Refrigeration Machine Operating on R113: Etude Expérimentale d’une Machine Frigorifique à Éjecteur Au R113. Int. J. Refrig. 1998, 21, 617–625. [Google Scholar] [CrossRef]
- Yan, J.; Chen, G.; Liu, C.; Tang, L.; Chen, Q. Experimental Investigations on a R134a Ejector Applied in a Refrigeration System. Appl. Therm. Eng. 2017, 110, 1061–1065. [Google Scholar] [CrossRef]
- Huang, B.J.; Chang, J.M.; Wang, C.P.; Petrenko, V.A. A 1-D Analysis of Ejector Performance. Int. J. Refrig. 1999, 22, 354–364. [Google Scholar] [CrossRef]
- Boumaraf, L.; Lallemand, A. Modeling of an Ejector Refrigerating System Operating in Dimensioning and Off-Dimensioning Conditions with the Working Fluids R142b and R600a. Appl. Therm. Eng. 2009, 29, 265–274. [Google Scholar] [CrossRef]
- Aghagoli, A.; Sorin, M. CFD Modelling and Exergy Analysis of a Heat Pump Cycle with Tesla Turbine Using CO2 as a Working Fluid. Appl. Therm. Eng. 2020, 178, 115587. [Google Scholar] [CrossRef]
- Hamzaoui, M.; Nesreddine, H.; Aidoun, Z.; Balistrou, M. Experimental Study of a Low Grade Heat Driven Ejector Cooling System Using the Working Fluid R245fa. Int. J. Refrig. 2018, 86, 388–400. [Google Scholar] [CrossRef]
- Ruangtrakoon, N.; Aphornratana, S. Development and Performance of Steam Ejector Refrigeration System Operated in Real Application in Thailand. Int. J. Refrig. 2014, 48, 142–152. [Google Scholar] [CrossRef]
- Sankarlal, T.; Mani, A. Experimental Investigations on Ejector Refrigeration System with Ammonia. Renew. Energy 2007, 32, 1403–1413. [Google Scholar] [CrossRef]
- Kumar, J.; Jain, N. Performance Analysis of Heat Operated Ejector Refrigeration System with Natural Refrigerants R-717 and Propane. Int. J. Sci. Res. 2013, 2, 139–142. [Google Scholar]
- Mwesigye, A.; Dworkin, S.B. Performance Analysis and Optimization of an Ejector Refrigeration System Using Alternative Working Fluids under Critical and Subcritical Operation Modes. Energy Convers. Manag. 2018, 176, 209–226. [Google Scholar] [CrossRef]
- Pridasawas, W.; Lundqvist, P. A Year-Round Dynamic Simulation of a Solar-Driven Ejector Refrigeration System with Iso-Butane as a Refrigerant. Int. J. Refrig. 2007, 30, 840–850. [Google Scholar] [CrossRef]
- Zheng, N.; Song, W.; Zhao, L. Theoretical and Experimental Investigations on the Changing Regularity of the Extreme Point of the Temperature Difference between Zeotropic Mixtures and Heat Transfer Fluid. Energy 2013, 55, 541–552. [Google Scholar] [CrossRef]
- Yang, X.; Xu, J.; Miao, Z.; Zou, J.; Qi, F. The Definition of Non-Dimensional Integration Temperature Difference and Its Effect on Organic Rankine Cycle. Appl. Energy 2016, 167, 17–33. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, J.; Zhao, L.; Deng, S.; Zhang, Y. Novel Experimental Research on the Compression Process in Organic Rankine Cycle (ORC). Energy Convers. Manag. 2017, 137, 1–11. [Google Scholar] [CrossRef]
- Chen, J.; Havtun, H.; Palm, B. Screening of Working Fluids for the Ejector Refrigeration System. Int. J. Refrig. 2014, 47, 1–14. [Google Scholar] [CrossRef]
- Buyadgie, D.; Buyadgie, O.; Artemenko, S.; Chamchine, A.; Drakhnia, O. Conceptual Design of Binary/Multicomponent Fluid Ejector Refrigeration Systems. Int. J. Low-Carbon Technol. 2012, 7, 120–127. [Google Scholar] [CrossRef]
- Kasperski, J.; Gil, B. Performance Estimation of Ejector Cycles Using Heavier Hydrocarbon Refrigerants. Appl. Therm. Eng. 2014, 71, 197–203. [Google Scholar] [CrossRef]
- Gil, B.; Kasperski, J. Efficiency Analysis of Alternative Refrigerants for Ejector Cooling Cycles. Energy Convers. Manag. 2015, 94, 12–18. [Google Scholar] [CrossRef]
- Śmierciew, K.; Pawluczuk, A.; Gagan, J.; Butrymowicz, D. Thermodynamic Analysis of Two-Phase Injector for Various Working Fluids. Appl. Therm. Eng. 2019, 157, 113713. [Google Scholar] [CrossRef]
- Xu, W.; Deng, S.; Zhao, L.; Su, W.; Zhang, Y.; Li, S.; Ma, M. How to Quantitatively Describe the Role of the Pure Working Fluids in Subcritical Organic Rankine Cycle: A Limitation on Efficiency. Energy Convers. Manag. 2018, 172, 316–327. [Google Scholar] [CrossRef]
- Calm, J.M.; Hourahan, G.C. Physical, Safety, and Environmental Data for Current and Alternative Refrigerants. In Proceedings of the Proceedings of 23rd International Congress of Refrigeration (ICR2011), Prague, Czech Republic, 21–26 August 2011. [Google Scholar]
- Lemmon, E.W.; Huber, M.L.; Mclinden, M.O. NIST Standard ReferenceDatabase 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP. 9.0; National Institute of Standards and Technology: Boulder, CO, USA, 2010. [Google Scholar]


| Working Fluid | Environmental and Safety Data [27] | Physical Data [28] | Classification | |||||
|---|---|---|---|---|---|---|---|---|
| Refrigerant number | Chemical formula | ODP | GWP 100yr | Safety group | Tbo, K | Tcr, K | Slope * | Type |
| R134a | CH2FCF3 | 0 | 1370 | A1 | 247.1 | 374.2 | −0.3727 | Wet |
| R152a | CH3CHF2 | 0 | 133 | A2 | 249.1 | 386.4 | −0.4276 | Wet |
| R290 | CH3CH2CH3 | 0 | 20 | A3 | 231.0 | 369.9 | −0.1225 | Wet |
| R123 | CF3CHCl2 | 0.01 | 77 | B1 | 300.9 | 456.8 | 2.4578 | Dry |
| R227ea | CF3CHFCF3 | 0 | 3580 | A1 | 256.8 | 374.9 | −1.5428 | Dry |
| R236fa | CF3CH2CF3 | 0 | 9820 | A1 | 271.6 | 398.1 | 3.6318 | Dry |
| R245fa | CF3CH2CHF2 | 0 | 1050 | B1 | 288.2 | 427.0 | 1.8363 | Dry |
| R365mfc | CH3CH2CF2CH3 | 0 | 890 | A2 | 313.3 | 460.0 | 0.8124 | Dry |
| R600 | CH3CH2CH2CH3 | 0 | 20 | A3 | 272.6 | 425.1 | 0.8897 | Dry |
| R600a | CH(CH3)2CH3 | 0 | 20 | A3 | 261.4 | 407.8 | 1.3193 | Dry |
| R601 | CH3CH2CH2CH2CH3 | 0 | 20 | A3 | 309.2 | 469.7 | 0.5027 | Dry |
| R141b | CH3CCl2F | 0.12 | 717 | \ | 305.2 | 477.5 | 3.2231 | Isentropic |
| R142b | CH3CClF2 | 0.06 | 2220 | A2 | 264.0 | 410.3 | −7.1431 | Isentropic |
| R1234ze | CHF=CCF3 | 0 | 6 | A2L | 254.1 | 382.5 | −1.0939 | Isentropic |
| R1234yf | CH2=CFCF3 | 0 | <4.4 | A2L | 243.6 | 367.8 | −0.2411 | Isentropic |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, J.; Liu, Z.; Yang, X.; Jin, S.; Ye, J. Limiting Performance of the Ejector Refrigeration Cycle with Pure Working Fluids. Entropy 2023, 25, 223. https://doi.org/10.3390/e25020223
Fu J, Liu Z, Yang X, Jin S, Ye J. Limiting Performance of the Ejector Refrigeration Cycle with Pure Working Fluids. Entropy. 2023; 25(2):223. https://doi.org/10.3390/e25020223
Chicago/Turabian StyleFu, Jiawei, Zhenhua Liu, Xingyang Yang, Sumin Jin, and Jilei Ye. 2023. "Limiting Performance of the Ejector Refrigeration Cycle with Pure Working Fluids" Entropy 25, no. 2: 223. https://doi.org/10.3390/e25020223
APA StyleFu, J., Liu, Z., Yang, X., Jin, S., & Ye, J. (2023). Limiting Performance of the Ejector Refrigeration Cycle with Pure Working Fluids. Entropy, 25(2), 223. https://doi.org/10.3390/e25020223






