Generalized Survival Probability
Abstract
1. Introduction
[the time-energy uncertainty relation] may be viewed as a consequence of the general theorem of Fock and Krylov on the connection between the decay law and the energy distribution function.
2. Models
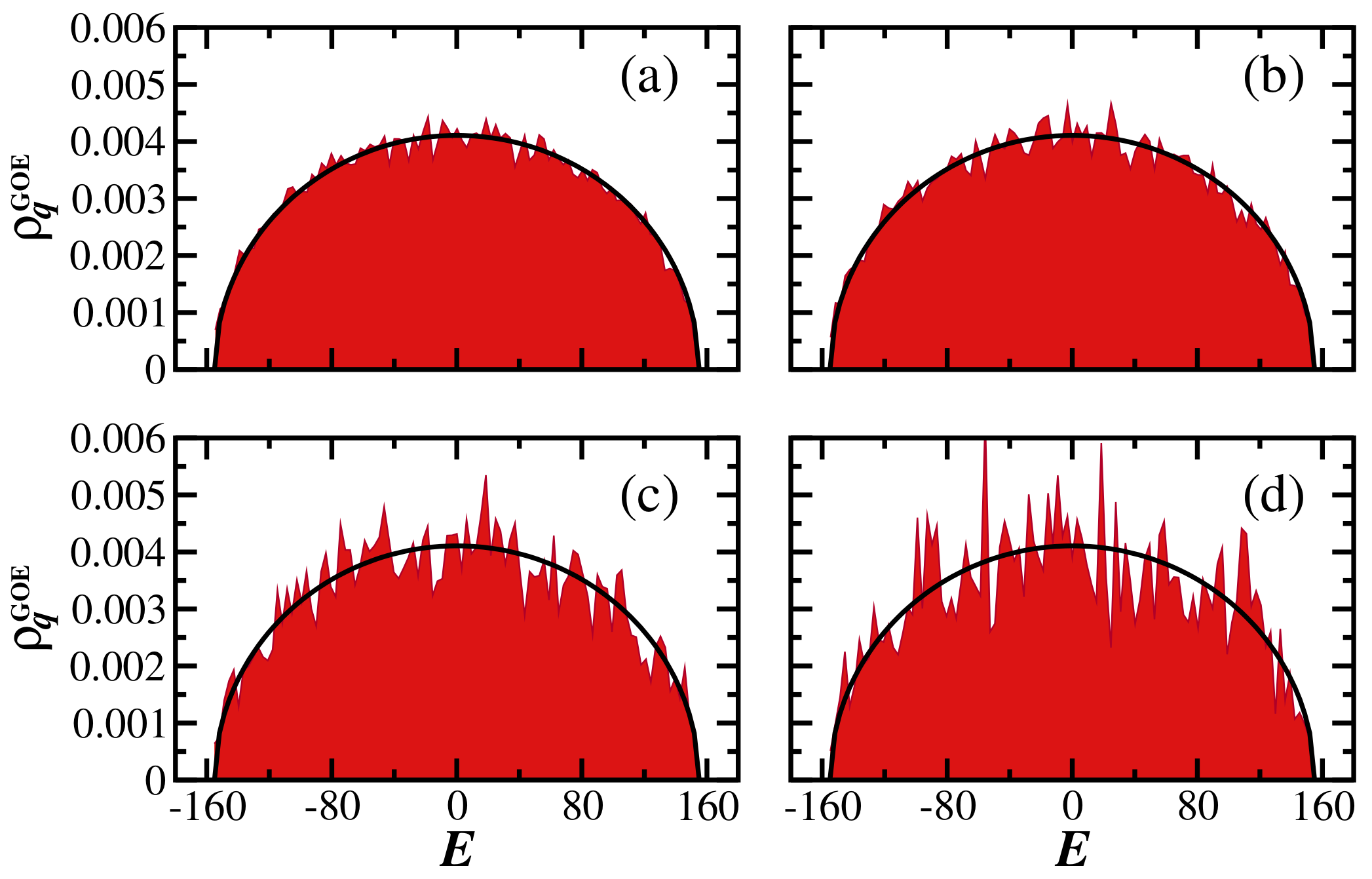
2.1. Gaussian Orthogonal Ensemble
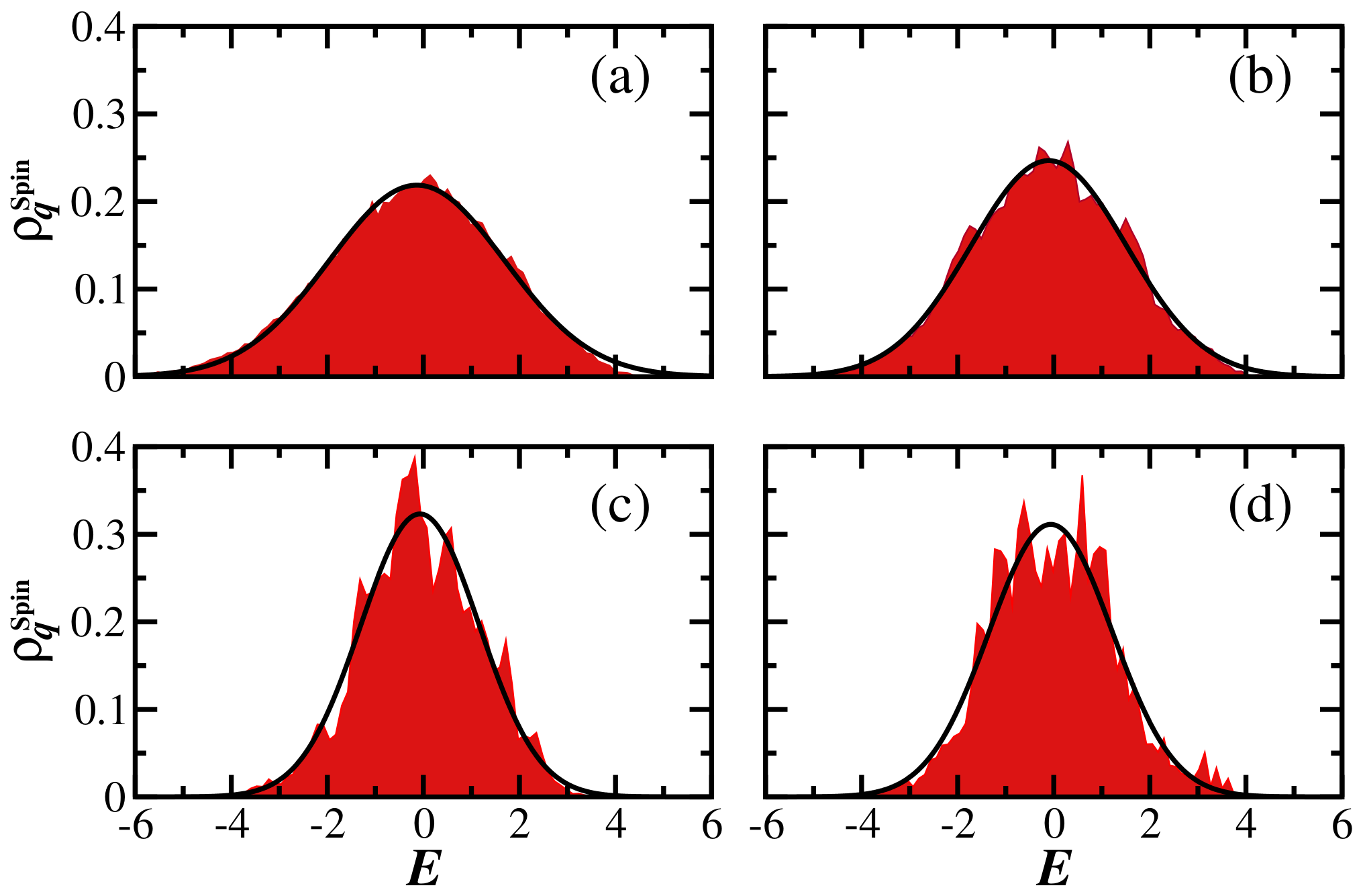
2.2. Disordered Spin-1/2 Model
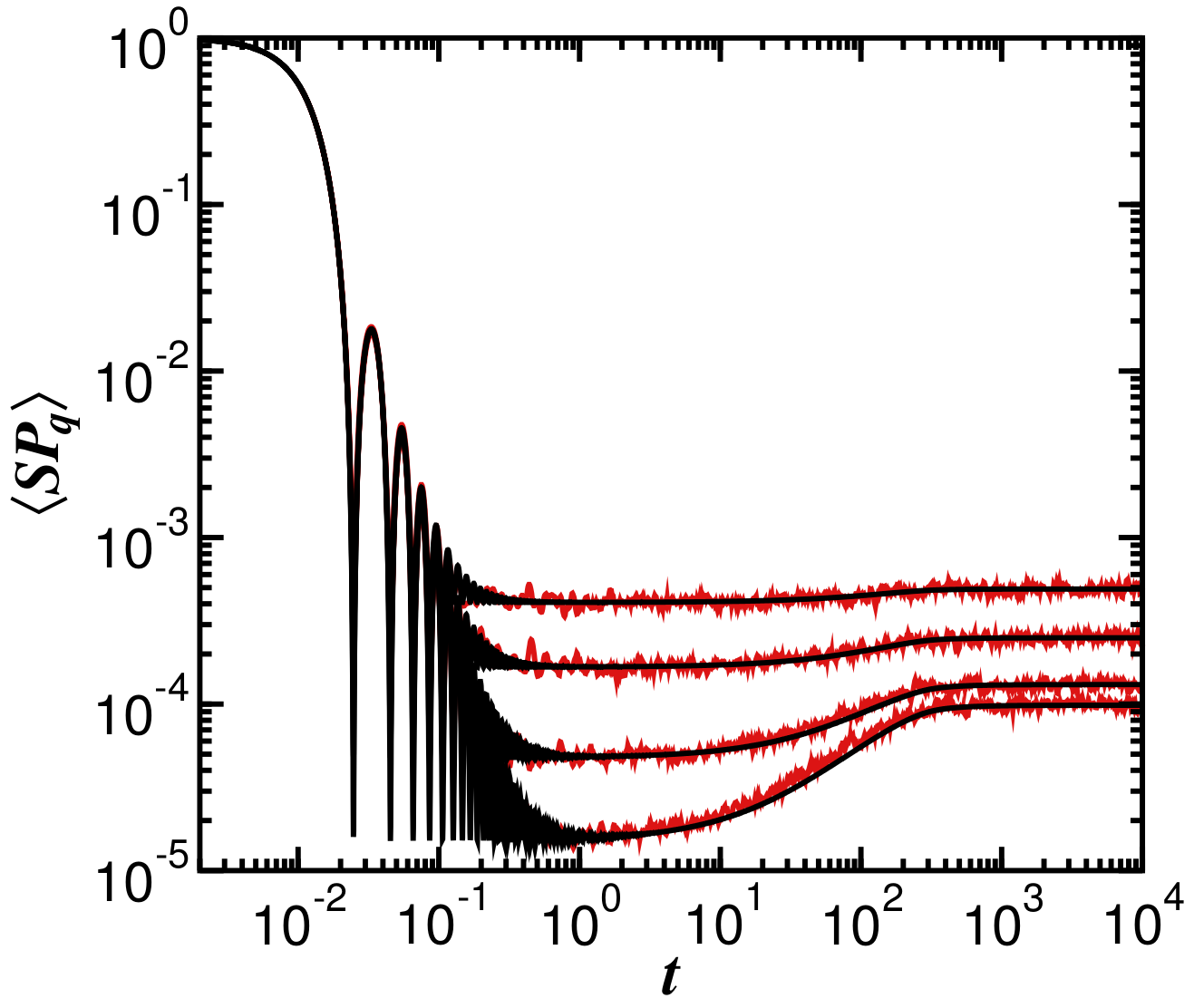
3. Generalized Survival Probability
Generalized LDoS
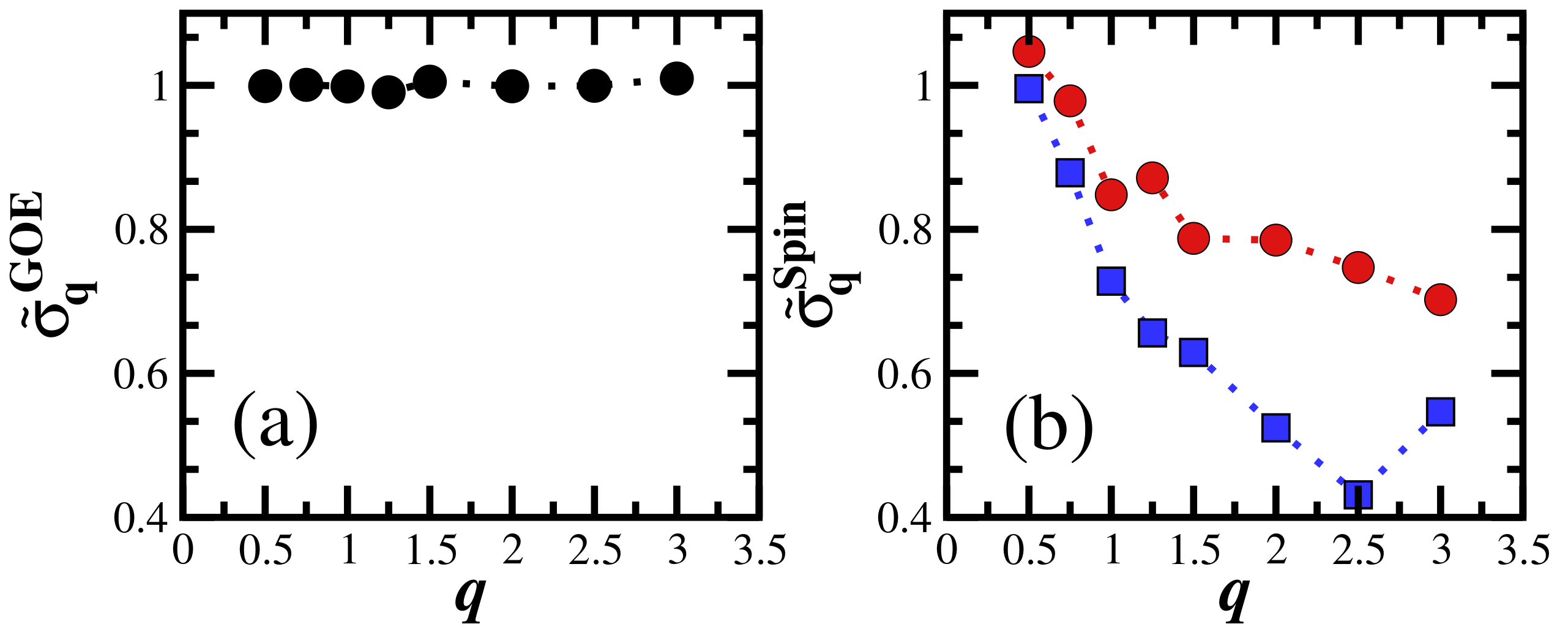
4. Evolution of the Generalized Survival Probability under the GOE Model: Analytical Expression
5. Evolution of the Generalized Survival Probability under the Spin Model
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DoS | Density of states |
| LDoS | Local density of states |
| gLDoS | Generalized local density of states |
| GOE | Gaussian orthogonal ensemble |
References
- Krylov, N.; Fock, V. On the uncertainity relation between time and energy. J. Phys. USSR 1947, 11, 112–120. [Google Scholar]
- Krylov, N.; Fock, V. On two interpretations of the uncertainty relations between energy and time. JETP 1947, 17, 93–107. [Google Scholar]
- Fock, V.A. Criticism of an attempt to disprove the uncertainty relation between time and energy. Sov. Phys. JETP 1962, 15, 784. [Google Scholar]
- Torres-Herrera, J.; Karp, J.; Távora, M.; Santos, L.F. Realistic Many-Body Quantum Systems vs. Full Random Matrices: Static and Dynamical Properties. Entropy 2016, 18, 359. [Google Scholar] [CrossRef]
- Casati, G.; Chirikov, B.V.; Guarneri, I.; Izrailev, F.M. Quantum ergodicity and localization in conservative systems: The Wigner band random matrix model. Phys. Lett. A 1996, 223, 430. [Google Scholar] [CrossRef]
- Fyodorov, Y.V.; Chubykalo, O.A.; Izrailev, F.M.; Casati, G. Wigner Random Banded Matrices with Sparse Structure: Local Spectral Density of States. Phys. Rev. Lett. 1996, 76, 1603–1606. [Google Scholar] [CrossRef]
- Bertulani, C.A.; Zelevinsky, V.G. Excitation of multiphonon giant resonance states in relativistic heavy-ion collisions. Nuc. Phys. A 1994, 568, 931–952. [Google Scholar] [CrossRef]
- Lewenkopf, C.H.; Zelevinsky, V.G. Single and multiple giant resonances: Counterplay of collective and chaotic dynamics. Nucl. Phys. A 1994, 569, 183–193. [Google Scholar] [CrossRef]
- Frazier, N.; Brown, B.A.; Zelevinsky, V. Strength functions and spreading widths of simple shell model configurations. Phys. Rev. C 1996, 54, 1665–1674. [Google Scholar] [CrossRef]
- Zelevinsky, V.; Brown, B.A.; Frazier, N.; Horoi, M. The nuclear shell model as a testing ground for many-body quantum chaos. Phys. Rep. 1996, 276, 85–176. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Izrailev, F.M. Statistical theory of finite Fermi systems based on the structure of chaotic eigenstates. Phys. Rev. E 1997, 56, 5144. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Izrailev, F.M. Excited eigenstates and strength functions for isolated systems of interacting particles. Phys. Rev. E 2000, 61, 2539. [Google Scholar] [CrossRef]
- Flambaum, V.V. Time Dynamics in Chaotic Many-body Systems: Can Chaos Destroy a Quantum Computer? Aust. J. Phys. 2000, 53, 489–497. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Izrailev, F.M. Unconventional decay law for excited states in closed many-body systems. Phys. Rev. E 2001, 64, 026124. [Google Scholar] [CrossRef] [PubMed]
- Flambaum, V.V.; Izrailev, F.M. Entropy production and wave packet dynamics in the Fock space of closed chaotic many-body systems. Phys. Rev. E 2001, 64, 036220. [Google Scholar] [CrossRef] [PubMed]
- Kota, V.K.B.; Sahu, R. Structure of wave functions in (1+2)-body random matrix ensembles. Phys. Rev. E 2001, 64, 016219. [Google Scholar] [CrossRef]
- Chavda, N.; Potbhare, V.; Kota, V. Strength functions for interacting bosons in a mean-field with random two-body interactions. Phys. Lett. A 2004, 326, 47. [Google Scholar] [CrossRef]
- Angom, D.; Ghosh, S.; Kota, V.K.B. Strength functions, entropies, and duality in weakly to strongly interacting fermionic systems. Phys. Rev. E 2004, 70, 016209. [Google Scholar] [CrossRef]
- Kota, V.K.B.; Chavda, N.D.; Sahu, R. Bivariate-t distribution for transition matrix elements in Breit-Wigner to Gaussian domains of interacting particle systems. Phys. Rev. E 2006, 73, 047203. [Google Scholar] [CrossRef]
- Kota, V.K.B. Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 884. [Google Scholar]
- Santos, L.F.; Borgonovi, F.; Izrailev, F.M. Chaos and Statistical Relaxation in Quantum Systems of Interacting Particles. Phys. Rev. Lett. 2012, 108, 094102. [Google Scholar] [CrossRef]
- Santos, L.F.; Borgonovi, F.; Izrailev, F.M. Onset of chaos and relaxation in isolated systems of interacting spins-1/2: Energy shell approach. Phys. Rev. E 2012, 85, 036209. [Google Scholar] [CrossRef] [PubMed]
- Torres-Herrera, E.J.; Vyas, M.; Santos, L.F. General Features of the Relaxation Dynamics of Interacting Quantum Systems. New J. Phys. 2014, 16, 063010. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Santos, L.F. Nonexponential fidelity decay in isolated interacting quantum systems. Phys. Rev. A 2014, 90, 033623. [Google Scholar] [CrossRef]
- Khalfin, L.A. Contribution to the decay theory of a quasi-stationary state. Sov. Phys. JETP 1958, 6, 1053. [Google Scholar]
- Ersak, I. The number of wave functions of an unstable particle. Sov. J. Nucl. Phys. 1969, 9, 263. [Google Scholar]
- Fleming, G.N. A Unitarity Bound on the Evolution of Nonstationary States. Il Nuovo Cimento A 1973, 16, 232. [Google Scholar] [CrossRef]
- Knight, P. Interaction Hamiltonians, spectral lineshapes and deviations from the exponential decay law at long times. Phys. Lett. A 1977, 61, 25–26. [Google Scholar] [CrossRef]
- Fonda, L.; Ghirardi, G.C.; Rimini, A. Decay theory of unstable quantum systems. Rep. Prog. Phys. 1978, 41, 587. [Google Scholar] [CrossRef]
- Erdélyi, A. Asymptotic Expansions Of Fourier Integrals Involving Logarithmic Singularities. J. Soc. Indust. Appr. Math. 1956, 4, 38. [Google Scholar] [CrossRef]
- Urbanowski, K. General properties of the evolution of unstable states at long times. Eur. Phys. J. D 2009, 54, 25–29. [Google Scholar] [CrossRef]
- Távora, M.; Torres-Herrera, E.J.; Santos, L.F. Inevitable power-law behavior of isolated many-body quantum systems and how it anticipates thermalization. Phys. Rev. A 2016, 94, 041603. [Google Scholar] [CrossRef]
- Távora, M.; Torres-Herrera, E.J.; Santos, L.F. Power-law decay exponents: A dynamical criterion for predicting thermalization. Phys. Rev. A 2017, 95, 013604. [Google Scholar] [CrossRef]
- Ketzmerick, R.; Petschel, G.; Geisel, T. Slow decay of temporal correlations in quantum systems with Cantor spectra. Phys. Rev. Lett. 1992, 69, 695–698. [Google Scholar] [CrossRef] [PubMed]
- Huckestein, B.; Schweitzer, L. Relation between the correlation dimensions of multifractal wave functions and spectral measures in integer quantum Hall systems. Phys. Rev. Lett. 1994, 72, 713–716. [Google Scholar] [CrossRef] [PubMed]
- Huckestein, B.; Klesse, R. Wave-packet dynamics at the mobility edge in two- and three-dimensional systems. Phys. Rev. B 1999, 59, 9714–9717. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Santos, L.F. Dynamics at the many-body localization transition. Phys. Rev. B 2015, 92, 014208. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Távora, M.; Santos, L.F. Survival Probability of the Néel State in Clean and Disordered Systems: An Overview. Braz. J. Phys. 2015, 46, 239. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Santos, L.F. Extended nonergodic states in disordered many-body quantum systems. Ann. Phys. 2017, 529, 1600284. [Google Scholar] [CrossRef]
- Leviandier, L.; Lombardi, M.; Jost, R.; Pique, J.P. Fourier Transform: A Tool to Measure Statistical Level Properties in Very Complex Spectra. Phys. Rev. Lett. 1986, 56, 2449–2452. [Google Scholar] [CrossRef]
- Pique, J.P.; Chen, Y.; Field, R.W.; Kinsey, J.L. Chaos and dynamics on 0.5–300 ps time scales in vibrationally excited acetylene: Fourier transform of stimulated-emission pumping spectrum. Phys. Rev. Lett. 1987, 58, 475–478. [Google Scholar] [CrossRef]
- Guhr, T.; Weidenmüller, H. Correlations in anticrossing spectra and scattering theory. Analytical aspects. Chem. Phys. 1990, 146, 21–38. [Google Scholar] [CrossRef]
- Hartmann, U.; Weidenmüller, H.; Guhr, T. Correlations in anticrossing spectra and scattering theory: Numerical simulations. Chem. Phys. 1991, 150, 311–320. [Google Scholar] [CrossRef]
- Alhassid, Y.; Levine, R.D. Spectral autocorrelation function in the statistical theory of energy levels. Phys. Rev. A 1992, 46, 4650–4653. [Google Scholar] [CrossRef]
- Lombardi, M.; Seligman, T.H. Universal and nonuniversal statistical properties of levels and intensities for chaotic Rydberg molecules. Phys. Rev. A 1993, 47, 3571–3586. [Google Scholar] [CrossRef]
- Michaille, L.; Pique, J.P. Influence of Experimental Resolution on the Spectral Statistics Used to Show Quantum Chaos: The Case of Molecular Vibrational Chaos. Phys. Rev. Lett. 1999, 82, 2083–2086. [Google Scholar] [CrossRef]
- Gorin, T.; Prosen, T.; Seligman, T.H. A random matrix formulation of fidelity decay. New J. Phys. 2004, 6, 20. [Google Scholar] [CrossRef]
- Alhassid, Y.; Fyodorov, Y.V.; Gorin, T.; Ihra, W.; Mehlig, B. Fano interference and cross-section fluctuations in molecular photodissociation. Phys. Rev. A 2006, 73, 042711. [Google Scholar] [CrossRef]
- Leyvraz, F.; García, A.; Kohler, H.; Seligman, T.H. Fidelity under isospectral perturbations: A random matrix study. J. Phys. A 2013, 46, 275303. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Santos, L.F. Dynamical manifestations of quantum chaos: Correlation hole and bulge. Philos. Trans. R. Soc. A 2017, 375, 20160434. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; García-García, A.M.; Santos, L.F. Generic dynamical features of quenched interacting quantum systems: Survival probability, density imbalance, and out-of-time-ordered correlator. Phys. Rev. B 2018, 97, 060303. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Santos, L.F. Signatures of chaos and thermalization in the dynamics of many-body quantum systems. Eur. Phys. J. Spec. Top. 2019, 227, 1897–1910. [Google Scholar] [CrossRef]
- Schiulaz, M.; Torres-Herrera, E.J.; Santos, L.F. Thouless and relaxation time scales in many-body quantum systems. Phys. Rev. B 2019, 99, 174313. [Google Scholar] [CrossRef]
- Lerma-Hernández, S.; Villaseñor, D.; Bastarrachea-Magnani, M.A.; Torres-Herrera, E.J.; Santos, L.F.; Hirsch, J.G. Dynamical signatures of quantum chaos and relaxation time scales in a spin-boson system. Phys. Rev. E 2019, 100, 012218. [Google Scholar] [CrossRef] [PubMed]
- Lezama, T.L.; Torres-Herrera, E.J.; Pérez-Bernal, F.; Lev, Y.B.; Santos, L.F. Equilibration time in many-body quantum systems. Phys. Rev. B 2021, 104, 085117. [Google Scholar] [CrossRef]
- Santos, L.F.; Pérez-Bernal, F.; Torres-Herrera, E.J. Speck of chaos. Phys. Rev. Res. 2020, 2, 043034. [Google Scholar] [CrossRef]
- Dag, C.B.; Mistakidis, S.I.; Chan, A.; Sadeghpour, H.R. Many-body quantum chaos in stroboscopically-driven cold atoms. arXiv 2022, arXiv:2210.03840. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Evers, F.; Mirlin, A.D. Anderson transitions. Rev. Mod. Phys. 2008, 80, 1355–1417. [Google Scholar] [CrossRef]
- Wegner, F. Inverse Participation Ratio in 2 + ε Dimensions. Z. Phys. B 1980, 36, 209. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Economou, E.N. Fractal Character of Eigenstates in Disordered Systems. Phys. Rev. Lett. 1984, 52, 565–568. [Google Scholar] [CrossRef]
- Atas, Y.Y.; Bogomolny, E.; Giraud, O.; Roux, G. Distribution of the Ratio of Consecutive Level Spacings in Random Matrix Ensembles. Phys. Rev. Lett. 2013, 110, 084101. [Google Scholar] [CrossRef]
- Atas, Y.Y.; Bogomolny, E. Calculation of multi-fractal dimensions in spin chains. Phil. Trans. R. Soc. A 2013, 372. [Google Scholar] [CrossRef]
- Solórzano, A.; Santos, L.F.; Torres-Herrera, E.J. Multifractality and self-averaging at the many-body localization transition. Phys. Rev. Res. 2021, 3, L032030. [Google Scholar] [CrossRef]
- Pilatowsky-Cameo, S.; Villaseñor, D.; Bastarrachea-Magnani, M.A.; Lerma-Hernández, S.; F. Santos, L.; Hirsch, J.G. Identification of quantum scars via phase-space localization measures. Quantum 2022, 6, 644. [Google Scholar] [CrossRef]
- Santos, L.F.; Rigolin, G.; Escobar, C.O. Entanglement versus chaos in disordered spin systems. Phys. Rev. A 2004, 69, 042304. [Google Scholar] [CrossRef]
- Santos, L.F.; Dykman, M.I.; Shapiro, M.; Izrailev, F.M. Strong many-particle localization and quantum computing with perpetually coupled qubits. Phys. Rev. A 2005, 71, 012317. [Google Scholar] [CrossRef]
- Dukesz, F.; Zilbergerts, M.; Santos, L.F. Interplay between interaction and (un)correlated disorder in one-dimensional many-particle systems: Delocalization and global entanglement. New J. Phys. 2009, 11, 043026. [Google Scholar] [CrossRef]
- Nandkishore, R.; Huse, D. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Condens. Matter Phys. 2015, 6, 15. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices; Academic Press: Boston, MA, USA, 1991. [Google Scholar]
- French, J.B.; Wong, S.S.M. Validity of random matrix theories for many-particle systems. Phys. Lett. B 1970, 33, 449. [Google Scholar] [CrossRef]
- Brody, T.A.; Flores, J.; French, J.B.; Mello, P.A.; Pandey, A.; Wong, S.S.M. Random-matrix physics: Spectrum and strength fluctuations. Rev. Mod. Phys. 1981, 53, 385. [Google Scholar] [CrossRef]
- Berry, M.V. Regular and irregular semiclassical wavefunctions. J. Phys. A 1977, 10, 2083. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Gribakina, A.A.; Gribakin, G.F.; Kozlov, M.G. Structure of compound states in the chaotic spectrum of the Ce atom: Localization properties, matrix elements, and enhancement of weak perturbations. Phys. Rev. A 1994, 50, 267–296. [Google Scholar] [CrossRef] [PubMed]
- Flambaum, V.V.; Gribakin, G.F.; Izrailev, F.M. Correlations within eigenvectors and transition amplitudes in the two-body random interaction model. Phys. Rev. E 1996, 53, 5729–5741. [Google Scholar] [CrossRef] [PubMed]
- Flambaum, V.V.; Izrailev, F.M.; Casati, G. Towards a statistical theory of finite Fermi systems and compound states: Random two-body interaction approach. Phys. Rev. E 1996, 54, 2136–2139. [Google Scholar] [CrossRef] [PubMed]
- Borgonovi, F.; Guarnieri, I.; Izrailev, F.M.; Casati, G. Chaos and thermalization in a dynamical model of two interacting particles. Phys. Lett. A 1998, 247, 140–144. [Google Scholar] [CrossRef]
- Borgonovi, F.; Izrailev, F.M.; Santos, L.F.; Zelevinsky, V.G. Quantum chaos and thermalization in isolated systems of interacting particles. Phys. Rep. 2016, 626, 1. [Google Scholar] [CrossRef]
- Luca, A.D.; Scardicchio, A. Ergodicity breaking in a model showing many-body localization. Europhys. Lett. 2013, 101, 37003. [Google Scholar] [CrossRef]
- Luitz, D.J.; Alet, F.; Laflorencie, N. Universal Behavior beyond Multifractality in Quantum Many-Body Systems. Phys. Rev. Lett. 2014, 112, 057203. [Google Scholar] [CrossRef]
- Li, X.; Ganeshan, S.; Pixley, J.; Sarma, S.D. Many-Body Localization and Quantum Nonergodicity in a Model with a Single-Particle Mobility Edge. Phys. Rev. Lett. 2015, 115, 186601. [Google Scholar] [CrossRef]
- Kohlert, T.; Scherg, S.; Li, X.; Lüschen, H.P.; Sarma, S.D.; Bloch, I.; Aidelsburger, M. Observation of Many-Body Localization in a One-Dimensional System with a Single-Particle Mobility Edge. Phys. Rev. Lett. 2019, 122, 170403. [Google Scholar] [CrossRef]
- Macé, N.; Alet, F.; Laflorencie, N. Multifractal Scalings Across the Many-Body Localization Transition. Phys. Rev. Lett. 2019, 123, 180601. [Google Scholar] [CrossRef]
- Santos, L.F.; Torres-Herrera, E.J. Analytical expressions for the evolution of many-body quantum systems quenched far from equilibrium. AIP Conf. Proc. 2017, 1912, 020015. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zarate-Herrada, D.A.; Santos, L.F.; Torres-Herrera, E.J. Generalized Survival Probability. Entropy 2023, 25, 205. https://doi.org/10.3390/e25020205
Zarate-Herrada DA, Santos LF, Torres-Herrera EJ. Generalized Survival Probability. Entropy. 2023; 25(2):205. https://doi.org/10.3390/e25020205
Chicago/Turabian StyleZarate-Herrada, David A., Lea F. Santos, and E. Jonathan Torres-Herrera. 2023. "Generalized Survival Probability" Entropy 25, no. 2: 205. https://doi.org/10.3390/e25020205
APA StyleZarate-Herrada, D. A., Santos, L. F., & Torres-Herrera, E. J. (2023). Generalized Survival Probability. Entropy, 25(2), 205. https://doi.org/10.3390/e25020205





