A Link Prediction Algorithm Based on Weighted Local and Global Closeness
Abstract
:1. Introduction
2. Algorithm Description
2.1. Problem Description
2.2. Classical Algorithm Similarity Metric
2.3. LGC Algorithm and LGC* Algorithm
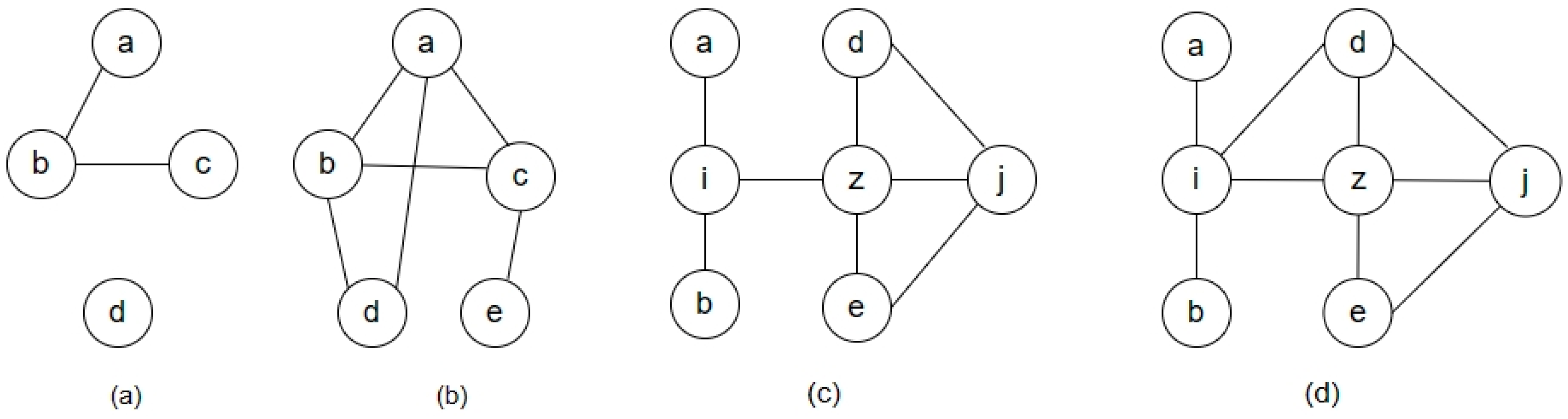
2.3.1. Node Closeness
2.3.2. Local Closeness and Global Closeness
2.3.3. Link Prediction Algorithm Based on Weighted Local and Global Closeness (LGC)
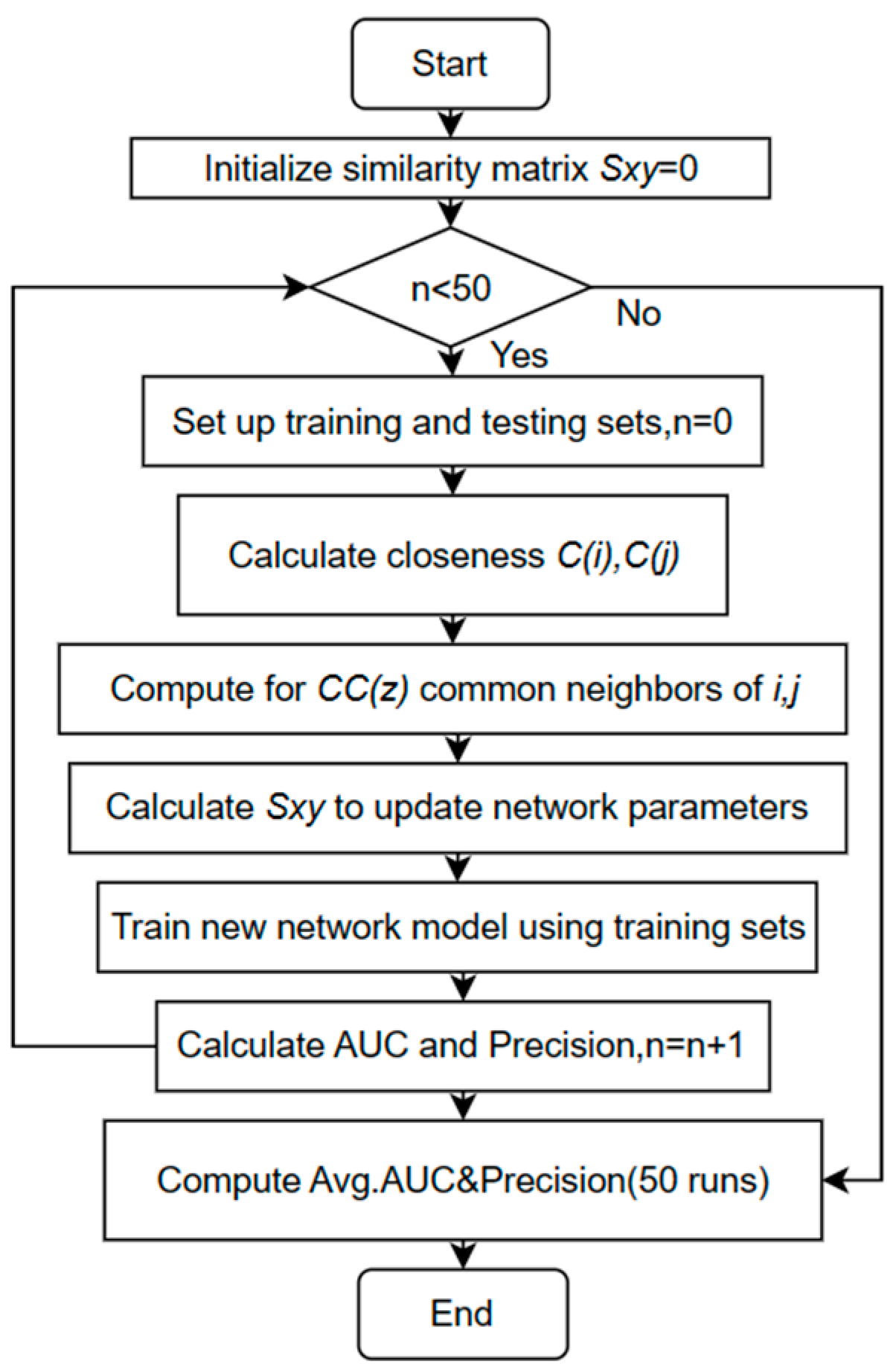
3. Results and Analysis
3.1. Datasets
3.2. Evaluation Metrics
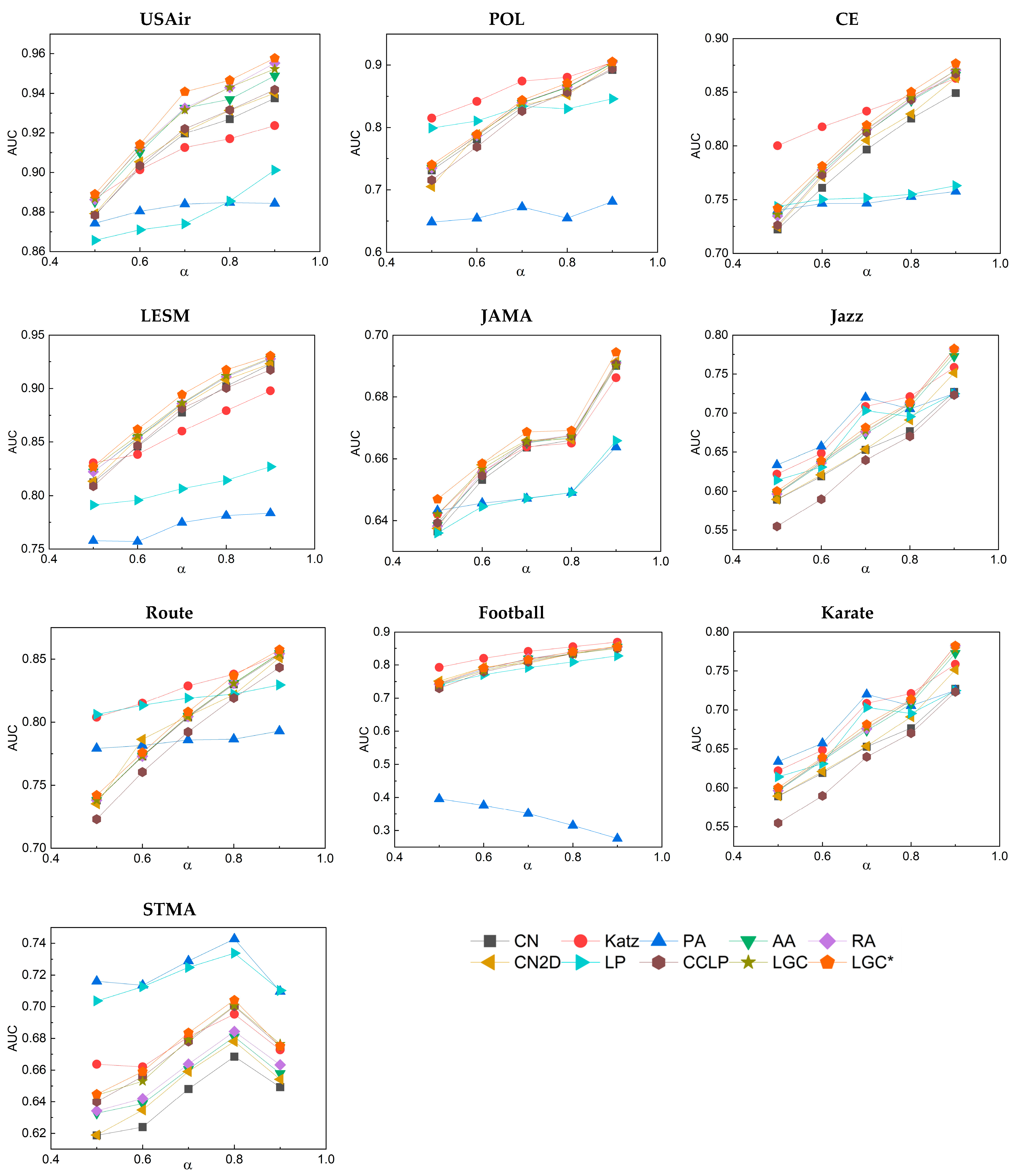
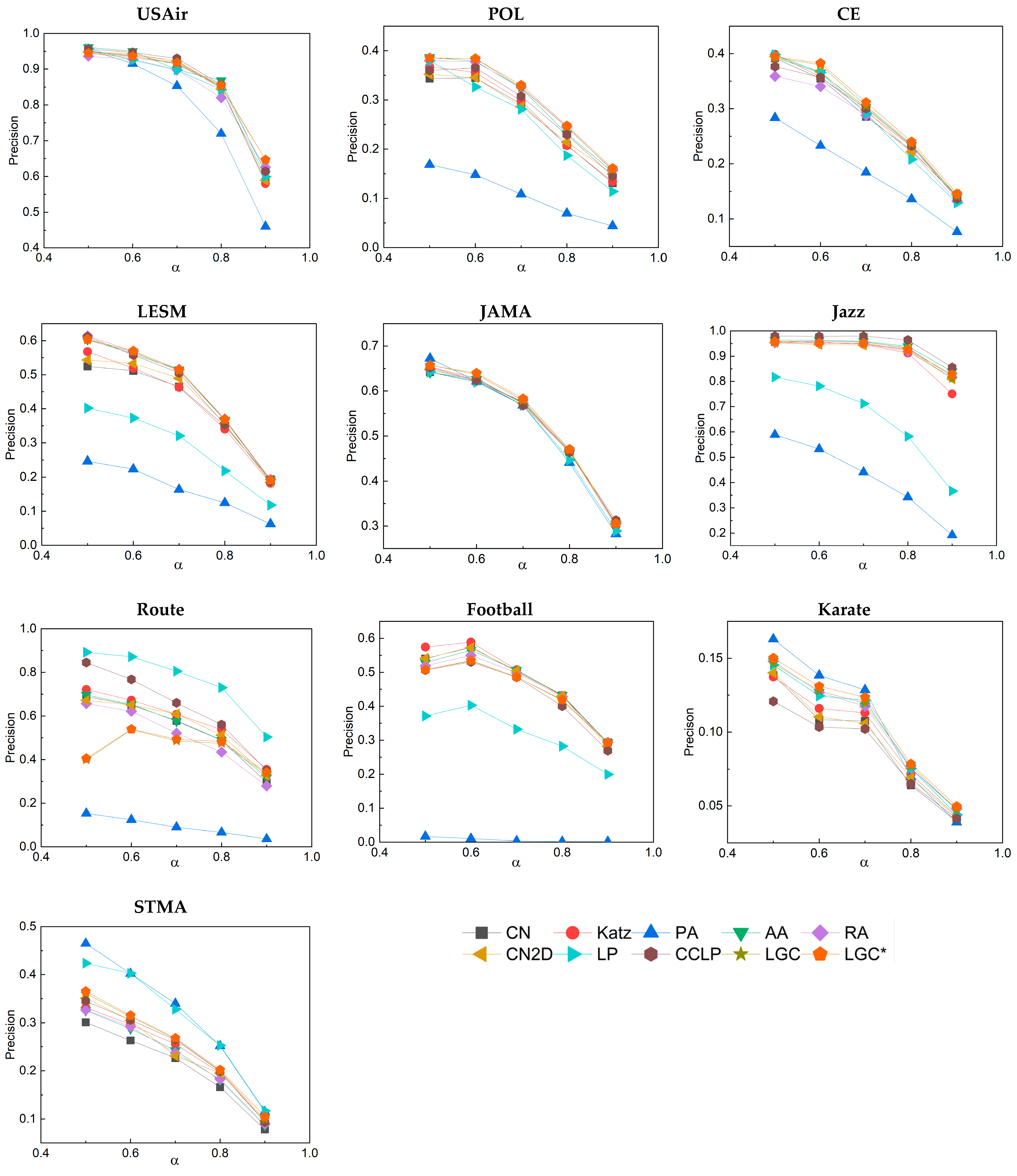
3.3. Analysis of Results
3.4. Complexity Analysis
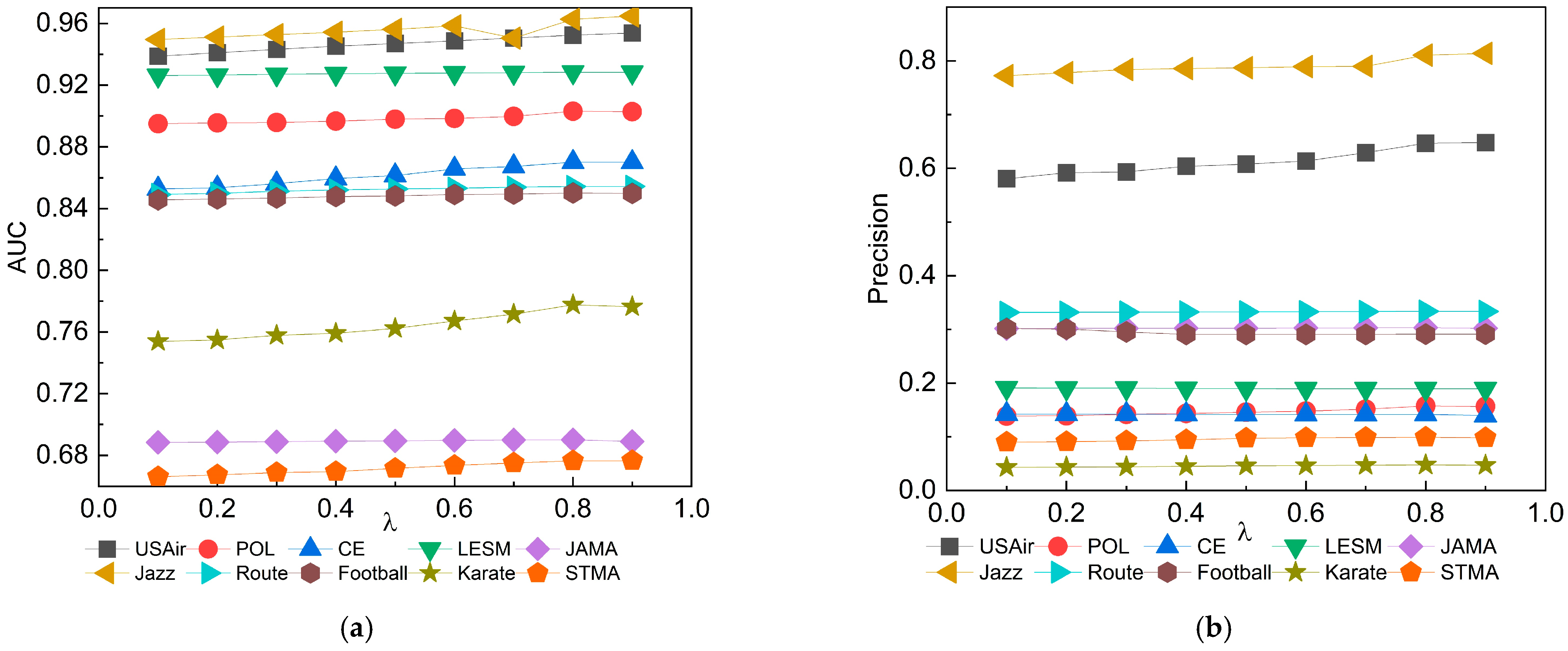
3.5. Robustness Analysis
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hoyt, J.R.; Langwig, K.E.; White, J.P.; Kaarakka, H.M.; Redell, J.A.; Kurta, A.; DePue, J.E.; Scullon, W.H.; Parise, K.L.; Foster, J.T.; et al. Cryptic connections illuminate pathogen transmission within community networks. Nature 2018, 563, 710–713. [Google Scholar] [CrossRef] [PubMed]
- Bonifazi, G.; Corradini, E.; Ursino, D.; Virgili, L. A social network analysis–based approach to investigate user behavior during a cryptocurrency speculative bubble. J. Inf. Sci. 2021, 49, 1060–1085. [Google Scholar] [CrossRef]
- Buccafurri, F.; Lax, G.; Nocera, A.; Ursino, D. Discovering missing me edges across social networks. Inf. Sci. 2015, 319, 18–37. [Google Scholar] [CrossRef]
- Valdeolivas, A.; Tichit, L.; Navarro, C.; Perrin, S.; Odelin, G.; Levy, N.; Cau, P.; Remy, E.; Baudot, A. Random walk with restart on multiplex and heterogeneous biological networks. Bioinformatics 2019, 35, 497–505. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y. Scientific collaboration and endorsement: Network analysis of coauthorship and citation networks. J. Informetr. 2011, 5, 187–203. [Google Scholar] [CrossRef]
- Bonifazi, G.; Cauteruccio, F.; Corradini, E.; Marchetti, M.; Pierini, A.; Terracina, G.; Ursino, D.; Virgili, L. An approach to detect backbones of information diffusers among different communities of a social platform. Data Knowl. Eng. 2022, 140, 102048. [Google Scholar] [CrossRef]
- Buccafurri, F.; Lax, G. Improving similarity-based methods for information propagation on social networks. In Proceedings of the International Conference on Networked Digital Technologies, Prague, Czech Republic, 7–9 July 2010. [Google Scholar]
- Rosvall, M.; Bergstrom, C.T. Mapping change in large networks. PLoS ONE 2010, 5, e8694. [Google Scholar] [CrossRef]
- Martínez, V.; Berzal, F.; Cubero, J.C. A survey of link prediction in complex networks. ACM Comput. Surv. 2016, 49, 1–33. [Google Scholar] [CrossRef]
- Li, R.H.; Yu, J.X.; Liu, J. Link prediction: The power of maximal entropy random walk. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow, UK, 24–28 October 2011. [Google Scholar]
- Zhao, J.; Feng, X.; Dong, L.; Liang, X.; Xu, K. Performance of local information-based link prediction: A sampling perspective. J. Phys. A Math. Theor. 2012, 45, 345001. [Google Scholar] [CrossRef]
- Li, S.; Huang, J.; Zhang, Z.; Liu, J.; Huang, T.; Chen, H. Similarity-based future common neighbors model for link prediction in complex networks. Sci. Rep. 2018, 8, 17014. [Google Scholar] [CrossRef]
- Newman, M.E. Clustering and preferential attachment in growing networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2001, 64, 025102. [Google Scholar] [CrossRef]
- Adamic, L.A.; Adar, E. Friends and neighbors on the web. Soc. Netw. 2003, 25, 211–230. [Google Scholar] [CrossRef]
- Zhou, T.; Lü, L.; Zhang, Y.C. Predicting missing links via local information. Eur. Phys. J. B 2009, 71, 623–630. [Google Scholar] [CrossRef]
- Lu, L.; Zhou, T. Link prediction in complex networks: A survey. Phys. A Stat. Mech. Its Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Ou, Q.; Jin, Y.-D.; Zhou, T.; Wang, B.-H.; Yin, B.-Q. Power-law strength-degree correlation from resource-allocation dynamics on weighted networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007, 75, 021102. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Lin, Y.; Wang, J.; Gregory, S. Link prediction with node clustering coefficient. Phys. A Stat. Mech. Its Appl. 2016, 452, 1–8. [Google Scholar] [CrossRef]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, Y.; Luo, Z.; Yang, Y.; Wang, X.; Gao, T.; Yu, Q. Link prediction algorithm based on clustering coefficient and node centrality. J. Tsinghua Univ. 2022, 62, 98–104. [Google Scholar]
- Lü, L.; Jin, C.H.; Zhou, T. Similarity index based on local paths for link prediction of complex networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 80, 046122. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.S.; Singh, K.; Biswas, B. Link prediction techniques, applications, and performance: A survey. Phys. A Stat. Mech. Its Appl. 2020, 553, 124289. [Google Scholar] [CrossRef]
- Lichtenwalter, R.N.; Lussier, J.T.; Chawla, N.V. New perspectives and methods in link prediction. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–28 July 2010; pp. 243–252. [Google Scholar] [CrossRef]
- Hasan, M.A.; Zaki, M.J. A survey of link prediction in social networks. In Social Network Data Analytics; Aggarwal, C.C., Ed.; Springer: Boston, MA, USA, 2011; pp. 243–275. [Google Scholar]
- García-Pérez, G.; Aliakbarisani, R.; Ghasemi, A.; Serrano, M. Predictability of missing links in complex networks. arXiv 2019, arXiv:1902.00035. [Google Scholar]
- Al Hasan, M.; Chaoji, V.; Salem, S.; Zaki, M. Link prediction using supervised learning. In Proceedings of the SDM06: Workshop on Link Analysis, Counter-Terrorism and Security, Bethesda, MD, USA, 19 April 2006. [Google Scholar]
- Ahn, M.W.; Jung, W.S. Accuracy test for link prediction in terms of similarity index: The case of WS and BA models. Phys. A Stat. Mech. Its Appl. 2015, 429, 177–183. [Google Scholar] [CrossRef]
| Symbols | Definitions |
|---|---|
| Similarity Score of Node Sum | |
| Weight Factor | |
| Degree of a Node | |
| Degree of a Node | |
| Neighbor Set of a Node | |
| Clustering Coefficient of a Node | |
| Common Neighbors of and |
| Algorithm Acronym | Definitions |
|---|---|
| CN | |
| Katz | |
| PA | |
| AA | |
| RA | |
| CN2D | |
| LP | |
| CCLP |
| Networks | N | M | D | ||
|---|---|---|---|---|---|
| USAir | 332 | 2162 | 0.749 | 12.807 | 0.039 |
| POL | 105 | 441 | 0.487 | 8.400 | 0.081 |
| CE | 297 | 2148 | 0.308 | 14.465 | 0.053 |
| LESM | 77 | 254 | 0.735 | 6.597 | 0.087 |
| JAMA | 62 | 1187 | 0.667 | 37.645 | 0.617 |
| Jazz | 198 | 2742 | 0.618 | 27.697 | 0.141 |
| Route | 2113 | 6632 | 0.123 | 3.139 | 0.003 |
| Football | 115 | 613 | 0.403 | 10.66 | 0.309 |
| Karate | 34 | 78 | 0.571 | 4.588 | 0.256 |
| STMA | 54 | 350 | 0.413 | 12.963 | 0.245 |
| Network | CN | Katz | PA | AA | RA | CN2D | LP | CCLP | LGC | LGC* |
|---|---|---|---|---|---|---|---|---|---|---|
| USAir | 0.9375 | 0.9237 | 0.8844 | 0.9488 | 0.9552 | 0.9401 | 0.9012 | 0.9418 | 0.9523 | 0.9577 |
| POL | 0.8923 | 0.9044 | 0.6811 | 0.9025 | 0.9047 | 0.9005 | 0.8460 | 0.8944 | 0.9031 | 0.9082 |
| CE | 0.8491 | 0.8628 | 0.7576 | 0.8658 | 0.8704 | 0.8631 | 0.7631 | 0.8670 | 0.8701 | 0.8766 |
| LESM | 0.9225 | 0.8978 | 0.7837 | 0.9275 | 0.9276 | 0.9231 | 0.8271 | 0.9173 | 0.9284 | 0.9305 |
| JAMA | 0.6900 | 0.6862 | 0.6637 | 0.6907 | 0.6910 | 0.6914 | 0.6658 | 0.6906 | 0.6901 | 0.6954 |
| Jazz | 0.9521 | 0.9383 | 0.7655 | 0.9593 | 0.9656 | 0.9575 | 0.8370 | 0.9561 | 0.9627 | 0.9684 |
| Route | 0.8532 | 0.8539 | 0.7929 | 0.8545 | 0.8543 | 0.8511 | 0.8296 | 0.8434 | 0.8543 | 0.8674 |
| Football | 0.8534 | 0.8693 | 0.2758 | 0.8543 | 0.8545 | 0.8569 | 0.8272 | 0.8499 | 0.8501 | 0.8543 |
| Karate | 0.7271 | 0.7584 | 0.7250 | 0.7725 | 0.7820 | 0.7514 | 0.7248 | 0.7231 | 0.7776 | 0.7823 |
| STMA | 0.6493 | 0.6728 | 0.7097 | 0.6579 | 0.6633 | 0.6542 | 0.7103 | 0.6750 | 0.6765 | 0.6851 |
| Network | CN | Katz | PA | AA | RA | CN2D | LP | CCLP | LGC | LGC* |
|---|---|---|---|---|---|---|---|---|---|---|
| USAir | 0.5850 | 0.5800 | 0.4605 | 0.6070 | 0.6255 | 0.5891 | 0.5989 | 0.6145 | 0.6465 | 0.6475 |
| POL | 0.1310 | 0.1340 | 0.0440 | 0.1535 | 0.1565 | 0.1496 | 0.1140 | 0.1455 | 0.1575 | 0.1610 |
| CE | 0.1405 | 0.1415 | 0.0765 | 0.1400 | 0.1320 | 0.1450 | 0.1290 | 0.1365 | 0.1410 | 0.1457 |
| LESM | 0.1935 | 0.1820 | 0.0625 | 0.1930 | 0.1930 | 0.1847 | 0.1180 | 0.1875 | 0.1895 | 0.1913 |
| JAMA | 0.3050 | 0.3000 | 0.2825 | 0.3050 | 0.3055 | 0.3041 | 0.2890 | 0.3125 | 0.3030 | 0.3161 |
| Jazz | 0.8210 | 0.7500 | 0.1920 | 0.8390 | 0.8155 | 0.8089 | 0.3665 | 0.8560 | 0.8105 | 0.8275 |
| Route | 0.2960 | 0.3550 | 0.0360 | 0.3185 | 0.2795 | 0.3265 | 0.5035 | 0.3500 | 0.3335 | 0.3412 |
| Football | 0.2935 | 0.2895 | 0.0015 | 0.2935 | 0.2935 | 0.2815 | 0.1995 | 0.2695 | 0.2881 | 0.2948 |
| Karate | 0.0395 | 0.0430 | 0.0390 | 0.0475 | 0.0480 | 0.0425 | 0.0440 | 0.0415 | 0.0482 | 0.0496 |
| STMA | 0.0780 | 0.0940 | 0.1150 | 0.0860 | 0.0890 | 0.0961 | 0.1170 | 0.0935 | 0.0990 | 0.1053 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ning, J.; Nie, L.; Liu, Q.; Zhao, N. A Link Prediction Algorithm Based on Weighted Local and Global Closeness. Entropy 2023, 25, 1517. https://doi.org/10.3390/e25111517
Wang J, Ning J, Nie L, Liu Q, Zhao N. A Link Prediction Algorithm Based on Weighted Local and Global Closeness. Entropy. 2023; 25(11):1517. https://doi.org/10.3390/e25111517
Chicago/Turabian StyleWang, Jian, Jun Ning, Lingcong Nie, Qian Liu, and Na Zhao. 2023. "A Link Prediction Algorithm Based on Weighted Local and Global Closeness" Entropy 25, no. 11: 1517. https://doi.org/10.3390/e25111517
APA StyleWang, J., Ning, J., Nie, L., Liu, Q., & Zhao, N. (2023). A Link Prediction Algorithm Based on Weighted Local and Global Closeness. Entropy, 25(11), 1517. https://doi.org/10.3390/e25111517






