Constraints on Tsallis Cosmology from Big Bang Nucleosynthesis and the Relic Abundance of Cold Dark Matter Particles
Abstract
1. Introduction
2. Thermodynamics Based on and Cosmological Equations
2.1. -Entropy and the First and Second Laws of Thermodynamics
2.2. -Entropy and Friedmann Equations
3. Tsallis Cosmology and Bounds from BBN
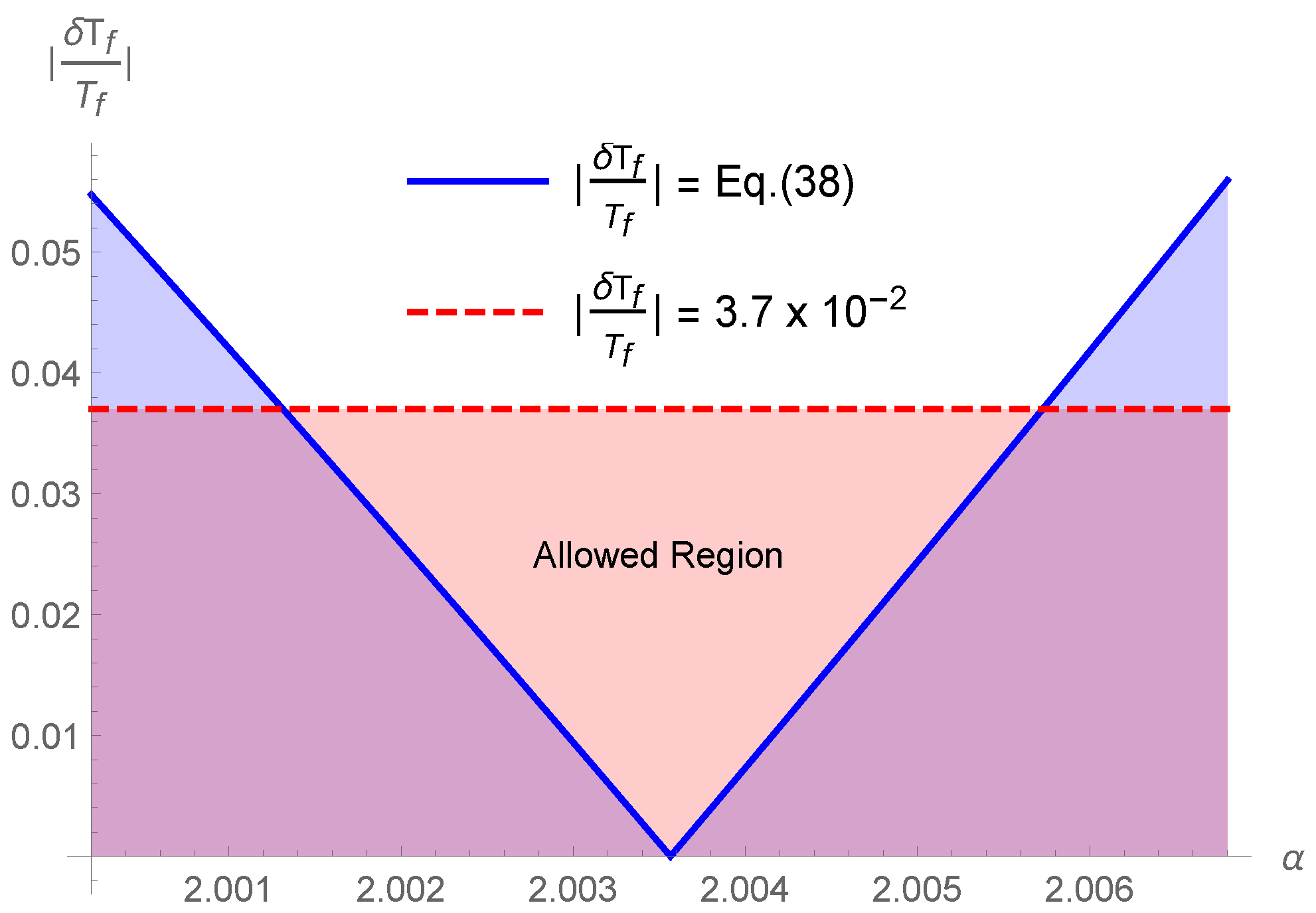
3.1. General Analysis
3.2. Constraints on Tsallis Cosmology from Primordial Abundance of Light Elements
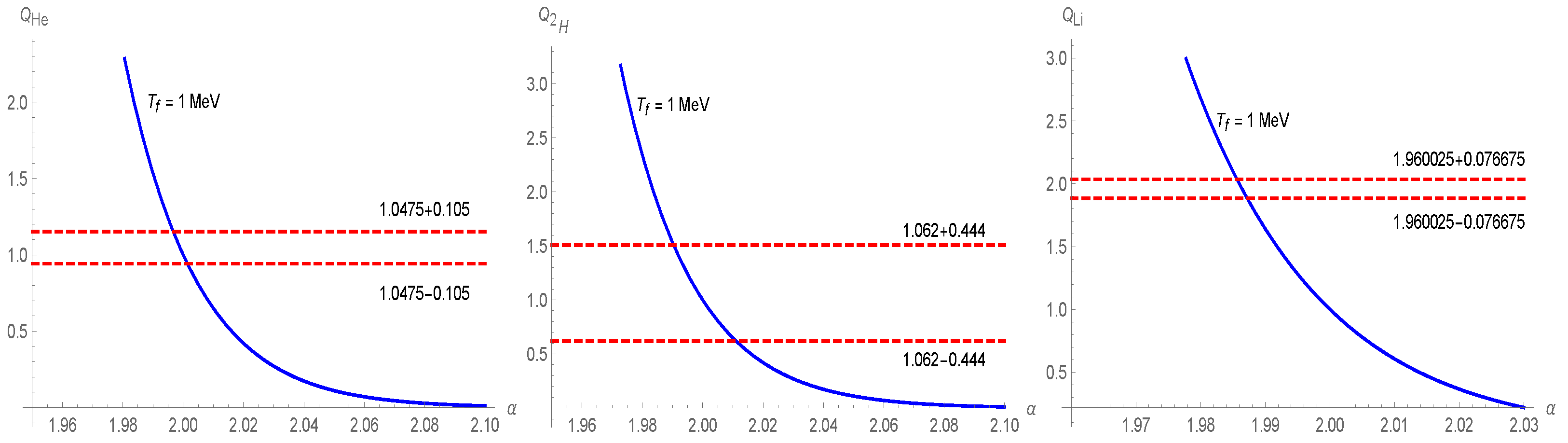
- abundance—Helium production is generated by deuterium production by means of a neutron and a proton. This is then converted into and tritium (the relevant reactions we are considering are , , and . Helium is produced by the reactions .). The best fit for the primordial abundance is given by [84,85]where Q is the amplification factor (in our case described by (33)) and (the baryon density parameter) is defined as ; see, e.g., [86,87], where is the baryon-to-photon ratio [88]. The values and correspond to the standard BBN result for the mass fraction based on the standard cosmological model (St.Cosm.), which yields . Using the observational data [89] and (see, e.g., [86,87]), one obtains the correct phenomenological helium mass abundance , cf. Equation (39), providedThis relation provides the sought constrain on Q. By taking Q to be equal to (see, e.g., Ref. [82]), we obtain . Figure 2 displays the latter relation with Q arising from the Tsallis cosmology, cf. Equation (33). This also imposes a constraint on admissible values of . The permissible range of ’s in relation to helium abundance is
- abundance—Neutron–proton interactions, that is, , produce deuterium, . Presently, the best fit for deuterium abundance is given by [86]The values of and once again result in a standard cosmology with the value of . The observational constraint on deuterium abundance , cf. Ref. [89] and Equation (45), implyleading to the constraint on given by . Following the same strategy as in the helium abundance case, we compare the latter with the amplification factor (33). The result is reported in Figure 2. From this, we can deduce the corresponding range of variability of for abundance, namely
- abundance—When considering lithium abundance, the parameter successfully fits the abundances of and , but it does not align with the observations of . This fact is known as the lithium problem [81]. In standard cosmology, the ratio of the expected value of abundance and the observed value (Obs.) is , cf., e.g., [81,90]. The best fit for abundance is presently given by [86], namelySuch a value does not overlap with the constraints on and abundances. In fact, from Figure 2, we see that the range for admissible s is
4. Tsallis Cosmology and Bounds from the Relic Abundance of Cold Dark Matter Particles
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BH | Bekenstein–Hawking |
| GR | General relativity |
| QFT | Quantum Field Theory |
| BBN | Big Bang nucleosynthesis |
| FRW | Friedmann–Robertson–Walker |
| CMB | Cosmic Microwave Background |
| DM | Dark Matter |
| WIMP | Weakly-interacting massive particle |
| CDM | Cold dark matter |
Appendix A. Zeroth Law of Thermodynamics and Entropy
Appendix B. BBN Physics—A Short Review
References
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Comm. Math. Phys. 1975, 43, 199–220, Erratum in Comm. Math. Phys. 1976, 46, 206–206. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of space-time: The Einstein equation of state. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef]
- Verlinde, E. On the origin of gravity and the laws of Newton. JHEP J. High Energy Phys. 2011, 1104, 029. [Google Scholar] [CrossRef]
- Padmanabhan, T. Gravity and the thermodynamics of horizons. Phys. Rept. 2005, 406, 49–125. [Google Scholar] [CrossRef]
- Padmanabhan, T. Thermodynamical Aspects of Gravity: New insights. Rep. Prog. Phys. 2010, 73, 046901. [Google Scholar] [CrossRef]
- Eling, C.; Guedens, R.; Jacobson, T. Nonequilibrium Thermodynamics of Spacetime. Phys. Rev. Lett. 2006, 96, 121301. [Google Scholar] [CrossRef]
- Akbar, M.; Cai, R.G. Friedmann equations of FRW universe in scalar–tensor gravity, f(R) gravity and first law of thermodynamics. Phys. Lett. B 2006, 635, 7–16. [Google Scholar] [CrossRef]
- Padmanabhan, T.; Paranjape, A. Entropy of null surfaces and dynamics of spacetime. Phys. Rev. D 2007, 75, 064004. [Google Scholar] [CrossRef]
- Akbar, M.; Cai, R.G. Thermodynamic behavior of the Friedmann equation at the apparent horizon of the FRW universe. Phys. Rev. D 2007, 75, 084003. [Google Scholar] [CrossRef]
- Cai, R.G.; Cao, L.M. Unified first law and the thermodynamics of the apparent horizon in the FRW universe. Phys. Rev. D 2007, 75, 064008. [Google Scholar] [CrossRef]
- Cai, R.G.; Kim, S.P. First law of thermodynamics and Friedmann equations of Friedmann–Robertson–Walker universe. JHEP J. High Energy Phys. 2005, 0502, 050. [Google Scholar] [CrossRef]
- Bousso, R. Cosmology and the S matrix. Phys. Rev. D 2005, 71, 064024. [Google Scholar] [CrossRef]
- Cai, R.G.; Myung, Y.S. Holography in a radiation-dominated universe with a positive cosmological constant. Phys. Rev. D 2003, 67, 124021. [Google Scholar] [CrossRef]
- Cai, R.G.; Cao, L.M. Thermodynamics of Apparent Horizon in Brane World Scenario. Nucl. Phys. B 2007, 785, 135–148. [Google Scholar] [CrossRef]
- Cai, R.G.; Cao, L.M.; Hu, Y.P. Corrected Entropy-Area Relation and Modified Friedmann Equations. JHEP J. High Energy Phys. 2008, 0808, 090. [Google Scholar] [CrossRef]
- Sheykhi, A.; Wang, B.; Cai, R.G. Thermodynamical Properties of Apparent Horizon in Warped DGP Braneworld. Nucl. Phys. B 2007, 779, 1–12. [Google Scholar] [CrossRef]
- Sheykhi, A.; Wang, B.; Cai, R.G. Deep connection between thermodynamics and gravity in Gauss-Bonnet braneworlds. Phys. Rev. D 2007, 76, 023515. [Google Scholar] [CrossRef]
- Tsallis, C.; Cirto, L.J.L. Black hole thermodynamical entropy. Eur. Phys. J. C 2013, 73, 2487. [Google Scholar] [CrossRef]
- Komatsu, N.; Kimura, S. Entropic cosmology for a generalized black-hole entropy. Phys. Rev. D 2013, 88, 083534. [Google Scholar] [CrossRef]
- Barboza, E.M., Jr.; Nunes, R.d.C.; Abreu, E.M.C.; Ananias Neto, J. Dark energy models through non-extensive Tsallis statistics. Phys. A 2015, 436, 301–310. [Google Scholar] [CrossRef]
- Lymperis, A.; Saridakis, E.N. Modified cosmology through nonextensive horizon thermodynamics. Eur. Phys. J. C 2018, 78, 993. [Google Scholar] [CrossRef] [PubMed]
- Saridakis, E.N.; Bamba, K.; Myrzakulov, R.; Anagnostopoulos, F.K. Holographic dark energy through Tsallis entropy. JCAP J. Cosmol. Astropart. Phys. 2018, 1812, 012. [Google Scholar] [CrossRef]
- Sheykhi, A. Modified Friedmann equations from Tsallis entropy. Phys. Lett. B 2018, 785, 118–126. [Google Scholar] [CrossRef]
- Artymowski, M.; Mielczarek, J. Quantum Hubble horizon. Eur. Phys. J. C 2019, 79, 632. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A.; Mendes, A.C.R.; Bonilla, A. Tsallis and Kaniadakis statistics from a point of view of the holographic equipartition law. Europhys. Lett. 2018, 121, 45002. [Google Scholar] [CrossRef]
- Jawad, A.; Iqbal, A. Modified cosmology through Renyi and logarithmic entropies. Int. J. Geom. Meth. Mod. Phys. 2018, 15, 1850130. [Google Scholar] [CrossRef]
- Abdollahi Zadeh, M.; Sheykhi, A.; Moradpour, H. Tsallis Agegraphic Dark Energy Model. Mod. Phys. Lett. A 2019, 34, 11. [Google Scholar]
- da Silva, W.J.C.; Silva, R. Extended ΛCDM model and viscous dark energy: A Bayesian analysis. JCAP J. Cosmol. Astropart. Phys. 2019, 2019, 036–040. [Google Scholar] [CrossRef]
- Cai, Y.F.; Liu, J.; Li, H. Entropic cosmology: A unified model of inflation and late-time acceleration. Phys. Lett. B 2010, 690, 213–219. [Google Scholar] [CrossRef]
- Das, S.; Majumdar, P.; Bhaduri, R.K. General Logarithmic Corrections to Black Hole Entropy. Class. Quant. Grav. 2002, 19, 2355–2368. [Google Scholar] [CrossRef]
- Ashtekar, A.; Baez, J.; Corichi, A.; Krasnov, K. Quantum Geometry and Black Hole Entropy. Phys. Rev. Lett. 1998, 80, 904–907. [Google Scholar] [CrossRef]
- Banerjee, R.; Majhi, B.R. Quantum Tunneling and Back Reaction. Phys. Lett. B 2008, 662, 62–65. [Google Scholar] [CrossRef]
- Das, S.; Shankaranarayanan, S.; Sur, S. Entanglement and corrections to Bekenstein–Hawking entropy. arXiv 2010, arXiv:1002.1129. [Google Scholar]
- Das, S.; Shankaranarayanan, S.; Sur, S. Black hole entropy from entanglement: A review. arXiv 2008, arXiv:0806.0402. [Google Scholar]
- Das, S.; Shankaranarayanan, S.; Sur, S. Power-law corrections to entanglement entropy of horizons. Phys. Rev. D 2008, 77, 064013. [Google Scholar] [CrossRef]
- Radicella, N.; Pavon, D. The generalized second law in universes with quantum corrected entropy relations. Phys. Lett. B 2010, 691, 121–126. [Google Scholar] [CrossRef]
- Iorio, A.; Lambiase, G.; Vitiello, G. Entangled quantum fields near the event horizon and entropy. Ann. Phys. 2004, 309, 151–165. [Google Scholar] [CrossRef]
- Jizba, P.; Lambiase, G.; Luciano, G.G.; Petruzziello, L. Decoherence limit of quantum systems obeying generalized uncertainty principle: New paradigm for Tsallis thermostatistics. Phys. Rev. D 2022, 105, L121501. [Google Scholar] [CrossRef]
- Jizba, P.; Lambiase, G.; Luciano, G.G.; Petruzziello, L. Coherent states for generalized uncertainty relations as Tsallis probability amplitudes: New route to nonextensive thermostatistics. Phys. Rev. D 2023, 108, 064024. [Google Scholar] [CrossRef]
- Jizba, P.; Lambiase, G. Tsallis cosmology and its applications in dark matter physics with focus on IceCube high-energy neutrino data. Eur. Phys. J. C 2022, 82, 1123. [Google Scholar] [CrossRef]
- Tsallis, C. Black Hole Entropy: A Closer Look. Entropy 2020, 22, 17. [Google Scholar] [CrossRef]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity; A Survey of Gravitational Theories for Cosmology and Astrophysics; Springer: London, UK, 2011. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Barrow, J.D. The Area of a Rough Black Hole. Phys. Lett. B 2020, 808, 135643. [Google Scholar] [CrossRef] [PubMed]
- Jalalzadeh, S.; da Silva, F.R.; Moniz, P.V. Prospecting black hole thermodynamics with fractional quantum mechanics. Eur. Phys. J. C 2021, 81, 632. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; Costa, E.W.O.; Moniz, P.V. de Sitter fractional quantum cosmology. Phys. Rev. D 2022, 105, L121901. [Google Scholar] [CrossRef]
- ’t Hooft, G. On the quantum structure of a black hole. Nucl. Phys. B 1985, 256, 727–745. [Google Scholar] [CrossRef]
- Wheeler, J.A. Geons. Phys. Rev. 1955, 97, 511–536. [Google Scholar] [CrossRef]
- Tang, H.P.; Wang, J.Z.; Zhu, J.L.; Ao, Q.B.; Wang, J.Y.; Yang, B.J.; Li, Y.N. Fractal dimension of pore-structure of porous metal materials made by stainless steel powder. Powder Technol. 2012, 217, 383–387. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B. Developing a new form of permeability and Kozeny–Carman constant for homogeneous porous media by means of fractal geometry. Adv. Water Resour. 2008, 31, 74–81. [Google Scholar] [CrossRef]
- Dagotto, E.; Kocić, A.; Kogut, J.B. Collapse of the wave function, anomalous dimensions and continuum limits in model scalar field theories. Phys. Lett. B 1990, 237, 268–273. [Google Scholar] [CrossRef]
- Kobayashi, T.; Nakano, H.; Terao, H. Induced top-Yukawa coupling and suppressed Higgs mass parameters. Phys. Rev. D 2005, 71, 115009. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Statist. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Lyra, M.L.; Tsallis, C. Non-extensivity and multifractality in low dissipative systems. Phys. Rev. Lett. 1998, 80, 53–56. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Interpretation of the Nonextensivity Parameter q in Some Applications of Tsallis Statistics and Lévy Distributions. Phys. Rev. Lett. 2000, 84, 2770–2773. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saridakis, E.N. Modified cosmology from extended entropy with varying exponent. Eur. Phys. J. C 2019, 79, 242. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Faraoni, V. From nonextensive statistics and black hole entropy to the holographic dark universe. Phys. Rev. D 2022, 105, 044042. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Paul, T. Early and late universe holographic cosmology from a new generalized entropy. Phys. Lett. B 2022, 831, 137189. [Google Scholar] [CrossRef]
- Landsberg, P.T. A Deduction of Carathéodory’s Principle from Kelvin’s Principle. Nature 1964, 201, 485. [Google Scholar] [CrossRef]
- Zemansky, M.W. Kelvin and Carathéodory—A Reconciliation. Am. J. Phys. 1966, 34, 914. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics, and particle creation. Phys. Rev. D 1977, 15, 2738–2751. [Google Scholar] [CrossRef]
- ‘t Hooft, G. Dimensional Reduction in Quantum Gravity. arXiv 1993, arXiv:gr-qc/9310026. [Google Scholar]
- Susskind, L. The World as a Hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Caratheodory, C. Untersuchungen über die Grundlagen der Thermodynamik. Math. Ann. 1909, 67, 355–386. [Google Scholar] [CrossRef]
- Buchdahl, H.A. On the Unrestricted Theorem of Carathéodory and Its Application in the Treatment of the Second Law of Thermodynamics. Am. J. Phys. 1949, 17, 212–218. [Google Scholar] [CrossRef]
- Huang, K. Statistical Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1987. [Google Scholar]
- Li, R.; Ren, J.R.; Shi, D.F. Fermions tunneling from apparent horizon of FRW universe. Phys. Lett. B 2009, 670, 446–448. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua1, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Spergel, D.N.; Bean, R.; Doré, O.; Nolta, M.R.; Bennett, C.L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.E.; Komatsu, E.; Page, L.; et al. Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology. Astrophys. J. Suppl. 2007, 170, 377–408. [Google Scholar] [CrossRef]
- Tegmark, M.; Strauss, M.A.; Blanton, M.R.; Abazajian, K.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.H.; Zehavi, I.; Bahcall, N.A.; et al. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004, 69, 103501–103525. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Kolb, E.W.; Turner, M.S. The Early Universe; Addison Wesley Publishing Company: New York, NY, USA, 1989. [Google Scholar]
- Bernstein, J.; Brown, L.S.; Feinberg, G. Cosmological helium production simplified. Rev. Mod. Phys. 1989, 61, 25–39. [Google Scholar] [CrossRef]
- Torres, D.F.; Vucetich, H.; Plastino, A. Early Universe Test of Nonextensive Statistics. Phys. Rev. Lett. 1997, 79, 1588–1590. [Google Scholar] [CrossRef]
- Capozziello, S.; Lambiase, G.; Saridakis, E. Constraining f(T) teleparallel gravity by big bang nucleosynthesis f(T) cosmology and BBN. Eur. Phys. J. C 2017, 77, 576. [Google Scholar] [CrossRef] [PubMed]
- Aver, E.; Olive, K.A.; Skillmann, E.D. The effects of He I λ 10830 on helium abundance determinations. JCAP J. Cosmol. Astropart. Phys. 2015, 07, 011. [Google Scholar] [CrossRef]
- Izotov, Y.I.; Thuan, T.X.; Guseva, N.G. A new determination of the primordial He abundance using the He I λ 10830 Å emission line: Cosmological implications. Mon. Not. R. Astron. Soc 2014, 445, 778–793. [Google Scholar] [CrossRef]
- Boran, S.; Kahya, E.O. Testing a Dilaton Gravity Model using Nucleosynthesis. Adv. High Energy Phys. 2014, 2014, 282675. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Sahoo, P.K. Big bang nucleosynthesis and entropy evolution in f(R,T) gravity. Eur. Phys. J. Plus 2020, 135, 350. [Google Scholar] [CrossRef]
- Katurci, N.; Kavuk, M. f(R,TμνTμν) gravity and Cardassian-like expansion as one of its consequences. Eur. Phys. J. Plus 2014, 129, 163. [Google Scholar] [CrossRef]
- Kneller, J.P.; Steigman, G. BBN for pedestrians. New J. Phys. 2004, 6, 117. [Google Scholar] [CrossRef]
- Steigman, G. Primordial Nucleosynthesis in the Precision Cosmology Era. Annu. Rev. Nucl. Part. Sci. 2007, 57, 463–491. [Google Scholar] [CrossRef]
- Steigman, G. Neutrinos and Big Bang Nucleosynthesis. Adv. High Energy Phys 2012, 2012, 268321. [Google Scholar] [CrossRef]
- Simha, V.; Steigman, G. Constraining the early-Universe baryon density and expansion rate. JCAP J. Cosmol. Astropart. Phys. 2008, 06, 016. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Fields, B.D.; Olive, K.A.; Yeh, T.-H.; Young, C. Big-Bang Nucleosynthesis after Planck. JCAP J. Cosmol. Astropart. Phys. 2020, 03, 010. [Google Scholar] [CrossRef]
- Fields, B.D. The Primordial Lithium Problem. Annu. Rev. Nucl. Part. Sci. 2011, 61, 47–68. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Lambiase, L. Cosmic relic abundance and f(R) gravity. Phys. Lett. B 2012, 715, 1–8. [Google Scholar] [CrossRef]
- Kang, J.U.; Panotopoulos, G. Big-bang nucleosynthesis and WIMP dark matter in modified gravity. Phys. Lett. B 2009, 677, 6–11. [Google Scholar] [CrossRef][Green Version]
- Capozziello, S.; Galluzzi, V.; Lambiase, G.; Pizza, L. Cosmological evolution of thermal relic particles in f(R) gravity. Phys. Rev. D 2015, 2015 92, 084006. [Google Scholar] [CrossRef]
- Iorio, A.; Lambiase, G. Thermal relics in cosmology with bulk viscosity. Eur. Phys. J. C 2015, 75, 115. [Google Scholar] [CrossRef]
- Bernal, N.; Ghoshal, A.; Hajkarim, F.; Lambiase, G. Primordial Gravitational Wave Signals in Modified Cosmologies. JCAP J. Cosmol. Astropart. Phys. 2020, 11, 051. [Google Scholar] [CrossRef]
- Olive, K.A.; Agashe, K.; Amsler, C.; Antonelli, M.; Arguin, J.F.; Asner, D.M.; Baer, H.; Band, H.R.; Barnett, R.M.; Basaglia, T.; et al. Review of Particle Physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jizba, P.; Lambiase, G. Constraints on Tsallis Cosmology from Big Bang Nucleosynthesis and the Relic Abundance of Cold Dark Matter Particles. Entropy 2023, 25, 1495. https://doi.org/10.3390/e25111495
Jizba P, Lambiase G. Constraints on Tsallis Cosmology from Big Bang Nucleosynthesis and the Relic Abundance of Cold Dark Matter Particles. Entropy. 2023; 25(11):1495. https://doi.org/10.3390/e25111495
Chicago/Turabian StyleJizba, Petr, and Gaetano Lambiase. 2023. "Constraints on Tsallis Cosmology from Big Bang Nucleosynthesis and the Relic Abundance of Cold Dark Matter Particles" Entropy 25, no. 11: 1495. https://doi.org/10.3390/e25111495
APA StyleJizba, P., & Lambiase, G. (2023). Constraints on Tsallis Cosmology from Big Bang Nucleosynthesis and the Relic Abundance of Cold Dark Matter Particles. Entropy, 25(11), 1495. https://doi.org/10.3390/e25111495






