Recovering Power Grids Using Strategies Based on Network Metrics and Greedy Algorithms
Abstract
:1. Introduction
- We examined recovery strategies based on various network metrics, including degree, betweenness, flow betweenness, eigenvector centrality, weighted eigenvector centrality, closeness, electrical closeness, electrical weighted closeness, zeta vector centrality, and weighted zeta vector centrality. Additionally, we compared these strategies to the random recovery, greedy, and two-step greedy strategies.
- To assess the effectiveness of recovery methods, we utilized the general recoverability framework proposed by He et al. [23], to measure power grid recoverability in the context of random link removals, where recoverability signifies a network’s ability to return to a predefined desired performance level.
- Our study did not consider cascading failures after the recovery or removal of a single transmission line. Instead, we used the direct current (DC) power flow model to maximize power flow satisfaction for loads after a link removal or addition.
2. Preliminary for Network Robustness
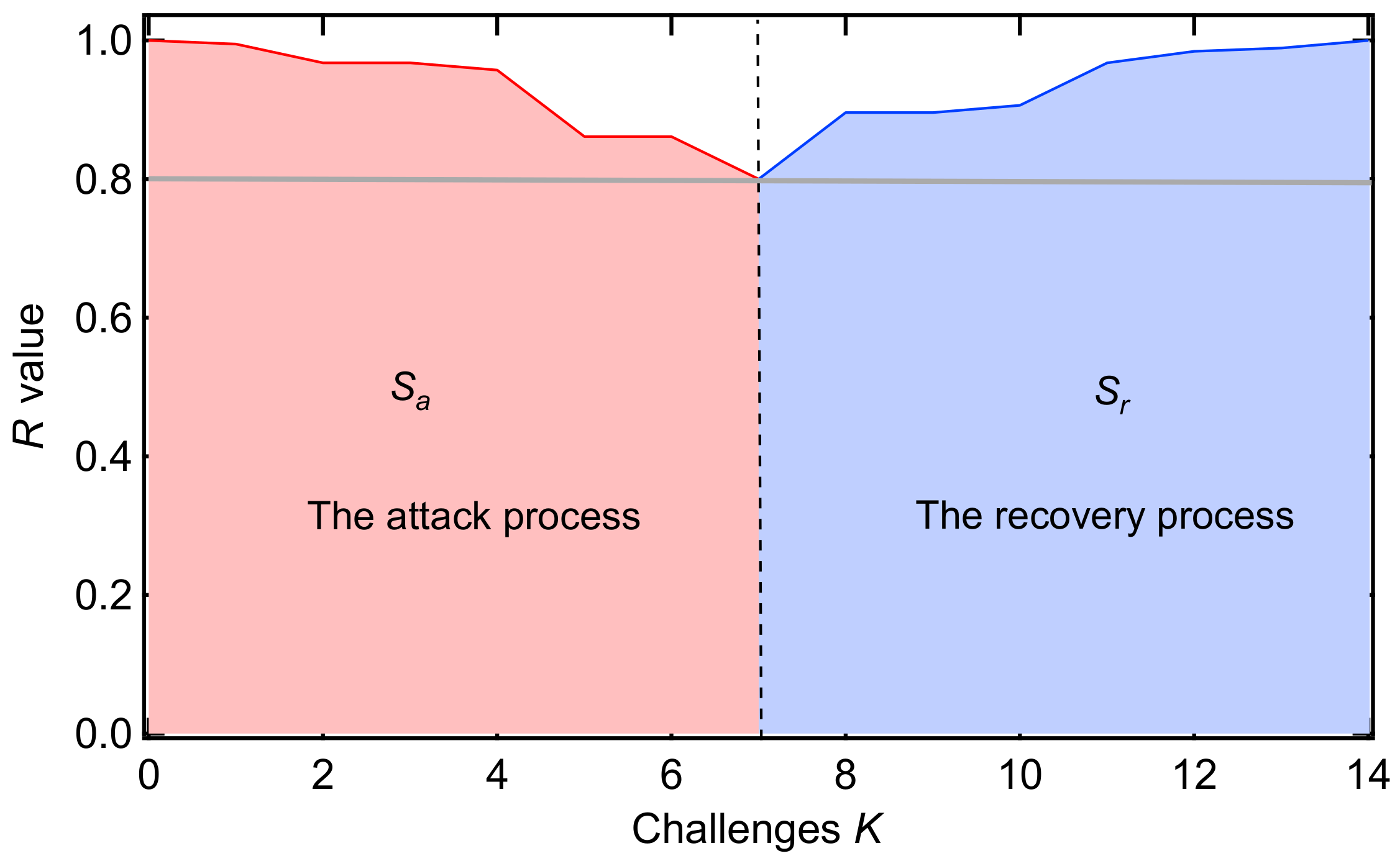
2.1. R-Value and Challenges
2.2. Recoverability Indicator of a Recovery Strategy
3. Modeling Power Grids
3.1. Network Model of Power Grids
3.2. Performance of Power Grids
3.3. Optimizing the DC Power Flow Model
4. The Attack and Recovery Process
4.1. The Attack Process
4.2. The Recovery Process
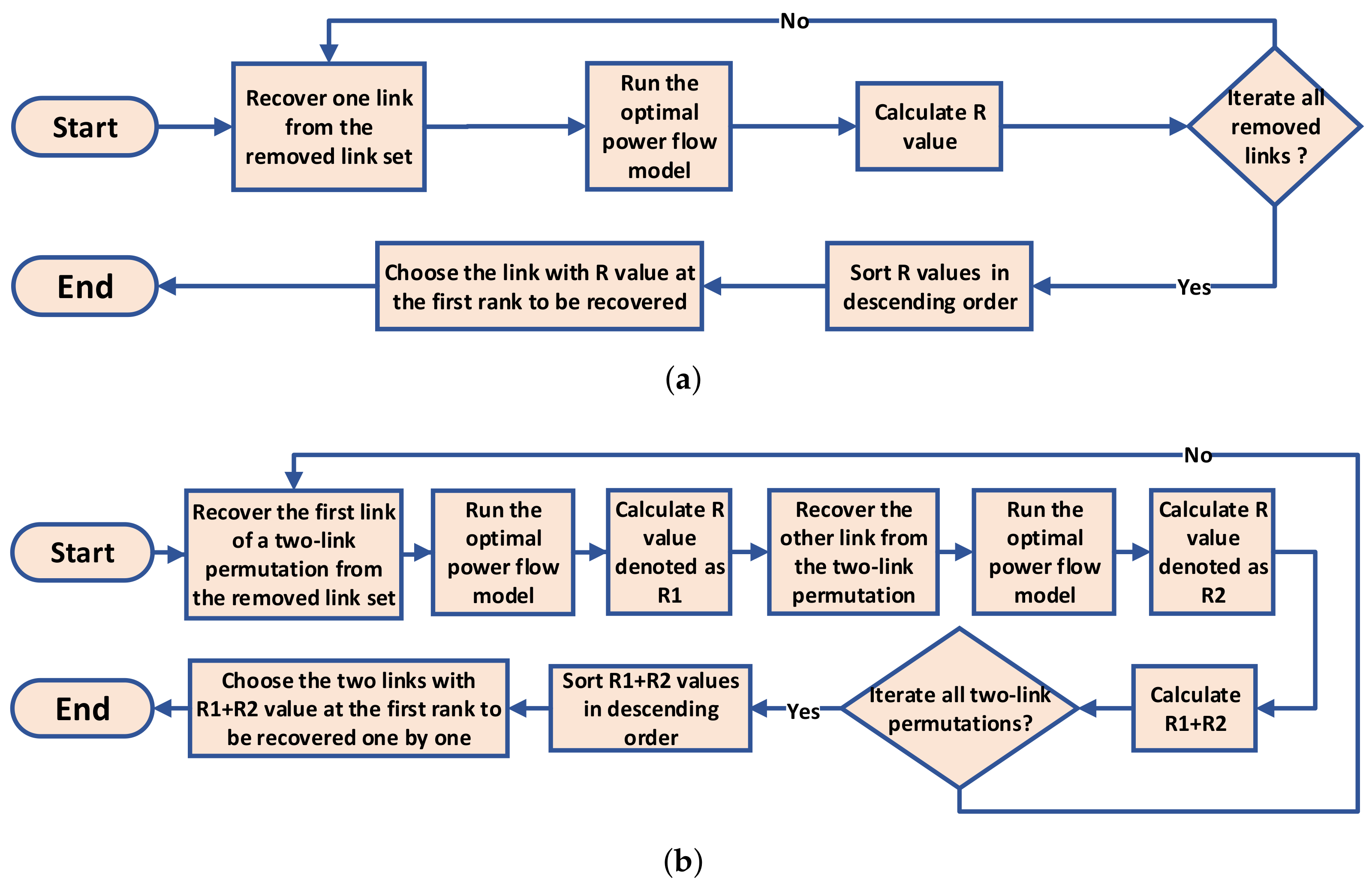
4.2.1. Random Recovery Strategy (Rand)
4.2.2. Greedy and Two-Step Greedy Recovery Strategies (Greedy and TwoGreedy)
4.2.3. Degree Recovery Strategy (Degree)
4.2.4. Betweenness and Flow Betweenness Recovery Strategies (Bet and FlowBet)
4.2.5. Eigenvector and Weighted Eigenvector Recovery Strategies (Eigen and WeiEigen)
4.2.6. Closeness, Electrical Closeness, and Electrical Weighted Closeness Recovery Strategies (Close, EleClose, and EleWeiClose)
4.2.7. Zeta Vector and Weighted Zeta Recovery Strategies (Zeta and WeiZeta)
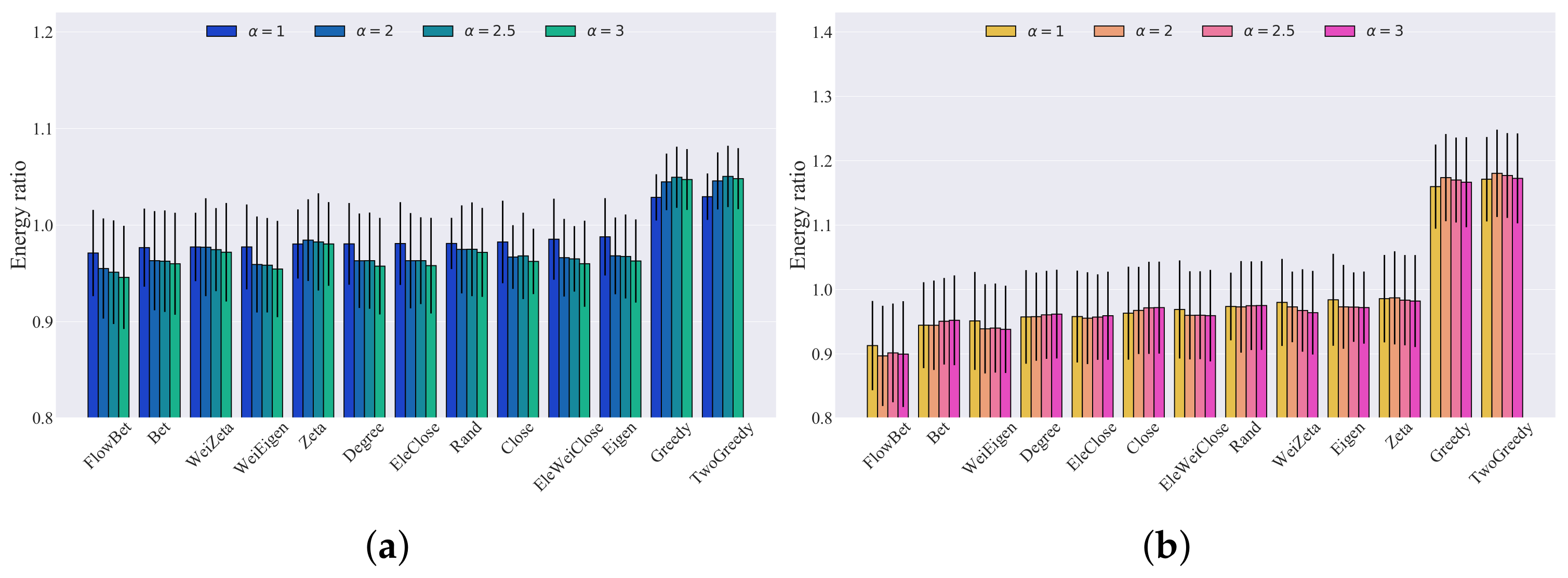
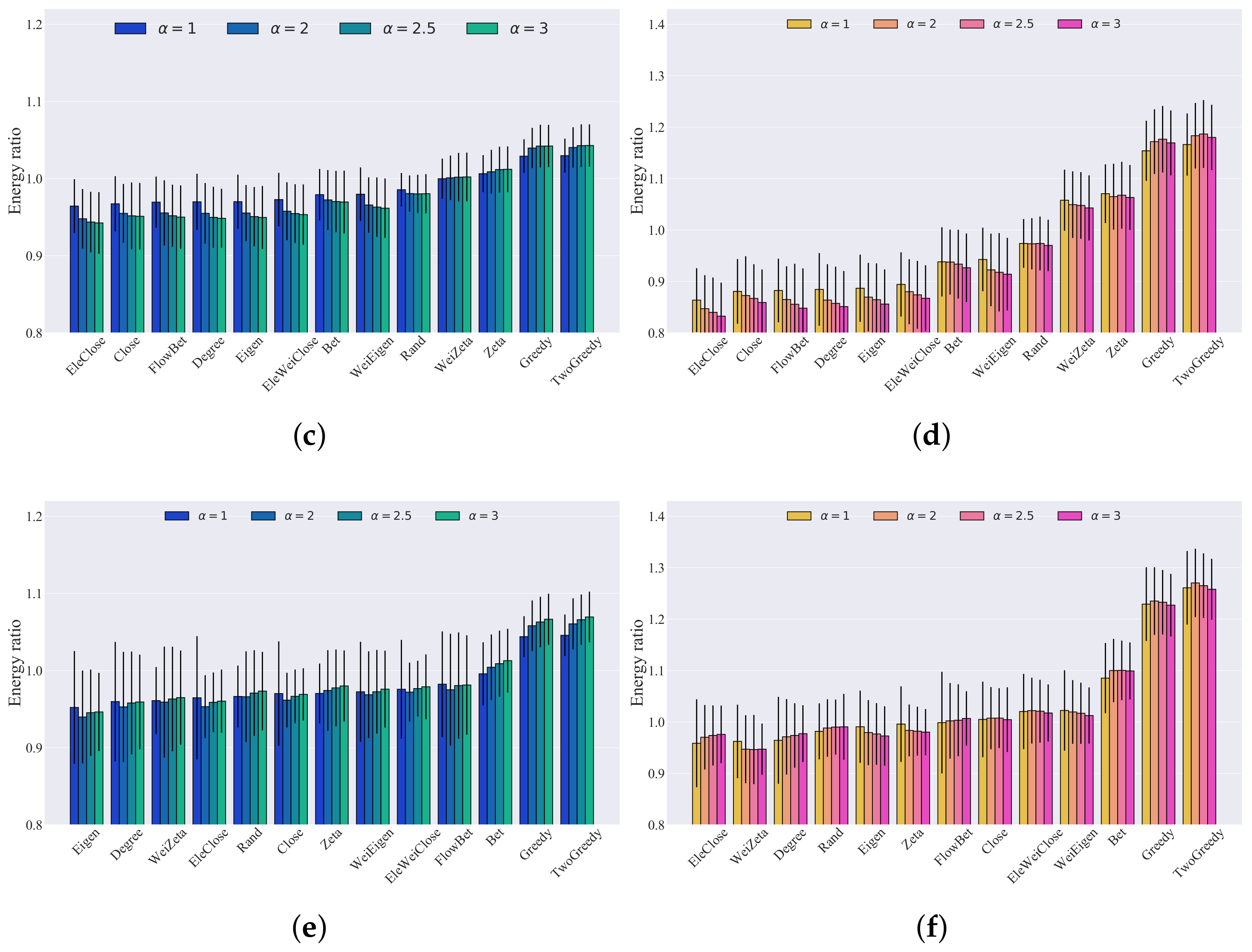
5. Results
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| the number of challenges in the attack process; | |
| the number of challenges in the recovery process; | |
| the value of R at challenge k; | |
| the attack strength; | |
| the recovery strength; | |
| the recoverability energy ratio; | |
| a graph; | |
| N | the number of nodes in a graph; |
| the set of N nodes; | |
| L | the number of links in a graph; |
| the set of L links; | |
| A | the adjacency matrix; |
| the element of the adjacency matrix; | |
| the link connecting node i and node j; | |
| the impedance of transmission line ; | |
| the weighted adjacency matrix; | |
| the element of the weighted adjacency matrix; | |
| the average degree; | |
| the amount of satisfied demand at bus i at challenge k; | |
| the amount of supply at bus i at challenge k; | |
| the injected power at node i; | |
| the weighted Laplacian matrix; | |
| the weighted degree matrix; | |
| the phase angle of bus i; | |
| the vector with elements ; | |
| the weighted incidence matrix; | |
| the element of the weighted incidence matrix; | |
| the supply vector, including the supply of each bus i at challenge k; | |
| the demand vector, including the demand of each bus i at challenge k; | |
| the active power flow vector at challenge k; | |
| the power flow of line at challenge k; | |
| the capacity vector, including the capacity of all transmission lines; | |
| the capacity of each transmission line ; | |
| the tolerance level; | |
| the degree of node i; | |
| the degree of link ; | |
| the betweenness of link ; | |
| the number of shortest paths from node s to node t; | |
| the number of shortest paths from node s to node t through link ; | |
| the flow betweenness; | |
| the magnitude of flow through the link when we inject one unit of active power to node s and extract one unit of active power from node t; | |
| the eigenvector centrality of node i; | |
| the product of the eigenvector centrality values of the end points of link ; | |
| the weighted eigenvector centrality of node i; | |
| the product of the weighted eigenvector centrality values of the end points of link ; | |
| the distance of the shortest path between node i and node j; | |
| the closeness of node i; | |
| the product of the closeness values of the end points of link ; | |
| Q | the Laplacian matrix of adjacency matrix A; |
| the pseudo-inverse Laplacian matrix of the Laplacian matrix Q; | |
| the effective resistance between node i and node j, calculated by using the pseudo-inverse matrix ; | |
| the electrical closeness of node i; | |
| the product of the electrical closeness values of the end points of link ; | |
| the pseudo-inverse matrix of the weighted Laplacian matrix ; | |
| the effective resistance between node i and node j, calculated by using the pseudo-inverse matrix ; | |
| the electrical weighted closeness of node i; | |
| the product of the electrical weighted closeness values of the end points of link ; | |
| the zeta vector; | |
| the weighted vector; | |
| the product of the zeta vector values of the end points of link ; | |
| the product of the weighted zeta vector values of the end points of link . |
Appendix A. Link Measurements Based on Whether Links Are Connected to Generators
| Metrics | Connected to Generators | Not Connected to Generators | ||
|---|---|---|---|---|
| Mean | Std | Mean | Std | |
| FlowBet | 94.770551 | 44.594022 | 114.742752 | 47.264862 |
| Degree | 10.400000 | 6.231258 | 12.269231 | 9.101902 |
| Zeta | 0.528584 | 0.296456 | 0.492346 | 0.434582 |
| Bet | 0.081226 | 0.044353 | 0.080283 | 0.063794 |
| Eigen | 0.032307 | 0.042318 | 0.050533 | 0.055398 |
| WeiZeta | 0.025984 | 0.031659 | 0.024918 | 0.050187 |
| EleWeiClose | 0.012889 | 0.004615 | 0.014670 | 0.005090 |
| WeiEigen | 0.045759 | 0.122430 | 0.009824 | 0.037966 |
| EleClose | 0.000488 | 0.000132 | 0.000535 | 0.000167 |
| Close | 0.000123 | 0.000029 | 0.000136 | 0.000038 |
| Metrics | Connected to Generators | Not Connected to Generators | ||
|---|---|---|---|---|
| Mean | Std | Mean | Std | |
| FlowBet | 96.370201 | 45.321198 | 240.779292 | 107.181289 |
| Degree | 3.272727 | 0.646670 | 8.800000 | 2.654630 |
| Zeta | 3.114607 | 1.747125 | 1.138656 | 0.685581 |
| EleWeiClose | 0.229349 | 0.068645 | 0.437775 | 0.126349 |
| Bet | 0.050301 | 0.005854 | 0.119877 | 0.072109 |
| Eigen | 0.008464 | 0.004923 | 0.037058 | 0.016150 |
| WeiEigen | 0.003469 | 0.010297 | 0.030148 | 0.074798 |
| WeiZeta | 0.001033 | 0.000709 | 0.000310 | 0.000363 |
| EleClose | 0.000070 | 0.000018 | 0.000115 | 0.000027 |
| Close | 0.000026 | 0.000005 | 0.000039 | 0.000010 |
| Metrics | Connected to Generators | Not Connected to Generators | ||
|---|---|---|---|---|
| Mean | Std | Mean | Std | |
| FlowBet | 832.375534 | 764.6106 | 778.816749 | 542.1641 |
| Degree | 19.189189 | 10.90265 | 10.761905 | 5.989612 |
| Zeta | 1.091884 | 1.30306 | 1.338246 | 0.9381184 |
| Bet | 0.046504 | 0.0607467 | 0.027309 | 0.0374265 |
| WeiZeta | 0.009382 | 0.0138922 | 0.011388 | 0.0088103 |
| WeiEigen | 0.002517 | 0.0154307 | 0.005404 | 0.0468745 |
| Eigen | 0.020586 | 0.022895 | 0.005041 | 0.008672 |
| EleWeiClose | 0.002065 | 0.0006941 | 0.001772 | 0.0005885 |
| EleClose | 0.000017 | 0.0000051 | 0.000014 | 0.0000038 |
| Close | 0.000002 | 0.0000008 | 0.000002 | 0.0000006 |
References
- Nuti, C.; Rasulo, A.; Vanzi, I. Seismic safety evaluation of electric power supply at urban level. Earthq. Eng. Struct. Dyn. 2007, 36, 245–263. [Google Scholar] [CrossRef]
- Zhou, X.; Yan, C. A blackout in Hainan Island power system: Causes and restoration procedure. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, C.; Ju, P.; Wu, F.; Pan, X.; Wang, Z. A systematic review on power system resilience from the perspective of generation, network, and load. Renew. Sustain. Energy Rev. 2022, 167, 112567. [Google Scholar] [CrossRef]
- Muir, A.; Lopatto, J. Final Report on the August 14, 2003 Blackout in the United States and Canada: Causes and Recommendations; Technical Report; U.S.-Canada Power System Outage Task Force: Ottawa, ON, Canada; Washington, DC, USA, 2004.
- LaCommare, K.H.; Eto, J.H. Understanding the Cost of Power Interruptions to US Electricity Consumers; Technical Report; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2004. [Google Scholar]
- Hines, P.; Apt, J.; Talukdar, S. Large blackouts in North America: Historical trends and policy implications. Energy Policy 2009, 37, 5249–5259. [Google Scholar] [CrossRef]
- Van Mieghem, P.; Doerr, C.; Wang, H.; Hernandez, J.M.; Hutchison, D.; Karaliopoulos, M.; Kooij, R. A Framework for Computing Topological Network Robustness; Report20101218; Delft University of Technology: Delft, The Netherlands, 2010. [Google Scholar]
- Cetinay, H.; Devriendt, K.; Van Mieghem, P. Nodal vulnerability to targeted attacks in power grids. Appl. Netw. Sci. 2018, 3, 34. [Google Scholar] [CrossRef]
- Schäfer, B.; Witthaut, D.; Timme, M.; Latora, V. Dynamically induced cascading failures in power grids. Nat. Commun. 2018, 9, 1975. [Google Scholar] [CrossRef]
- Pagani, G.A.; Aiello, M. The power grid as a complex network: A survey. Phys. A Stat. Mech. Its Appl. 2013, 392, 2688–2700. [Google Scholar] [CrossRef]
- Rocchetta, R. Enhancing the resilience of critical infrastructures: Statistical analysis of power grid spectral clustering and post-contingency vulnerability metrics. Renew. Sustain. Energy Rev. 2022, 159, 112185. [Google Scholar] [CrossRef]
- Kyriacou, A.; Demetriou, P.; Panayiotou, C.; Kyriakides, E. Controlled Islanding Solution for Large-Scale Power Systems. IEEE Trans. Power Syst. 2018, 33, 1591–1602. [Google Scholar] [CrossRef]
- Younesi, A.; Shayeghi, H.; Wang, Z.; Siano, P.; Mehrizi-Sani, A.; Safari, A. Trends in modern power systems resilience: State-of-the-art review. Renew. Sustain. Energy Rev. 2022, 162, 112397. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, R.; Terzija, V. Power system restoration: A literature review from 2006 to 2016. J. Mod. Power Syst. Clean Energy 2016, 4, 332–341. [Google Scholar] [CrossRef]
- Sun, W.; Liu, C.C.; Zhang, L. Optimal generator start-up strategy for bulk power system restoration. IEEE Trans. Power Syst. 2010, 26, 1357–1366. [Google Scholar] [CrossRef]
- Sarmadi, S.A.N.; Dobakhshari, A.S.; Azizi, S.; Ranjbar, A.M. A sectionalizing method in power system restoration based on WAMS. IEEE Trans. Smart Grid 2011, 2, 190–197. [Google Scholar] [CrossRef]
- Wu, J.; Fang, B.; Fang, J.; Chen, X.; Chi, K.T. Sequential topology recovery of complex power systems based on reinforcement learning. Phys. A Stat. Mech. Its Appl. 2019, 535, 122487. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Chen, Z.; Huang, Y.; Zheng, Z. Sequential Node/Link Recovery Strategy of Power Grids Based on Q-Learning Approach. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, X.; Guo, J.; Shan, X.; Wang, Z.; Li, Z.; Tse, C.K. Integrating Reinforcement Learning and Optimal Power Dispatch to Enhance Power Grid Resilience. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1402–1406. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Z.; Zhang, Y.; Xia, Y.; Chen, X. Sequential Recovery of Complex Networks Suffering from Cascading Failure Blackouts. IEEE Trans. Netw. Sci. Eng. 2020, 7, 2997–3007. [Google Scholar] [CrossRef]
- Igder, M.A.; Liang, X. Service Restoration Using Deep Reinforcement Learning and Dynamic Microgrid Formation in Distribution Networks. IEEE Trans. Ind. Appl. 2023, 59, 5453–5472. [Google Scholar] [CrossRef]
- Yeh, W.C.; He, M.F.; Huang, C.L.; Tan, S.Y.; Zhang, X.; Huang, Y.; Li, L. New genetic algorithm for economic dispatch of stand-alone three-modular microgrid in DongAo Island. Appl. Energy 2020, 263, 114508. [Google Scholar] [CrossRef]
- He, Z.; Sun, P.; Van Mieghem, P. Topological Approach to Measure Network Recoverability. In Proceedings of the 2019 11th International Workshop on Resilient Networks Design and Modeling (RNDM), Nicosia, Cyprus, 14–16 October 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Trajanovski, S.; Martín-Hernández, J.; Winterbach, W.; Van Mieghem, P. Robustness envelopes of networks. J. Complex Netw. 2013, 1, 44–62. [Google Scholar] [CrossRef]
- Sun, P.; He, Z.; Kooij, R.E.; Van Mieghem, P. Topological approach to measure the recoverability of optical networks. Opt. Switch. Netw. 2021, 41, 100617. [Google Scholar] [CrossRef]
- Van Mieghem, P.; Devriendt, K.; Cetinay, H. Pseudoinverse of the Laplacian and best spreader node in a network. Phys. Rev. E 2017, 96, 032311. [Google Scholar] [CrossRef]
- Koç, Y.; Verma, T.; Araujo, N.A.M.; Warnier, M. MATCASC: A tool to analyse cascading line outages in power grids. In Proceedings of the 2013 IEEE International Workshop on Inteligent Energy Systems (IWIES), Vienna, Austria, 14 November 2013; pp. 143–148. [Google Scholar] [CrossRef]
- Cetinay, H.; Soltan, S.; Kuipers, F.A.; Zussman, G.; Van Mieghem, P. Comparing the effects of failures in power grids under the AC and DC power flow models. IEEE Trans. Netw. Sci. Eng. 2017, 5, 301–312. [Google Scholar] [CrossRef]
- Motter, A.E.; Lai, Y.C. Cascade-based attacks on complex networks. Phys. Rev. E 2002, 66, 065102. [Google Scholar] [CrossRef] [PubMed]
- Van Mieghem, P.; Stevanović, D.; Kuipers, F.; Li, C.; van de Bovenkamp, R.; Liu, D.; Wang, H. Decreasing the spectral radius of a graph by link removals. Phys. Rev. E 2011, 84, 016101. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E. A measure of betweenness centrality based on random walks. Soc. Netw. 2005, 27, 39–54. [Google Scholar] [CrossRef]
- Newman, M.E. The mathematics of networks. In The New Palgrave Dictionary of Economics; Palgrave Macmillan: London, UK, 2008; Volume 2, pp. 1–12. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Cetinay, H.; Kuipers, F.A.; Van Mieghem, P. A topological investigation of power flow. IEEE Syst. J. 2016, 12, 2524–2532. [Google Scholar] [CrossRef]
- Ellens, W.; Spieksma, F.; Van Mieghem, P.; Jamakovic, A.; Kooij, R. Effective graph resistance. Linear Algebra Its Appl. 2011, 435, 2491–2506. [Google Scholar] [CrossRef]



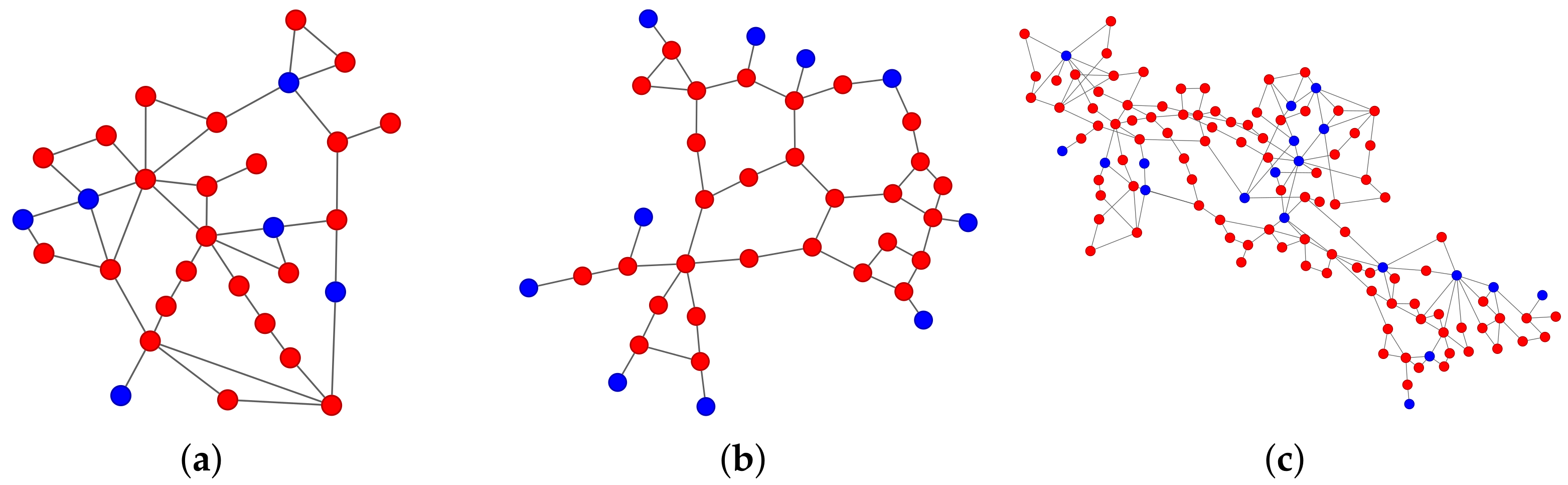
| Name | N | L | |
|---|---|---|---|
| IEEE 30 | 30 | 41 | 2.73 |
| IEEE 39 | 39 | 46 | 2.36 |
| IEEE 118 | 118 | 179 | 3.03 |
| Abbreviation | Full Name |
|---|---|
| TwoGreedy | Two-step greedy recovery strategy |
| Greedy | Greedy recovery strategy |
| Bet | Betweenness recovery strategy |
| FlowBet | Flow betweenness recovery strategy |
| EleWeiClose | Electrical weighted closeness recovery strategy |
| WeiEigen | Weighted eigenvector recovery strategy |
| Close | Closeness recovery strategy |
| EleClose | Electrical closeness recovery strategy |
| Rand | Random recovery strategy |
| Degree | Degree recovery strategy |
| Zeta | Zeta vector recovery strategy |
| WeiZeta | Weighted zeta vector recovery strategy |
| Degree | Degree recovery strategy |
| Eigen | Eigenvector recovery strategy |
| Rank | Threshold = 0.8 | Threshold = 0.5 | ||||
|---|---|---|---|---|---|---|
| Strategy | Mean | Std | Strategy | Mean | Std | |
| 1 | TwoGreedy | 1.0292 | 0.0241 | TwoGreedy | 1.1710 | 0.0656 |
| 2 | Greedy | 1.0285 | 0.0240 | Greedy | 1.1595 | 0.0654 |
| 3 | Eigen | 0.9877 | 0.0400 | Zeta | 0.9854 | 0.0679 |
| 4 | EleWeiClose | 0.9852 | 0.0420 | Eigen | 0.9837 | 0.0714 |
| 5 | Close | 0.9823 | 0.0427 | WeiZeta | 0.9796 | 0.0676 |
| 6 | Rand | 0.9808 | 0.0265 | Rand | 0.9733 | 0.0526 |
| 7 | EleClose | 0.9807 | 0.0429 | EleWeiClose | 0.9687 | 0.0762 |
| 8 | Degree | 0.9804 | 0.0423 | Close | 0.9629 | 0.0722 |
| 9 | Zeta | 0.9803 | 0.0358 | EleClose | 0.9576 | 0.0713 |
| 10 | WeiEigen | 0.9772 | 0.0440 | Degree | 0.9571 | 0.0727 |
| 11 | WeiZeta | 0.9772 | 0.0354 | WeiEigen | 0.9509 | 0.0761 |
| 12 | Bet | 0.9765 | 0.0404 | Bet | 0.9442 | 0.0667 |
| 13 | FlowBet | 0.9709 | 0.0447 | FlowBet | 0.9126 | 0.0693 |
| Rank | Threshold = 0.8 | Threshold = 0.5 | ||||
|---|---|---|---|---|---|---|
| Strategy | Mean | Std | Strategy | Mean | Std | |
| 1 | TwoGreedy | 1.0299 | 0.0221 | TwoGreedy | 1.1665 | 0.0605 |
| 2 | Greedy | 1.0292 | 0.0219 | Greedy | 1.1543 | 0.0585 |
| 3 | Zeta | 1.0065 | 0.0240 | Zeta | 1.0709 | 0.0571 |
| 4 | WeiZeta | 1.0000 | 0.0260 | WeiZeta | 1.0582 | 0.0594 |
| 5 | Rand | 0.9858 | 0.0217 | Rand | 0.9741 | 0.0474 |
| 6 | WeiEigen | 0.9800 | 0.0347 | WeiEigen | 0.9430 | 0.0618 |
| 7 | Bet | 0.9794 | 0.0333 | Bet | 0.9384 | 0.0673 |
| 8 | EleWeiClose | 0.9730 | 0.0347 | EleWeiClose | 0.8945 | 0.0625 |
| 9 | Eigen | 0.9703 | 0.0351 | Eigen | 0.8871 | 0.0653 |
| 10 | Degree | 0.9701 | 0.0363 | Degree | 0.8848 | 0.0706 |
| 11 | FlowBet | 0.9697 | 0.0331 | FlowBet | 0.8827 | 0.0618 |
| 12 | Close | 0.9675 | 0.0358 | Close | 0.8809 | 0.0629 |
| 13 | EleClose | 0.9646 | 0.0348 | EleClose | 0.8639 | 0.0621 |
| Rank | Threshold = 0.8 | Threshold = 0.5 | ||||
|---|---|---|---|---|---|---|
| Strategy | Mean | Std | Strategy | Mean | Std | |
| 1 | TwoGreedy | 1.0458 | 0.0270 | TwoGreedy | 1.2611 | 0.0715 |
| 2 | Greedy | 1.0441 | 0.0266 | Greedy | 1.2294 | 0.0717 |
| 3 | Bet | 0.9959 | 0.0409 | Bet | 1.0855 | 0.0683 |
| 4 | FlowBet | 0.9824 | 0.0685 | WeiEigen | 1.0225 | 0.0782 |
| 5 | EleWeiClose | 0.9759 | 0.0639 | EleWeiClose | 1.0206 | 0.0732 |
| 6 | WeiEigen | 0.9726 | 0.0648 | Close | 1.0051 | 0.0734 |
| 7 | Zeta | 0.9705 | 0.0388 | FlowBet | 0.9989 | 0.0988 |
| 8 | Close | 0.9703 | 0.0677 | Zeta | 0.9961 | 0.0735 |
| 9 | Rand | 0.9666 | 0.0400 | Eigen | 0.9909 | 0.0701 |
| 10 | EleClose | 0.9649 | 0.0799 | Rand | 0.9819 | 0.0545 |
| 11 | WeiZeta | 0.9611 | 0.0435 | Degree | 0.9646 | 0.0846 |
| 12 | Degree | 0.9599 | 0.0774 | WeiZeta | 0.9624 | 0.0715 |
| 13 | Eigen | 0.9523 | 0.0731 | EleClose | 0.9589 | 0.0855 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Cetinay, H.; He, Z.; Liu, L.; Van Mieghem, P.; Kooij, R.E. Recovering Power Grids Using Strategies Based on Network Metrics and Greedy Algorithms. Entropy 2023, 25, 1455. https://doi.org/10.3390/e25101455
Wang F, Cetinay H, He Z, Liu L, Van Mieghem P, Kooij RE. Recovering Power Grids Using Strategies Based on Network Metrics and Greedy Algorithms. Entropy. 2023; 25(10):1455. https://doi.org/10.3390/e25101455
Chicago/Turabian StyleWang, Fenghua, Hale Cetinay, Zhidong He, Le Liu, Piet Van Mieghem, and Robert E. Kooij. 2023. "Recovering Power Grids Using Strategies Based on Network Metrics and Greedy Algorithms" Entropy 25, no. 10: 1455. https://doi.org/10.3390/e25101455
APA StyleWang, F., Cetinay, H., He, Z., Liu, L., Van Mieghem, P., & Kooij, R. E. (2023). Recovering Power Grids Using Strategies Based on Network Metrics and Greedy Algorithms. Entropy, 25(10), 1455. https://doi.org/10.3390/e25101455






