Entanglement Dynamics and Classical Complexity
Abstract
1. Introduction
2. Analytical Results
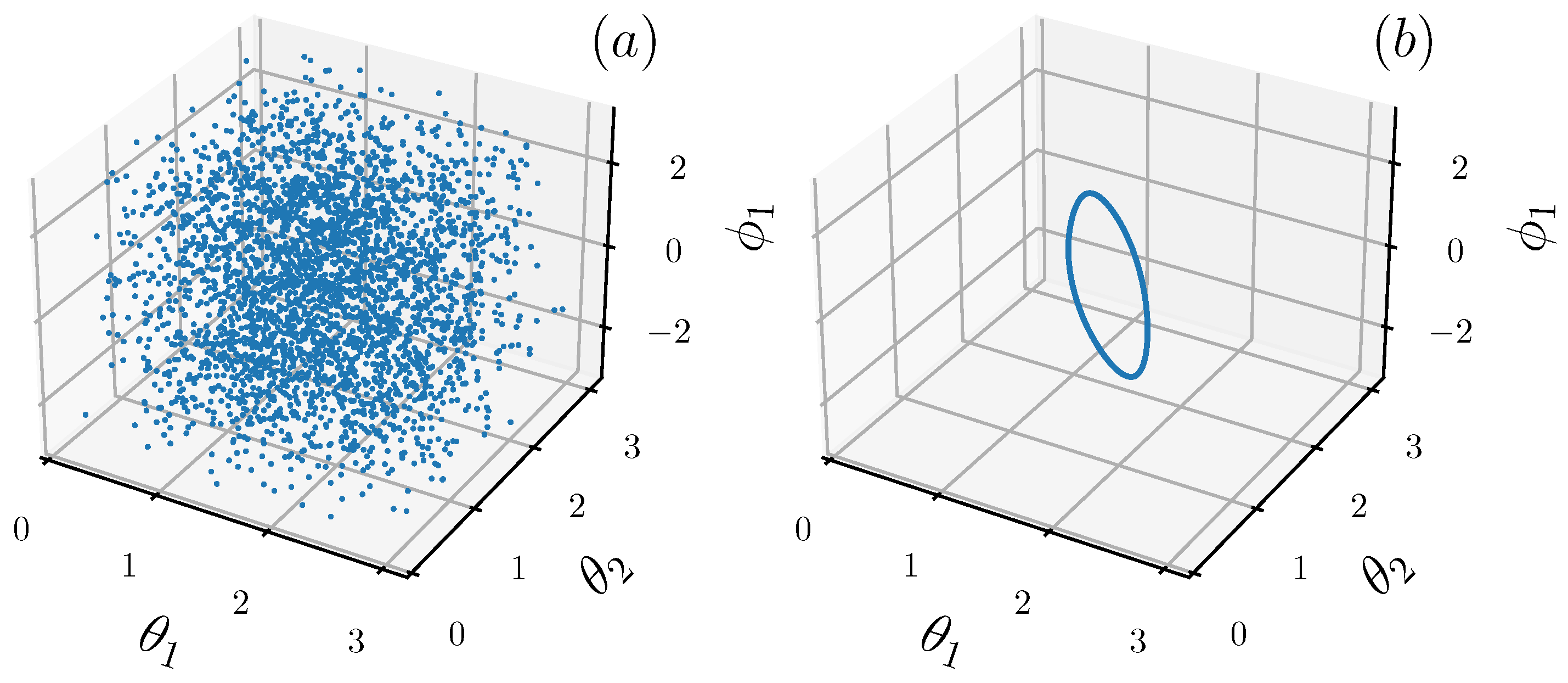
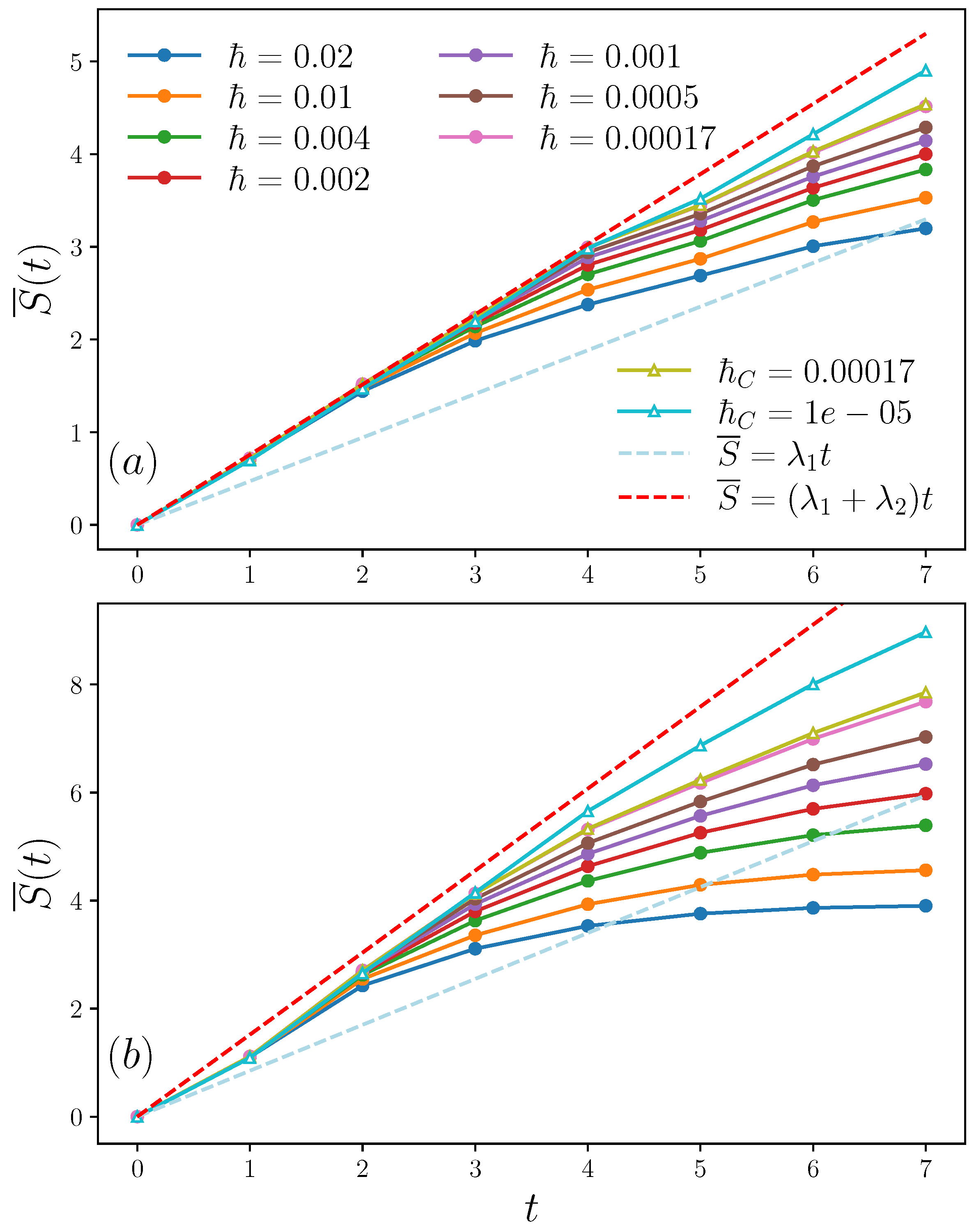
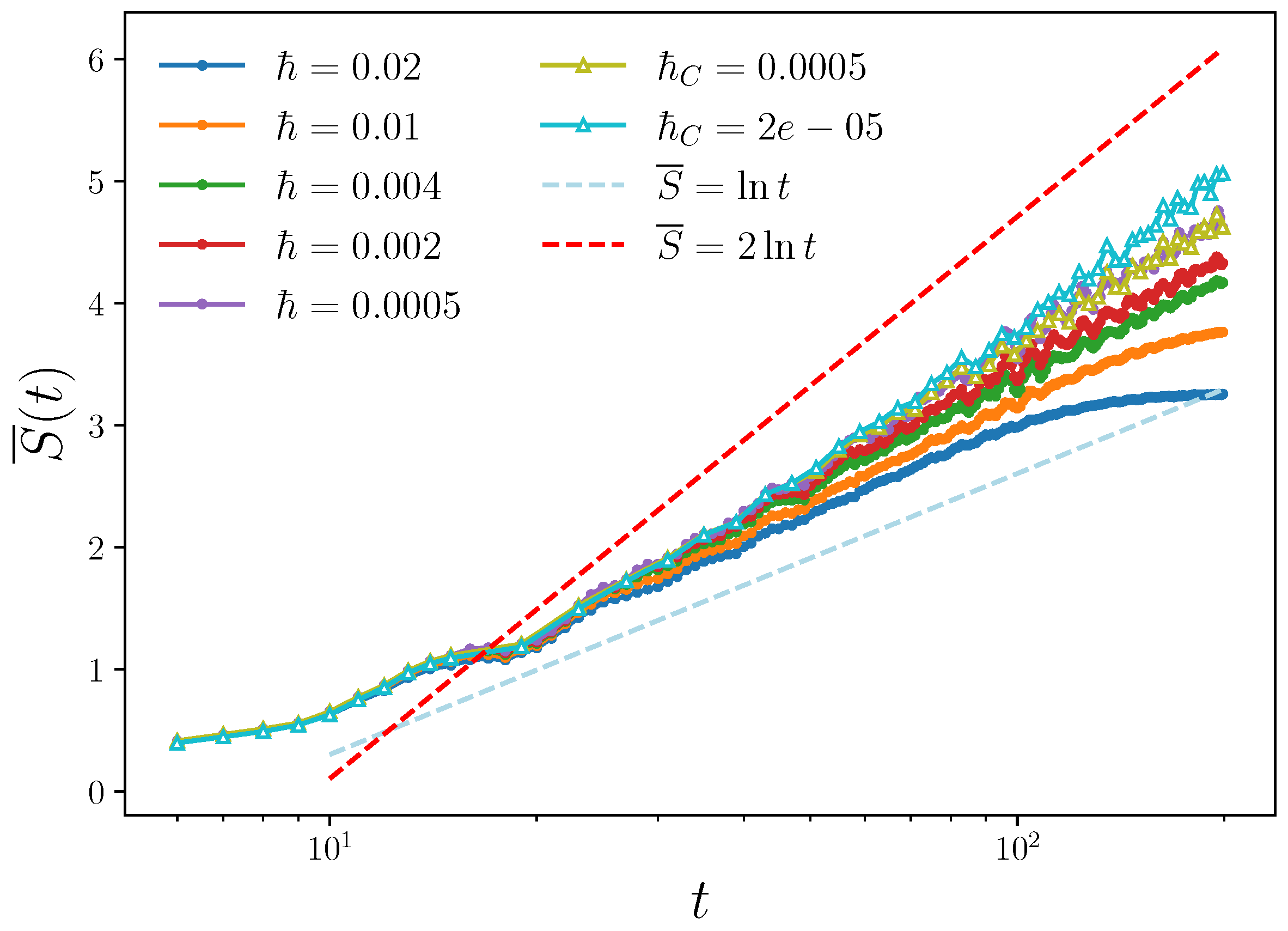
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Equation (24)
References
- Dowling, J.P.; Milburn, G.J. Quantum technology: The second quantum revolution. Phil. Trans. R. Soc. A 2003, 361, 1655–1674. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Sciarrino, F.; Laing, A.; Thompson, M.G. Integrated photonic quantum technologies. Nat. Photonics 2020, 14, 273–284. [Google Scholar] [CrossRef]
- Benenti, G.; Casati, G.; Rossini, D.; Strini, G. Principles of Quantum Computation and Information (A Comprehensive Textbook); World Scientific Singapore: Singapore, 2019. [Google Scholar]
- Cornfeld, I.P.; Fomin, S.V.; Sinai, Y.G. Ergodic Theory; Springer: New York, NY, USA, 1982. [Google Scholar] [CrossRef]
- Gu, Y. Evidences of classical and quantum chaos in the time evolution of nonequilibrium ensembles. Phys. Lett. 1990, 149, 95–100. [Google Scholar] [CrossRef]
- Ford, J.; Mantica, G.; Ristow, G.H. The Arnol’d cat: Failure of the correspondence principle. Phys. Nonlinear Phenom. 1991, 50, 493–520. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, J. Time evolution of coarse-grained entropy in classical and quantum motions of strongly chaotic systems. Phys. Lett. 1997, 229, 208–216. [Google Scholar] [CrossRef]
- Pattanayak, A.K.; Brumer, P. Chaos and Lyapunov exponents in classical and quantal distribution dynamics. Phys. Rev. E 1997, 56, 5174–5177. [Google Scholar] [CrossRef]
- Sokolov, V.V.; Zhirov, O.V.; Benenti, G.; Casati, G. Complexity of quantum states and reversibility of quantum motion. Phys. Rev. E 2008, 78, 046212. [Google Scholar] [CrossRef]
- Benenti, G.; Casati, G. How complex is quantum motion? Phys. Rev. E 2009, 79, 025201. [Google Scholar] [CrossRef]
- Balachandran, V.; Benenti, G.; Casati, G.; Gong, J. Phase-space characterization of complexity in quantum many-body dynamics. Phys. Rev. E 2010, 82, 046216. [Google Scholar] [CrossRef]
- Prosen, T. Complexity and nonseparability of classical Liouvillian dynamics. Phys. Rev. E 2011, 83, 031124. [Google Scholar] [CrossRef]
- Benenti, G.; Carlo, G.G.; Prosen, T. Wigner separability entropy and complexity of quantum dynamics. Phys. Rev. E 2012, 85, 051129. [Google Scholar] [CrossRef] [PubMed]
- Qin, P.; Wang, W.G.; Benenti, G.; Casati, G. Complexity and instability of quantum motion near a quantum phase transition. Phys. Rev. E 2014, 89, 032120. [Google Scholar] [CrossRef] [PubMed]
- Rozenbaum, E.B.; Ganeshan, S.; Galitski, V. Lyapunov Exponent and Out-of-Time-Ordered Correlator’s Growth Rate in a Chaotic System. Phys. Rev. Lett. 2017, 118, 086801. [Google Scholar] [CrossRef]
- Rammensee, J.; Urbina, J.D.; Richter, K. Many-Body Quantum Interference and the Saturation of Out-of-Time-Order Correlators. Phys. Rev. Lett. 2018, 121, 124101. [Google Scholar] [CrossRef] [PubMed]
- García-Mata, I.; Saraceno, M.; Jalabert, R.A.; Roncaglia, A.J.; Wisniacki, D.A. Chaos Signatures in the Short and Long Time Behavior of the Out-of-Time Ordered Correlator. Phys. Rev. Lett. 2018, 121, 210601. [Google Scholar] [CrossRef]
- Bergamasco, P.D.; Carlo, G.G.; Rivas, A.M.F. Out-of-time ordered correlators, complexity, and entropy in bipartite systems. Phys. Rev. Res. 2019, 1, 033044. [Google Scholar] [CrossRef]
- Prakash, R.; Lakshminarayan, A. Scrambling in strongly chaotic weakly coupled bipartite systems: Universality beyond the Ehrenfest timescale. Phys. Rev. B 2020, 101, 121108. [Google Scholar] [CrossRef]
- Wang, J.; Benenti, G.; Casati, G.; Wang, W.G. Complexity of quantum motion and quantum-classical correspondence: A phase-space approach. Phys. Rev. Res. 2020, 2, 043178. [Google Scholar] [CrossRef]
- Bennett, C.H.; Bernstein, H.J.; Popescu, S.; Schumacher, B. Concentrating partial entanglement by local operations. Phys. Rev. A 1996, 53, 2046–2052. [Google Scholar] [CrossRef]
- Lerose, A.; Pappalardi, S. Bridging entanglement dynamics and chaos in semiclassical systems. Phys. Rev. A 2020, 102, 032404. [Google Scholar] [CrossRef]
- Bianchi, E.; Hackl, L.; Yokomizo, N. Linear growth of the entanglement entropy and the Kolmogorov-Sinai rate. J. High Energy Phys. 2018, 2018, 25. [Google Scholar] [CrossRef]
- Miller, P.A.; Sarkar, S. Signatures of chaos in the entanglement of two coupled quantum kicked tops. Phys. Rev. E 1999, 60, 1542–1550. [Google Scholar] [CrossRef] [PubMed]
- Fujisaki, H.; Miyadera, T.; Tanaka, A. Dynamical aspects of quantum entanglement for weakly coupled kicked tops. Phys. Rev. E 2003, 67, 066201. [Google Scholar] [CrossRef] [PubMed]
- Jacquod, P. Semiclassical Time Evolution of the Reduced Density Matrix and Dynamically Assisted Generation of Entanglement for Bipartite Quantum Systems. Phys. Rev. Lett. 2004, 92, 150403. [Google Scholar] [CrossRef]
- Petitjean, C.; Jacquod, P. Lyapunov Generation of Entanglement and the Correspondence Principle. Phys. Rev. Lett. 2006, 97, 194103. [Google Scholar] [CrossRef] [PubMed]
- Husimi, K. Some formal properties of the density matrix. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264. [Google Scholar]
- Emerson, J.; Ballentine, L. Characteristics of quantum-classical correspondence for two interacting spins. Phys. Rev. A 2001, 63, 052103. [Google Scholar] [CrossRef]
- Haake, F.; Gnutzmann, S.; Kuś, M. Quantum Signatures of Chaos; Springer: Heidelberg, Germany, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Dietz, B.; Rosa, D.; Benenti, G. Entanglement Dynamics and Classical Complexity. Entropy 2023, 25, 97. https://doi.org/10.3390/e25010097
Wang J, Dietz B, Rosa D, Benenti G. Entanglement Dynamics and Classical Complexity. Entropy. 2023; 25(1):97. https://doi.org/10.3390/e25010097
Chicago/Turabian StyleWang, Jiaozi, Barbara Dietz, Dario Rosa, and Giuliano Benenti. 2023. "Entanglement Dynamics and Classical Complexity" Entropy 25, no. 1: 97. https://doi.org/10.3390/e25010097
APA StyleWang, J., Dietz, B., Rosa, D., & Benenti, G. (2023). Entanglement Dynamics and Classical Complexity. Entropy, 25(1), 97. https://doi.org/10.3390/e25010097








