A Networked Method for Multi-Evidence-Based Information Fusion
Abstract
1. Introduction
2. Preliminaries
2.1. Dempster–Shafer Evidence Theory
2.2. Graph Theory
2.3. The Distance Measure between Basic Belief Assignments
3. Evidence Interaction
4. The Proposed Method
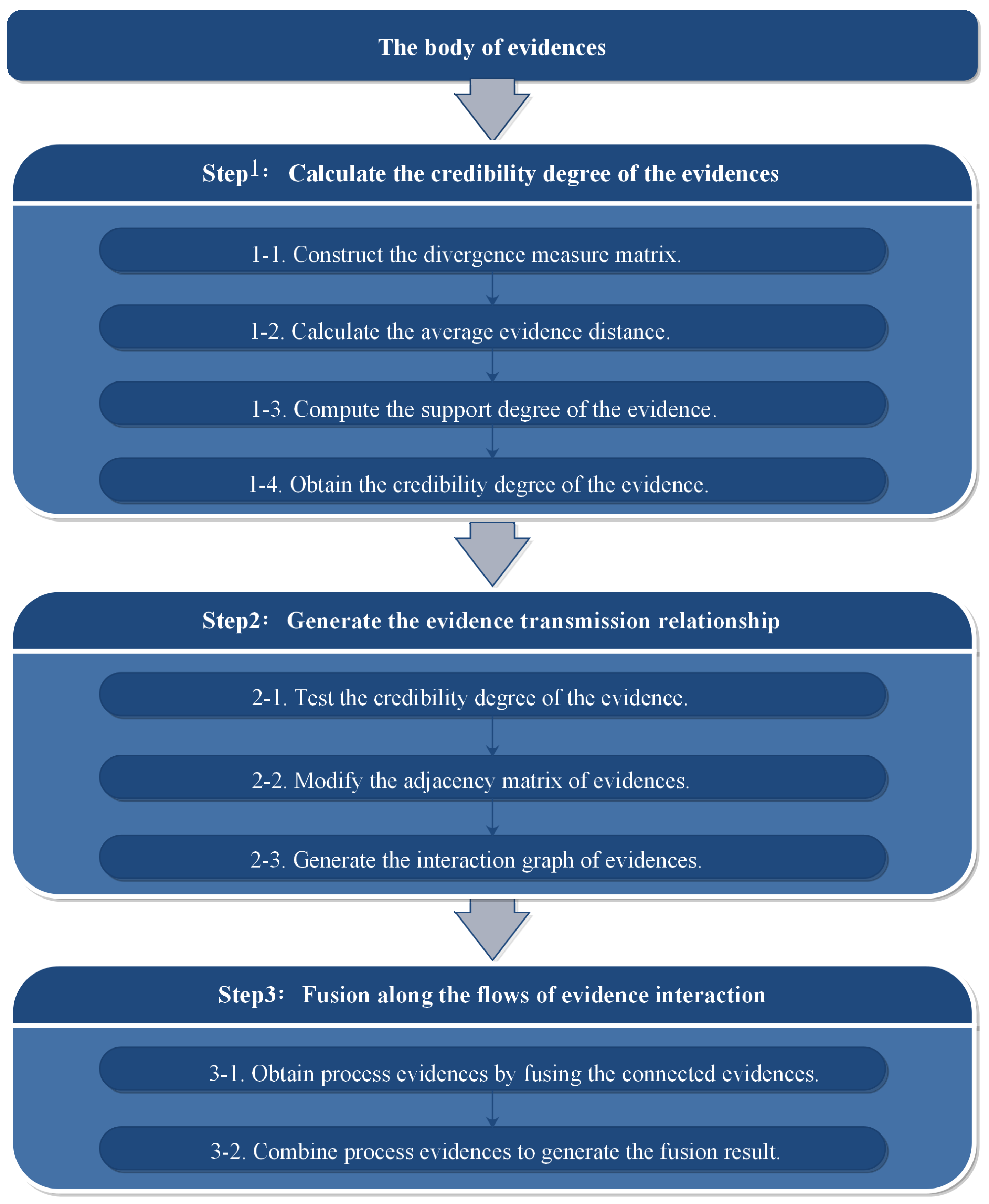
4.1. Calculate the Credibility Degree of the Evidence
- Step 1-1: By mean of Jousselme’s distance, the divergence measure matrix DMM can be constructed as (10).
- Step 1-2: For , the average distance from other evidence can be calculated by
- Step 1-3: The support degree of is defined as
- Step 1-4: The credibility degree of is calculated by
4.2. Generate the Evidence Transmission Relationship
4.3. Fusion along the Flows of Evidence Interaction
- Step 3-1: For each evidence in connected part of the interaction graph , fuse evidence and evidence connected to directly via the Dempster’s combination rule (6); the fusion result is represented as process evidence .
- Step 3-2: All process evidence obtained in the previous step are fused via Dempster’s combination rule (6). Hence, the final combination result is obtained.
5. Example Illustration
5.1. Case 1
- Problem statement
- The fusion approach
- Step 1-1: Construct the divergence measure matrix as follows:
- Step 1-2: Obtain the average evidence distance of as:
- Step 1-3: Calculate the support degree of as:
- Step 1-4: Compute the credibility degree of as:
- Step 2-1: Calculate the test value of the credibility degree of as:
- Step 2-2: Modify the adjacency matrix A to :
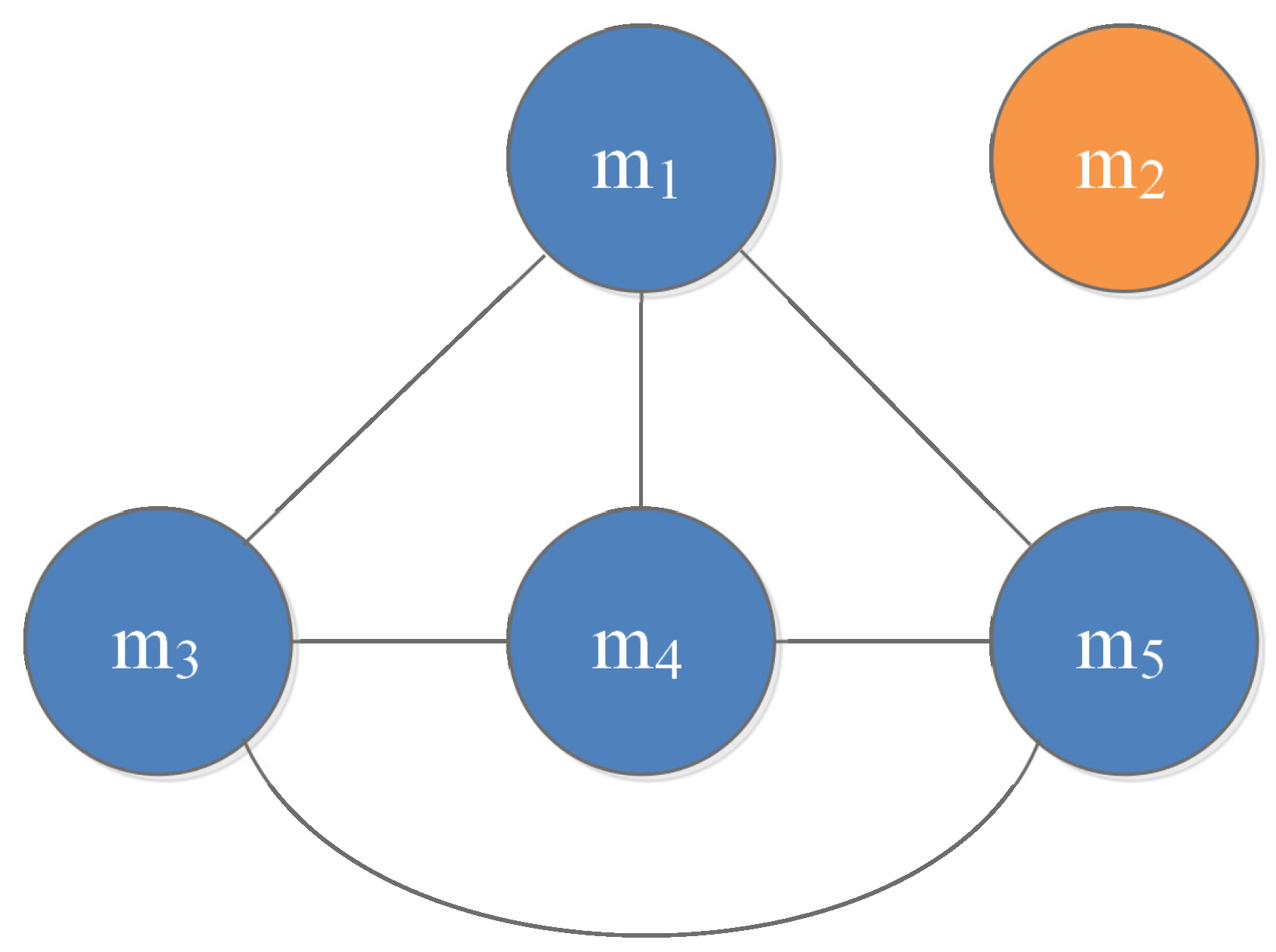
- Step 2-3: Generate the interaction graph between evidence as Figure 2.
- Step 3-1: Fuse the connected evidence via the Dempster’s rule of combination; the process evidence is computed. Since the connection graph is modified by a full connected graph, the process evidence generated by the proposed method is also the same. The process evidence is shown as follows:
- Step 3-2: Fuse the process evidence via Dempster’s combination rule; the fusion results are shown in Table 2.
- Discussion
5.2. Case2
- The decision-making application
- The fusion approach
- Step 1-1: Construct the divergence measure matrix as follows:
- Step 1-2: Obtain the average evidence distance of as:
- Step 1-3: Calculate the support degree of as:
- Step 1-4: Compute the credibility degree of as:
- Step 2-1: Calculate the test value of the credibility degree of as:
- Step 2-2: Modify the adjacency matrix A to :
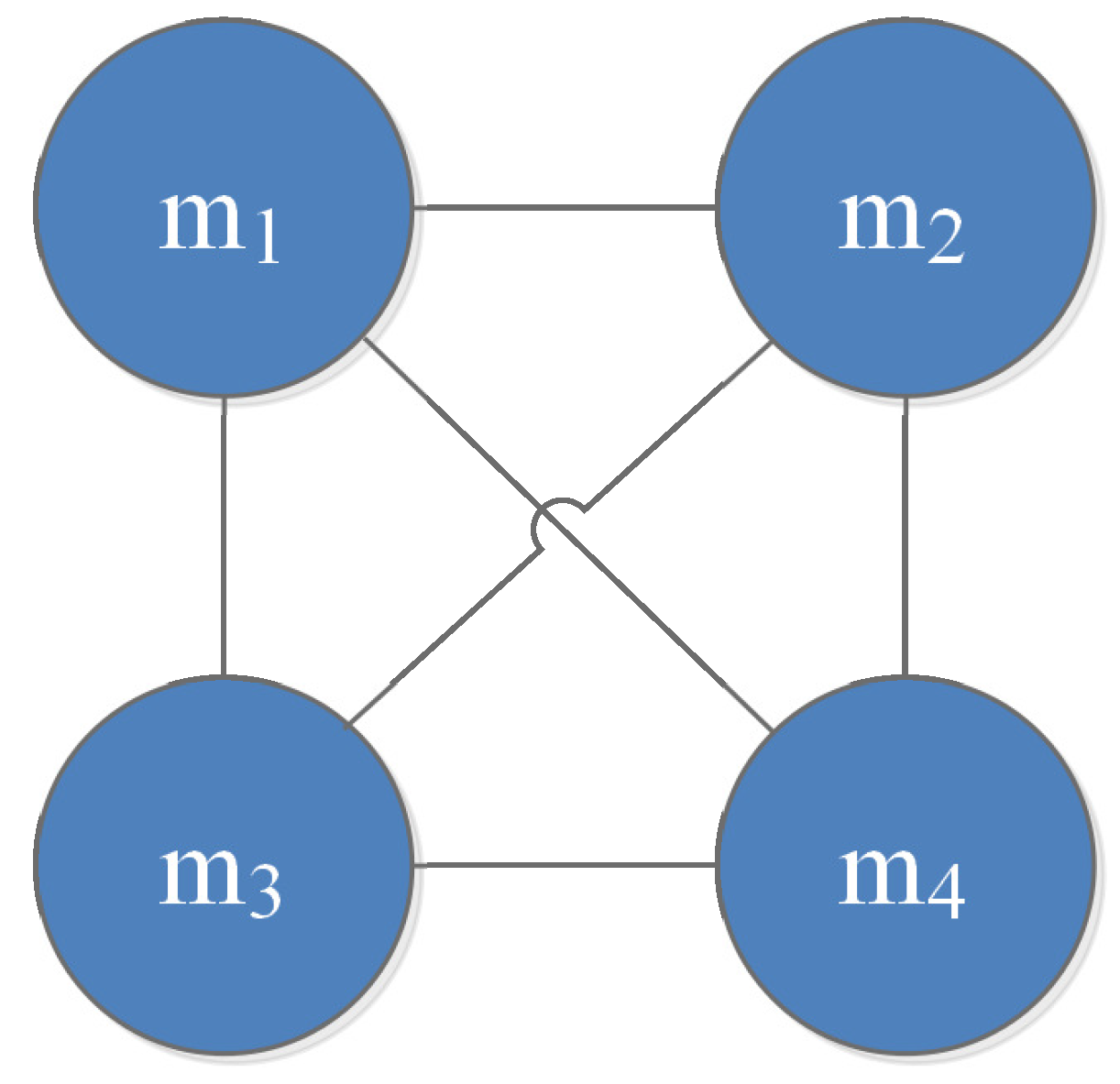
- Step 2-3: Generate the interaction graph between evidence as Figure 3.
- Step 3-1: Fuse the connected evidence via the Dempster’s rule of combination; the process evidence is computed. Since the connection graph is modified by a fully connected graph, the process evidence generated by the proposed method is also the same. The process evidence is shown as follows:
- Step 3-2: Fuse the process evidence via Dempster’s combination rule; the fusion results are shown in Table 4.
- Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vandecasteele, F.; Merci, B.; Verstockt, S. Reasoning on multi-sensor geographic smoke spread data for fire development and risk analysis. Fire Saf. J. 2016, 86, 65–74. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Zhu, H.; AbouRizk, S.M. Perceiving safety risk of buildings adjacent to tunneling excavation: An information fusion approach. Autom. Constr. 2017, 73, 88–101. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.; Cheng, M. Fault diagnosis of wind turbine based on multi-sensors information fusion technology. Iet Renew. Power Gener. 2014, 8, 289–298. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, C.; Zhuang, M.; Shou, Y.; Tang, Y. Sensor data fusion with z-numbers and its application in fault diagnosis. Sensors 2016, 16, 1509. [Google Scholar] [CrossRef] [PubMed]
- Dong, M.; He, D. Hidden semi-Markov model-based methodology for multi-sensor equipment health diagnosis and prognosis. Eur. J. Oper. Res. 2007, 178, 858–878. [Google Scholar] [CrossRef]
- Yang, F.; Wei, H. Fusion of infrared polarization and intensity images using support value transform and fuzzy combination rules. Infrared Phys. Technol. 2013, 60, 235–243. [Google Scholar] [CrossRef]
- Shen, X.; Varshney, P.K. Sensor selection based on generalized information gain for target tracking in large sensor networks. IEEE Trans. Signal Process. 2013, 62, 363–375. [Google Scholar] [CrossRef]
- Walczak, B.; Massart, D. Rough sets theory. Chemom. Intell. Lab. Syst. 1999, 47, 1–16. [Google Scholar] [CrossRef]
- Shen, L.; Tay, F.E.; Qu, L.; Shen, Y. Fault diagnosis using rough sets theory. Comput. Ind. 2000, 43, 61–72. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A Zadeh; World Scientific: Singapore, 1996; pp. 394–432. [Google Scholar]
- Liu, H.C.; Liu, L.; Lin, Q.L. Fuzzy failure mode and effects analysis using fuzzy evidential reasoning and belief rule-based methodology. IEEE Trans. Reliab. 2013, 62, 23–36. [Google Scholar] [CrossRef]
- Jiang, W.; Wei, B. Intuitionistic fuzzy evidential power aggregation operator and its application in multiple criteria decision-making. Int. J. Syst. Sci. 2018, 49, 582–594. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. In Classic Works of the Dempster-Shafer Theory of Belief Functions; Springer: Berlin/Heidelberg, Germany, 2008; pp. 57–72. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 42. [Google Scholar]
- Deng, X.; Han, D.; Dezert, J.; Deng, Y.; Shyr, Y. Evidence combination from an evolutionary game theory perspective. IEEE Trans. Cybern. 2015, 46, 2070–2082. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. A note on Z-numbers. Inf. Sci. 2011, 181, 2923–2932. [Google Scholar] [CrossRef]
- Kang, B.; Chhipi-Shrestha, G.; Deng, Y.; Hewage, K.; Sadiq, R. Stable strategies analysis based on the utility of Z-number in the evolutionary games. Appl. Math. Comput. 2018, 324, 202–217. [Google Scholar] [CrossRef]
- Deng, X.; Hu, Y.; Deng, Y.; Mahadevan, S. Environmental impact assessment based on D numbers. Expert Syst. Appl. 2014, 41, 635–643. [Google Scholar] [CrossRef]
- Xiao, F. An intelligent complex event processing with numbers under fuzzy environment. Math. Probl. Eng. 2016, 2016, 1–10. [Google Scholar]
- Smets, P. Decision making in the TBM: The necessity of the pignistic transformation. Int. J. Approx. Reason. 2005, 38, 133–147. [Google Scholar] [CrossRef]
- Dezert, J.; Smarandache, F. A new probabilistic transformation of belief mass assignment. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–8. [Google Scholar]
- Zadeh, L.A. A simple view of the Dempster-Shafer theory of evidence and its implication for the rule of combination. AI Mag. 1986, 7, 85. [Google Scholar]
- Yager, R.R. On the Dempster-Shafer framework and new combination rules. Inf. Sci. 1987, 41, 93–137. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Representation and combination of uncertainty with belief functions and possibility measures. Comput. Intell. 1988, 4, 244–264. [Google Scholar] [CrossRef]
- Smets, P. The combination of evidence in the transferable belief model. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 447–458. [Google Scholar] [CrossRef]
- Martin, A.; Osswald, C. A new generalization of the proportional conflict redistribution rule stable in terms of decision. In Advances and Applications of DSmT for Information Fusion: Collected Works Volume 2; American Research Press: New York, NY, USA, 2006; Volume 2, pp. 69–88. [Google Scholar]
- Smarandache, F.; Dezert, J. Advances and Applications of DSmT for Information Fusion, Vol. IV: Collected Works; American Research Press: New York, NY, USA, 2015. [Google Scholar]
- Murphy, C.K. Combining belief functions when evidence conflicts. Decis. Support Syst. 2000, 29, 1–9. [Google Scholar] [CrossRef]
- Yong, D.; WenKang, S.; ZhenFu, Z.; Qi, L. Combining belief functions based on distance of evidence. Decis. Support Syst. 2004, 38, 489–493. [Google Scholar] [CrossRef]
- Yuan, K.; Xiao, F.; Fei, L.; Kang, B.; Deng, Y. Conflict management based on belief function entropy in sensor fusion. SpringerPlus 2016, 5, 1–12. [Google Scholar] [CrossRef]
- Yang, B.; Gan, D.; Tang, Y.; Lei, Y. Incomplete Information Management Using an Improved Belief Entropy in Dempster-Shafer Evidence Theory. Entropy 2020, 22, 993. [Google Scholar] [CrossRef]
- Xiao, F. Evidence combination based on prospect theory for multi-sensor data fusion. ISA Trans. 2020, 106, 253–261. [Google Scholar] [CrossRef]
- Xiao, F. Multi-sensor data fusion based on the belief divergence measure of evidences and the belief entropy. Inf. Fusion 2019, 46, 23–32. [Google Scholar] [CrossRef]
- Sader, M.; Chen, Z.; Liu, Z.; Deng, C. Distributed robust fault-tolerant consensus control for a class of nonlinear multi-agent systems with intermittent communications. Appl. Math. Comput. 2021, 403, 126166. [Google Scholar] [CrossRef]
- Liu, J.; Tang, Y. Conflict data fusion in a multi-agent system premised on the base basic probability assignment and evidence distance. Entropy 2021, 23, 820. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W.; Atkins, E.M. A survey of consensus problems in multi-agent coordination. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 1859–1864. [Google Scholar]
- Jousselme, A.L.; Grenier, D.; Bossé, É. A new distance between two bodies of evidence. Inf. Fusion 2001, 2, 91–101. [Google Scholar] [CrossRef]
- Wang, H.; Deng, X.; Jiang, W.; Geng, J. A new belief divergence measure for Dempster–Shafer theory based on belief and plausibility function and its application in multi-source data fusion. Eng. Appl. Artif. Intell. 2021, 97, 104030. [Google Scholar] [CrossRef]
- Jiang, W.; Wei, B.; Xie, C.; Zhou, D. An evidential sensor fusion method in fault diagnosis. Adv. Mech. Eng. 2016, 8, 1–7. [Google Scholar] [CrossRef]
| A | B | C | ||
|---|---|---|---|---|
| 0.41 | 0.29 | 0.30 | 0.00 | |
| 0.00 | 0.90 | 0.10 | 0.00 | |
| 0.58 | 0.07 | 0.00 | 0.35 | |
| 0.55 | 0.10 | 0.00 | 0.35 | |
| 0.60 | 0.10 | 0.00 | 0.30 |
| Method | A | B | C | Target | |
|---|---|---|---|---|---|
| Dempster [13] | 0.0000 | 0.1422 | 0.8578 | 0.0000 | C |
| Dubois and Prade [24] | 0.7504 | 0.0160 | 0.0158 | 0.0832 | A |
| PCR6 [26] | 0.4518 | 0.3624 | 0.0438 | 0.1420 | A |
| Murphy [28] | 0.9620 | 0.0210 | 0.0138 | 0.0032 | A |
| Deng et al. [29] | 0.9820 | 0.0039 | 0.0107 | 0.0034 | A |
| Yuan et al. [30] | 0.9886 | 0.0002 | 0.0072 | 0.0039 | A |
| Xiao [33] | 0.9905 | 0.0002 | 0.0061 | 0.0043 | A |
| Proposed method | 1.0000 | 0.0000 | 0.0000 | 0.0000 | A |
| 0.648 | 0.153 | 0.090 | 0.009 | 0.100 | |
| 0.621 | 0.072 | 0.198 | 0.009 | 0.100 | |
| 0.729 | 0.054 | 0.099 | 0.018 | 0.100 | |
| 0.747 | 0.063 | 0.081 | 0.009 | 0.100 |
| Target | |||||
|---|---|---|---|---|---|
| Dempster [13] | 0.9918 | 0.0027 | 0.0051 | 0.0001 | |
| Dubious and Prade [24] | 0.7704 | 0.0110 | 0.0200 | 0.0003 | |
| PCR6 [26] | 0.9158 | 0.0246 | 0.0428 | 0.0005 | |
| Xiao [33] | 0.9919 | 0.0026 | 0.0051 | 0.0001 | |
| Jiang et al. [40] | 0.9908 | 0.0030 | 0.0058 | 0.0001 | |
| Wang et al. [39] | 0.9921 | 0.0025 | 0.0050 | 0.0001 | |
| Proposed method | 1.0000 | 0.0000 | 0.0000 | 0.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Q.; Liu, Z.; Chen, Z. A Networked Method for Multi-Evidence-Based Information Fusion. Entropy 2023, 25, 69. https://doi.org/10.3390/e25010069
Liang Q, Liu Z, Chen Z. A Networked Method for Multi-Evidence-Based Information Fusion. Entropy. 2023; 25(1):69. https://doi.org/10.3390/e25010069
Chicago/Turabian StyleLiang, Qian, Zhongxin Liu, and Zengqiang Chen. 2023. "A Networked Method for Multi-Evidence-Based Information Fusion" Entropy 25, no. 1: 69. https://doi.org/10.3390/e25010069
APA StyleLiang, Q., Liu, Z., & Chen, Z. (2023). A Networked Method for Multi-Evidence-Based Information Fusion. Entropy, 25(1), 69. https://doi.org/10.3390/e25010069





