Vanishing Opinions in Latané Model of Opinion Formation
Abstract
1. Introduction
2. Model
3. Results
3.1. How Influential Are the Nearest-Neighbours in Respect to the Entire Population?
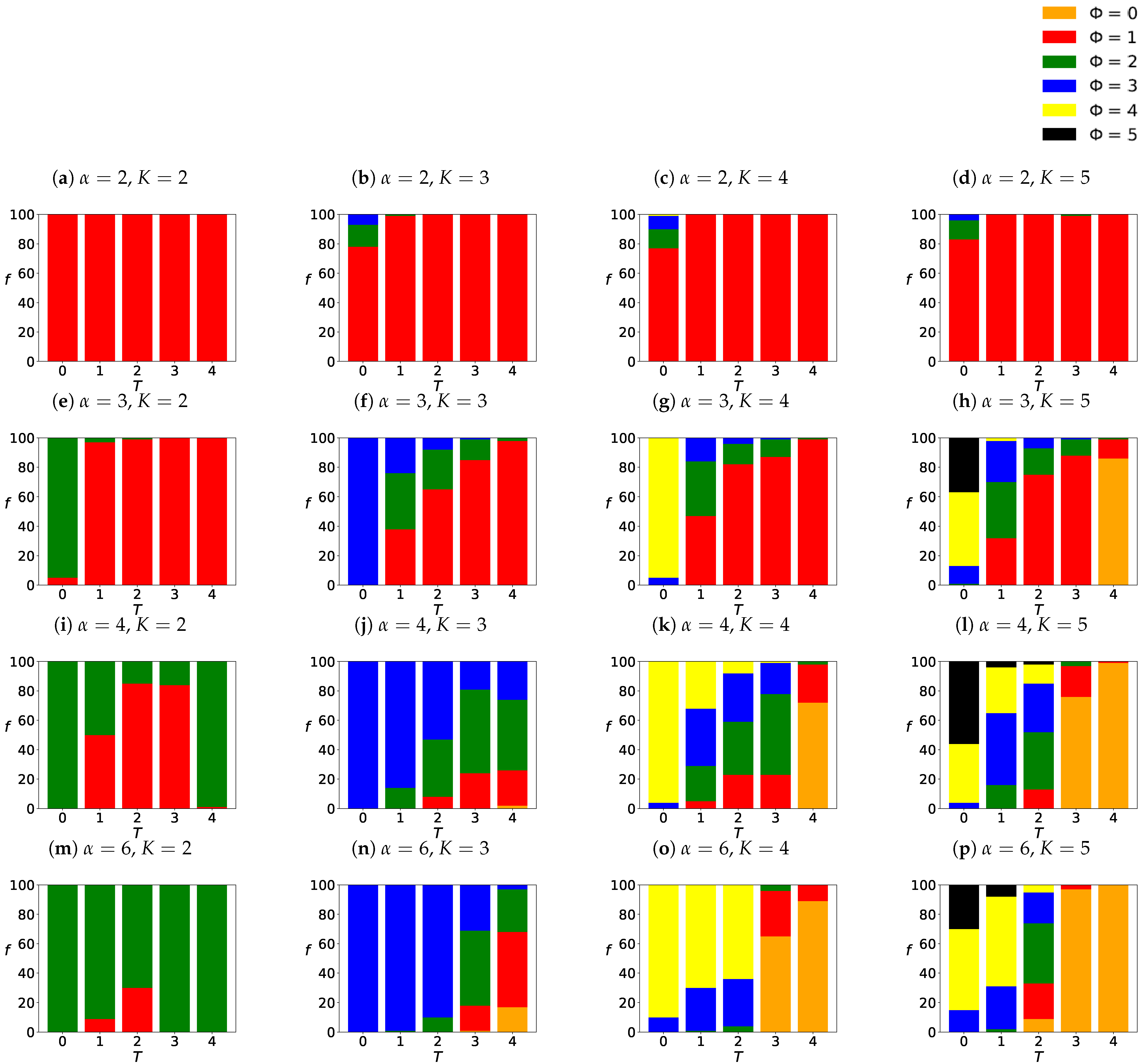
3.2. The Final Opinions Distributions
3.3. Opinion Clustering
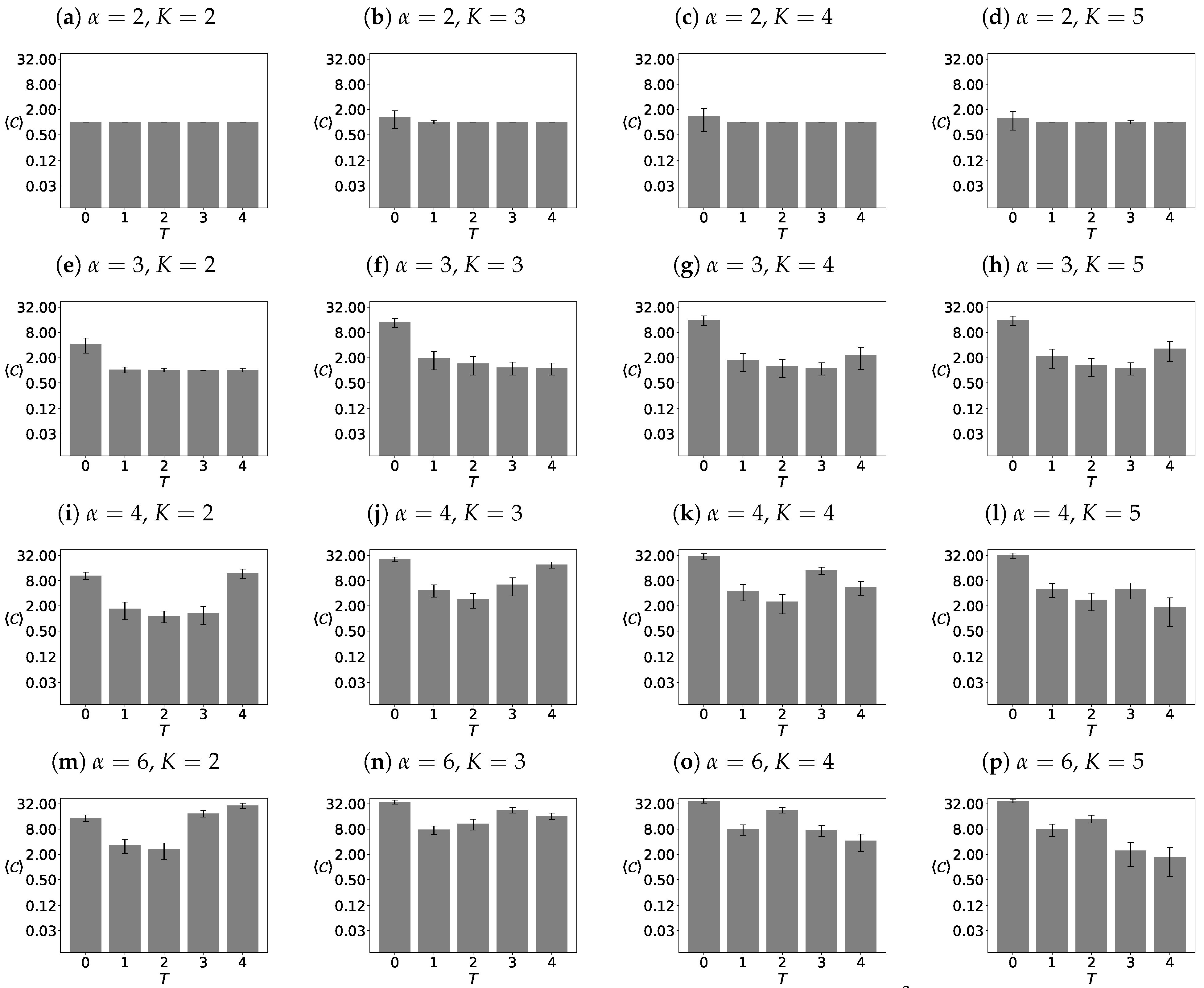
3.3.1. Average Number of Opinion Clusters
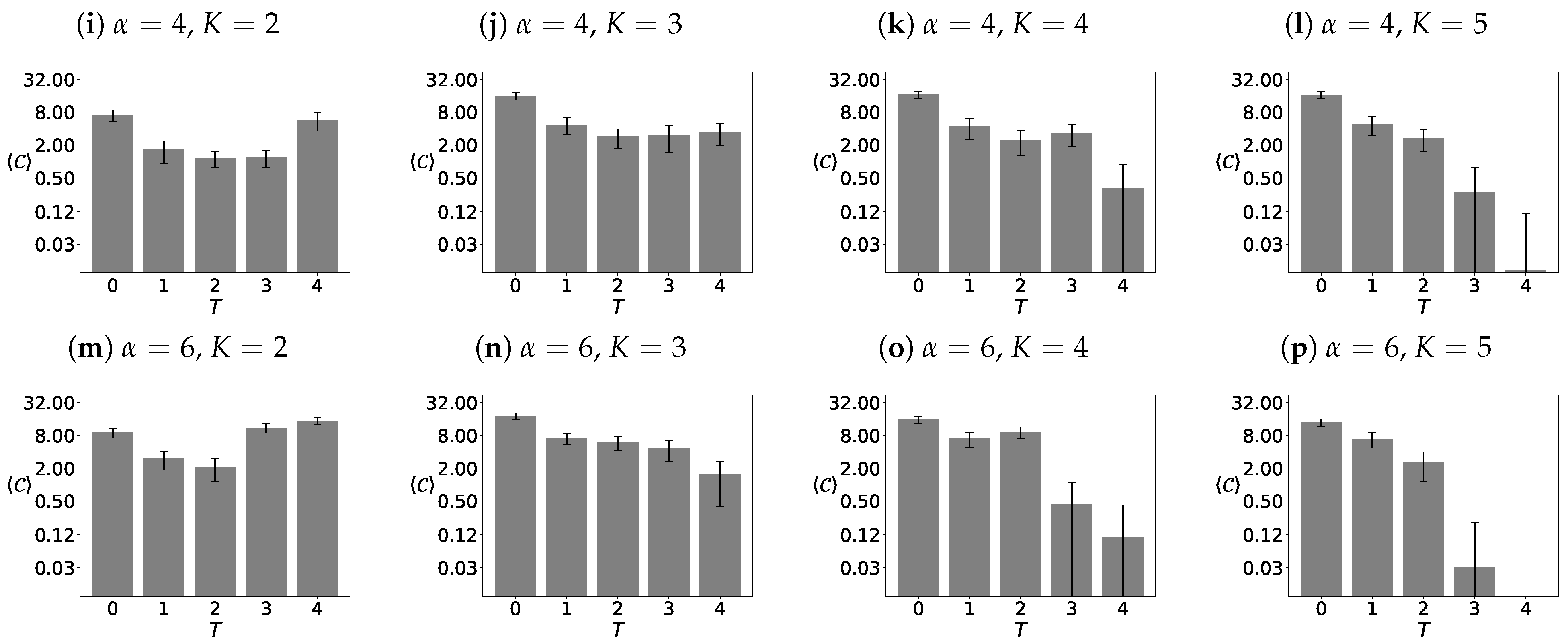
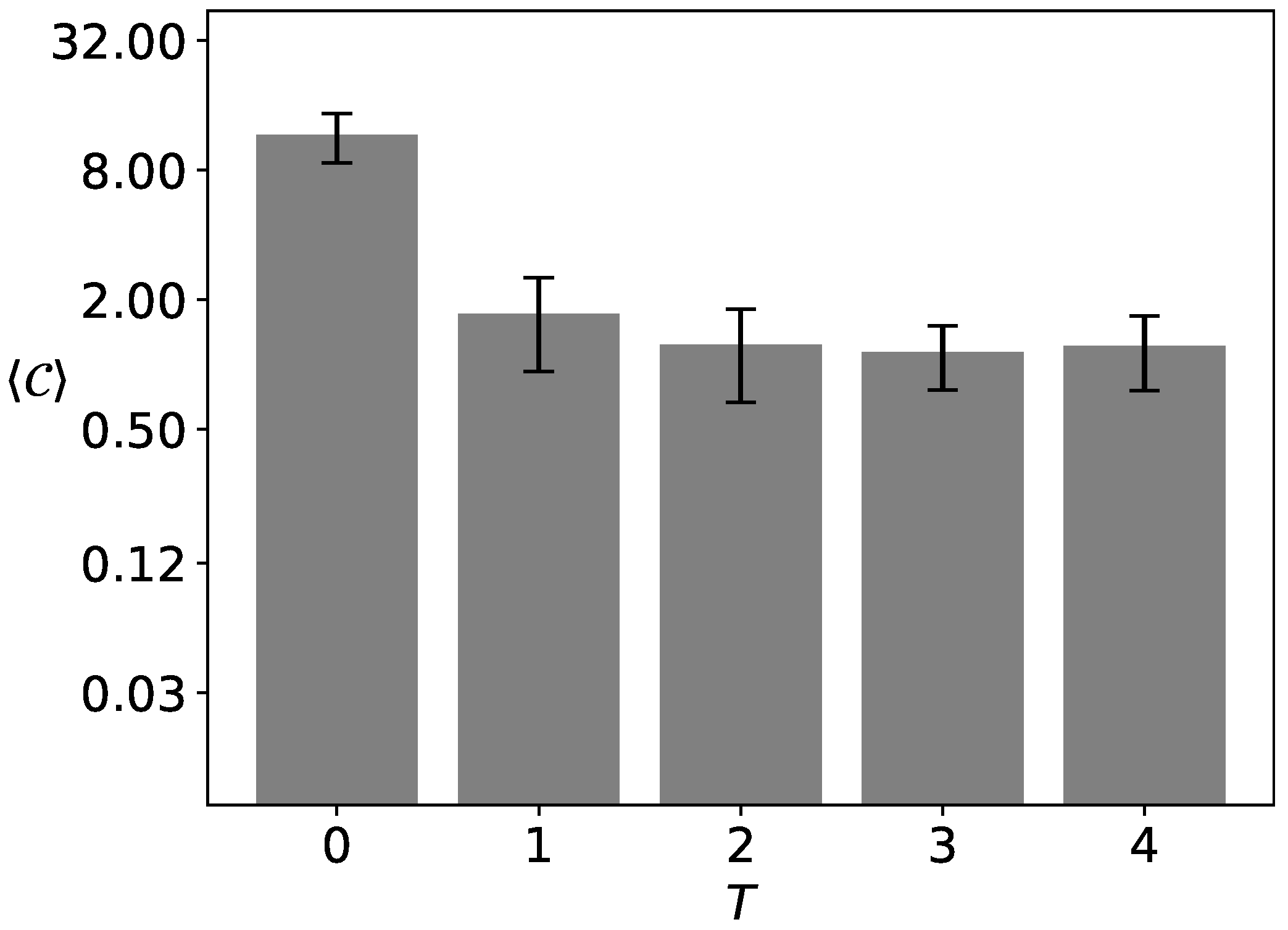
3.3.2. The Sizes of the Largest Clusters
3.4. Distribution of Surviving Opinions
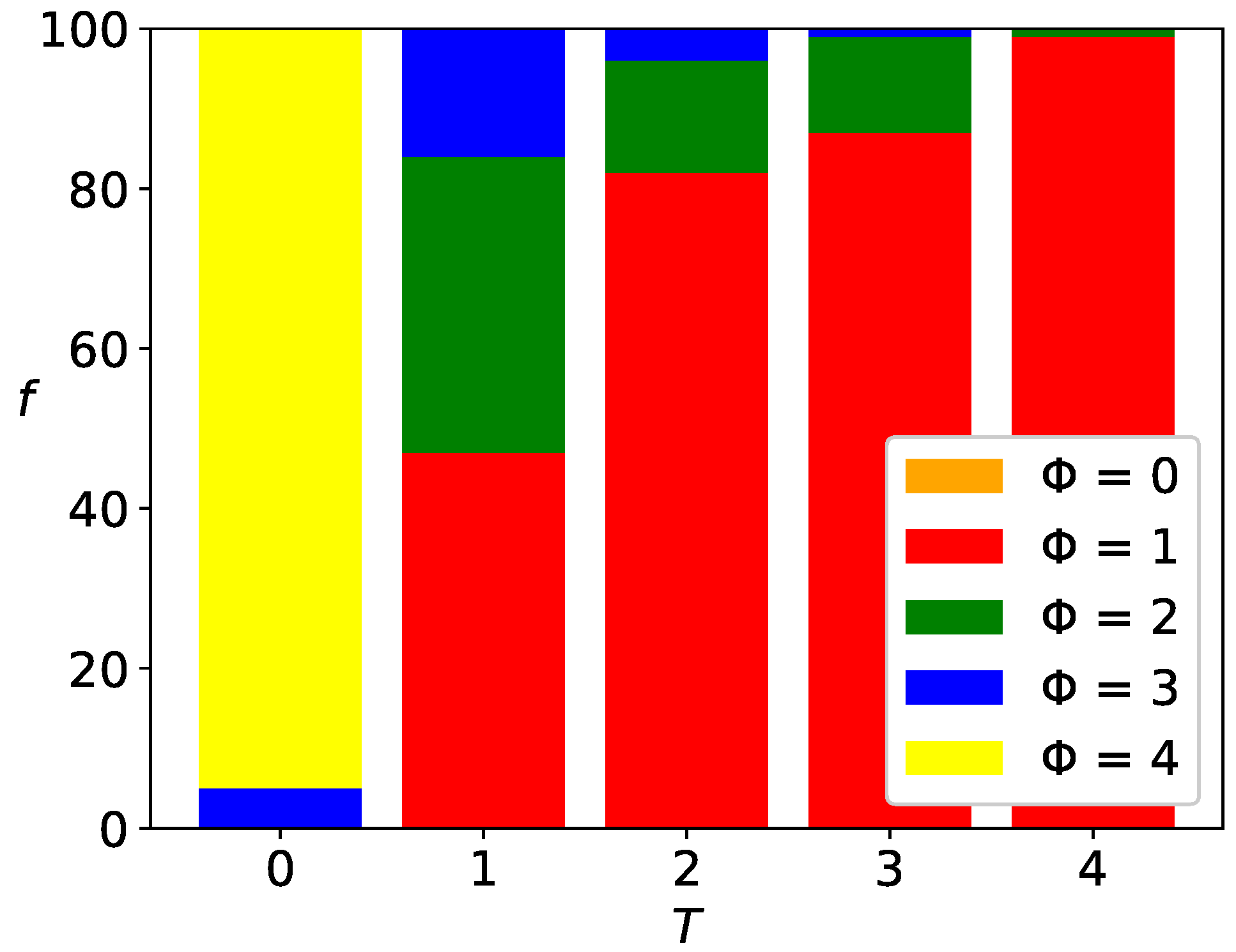
3.4.1. Histograms of Surviving Opinions
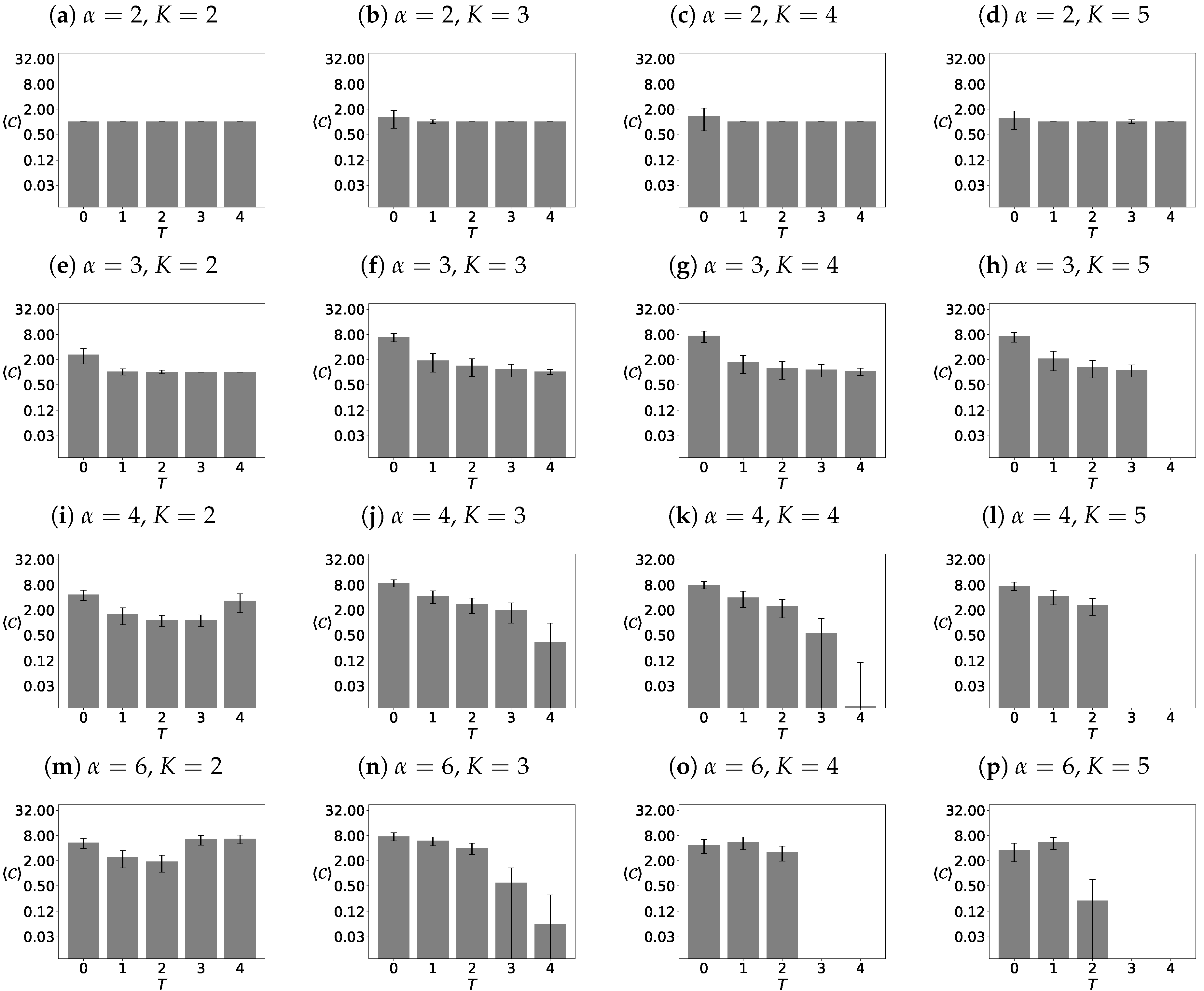
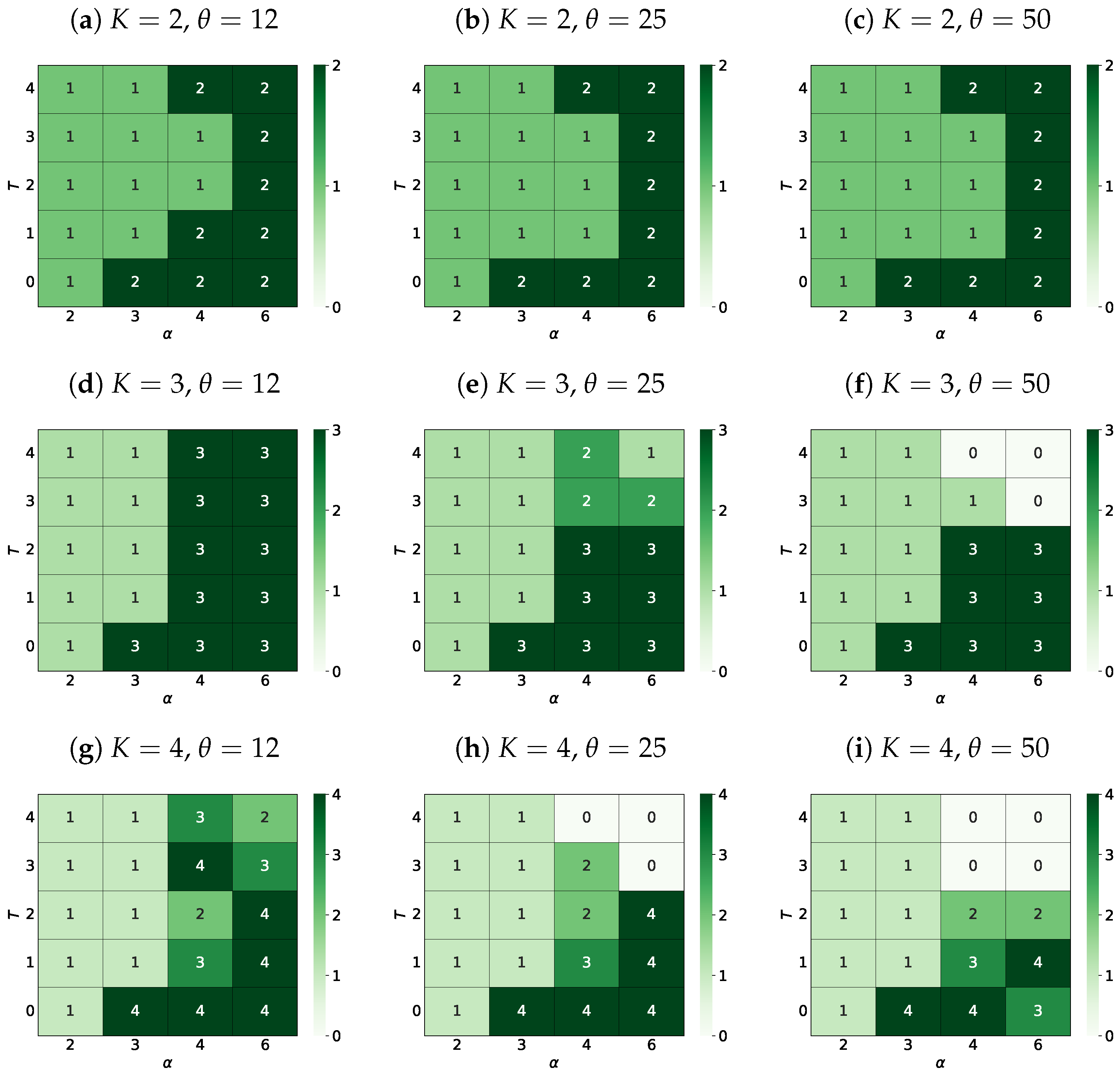
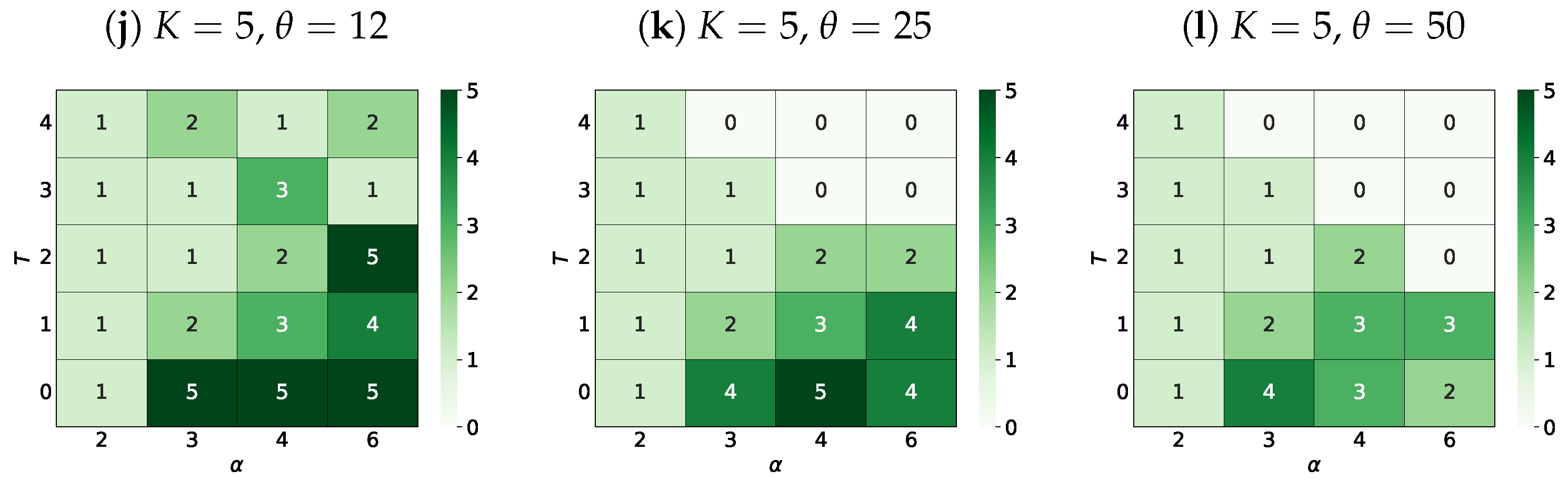
3.4.2. The Most Probable Number of Surviving Opinions
4. Discussion
4.1. Average Number of Opinion Clusters
4.2. The Sizes of the Largest Clusters
4.3. Histograms of Surviving Opinions
4.4. The Most Probable Number of Surviving Opinions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
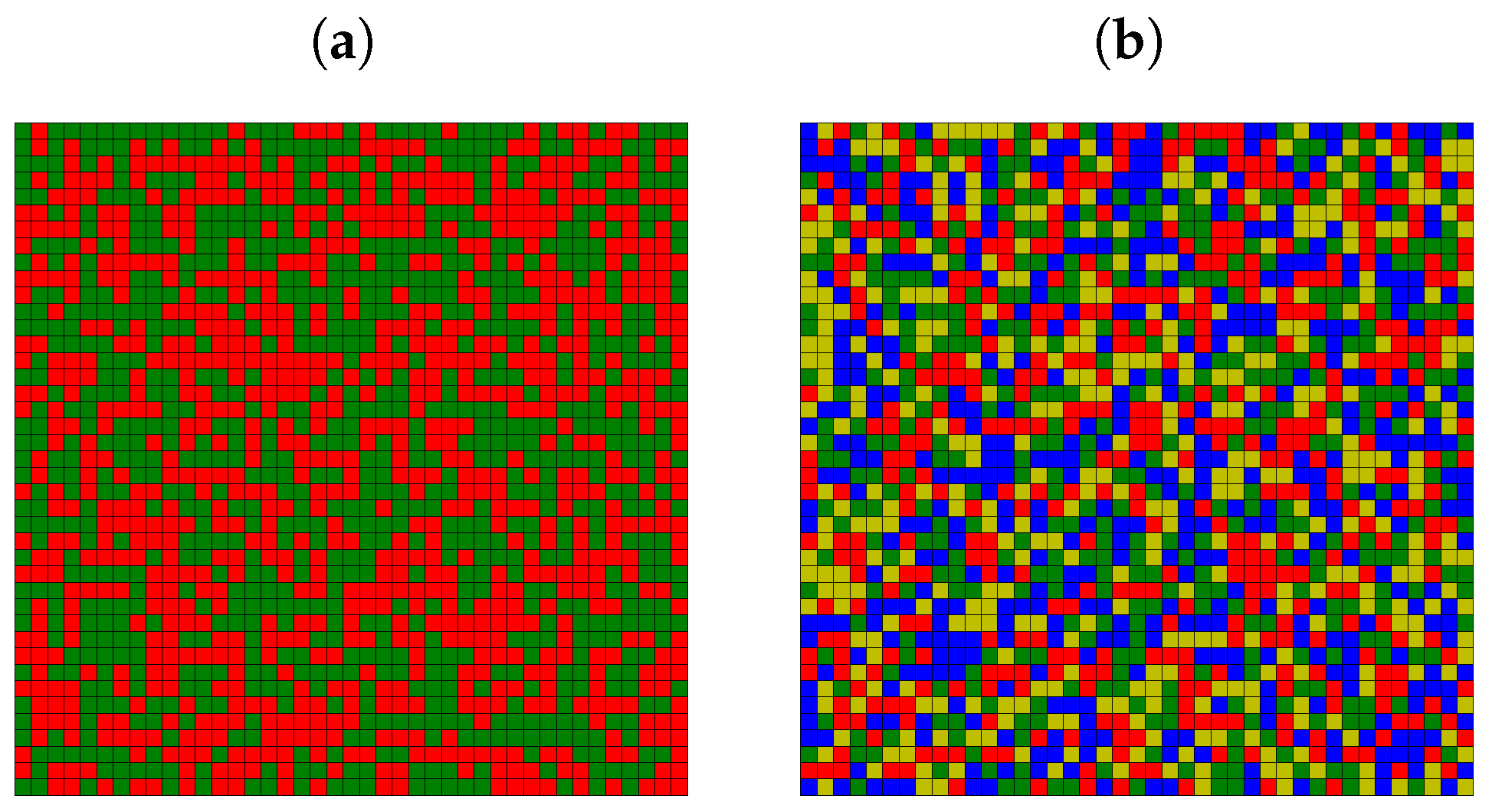
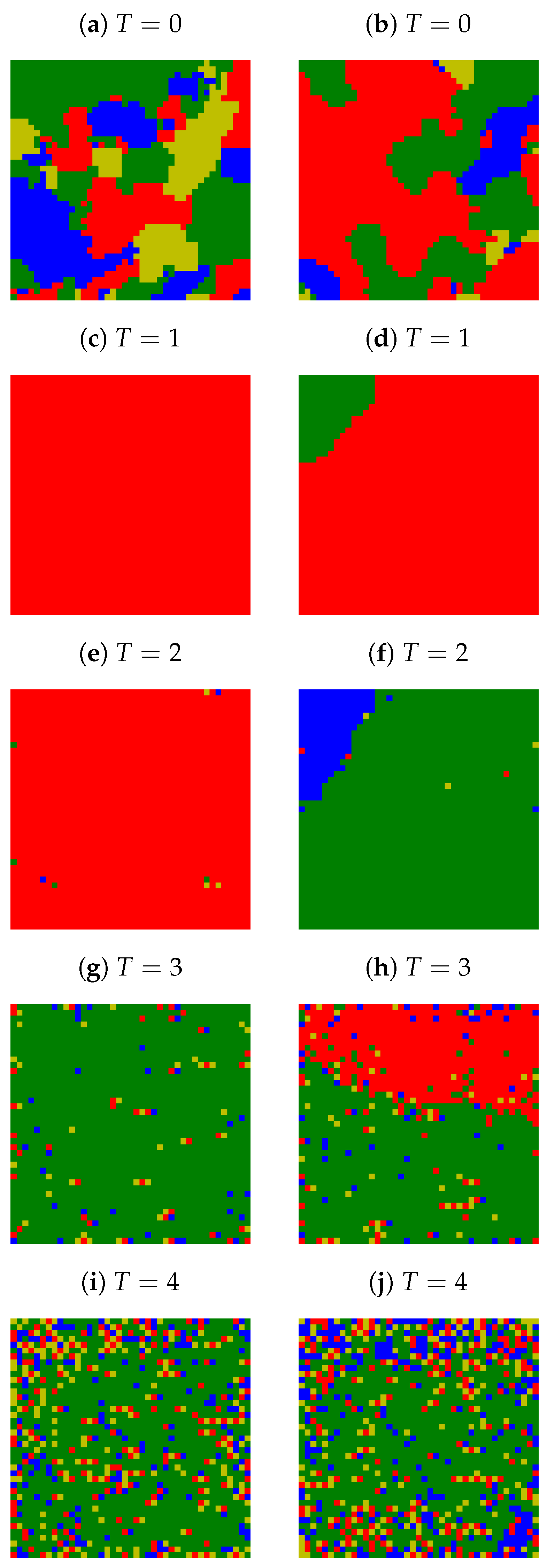
Appendix A. Examples of Final Spatial Opinion Distribution

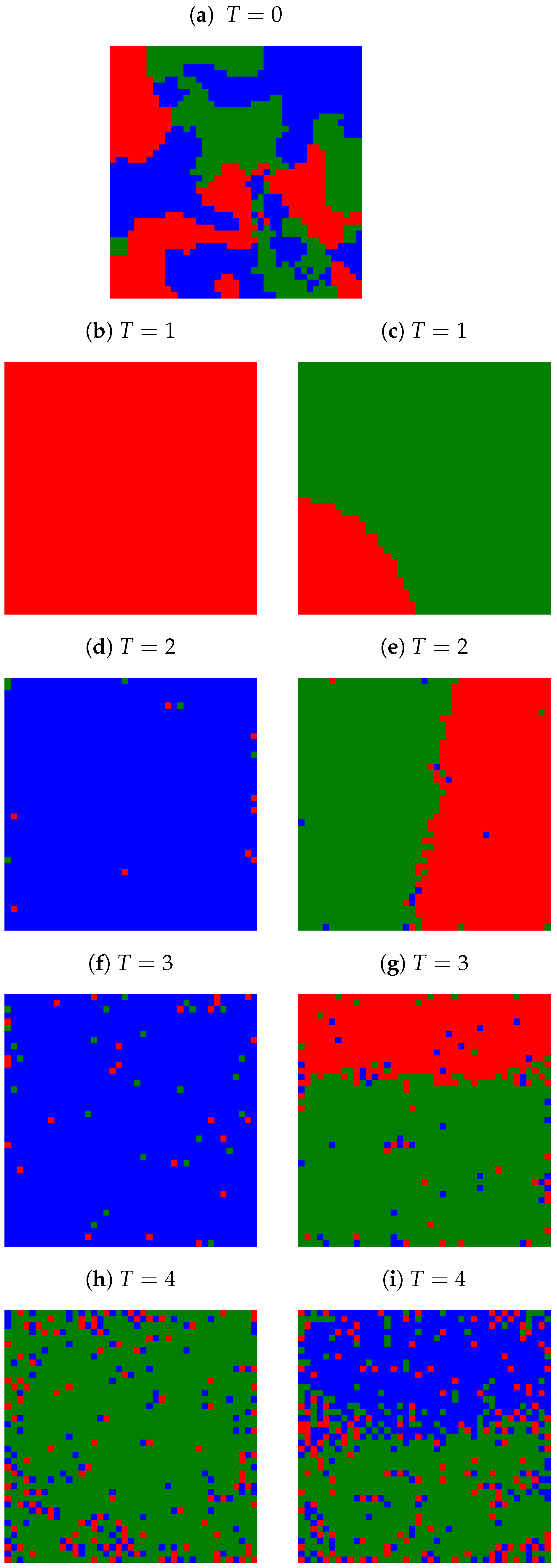
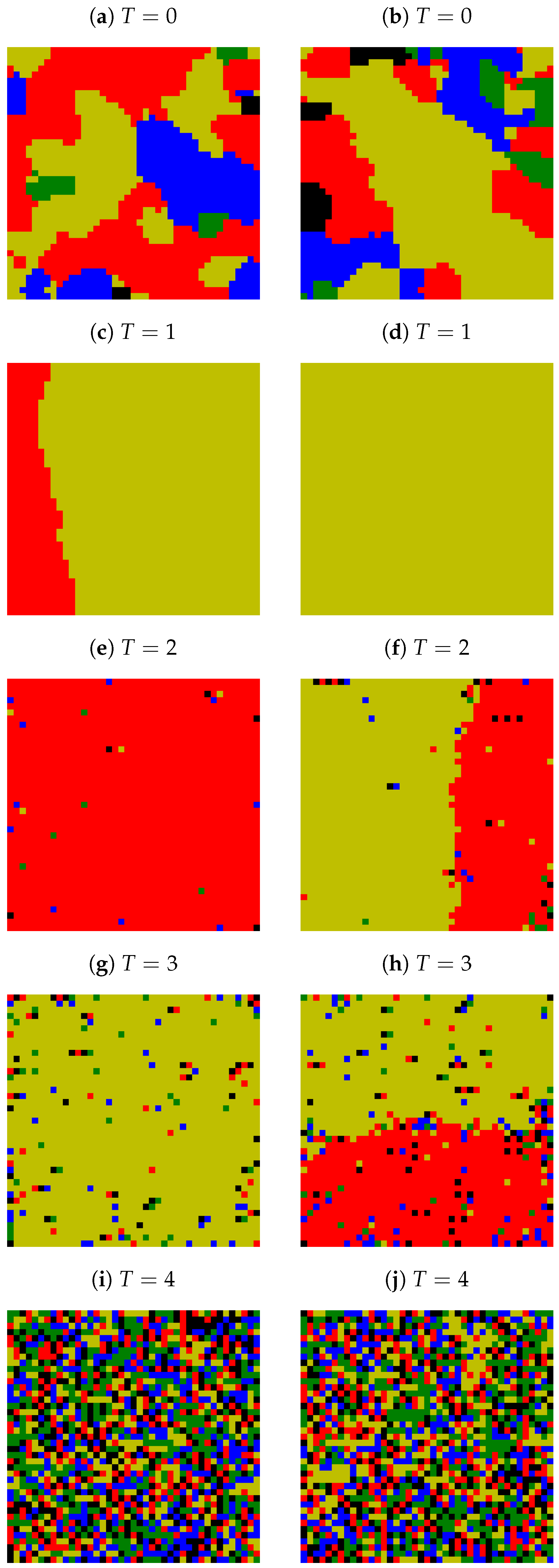
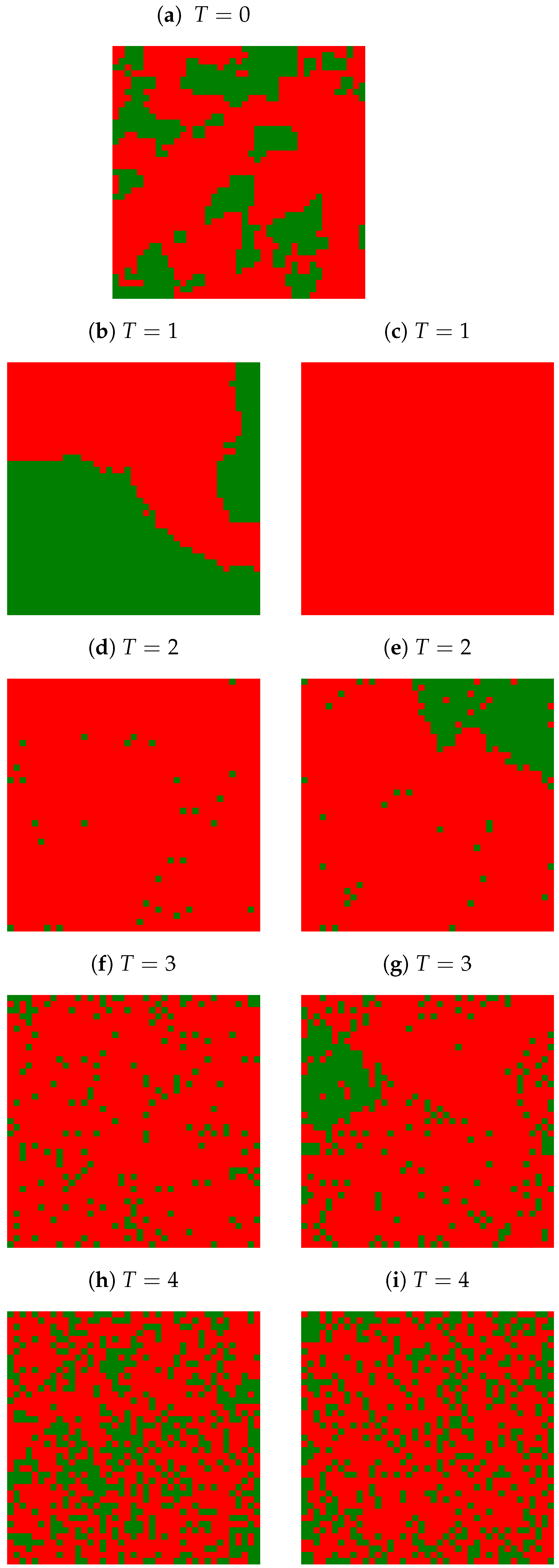
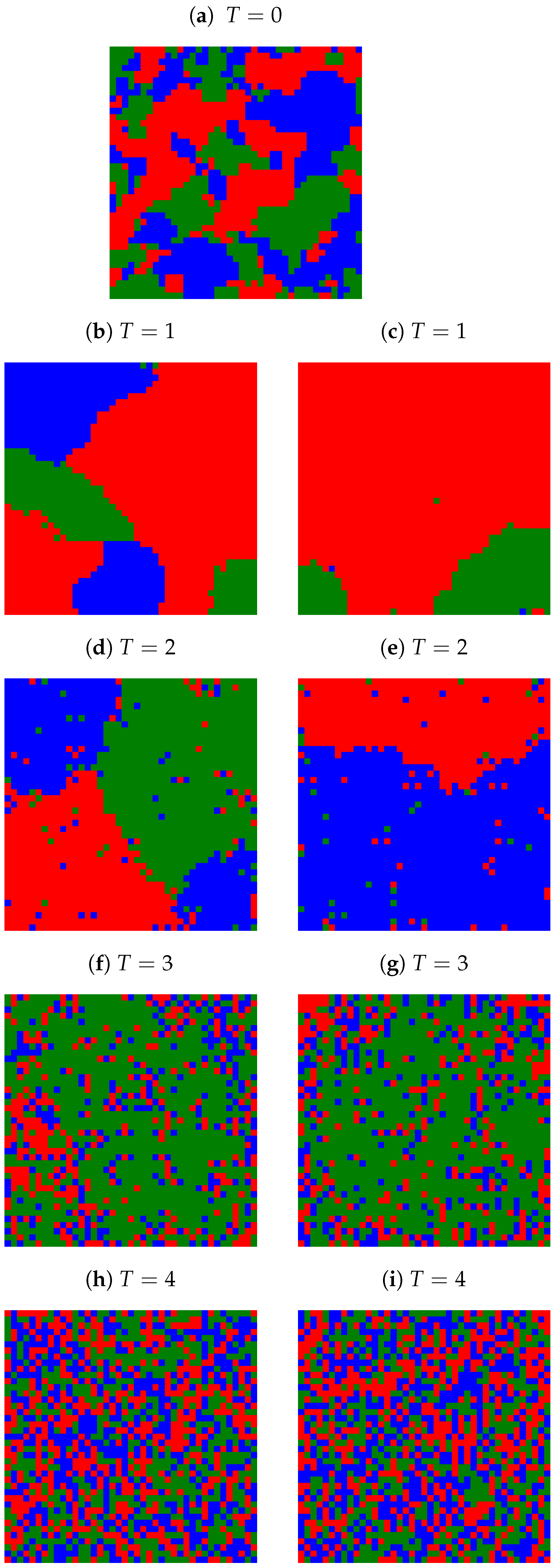



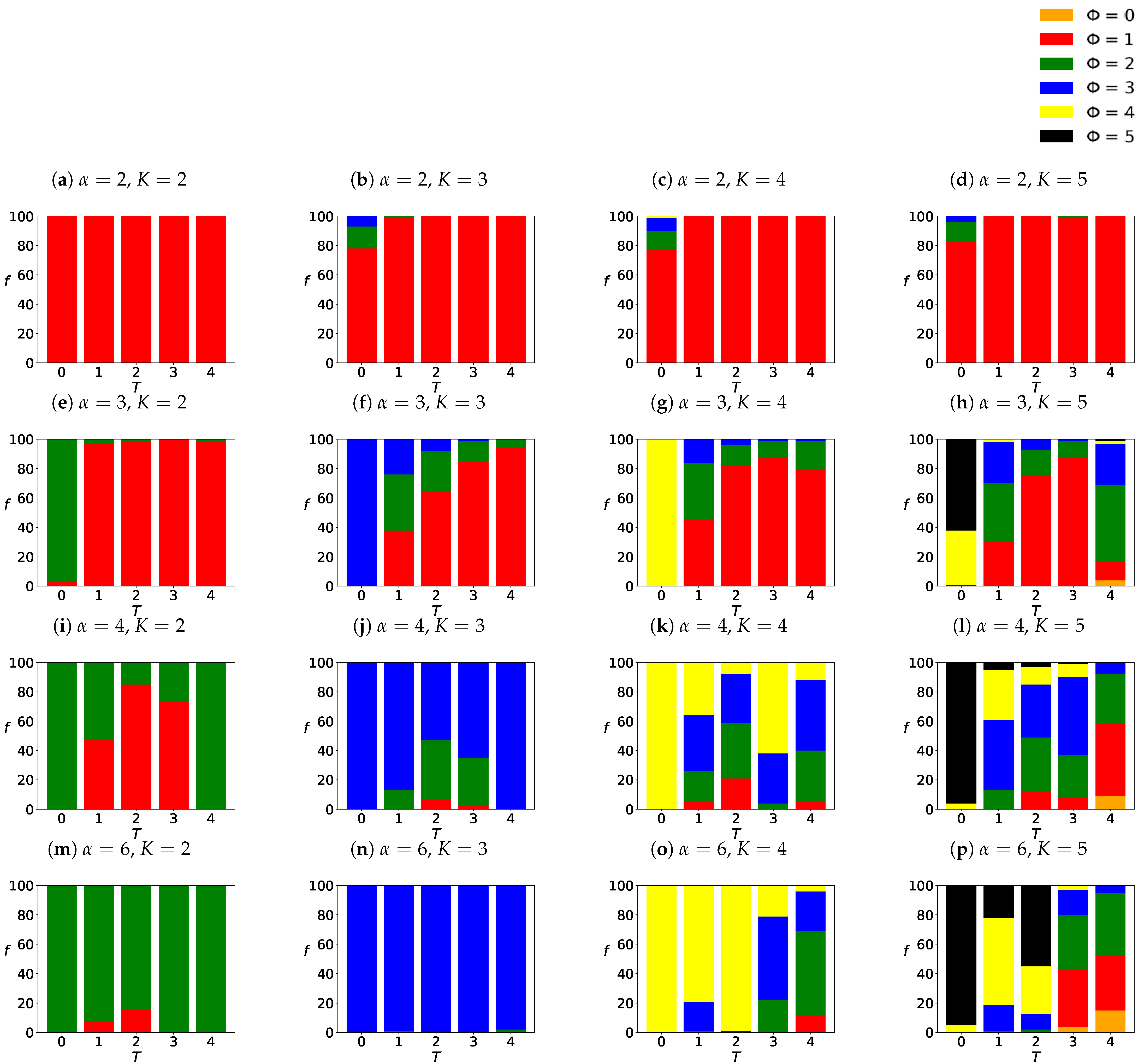

Appendix B. Average Number of Clusters
Appendix C. The Number of Surviving Opinions
References
- Galam, S. Opinion Dynamics and Unifying Principles: A Global Unifying Frame. Entropy 2022, 24, 1201. [Google Scholar] [CrossRef]
- Kozitsin, I. A general framework to link theory and empirics in opinion formation models. Sci. Rep. 2022, 12, 5543. [Google Scholar] [CrossRef]
- Weron, T.; Szwabiński, J. Opinion Evolution in Divided Community. Entropy 2022, 24, 185. [Google Scholar] [CrossRef]
- Galam, S.; Brooks, R.R.W. Radicalism: The asymmetric stances of radicals versus conventionals. Phys. Rev. E 2022, 105, 044112. [Google Scholar] [CrossRef]
- Muslim, R.; Kholili, M.; Nugraha, A. Opinion dynamics involving contrarian and independence behaviors based on the Sznajd model with two-two and three-one agent interactions. Phys. D Nonlinear Phenom. 2022, 439, 133379. [Google Scholar] [CrossRef]
- Lian, Y.; Dong, X. An opinion dynamics model for unrelated discrete opinions. Knowl.-Based Syst. 2022, 251, 109133. [Google Scholar] [CrossRef]
- Su, W.; Chen, X.; Yu, Y.; Chen, G. Noise-Based Control of Opinion Dynamics. IEEE Trans. Autom. Control 2022, 67, 3134–3140. [Google Scholar] [CrossRef]
- Zachary, D.S. Modelling shifts in social opinion through an application of classical physics. Sci. Rep. 2022, 12, 5485. [Google Scholar] [CrossRef]
- Nguyen, V.X.; Xiao, G.; Xu, X.J.; Wu, Q.; Xia, C.Y. Dynamics of opinion formation under majority rules on complex social networks. Sci. Rep. 2020, 10, 456. [Google Scholar] [CrossRef]
- Galam, S.; Cheon, T. Asymmetric Contrarians in Opinion Dynamics. Entropy 2020, 22, 25. [Google Scholar] [CrossRef]
- Galam, S.; Cheon, T. Tipping Points in Opinion Dynamics: A Universal Formula in Five Dimensions. Front. Phys. 2020, 8, 566580. [Google Scholar] [CrossRef]
- Malarz, K.; Szvetelszky, Z.; Szekfü, B.; Kułakowski, K. Gossip in random networks. Acta Phys. Pol. B 2006, 37, 3049–3058. [Google Scholar]
- Choi, D.; Chun, S.; Oh, H.; Han, J.; Kwon, T.T. Rumor Propagation is Amplified by Echo Chambers in Social Media. Sci. Rep. 2020, 10, 310. [Google Scholar] [CrossRef]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591–646. [Google Scholar] [CrossRef]
- Stauffer, D. A Biased Review of Sociophysics. J. Stat. Phys. 2013, 151, 9–20. [Google Scholar] [CrossRef]
- Galam, S. The Trump phenomenon: An explanation from sociophysics. Int. J. Mod. Phys. B 2017, 31, 1742015. [Google Scholar] [CrossRef]
- Ishii, A.; Kawahata, Y. Sociophysics analysis of the dynamics of peoples’ interests in society. Front. Phys. 2018, 6, 089. [Google Scholar] [CrossRef]
- Schweitzer, F. Sociophysics. Phys. Today 2018, 71, 40–46. [Google Scholar] [CrossRef]
- Sobkowicz, P. Social Simulation Models at the Ethical Crossroads. Sci. Eng. Ethics 2019, 25, 143–157. [Google Scholar] [CrossRef]
- Jusup, M.; Holme, P.; Kanazawa, K.; Takayasu, M.; Romić, I.; Wang, Z.; Geček, S.; Lipić, T.; Podobnik, B.; Wang, L.; et al. Social physics. Phys. Rep. 2022, 948, 1–148. [Google Scholar] [CrossRef]
- Fortunato, S.; Stauffer, D. Computer Simulations of Opinions. arXiv 2005. [Google Scholar] [CrossRef]
- Grabisch, M.; Rusinowska, A. A Survey on Nonstrategic Models of Opinion Dynamics. Games 2020, 11, 65. [Google Scholar] [CrossRef]
- Hegselmann, R.; Krause, U. Opinion dynamics and bounded confidence: Models, analysis and simulation. JASSS—J. Artif. Soc. Soc. Simul. 2002, 5, 2. [Google Scholar]
- Schawe, H.; Hernández, L. When open mindedness hinders consensus. Sci. Rep. 2020, 10, 8273. [Google Scholar] [CrossRef]
- Schawe, H.; Hernández, L. Collective effects of the cost of opinion change. Sci. Rep. 2020, 10, 13825. [Google Scholar] [CrossRef]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing beliefs among interacting agents. Adv. Complex Syst. 2000, 3, 87. [Google Scholar] [CrossRef]
- Deffuant, G. Comparing extremism propagation patterns in continuous opinion models. JASSS—J. Artif. Soc. Soc. Simul. 2006, 9, 8. [Google Scholar]
- Malarz, K. Truth seekers in opinion dynamics models. Int. J. Mod. Phys. C 2006, 17, 1521–1524. [Google Scholar] [CrossRef]
- Mathias, J.D.; Huet, S.; Deffuant, G. Bounded confidence model with fixed uncertainties and extremists: The opinions can keep fluctuating indefinitely. JASSS—J. Artif. Soc. Soc. Simul. 2016, 19, 6. [Google Scholar] [CrossRef]
- Chen, G.; Cheng, H.; Huang, C.; Han, W.; Dai, Q.; Li, H.; Yang, J. Deffuant model on a ring with repelling mechanism and circular opinions. Phys. Rev. E 2017, 95, 042118. [Google Scholar] [CrossRef]
- Kułakowski, K. Opinion polarization in the Receipt–Accept–Sample model. Physica A 2009, 388, 469–476. [Google Scholar] [CrossRef][Green Version]
- Malarz, K.; Gronek, P.; Kułakowski, K. Zaller–Deffuant model of mass opinion. JASSS—J. Artif. Soc. Soc. Simul. 2011, 14, 2. [Google Scholar] [CrossRef]
- Malarz, K.; Kułakowski, K. Bounded confidence model: Addressed information maintain diversity of opinions. Acta Phys. Pol. A 2012, 121, B86–B88. [Google Scholar] [CrossRef]
- Malarz, K.; Kułakowski, K. Mental ability and common sense in an artificial society. Europhys. News 2014, 45, 21–23. [Google Scholar] [CrossRef][Green Version]
- Weisbuch, G.; Deffuant, G.; Amblard, F.; Nadal, J.P. Interacting Agents and Continuous Opinions Dynamics. In Heterogenous Agents, Interactions and Economic Performance; Cowan, R., Jonard, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 225–242. [Google Scholar] [CrossRef]
- Ben-Naim, E.; Krapivsky, P.L.; Redner, S. Bifurcations and patterns in compromise processes. Phys. D Nonlinear Phenom. 2003, 183, 190–204. [Google Scholar] [CrossRef]
- Ben-Naim, E.; Krapivsky, P.L.; Vazquez, F.; Redner, S. Unity and discord in opinion dynamics. Phys. A Stat. Mech. Its Appl. 2003, 330, 99–106. [Google Scholar] [CrossRef]
- Weisbuch, G.; Deffuant, G.; Amblard, F.; Nadal, J.P. Meet, discuss, and segregate! Complexity 2002, 7, 55–63. [Google Scholar] [CrossRef]
- Laguna, M.F.; Abramson, G.; Zanette, D.H. Minorities in a model for opinion formation. Complexity 2004, 9, 31–36. [Google Scholar] [CrossRef]
- Galam, S. Minority opinion spreading in random geometry. Eur. Phys. J. B 2002, 25, 403–406. [Google Scholar] [CrossRef]
- Oliveira, L.S.; Rodrigues, A.C.; Forgerini, F.L. Reputation in Majority Rule Model leading to democratic states. J. Phys. Conf. Ser. 2019, 1391, 012042. [Google Scholar] [CrossRef]
- Holley, R.A.; Liggett, T.M. Ergodic theorems for weakly interacting infinite systems and voter model. Ann. Probab. 1975, 3, 643–663. [Google Scholar] [CrossRef]
- Lima, F.W.S.; Malarz, K. Majority-vote model on (3,4,6,4) and (34,6) Archimedean lattices. Int. J. Mod. Phys. C 2006, 17, 1273–1283. [Google Scholar] [CrossRef]
- Fernandez-Gracia, J.; Suchecki, K.; Ramasco, J.J.; San Miguel, M.; Eguiluz, V.M. Is the Voter Model a Model for Voters? Phys. Rev. Lett. 2014, 112, 158701. [Google Scholar] [CrossRef] [PubMed]
- Sznajd-Weron, K.; Sznajd, J. Opinion evolution in closed community. Int. J. Mod. Phys. C 2000, 11, 1157–1165. [Google Scholar] [CrossRef]
- Sznajd-Weron, K. Sznajd model and its applications. Acta Phys. Pol. B 2005, 36, 2537–2547. [Google Scholar]
- Sznajd-Weron, K.; Sznajd, J. Who is left, who is right? Physica A 2005, 351, 593–604. [Google Scholar] [CrossRef]
- Malarz, K.; Kułakowski, K. The Sznajd dynamics on a directed clustered network. Acta Phys. Pol. A 2008, 114, 581–588. [Google Scholar] [CrossRef]
- Sznajd-Weron, K.; Sznajd, J.; Weron, T. A review on the Sznajd model—20 years after. Physica A 2021, 565, 125537. [Google Scholar] [CrossRef]
- Galam, S. Unifying Local Dynamics in Two-State Spin Systems. arXiv 2004. [Google Scholar] [CrossRef]
- Galam, S. Sociophysics: A review of Galam models. Int. J. Mod. Phys. C 2008, 19, 409–440. [Google Scholar] [CrossRef]
- Gekle, S.; Peliti, L.; Galam, S. Opinion dynamics in a three-choice system. Eur. Phys. J. B 2005, 45, 569–575. [Google Scholar] [CrossRef]
- Malarz, K.; Kułakowski, K. Indifferents as an interface between Contra and Pro. Acta Phys. Pol. A 2010, 117, 695–699. [Google Scholar] [CrossRef]
- Öztürk, M.K. Dynamics of discrete opinions without compromise. Adv. Complex Syst. 2013, 16, 1350010. [Google Scholar] [CrossRef]
- Bańcerowski, P.; Malarz, K. Multi-choice opinion dynamics model based on Latané theory. Eur. Phys. J. B 2019, 92, 219. [Google Scholar] [CrossRef]
- Kowalska-Styczeń, A.; Malarz, K. Noise induced unanimity and disorder in opinion formation. PLoS ONE 2020, 15, e0235313. [Google Scholar] [CrossRef]
- Martins, A.C.R. Discrete opinion dynamics with M choices. Eur. Phys. J. B 2020, 93, 1. [Google Scholar] [CrossRef]
- Zubillaga, B.; Vilela, A.; Wang, M.; Du, R.; Dong, G.; Stanley, H. Three-state majority-vote model on small-world networks. Sci. Rep. 2022, 12, 282. [Google Scholar] [CrossRef]
- Li, L.; Zeng, A.; Fan, Y.; Di, Z. Modeling multi-opinion propagation in complex systems with heterogeneous relationships via Potts model on signed networks. Chaos 2022, 32, 083101. [Google Scholar] [CrossRef]
- Doniec, M.; Lipiecki, A.; Sznajd-Weron, K. Consensus, Polarization and Hysteresis in the Three-State Noisy q-Voter Model with Bounded Confidence. Entropy 2022, 24, 983. [Google Scholar] [CrossRef]
- Xiong, F.; Liu, Y.; Wang, L.; Wang, X. Analysis and application of opinion model with multiple topic interactions. Chaos 2017, 27, 083113. [Google Scholar] [CrossRef]
- Galam, S. The drastic outcomes from voting alliances in three-party democratic voting (1990–2013). J. Stat. Phys. 2013, 151, 46–68. [Google Scholar] [CrossRef]
- Wu, D.; Szeto, K.Y. Analysis of timescale to consensus in voting dynamics with more than two options. Phys. Rev. E 2018, 97, 042320. [Google Scholar] [CrossRef] [PubMed]
- Nowak, A.; Szamrej, J.; Latané, B. From private attitude to public opinion: A dynamic theory of social impact. Psychol. Rev. 1990, 97, 362–376. [Google Scholar] [CrossRef]
- Darley, J.M.; Latané, B. Bystander intervention in emergencies—Diffusion of responsibility. J. Personal. Soc. Psychol. 1968, 8, 377–383. [Google Scholar] [CrossRef] [PubMed]
- Latané, B.; Harkins, S. Cross-modality matches suggest anticipated stage fright a multiplicative power function of audience size and status. Percept. Psychophys. 1976, 20, 482–488. [Google Scholar] [CrossRef]
- Latané, B. The psychology of social impact. Am. Psychol. 1981, 36, 343–356. [Google Scholar] [CrossRef]
- Kacperski, K.; Hołyst, J.A. Phase transitions as a persistent feature of groups with leaders in models of opinion formation. Physica A 2000, 287, 631–643. [Google Scholar] [CrossRef]
- Hołyst, J.A.; Kacperski, K.; Schweitzer, F. Phase transitions in social impact models of opinion formation. Physica A 2000, 285, 199–210. [Google Scholar] [CrossRef]
- Kowalska-Styczeń, A.; Malarz, K. Are randomness of behavior and information flow important to opinion forming in organization? In Proceedings of the 36th International Business Information Management Association Conference, Granada, Spain, 4–5 November 2020; Soliman, K.S., Ed.; International Business Information Management Associationa: King of Prussia, PA, USA, 2020; pp. 10691–10698. [Google Scholar] [CrossRef]
- Hołyst, J.A.; Kacperski, K.; Schweitzer, F. Social Impact Models of Opinion Dynamics. In Annual Reviews of Computational Physics IX; Stauffer, D., Ed.; World Scientific: Singapore, 2011; pp. 253–273. [Google Scholar] [CrossRef]
- Bańcerowski, P. Modeling of Opinion Formation Based on Latané Theory. Master’s Thesis, AGH University of Science and Technology, Kraków, Poland, 2017. (In Polish). [Google Scholar]
- Dworak, M. Modeling of Public Opinion Dynamics in a System with Many Available Discrete Opinions. Master’s Thesis, AGH University of Science and Technology, Kraków, Poland, 2022. (In Polish). [Google Scholar]
- Kułakowski, K. A note on temperature without energy—A social example. arXiv 2008, arXiv:0807.0711. [Google Scholar]
- Available online: http://www.zis.agh.edu.pl/app/MSc/Maciej_Dworak/ (accessed on 5 December 2022).
- Landau, D.P.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Hoshen, J.; Kopelman, R. Percolation and cluster distribution. 1. Cluster multiple labeling technique and critical concentration algorithm. Phys. Rev. B 1976, 14, 3438–3445. [Google Scholar] [CrossRef]
- Frijters, S.; Krüger, T.; Harting, J. Parallelised Hoshen–Kopelman algorithm for lattice-Boltzmann simulations. Comput. Phys. Commun. 2015, 189, 92–98. [Google Scholar] [CrossRef]
- Kotwica, M.; Gronek, P.; Malarz, K. Efficient space virtualisation for Hoshen–Kopelman algorithm. Int. J. Mod. Phys. C 2019, 30, 1950055. [Google Scholar] [CrossRef]
- Ren, J.; Wang, W.X.; Qi, F. Randomness enhances cooperation: A resonance-type phenomenon in evolutionary games. Phys. Rev. E 2007, 75, 045101. [Google Scholar] [CrossRef] [PubMed]
- Shirado, H.; Christakis, N.A. Locally noisy autonomous agents improve global human coordination in network experiments. Nature 2017, 545, 370–374. [Google Scholar] [CrossRef] [PubMed]
- De Sanctis, L.; Galla, T. Effects of noise and confidence thresholds in nominal and metric Axelrod dynamics of social influence. Phys. Rev. E 2009, 79, 046108. [Google Scholar] [CrossRef] [PubMed]
- Biondo, A.E.; Pluchino, A.; Rapisarda, A. The Beneficial Role of Random Strategies in Social and Financial Systems. J. Stat. Phys. 2013, 151, 607–622. [Google Scholar] [CrossRef]
- Su, W.; Chen, G.; Hong, Y. Noise leads to quasi-consensus of Hegselmann–Krause opinion dynamics. Automatica 2017, 85, 448–454. [Google Scholar] [CrossRef]
- Dunbar, R.; Gamble, C.; Gowlett, J. Social Brain, Distributed Mind; British Academy: London, UK, 2010. [Google Scholar] [CrossRef]
- Sutcliffe, A.; Dunbar, R.; Binder, J.; Arrow, H. Relationships and the social brain: Integrating psychological and evolutionary perspectives. Br. J. Psychol. 2012, 103, 149–168. [Google Scholar] [CrossRef]
- Arnaboldi, V.; Conti, M.; La Gala, M.; Passarella, A.; Pezzoni, F. Ego network structure in online social networks and its impact on information diffusion. Comput. Commun. 2016, 76, 26–41. [Google Scholar] [CrossRef]
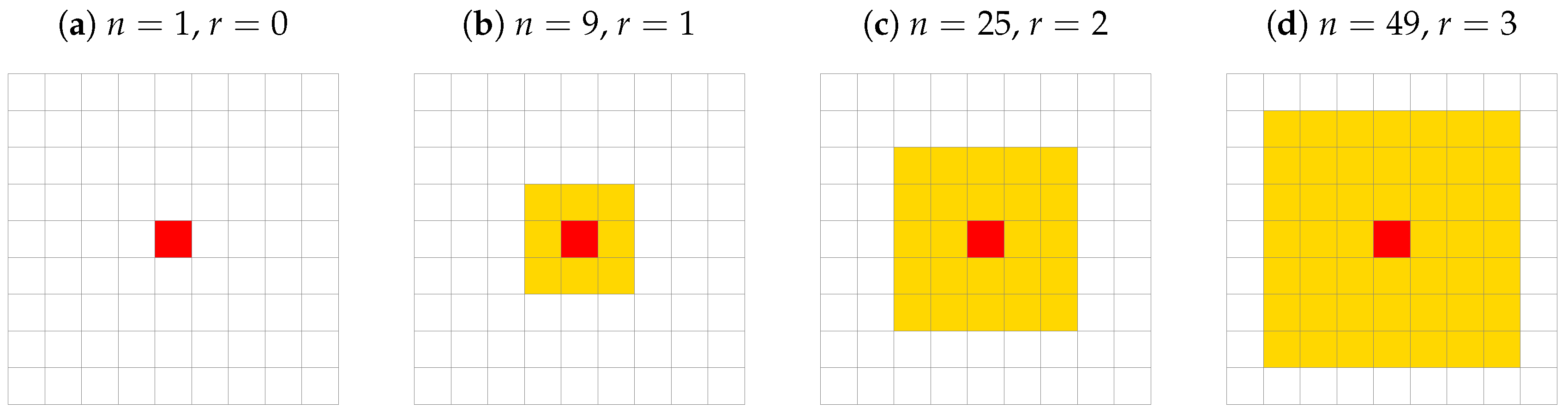

| 2 | 3 | 4 | 6 | |
|---|---|---|---|---|
| n | ||||
| 1 | 0.05987(13) | 0.14973(63) | 0.2209(13) | 0.2902(16) |
| 9 | 0.25269(45) | 0.58795(79) | 0.80513(74) | 0.95820(21) |
| 25 | 0.39642(56) | 0.76437(75) | 0.92761(38) | 0.993687(41) |
| 49 | 0.49898(57) | 0.84573(64) | 0.96450(21) | 0.998328(12) |
| 81 | 0.57600(53) | 0.89073(54) | 0.97971(13) | 0.9994007(45) |
| 121 | 0.63641(46) | 0.91866(44) | 0.987262(83) | 0.9997408(20) |
| 169 | 0.68530(41) | 0.93739(36) | 0.991477(58) | 0.9998727(10) |
| 225 | 0.72578(35) | 0.95064(29) | 0.994033(42) | 0.99993158(54) |
| 289 | 0.75989(31) | 0.96039(24) | 0.995680(31) | 0.99996061(31) |
| 361 | 0.78903(28) | 0.96778(20) | 0.996790(23) | 0.99997609(18) |
| n | ||||
| 1 | 0.05990(17) | 0.15080(92) | 0.2232(16) | 0.2937(22) |
| 9 | 0.25275(62) | 0.5873(15) | 0.8041(10) | 0.95793(26) |
| 25 | 0.39649(85) | 0.7635(13) | 0.92698(53) | 0.993625(52) |
| 49 | 0.49906(96) | 0.8449(11) | 0.96414(29) | 0.998311(15) |
| 81 | 0.5761(10) | 0.89006(90) | 0.97950(18) | 0.9993947(53) |
| 121 | 0.6365(10) | 0.91812(72) | 0.98712(12) | 0.9997382(22) |
| 169 | 0.6854(10) | 0.93694(59) | 0.991385(81) | 0.9998715(10) |
| 225 | 0.72586(96) | 0.95027(48) | 0.993969(57) | 0.99993091(62) |
| 289 | 0.75996(93) | 0.96008(39) | 0.995633(41) | 0.99996022(35) |
| 361 | 0.78909(88) | 0.96753(32) | 0.996755(31) | 0.99997585(21) |
| n | ||||
| 1 | 0.05990(16) | 0.15095(98) | 0.2247(20) | 0.2962(27) |
| 9 | 0.25275(50) | 0.5871(15) | 0.80338(98) | 0.95757(28) |
| 25 | 0.39649(65) | 0.7633(14) | 0.92657(51) | 0.993549(51) |
| 49 | 0.49906(70) | 0.8448(11) | 0.96393(29) | 0.998291(15) |
| 81 | 0.57609(70) | 0.88999(90) | 0.97938(18) | 0.9993876(54) |
| 121 | 0.63649(69) | 0.91807(74) | 0.98705(12) | 0.9997353(22) |
| 169 | 0.68538(66) | 0.93690(60) | 0.991331(79) | 0.9998701(12) |
| 225 | 0.72586(63) | 0.95024(49) | 0.993931(56) | 0.99993012(63) |
| 289 | 0.75997(59) | 0.96006(41) | 0.995605(40) | 0.99995976(36) |
| 361 | 0.78911(56) | 0.96751(34) | 0.996735(30) | 0.99997557(21) |
| n | ||||
| 1 | 0.05988(15) | 0.1511(10) | 0.2248(21) | 0.2976(26) |
| 9 | 0.25267(48) | 0.5867(15) | 0.8029(11) | 0.95741(29) |
| 25 | 0.39638(58) | 0.7629(13) | 0.92634(61) | 0.993525(55) |
| 49 | 0.49893(59) | 0.8445(11) | 0.96380(34) | 0.998284(15) |
| 81 | 0.57595(57) | 0.88970(90) | 0.97930(21) | 0.9993847(57) |
| 121 | 0.63634(55) | 0.91784(73) | 0.98700(14) | 0.9997340(25) |
| 169 | 0.68523(53) | 0.93673(60) | 0.991302(92) | 0.9998694(12) |
| 225 | 0.72571(51) | 0.95010(49) | 0.993909(65) | 0.99992979(66) |
| 289 | 0.75982(49) | 0.95995(40) | 0.995590(46) | 0.99995958(37) |
| 361 | 0.78896(49) | 0.96742(33) | 0.996723(35) | 0.99997546(24) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dworak, M.; Malarz, K. Vanishing Opinions in Latané Model of Opinion Formation. Entropy 2023, 25, 58. https://doi.org/10.3390/e25010058
Dworak M, Malarz K. Vanishing Opinions in Latané Model of Opinion Formation. Entropy. 2023; 25(1):58. https://doi.org/10.3390/e25010058
Chicago/Turabian StyleDworak, Maciej, and Krzysztof Malarz. 2023. "Vanishing Opinions in Latané Model of Opinion Formation" Entropy 25, no. 1: 58. https://doi.org/10.3390/e25010058
APA StyleDworak, M., & Malarz, K. (2023). Vanishing Opinions in Latané Model of Opinion Formation. Entropy, 25(1), 58. https://doi.org/10.3390/e25010058







