Quantitative Study of Non-Linear Convection Diffusion Equations for a Rotating-Disc Electrode
Abstract
1. Introduction
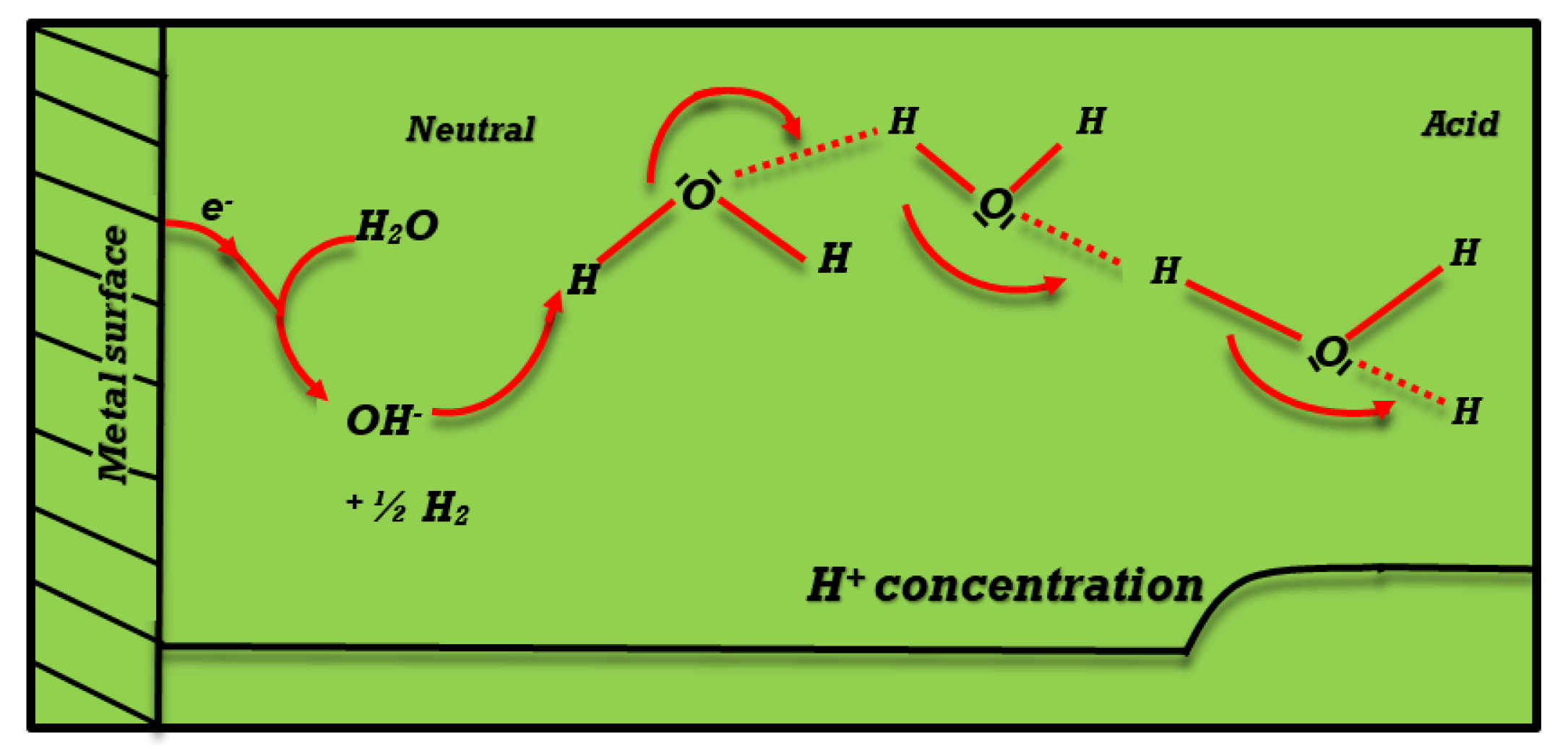
- This study’s primary goals were to analyze a mathematical model for the reduction of ions and electrolysis of in non-buffered aqueous electrolyte solutions and to investigate how specific parameters affect the e entropy of hydrogen () and hydroxide () ions in a rotating-disc electrode (RDE).
- The mathematical model of the convection-diffusion equation for the non-dimensional hydrogen () and hydroxide () ion concentrations on a rotating-disc electrode (RDE) has been solved for this problem.
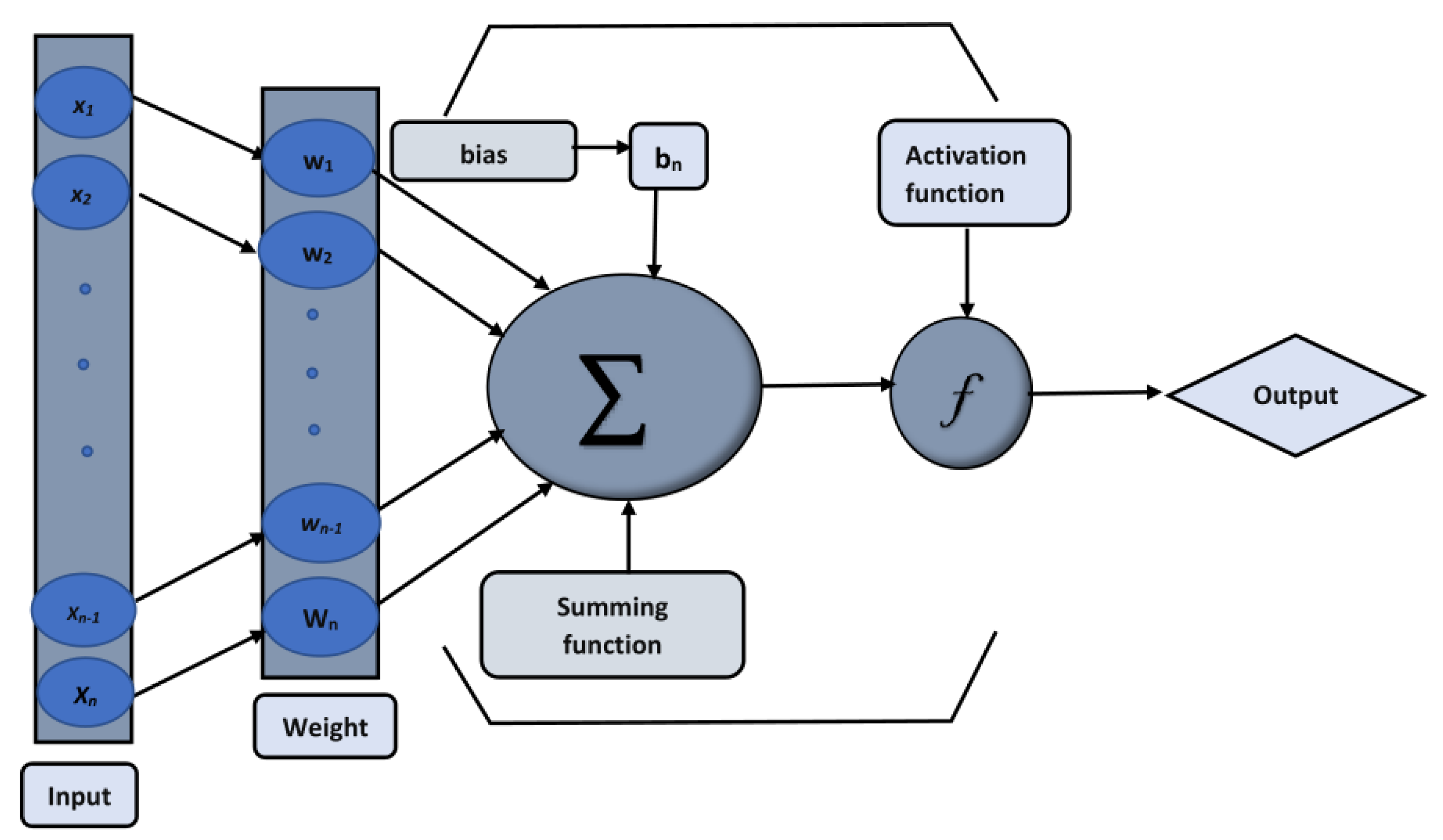
- The behavior of the hydrogen () and hydroxide () ion concentrations are studied using the backpropagated Levenberg–Marquardt algorithm (BLMA) and neural networks (NNs).
- The reference data of target solutions were produced by the Runge–Kutta technique and were successfully used in the supervised learning phase of the NNs-BLMA.
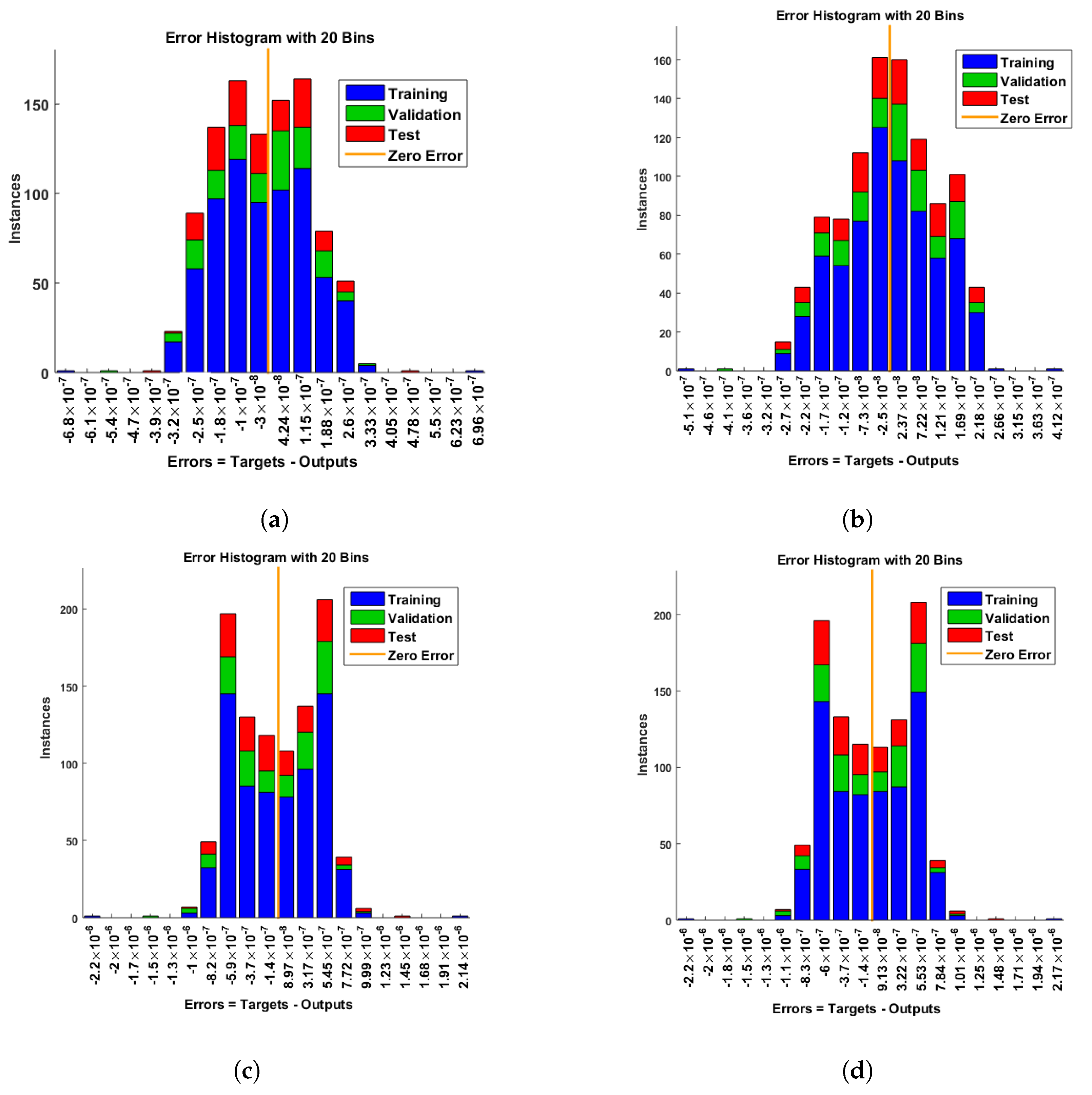
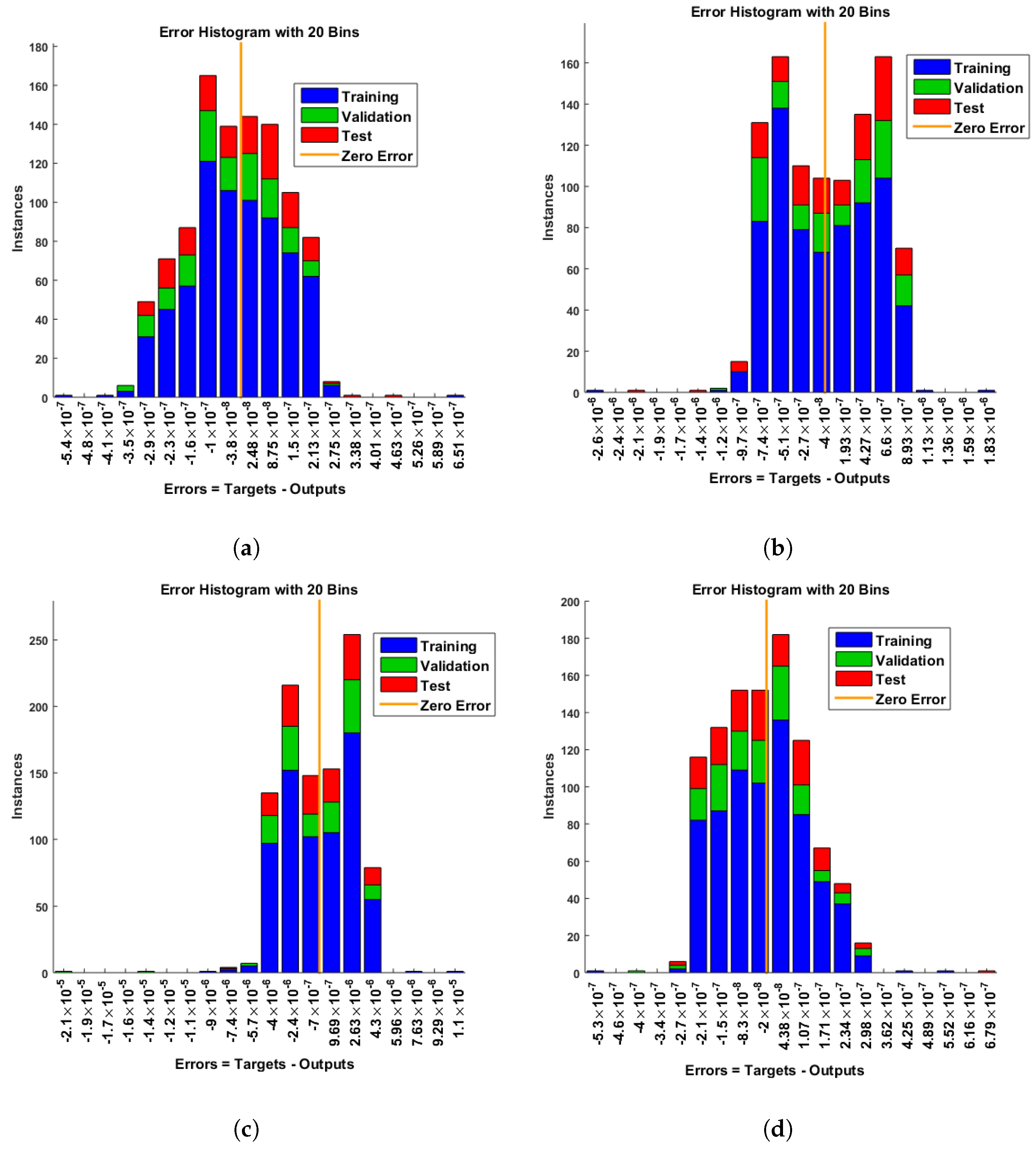
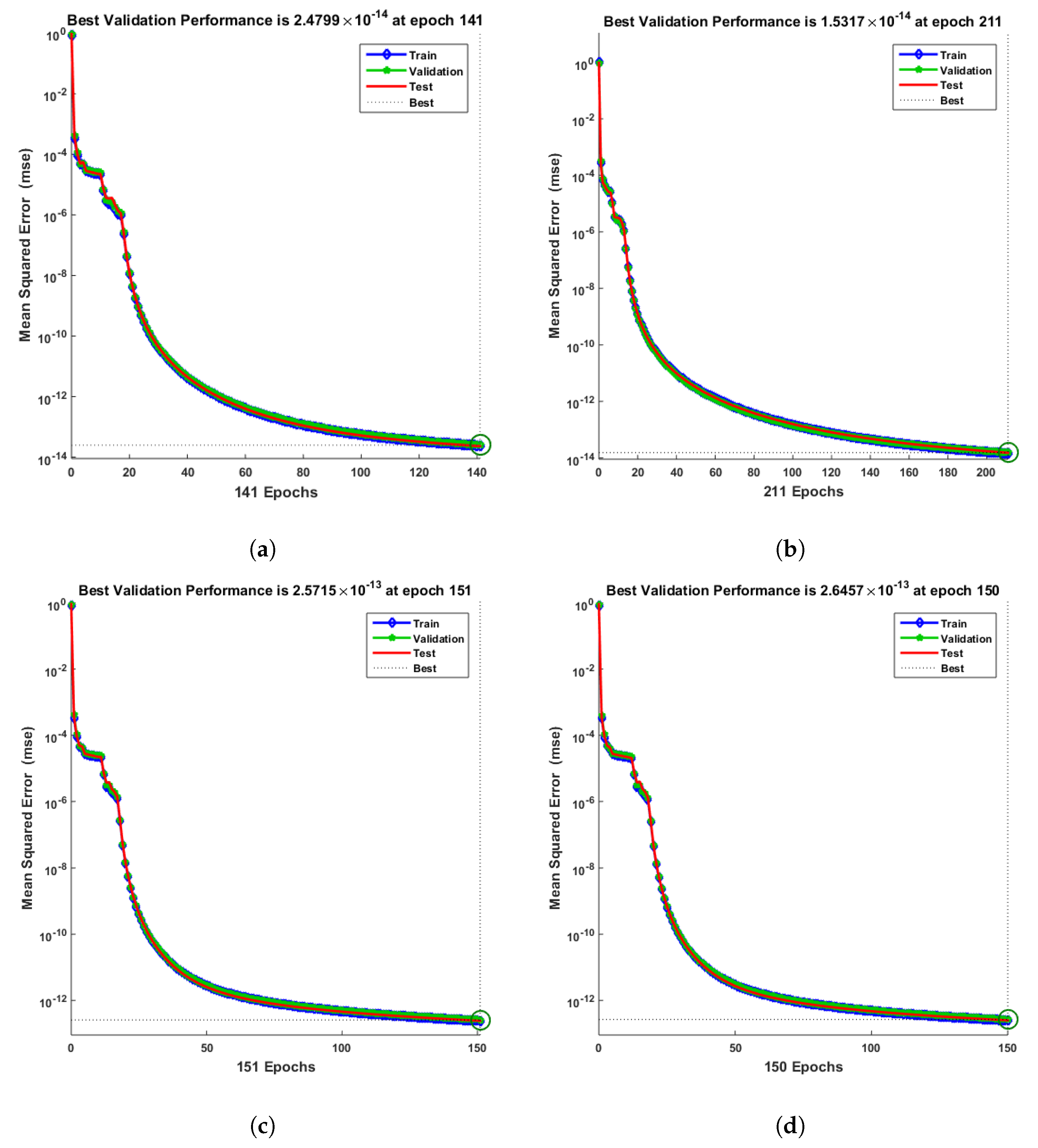
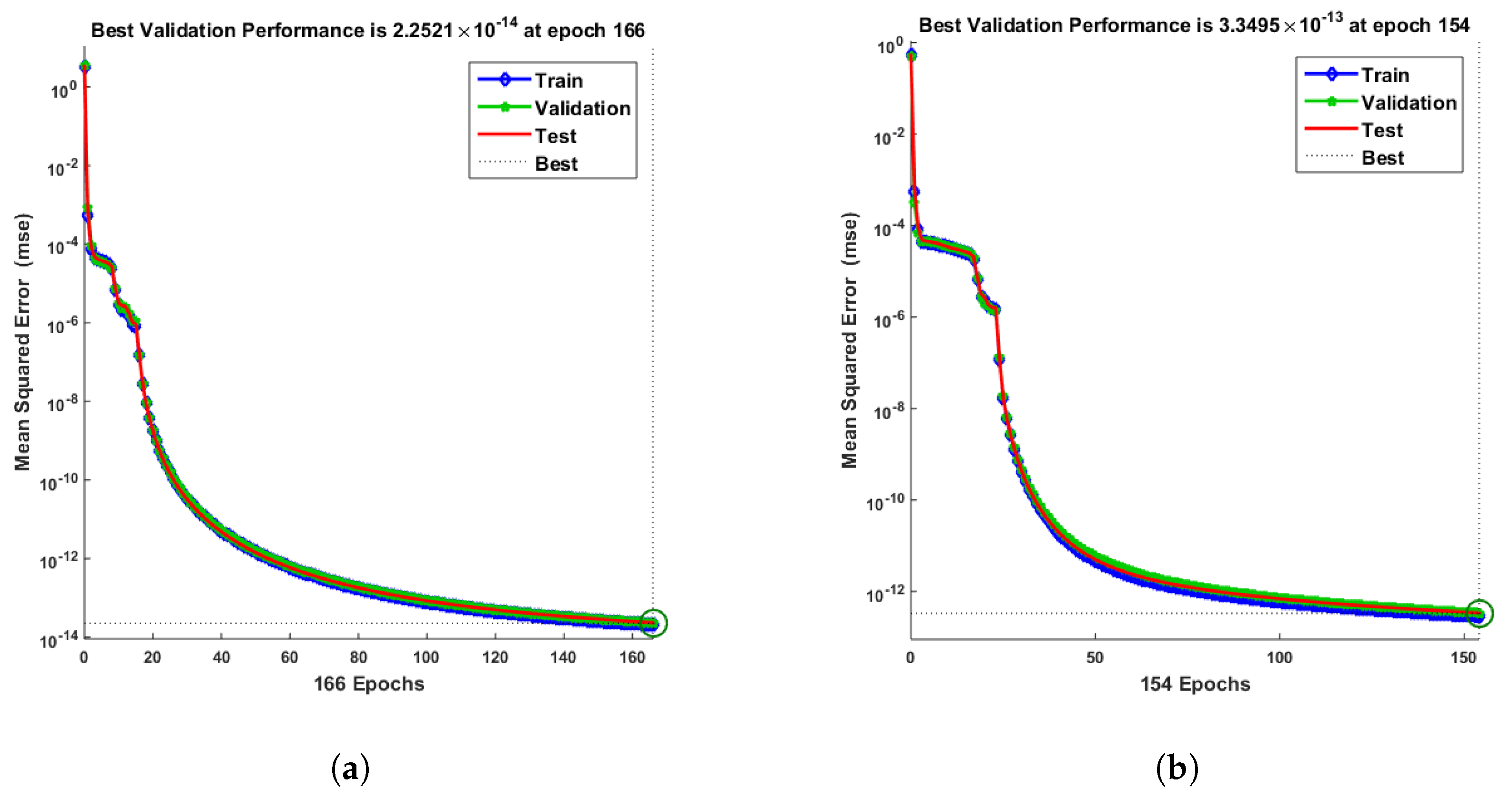
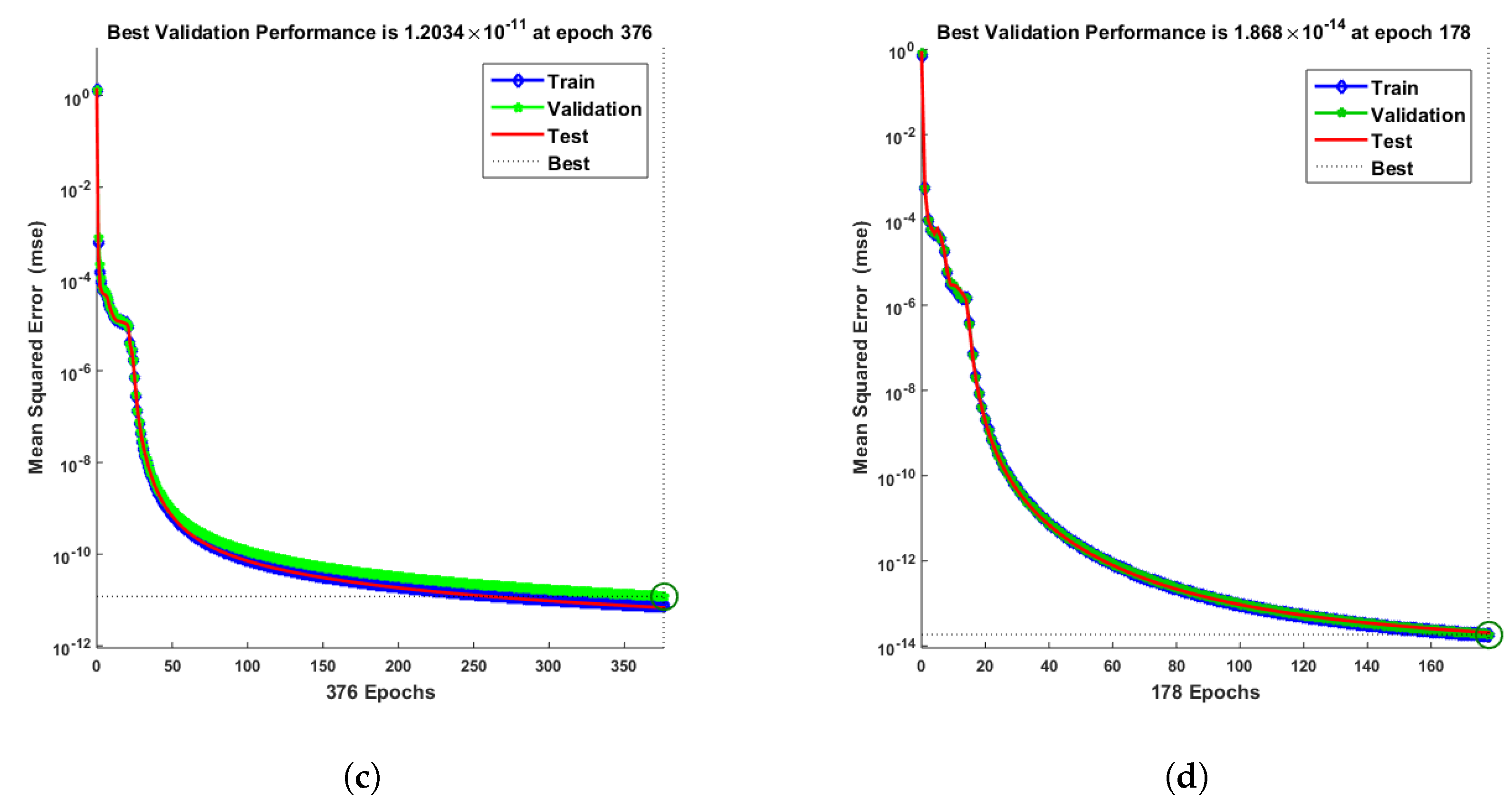
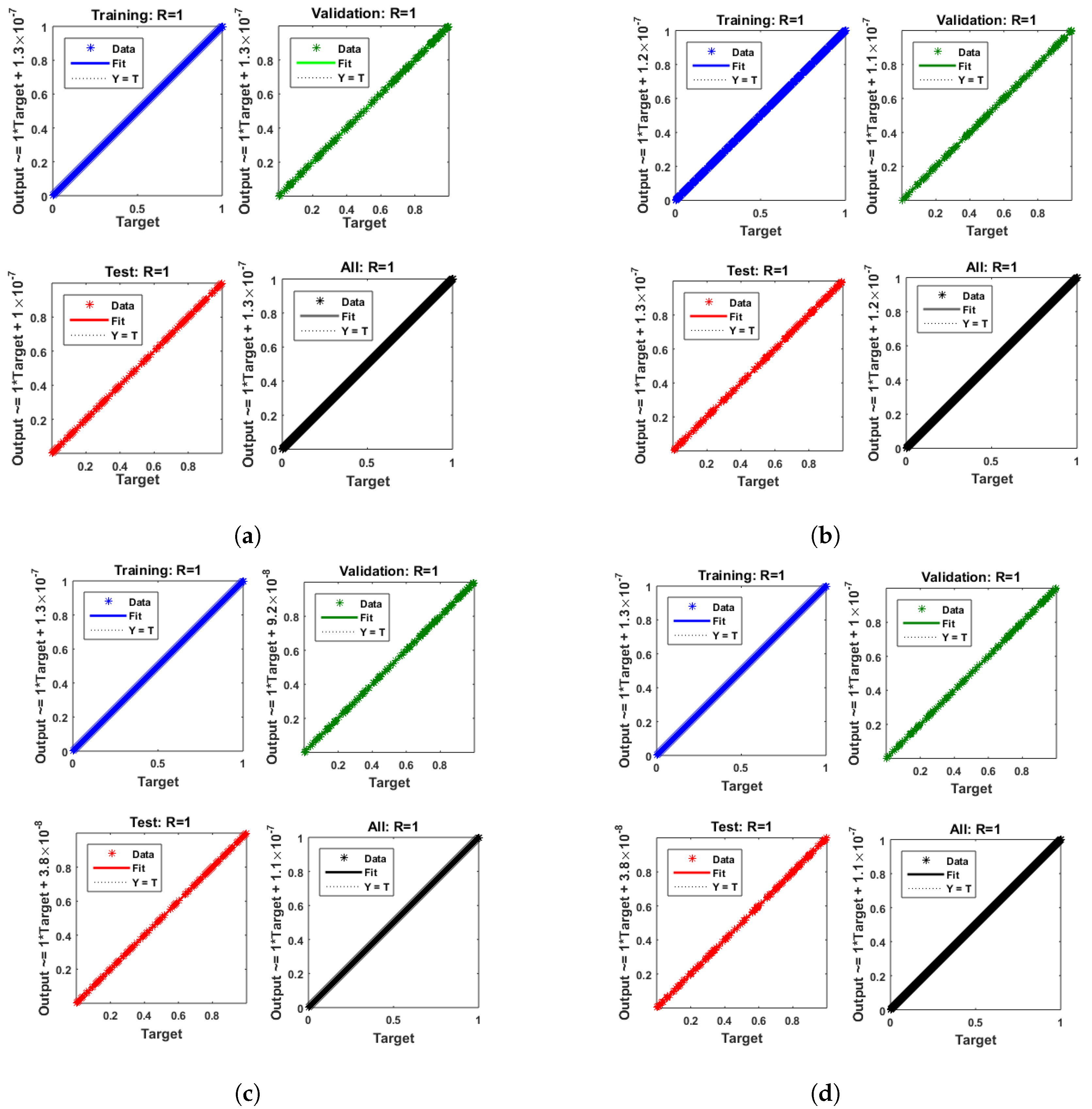
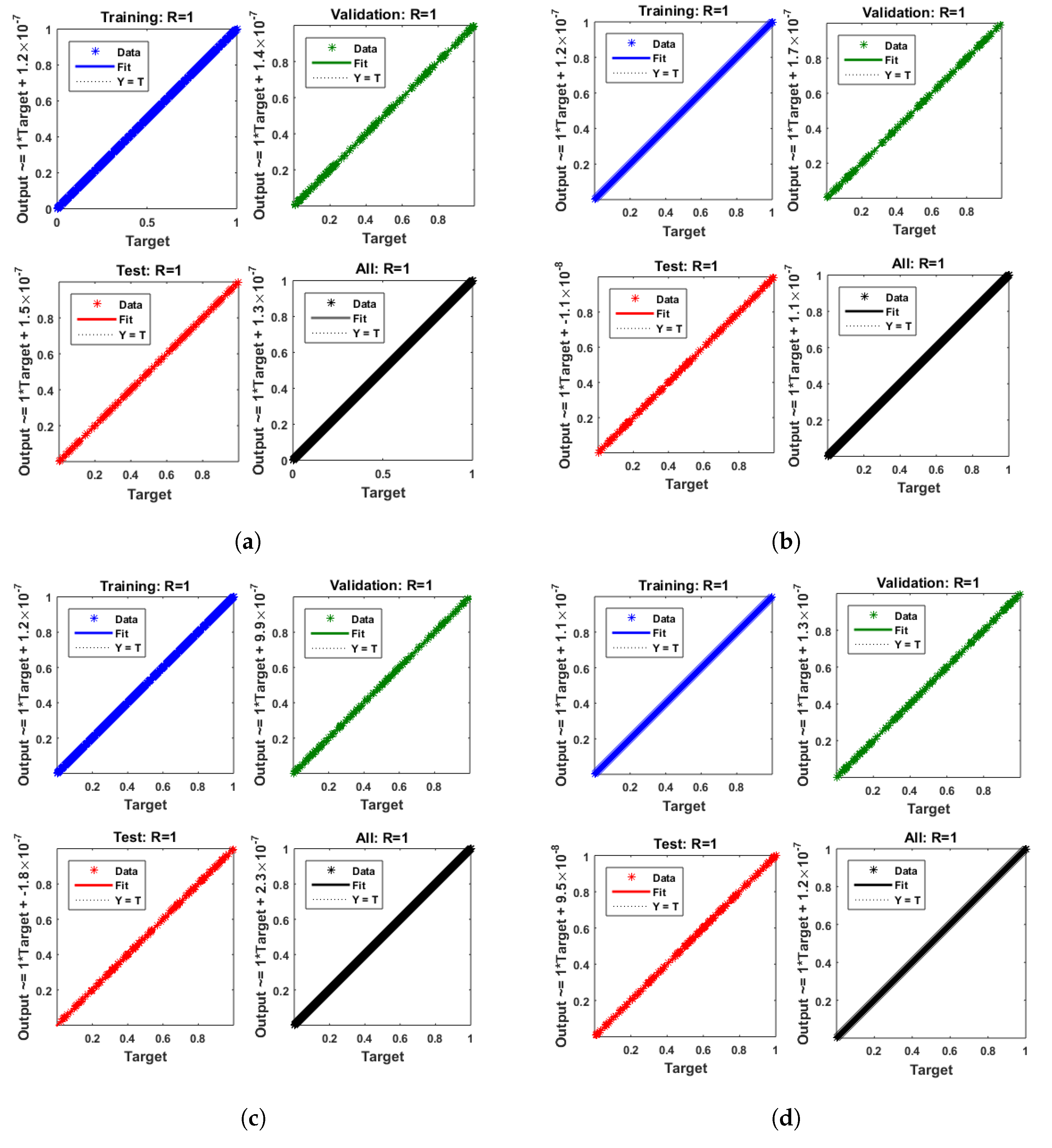
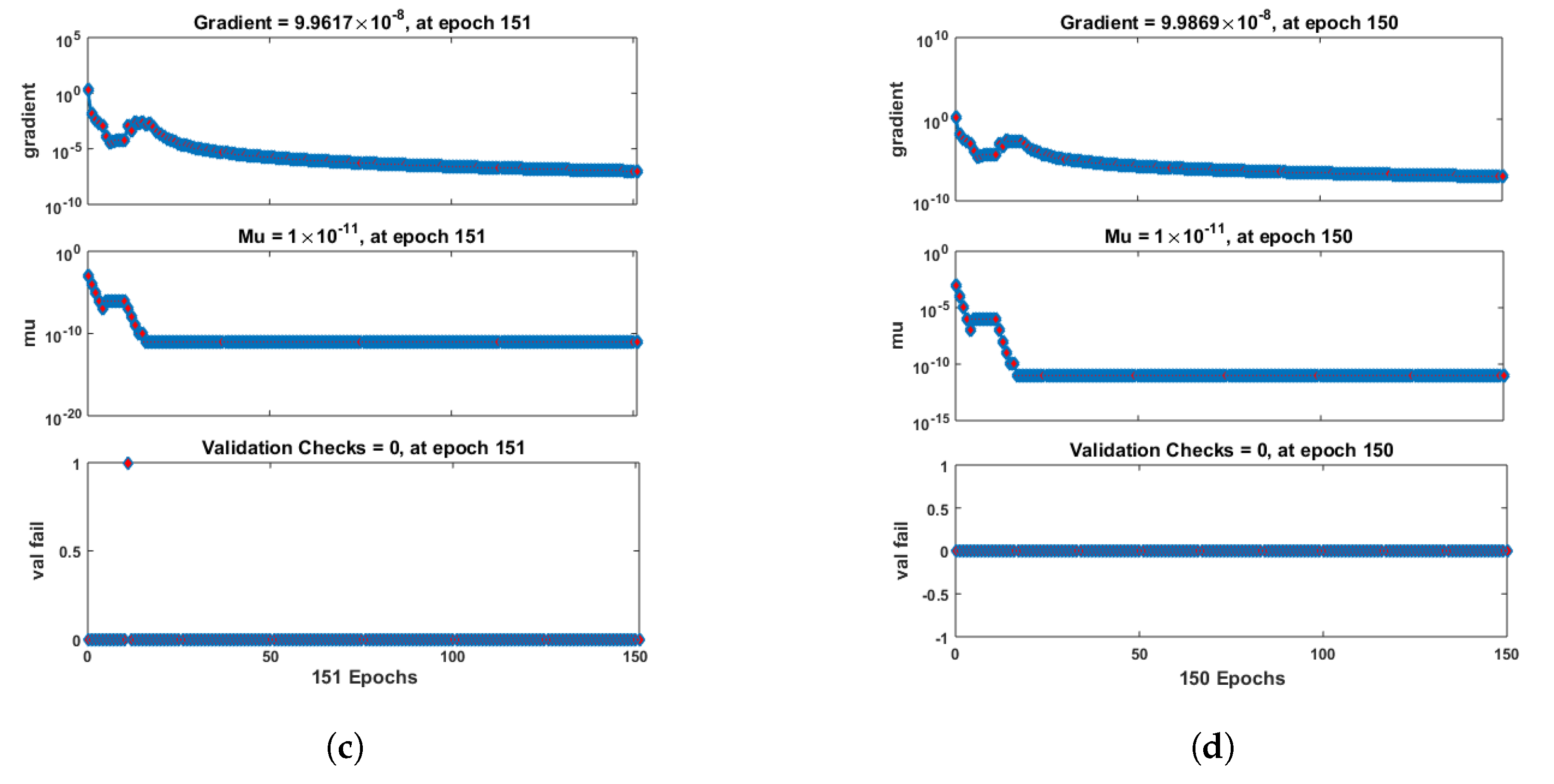
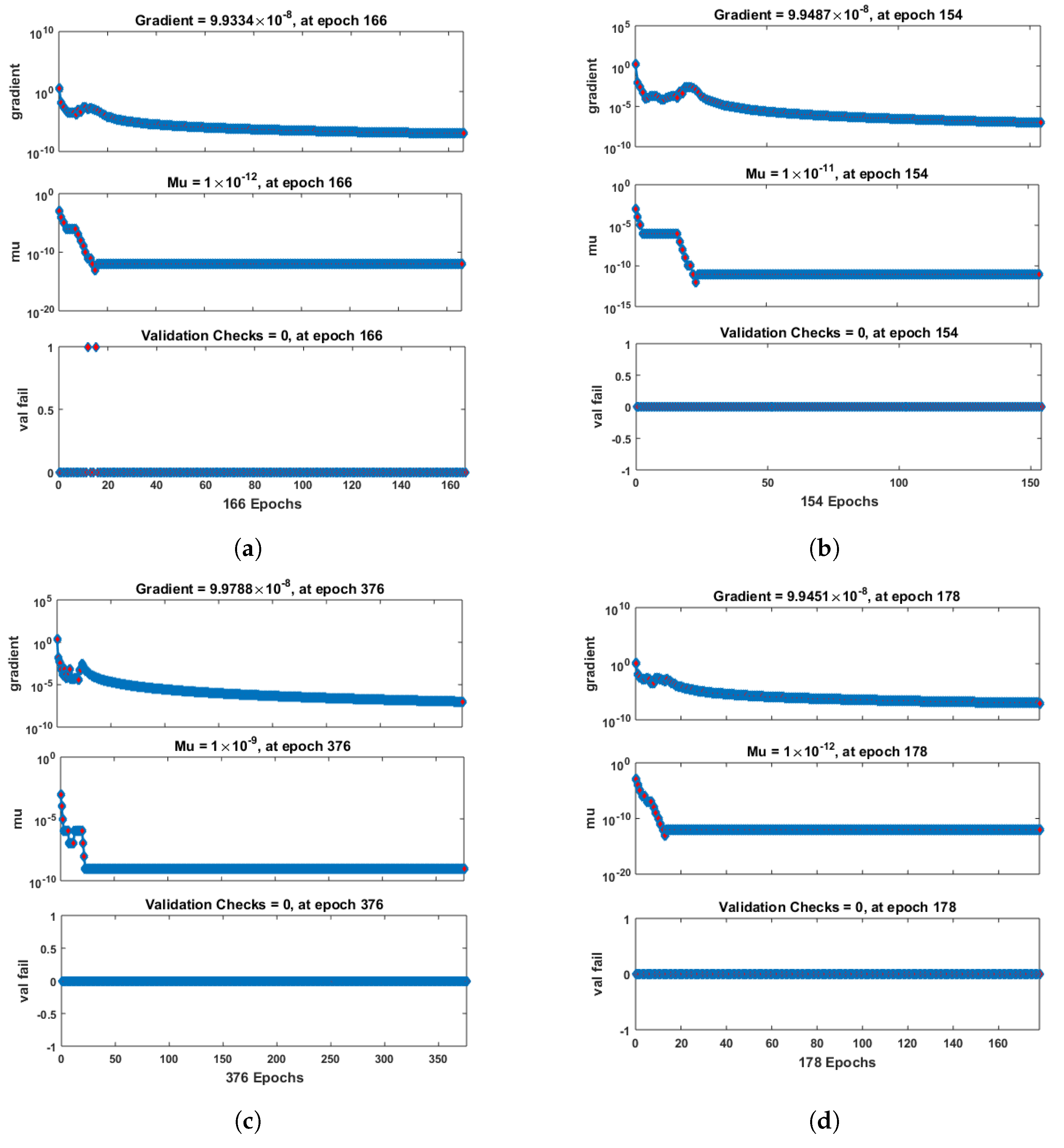
- Convergence analysis based on curve fitting, mean-square error, error histograms, and regression analysis by reference data was used to verify the effectiveness of the designed NN-BLMA. The results establish that the suggested method is slick and straightforward, extending to more complex problems.
2. Mathematical Formulation of the Problem
- (i)
- At z = 0, the two species become
- (ii)
- As z →∞, the concentration of ions () equals the bulk concentration of ions (), and the concentration of ions () approaches zero. That is,
- (iii)
- In the first step, a numerical solution is computed using the Runge–Kutta technique of fourth order () using Mathematica’s “ND Solve” module to create an initial dataset.
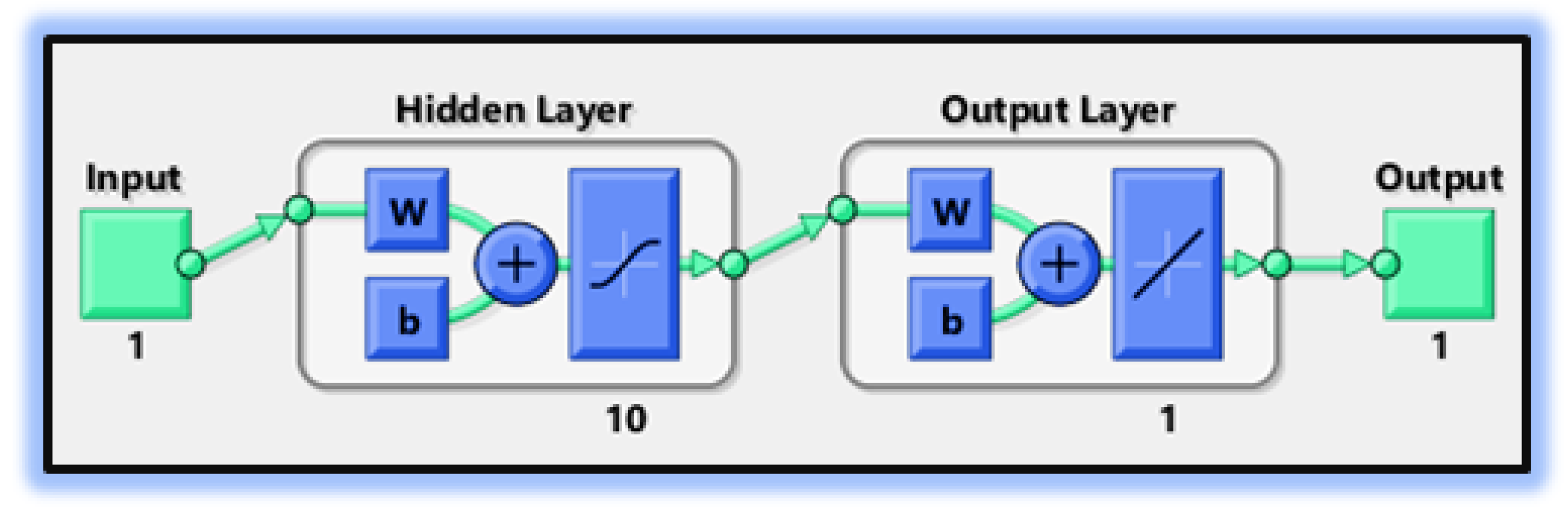
- In the second step, using the “nftool” from the MATLAB package, the BLM algorithm is run with the proper hidden neuron parameters and test data. Additionally, BLM employs the training, testing, and validation process and a reference solution to provide approximations for various nonlinear equation instances. Figure 2 and Figure 3 illustrate the NNs-LM technique using a single neuron model.
3. Comparison of Numerical Solutions
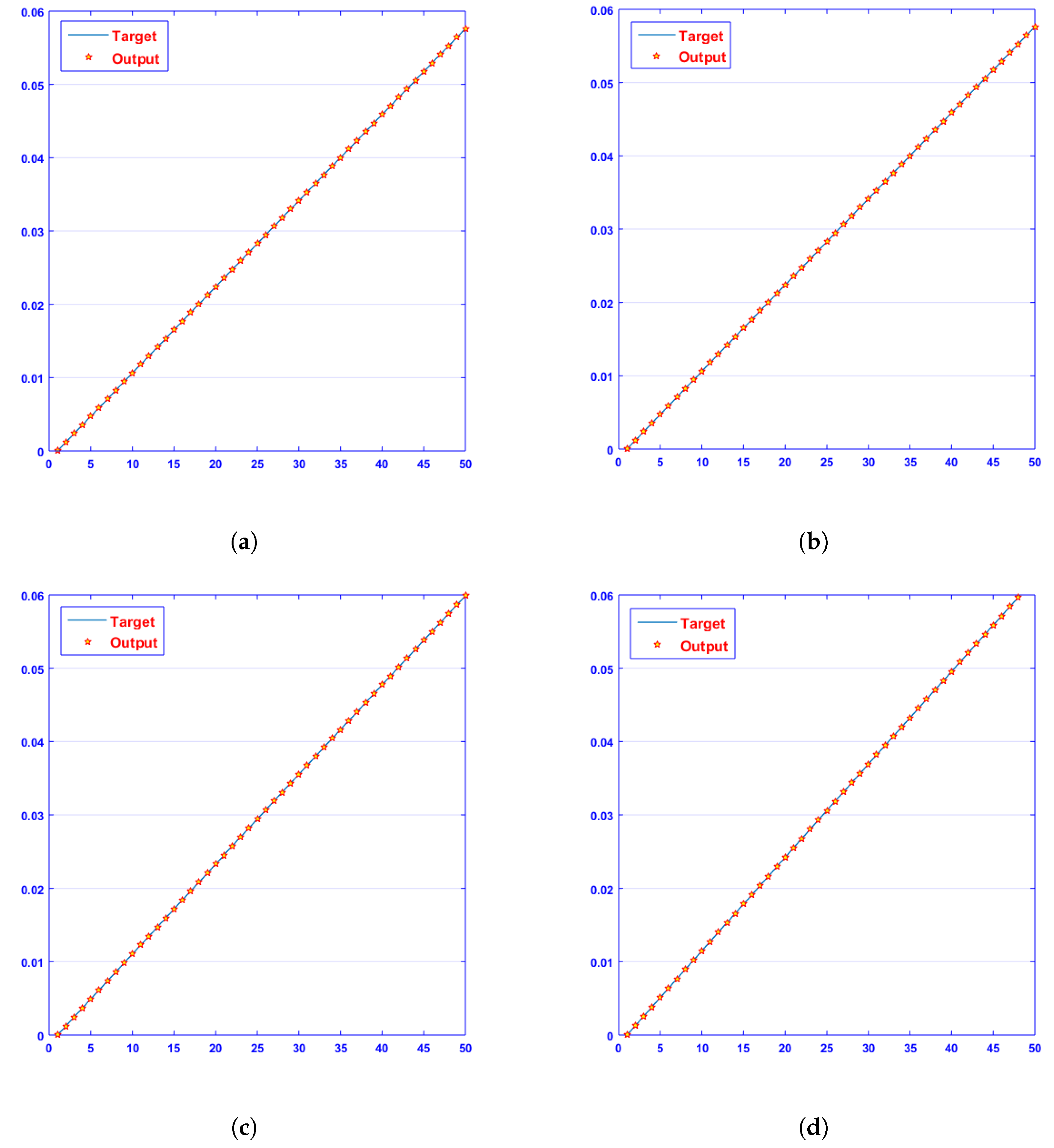
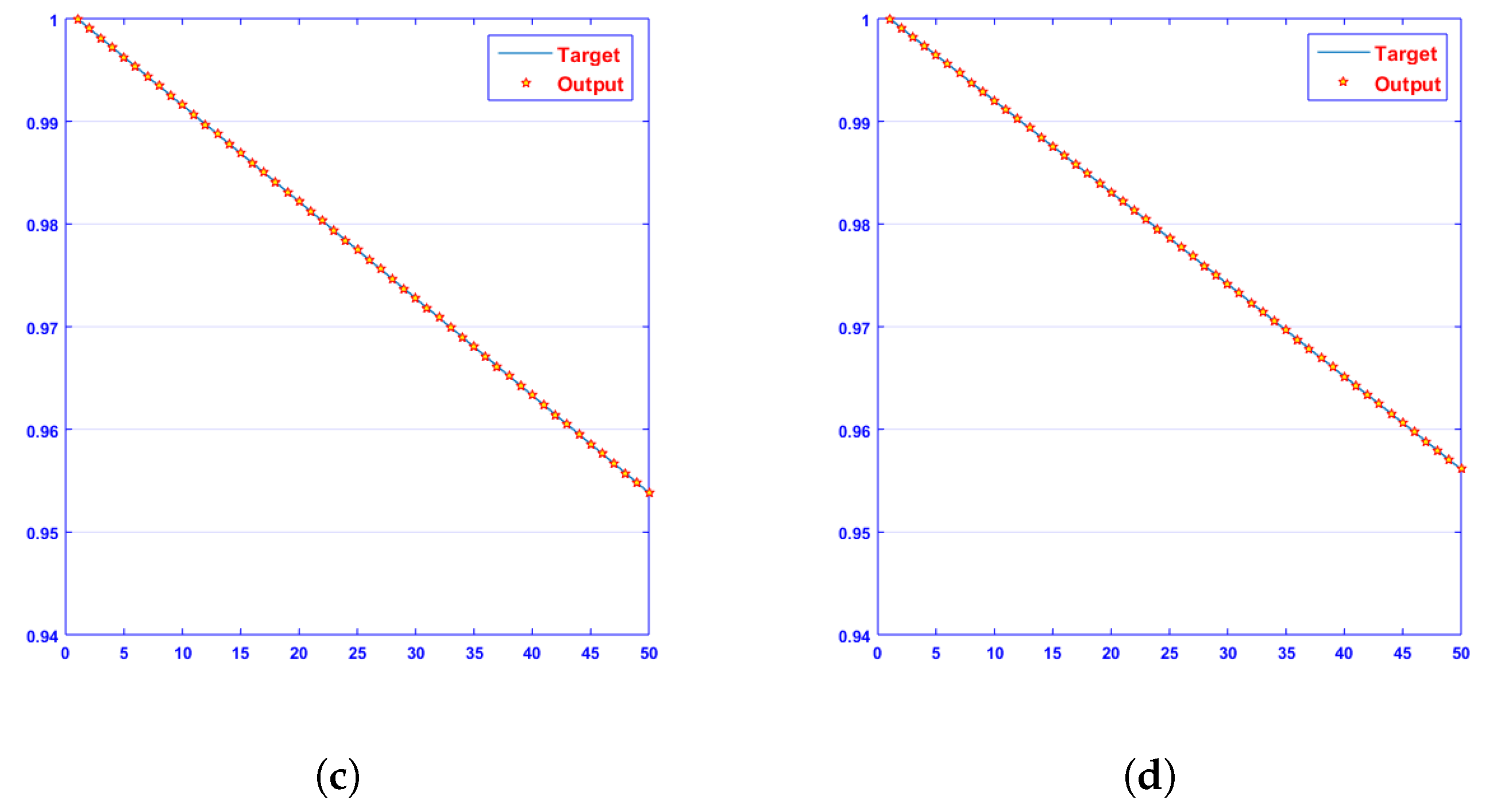
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| ion concentration | mol cm−3 | |
| ion concentration | mol cm−3 | |
| ion bulk concentration | mol cm−3 | |
| ion bulk concentration | mol cm−3 | |
| coefficient of diffusion of ions | cm−2 s−1 | |
| coefficient of diffusion of ions | cm−2 s−1 | |
| kinematic viscosity | cm2 s−1 | |
| rotation rate | s−1 | |
| forward rate coefficient | mol−1 s−1 cm3 | |
| backward rate coefficient | mol s−1 cm−3 | |
| = −0.51 | velocity | cm s−1 |
| a = 0.51023 | parameter | cm−1 s−1 |
| = | dimensionless backward rate coefficient | none |
| = | dimensionless forward rate coefficient | none |
| m = uv + | parameter | none |
| current | Ampere (or) C s−1 | |
| potential | volt | |
| F | Faraday constant | C mol−1 |
| A | area | cm−2 |
| T | temperature | K |
| dimensionless axial distance | none | |
| Z | axial distance | cm |
References
- Albery, W.J.; Bruckenstein, S. Uniformly accessible electrodes. J. Electroanal. Chem. Interfacial Electrochem. 1983, 144, 105–112. [Google Scholar] [CrossRef]
- Shi, M.; Wang, R.; Li, L.; Chen, N.; Xiao, P.; Yan, C.; Yan, X. Redox-Active Polymer Integrated with MXene for Ultra-Stable and Fast Aqueous Proton Storage. Adv. Funct. Mater. 2022. [CrossRef]
- Levich, V.G. Physicochemical Hydrodynamics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]
- Koutecky, J.; Levich, V. The use of a rotating disk electrode in the studies of electrochemical kinetics and electrolytic processes. Russ. J. Phys. Chem. A 1958, 32, 1565–1575. [Google Scholar]
- Bockris, J.O.; Conway, B.E.; White, R.E. Modern Aspects of Electrochemistry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1992; Volume 22. [Google Scholar]
- Kármán, T.v. Über laminare und turbulente Reibung. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. 1921, 1, 233–252. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Fedorov, R.V.; Karpukhina, T.V.; Simos, T.E.; Tsitouras, C. Runge–Kutta Embedded Methods of Orders 8 (7) for Use in Quadruple Precision Computations. Mathematics 2022, 10, 3247. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M. Heat transfer and thermal conductivity of magneto micropolar fluid with thermal non-equilibrium condition passing through the vertical porous medium. Waves Random Complex Media 2022, 1–25. [Google Scholar] [CrossRef]
- Bruckenstein, S.; Miller, B. Unraveling reactions with rotating electrodes. Accounts Chem. Res. 1977, 10, 54–61. [Google Scholar] [CrossRef]
- Popović, N.D.; Johnson, D.C. A Ring- Disk Study of the Competition between Anodic Oxygen-Transfer and Dioxygen-Evolution Reactions. Anal. Chem. 1998, 70, 468–472. [Google Scholar] [CrossRef]
- Chang, H.; Johnson, D.C. Electrocatalysis of anodic oxygen-transfer reactions: Chronoamperometric and voltammetric studies of the nucleation and electrodeposition of β-lead dioxide at a rotated gold disk electrode in acidic media. J. Electrochem. Soc. 1989, 136, 17. [Google Scholar] [CrossRef]
- Treimer, S.E.; Feng, J.; Scholten, M.D.; Johnson, D.C.; Davenport, A.J. Comparison of Voltammetric Responses of Toluene and Xylenes at Iron (III)-Doped, Bismuth (V)-Doped, and Undoped β-Lead Dioxide Film Electrodes in 0.50 M H2SO4. J. Electrochem. Soc. 2001, 148, E459. [Google Scholar] [CrossRef]
- Treimer, S.; Tang, A.; Johnson, D.C. A Consideration of the application of Kouteckỳ-Levich plots in the diagnoses of charge-transfer mechanisms at rotated disk electrodes. Electroanalysis 2002, 14, 165–171. [Google Scholar] [CrossRef]
- Borrás, C.; Rodríguez, P.; Laredo, T.; Mostany, J.; Scharifker, B. Electrooxidation of aqueous p-methoxyphenol on lead oxide electrodes. J. Appl. Electrochem. 2004, 34, 583–589. [Google Scholar] [CrossRef]
- Cahan, B.; Villullas, H. The hanging meniscus rotating disk (HMRD). J. Electroanal. Chem. Interfacial Electrochem. 1991, 307, 263–268. [Google Scholar] [CrossRef]
- Khan, M.F.; Sulaiman, M.; Alshammari, F.S. A hybrid heuristic-driven technique to study the dynamics of savanna ecosystem. Stoch. Environ. Res. Risk Assess. 2022, 1–25. [Google Scholar] [CrossRef]
- Newman, J. Current distribution on a rotating disk below the limiting current. J. Electrochem. Soc. 1966, 113, 1235. [Google Scholar] [CrossRef]
- Lu, S.; Yin, Z.; Liao, S.; Yang, B.; Liu, S.; Liu, M.; Yin, L.; Zheng, W. An asymmetric encoder–decoder model for Zn-ion battery lifetime prediction. Energy Rep. 2022, 8, 33–50. [Google Scholar] [CrossRef]
- Eddowes, M.J. Numerical methods for the solution of the rotating disc electrode system. J. Electroanal. Chem. Interfacial Electrochem. 1983, 159, 1–22. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Alshammari, F.S. Analysis of heat transmission in convective, radiative and moving rod with thermal conductivity using meta-heuristic-driven soft computing technique. Struct. Multidiscip. Optim. 2022, 65, 317. [Google Scholar] [CrossRef]
- Nolan, J.E.; Plambeck, J.A. The EC-catalytic mechanism at the rotating disk electrode: Part I. Approximate theories for the pseudo-first-order case and applications to the Fenton reaction. J. Electroanal. Chem. Interfacial Electrochem. 1990, 286, 1–21. [Google Scholar] [CrossRef]
- Chung, K.L.; Tian, H.; Wang, S.; Feng, B.; Lai, G. Miniaturization of microwave planar circuits using composite microstrip/coplanar-waveguide transmission lines. Alex. Eng. J. 2022, 61, 8933–8942. [Google Scholar] [CrossRef]
- Nolan, J.E.; Plambeck, J.A. The EC-catalytic mechanism at the rotating disk electrode: Part II. Comparison of approximate theories for the second-order case and application to the reaction of bipyridinium cation radicals with dioxygen in non-aqueous solutions. J. Electroanal. Chem. Interfacial Electrochem. 1990, 294, 1–20. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Seidu, J.; Alshammari, F.S. Mathematical Analysis of the Prey-Predator System with Immigrant Prey Using the Soft Computing Technique. Discret. Dyn. Nat. Soc. 2022, 2022, 1241761. [Google Scholar] [CrossRef]
- Rani, P.J.; Kirthiga, M.; Molina, A.; Laborda, E.; Rajendran, L. Analytical solution of the convection-diffusion equation for uniformly accessible rotating disk electrodes via the homotopy perturbation method. J. Electroanal. Chem. 2017, 799, 175–180. [Google Scholar] [CrossRef]
- Wu, H.; Jin, S.; Yue, W. Pricing Policy for a Dynamic Spectrum Allocation Scheme with Batch Requests and Impatient Packets in Cognitive Radio Networks. J. Syst. Sci. Syst. Eng. 2022, 31, 133–149. [Google Scholar] [CrossRef]
- Devi, M.C.; Rajendran, L.; Yousaf, A.B.; Fernandez, C. Non-linear differential equations and rotating disc electrodes: Padé approximationtechnique. Electrochim. Acta 2017, 243, 1–6. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Khan, M.F.; Sulaiman, M.; Alshammari, F.S.; Laouini, G. Analysis of MHD Falkner-Skan Boundary Layer Flow and Heat Transfer Due to Symmetric Dynamic Wedge: A Numerical Study via the SCA-SQP-ANN Technique. Symmetry 2022, 14, 2180. [Google Scholar] [CrossRef]
- Dong, Q.; Santhanagopalan, S.; White, R.E. Simulation of the oxygen reduction reaction at an RDE in 0.5 m H2SO4 including an adsorption mechanism. J. Electrochem. Soc. 2007, 154, A888. [Google Scholar] [CrossRef]
- Alhakami, H.; Kamal, M.; Sulaiman, M.; Alhakami, W.; Baz, A. A Machine Learning Strategy for the Quantitative Analysis of the Global Warming Impact on Marine Ecosystems. Symmetry 2022, 14, 2023. [Google Scholar] [CrossRef]
- Grozovski, V.; Vesztergom, S.; Láng, G.G.; Broekmann, P. Electrochemical hydrogen evolution: H+ or H2O reduction? A rotating disk electrode study. J. Electrochem. Soc. 2017, 164, E3171. [Google Scholar] [CrossRef]
- Kamal, M.; Sulaiman, M.; Alshammari, F.S. Quantitative features analysis of a model for separation of dissolved substances from a fluid flow by using a hybrid heuristic. Eur. Phys. J. Plus 2022, 137, 1062. [Google Scholar] [CrossRef]
- Sylvia, S.V.; Salomi, R.J.; Rajendran, L. Mathematical modeling of hydrogen evolution at a rotating disk electrode. Proc. AIP Conf. Proc. 2020, 2277, 130012. [Google Scholar]
- Lin, Z.; Wang, H.; Li, S. Pavement anomaly detection based on transformer and self-supervised learning. Autom. Constr. 2022, 143, 104544. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R.; White, H.S. Electrochemical Methods: Fundamentals and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Ye, R.; Liu, P.; Shi, K.; Yan, B. State damping control: A novel simple method of rotor UAV with high performance. IEEE Access 2020, 8, 214346–214357. [Google Scholar] [CrossRef]
- Kanzaki, Y.; Tokuda, K.; Bruckenstein, S. Dissociation rates of weak acids using sinusoidal hydrodynamic modulated rotating disk electrode employing Koutecky-Levich equation. J. Electrochem. Soc. 2014, 161, H770. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Kumam, P.; Alarfaj, F.K. Application of Legendre polynomials based neural networks for the analysis of heat and mass transfer of a non-Newtonian fluid in a porous channel. Adv. Contin. Discret. Model. 2022, 2022, 7. [Google Scholar] [CrossRef]
- Guo, J.; Khan, A.; Sulaiman, M.; Kumam, P. A Novel Neuroevolutionary Paradigm for Solving Strongly Nonlinear Singular Boundary Value Problems in Physiology. IEEE Access 2022, 10, 21979–22002. [Google Scholar] [CrossRef]
- Cochran, W. The flow due to a rotating disc. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1934; Volume 30, pp. 365–375. [Google Scholar]
- Diard, J.P.; Montella, C. Re-examination of steady-state concentration profile near a uniformly accessible rotating disk electrode. J. Electroanal. Chem. 2013, 703, 52–55. [Google Scholar] [CrossRef]
- Michel, R.; Montella, C. Diffusion–convection impedance using an efficient analytical approximation of the mass transfer function for a rotating disk. J. Electroanal. Chem. 2015, 736, 139–146. [Google Scholar] [CrossRef]
- Compton, R.G.; Banks, C.E. Understanding Voltammetry; World Scientific: Singapore, 2018. [Google Scholar]
- Sulaiman, M.; Umar, M.; Nonlaopon, K.; Alshammari, F.S. The Quantitative Features Analysis of the Nonlinear Model of Crop Production by Hybrid Soft Computing Paradigm. Agronomy 2022, 12, 799. [Google Scholar] [CrossRef]
- Fawad Khan, M.; Bonyah, E.; Alshammari, F.S.; Ghufran, S.M.; Sulaiman, M. Modelling and Analysis of Virotherapy of Cancer Using an Efficient Hybrid Soft Computing Procedure. Complexity 2022, 2022, 9660746. [Google Scholar] [CrossRef]
- Ganie, A.H.; Fazal, F.; Romero, C.A.T.; Sulaiman, M. Quantitative Features Analysis of Water Carrying Nanoparticles of Alumina over a Uniform Surface. Nanomaterials 2022, 12, 878. [Google Scholar] [CrossRef] [PubMed]
- Khan, N.A.; Sulaiman, M.; Bonyah, E.; Seidu, J.; Alshammari, F.S. Investigation of Three-Dimensional Condensation Film Problem over an Inclined Rotating Disk Using a Nonlinear Autoregressive Exogenous Model. Comput. Intell. Neurosci. 2022, 2022, 2930920. [Google Scholar] [CrossRef] [PubMed]
- Khan, N.A.; Sulaiman, M.; Tavera Romero, C.A.; Laouini, G.; Alshammari, F.S. Study of Rolling Motion of Ships in Random Beam Seas with Nonlinear Restoring Moment and Damping Effects Using Neuroevolutionary Technique. Materials 2022, 15, 674. [Google Scholar] [CrossRef] [PubMed]
- Ganie, A.H.; Rahman, I.U.; Sulaiman, M.; Nonlaopon, K. Solution of Nonlinear Reaction-Diffusion Model in Porous Catalysts Arising in Micro-Vessel and Soft Tissue Using a Metaheuristic. IEEE Access 2022, 10, 41813–41827. [Google Scholar] [CrossRef]
- Khan, N.A.; Sulaiman, M.; Alshammari, F.S. Heat transfer analysis of an inclined longitudinal porous fin of trapezoidal, rectangular and dovetail profiles using cascade neural networks. Struct. Multidiscip. Optim. 2022, 65, 251. [Google Scholar] [CrossRef]





| m() | BLMA | Error | ||
|---|---|---|---|---|
| At c = 0.1 | 0 | 0 | ||
| 0.1 | 0.112628 | 0.112628 | ||
| 0.2 | 0.224126 | 0.224126 | ||
| 0.3 | 0.334163 | 0.334163 | ||
| 0.4 | 0.442201 | 0.442201 | ||
| 0.5 | 0.547518 | 0.547518 | ||
| 0.6 | 0.649234 | 0.649234 | ||
| 0.7 | 0.74636 | 0.74636 | ||
| 0.8 | 0.837858 | 0.837858 | ||
| 0.9 | 0.922711 | 0.922711 | ||
| 1 | 1 | 1 | ||
| At c = 0.2 | 0 | 0 | ||
| 0.1 | 0.117043 | 0.117043 | ||
| 0.2 | 0.231951 | 0.231951 | ||
| 0.3 | 0.344387 | 0.344387 | 4.47 | |
| 0.4 | 0.453808 | 0.453808 | ||
| 0.5 | 0.559495 | 0.559495 | ||
| 0.6 | 0.660585 | 0.660585 | ||
| 0.7 | 0.756128 | 0.756128 | ||
| 0.8 | 0.845145 | 0.845145 | ||
| 0.9 | 0.926705 | 0.926705 | ||
| 1 | 1 | 1 | ||
| At c = 0.3 | 0 | 0 | ||
| 0.1 | 0.121457 | 0.121457 | ||
| 0.2 | 0.239776 | 0.239776 | ||
| 0.3 | 0.354611 | 0.354611 | ||
| 0.4 | 0.465415 | 0.465415 | ||
| 0.5 | 0.571471 | 0.571471 | 8.12 | |
| 0.6 | 0.671937 | 0.671937 | ||
| 0.7 | 0.765896 | 0.765896 | 5.86 | |
| 0.8 | 0.852433 | 0.852433 | ||
| 0.9 | 0.930699 | 0.930699 | ||
| 1 | 1 | 1 | ||
| At c = 0.4 | 0 | 0 | ||
| 0.1 | 0.125872 | 0.125872 | ||
| 0.2 | 0.247601 | 0.247601 | ||
| 0.3 | 0.364835 | 0.364835 | ||
| 0.4 | 0.477022 | 0.477022 | ||
| 0.5 | 0.583448 | 0.583448 | ||
| 0.6 | 0.683288 | 0.683288 | ||
| 0.7 | 0.775665 | 0.775665 | ||
| 0.8 | 0.85972 | 0.85972 | ||
| 0.9 | 0.934694 | 0.934694 | ||
| 1 | 1 | 1 |
| n() | BLMA | Error | ||
|---|---|---|---|---|
| At c = 0.1 | 0 | 1 | 1 | |
| 0.1 | 0.896201 | 0.896201 | ||
| 0.2 | 0.791525 | 0.791524 | ||
| 0.3 | 0.686286 | 0.686286 | ||
| 0.4 | 0.581012 | 0.581012 | ||
| 0.5 | 0.476435 | 0.476435 | ||
| 0.6 | 0.373469 | 0.373469 | ||
| 0.7 | 0.273176 | 0.273176 | ||
| 0.8 | 0.176716 | 0.176716 | ||
| 0.9 | 0.085278 | 0.085278 | ||
| 1 | ||||
| At c = 0.2 | 0 | 1 | 0.999998 | |
| 0.1 | 0.900616 | 0.900615 | ||
| 0.2 | 0.79935 | 0.799349 | ||
| 0.3 | 0.69651 | 0.69651 | ||
| 0.4 | 0.592619 | 0.592619 | ||
| 0.5 | 0.488411 | 0.488411 | ||
| 0.6 | 0.38482 | 0.384819 | ||
| 0.7 | 0.282944 | 0.282944 | ||
| 0.8 | 0.184004 | 0.184004 | ||
| 0.9 | 0.089272 | 0.089272 | 3.53 | |
| 1 | ||||
| At c = 0.3 | 0 | 1 | 1 | |
| 0.1 | 0.905031 | 0.90503 | ||
| 0.2 | 0.807175 | 0.807175 | ||
| 0.3 | 0.706734 | 0.706734 | ||
| 0.4 | 0.604225 | 0.604225 | ||
| 0.5 | 0.500388 | 0.500388 | ||
| 0.6 | 0.396172 | 0.396172 | ||
| 0.7 | 0.292713 | 0.292713 | ||
| 0.8 | 0.191291 | 0.191291 | ||
| 0.9 | 0.093267 | 0.093267 | ||
| 1 | ||||
| At c = 0.4 | 0 | 1 | 0.999999 | |
| 0.1 | 0.909445 | 0.909445 | 7.94 | |
| 0.2 | 0.815 | 0.815 | ||
| 0.3 | 0.716958 | 0.716958 | ||
| 0.4 | 0.615832 | 0.615832 | ||
| 0.5 | 0.512365 | 0.512365 | 1.35 | |
| 0.6 | 0.407523 | 0.407523 | ||
| 0.7 | 0.302481 | 0.302481 | ||
| 0.8 | 0.198578 | 0.198578 | ||
| 0.9 | 0.097261 | 0.097261 | ||
| 1 |
| Training | Testing | Validation | Max.iteration | Hidden Neurons | Performance Function |
|---|---|---|---|---|---|
| 70% | 15% | 15% | 1000 | 10 | Mean square error |
| Mean Square Error | ||||||||
|---|---|---|---|---|---|---|---|---|
| c | Neurons | Epochs | Gradient | Mu | Training | Testing | Validation | Regression |
| 0.1 | 10 | 141 | 1.00 | 1 | ||||
| 0.2 | 10 | 211 | 1 | |||||
| 0.3 | 10 | 151 | 1 | |||||
| 0.4 | 10 | 150 | 1 | |||||
| Mean Square Error | ||||||||
|---|---|---|---|---|---|---|---|---|
| c | Neurons | Epochs | Gradient | Mu | Training | Testing | Validation | Regression |
| 0.1 | 10 | 166 | 1 | |||||
| 0.2 | 10 | 154 | 1 | |||||
| 0.3 | 10 | 376 | 1 | |||||
| 0.4 | 10 | 178 | 1 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, F.S.; Jan, H.; Sulaiman, M.; Prathumwan, D.; Laouini, G. Quantitative Study of Non-Linear Convection Diffusion Equations for a Rotating-Disc Electrode. Entropy 2023, 25, 134. https://doi.org/10.3390/e25010134
Alshammari FS, Jan H, Sulaiman M, Prathumwan D, Laouini G. Quantitative Study of Non-Linear Convection Diffusion Equations for a Rotating-Disc Electrode. Entropy. 2023; 25(1):134. https://doi.org/10.3390/e25010134
Chicago/Turabian StyleAlshammari, Fahad Sameer, Hamad Jan, Muhammad Sulaiman, Din Prathumwan, and Ghaylen Laouini. 2023. "Quantitative Study of Non-Linear Convection Diffusion Equations for a Rotating-Disc Electrode" Entropy 25, no. 1: 134. https://doi.org/10.3390/e25010134
APA StyleAlshammari, F. S., Jan, H., Sulaiman, M., Prathumwan, D., & Laouini, G. (2023). Quantitative Study of Non-Linear Convection Diffusion Equations for a Rotating-Disc Electrode. Entropy, 25(1), 134. https://doi.org/10.3390/e25010134







