Quantum Manifestation of the Classical Bifurcation in the Driven Dissipative Bose–Hubbard Dimer
Abstract
1. Introduction
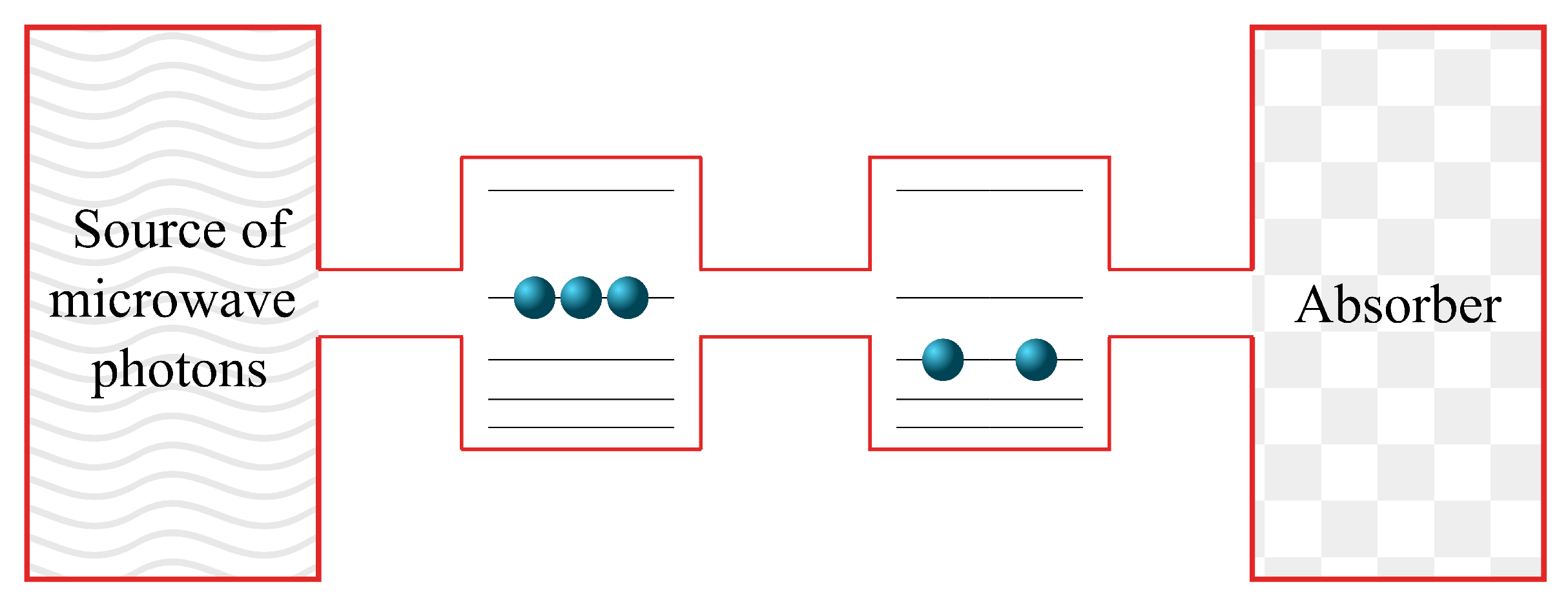
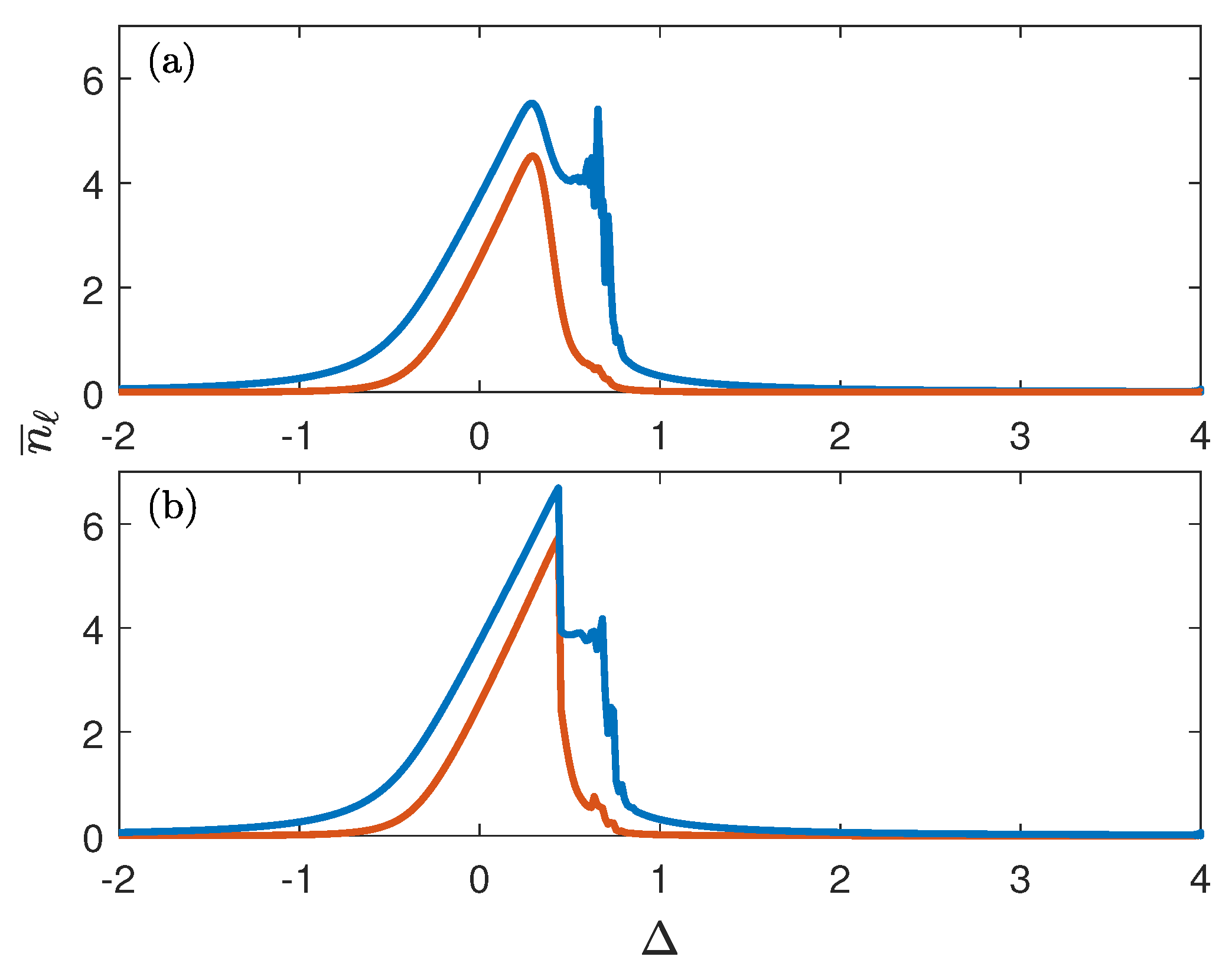
2. Quantum Dynamics
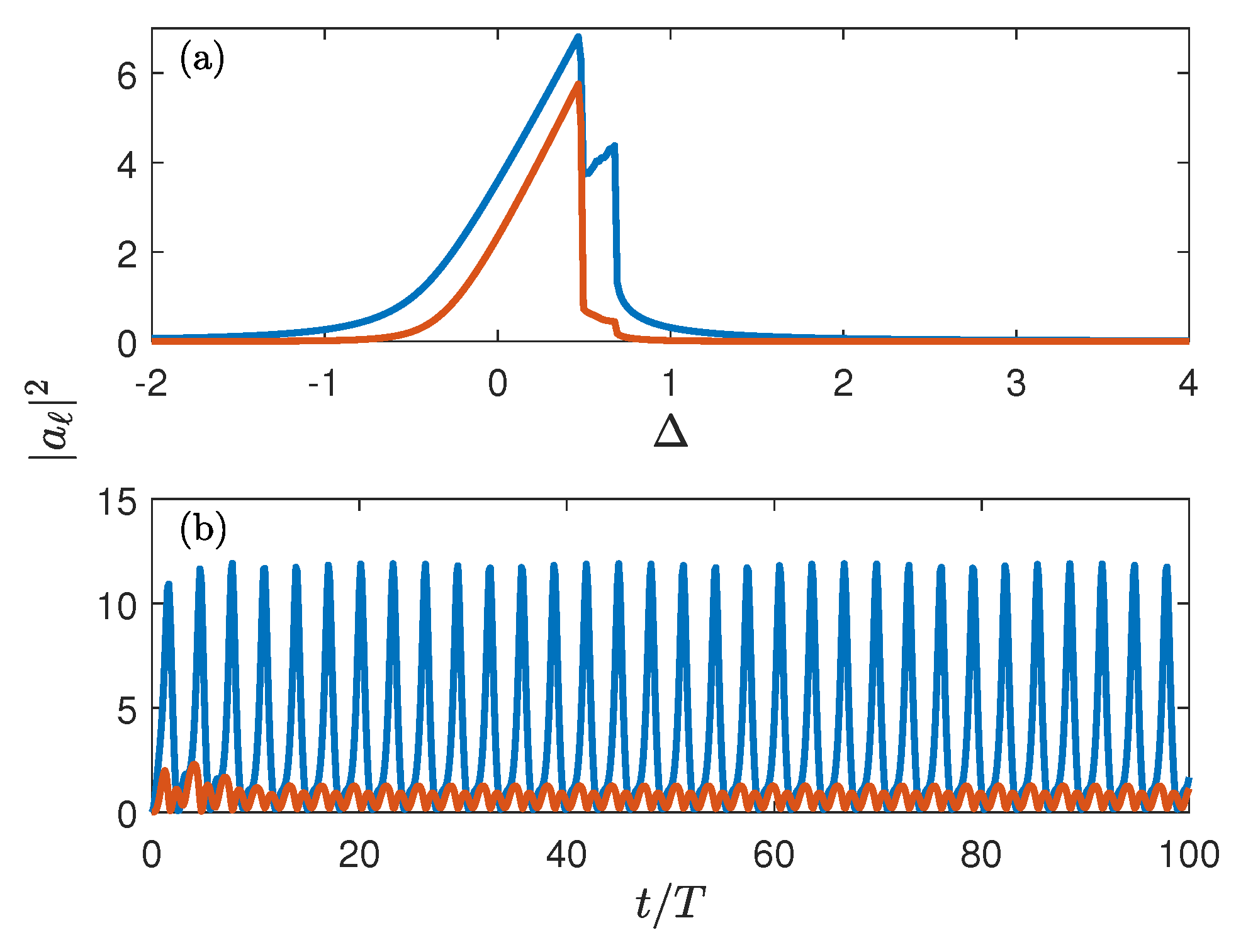
3. Classical Dynamics
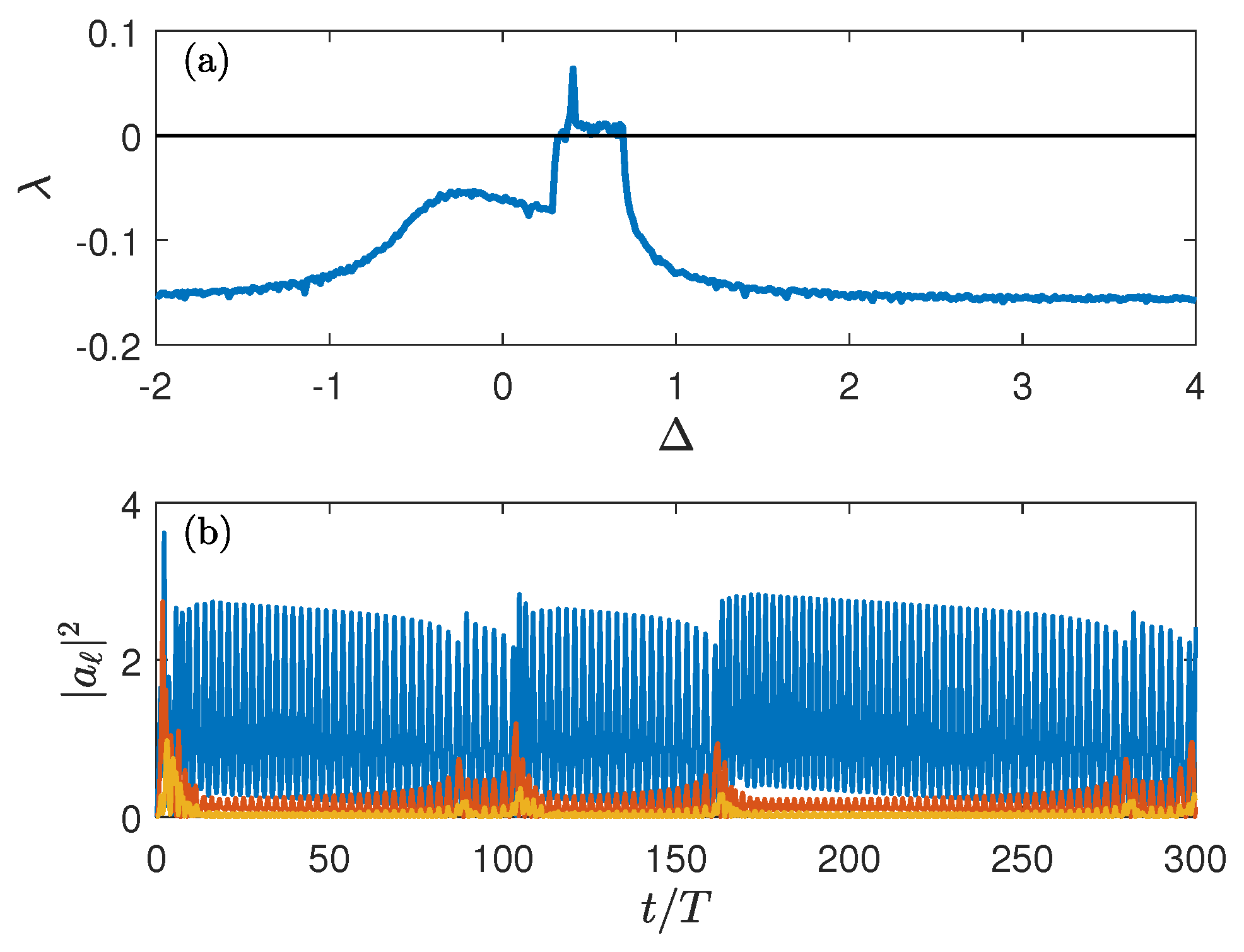
4. Dissipative BH Trimer
5. Summary
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BH | Bose–Hubbard |
| SPDM | Single-particle density matrix |
References
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S.R. Quantum Coherent Atomic Tunneling between Two Trapped Bose-Einstein Condensates. Phys. Rev. Lett. 1997, 79, 4950–4953. [Google Scholar] [CrossRef]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct Observation of Tunneling and Nonlinear Self-Trapping in a Single Bosonic Josephson Junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef] [PubMed]
- Levy, S.; Lahoud, E.; Shomroni, I.; Steinhauer, J. The a.c. and d.c. Josephson effects in a Bose–Einstein condensate. Nature 2007, 449, 579–583. [Google Scholar] [CrossRef] [PubMed]
- Abbarchi, M.; Amo, A.; Sala, V.G.; Solnyshkov, D.D.; Flayac, H.; Ferrier, L.; Sagnes, I.; Galopin, E.; Lemaître, A.; Malpuech, G.; et al. Macroscopic quantum self-trapping and Josephson oscillations of exciton polaritons. Nat. Phys. 2013, 9, 275–279. [Google Scholar] [CrossRef]
- Kolovsky, A. Bistability in the dissipative quantum systems I: Damped and driven nonlinear oscillator. arXiv 2020, arXiv:2002.11373. [Google Scholar] [CrossRef]
- Giraldo, A.; Krauskopf, B.; Broderick, N.G.R.; Levenson, J.A.; Yacomotti, A.M. The driven-dissipative Bose–Hubbard dimer: Phase diagram and chaos. New J. Phys. 2020, 22, 043009. [Google Scholar] [CrossRef]
- Giraldo, A.; Masson, S.J.; Broderick, N.G.R.; Krauskopf, B. Semiclassical bifurcations and quantum trajectories: A case study of the open Bose–Hubbard dimer. Eur. Phys. J. Spec. Top. 2022, 231, 385–401. [Google Scholar] [CrossRef]
- Lledó, C.; Mavrogordatos, T.K.; Szymańska, M.H. Driven Bose-Hubbard dimer under nonlocal dissipation: A bistable time crystal. Phys. Rev. B 2019, 100, 054303. [Google Scholar] [CrossRef]
- Lledó, C.; Szymańska, M.H. A dissipative time crystal with or without Z2 symmetry breaking. New J. Phys. 2020, 22, 075002. [Google Scholar] [CrossRef]
- Braun, D. Dissipative Quantum Chaos and Decoherence; Springer: Berlin/Heidelberg, Germany, 2001; Volume 172. [Google Scholar] [CrossRef]
- Sá, L.; Ribeiro, P.; Prosen, T. Complex Spacing Ratios: A Signature of Dissipative Quantum Chaos. Phys. Rev. X 2020, 10, 021019. [Google Scholar] [CrossRef]
- Lagoudakis, K.G.; Pietka, B.; Wouters, M.; André, R.; Deveaud-Plédran, B. Coherent Oscillations in an Exciton-Polariton Josephson Junction. Phys. Rev. Lett. 2010, 105, 120403. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, S.R.K.; Amo, A.; Sagnes, I.; Gratiet, L.L.; Galopin, E.; Lemaître, A.; Bloch, J. Interaction-induced hopping phase in driven-dissipative coupled photonic microcavities. Nat. Commun. 2016, 7, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Eichler, C.; Salathe, Y.; Mlynek, J.; Schmidt, S.; Wallraff, A. Quantum-Limited Amplification and Entanglement in Coupled Nonlinear Resonators. Phys. Rev. Lett. 2014, 113, 110502. [Google Scholar] [CrossRef] [PubMed]
- Raftery, J.; Sadri, D.; Schmidt, S.; Türeci, H.; Houck, A. Observation of a Dissipation-Induced Classical to Quantum Transition. Phys. Rev. X 2014, 4, 031043. [Google Scholar] [CrossRef]
- Fitzpatrick, M.; Sundaresan, N.M.; Li, A.C.Y.; Koch, J.; Houck, A. Observation of a Dissipative Phase Transition in a One-Dimensional Circuit QED Lattice. Phys. Rev. X 2017, 7, 011016. [Google Scholar] [CrossRef]
- Fedorov, G.; Remizov, S.; Shapiro, D.; Pogosov, W.; Egorova, E.; Tsitsilin, I.; Andronik, M.; Dobronosova, A.; Rodionov, I.; Astafiev, O.; et al. Photon Transport in a Bose-Hubbard Chain of Superconducting Artificial Atoms. Phys. Rev. Lett. 2021, 126, 180503. [Google Scholar] [CrossRef] [PubMed]
- Muraev, P.S.; Maksimov, D.N.; Kolovsky, A.R. Ballistic transport of interacting Bose particles in a tight-binding chain. Phys. Rev. E 2022, 106, 064203. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muraev, P.; Maksimov, D.; Kolovsky, A. Quantum Manifestation of the Classical Bifurcation in the Driven Dissipative Bose–Hubbard Dimer. Entropy 2023, 25, 117. https://doi.org/10.3390/e25010117
Muraev P, Maksimov D, Kolovsky A. Quantum Manifestation of the Classical Bifurcation in the Driven Dissipative Bose–Hubbard Dimer. Entropy. 2023; 25(1):117. https://doi.org/10.3390/e25010117
Chicago/Turabian StyleMuraev, Pavel, Dmitrii Maksimov, and Andrey Kolovsky. 2023. "Quantum Manifestation of the Classical Bifurcation in the Driven Dissipative Bose–Hubbard Dimer" Entropy 25, no. 1: 117. https://doi.org/10.3390/e25010117
APA StyleMuraev, P., Maksimov, D., & Kolovsky, A. (2023). Quantum Manifestation of the Classical Bifurcation in the Driven Dissipative Bose–Hubbard Dimer. Entropy, 25(1), 117. https://doi.org/10.3390/e25010117





