Local-Forest Method for Superspreaders Identification in Online Social Networks
Abstract
:1. Introduction
2. Push-Republish Model
2.1. Description of the Push-Republish Model
- 1.
- Step 1: At the time t, for node i in the set , its neighbors in S state will become R state (i.e., the “push” mechanism). Meanwhile, such neighbors who receive the message for the first time will choose to republish the massage with probability (i.e., the “republish” behavior). Add the neighbors who choose to republish the message to the set .
- 2.
- Step 2: Remove i from .
- 3.
- Step 3: Perform steps 1–2 until , then perform step 4.
- 4.
- Step 4: Update the propagation process to the next time step, i.e., set . If there is no node in set , the propagation process ends. Denote the ending time as the propagation duration T. Otherwise, repeat step 3.
2.2. Comparison between PR Model and SIR Model
3. Local-Forest Method
4. Simulation Results
4.1. Experimental Setup
4.2. Methods Evaluation
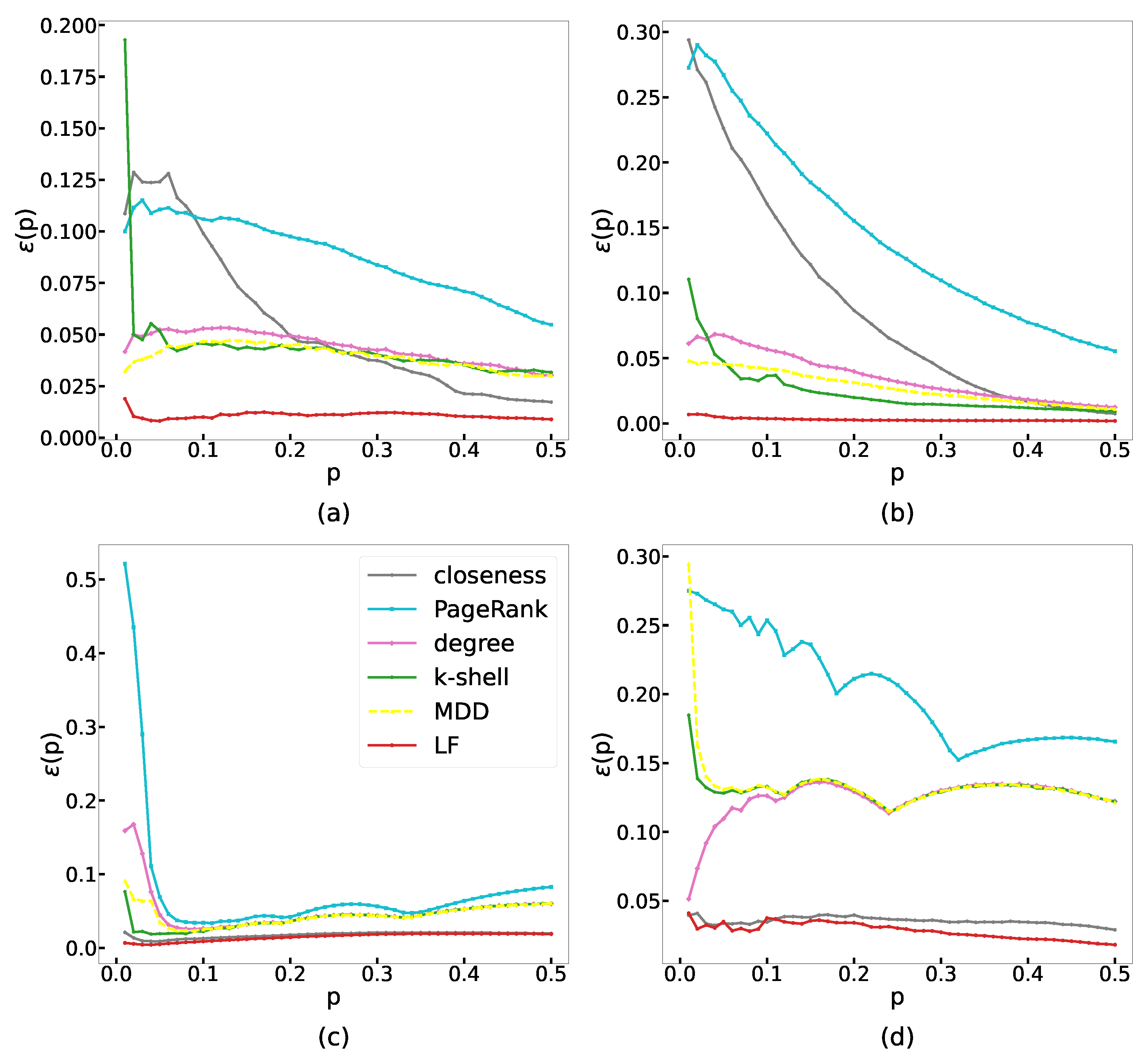
4.2.1. Imprecision Function
4.2.2. Recognition Rate
4.2.3. Kendall Correlation Coefficient
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. SIR Model
Appendix B. Classic Centrality Measures
- 1.
- Degree.The degree (denoted as k) of a node is the number of nodes connected to it. For a directed network, the in-degree (denoted as ) of a node is the number of nodes pointing to it (such nodes are called in-neighbor), and the out-degree (denoted as ) is the number of nodes pointed by it.
- 2.
- K-shell centrality.In k-shell decomposition, firstly, remove all nodes with degree (set for directed networks). Then, there may appear nodes with again. Continue to remove all nodes with degree iteratively until there is no node with . The ks index of the removed nodes is 1, and here we define the k-shell centrality of these nodes as . We say the nodes with are in the 1-shell. Iteratively, remove the nodes with in a similar way and obtain the 2-shell. Continue the removing process to obtain higher-k shells until there is no more node in the network. Finally, the k-shell centrality of each node is clarified, and the network can be viewed as the union of all shells. Nodes in the inner-most shell possess the highest k-shell centrality (i.e., highest ks index).
- 3.
- Closeness centrality.The closeness centrality of node i is defined aswhere V is the set of all the nodes in the network and is the distance between node i and node j.
- 4.
- PageRank.The PageRank value of node i is calculated iteratively. The PageRank value of node i in step t is calculated as:where is the set of the neighbors of node i, is the out-degree of node j, is a constant, and N is the number of the nodes in the network. Conventionally, set for each node i, and . Finally, the converges to , which is the PageRank centrality of node i.
- 5.
- Mixed degree decomposition (MDD).Use the mixed degree to replace the degree k to decompose the network in the same way as the k-shell decomposition, where is the residual degree (number of links connecting to the remaining nodes) and is the exhausted degree (number of links connecting to the removed nodes). is a constant, which is set as 0.7 commonly.
References
- Wang, L.; Ma, L.; Wang, C.; Xie, N.G.; Koh, J.M.; Cheong, K.H. Identifying influential spreaders in social networks through discrete moth-flame optimization. IEEE Trans. Evol. Comput. 2021, 25, 1091–1102. [Google Scholar] [CrossRef]
- Goel, S.; Watts, D.J.; Goldstein, D.G. The structure of online diffusion networks. In Proceedings of the 13th ACM Conference on Electronic Commerce, Valencia, Spain, 4–8 June 2012; pp. 623–638. [Google Scholar]
- Zhao, J.; Wu, J.; Xu, K. Weak ties: Subtle role of information diffusion in online social networks. Phys. Rev. E 2010, 82, 016105. [Google Scholar] [CrossRef]
- Pei, S.; Morone, F.; Makse, H.A. Theories for influencer identification in complex networks. In Complex Spreading Phenomena in Social Systems; Springer: Cham, Switzerland, 2018; pp. 125–148. [Google Scholar]
- Liu, L.; Wang, X.; Zheng, Y.; Fang, W.; Tang, S.; Zheng, Z. Homogeneity trend on social networks changes evolutionary advantage in competitive information diffusion. New J. Phys. 2020, 22, 013019. [Google Scholar] [CrossRef]
- Wang, X.; Sirianni, A.D.; Tang, S.; Zheng, Z.; Fu, F. Public discourse and social network echo chambers driven by socio-cognitive biases. Phys. Rev. X 2020, 10, 041042. [Google Scholar] [CrossRef]
- Pei, S.; Makse, H.A. Spreading dynamics in complex networks. J. Stat. Mech. Theory Exp. 2013, 2013, P12002. [Google Scholar] [CrossRef]
- Pei, S.; Muchnik, L.; Andrade, J.S., Jr.; Zheng, Z.; Makse, H.A. Searching for superspreaders of information in real-world social media. Sci. Rep. 2014, 4, 5547. [Google Scholar] [CrossRef]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef]
- Chen, D.; Lü, L.; Shang, M.S.; Zhang, Y.C.; Zhou, T. Identifying influential nodes in complex networks. Phys. A Stat. Mech. Its Appl. 2012, 391, 1777–1787. [Google Scholar] [CrossRef]
- Abrahamson, E.; Rosenkopf, L. Social network effects on the extent of innovation diffusion: A computer simulation. Organ. Sci. 1997, 8, 289–309. [Google Scholar] [CrossRef]
- Richardson, M.; Domingos, P. Mining knowledge-sharing sites for viral marketing. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 61–70. [Google Scholar]
- Muchnik, L.; Aral, S.; Taylor, S.J. Social influence bias: A randomized experiment. Science 2013, 341, 647–651. [Google Scholar] [CrossRef] [Green Version]
- Lü, L.; Chen, D.; Ren, X.L.; Zhang, Q.M.; Zhang, Y.C.; Zhou, T. Vital nodes identification in complex networks. Phys. Rep. 2016, 650, 1–63. [Google Scholar] [CrossRef]
- Erkol, Ş.; Castellano, C.; Radicchi, F. Systematic comparison between methods for the detection of influential spreaders in complex networks. Sci. Rep. 2019, 9, 15095. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef] [PubMed]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, M.; Zhou, T.; Do, Y. Core-like groups result in invalidation of identifying super-spreader by k-shell decomposition. Sci. Rep. 2015, 5, 9602. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Li, W.; Guo, Y.; Peng, X.; Li, Y. Identifying influential spreaders in complex networks based on improved k-shell method. Phys. A Stat. Mech. Its Appl. 2020, 554, 124229. [Google Scholar] [CrossRef]
- Ma, L.L.; Ma, C.; Zhang, H.F.; Wang, B.H. Identifying influential spreaders in complex networks based on gravity formula. Phys. A Stat. Mech. Its Appl. 2016, 451, 205–212. [Google Scholar] [CrossRef]
- Li, Z.; Huang, X. Identifying influential spreaders in complex networks by an improved gravity model. Sci. Rep. 2021, 11, 22194. [Google Scholar] [CrossRef]
- Hou, B.; Yao, Y.; Liao, D. Identifying all-around nodes for spreading dynamics in complex networks. Phys. A Stat. Mech. Its Appl. 2012, 391, 4012–4017. [Google Scholar] [CrossRef]
- Lin, J.H.; Guo, Q.; Dong, W.Z.; Tang, L.Y.; Liu, J.G. Identifying the node spreading influence with largest k-core values. Phys. Lett. A 2014, 378, 3279–3284. [Google Scholar] [CrossRef]
- Bae, J.; Kim, S. Identifying and ranking influential spreaders in complex networks by neighborhood coreness. Phys. A Stat. Mech. Its Appl. 2014, 395, 549–559. [Google Scholar] [CrossRef]
- Zeng, A.; Zhang, C.J. Ranking spreaders by decomposing complex networks. Phys. Lett. A 2013, 377, 1031–1035. [Google Scholar] [CrossRef]
- Wei, B.; Liu, J.; Wei, D.; Gao, C.; Deng, Y. Weighted k-shell decomposition for complex networks based on potential edge weights. Phys. A Stat. Mech. Its Appl. 2015, 420, 277–283. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Y.; Xi, J.; Du, C. Fast ranking influential nodes in complex networks using a k-shell iteration factor. Phys. A Stat. Mech. Its Appl. 2016, 461, 171–181. [Google Scholar] [CrossRef]
- Fu, Y.H.; Huang, C.Y.; Sun, C.T. Identifying super-spreader nodes in complex networks. Math. Probl. Eng. 2015, 2015, 675713. [Google Scholar] [CrossRef]
- Yu, Y.; Zhou, B.; Chen, L.; Gao, T.; Liu, J. Identifying Important Nodes in Complex Networks Based on Node Propagation Entropy. Entropy 2022, 24, 275. [Google Scholar] [CrossRef]
- Namtirtha, A.; Dutta, B.; Dutta, A. Semi-global triangular centrality measure for identifying the influential spreaders from undirected complex networks. Expert Syst. Appl. 2022, 206, 117791. [Google Scholar] [CrossRef]
- Li, H.; Shang, Q.; Deng, Y. A generalized gravity model for influential spreaders identification in complex networks. Chaos Solitons Fractals 2021, 143, 110456. [Google Scholar] [CrossRef]
- Zeng, Q.; Liu, Y.; Tang, M.; Gong, J. Identifying super-spreaders in information–epidemic coevolving dynamics on multiplex networks. Knowl.-Based Syst. 2021, 229, 107365. [Google Scholar] [CrossRef]
- Kempe, D.; Kleinberg, J.; Tardos, É. Maximizing the spread of influence through a social network. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 137–146. [Google Scholar]
- Morone, F.; Makse, H.A. Influence maximization in complex networks through optimal percolation. Nature 2015, 524, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Cao, T.; Wu, X.; Wang, S.; Hu, X. OASNET: An optimal allocation approach to influence maximization in modular social networks. In Proceedings of the 2010 ACM Symposium on Applied Computing, Sierre, Switzerland, 22–26 March 2010; pp. 1088–1094. [Google Scholar]
- Estevez, P.A.; Vera, P.; Saito, K. Selecting the most influential nodes in social networks. In Proceedings of the 2007 International Joint Conference on Neural Networks, Orlando, FL, USA, 12–17 August 2007; pp. 2397–2402. [Google Scholar]
- Ullah, A.; Wang, B.; Sheng, J.; Long, J.; Khan, N.; Sun, Z. Identifying vital nodes from local and global perspectives in complex networks. Expert Syst. Appl. 2021, 186, 115778. [Google Scholar] [CrossRef]
- Goyal, A.; Lu, W.; Lakshmanan, L.V. Celf++ optimizing the greedy algorithm for influence maximization in social networks. In Proceedings of the 20th International Conference Companion on World Wide Web, Hyderabad, India, 28 March–1 April 2011; pp. 47–48. [Google Scholar]
- Wang, Y.; Cong, G.; Song, G.; Xie, K. Community-based greedy algorithm for mining top-k influential nodes in mobile social networks. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–28 July 2010; pp. 1039–1048. [Google Scholar]
- Zareie, A.; Sheikhahmadi, A.; Jalili, M. Identification of influential users in social network using gray wolf optimization algorithm. Expert Syst. Appl. 2020, 142, 112971. [Google Scholar] [CrossRef]
- Antelmi, A.; Cordasco, G.; Spagnuolo, C.; Szufel, P. Social influence maximization in hypergraphs. Entropy 2021, 23, 796. [Google Scholar] [CrossRef]
- Fu, B.; Zhang, J.; Bai, H.; Yang, Y.; He, Y. An Influence Maximization Algorithm for Dynamic Social Networks Based on Effective Links. Entropy 2022, 24, 904. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, J.; Feng, X.; Xiong, H.; Xu, K. Information propagation in online social networks: A tie-strength perspective. Knowl. Inf. Syst. 2012, 32, 589–608. [Google Scholar] [CrossRef]
- Kempe, D.; Kleinberg, J.; Tardos, É. Influential nodes in a diffusion model for social networks. In Proceedings of the International Colloquium on Automata, Languages, and Programming, Lisbon, Portugal, 11–15 July 2005; pp. 1127–1138. [Google Scholar]
- Ruan, Z.; Wang, J.; Xuan, Q.; Fu, C.; Chen, G. Information filtering by smart nodes in random networks. Phys. Rev. E 2018, 98, 022308. [Google Scholar] [CrossRef]
- Xuan, Q.; Shu, X.; Ruan, Z.; Wang, J.; Fu, C.; Chen, G. A self-learning information diffusion model for smart social networks. IEEE Trans. Netw. Sci. Eng. 2019, 7, 1466–1480. [Google Scholar] [CrossRef]
- Watts, D.J.; Dodds, P.S. Influentials, networks, and public opinion formation. J. Consum. Res. 2007, 34, 441–458. [Google Scholar] [CrossRef]
- De Arruda, G.F.; Barbieri, A.L.; Rodriguez, P.M.; Rodrigues, F.A.; Moreno, Y.; da Fontoura Costa, L. Role of centrality for the identification of influential spreaders in complex networks. Phys. Rev. E 2014, 90, 032812. [Google Scholar] [CrossRef] [PubMed]
- Viswanath, B.; Mislove, A.; Cha, M.; Gummadi, K.P. On the evolution of user interaction in facebook. In Proceedings of the 2nd ACM Workshop on Online Social Networks, Barcelona, Spain, 17 August 2009; pp. 37–42. [Google Scholar]
- Liu, D.; Nie, H.; Zhao, J.; Wang, Q. Identifying influential spreaders in large-scale networks based on evidence theory. Neurocomputing 2019, 359, 466–475. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Wu, L.; Zhang, J. Identifying Influential Nodes in Complex Networks Based on Multiple Local Attributes and Information Entropy. Entropy 2022, 24, 293. [Google Scholar] [CrossRef] [PubMed]
- Kunegis, J. Konect: The koblenz network collection. In Proceedings of the 22nd International Conference on World Wide Web, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 1343–1350. [Google Scholar]
- Cho, E.; Myers, S.A.; Leskovec, J. Friendship and mobility: User movement in location-based social networks. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 1082–1090. [Google Scholar]
- Zafarani, R.; Liu, H. Social Computing Data Repository at ASU. 2009. Available online: http://datasets.syr.edu/ (accessed on 7 September 2022).
- De Choudhury, M.; Lin, Y.R.; Sundaram, H.; Candan, K.S.; Xie, L.; Kelliher, A. How does the data sampling strategy impact the discovery of information diffusion in social media? In Proceedings of the Fourth International AAAI Conference on Weblogs and Social Media, Washington, DC, USA, 23–26 May 2010.
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Berry, K.J.; Johnston, J.E.; Zahran, S.; Mielke, P.W. Stuart’s tau measure of effect size for ordinal variables: Some methodological considerations. Behav. Res. Methods 2009, 41, 1144–1148. [Google Scholar] [CrossRef]
- Stuart, A. The estimation and comparison of strengths of association in contingency tables. Biometrika 1953, 40, 105–110. [Google Scholar] [CrossRef]
- Wang, X.; Li, W.; Liu, L.; Pei, S.; Tang, S.; Zheng, Z. Promoting information diffusion through interlayer recovery processes in multiplex networks. Phys. Rev. E 2017, 96, 032304. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Tang, S.; Zheng, H.; Zheng, Z. Multilayer social reinforcement induces bistability on multiplex networks. J. Stat. Mech. Theory Exp. 2021, 2021, 063402. [Google Scholar] [CrossRef]


| Centrality Measure | 3 | 16 | 4 | 5 | 6 | 11 | 7 | 17 | 1,2 | 24 | 9 | 14,15 | 18–23 | 12,13 | 8 | 25,26 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k-shell | 3 | 1 | 3 | 3 | 3 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| degree | 8 | 8 | 4 | 5 | 4 | 4 | 4 | 2 | 2 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |
| LT | 13 | 12 | 19 | 14 | 13 | 13 | 10 | 11 | 8 | 4 | 5 | 8 | 8 | 4 | 4 | 3 | 2 |
| LF | 91 | 78 | 52 | 68 | 56 | 35 | 36 | 16 | 21 | 17 | 12 | 13 | 12 | 13 | 10 | 4 | 5 |
| Network | N | M | MC | ||||
|---|---|---|---|---|---|---|---|
| Brightkite | 56,739 | 425,890 | 7.506 | 1000 | 0.015618 | 0.016 | 90.9% |
| 63,392 | 816,831 | 25.771 | 1000 | 0.011358 | 0.012 | 78.9% | |
| DouBan | 154,908 | 654,324 | 4.224 | 500 | 0.027100 | 0.028 | 91.8% |
| 465,017 | 834,797 | 1.795 | 200 | 0.116572 | 0.120 | 82.6% |
| Network | Degree | k-Shell | Closeness | PageRank | MDD | LF |
|---|---|---|---|---|---|---|
| Brightkite | 0.04799 | 1.73308 | 11,845.25111 | 14.45678 | 28.02683 | 0.95804 |
| 0.03003 | 2.15947 | 24,302.80110 | 29.29709 | 44.02255 | 1.19346 | |
| DouBan | 0.12007 | 1.50177 | 59,277.99047 | 27.76005 | 50.87384 | 1.72524 |
| 0.24067 | 4.83157 | 1813.34151 | 14.19303 | 192.96852 | 2.10739 |
| Network | Degree | k-Shell | Closeness | PageRank | MDD | LF |
|---|---|---|---|---|---|---|
| Brightkite | 0.42768 | 0.45701 | 0.68762 | 0.22887 | 0.42658 | 0.69770 |
| 0.79352 | 0.83248 | 0.80367 | 0.55818 | 0.80476 | 0.90089 | |
| DouBan | 0.65134 | 0.65002 | 0.72248 | 0.45388 | 0.65896 | 0.78665 |
| 0.34802 | 0.35625 | 0.63684 | 0.17299 | 0.34434 | 0.70861 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Y.; Tang, S.; Liu, L.; Zheng, H.; Wang, X.; Zheng, Z. Local-Forest Method for Superspreaders Identification in Online Social Networks. Entropy 2022, 24, 1279. https://doi.org/10.3390/e24091279
Hao Y, Tang S, Liu L, Zheng H, Wang X, Zheng Z. Local-Forest Method for Superspreaders Identification in Online Social Networks. Entropy. 2022; 24(9):1279. https://doi.org/10.3390/e24091279
Chicago/Turabian StyleHao, Yajing, Shaoting Tang, Longzhao Liu, Hongwei Zheng, Xin Wang, and Zhiming Zheng. 2022. "Local-Forest Method for Superspreaders Identification in Online Social Networks" Entropy 24, no. 9: 1279. https://doi.org/10.3390/e24091279
APA StyleHao, Y., Tang, S., Liu, L., Zheng, H., Wang, X., & Zheng, Z. (2022). Local-Forest Method for Superspreaders Identification in Online Social Networks. Entropy, 24(9), 1279. https://doi.org/10.3390/e24091279





