Performance of Bearing Ball Defect Classification Based on the Fusion of Selected Statistical Features
Abstract
:1. Introduction
2. Paper Contribution
3. The Fault Diagnosis Methodology
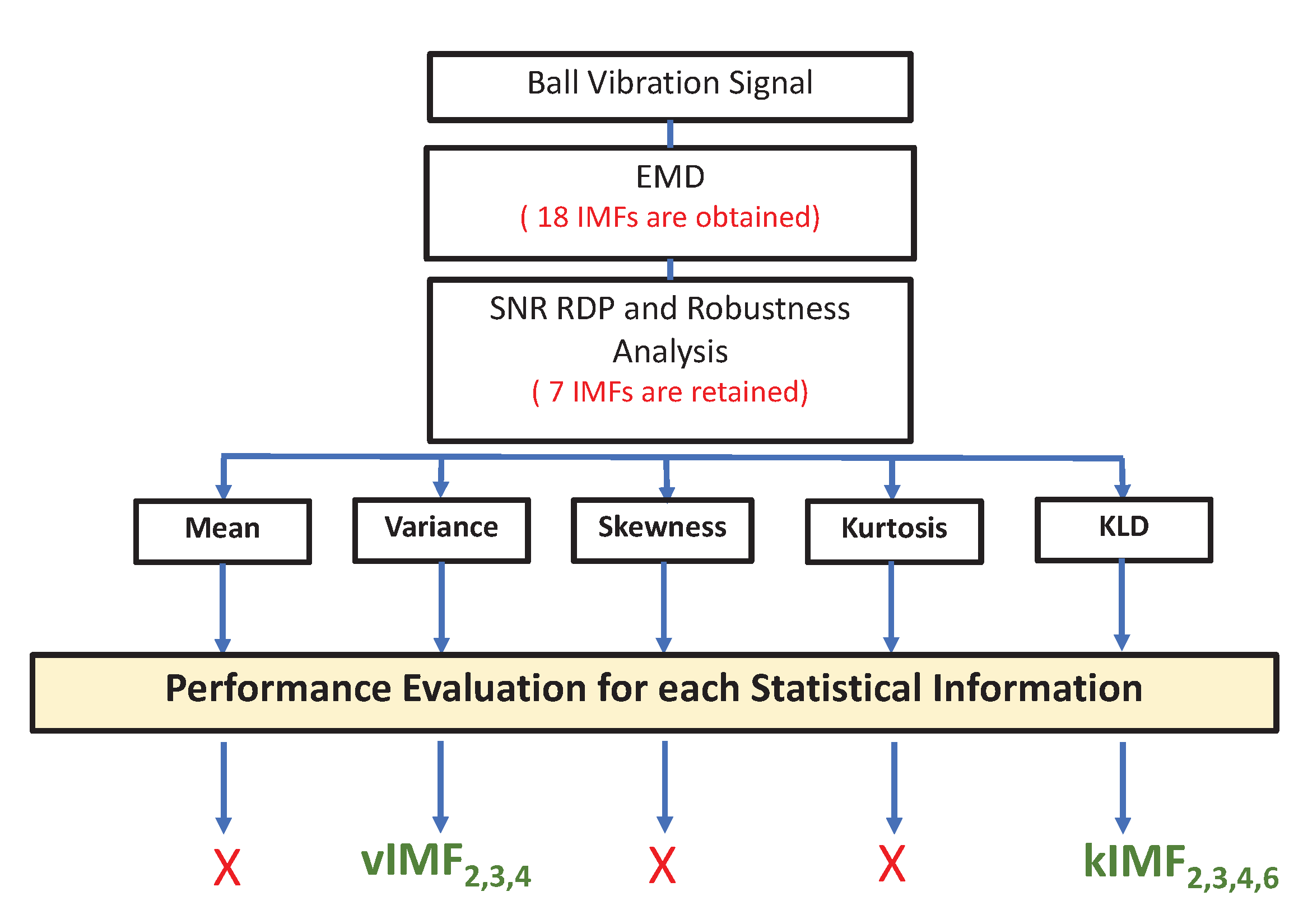
3.1. Preprocessing and Feature Extraction and Selection
- The mean and the skewness had very poor detection performance
- The kurtosis had a very low sensitivity to the ball fault level.
- Variance: , and ; denoted as
- KLD: , , and ; denoted as .
3.2. Feature Analysis
3.2.1. Principal Component Analysis (PCA)
- Kernel-based techniques: kernel principal component analysis (KPCA) and support vector machine (SVM);
- Deterministic systematic exploration techniques: K-nearest neighbours (KNN) and decision tree (DT);
- Probabilistic systematic exploration techniques: naive Bayes classifiers (NB).
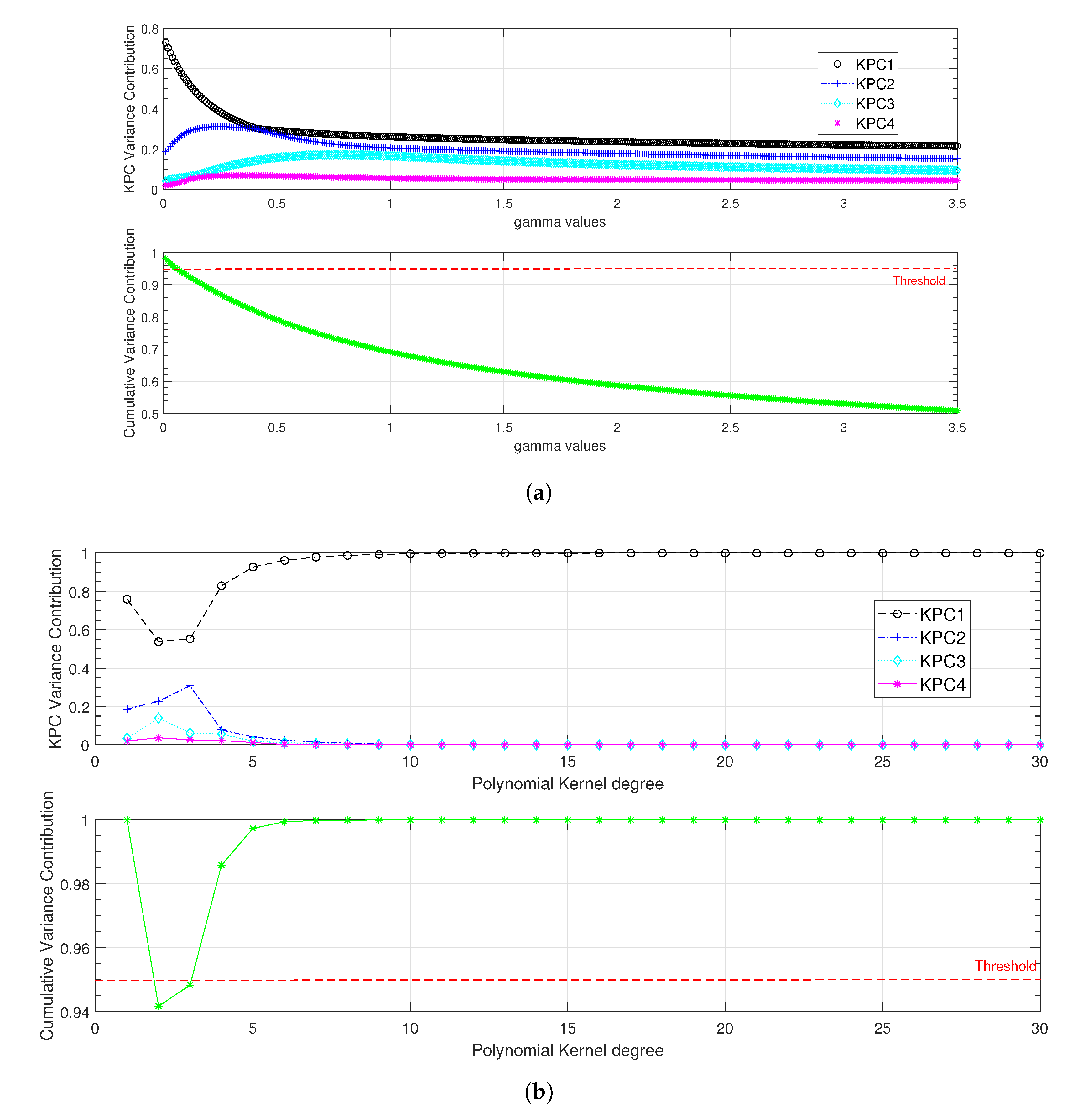
3.2.2. Kernel Principal Component Analysis (KPCA)
- The polynomial kernel defined as ( is the kernel’s order):
- The Gaussian kernel defined as ( is the standard deviation of the kernel):
3.2.3. Support Vector Machine (SVM)
3.2.4. K-Nearest Neighbours (KNN)
- Euclidean distance (Euc). It is defined by:
- City block distance (CB) given as:
3.2.5. Decision Tree (DT)
3.2.6. Naive Bayes (NB)
4. Results and Discussions
4.1. Experimental Data
- No-load condition (): of the nominal load;
- Half-loaded condition (): of the nominal load;
- Fully loaded condition (): of the nominal load;
- Overloaded condition (): of the nominal load;
- Combination of all the load conditions: ().
- H: corresponding to the healthy behaviour (no fault);
- : faulty case with a severity of inch;
- : faulty case with a severity of inch;
- : faulty case with a severity of inch.
4.2. Experimental Validation
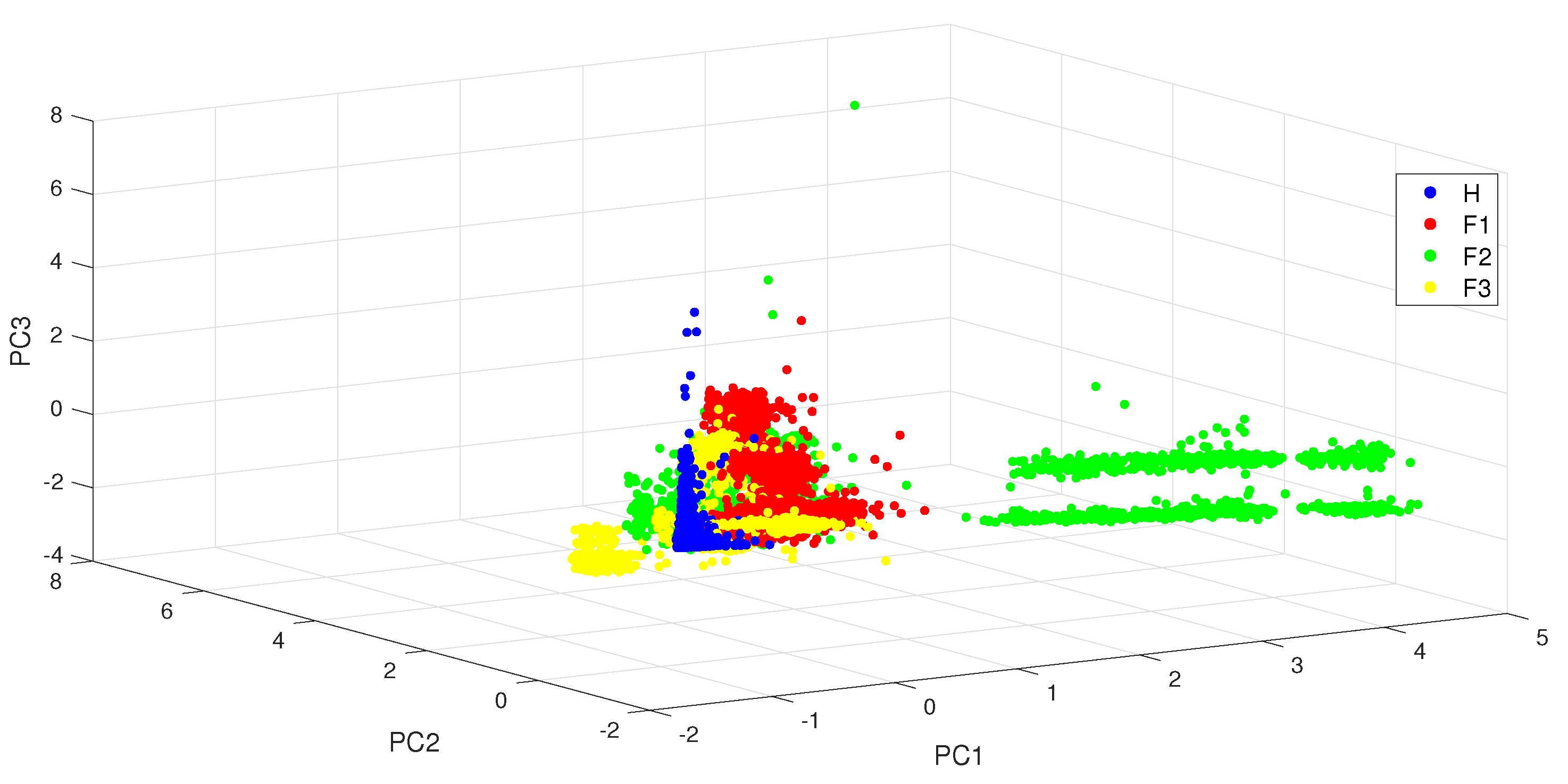
4.2.1. Linear Classification with PCA
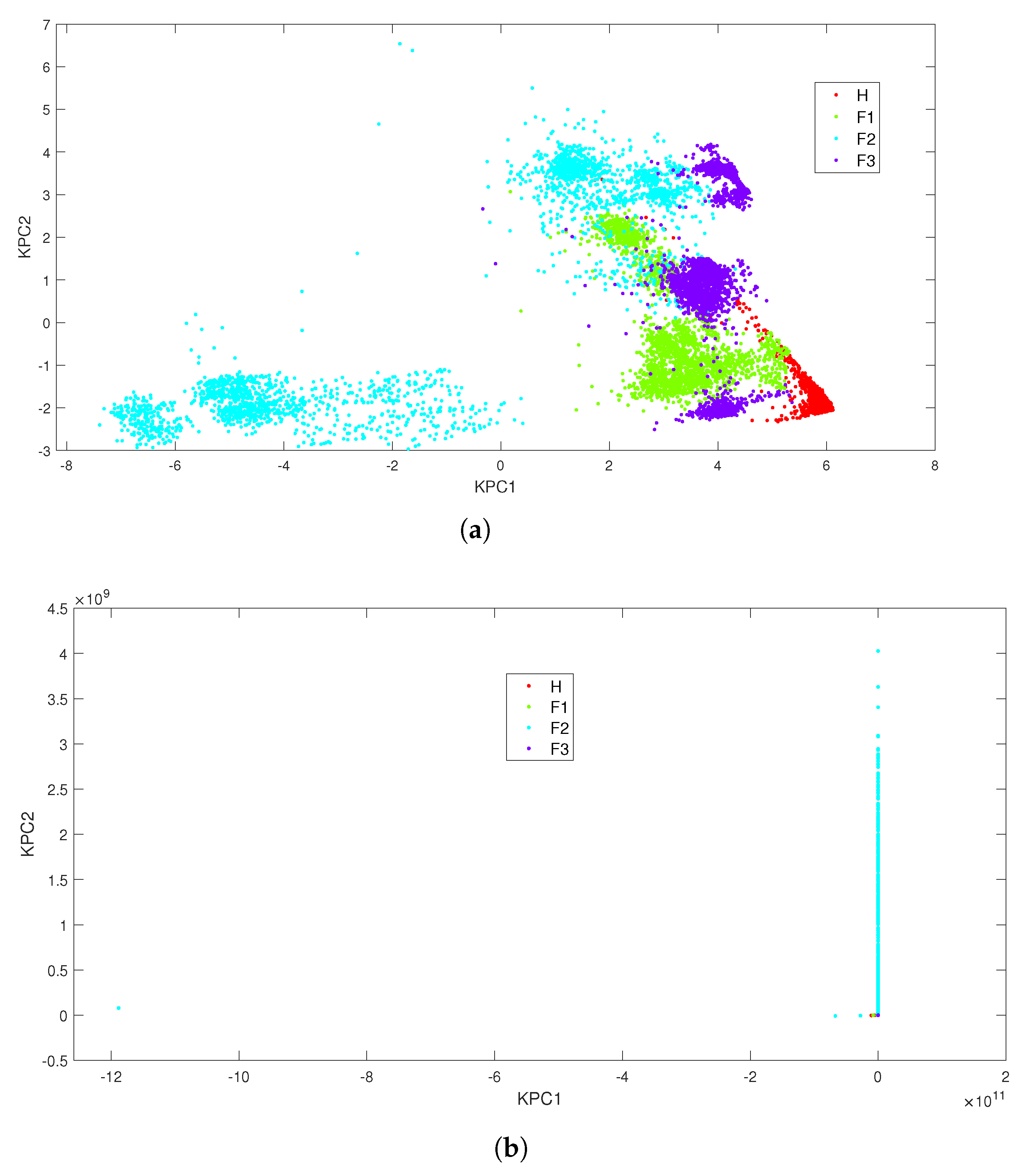
4.2.2. Kernel-Based Classifiers
4.2.3. Classification Results Based on the Systematic Data Exploration Strategy
- Under the single-load condition, all the three classifiers exhibited good performance despite a low testing accuracy rate of for the NB classifier;
- Under the combined-load condition, the performance of the NB classifier was severely degraded with and for the training accuracy rate and the testing accuracy rate, respectively.
- ■
- Case study with four features
- □
- KLD and variance of and , denoted as ;
In this case study, the KLD and the variance of the selected IMFs ( and ) were merged together for each load condition as in the following matrix.where and denote the KLD and variance of the jth component for their ith realisation, respectively. - ■
- Case study with two features
- □
- KLD and variance of , denoted as ;
- □
- KLD and variance of , denoted as ;
- □
- Variances of and , denoted as ;
- □
- KLD of and , denoted as .
- ■
- Case study with one feature
- □
- Variance of , denoted as ;
- □
- Variance of , denoted as ;
- □
- KLD of , denoted as ;
- □
- KLD of , denoted as .
- For both training and testing steps, whatever the load condition or the used classifier, case with the combination of KLD and variance for and offers the best performance.
- This analysis shows that it is possible to adapt to each case and meet the application requirements. Taking the example of load , we can choose to work with either four features (), two features () or even one feature (: variance of ) to reach of classification accuracy. This flexibility can address the computation time that is strongly linked to the number of used features corresponding to the input’s dimension of the classification system.
- Finally, we can conclude that in our study, the KNN classifier offers the most efficient combinations of features.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Huang, W.; Cheng, J.; Yang, Y. Rolling bearing fault diagnosis and performance degradation assessment under variable operation conditions based on nuisance attribute projection. Mech. Syst. Signal Process. 2019, 114, 165–188. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Y.; Xu, M.; Huang, W. A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery. Entropy 2019, 21, 409. [Google Scholar] [CrossRef] [PubMed]
- Tang, M.; Liao, Y.; Luo, F.; Li, X. A Novel Method for Fault Diagnosis of Rotating Machinery. Entropy 2022, 24, 681. [Google Scholar] [CrossRef] [PubMed]
- Zarei, J.; Tajeddini, M.A.; Karimi, H.R. Vibration analysis for bearing fault detection and classification using an intelligent filter. Mechatronics 2014, 24, 151–157. [Google Scholar] [CrossRef]
- Immovilli, F.; Bianchini, C.; Cocconcelli, M.; Bellini, A.; Rubini, R. Bearing fault model for induction motor with externally induced vibration. IEEE Trans. Ind. Electron. 2012, 60, 3408–3418. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Si, S.; Huang, S. Entropy based fault classification using the Case Western Reserve University data: A benchmark study. IEEE Trans. Reliab. 2019, 69, 754–756. [Google Scholar] [CrossRef]
- Tahir, M.M.; Khan, A.Q.; Iqbal, N.; Hussain, A.; Badshah, S. Enhancing fault classification accuracy of ball bearing using central tendency based time domain features. IEEE Access 2016, 5, 72–83. [Google Scholar] [CrossRef]
- Boudiaf, A.; Moussaoui, A.; Dahane, A.; Atoui, I. A comparative study of various methods of bearing faults diagnosis using the Case Western Reserve University data. J. Fail. Anal. Prev. 2016, 16, 271–284. [Google Scholar] [CrossRef]
- Safizadeh, M.; Latifi, S. Using multi-sensor data fusion for vibration fault diagnosis of rolling element bearings by accelerometer and load cell. Inf. Fusion 2014, 18, 1–8. [Google Scholar] [CrossRef]
- Kaya, Y.; Kuncan, M.; Kaplan, K.; Minaz, M.R.; Ertunç, H.M. A new feature extraction approach based on one dimensional gray level co-occurrence matrices for bearing fault classification. J. Exp. Theor. Artif. Intell. 2021, 33, 161–178. [Google Scholar] [CrossRef]
- Delpha, C.; Diallo, D.; Harmouche, J.; Benbouzid, M.; Amirat, Y.; Elbouchickhi, E. Bearing Fault Diagnosis in Rotating Machines. In Electrical Systems 2: From Diagnosis to Prognosis; Soualhi, A., Razik, H., Eds.; ISTE: London, UK, 2020; pp. 123–152. [Google Scholar]
- Neupane, D.; Seok, J. Bearing Fault Detection and Diagnosis Using Case Western Reserve University Dataset With Deep Learning Approaches: A Review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Qi, J.; Gao, X.; Huang, N. Mechanical Fault Diagnosis of a High Voltage Circuit Breaker Based on High-Efficiency Time-Domain Feature Extraction with Entropy Features. Entropy 2020, 22, 478. [Google Scholar] [CrossRef]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483. [Google Scholar] [CrossRef]
- Liu, M.K.; Weng, P.Y. Fault Diagnosis of Ball Bearing Elements: A Generic Procedure based on Time-Frequency Analysis. Meas. Sci. Rev. 2019, 19, 185–194. [Google Scholar] [CrossRef]
- Du, C.; Gao, S.; Jia, N.; Kong, D.; Jiang, J.; Tian, G.; Su, Y.; Wang, Q.; Li, C. A High-Accuracy Least-Time-Domain Mixture Features Machine-Fault Diagnosis Based on Wireless Sensor Network. IEEE Syst. J. 2020, 14, 4101–4109. [Google Scholar] [CrossRef]
- Griffin, D.; Lim, J. Signal estimation from modified short-time Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 236–243. [Google Scholar] [CrossRef]
- Allen, J.B.; Rabiner, L.R. A unified approach to short-time Fourier analysis and synthesis. Proc. IEEE 1977, 65, 1558–1564. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Shensa, M.J. The discrete wavelet transform: Wedding the a trous and Mallat algorithms. IEEE Trans. Signal Process. 1992, 40, 2464–2482. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. Hilbert–Huang transform-based vibration signal analysis for machine health monitoring. IEEE Trans. Instrum. Meas. 2006, 55, 2320–2329. [Google Scholar] [CrossRef]
- Susanto, A.; Liu, C.H.; Yamada, K.; Hwang, Y.R.; Tanaka, R.; Sekiya, K. Application of Hilbert–Huang transform for vibration signal analysis in end-milling. Precis. Eng. 2018, 53, 263–277. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, T.; Yan, S.; Qian, M. Revised empirical wavelet transform based on auto-regressive power spectrum and its application to the mode decomposition of deployable structure. J. Sound Vib. 2018, 431, 70–87. [Google Scholar] [CrossRef]
- Amirat, Y.; Elbouchickhi, E.; Delpha, C.; Benbouzid, M.; Diallo, D. Modal Decomposition for Bearing Fault Detection. In Electrical Systems 1: From Diagnosis to Prognosis; Soualhi, A., Razik, H., Eds.; ISTE: London, UK, 2020; pp. 121–168. [Google Scholar]
- Shi, R.; Wang, B.; Wang, Z.; Liu, J.; Feng, X.; Dong, L. Research on Fault Diagnosis of Rolling Bearings Based on Variational Mode Decomposition Improved by the Niche Genetic Algorithm. Entropy 2022, 24, 825. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Shen, Z.; Long, S.; Wu, M.; Shih, H.; Zheng, Q.; Tung, C.; Liu, H. The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc. R. Soc. A 1998, 545, 903–995. [Google Scholar] [CrossRef]
- Ahmed, H.O.A.; Nandi, A.K. Intrinsic Dimension Estimation-Based Feature Selection and Multinomial Logistic Regression for Classification of Bearing Faults Using Compressively Sampled Vibration Signals. Entropy 2022, 24, 511. [Google Scholar] [CrossRef]
- Tabrizi, A.; Garibaldi, L.; Fasana, A.; Marchesiello, S. Early damage detection of roller bearings using wavelet packet decomposition, ensemble empirical mode decomposition and support vector machine. Meccanica 2015, 50, 865–874. [Google Scholar] [CrossRef]
- Han, H.; Cho, S.; Kwon, S.; Cho, S.B. Fault diagnosis using improved complete ensemble empirical mode decomposition with adaptive noise and power-based intrinsic mode function selection algorithm. Electronics 2018, 7, 16. [Google Scholar] [CrossRef]
- Ge, J.; Niu, T.; Xu, D.; Yin, G.; Wang, Y. A Rolling Bearing Fault Diagnosis Method Based on EEMD-WSST Signal Reconstruction and Multi-Scale Entropy. Entropy 2020, 22, 290. [Google Scholar] [CrossRef]
- Kumar, P.S.; Kumaraswamidhas, L.A.; Laha, S.K. Selecting effective intrinsic mode functions of empirical mode decomposition and variational mode decomposition using dynamic time warping algorithm for rolling element bearing fault diagnosis. Trans. Inst. Meas. Control 2019, 41, 1923–1932. [Google Scholar] [CrossRef]
- Tang, G.; Luo, G.; Zhang, W.; Yang, C.; Wang, H. Underdetermined blind source separation with variational mode decomposition for compound roller bearing fault signals. Sensors 2016, 16, 897. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Wang, Y.; Deng, W. Fault Diagnosis for Rolling Bearings Using Optimized Variational Mode Decomposition and Resonance Demodulation. Entropy 2020, 22, 739. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P. On empirical mode decomposition and its algorithms. In Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing, Grado, Italy, 8–11 June 2003; Volume 3, pp. 8–11. [Google Scholar]
- Yu, D.; Cheng, J.; Yang, Y. Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings. Mech. Syst. Signal Process. 2005, 19, 259–270. [Google Scholar] [CrossRef]
- Moore, K.J.; Kurt, M.; Eriten, M.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Wavelet-bounded empirical mode decomposition for measured time series analysis. Mech. Syst. Signal Process. 2018, 99, 14–29. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: New York, NY, USA, 2002. [Google Scholar]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Mucherino, A.; Papajorgji, P.J.; Pardalos, P.M. k-Nearest Neighbor Classification. In Data Mining in Agriculture; Mucherino, A., Papajorgji, P.J., Pardalos, P.M., Eds.; Springer: New York, NY, USA, 2009; pp. 83–106. [Google Scholar]
- Izenman, A.J. Modern Multivariate Statistical Techniques: Regression, Classification, and Manifold Learning; Springer: New York, NY, USA, 2008. [Google Scholar]
- Webb, G.I. Naïve Bayes. In Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2010; pp. 713–714. [Google Scholar]
- Case Western Reserve University, USA. Bearing Data Centre. 2020. Available online: http://csegroups.case.edu/bearingdatacenter/pages/download-data-file/ (accessed on 2 March 2020).
- Harmouche, J.; Delpha, C.; Diallo, D. Incipient fault detection and diagnosis based on Kullback–Leibler divergence using principal component analysis: Part I. Signal Process. 2014, 94, 278–287. [Google Scholar] [CrossRef]
- Cai, P.; Deng, X. Incipient fault detection for nonlinear processes based on dynamic multi-block probability related kernel principal component analysis. ISA Trans. 2020, 105, 210–220. [Google Scholar] [CrossRef]
- Delpha, C.; Diallo, D. Kullback—Leibler divergence for incipient fault diagnosis. In Signal Processing for Fault Detection and Diagnosis in Electric Machines and Systems; Benbouzid, M., Ed.; IET, The Institution of Engineering and Technology: London, UK, 2020; pp. 87–118. [Google Scholar]
- Mezni, Z.; Delpha, C.; Diallo, D.; Braham, A. Bearing fault detection using intrinsic mode functions statistical information. In Proceedings of the 2018 15th International Multi-Conference on Systems, Signals & Devices (SSD), Yasmine Hammamet, Tunisia, 19–22 March 2018; pp. 870–875. [Google Scholar]
- Mezni, Z.; Delpha, C.; Diallo, D.; Braham, A. Intrinsic Mode Function Selection and Statistical Information Analysis for Bearing Ball Fault Detection. In Diagnosis, Fault Detection & Tolerant Control; Derbel, N., Ghommam, J., Zhu, Q., Eds.; Springer: Singapore, Singapore, 2020; pp. 111–135. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.R. Kernel principal component analysis. In Proceedings of the International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 1997; pp. 583–588. [Google Scholar]
- Lu, H.; Meng, Y.; Yan, K.; Gao, Z. Kernel principal component analysis combining rotation forest method for linearly inseparable data. Cogn. Syst. Res. 2019, 53, 111–122. [Google Scholar] [CrossRef]
- Dong, S.; Luo, T.; Zhong, L.; Chen, L.; Xu, X. Fault diagnosis of bearing based on the kernel principal component analysis and optimized k-nearest neighbour model. J. Low Freq. Noise Vib. Act. Control 2017, 36, 354–365. [Google Scholar] [CrossRef]
- Wu, G.; Yuan, H.; Gao, B.; Li, S. Fault diagnosis of power transformer based on feature evaluation and kernel principal component analysis. High Volt. Eng. 2017, 43, 2533–2540. [Google Scholar]
- Zhang, X.; Delpha, C. Improved Incipient Fault Detection Using Jensen-Shannon Divergence and KPCA. In Proceedings of the 2020 Prognostics and Health Management Conference (PHM 2020), Besancon, France, 4–7 May 2020; pp. 241–246. [Google Scholar]
- Fauvel, M.; Chanussot, J.; Benediktsson, J.A. Kernel principal component analysis for the classification of hyperspectral remote sensing data over urban areas. EURASIP J. Adv. Signal Process. 2009, 2009, 783194. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Wu, Y.; Ianakiev, K.; Govindaraju, V. Improved k-Nearest Neighbor classification. Pattern Recognit. 2002, 35, 2311–2318. [Google Scholar] [CrossRef]
- Mezni, Z.; Delpha, C.; Diallo, D.; Braham, A. Bearing Fault Severity Classification Based on EMD-KLD: A Comparative Study for Incipient Ball Faults. In Proceedings of the 2020 Prognostics and Health Management Conference (PHM-Besançon), Besancon, France, 4–7 May 2020; pp. 257–262. [Google Scholar]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Polat, K.; Güneş, S. Classification of epileptiform EEG using a hybrid system based on decision tree classifier and fast Fourier transform. Appl. Math. Comput. 2007, 187, 1017–1026. [Google Scholar] [CrossRef]
- Saimurugan, M.; Ramachandran, K.; Sugumaran, V.; Sakthivel, N. Multi component fault diagnosis of rotational mechanical system based on decision tree and support vector machine. Expert Syst. Appl. 2011, 38, 3819–3826. [Google Scholar] [CrossRef]
- Zhang, N.; Wu, L.; Yang, J.; Guan, Y. Naive bayes bearing fault diagnosis based on enhanced independence of data. Sensors 2018, 18, 463. [Google Scholar] [CrossRef]
- Addin, O.; Sapuan, S.; Othman, M.; Ali, B.A. Comparison of Naïve bayes classifier with back propagation neural network classifier based on f-folds feature extraction algorithm for ball bearing fault diagnostic system. Int. J. Phys. Sci. 2011, 6, 3181–3188. [Google Scholar]
- Vernekar, K.; Kumar, H.; Gangadharan, K. Engine gearbox fault diagnosis using empirical mode decomposition method and Naïve Bayes algorithm. Sādhanā 2017, 42, 1143–1153. [Google Scholar] [CrossRef]
- Mezni, Z.; Delpha, C.; Diallo, D.; Braham, A. A comparative study for ball bearing fault classification using kernel-SVM with Kullback Leibler divergence selected features. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 6969–6974. [Google Scholar]
- Sharma, A.; Amarnath, M.; Kankar, P. Feature extraction and fault severity classification in ball bearings. J. Vib. Control 2016, 22, 176–192. [Google Scholar] [CrossRef]
- Attoui, I.; Fergani, N.; Boutasseta, N.; Oudjani, B.; Deliou, A. A new time–frequency method for identification and classification of ball bearing faults. J. Sound Vib. 2017, 397, 241–265. [Google Scholar] [CrossRef]
- Babouri, M.K.; Djebala, A.; Ouelaa, N.; Oudjani, B.; Younes, R. Rolling bearing faults severity classification using a combined approach based on multi-scales principal component analysis and fuzzy technique. Int. J. Adv. Manuf. Technol. 2020, 107, 4301–4316. [Google Scholar] [CrossRef]


| IMF Rank | SNR RDP (%) |
|---|---|
| 1 | 5 |
| 2 | 11.7 |
| 3 | 21.6 |
| 4 | 20 |
| 5 | 17.3 |
| 6 | 22.3 |
| 7 | 28.2 |
| 8 | 34.8 |
| 9 | 44.9 |
| 10 | 51.8 |
| 11 | 59.2 |
| 12 | 62.1 |
| 13 | 68.2 |
| 14 | 68.9 |
| 15 | 59.1 |
| 16 | 62.1 |
| 17 | 83 |
| 18 | 81.1 |
| AUC for Mean | AUC for Variance | AUC for Skewness | AUC for Kurtosis | AUC for KLD | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IMF | ||||||||||||||||||||
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||||
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||||||
| 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||||
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||||
| 6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||
| 7 | 1 | 1 | 1 | |||||||||||||||||
| 8 | 1 | 1 | 1 | |||||||||||||||||
| Load Condition | PC | Eigenvalue | Variance Contribution (%) | Cumulative Variance (%) |
|---|---|---|---|---|
| 1 | 2.638 | 65.956 | 65.956 | |
| 2 | 0.982 | 24.572 | 90.53 | |
| 3 | 0.277 | 6.932 | 97.46 | |
| 4 | 0.105 | 2.537 | 100 | |
| 1 | 1.672 | 41.814 | 41.814 | |
| 2 | 1.475 | 36.847 | 78.69 | |
| 3 | 0.482 | 12.071 | 90.76 | |
| 4 | 0.369 | 9.239 | 100 | |
| 1 | 3.073 | 75.927 | 75.927 | |
| 2 | 0.744 | 18.617 | 94.55 | |
| 3 | 0.136 | 3.422 | 97.97 | |
| 4 | 0.081 | 2.031 | 100 | |
| 1 | 2.706 | 67.653 | 67.653 | |
| 2 | 1.039 | 25.996 | 93.65 | |
| 3 | 0.172 | 4.31 | 97.96 | |
| 4 | 0.081 | 2.01 | 100 | |
| 1 | 1.829 | 45.747 | 45.747 | |
| 2 | 1.132 | 28.322 | 74.07 | |
| 3 | 0.806 | 20.151 | 94.22 | |
| 4 | 0.231 | 5.779 | 100 |
| KPC | Variance Contribution | Cumulative Variance (%) | ||
|---|---|---|---|---|
| Gaussian Kernel | Polynomial Kernel | Gaussian Kernel | Polynomial Kernel | |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | 100 | 100 | ||
| Classifier | KNN | DT | NB | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Load (hp) | |||||||||||||||
| Training accuracy rate (%) | 100 | 99 | 100 | 100 | 98 | 98 | 82.3 | ||||||||
| Testing accuracy rate (%) | 81.92 | ||||||||||||||
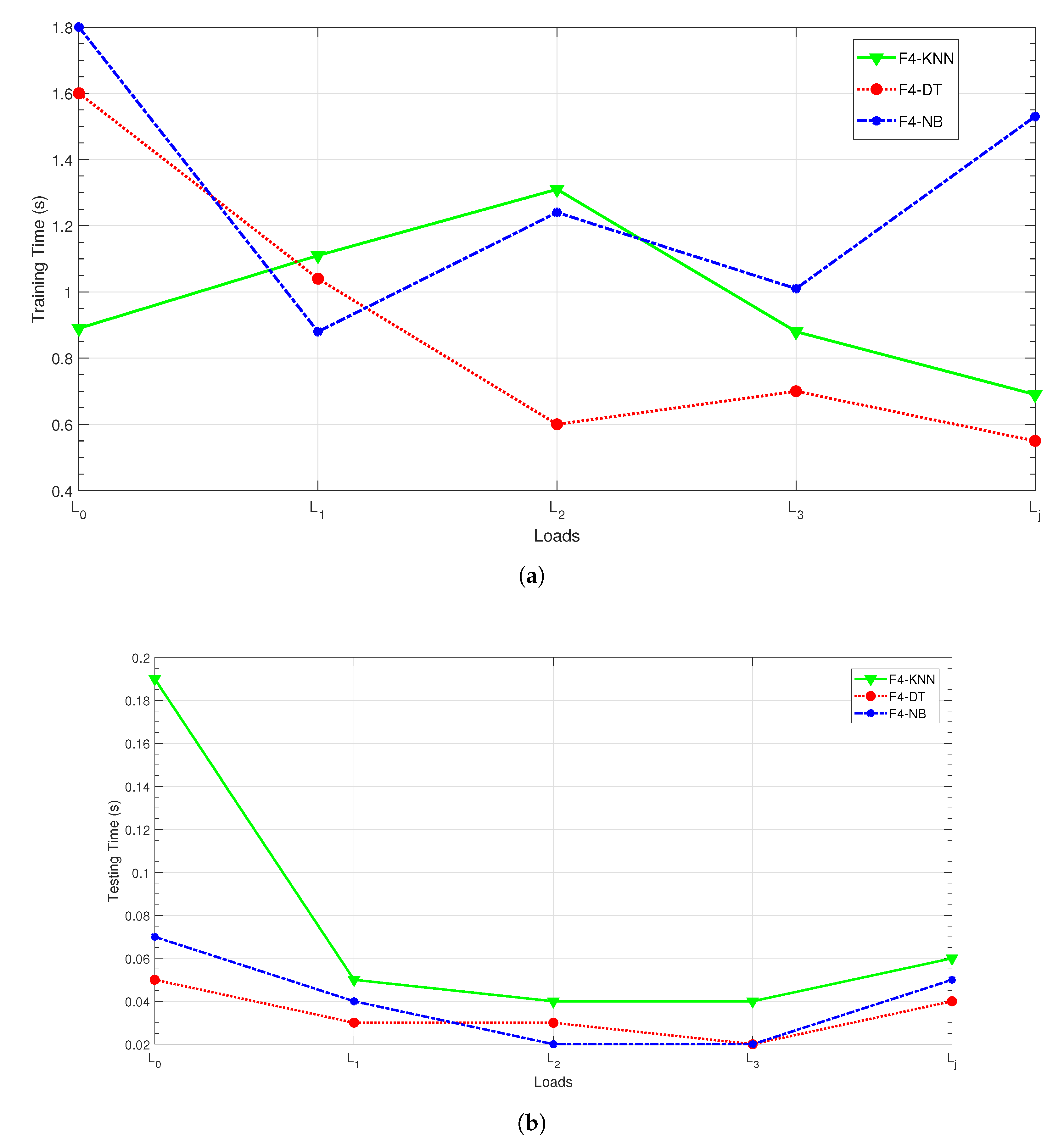
| Training time (s) | 1 | ||||||||||||||
| Testing time (s) | |||||||||||||||
| Features | Relevant | |||
|---|---|---|---|---|
| Variance | ||||
| KLD | ||||
| Classifier | KNN | DT | NB | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Load (hp) | |||||||||||||||
| Training accuracy rate (%) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | ||||
| Testing accuracy rate (%) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | ||
| Training time (s) | |||||||||||||||
| Testing time (s) | |||||||||||||||
| Ref | Fault Type | Ball | ||||||
|---|---|---|---|---|---|---|---|---|
| Load (hp) | Mean | |||||||
| Algorithm | Testing Accuracy Rates (%) | |||||||
| [6] | MPE | KNN | 93 | 99 | 100 | 100 | Not provided | 98 |
| SVM | 81 | 99 | 100 | 98 | Not provided | 94.5 | ||
| Logic regression | 96 | 99 | 100 | 100 | Not provided | 98.75 | ||
| Backpropagation NN | 70 | 91 | 90 | 93 | Not provided | 86 | ||
| Extreme learning Machine | 92 | 90 | 100 | 100 | Not provided | 97.5 | ||
| Soft regression | 94 | 99 | 100 | 100 | Not provided | 98.25 | ||
| Proposed technique | KLD and variance | KNN | 100 | 100 | 100 | 100 | 100 | 100 |
| DT | 100 | 100 | 100 | 100 | 100 | 100 | ||
| NB | 99.83 | 100 | 99.85 | 100 | 100 | 99.92 | ||
| KNN | DT | NB | ||||
|---|---|---|---|---|---|---|
| Load Condition | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mezni, Z.; Delpha, C.; Diallo, D.; Braham, A. Performance of Bearing Ball Defect Classification Based on the Fusion of Selected Statistical Features. Entropy 2022, 24, 1251. https://doi.org/10.3390/e24091251
Mezni Z, Delpha C, Diallo D, Braham A. Performance of Bearing Ball Defect Classification Based on the Fusion of Selected Statistical Features. Entropy. 2022; 24(9):1251. https://doi.org/10.3390/e24091251
Chicago/Turabian StyleMezni, Zahra, Claude Delpha, Demba Diallo, and Ahmed Braham. 2022. "Performance of Bearing Ball Defect Classification Based on the Fusion of Selected Statistical Features" Entropy 24, no. 9: 1251. https://doi.org/10.3390/e24091251
APA StyleMezni, Z., Delpha, C., Diallo, D., & Braham, A. (2022). Performance of Bearing Ball Defect Classification Based on the Fusion of Selected Statistical Features. Entropy, 24(9), 1251. https://doi.org/10.3390/e24091251







