A Realization Approach to Lossy Network Compression of a Tuple of Correlated Multivariate Gaussian RVs †
Abstract
:1. Introduction
1.1. Literature Review
1.2. Main Theorems and Discussion
1.3. Structure of the Paper
2. Probabilistic Properties of Tuples of Random Variables
2.1. Notation of Elements of Probability Theory
2.2. Geometric Approach of Gaussian Random Variables and Canonical Variable Form
| identical information of and | |
| correlated information of with respect to | |
| private information of with respect to | |
| identical information of and | |
| correlated information of with respect to | |
| private information of with respect to |
2.3. Conditional Independence of a Triple of Gaussian Random Variables
2.4. Weak Realization of a Gaussian Probability Measure on a Tuple of Random Variables
- (1)
- The measure restricted to the first two Gaussian random variables is equal to the considered probability measure;
- (2)
- The third Gaussian random variable makes the other two random variables conditionally independent. This problem does not have a unique solution, there is a set of Gaussian probability measures which meets those conditions. Needed is the parameterization of this set of solutions.
- At the encoder, first compute the variables,then, the tripleof jointly Gaussian random variables are such thatandindependent of W.
- The tuple of random variablesare represented according to
- At the encoder, compute first the variables,then the tripleof jointly Gaussian random variables are independent.
- The tuple of random variablesare represented according to,
- (a)
- At the encoder, the conditional expectations are correct and the definitions of and of are well defined.
- (b)
- The three random variables are independent. Consequently, the three sequences, and messages generated by the Gray–Wyner encoder,are independent.
2.5. Characterization of Minimal Conditional Independence of a Triple of Gaussian Random Variables
3. Wyner’s Common Information
3.1. Reduction of the Calculation of Wyner’s Common Information
3.2. Wyner’s Common Information of Correlated Random Variables
3.3. Wyner’s Common Information of Arbitrary Gaussian Random Variables
- (a)
- The minimal σ-algebra which makes conditionally independent is the trivial σ-algebra denoted by . Thus, . The random variable W, in this case, is the constant , hence .
- (b)
- Then, and
- (c)
- The weak stochastic realization that achieves is
- (a)
- The only minimal σ-algebra which makes and Gaussian conditional-independent is . The state variable is thus, and .
- (b)
- Then .
- (c)
- The weak stochastic realization is again simple, the variable W equals the identical component and there is no need to use the signals and . Thus, the representations are,
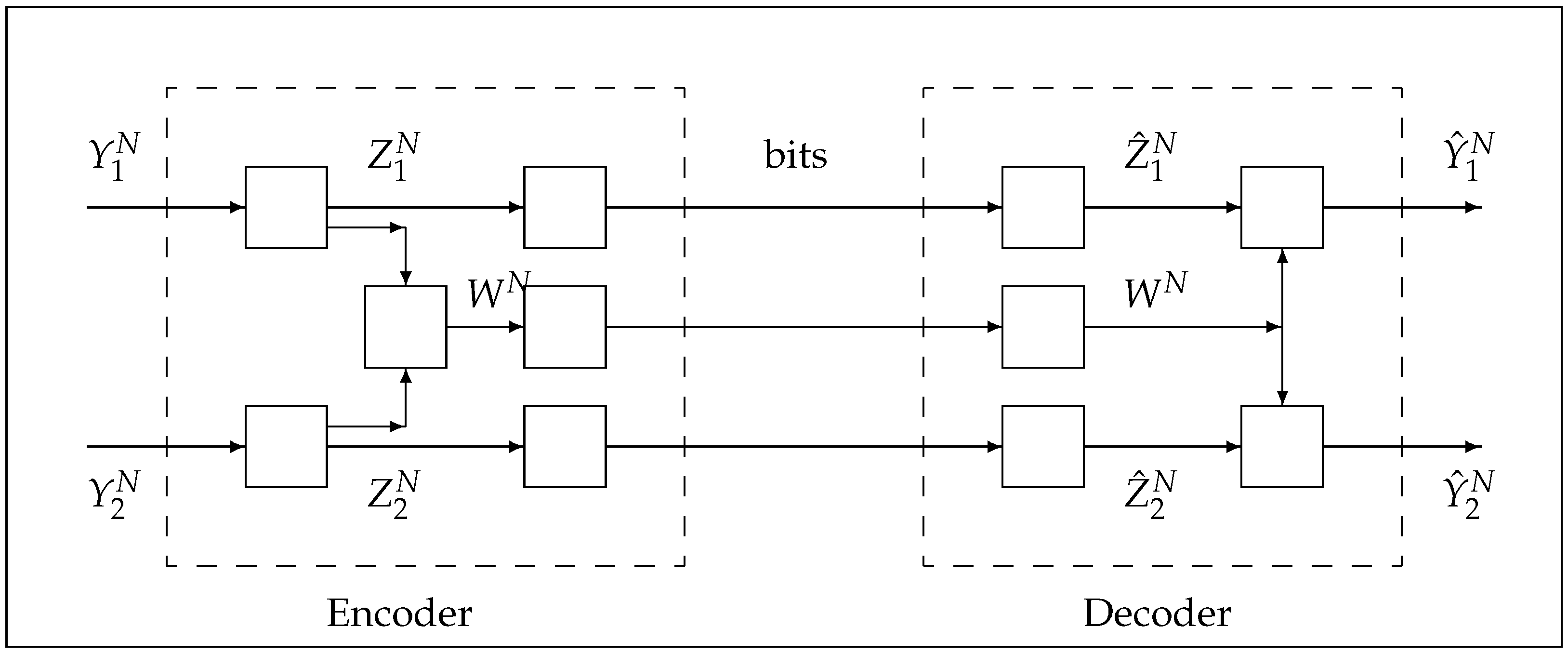
4. Parametrization of Gray and Wyner Rate Region and Wyner’s Lossy Common Information
4.1. Characterizations of Joint, Conditional and Marginal RDFs
4.2. Wyner’s Lossy Common Information of Correlated Gaussian Vectors
4.3. Applications to Problems of the Literature [15,16,17]
4.4. Characterization and Parameterization of the Gray and Wyner Rate Region by Jointly Gaussian RVs
- (1)
- Theorem 5—the characterizations of the rate region , and
- (2)
- The characterization of rates that lie on Pangloss Plane.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Algorithm to Generate the Canonical Variable Form
- 1
- Perform singular-value decompositions:with orthogonal () andand satisfying corresponding conditions.
- 2
- Perform a singular-value decomposition ofwith , orthogonal and
- 3
- Compute the new variance matrix according to
- 4
- The transformation to the canonical variable representationis then
Appendix A.2. Information Theory
Appendix A.3. An Inequality for Determinants
References
- Gray, R.M.; Wyner, A.D. Source coding for a simple network. Bell Syst. Tech. J. 1974, 53, 1681–1721. [Google Scholar] [CrossRef]
- Wyner, A.D. The common information of two dependent random variables. IEEE Trans. Inf. Theory 1975, 21, 163–179. [Google Scholar] [CrossRef]
- Witsenhausen, H.S. Values and bounds for common information of two discrete variables. SIAM J. Appl. Math. 1976, 31, 313–333. [Google Scholar] [CrossRef]
- Witsenhausen, H.S. On sequences of pairs of dependent random variables. SIAM J. Appl. Math. 1975, 28, 100–113. [Google Scholar] [CrossRef]
- Gacs, P.; Korner, J. Common information is much less than mutual information. Probl. Control Inf. Theory 1973, 2, 149–162. [Google Scholar]
- Benammar, M.; Zaidi, A. Rate-distortion region of a Gray-Wyner model with side information. Entropy 2018, 20, 2. [Google Scholar] [CrossRef] [PubMed]
- Benammar, M.; Zaidi, A. Rate-distortion region of a Gray-Wyner problem with side information. In Proceedings of the IEEE International Symposium on Information Theory (ISIT.2017), Aachen, Germany, 25–30 June 2017; pp. 106–110. [Google Scholar]
- Benammar, M.; Zaidi, A. Rate-distortion function for a Heegard-Berger problem with two sources and degraded reconstruction sets. IEEE Trans. Inf. Theory 2016, 62, 5080–5092. [Google Scholar] [CrossRef]
- Benammar, M.; Zaidi, A. Rate-distortion function for a Heegard-Berger problem with common reconstruction constraint. In Proceedings of the IEEE International Theory Workshop (ITW.2015), Jeju Island, Korea, 11–15 October 2015. [Google Scholar]
- Heegard, C.; Berger, T. Rate distortion when side information may be absent. IEEE Trans. Inf. Theory 1985, 31, 727–734. [Google Scholar] [CrossRef]
- Cuff, P.W.; Permuter, H.H.; Cover, T.M. Coordination Capacity. IEEE Trans. Inf. Theory 2010, 56, 4181–4206. [Google Scholar] [CrossRef]
- Kumar, B.; Viswanatha, E.A.; Rose, K. The lossy common information of correlated sources. IEEE Trans. Inf. Theory 2014, 60, 3238–3253. [Google Scholar]
- Xu, G.; Liu, W.; Chen, B. A lossy source coding interpretation of Wyner’s common information. IEEE Trans. Inf. Theory 2016, 62, 754–768. [Google Scholar] [CrossRef]
- Xiao, J.-J.; Luo, Z.-Q. Compression of Correlated Gaussian Sources under Individual Distortion Criteria. In Proceedings of the 43rd Annual Allerton Conference on Communication, Control and Computing, Monticello, IL, USA, 28–30 September 2005; pp. 438–447. [Google Scholar]
- Satpathy, S.; Cuff, P. Gaussian secure source coding and Wyner’s common information. In Proceedings of the IEEE International Symposium on Information Theory (ISIT.2015), Hong Kong, China, 14–19 July 2015; pp. 116–120. [Google Scholar]
- Veld, G.J.O.; Gastpar, M.C. Total correlation of Gaussian vector sources on the Gray-Wyner network. In Proceedings of the 54th Annual Allerton Conference on Communication, Control and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016; pp. 385–392. [Google Scholar]
- Sula, E.; Gastpar, M. Relaxed Wyner’s common information. arXiv 2019, arXiv:1912.07083. [Google Scholar]
- Hotelling, H. Relation between two sets of variates. Biometrika 1936, 28, 321–377. [Google Scholar] [CrossRef]
- Gelfand, M.I.; Yaglom, M. Calculation of the amount of information about a random function contained in another such function. Am. Math. Soc. Transl. 1959, 2, 199–246. [Google Scholar]
- van Schuppen, J.H. Common, correlated, and private information in control of decentralized systems. In Coordination Control of Distributed Systems; van Schuppen, J.H., Villa, T., Eds.; Number 456 in Lecture Notes in Control and Information Sciences; Springer International Publishing: Cham, Switzerland, 2015; pp. 215–222. [Google Scholar]
- Charalambous, C.D.; van Schuppen, J.H. A new approach to lossy network compression of a tuple of correlated multivariate Gaussian RVs. arXiv 2019, arXiv:1905.12695. [Google Scholar]
- van Putten, C.; van Schuppen, J.H. The weak and strong Gaussian probabilistic realization problem. J. Multivar. Anal. 1983, 13, 118–137. [Google Scholar] [CrossRef]
- Noble, B. Applied Linear Algebra; Prentice-Hall: Englewood Cliffs, NJ, USA, 1969. [Google Scholar]
- Stylianou, E.; Charalambous, C.D.; Charalambous, T. Joint rate distortion function of a tuple of correlated multivariate Gaussian sources with individual fidelity criteria. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT.2021), Melbourne, Australia, 12–20 July 2021; pp. 2167–2172. [Google Scholar]
- Gkagkos, M.; Charalambous, C.D. Structural properties of optimal test channels for distributed source coding with decoder side information for multivariate Gaussian sources with square-error fidelity. arXiv 2020, arXiv:2011.10941. [Google Scholar]
- Gkangos, M.; Charalambous, C.D. Structural properties of test channels of the RDF for Gaussian multivariate distributed sources. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT.2021), Melbourne, Australia, 12–20 July 2021; pp. 2631–2636. [Google Scholar]
- Charalambous, C.D.; van Schuppen, J.H. Characterization of conditional independence and weak realizations of multivariate gaussian random variables: Applications to networks. In Proceedings of the IEEE International Symposium on Information Theory (ISIT.2020), Los Angeles, CA, USA, 21–26 June 2020. [Google Scholar]
- Gray, R.M. A new class of lower bounds to information rates of stationary via conditional rate-distortion functions. IEEE Trans. Inf. Theory 1973, 19, 480–489. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Gallager, R.G. Information Theory and Reliable Communication; John Wiley & Sons: New York, NY, USA, 1968. [Google Scholar]
- Yaglom, A.M.; Yaglom, I.M. Probability and Information; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Marshall, A.W.; Olkin, I. Inequalities: Theory of Majorization and Its Applications; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Hua, L.K. Inequalies involving determinants. Acta Math. Sin. 1955, 5, 463–470, (In Chinese; English summary). [Google Scholar]
- Zhang, F. Positive semidefinite matrices. In Matrix Theory: Basic Results and Techniques; Springer Science+Business Media: New York, NY, USA, 2011; pp. 199–252. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charalambous, C.D.; van Schuppen, J.H. A Realization Approach to Lossy Network Compression of a Tuple of Correlated Multivariate Gaussian RVs. Entropy 2022, 24, 1227. https://doi.org/10.3390/e24091227
Charalambous CD, van Schuppen JH. A Realization Approach to Lossy Network Compression of a Tuple of Correlated Multivariate Gaussian RVs. Entropy. 2022; 24(9):1227. https://doi.org/10.3390/e24091227
Chicago/Turabian StyleCharalambous, Charalambos D., and Jan H. van Schuppen. 2022. "A Realization Approach to Lossy Network Compression of a Tuple of Correlated Multivariate Gaussian RVs" Entropy 24, no. 9: 1227. https://doi.org/10.3390/e24091227
APA StyleCharalambous, C. D., & van Schuppen, J. H. (2022). A Realization Approach to Lossy Network Compression of a Tuple of Correlated Multivariate Gaussian RVs. Entropy, 24(9), 1227. https://doi.org/10.3390/e24091227






