Abstract
Properties of data distributions can be assessed at both global and local scales. At a highly localized scale, a fundamental measure is the local intrinsic dimensionality (LID), which assesses growth rates of the cumulative distribution function within a restricted neighborhood and characterizes properties of the geometry of a local neighborhood. In this paper, we explore the connection of LID to other well known measures for complexity assessment and comparison, namely, entropy and statistical distances or divergences. In an asymptotic context, we develop analytical new expressions for these quantities in terms of LID. This reveals the fundamental nature of LID as a building block for characterizing and comparing data distributions, opening the door to new methods for distributional analysis at a local scale.
1. Introduction
Fundamental activities for analyzing data include both an ability to characterize data complexity and an ability to make comparisons between distributions. Widely used measures for these activities include entropy (for assessing uncertainty) and statistical divergences or distances (to compare distributions) []. Such analysis can be performed at either a global scale across the entire data distribution or at a local scale, in the vicinity of a given location in the distribution.
An important measure of global complexity is intrinsic dimensionality, which captures the effective number of degrees of freedom needed to describe the entire dataset. On the other hand, local intrinsic dimensionality (LID) [] is capable of characterizing the complexity of the data distribution around a specified query location, thus capturing the number of degrees of freedom present at a local scale. LID is a unitless quantity that can also be interpreted as a relative growth rate of probability measure within an expanding neighborhood around the specified query location, or the intrinsic dimension of the space immediately around the query point.
Our focus in this paper is to characterize entropy and statistical divergences at a highly local scale, for an asymptotically small vicinity around a specified location. We show that it is possible to leverage properties that arise from LID based characterizations of lower tail distributions [], to develop analytical expressions for a wide selection of entropy variants and statistical divergences, in both univariate and multivariate settings. This yields expressions for tail entropies and tail divergences.
Analytical characterizations for tail divergences and tail entropies are appealing from a number of perspectives. These are as follows:
- For univariate scenarios, if working with the tail of a distribution that has a single variable, we can conduct:
- –
- Temporal analysis: when a distribution models some property varying over time (e.g., survival analysis), we can analyze the entropy of a univariate distribution within an asymptotically short window of time, or the divergence between two univariate distributions within an asymptotically short window of time.
- –
- Distance-based analysis: when a distribution models distances from a query location to its nearest neighbors and the distances are induced by a global data distribution. Here, our results can be used for analysis of tail entropy or divergence between distributions within an asymptotically small distance interval. In the case of the latter, this can provide insight into multivariate properties, since under minimal assumptions the divergences between univariate distance distributions provide lower bounds for distances between multivariate distributions [,]. This is applicable for models such as generative adversarial networks (GANs), where it is important to test correspondence between synthetic and true distributions at a local level [].
- For multivariate scenarios where we are analyzing distributions with multiple variables:
- –
- If an assumption of locally spherical symmetry of the distribution holds, then we can directly compute the tail entropy of a distribution or the divergence between two tail distributions in the vicinity of a single point. Such an assumption is suitable for analyzing data distributions for many types of physical systems such as fluids, glasses, metals and polymers, where local isotropy holds.
A key challenge in developing analytical characterizations for tail entropies and tail divergences is how to avoid or minimize assumptions about the form of the local distribution in the vicinity of the query (for example, assumptions such as a local normal distribution or a local uniform distribution). As we will see, analytical results are in fact possible—as the neighborhood radius asymptotically tends to zero, the tail distribution (a truncated distribution induced from the global distribution) is guaranteed to converge to a generalized pareto distribution (GPD), with the GPD parameter determined by the LID value of the tail distribution. The technical challenge is to rigorously delineate under what circumstances it is possible to leverage this relationship to achieve a dramatic simplification of the integrals that are required to compute varieties of tail entropy or distribution divergences. Our results in this paper show that such simplifications are in fact possible, for a wide range of tail entropies and divergences. This allows us to characterize and analyze fundamental properties of local neighborhood geometry, with results holding asymptotically for essentially all smooth data distributions.
In summary, our key contributions are the development of substantial new theory that asymptotically relates tail entropy, divergences and LID. It builds on and extends an earlier work by Bailey et al. [], which focused solely on univariate entropies, without reference to divergences or multivariate settings. Specifically in this paper, we:
- Formulate technical lemmas which delineate when it is possible to substitute certain types of tail distributions by simple formulations that depend only on their associated LID values.
- Use these lemmas to compute univariate tail formulations of entropy, cross entropy, cumulative entropy, entropy power and generalized q-entropies, all in terms of the LID values of the original tail distributions.
- Use these lemmas to compute tail formulations of univariate statistical divergences and distances (Kullback–Leibler divergence, Jensen–Shannon divergence, Hellinger distance, divergence, -divergence, Wasserstein distance and distance).
- Extend the univariate results to a multivariate context, when local spherical symmetry of the distribution holds.
2. Related Work
The core of our study involves intrinsic dimensionality (ID) and we begin by reviewing previous work on this topic.
There is a long history of work on ID, and this can be assessed either globally (for every data point) or locally (with respect to a chosen query point). Surveys of the field provide a good overview [,,]. In the global case, a range of previous works have focused on topological models and appropriate estimation methods [,,]. Such examples encompass techniques such as PCA and its variants [], graph based methods [] and fractal models [,]. Other approaches such as IDEA [,], DANCo [] or 2-NN estimate the (global) intrinsic dimension based on concentration of norms and angles, or 2-nearest neighbors [].
Local intrinsic dimensionality focuses on the intrinsic dimension of a particular query point and has been used in a range of applications. These include modeling deformation in granular materials [,], climate science [,], dimension reduction via local PCA [], similarity search [], clustering [], outlier detection [], statistical manifold learning [], adversarial example detection [], adversarial nearest neighbor characterization [,] and deep learning understanding [,]. In deep learning, it has been shown that adversarial examples are associated with high LID estimates, a characteristic that can be leveraged to build accurate adversarial example detectors []. It has also been found that the LID of deep representations [] learned by Deep Neural Networks (DNNs) or the raw input data [,] is correlated with the generalization performance of DNNs. A ‘dimensionality expansion’ phenomenon has been observed when DNNs overfit to noisy class labels [] and this can be leveraged to develop improved loss functions. The use of a “cross-LID” measure to evaluate the quality of synthetic examples generated by GANs has been proposed in []. Connections between local intrinsic dimensionality and global intrinsic dimensionality were explored by Romano et al in []. In the area of climate science and dynamical systems, a formulation similar to local intrinsic dimensionality has been developed and referred to as local dimension or instantaneous dimension [,,], using links to extreme value theoretic methods. It has proved useful as measure to characterize predictability of states and explain system dynamics.
For local intrinsic dimensionality, a popular estimator is the maximum likelihood estimator, studied in the Euclidean setting by Levina and Bickel [] and later formulated under the more general assumptions of extreme value theory by Houle [] and Amsaleg et al. [], who showed it to be equivalent to the classic Hill estimator []. Other local estimators include expected simplex skewness [], the tight locality estimator [], the MiND framework [], manifold adaptive dimension [], statistical distance [] and angle-based approaches []. Smoothing approaches for estimation have also been used with success [,].
Local intrinsic dimensionality is closely related to (univariate) distance distributions. Fundamental relations for interpoint distances, connecting multivariate distributions and univariate distributions have been explored by both [,]. The former showed that two multivariate distributions are equal whenever the interpoint distances both within and between samples have the same univariate distribution, while the latter showed that two multivariate distributions F and G are different if their univariate distance distributions from some randomly chosen point z are different. This can form the basis of a two sample test for comparing F and G. These studies have implications for our work in this paper, since they characterize the role that comparison between univariate distributions can play as a necessary condition for comparing equality of multivariate distributions.
Our work in this paper formulates results for different varieties of entropy and different types of divergences. Entropy is a fundamental notion used across many scientific disciplines. A good overview of its role in information theory is presented in []. Entropy power (the exponential of entropy) is commonly used in signal processing and information theory, and is a building block for the well-known Shannon entropy power inequality which can be used to analyze the convolution of two independent random variables []. Entropy power goes under the name of perplexity in the field of natural language processing [] and true diversity in the field of ecology []. It also corresponds to the volume of the smallest set that contains most of the probability measure [], and it can be interpreted as a measure of statistical dispersion []. It is also related to Fisher information via Stam’s inequality [].
Cumulative entropy was formulated in [] and is a modification of cumulative residual entropy []. It is popular in reliability theory where it is used to characterize uncertainty over time intervals. Apart from reliability theory analysis, it has been used in data mining tasks such as dependency analysis [] and subspace cluster analysis [], where it has proved more effective due to good estimation properties. These data mining investigations have used cumulative entropy at a global level (over the entire data domain), rather than at the local (tail) level, as in our study. Generalized variants based on Tsallis q-statistics have been developed for both entropy [] and cumulative entropy []. Inclusion of the extra q parameter can assist with higher robustness to anomalies and better fitting to characteristics of data distributions. Tail entropy has been used in financial applications for measuring the expected shortfall [] in the upper tail using quantization. This is different from our context, where the our exclusive focus is on lower tails and we develop exact results for an asymptotic regime where lower tail size approaches zero.
Divergences between probability distributions are a fundamental building block in statistics and are used to assess the degree to which one probability distribution is different from another probability distribution. They have a wide range of formulations [] and applications, which range from use as objective functions in supervised and unsupervised machine learning [], to hypothesis and two sample or goodness of fit testing in statistics [], as well as generative modeling in deep learning, particularly using the Wasserstein distance []. Asymptotic forms of KL divergence have been investigated by Contreras-Reyes [], for comparison of multivariate asymmetric heavy-tailed distributions.
Finally, we note that this work considerably expands a recent study by Bailey et al. [], which established relationships between tail entropies and LID. This current paper extends and generalizes that work in several directions: (i) We establish general lemmas that provide sufficient conditions for when it is possible to substitute a tail distribution with components such as a power law, inside an integral. The techniques of [] were specially crafted for specific integrals. (ii) We provide results for statistical divergences and distances (the work of [] only considers entropy). (iii) We show how to formulate results for the multivariate context (as [] only considers univariate scenarios).
3. Local Intrinsic Dimensionality
In this section, we summarize the LID model using the presentation of []. LID can be regarded as a continuous extension of the expansion dimension [,]. Like earlier expansion-based models of intrinsic dimension, its motivation comes from the relationship between volume and radius in an expanding ball, where (as originally stated in []) the volume of the ball is taken to be the probability measure associated with the region it encloses. The probability as a function of radius—denoted by —has the form of a univariate cumulative distribution function (CDF). The model formulation (as stated in []) generalizes this notion to real-valued functions F for which , under appropriate assumptions of smoothness.
Definition 1
([]). Let F be a real-valued function that is non-zero over some open interval containing , . The intrinsic dimensionality of F at r is defined as follows whenever the limit exists:
When F satisfies certain smoothness conditions in the vicinity of r, its intrinsic dimensionality has a convenient known form:
Theorem 1
([]). Let F be a real-valued function that is non-zero over some open interval containing , . If F is continuously differentiable at r and using to denote the derivative , then
Let be a location of interest within a data domain for which the distance measure has been defined. To any generated sample we associate the distance ; in this way, a global distribution that produces the sample can be said to induce the random value from a local distribution of distances taken with respect to . The CDF of the local distance distribution is simply the probability of the sample distance lying within a threshold r—that is, . In characterizing the local intrinsic dimensionality in the vicinity of location , we are interested in the limit of as the distance r tends to 0, which we denote by
Henceforth, when we refer to the local intrinsic dimensionality (LID) of a function F, or of a point whose induced distance distribution has F as its CDF, we will take ‘LID’ to mean the quantity . In general, is not necessarily an integer. In practice, estimation of the LID at would give an indication of the dimension of the submanifold containing that best fits the distribution.
The function can be seen to fully characterize its associated function F. This result is analogous to a foundational result from the statistical theory of extreme values (EVT), in that it corresponds under an inversion transformation to the Karamata representation theorem [] for the upper tails of regularly varying functions. For more information on EVT and how the LID model relates to the extreme-value theoretic generalized pareto distribution, we refer the reader to [,,].
Theorem 2 (LID Representation Theorem
[]).Let be a real-valued function, and assume that exists. Let x and w be values for which and are both positive. If F is non-zero and continuously differentiable everywhere in the interval , then
whenever the integral exists.
In [], conditions on x and w are provided for which the factor can be seen to tend to 1 as . The convergence characteristics of F to its asymptotic form are expressed by the factor , which is related to the slowly varying component of functions as studied in EVT []. As we will shown in the next section, we make use of the LID Representation Theorem in our analysis of the limits of tail entropy variants under a form of normalization.
4. Definitions of Tail Entropies and Tail Dissimilarity Measures
In this section, we present the formulations of entropy, divergences and distances that will be studied in the later sections, in the light of the model of local intrinsic dimensionality outlined in Section 3. These entropies and dissimilarity measures will all be conditioned on the lower tails of smooth functions on domains bounded from below at zero. In each case, the formulations involve one or more non-negative real-valued functions whose restriction to satisfies certain smooth growth properties:
Definition 2.
Letbe a function that is positive except at. We say that F is a smooth growth function if
- There exists a value such that F is monotonically increasing over ;
- F is continuous over ;
- F is differentiable over ; and
- The local intrinsic dimensionality exists and is positive.
Given a smooth growth function F and a value , we define . If F is the CDF of some random variable , then , which can in turn be interpreted as the CDF of the distribution of X conditioned to the lower tail . It is easy to see that for a sufficiently small choice of w, must also be a smooth growth function. Its derivative exists since exists, and thus can be regarded as the probability density function (PDF) of the restriction of F to . In addition, it can easily be shown (using Theorem 1) that the LID of is identical to that of F.
If the monotonicity of the function F is strict over the domain of interest , its inverse function exists and satisfies the smooth growth conditions within some neighborhood of the origin. Moreover, is also a smooth growth function over , with and .
The following tail entropy, tail divergence and tail distance formulations all apply to any functions F and G satisfying the conditions stated above; in particular, they involve one or more of , , , , and (if the monotonicity of the functions is strict) and . In their definitions, the only difference between the tail variants and the original versions is that the distributions are conditioned on the lower tail . In the tail measures involving one or more of , , and , integration is performed over the lower tail and not the entire distributional range ; for the variant involving and , integration is performed over for values of w constrained to the lower tail.
We begin with (differential) tail entropy. Entropy is perhaps the most fundamental and widely used model of data complexity and can be regarded as a measure of the uncertainty of a distribution. Differential entropy assesses the expected surprisal of a random variable and can take negative values.
Definition 3
(Tail Entropy).The entropy of F conditioned on is
The tail entropy is equal to , the expected value of the (tail) log-likelihood. It is also possible to define the variance of the (tail) log-likelihood. This is known as the varentropy. Understanding this further, note that one may define the information content of a random variable X with density function f, to be . The entropy (uncertainty) then corresponds to the expected value of the information content of X and the varentropy corresponds to the variance of the information content of X. The varentropy was introduced by Song [] as an intrinsic measure of the shape of a distribution and has been explored in a range of studies [,,].
Definition 4
(Tail varentropy).The varentropy of F conditioned on is
The cumulative entropy is a variant of entropy proposed in [,] due to its attractive theoretical properties. Tail conditioning on the cumulative entropy has the same general form as that of the tail entropy. Cumulative entropy [,] is an information-theoretic measure popular in reliability theory, where it is used to model uncertainty over time intervals. It corresponds to the expected value of the mean inactivity time. Compared to ordinary Shannon differential entropy, cumulative entropy has certain attractive properties, such as non-negativity and ease of estimation.
Definition 5
(Cumulative Tail Entropy).The cumulative entropy of F conditioned on is
The entropy power is the exponential of the entropy, and is also known as perplexity in the natural language processing community. It corresponds to the volume of the smallest set that contains most of the probability measure [], and can be interpreted as a measure of statistical dispersion []. There are several standard definitions of entropy power in the research literature. For our purposes, we adopt the simplest—the exponential of Shannon entropy—for our definition conditioned to the tail.
Definition 6
(Tail Entropy Power).The entropy power of F conditioned on is defined to be
In the introduction, we briefly mentioned some motivation for the entropy power . We can add to this as follows:
- It can be interpreted as a diversity. Observe that when F is a (univariate) uniform distance distribution ranging over the interval , we have and . In other words, the entropy power is equal to the ‘effective diversity’ of the distribution (the number of neighbor distance possibilities).
- Given two different queries, each with its own neighborhood, one query with tail entropy power equal to 2 and the other with tail entropy power equal to 4, we can say that the distance distribution of the second query is twice as diverse as that of the first query.
For each of the tail entropy variants introduced above, we also propose analogous variants based on the q-entropy formulation due to Tsallis []. Generalized Tsallis entropies [,] are a family of entropies characterized via an exponent parameter q applied to the probabilities, in which the traditional (Shannon) entropy variants are obtained as the special case when q is allowed to tend to 1. The use of such a parameter q can often facilitate more accurate fitting of data characteristics and robustness to outliers.
Definition 7
(Tail q-Entropy).For any , the q-entropy of F conditioned on is defined to be
Definition 8
(Cumulative Tail q-Entropy).For any , the cumulative q-entropy of F conditioned on is defined to be
We define the tail q-entropy power using the q-exponential function from Tsallis statistics [], . Note that L’Hôpital’s rule can be used to show that as .
Definition 9
(Tail q-Entropy Power).For any , the q-entropy power of F conditioned on is defined to be
We next define the tail cross entropy. Cross entropy can be used to compare two probability distributions and is often employed as a loss function in machine learning, comparing a true distribution and a learned distribution. From an information theoretic perspective, cross entropy corresponds to the expected coding length when a wrong distribution G is assumed while the data actually follows a distribution F.
Definition 10
(Tail Cross Entropy).The cross entropy from F to G, conditioned on , is defined to be
Similar to entropy power, we can also define the cross entropy power, which is the exponential of the cross entropy.
Definition 11
(Tail Cross Entropy Power).The cross entropy power from F to G, conditioned on , is defined to be
A classic and fundamental method for comparing two probability distributions is the Kullback–Leibler divergence (KL Divergence) []. measures the degree to which a probability distribution G is different from a reference probability distribution F. It is a member of both the family of f-divergences and Bregman divergences. It is widely used in statistics, machine learning and information theory.
Definition 12
(Tail KL Divergence).The Kullback–Leibler divergence from F to G, conditioned on , is defined to be
The tail KL divergence can be connected to the tail entropy and the tail cross entropy according to the relationship .
The Jensen–Shannon divergence (JS divergence) [] is another popular measure of distance between probability distributions. It is based on the KL divergence, but unlike the KL, the square root of the JS divergence is a true metric.
Definition 13
(Tail JS Divergence).The Jensen–Shannon divergence between F and G, conditioned on , is defined to be
The tail JS divergence can also be written in terms of the tail entropies
The L2 distance is the squared Euclidean distance when comparing two probability distributions. It is part of the family of divergences when setting [].
Definition 14
(Tail L2 Distance).The L2 distance between F and G, conditioned on , is defined to be
The Hellinger distance [] is a true metric for comparing two probability distributions. The squared Hellinger distance a member of the family of f-divergences and is part of the family of divergences when setting [].
Definition 15
(Tail Hellinger Distance).The Hellinger distance between F and G, conditioned on , is defined to be
The divergence between two probability distributions [] is a member of the family of f divergences and is part of the family of divergences when setting [].
Definition 16
(Tail-Divergence).The divergence between F and G, conditioned on , is defined to be
The asymmetric -divergence [] is another member of the family of f divergences. When it is proportional to the divergence. When it is proportional to the squared Hellinger distance. When it corresponds to the KL-divergence.
Definition 17
(Tail-Divergence).The α-divergence from F to G, conditioned on , is defined to be
The Wasserstein distance between two probability distributions is also known as the Kantorovich–Rubinstein metric [] or the earth mover’s distance. It has become very popular as part of the loss function used in generative adversarial networks []. In the univariate case it can be expressed in a simple analytic form.
Definition 18
(Tail Wasserstein Distance).The p-th Wasserstein distance between F and G, conditioned on , is defined to be
For some of the aforementioned tail measures, we will also consider a normalization of the entropy, divergence or distance (as the case may be) with respect to w, the length of the tail. In Section 5 and Section 6, we will show that as w tends to zero, the limits of these (possibly normalized) tail entropies and tail divergences can be expressed in terms of the local intrinsic dimensionalities of F and G. The notation for these variants, and our results for their limits in terms of and , are summarized in Table 1.

Table 1.
Asymptotic equivalences between LID formulations and tail measures of entropy or divergence. In each case, the functions F and G are assumed to be smooth growth functions. In addition, for the Normalized Wasserstein Distance, F and G must be strictly monotonically increasing, thereby guaranteeing that the inverses of and exist near zero. In some cases, for the asymptotic limit to exist non-trivially (that is, to be both finite and non-zero), the tail entropy or tail divergence must be normalized by the multiplicative factor , w. For the Tail Entropy and Tail Cross Entropy, no reweighting by powers of w can lead to a non-trivial asymptotic limit as w tends to zero.
5. Simplification of Tail Measures
Next, we present the main theoretical contributions of the paper: three technical lemmas that will later be used to establish relationships between local intrinsic dimensionality and a variety of tail measures based on entropy, divergences or distances. The results presented in this section all apply asymptotically, as the tail boundary tends toward zero.
Each of the three lemmas allow, under certain conditions, the simplification of limits of integrals involving smooth growth functions of the form (as defined in Section 4), or its associated first derivative or inverse function . The limit integral simplifications allow for the substitution of the function (or derivative or inverse) by expressions that involve one or more of the following: the LID value of the function, the variable of integration or the tail boundary w. Moreover, the lemmas require that the integrand be monotone with respect to small variations in the targeted function.
The first lemma allows terms of the form (resembling the CDF of a tail-conditioned distribution) to be converted into a term that depends only on the variable of integration, the tail length w, and the local intrinsic dimension .
Lemma 1.
Let F be a smooth growth function over the interval . Consider the function admitting a representation of the form
where:
- ;
- ; and
- for all fixed choices of t and w satisfying , is monotone and continuously partially differentiable with respect to z over the interval .
Then
whenever the latter limit exists or diverges to or .
Proof.
Since F is assumed to be a smooth growth function, the limit exists and is positive. We present an ‘epsilon-delta’ argument based on this limit. For any real value satisfying , there must exist a value such that implies that . Therefore, when ,
Exponentiating, we obtain the bounds
Applying this bound together with Theorem 2, the ratio can be seen to satisfy
Over the domain of interest , the assumption that ensures that , and that the upper and lower bounds of Inequality (1) lie in the interval . Since has been assumed to be monotone with respect to , the maximum and minimum attained by over choices of z restricted to any (closed) subinterval of must occur at opposite endpoints of the subinterval. With this in mind, for any choice of , Inequality (1) implies that
where
Since and are also continuously partially differentiable with respect to z over ,
It therefore follows from the squeeze theorem for integrals that
whenever the right-hand limit exists or diverges. □
In a manner similar to that of the preceding lemma, the following result allows terms of the form (the inverse of ) to be converted into a term that depends only on the variable of integration, the tail length w and the local intrinsic dimension . Here, in order to ensure the existence of the inverse function, F (and by extension and ) must be strictly monotonically increasing over the tail.
Lemma 2.
Let F be a smooth growth function over the interval . Let us also assume that, over the interval, the monotonicity of F is strict. Consider the function admitting a representation of the form
where:
- ;
- for all , where is restricted to values of t in ; and
- for all fixed choices of u and w satisfying and , is monotone and continuously partially differentiable with respect to z over the interval .
Then
whenever the latter limit exists or diverges to or .
Proof.
First, we note that the strict monotonicity of F implies that for all and , the function is uniquely defined when is restricted to .
As in the proof of Lemma 1, an ‘epsilon-delta’ argument based on the existence of the limit yields the following: for any real value satisfying , there exists a value such that
holds for all . Solving for t through exponentiation of the bounds, and then setting , we obtain
The remainder of the proof follows essentially the same path as that of Lemma 1. Over the domain of interest , the assumption that ensures that , and that u lies in the interval . Since has been assumed to be monotone with respect to , the maximum and minimum attained by over choices of z restricted to any (closed) subinterval of must occur at opposite endpoints. Therefore, for any choice of ,
where
Since is also continuously partially differentiable with respect to z over ,
It therefore follows from the squeeze theorem for integrals that
whenever the right-hand limit exists or diverges. □
The third lemma facilitates the conversion of a term of the form to , together with a factor that depends only on the variable of integration and . Since F is assumed to be a smooth growth function, must be smooth as well, and therefore satisfies the conditions of Theorem 1 over . Hence, can be substituted by an expression involving :
The substitution comes at the cost of introducing a non-constant factor . The following lemma shows that can in turn be substituted by the constant , provided that certain monotonicity assumptions are satisfied.
Lemma 3.
Let F be a smooth growth function over the interval . Consider the function admitting a representation of the form
where:
- ;
- , and
- there exists a value such that for all fixed choices of t satisfying , is monotone with respect to z over the interval .
Then
whenever the latter limit exists or diverges to or .
Proof.
Since F is assumed to be a smooth growth function, the limit exists and is positive. We present an ‘epsilon-delta’ argument based on this limit. For any real value satisfying , there must exist a value such that implies that .
Since has been assumed to be monotone with respect to z over the interval , the restriction ensures that is monotone over the entire domain of interest . Therefore, the maximum and minimum attained by over choices of z restricted to any (closed) subinterval of must occur at opposite endpoints of the subinterval. As in the proof of Lemma 1,
where
Since is also continuously partially differentiable with respect to z over the range ,
It therefore follows from the squeeze theorem for integrals that
whenever the right-hand limit exists or diverges. □
6. Derivation of the Limits of Tail Measures
In this section, we will see how the three substitution lemmas can be applied to the limits of tail measures of entropy, divergence or distance, so as to produce formulations that depend only on the local intrinsic dimensions of the functions involved. All three lemmas require that the integral function be monotone with respect to small variations in the term that is targeted for substitution. In the discussion, we choose two tail measures as running examples: the tail KL divergence and the second tail Wasserstein distance ().
6.1. Handling Derivatives of Smooth Growth Functions
In the case of the tail KL divergence, Theorem 1 allows us to substitute out the first derivatives and for the functions and :
6.2. Substitution of LID Functions by Constants
In the limit of the tail KL divergence, the functions and can be replaced by the constants and , respectively, through three successive applications of Lemma 3. To verify that the monotonicity condition of the Lemma is satisfied, we choose one of the terms and replace it by a new variable, z:
For any fixed values of t and w, it is easy to see that the integrand is locally monotone in the vicinity of —here, if is positive, a small increase in z (above the value ) would result in an increase in the value of the integrand, and a small decrease would cause the integrand to decrease. If instead the logarithmic factor were negative, an increase in z would result in a decrease in the value of the integrand. Either way, the integrand would be monotone in the vicinity of at each fixed value of t and w. Its monotonicity condition thus being satisfied, Lemma 3 allows the targeted instance of to be substituted by :
Similarly, it can be verified that the new integrand is monotone in each of the remaining two factors and ; consequently, they too can be substituted by and , one at a time, to yield
6.3. Elimination of Tail-Conditioned Smooth Growth Functions
Now that the tail KL divergence has been reformulated in terms of the tail-conditioned smooth growth functions and , these two functions can be substituted out via three successive applications of Lemma 1, so as to obtain the limit of an integral involving only the variable of integration t, and the constants w, and :
As in the previous step in which and were substituted out, the monotonicity conditions of Lemma 1 can easily be verified.
Now that the integral involves only constants and the variable t, it can be solved straightforwardly using the integration-by-parts technique, yielding
6.4. Elimination of the Inverses of Tail-Conditioned Smooth Growth Functions
We now turn our attention to the limit of the tail Wasserstein distance for the case . Using Lemma 2, the inverse functions and can be substituted out, provided that the monotonicity requirements are satisfied. However, immediate application of the lemma to or does not necessarily work—to see this, consider substituting by the new variable z.
Clearly, the integrand is not necessarily monotone in z in the vicinity of those values of the integration variable u where .
Instead, we expand the squared difference and apply Lemma 3 to each of the resulting four occurrences of and , one by one. By way of illustration, we consider substitution by z for the factor of in the cross term:
With respect to small variations in the variable z about the value , noting that is always non-negative, the integrand is easily seen to be monotone in z when is non-zero: for any increase in z, the value of the integrand decreases, and for any decrease in z, the value of the integrand increases. Lemma 2 can therefore be applied, producing
After three more applications of Lemma 2, followed by taking the square root of the integral, we obtain
6.5. Normalization
Even though the limit of the second tail Wasserstein distance is zero and therefore uninteresting, we observe that by normalizing it by the tail length w, we arrive at a more useful result:
In general, reweighting by a power of w may be required to expose a relationship between the tail limit of an entropy measure or divergence and an expression in terms of the local intrinsic dimensions of the functions involved. Since local intrinsic dimension is a unitless quantity, in order to establish a non-trivial formulation solely in terms of LID values, any tail measure whose values are not unitless will generally require some form of normalization.
6.6. Summary of Results
Table 1 provides a summary of results. All the results stated in Table 1 can be derived either using the techniques outlined earlier in this section, or through direct substitution of another result in the table. The derivations are outlined in Table 2 (tail entropy variants), Table 3 (tail divergence variants), Table 4 (tail distance variants) and Table 5 (tail Wasserstein distances). Most of these derivations are straightforward; however, for two of the tail measures, some clarifications are required.

Table 2.
Derivations of asymptotic relationships between tail entropy variants and local intrinsic dimensionality. Each step shows the equivalences between the formulations when w is allowed to tend to zero. In the comments column, for each step of the derivation, the lemmas invoked are stated, as well as any additional assumptions made. If a normalization other weighting is needed to avoid divergence, or convergence to a constant (independent of F), the details are shown in a comment in the final step. In all cases, F is assumed to be a smooth growth function.

Table 3.
Derivations of asymptotic relationships between tail divergences and local intrinsic dimensionality. Each step shows the equivalences between the formulations when w is allowed to tend to zero. In the comments column, for each step of the derivation, the lemmas invoked are stated, as well as any additional assumptions made. If a normalization or weighting is needed, the details are shown in a comment in the final step. In all cases, F and G are assumed to be smooth growth functions.

Table 4.
Derivations of asymptotic relationships between tail distances and local intrinsic dimensionality. Each step shows the equivalences between the formulations when w is allowed to tend to zero. In the comments column, for each step of the derivation, the lemmas invoked are stated, as well as any additional assumptions made. For each tail distance, the first step of the derivations shows an expansion by which the monotonicity of each factor can be verified. If a normalization or weighting is needed, the details are shown in a comment in the final step. In all cases, F and G are assumed to be smooth growth functions.

Table 5.
Derivations of asymptotic relationships between tail Wasserstein distances and local intrinsic dimensionality. Each step shows the equivalences between the formulations when w is allowed to tend to zero. In the comments column, for each step of the derivation, the lemmas invoked are stated, as well as any additional assumptions made. Normalization details are shown in a comment in the final step. In all cases, F and G are assumed to be invertible smooth growth functions.
Generally speaking, for the normalized tail Wasserstein distances with p non-integer or p odd (Table 5), Lemma 2 cannot be applied, due to the absolute value operation in the integrand. It may happen that the functions and may have crossing points for many (possibly even infinitely many) values of u between 0 and 1. At these values of u, , and neither nor would be monotone in the vicinity of or , as the case may be.
For the tail JS divergence (Table 3), the derivation relies on the fact that the LID of the sum (or average) of two non-negative smooth growth functions is the smaller of the two individual LID values. This is an implication of the fact that whenever the smooth growth functions and have (see [] for more details). Accordingly, if , then the function (F or G) with smaller LID value must have the same LID value as the average function , and the other function (G or F) must have LID value equal to the maximum of the two. From these observations, the derivation can be seen to hold.
The result for the limit of the tail KL divergence has an interesting interpretation in light of the so-called Itakura–Saito (IS) divergence (or distance) []:
As the tail boundary w tends to 0, the tail KL divergence between smooth functions F and G tends to the (univariate) IS divergence between their associated LID values and :
When F and G are interpreted as the CDFs of distance distributions, the shape parameters of the extreme-value-theoretic generalized pareto distributions (GPDs) that asymptotically characterize their lower tails are known to equal and , respectively []. Since the ratio of these parameters is equal to (the reciprocal of) the ratio of LID values, the tail KL divergence between F and G can also be interpreted as tending to the IS divergence between GPD parameters.
The IS divergence is popular as an objective for matrix factorization of audio spectra [], for assessing the loss of using entry to approximate a true entry ; more precisely, to approximate a matrix by factorization , the loss is . The IS divergence is a convenient choice for this scenario due to its scale-free property ( for any ), thus giving the same relative weight to both small and large values of and , since they only appear as the ratio . This is important for scenarios such as audio spectra, where the magnitudes of and can vary greatly.
The Itakura–Saito divergence falls into the family of so-called Bregman divergences (or distances) [], which have a geometric interpretation as the difference between the value of a convex generator function at on the one hand, and the value at of a hyperplane function that is tangent to the generator curve at . Bregman divergences are a highly expressive family of distances with a wide range of applications []. For the IS divergence, the convex generator function is the negative logarithm . Interestingly, the KL divergence is also a Bregman divergence, with its convex generator being the negative entropy function [].
7. Extension to Multivariate Distributions
Thus far, our results have focused on a univariate scenario, wherein entropy and divergence variants were shown to be asymptotically equivalent to formulations involving the local intrinsic dimensionalities of smooth distributions of a single random variable. As discussed in Section 3, these results can be applied to distance-based analysis, through characterizations involving the LIDs of local (univariate) distance distributions induced by the overall (global) multivariate distribution. These characterizations are indirect, in that they do not explicitly involve (nor do they require) any knowledge of the underlying global distribution and its parameters. However, characterizations in terms of induced distance distributions may not be entirely satisfying when the nature of the global multivariate distribution is either known or assumed. In this section, we will assume that our domain is the n-dimensional space equipped with the Euclidean distance, . Within , we will also assume that we are given a data distribution with probability density function .
7.1. Multivariate Tail Distributions with Local Spherical Symmetry
Within the Euclidean domain, the challenge is to analyze distributions in terms of the probability measure captured within volumes associated with a distributional tail. However, unlike in univariate distributions, there is no universally accepted notion of ‘distributional tail’ for multivariate distributions. For our purposes, given a distance , we define the tail of of length r to be the region enclosed by the ball of radius r centered at the origin; that is, . The boundary of the tail is the -dimensional surface area of , which we denote by .
To enable tractable analysis, we will assume that the PDF can be expressed in terms of a locally spherically symmetrical function. One example of where local spherical symmetry can be expected to hold is for a locally isotropic context. This is a common assumption for physical systems, including metals, glasses, fluids and polymers, for which the distribution locally surrounding a particle in the system does not have a directional preference.
Formally, we say that a density function f is locally spherically symmetrical within radius w if for all , we have for some univariate function where . For f to be locally spherically symmetrical, it suffices that be equal to whenever . The assumption also implies the existence of a function for which , and therefore that f must be constant over all points of the sphere .
The probability measure captured by , which we denote by , is obtained through the integration of f over this ball:
It is not difficult to see that the univariate function F is simply the CDF of the distribution of distances to the origin induced by the global distribution . If F is differentiable over the tail interval , then the integral of over this interval exists, and equals F:
The derivative can therefore be interpreted as the PDF of the radial distance distribution as measured from the origin.
For spherically symmetric distributions in Euclidean spaces, the multivariate density and radial density is related through a factor that depends on the surface area of spherical volumes. The formulae for the volume of an n-sphere and its -dimensional surface area are given by
respectively. is the common gamma function if n is a positive integer and if n is a non negative integer. Furthermore, the volume and surface area have a simple relationship that allows for easy conversion between the two:
Lemma 4
([]). Let be an n-dimensional random vector that is spherically symmetric with a radial distribution . Then has a density if and only if has a density s and
If F is a smooth growth function that is locally spherically symmetric over , Equation (2) and Lemma 4 together give us the following relationship between the radial density and the multivariate density f:
whenever . Conditioning the distribution to the ball , the tail distribution PDF becomes
7.2. Multivariate Tail Entropy Variants
The aforementioned relationships between multivariate and radial densities can be immediately used to compute the various tail entropies for the locally spherically symmetric multivariate case. Useful background on evaluating radial integrals can be found in Baker []. For example, the multivariate Tail Entropy is
Although the multivariate formulation of Tail Entropy resembles that of the univariate formulation , the two are not identical. Nevertheless, the multivariate formulation can still be simplified using the technical lemmas introduced in Section 5. In much the same way as for the univariate Tail Entropy Power, we can use Theorem 1 together with Lemmas 1 and 3 to determine the limit of as w tends to 0. Replacing by , then by , and finally by , we obtain
Solving the integral, and then using Equation (3) to convert the surface area factor to an expression involving the volume , we eventually arrive at
which diverges even when the Tail Entropy is reweighted by (or indeed, by any other polynomial in w). However, the Tail Entropy Power, when normalized by , does converge to a strictly positive value:
As one might expect in the n-dimensional Euclidean setting, the (normalized asymptotic) multivariate Tail Entropy Power is maximized whenever , the local intrinsic dimensionality of the associated radial CDF F, is equal to n.
7.3. Multivariate Cumulative Tail Entropy
In the multivariate setting, cumulative entropy is defined in terms of the distributional tail, according to the notion laid out in Section 7.1. In place of the usual probability density , the entropy function is applied to the probability measure associated with the ball centered at the origin with radius ; that is, with
Note that since F takes the same value at and whenever , the quantity is locally spherically symmetric even when the underlying density function f is not.
We can adapt the multivariate formulation of cumulative residual entropy that was originally proposed by Rao []. The multivariate Cumulative Tail Entropy, conditioned to a distributional tail of radius w, is expressed as a multivariate integral involving , or as a radial integral involving , as follows:
As in the treatment of the univariate tail entropies, we can use Lemma 1 to determine the limit of as w tends to 0. Replacing by ,
Solving the integral, and then converting the surface area factor to a volume factor using Equation (3), we obtain
Although the multivariate Cumulative Tail Entropy vanishes as the tail boundary w tends to zero, when normalized by the tail volume it converges to a strictly positive value:
Again, as with the Normalized Tail Entropy Power, the (asymptotic) multivariate Tail Cumulative Entropy is maximized whenever . That is, when .
7.4. Multivariate Tail Divergences
Several of the tail divergence measures, when considered in the multivariate setting under the assumptions of locally spherical symmetry, turn out to be identical to those of the radial (univariate) setting. As an example, consider the multivariate Tail KL Divergence, defined as
Applying Lemma 4 and integrating radially over the tail, we see that
the Tail KL Divergence of F and G, which (as stated in Table 1) has the limit as the tail length w tends to zero.
Similarly, it can easily be seen that the multivariate versions of the JS Divergence, the Hellinger Distance, the -Divergence and the -Divergence all have radial integral formulations identical to their corresponding univariate versions.
7.5. Observations
The general strategy for deriving these results is essentially the same as for the multivariate Tail Entropy: first use Lemma 4 to convert the multidimensional integral to an integral in one dimension, then use the technical lemmas of Section 5 to simplify the univariate integral as before.
Our results for the locally spherically symmetric multivariate case are shown in Table 6; however, since their derivations greatly resemble those of the analogous univariate cases, we omit the details. Some remarks:

Table 6.
Asymptotic equivalences between LID formulations and tail measures of entropy or divergence for locally spherically symmetric distributions in the n-dimensional Euclidean setting. In each case, the density functions are assumed to be f and g, and the CDFs F and G of their induced distance distributions are assumed to be smooth growth functions. In the results, and denote the volume and surface area of the n-dimensional ball with radius r (respectively). In some cases, for the asymptotic limit to exist non-trivially (that is, to be both finite and non-zero), the tail entropy or tail divergence must be normalized by some multiplicative factor dependent on the tail volume .
- A result for the Wasserstein Distance is not included, since its formulation does not generalize straightforwardly to higher dimensions, unlike the other divergence measures.
- The normalizations and weightings used depend only on the tail volume and (for the Tsallis entropy variants) the parameter q. This generalizes our earlier univariate results where normalization was performed with regard to the tail length w.
- All the multivariate tail variants considered Table 6 are elegant generalizations of their corresponding univariate formulations, and all explicitly depend on the ratios between the LIDs and the dimension of the space n ( and ), or on the ratio of two LID values (). Among these, the Normalized Entropy Power and the Normalized Cumulative Entropy are maximized when , which can occur when the tail distribution is uniform. The Varentropy is minimized when , which can occur when the variance of the log-likelihood for a uniform distribution is equal to zero.
- As mentioned in Related Work, a number of previous studies in deep learning have found that the local intrinsic dimension in learned representations is lower than the dimension of the full space [,,,] (i.e., ) and that the learning process progressively reduces local intrinsic dimension. Consider a concrete example where and and the learning process is reducing at a point from 12 to 11. The consequent effect on entropy can be interpreted from two different perspectives, either as an increase in tail distance entropy or a decrease in tail location entropy:
- Considering univariate normalized entropy power or normalized cumulative entropy (Table 1), reduction of corresponds to an increase in entropy. Here, the entropy is measuring the uncertainty of the univariate random variable modeling distances to nearest neighbors. Thus, reduction of corresponds to an increase in “distance entropy”.
- Considering multivariate normalized entropy power or multivariate normalized cumulative entropy (Table 6), reduction of corresponds to an decrease in entropy. Here, the entropy is measuring the uncertainty of the multivariate random variable modeling locations of nearest neighbors, assuming local spherical symmetry. So reduction of corresponds to a decrease in “location entropy”.
We will see a visualization of these scenarios in Section 7.6.
- 5.
- All four of the multivariate tail divergences listed in Table 6, as well as the Hellinger Distance, have radial integral formulations that are identical to their univariate counterparts. All the divergences and distances (including the Weighted L2 Distance) are minimized when .
- 6.
- By setting , we can recover the univariate results from Table 1. However, note that the range of integration used in Table 6 is a hypersphere of radius w, where for it is the interval . In contrast, the integral formulations listed in Table 1 were taken over the interval . For some results, this means a minor (constant factor of 2) difference between Table 1 and the result from Table 6 when .
7.6. Visualization of Behavior
Our results in Table 6 relate local intrinsic dimensionality to entropies and divergences. If analyzing an n dimensional global distribution such as the standard normal distribution or uniform distribution, then the dimension of every sub-manifold (i.e., the local intrinsic dimensionality ) will be n. However, our interest is in situations where the local intrinsic dimensionality differs from the representation dimension n. To provide further intuition on this aspect, two plots are shown in Figure 1.
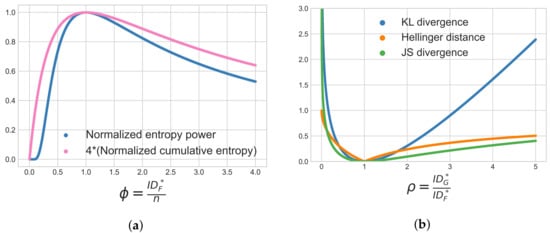
Figure 1.
Visualization of selected measures from Table 6 (a) Entropy behavior as the ratio varies; (b) Divergence/distance behavior as the ratio varies.
Figure 1a compares the behavior of the normalized entropy power and the normalized cumulative entropy (multiplied by a constant factor of 4) in n-dimensional space, as the ratio is varied. We see that these measures have similar trends and they are maximized when . We also see that when , these entropic measures will decrease if is decreased (for a fixed n). On the other hand, if and , then these entropic measures will increase if is decreased, where corresponds to the scenario where we are modeling the uncertainty of a distance distribution. This illustrates remark number 4 from Section 7.5 above.
Figure 1b compares the behavior of different tail divergences as the ratio varies. The divergences shown are the KL divergence, the Jensen–Shannon divergence and the Hellinger distance. These measures have similar trends as varies and are minimized and equal to zero when . Also, the Hellinger distance is bounded above by 1.
8. Conclusions
In this theoretical investigation, we have established asymptotic relationships between tail entropy variants, tail divergences and the theory of local intrinsic dimensionality. Our results are derived under the assumption that the distribution(s) under consideration are being analyzed in a highly local context, within the distribution tail(s), an asymptotically small neighborhood whose radius approaches zero. These results show that tail entropies and tail divergences depend in a fundamental way on local intrinsic dimensionality and help form a theoretical foundation for cross-fertilization between intrinsic dimensionality research and entropy research. As future work, we plan to investigate the potential of these new characterizations in a range of application settings. For example, for use as a basis in machine learning to characterize and improve representations and representation learning, as well as use in understanding behavior of physical systems such as fluids and helping characterize their critical transitions in time and space.
Our results from both univariate and multivariate cases, show that the tail entropies and divergences considered in this paper depend only on (i) the embedding (representation) dimension in which the distribution is situated, and (ii) the local intrinsic dimension(s) of the distribution(s). Furthermore, in many cases there is dependence involving the ratio between the intrinsic dimension and the embedding dimension.
Consider the context of distance based analysis, when a distribution models distances from a central query location to its nearest neighbors, and the distances are induced by global data. In this situation, our characterization of entropy might be termed as ‘personalized’, in that entropy expresses the uncertainty (or complexity) from the perspective of the query, in regard to the distances to samples within an asymptotically small neighborhood. Phrased another way, these local entropies are ‘observer-dependent’, since they are tied to the choice of query (the observer). This can be contrasted with the more common notion of entropy, where one analyzes a global distribution, and there is no requirement of a query point or its local neighborhood.
As alluded to in the introduction, divergences between tail distributions could be used for comparison of real and synthetic distributions, as is commonly required for generative adversarial networks (GANs). Given a particular query location we may either: (i) compute the divergence between the univariate tail distance distributions of synthetic and real examples, as measured from a query point; or (ii) compute the divergence between the multivariate tail distance distributions of synthetic and real examples, again as measured from the query, under an assumption of local isotropy. Our results show that under the assumption of local spherical symmetry, the use of divergences (such as KL) between tail distance distributions is asymptotically equivalent to the standard multivariate formulations with the same divergences, when restricted to the neighborhoods around locations of interest. For future work it will be interesting to consider whether it is possible to further extend our multivariate results to elliptically symmetric distributions or skew-elliptical distributions, such as those studied by Contreras-Reyes [].
Lastly, our results in Table 1 and Table 6 show theoretical relationships for entropies and divergences, but in practice one must estimate the measures using samples of data. A natural approach here is to first estimate local intrinsic dimensional values such as and using any desired estimator (such as the maximum likelihood estimator [,,]), and then plug in the estimated LID value into the desired tail entropy or tail divergence formula. For example, an estimator of the (univariate) Normalized Cumulative Entropy could be obtained by computing , where is the estimated LID of the distance distribution F.
Author Contributions
Conceptualization, J.B., M.E.H. and X.M.; methodology, J.B., M.E.H. and X.M.; formal analysis, J.B., M.E.H. and X.M.; writing—original draft preparation, J.B., M.E.H. and X.M.; writing—review and editing, J.B., M.E.H. and X.M. All authors have read and agreed to the published version of the manuscript.
Funding
James Bailey acknowledges the support of ARC Discovery Grant DP170102472. Michael E. Houle acknowledges the financial support of JSPS Kakenhi Kiban (B) Research Grant 18H03296.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Basseville, M. Divergence measures for statistical data processing—An annotated bibliography. Signal Process. 2013, 93, 621–633. [Google Scholar] [CrossRef]
- Houle, M.E. Local Intrinsic Dimensionality I: An Extreme-Value-Theoretic Foundation for Similarity Applications. In Proceedings of the International Conference on Similarity Search and Applications, Munich, Germany, 4–6 October 2017; pp. 64–79. [Google Scholar]
- Bailey, J.; Houle, M.E.; Ma, X. Relationships Between Local Intrinsic Dimensionality and Tail Entropy. In Proceedings of the Similarity Search and Applications—Proc. of the 14th International Conference, SISAP 2021, Dortmund, Germany, 29 September–1 October 2021. [Google Scholar]
- Heller, R.; Heller, Y. Multivariate tests of association based on univariate tests. In Advances in Neural Information Processing Systems 29 (NIPS 2016); Lee, D.D., Sugiyama, M., von Luxburg, U., Guyon, I., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2016; pp. 208–216. [Google Scholar]
- Maa, J.; Pearl, D.; Bartoszynski, R. Reducing multidimensional two-sample data to one-dimensional interpoint comparisons. Ann. Stat. 1996, 24, 1069–1074. [Google Scholar] [CrossRef]
- Li, A.; Qi, J.; Zhang, R.; Ma, X.; Ramamohanarao, K. Generative image inpainting with submanifold alignment. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, Hong Kong, 10–16 August 2019; pp. 811–817. [Google Scholar]
- Camastra, F.; Staiano, A. Intrinsic dimension estimation: Advances and open problems. Inf. Sci. 2016, 328, 26–41. [Google Scholar] [CrossRef]
- Campadelli, P.; Casiraghi, E.; Ceruti, C.; Rozza, A. Intrinsic Dimension Estimation: Relevant Techniques and a Benchmark Framework. Math. Probl. Eng. 2015, 2015, 759567. [Google Scholar] [CrossRef]
- Verveer, P.J.; Duin, R.P.W. An evaluation of intrinsic dimensionality estimators. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 81–86. [Google Scholar] [CrossRef]
- Bruske, J.; Sommer, G. Intrinsic dimensionality estimation with optimally topology preserving maps. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 572–575. [Google Scholar] [CrossRef]
- Pettis, K.W.; Bailey, T.A.; Jain, A.K.; Dubes, R.C. An intrinsic dimensionality estimator from near-neighbor information. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 25–37. [Google Scholar] [CrossRef]
- Navarro, G.; Paredes, R.; Reyes, N.; Bustos, C. An empirical evaluation of intrinsic dimension estimators. Inf. Syst. 2017, 64, 206–218. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Costa, J.A.; Hero III, A.O. Entropic Graphs for Manifold Learning. In Proceedings of the 37th Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 1, pp. 316–320. [Google Scholar]
- Hein, M.; Audibert, J.Y. Intrinsic dimensionality estimation of submanifolds in Rd. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 289–296. [Google Scholar]
- Rozza, A.; Lombardi, G.; Rosa, M.; Casiraghi, E.; Campadelli, P. IDEA: Intrinsic Dimension Estimation Algorithm. In Proceedings of the International Conference on Image Analysis and Processing, Ravenna, Italy, 14–16 September 2011; pp. 433–442. [Google Scholar]
- Rozza, A.; Lombardi, G.; Ceruti, C.; Casiraghi, E.; Campadelli, P. Novel High Intrinsic Dimensionality Estimators. Mach. Learn. 2012, 89, 37–65. [Google Scholar] [CrossRef]
- Ceruti, C.; Bassis, S.; Rozza, A.; Lombardi, G.; Casiraghi, E.; Campadelli, P. DANCo: An intrinsic dimensionality estimator exploiting angle and norm concentration. Pattern Recognit. 2014, 47, 2569–2581. [Google Scholar] [CrossRef]
- Facco, E.; d’Errico, M.; Rodriguez, A.; Laio, A. Estimating the intrinsic dimension of datasets by a minimal neighborhood information. Sci. Rep. 2017, 7, 12140. [Google Scholar] [CrossRef]
- Zhou, S.; Tordesillas, A.; Pouragha, M.; Bailey, J.; Bondell, H. On local intrinsic dimensionality of deformation in complex materials. Nat. Sci. Rep. 2021, 11, 10216. [Google Scholar] [CrossRef]
- Tordesillas, A.; Zhou, S.; Bailey, J.; Bondell, H. A representation learning framework for detection and characterization of dead versus strain localization zones from pre- to post- failure. Granul. Matter 2022, 24, 75. [Google Scholar] [CrossRef]
- Faranda, D.; Messori, G.; Yiou, P. Dynamical proxies of North Atlantic predictability and extremes. Sci. Rep. 2017, 7, 41278. [Google Scholar] [CrossRef]
- Messori, G.; Harnik, N.; Madonna, E.; Lachmy, O.; Faranda, D. A dynamical systems characterization of atmospheric jet regimes. Earth Syst. Dynam. 2021, 12, 233–251. [Google Scholar] [CrossRef]
- Kambhatla, N.; Leen, T.K. Dimension Reduction by Local Principal Component Analysis. Neural Comput. 1997, 9, 1493–1516. [Google Scholar] [CrossRef]
- Houle, M.E.; Ma, X.; Nett, M.; Oria, V. Dimensional Testing for Multi-Step Similarity Search. In Proceedings of the IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; pp. 299–308. [Google Scholar]
- Campadelli, P.; Casiraghi, E.; Ceruti, C.; Lombardi, G.; Rozza, A. Local Intrinsic Dimensionality Based Features for Clustering. In Proceedings of the International Conference on Image Analysis and Processing, Naples, Italy, 9–13 September 2013; pp. 41–50. [Google Scholar]
- Houle, M.E.; Schubert, E.; Zimek, A. On the correlation between local intrinsic dimensionality and outlierness. In Proceedings of the International Conference on Similarity Search and Applications, Lima, Peru, 7–9 October 2018; pp. 177–191. [Google Scholar]
- Carter, K.M.; Raich, R.; Finn, W.G.; Hero, A.O., III. FINE: Fisher Information Non-parametric Embedding. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2093–2098. [Google Scholar] [CrossRef]
- Ma, X.; Li, B.; Wang, Y.; Erfani, S.M.; Wijewickrema, S.N.R.; Schoenebeck, G.; Song, D.; Houle, M.E.; Bailey, J. Characterizing Adversarial Subspaces Using Local Intrinsic Dimensionality. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–15. [Google Scholar]
- Amsaleg, L.; Bailey, J.; Barbe, D.; Erfani, S.M.; Houle, M.E.; Nguyen, V.; Radovanović, M. The Vulnerability of Learning to Adversarial Perturbation Increases with Intrinsic Dimensionality. In Proceedings of the IEEE Workshop on Information Forensics and Security, Rennes, France, 4–7 December 2017; pp. 1–6. [Google Scholar]
- Amsaleg, L.; Bailey, J.; Barbe, A.; Erfani, S.M.; Furon, T.; Houle, M.E.; Radovanović, M.; Nguyen, X.V. High Intrinsic Dimensionality Facilitates Adversarial Attack: Theoretical Evidence. IEEE Trans. Inf. Forensics Secur. 2021, 16, 854–865. [Google Scholar] [CrossRef]
- Ma, X.; Wang, Y.; Houle, M.E.; Zhou, S.; Erfani, S.M.; Xia, S.; Wijewickrema, S.N.R.; Bailey, J. Dimensionality-Driven Learning with Noisy Labels. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 3361–3370. [Google Scholar]
- Ansuini, A.; Laio, A.; Macke, J.H.; Zoccolan, D. Intrinsic dimension of data representations in deep neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 6111–6122. [Google Scholar]
- Pope, P.; Zhu, C.; Abdelkader, A.; Goldblum, M.; Goldstein, T. The intrinsic dimension of images and its impact on learning. In Proceedings of the International Conference on Learning Representations, Virtual Event, 3–7 May 2021. [Google Scholar]
- Gong, S.; Boddeti, V.N.; Jain, A.K. On the intrinsic dimensionality of image representations. In Proceedings of the CVPR, Long Beach, CA, USA, 5–20 June 2019; pp. 3987–3996. [Google Scholar]
- Barua, S.; Ma, X.; Erfani, S.M.; Houle, M.H.; Bailey, J. Quality Evaluation of GANs Using Cross Local Intrinsic Dimensionality. arXiv 2019, arXiv:1905.00643. [Google Scholar]
- Romano, S.; Chelly, O.; Nguyen, V.; Bailey, J.; Houle, M.E. Measuring Dependency via Intrinsic Dimensionality. In Proceedings of the ICPR16, Cancun, Mexico, 4–8 December 2016; pp. 1207–1212. [Google Scholar]
- Lucarini, V.; Faranda, D.; de Freitas, A.; de Freitas, J.; Holland, M.; Kuna, T.; Nicol, M.; Todd, M.; Vaienti, S. Extremes and Recurrence in Dynamical Systems; Pure and Applied Mathematics: A Wiley Series of Texts, Monographs and Tracts; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Levina, E.; Bickel, P.J. Maximum Likelihood Estimation of Intrinsic Dimension. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 13–18 December 2004; pp. 777–784. [Google Scholar]
- Amsaleg, L.; Chelly, O.; Furon, T.; Girard, S.; Houle, M.E.; Kawarabayashi, K.; Nett, M. Extreme-Value-Theoretic Estimation of Local Intrinsic Dimensionality. Data Min. Knowl. Discov. 2018, 32, 1768–1805. [Google Scholar] [CrossRef]
- Hill, B.M. A Simple General Approach to Inference About the Tail of a Distribution. Ann. Stat. 1975, 3, 1163–1174. [Google Scholar] [CrossRef]
- Johnsson, K.; Soneson, C.; Fontes, M. Low bias local intrinsic dimension estimation from expected simplex skewness. IEEE TPAMI 2015, 37, 196–202. [Google Scholar] [CrossRef] [PubMed]
- Amsaleg, L.; Chelly, O.; Houle, M.E.; Kawarabayashi, K.; Radovanović, R.; Treeratanajaru, W. Intrinsic dimensionality estimation within tight localities. In Proceedings of the 2019 SIAM International Conference on Data Mining, Calgary, AB, Canada, 2–4 May 2019; pp. 181–189. [Google Scholar]
- Farahmand, A.M.; Szepesvári, C.; Audibert, J.Y. Manifold-adaptive dimension estimation. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, OR, USA, 20–24 June 2007; pp. 265–272. [Google Scholar]
- Block, A.; Jia, Z.; Polyanskiy, Y.; Rakhlin, A. Intrinsic Dimension Estimation Using Wasserstein Distances. arXiv 2021, arXiv:2106.04018. [Google Scholar]
- Thordsen, E.; Schubert, E. ABID: Angle Based Intrinsic Dimensionality—Theory and analysis. Inf. Syst. 2022, 108, 101989. [Google Scholar] [CrossRef]
- Carter, K.M.; Raich, R.; Hero III, A.O. On Local Intrinsic Dimension Estimation and Its Applications. IEEE Trans. Signal Process. 2010, 58, 650–663. [Google Scholar] [CrossRef]
- Tempczyk, P.; Golinski, A.; Spurek, P.; Tabor, J. LIDL: Local Intrinsic Dimension estimation using approximate Likelihood. In Proceedings of the ICLR 2021 Workshop on Geometrical and Topological Representation Learning, Online, 7 May 2021. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing); Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Rioul, O. Information Theoretic Proofs of Entropy Power Inequalities. IEEE Trans. Inf. Theory 2011, 57, 33–55. [Google Scholar] [CrossRef]
- Jelinek, F.; Mercer, R.L.; Bahl, L.R.; Baker, J.K. Perplexity—A measure of the difficulty of speech recognition tasks. J. Acoust. Soc. Am. 1977, 62, S63. [Google Scholar] [CrossRef]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Kostal, L.; Lansky, P.; Pokora, O. Measures of statistical dispersion based on Shannon and Fisher information concepts. Inf. Sci. 2013, 235, 214–223. [Google Scholar] [CrossRef]
- Stam, A.J. Some inequalities satisfied by the quantities of information of Fisher and Shannon. Inf. Control. 1959, 2, 101–112. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Longobardi, M. On cumulative entropies. J. Stat. Plan. Inference 2009, 139, 4072–4087. [Google Scholar] [CrossRef]
- Rao, M.; Chen, Y.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: A new measure of information. IEEE Trans. Inf. Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Mandros, P.; Vreeken, J. Universal Dependency Analysis. In Proceedings of the 2016 SIAM International Conference on Data Mining, Miami, FL, USA, 5–7 May 2016; pp. 792–800. [Google Scholar] [CrossRef]
- Böhm, K.; Keller, F.; Müller, E.; Nguyen, H.V.; Vreeken, J. CMI: An Information-Theoretic Contrast Measure for Enhancing Subspace Cluster and Outlier Detection. In Proceedings of the 13th SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; pp. 198–206. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Calì, C.; Longobardi, M.; Ahmadi, J. Some properties of cumulative Tsallis entropy. Phys. A Stat. Mech. Its Appl. 2017, 486, 1012–1021. [Google Scholar] [CrossRef]
- Pele, D.T.; Lazar, E.; Mazurencu-Marinescu-Pele, M. Modeling Expected Shortfall Using Tail Entropy. Entropy 2019, 21, 1204. [Google Scholar] [CrossRef]
- MacKay, D.J. Information Theory, Inference, and Learning Algorithms, 1st ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kac, M.; Kiefer, J.; Wolfowitz, J. On tests of normality and other tests of goodness of fit based on distance methods. Ann. Math. Stat. 1955, 26, 189–211. [Google Scholar] [CrossRef]
- Nowozin, S.; Cseke, B.; Tomioka, R. f-GAN: Training generative neural samplers using variational divergence minimization. In Proceedings of the 30th Annual Conference on Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 271–279. [Google Scholar]
- Contreras-Reyes, J. Asymptotic form of the Kullback-Leibler divergence for multivariate asymmetric heavy-tailed distributions. Phys. A Stat. Mech. Its Appl. 2014, 395, 200–208. [Google Scholar] [CrossRef]
- Houle, M.E.; Kashima, H.; Nett, M. Generalized Expansion Dimension. In Proceedings of the IEEE 12th International Conference on Data Mining Workshops, Brussels, Belgium, 10 December 2012; pp. 587–594. [Google Scholar]
- Karger, D.R.; Ruhl, M. Finding nearest neighbors in growth-restricted metrics. In Proceedings of the 34th ACM Symposium on Theory of Computing, Montreal, QC, Canada, 19–21 May 2002; pp. 741–750. [Google Scholar]
- Houle, M.E. Dimensionality, Discriminability, Density and Distance Distributions. In Proceedings of the IEEE 13th International Conference on Data Mining Workshops, Dallas, TX, USA, 7–10 December 2013; pp. 468–473. [Google Scholar]
- Karamata, J. Sur un mode de croissance régulière. Théorèmes fondamentaux. Bull. Société Mathématique Fr. 1933, 61, 55–62. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: Berlin/Heidelberg, Germany, 2001; Volume 208. [Google Scholar]
- Houle, M.E. Local Intrinsic Dimensionality II: Multivariate Analysis and Distributional Support. In Proceedings of the International Conference on Similarity Search and Applications, Munich, Germany, 4–6 October 2017; pp. 80–95. [Google Scholar]
- Song, K. Renyi information, log likelihood and an intrinsic distribution measure. J. Statist. Plann. Inference 2001, 93, 51–69. [Google Scholar] [CrossRef]
- Buono, F.; Longobardi, M. Varentropy of past lifetimes. arXiv 2020, arXiv:2008.07423. [Google Scholar]
- Maadani, S.; Borzadaran, G.R.M.; Roknabadi, A.H.R. Varentropy of order statistics and some stochastic comparisons. Commun. Stat. Theory Methods 2021, 51, 6447–6460. [Google Scholar] [CrossRef]
- Raqab, M.Z.; Bayoud, H.A.; Qiu, G. Varentropy of inactivity time of a random variable and its related applications. IMA J. Math. Control. Inf. 2021, 39, 132–154. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Basu, A.; Harris, I.R.; Hjort, N.L.; Jones, M.C. Robust and efficient estimation by minimising a density power divergence. Biometrika 1998, 85, 549–559. [Google Scholar] [CrossRef]
- Hellinger, E. Neue Begründung der Theorie quadratischer Formen von unendlichvielen Veränderlichen. J. Für Die Reine Und Angew. Math. 1909, 136, 210–271. [Google Scholar] [CrossRef]
- Cichocki, A.; Amari, S. Families of Alpha- Beta- and Gamma- Divergences: Flexible and Robust Measures of Similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Pearson, K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Kantorovich, L.V. Mathematical Methods of Organizing and Planning Production. Manag. Sci. 1939, 6, 366–422. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein Generative Adversarial Networks. In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney, NSW, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; PMLR: Cambridge, MA, USA, 2017; Volume 70, pp. 214–223. [Google Scholar]
- Houle, M.E. Local Intrinsic Dimensionality III: Density and Similarity. In Proceedings of the International Conference on Similarity Search and Applications, Copenhagen, Denmark, 30 September–2 October 2020. [Google Scholar]
- Itakura, F.; Saito, S. Analysis synthesis telephony based on the maximum likelihood method. In Proceedings of the 6th International Congress on Acoustics, Tokyo, Japan, 21–28 August 1968; pp. C17–C20. [Google Scholar]
- Fevotte, C.; Bertin, N.; Durrieu, J. Nonnegative Matrix Factorization with the Itakura-Saito Divergence: With Application to Music Analysis. Neural Comput. 2009, 21, 793–830. [Google Scholar] [CrossRef]
- Bregman, L.M. The relaxation method of finding the common points of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. Sided and symmetrized Bregman centroids. IEEE Trans. Inf. Theory 2009, 55, 2882–2904. [Google Scholar] [CrossRef]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman Divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Fang, K.W.; Kotz, S.; Wang Ng, K. Symmetric Multivariate and Related Distributions; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Baker, J.A. Integration of Radial Functions. Math. Mag. 1999, 72, 392–395. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).