Study of the Imbibition Phenomenon in Porous Media by the Smoothed Particle Hydrodynamic (SPH) Method
Abstract
:1. Introduction
2. Methodology
2.1. The Governing Equations
2.2. The SPH Model
2.3. The Relaxation of the Solid Boundary
3. Results and Discussion
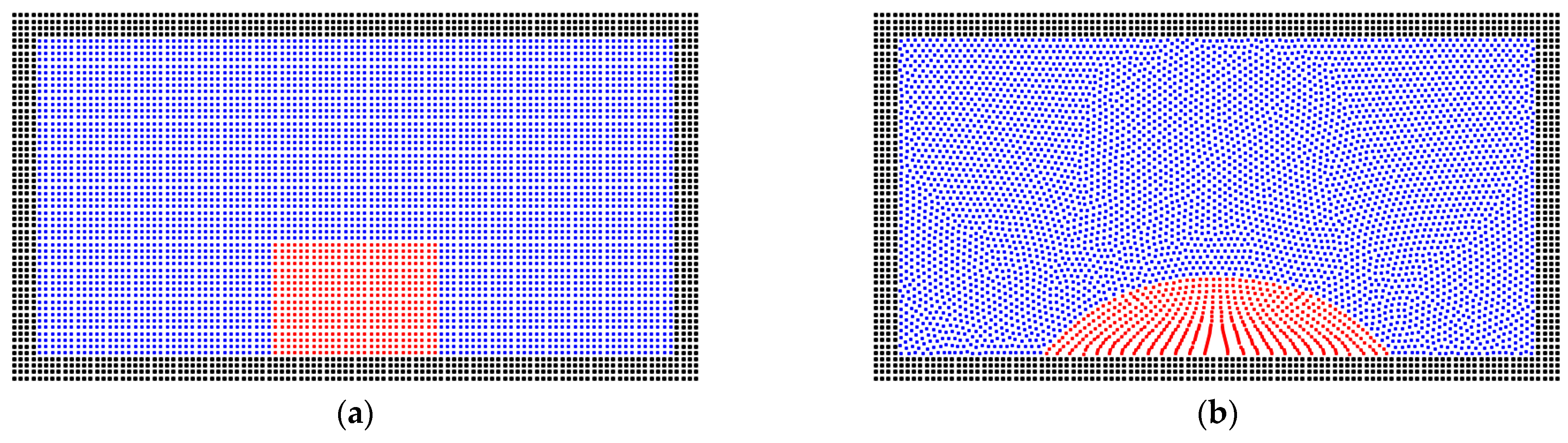
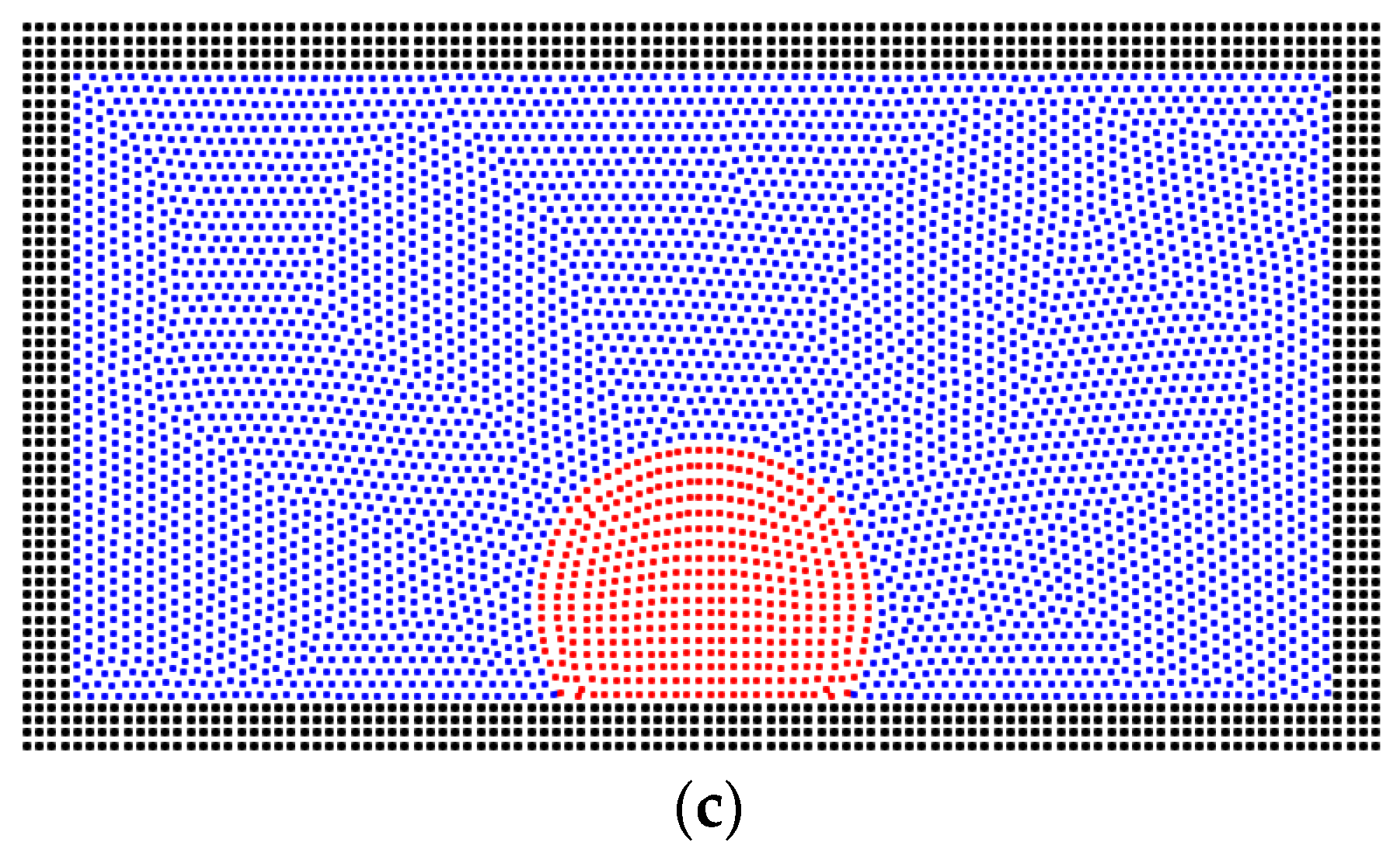
3.1. The Validation of the Scheme
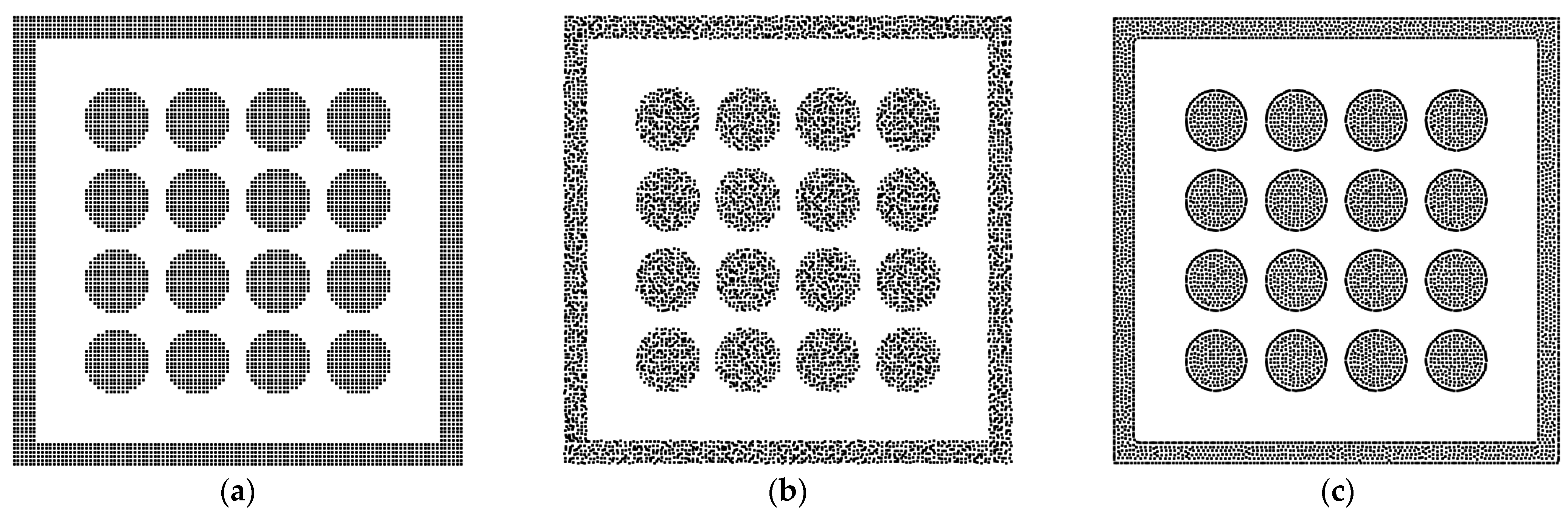
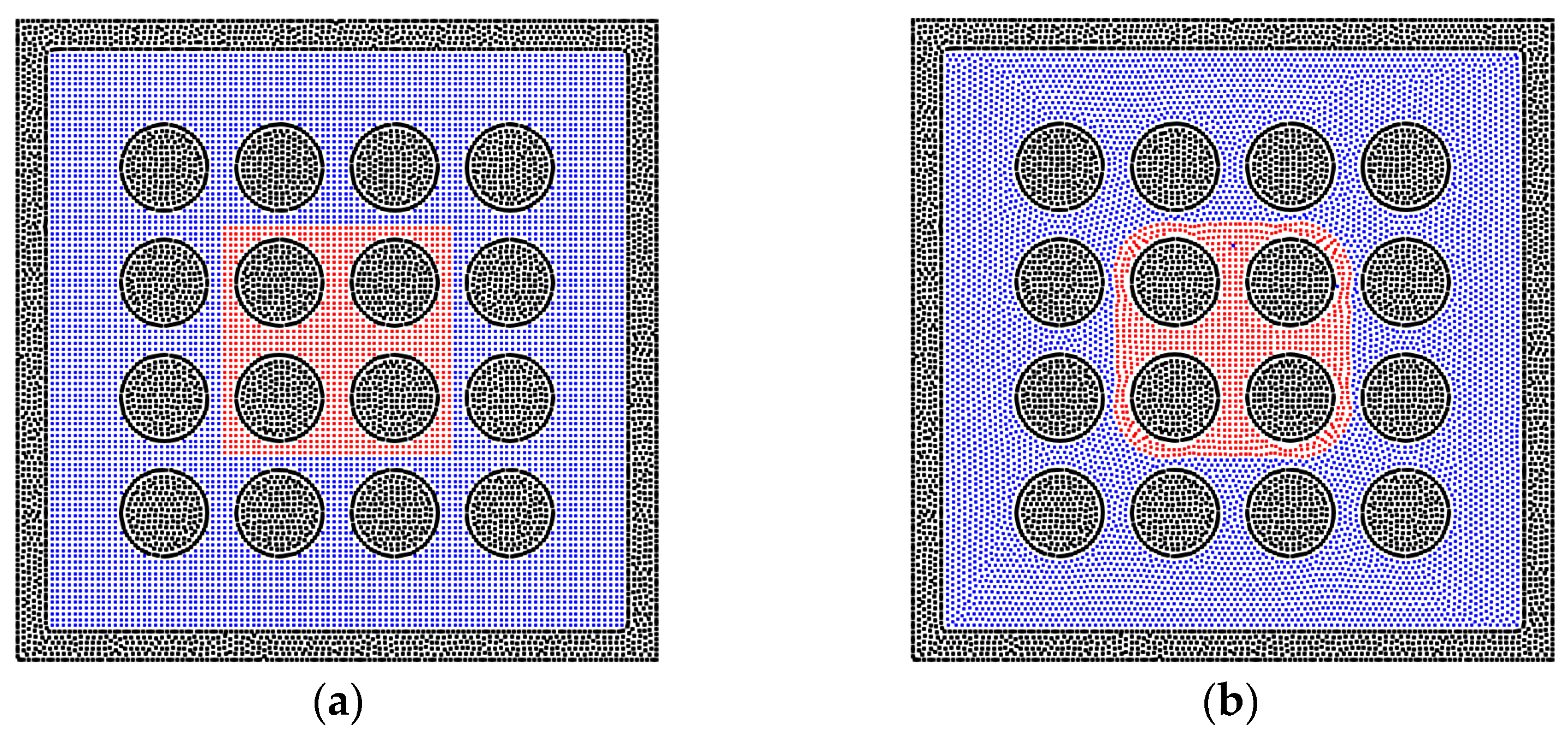
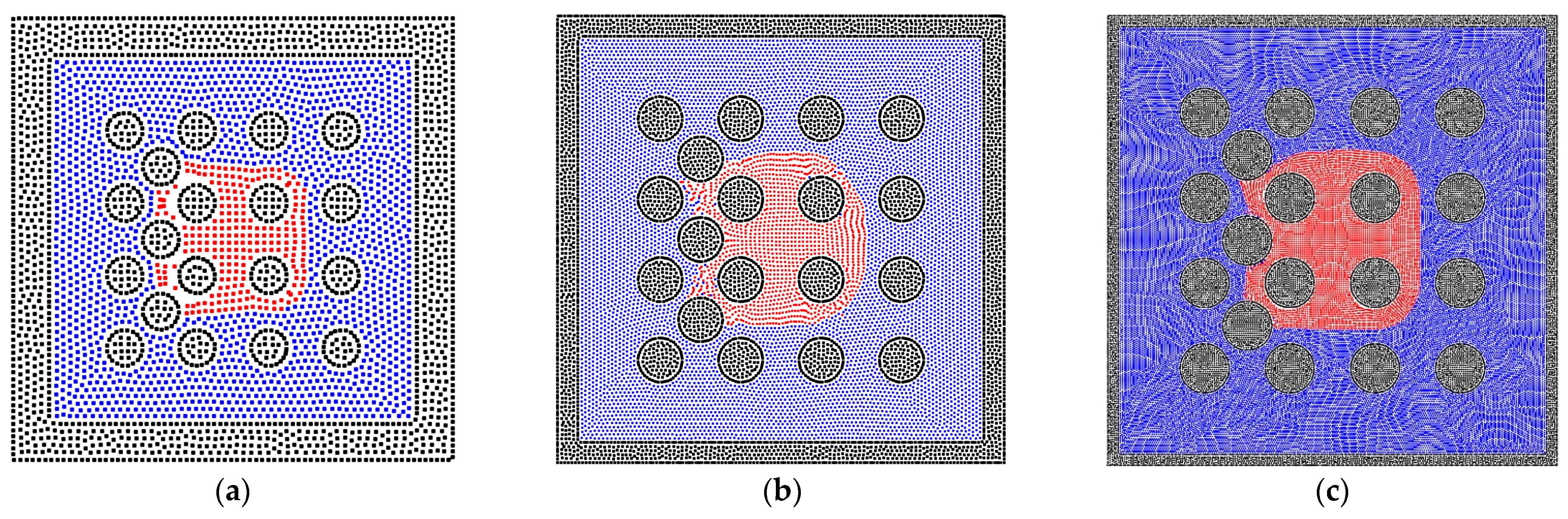
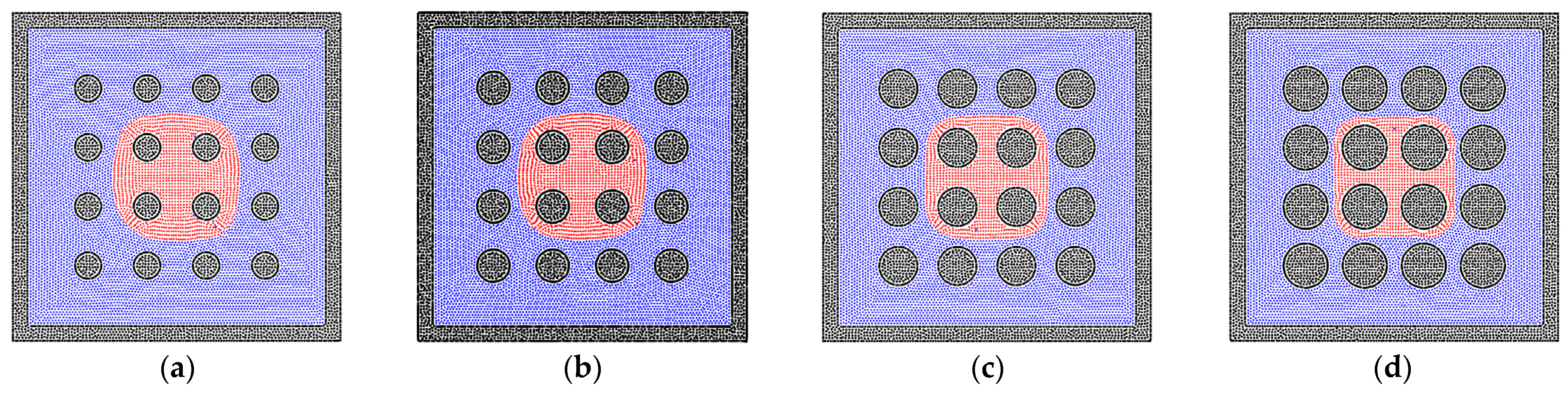
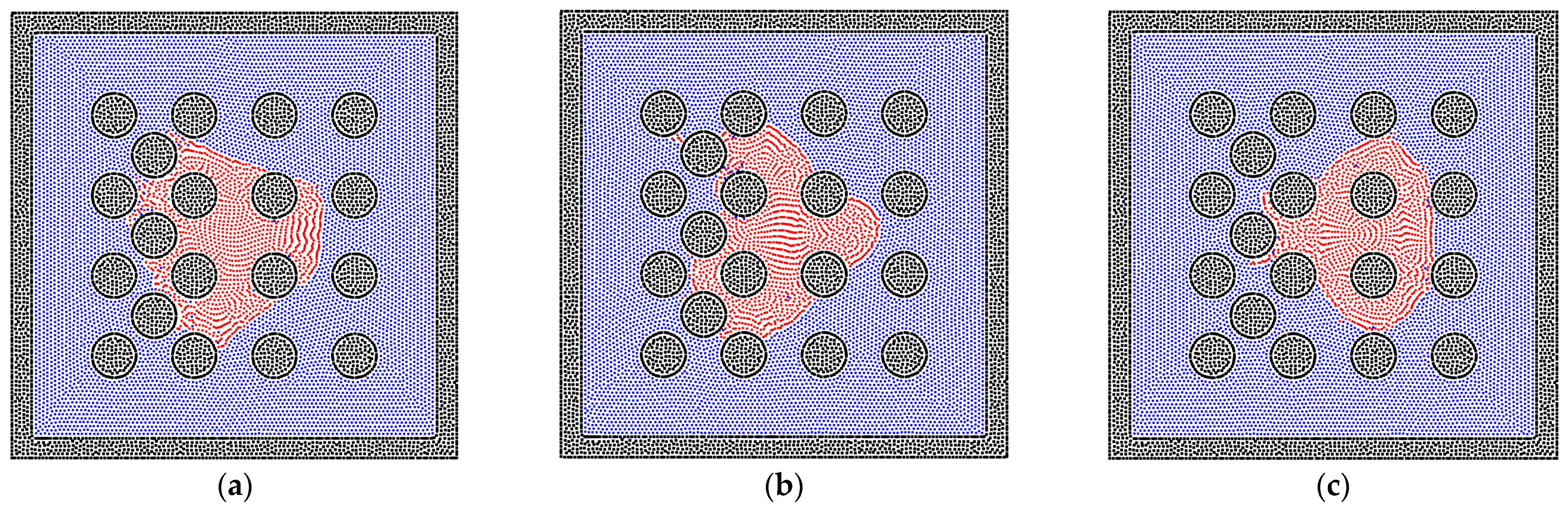
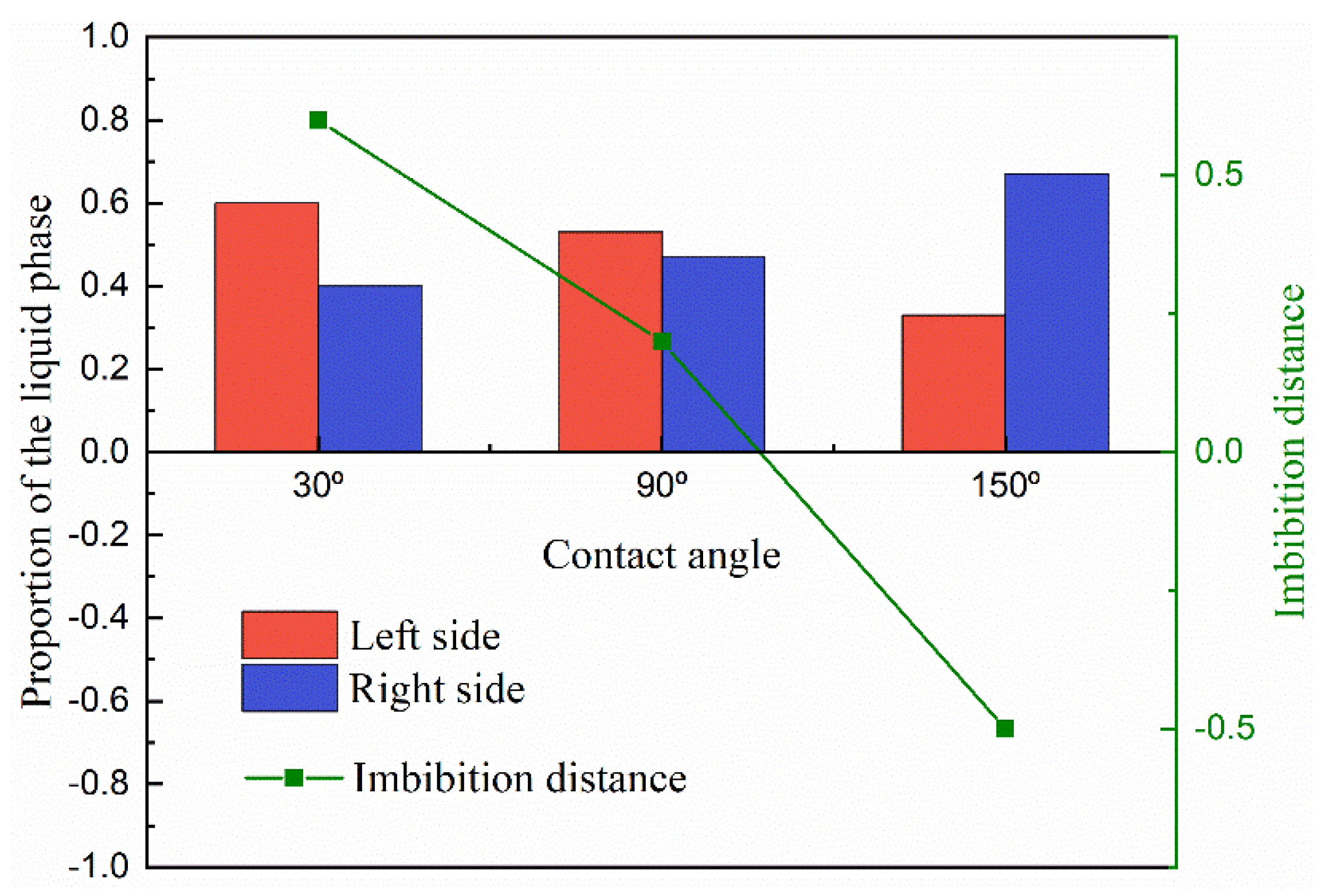
3.2. The Sensitivity of the Porous Media’s Structure for the Two-Phase Behavior
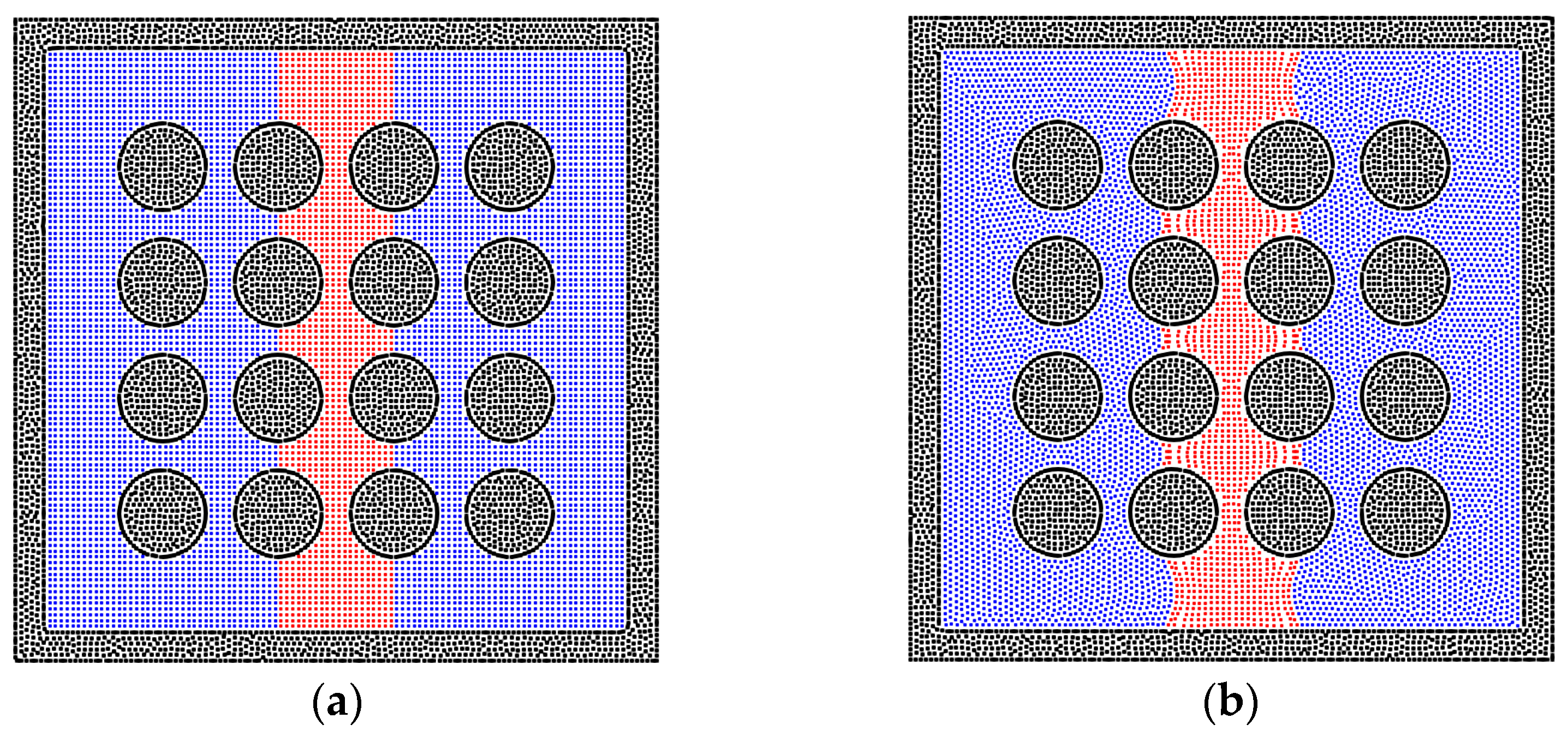
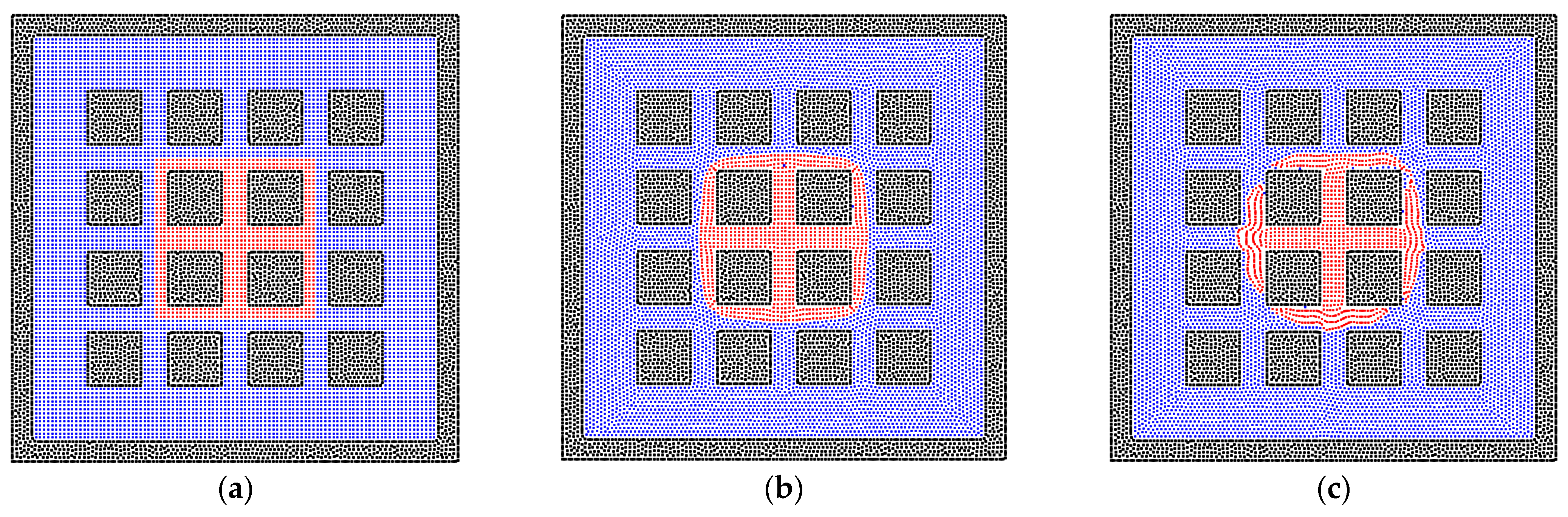
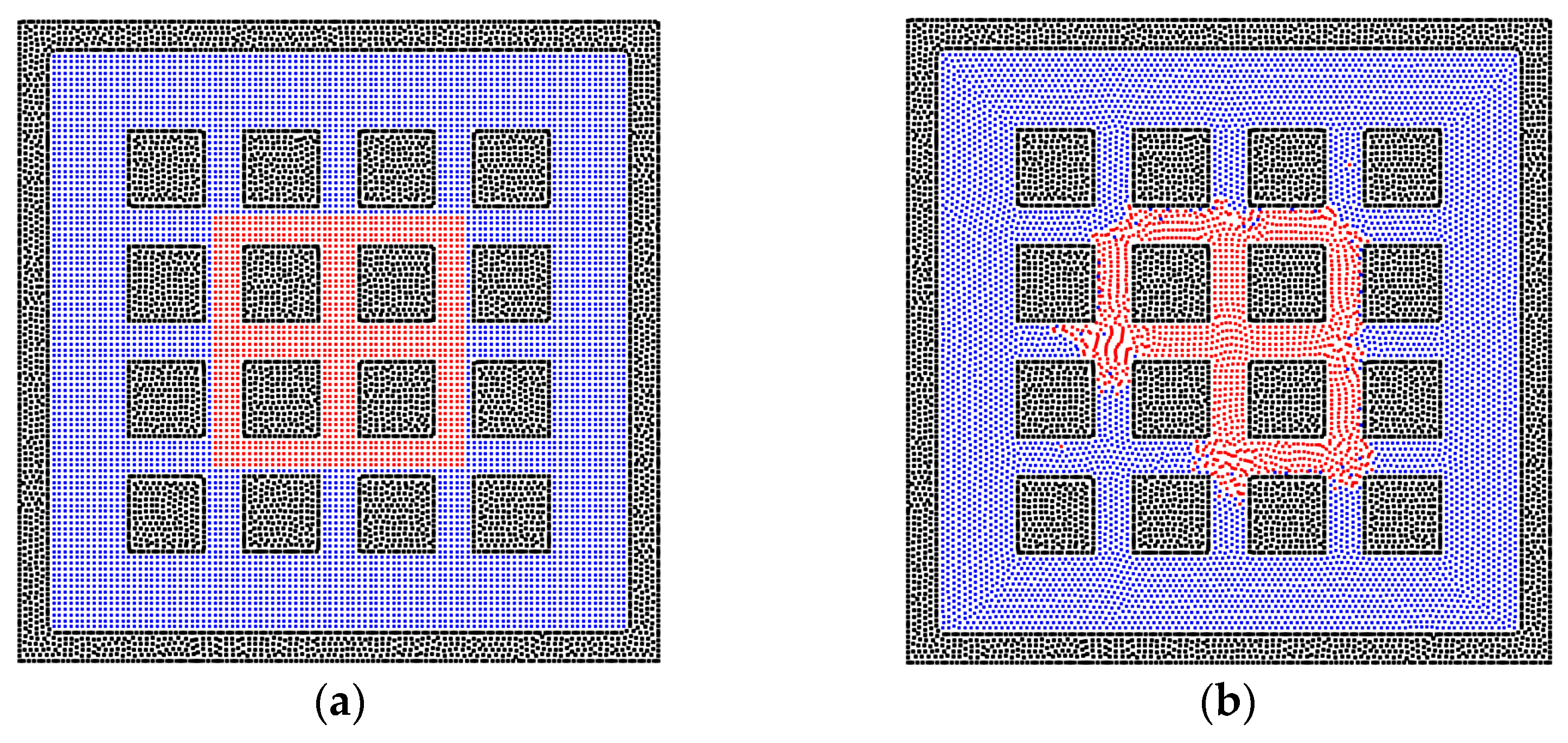
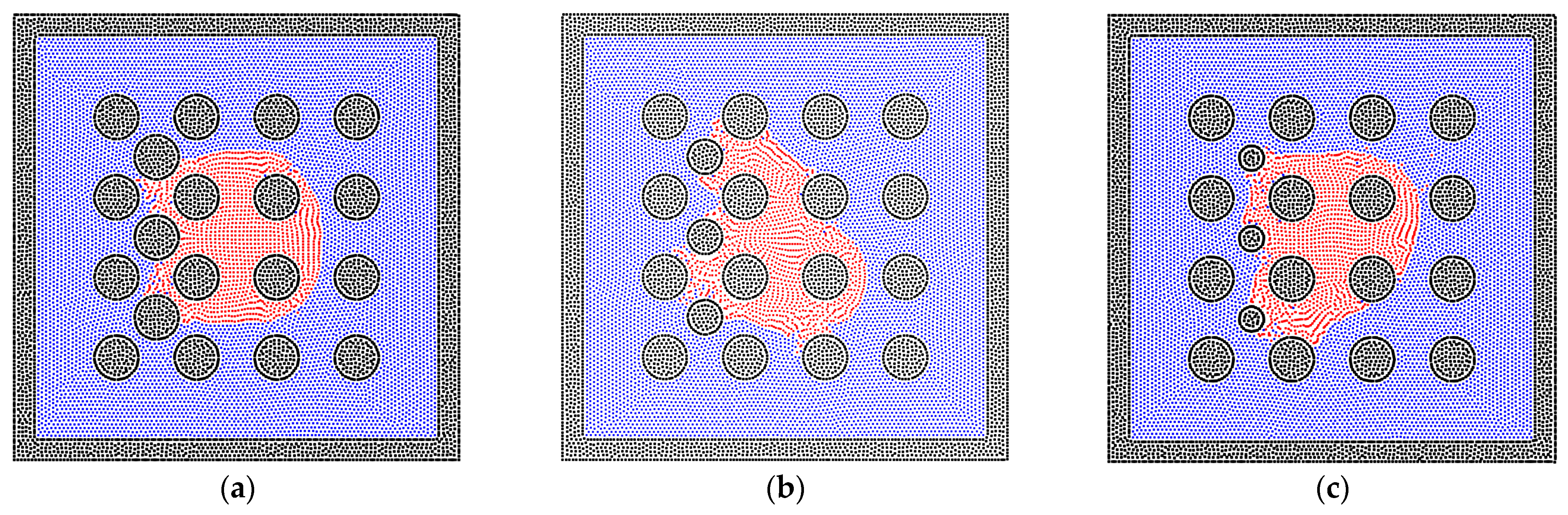
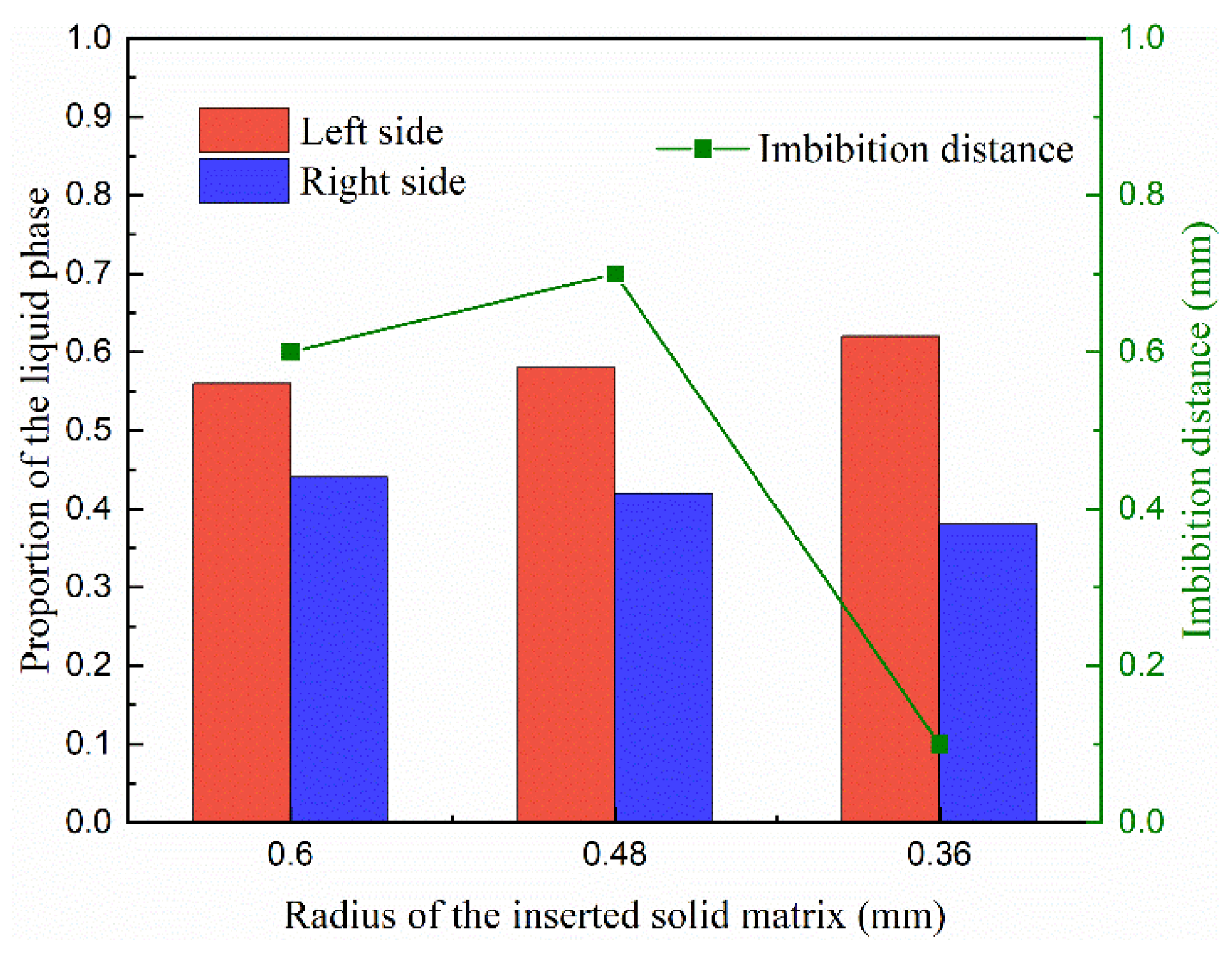
3.3. The Two-Phase Behavior in the Heterogeneous Porous Media
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stewart, H.B.; Wendroff, B. Two-phase flow: Models and methods. J. Comput. Phys. 1984, 56, 363–409. [Google Scholar] [CrossRef]
- Drew, D.A. Mathematical modeling of two-phase flow. Annu. Rev. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Yao, J.; Iglauer, S.; Luquot, L.; Zhang, K.; Sun, H.; Zhang, L.; Song, W.; Wang, Z. Dynamic pore-scale dissolution by CO2-saturated brine in carbonates: Impact of homogeneous versus fractured versus vuggy pore structure. Water Resour. Res. 2020, 56, e2019WR026112. [Google Scholar] [CrossRef]
- Wang, X.; Yin, H.; Zhao, X.; Li, B.; Yang, Y. Microscopic remaining oil distribution and quantitative analysis of polymer flooding based on CT scanning. Adv. Geo-Energy Res. 2019, 3, 448–456. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Y.; Sun, S.; Yao, J.; Kou, J. Flow Behaviors of Shale Oil in Kerogen Slit by Molecular Dynamics Simulation. Chem. Eng. J. 2022, 434, 134682. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Qiao, Z.; Sun, S. Two-phase fluid simulation using a diffuse interface model with Peng--Robinson equation of state. SIAM J. Sci. Comput. 2014, 36, B708–B728. [Google Scholar] [CrossRef]
- Zhu, G.; Kou, J.; Yao, B.; Wu, Y.-s.; Yao, J.; Sun, S. Thermodynamically consistent modelling of two-phase flows with moving contact line and soluble surfactants. J. Fluid Mech. 2019, 879, 327–359. [Google Scholar] [CrossRef]
- Kou, J.; Sun, S. A new treatment of capillarity to improve the stability of IMPES two-phase flow formulation. Comput. Fluids 2010, 39, 1923–1931. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Li, Y.; Sun, S.; Gao, X. A self-adaptive deep learning algorithm for accelerating multi-component flash calculation. Comput. Methods Appl. Mech. Eng. 2020, 369, 113207. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, S. A coupled Lattice Boltzmann approach to simulate gas flow and transport in shale reservoirs with dynamic sorption. Fuel 2019, 246, 196–203. [Google Scholar] [CrossRef]
- Douglas, J., Jr. Finite difference methods for two-phase incompressible flow in porous media. SIAM J. Numer. Anal. 1983, 20, 681–696. [Google Scholar] [CrossRef]
- Reichenberger, V.; Jakobs, H.; Bastian, P.; Helmig, R. A mixed-dimensional finite volume method for two-phase flow in fractured porous media. Adv. Water Resour. 2006, 29, 1020–1036. [Google Scholar] [CrossRef]
- Chessa, J.; Belytschko, T. An extended finite element method for two-phase fluids. J. Appl. Mech. 2003, 70, 10–17. [Google Scholar] [CrossRef]
- Durlofsky, L.J. A triangle based mixed finite element—finite volume technique for modeling two phase flow through porous media. J. Comput. Phys. 1993, 105, 252–266. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Y.; Yang, Y.; Mei, Q.; Yang, S.; Wang, C. Multicomponent Shale Oil Flow in Real Kerogen Structures via Molecular Dynamic Simulation. Energies 2020, 13, 3815. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Yao, J.; Kou, J.; Li, Z.; Wu, T.; Zhang, K.; Zhang, L.; Sun, H. Adsorption behaviors of shale oil in kerogen slit by molecular simulation. Chem. Eng. J. 2020, 387, 124054. [Google Scholar] [CrossRef]
- Feng, Q.; Xu, S.; Xing, X.; Zhang, W.; Wang, S. Advances and challenges in shale oil development: A critical review. Adv. Geo-Energy Res. 2020, 4, 406–418. [Google Scholar] [CrossRef]
- Liu, J.; Tang, Q.; Kou, J.; Xu, D.; Zhang, T.; Sun, S. A quantitative study on the approximation error and speed-up of the multi-scale MCMC (Monte Carlo Markov chain) method for molecular dynamics. J. Comput. Phys. 2022, 111491. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Xie, X.; Meng, Q.; Sun, S. Effects of Membrane Structure on Oil–Water Separation by Smoothed Particle Hydrodynamics. Membranes 2022, 12, 387. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Liu, Y.; Iglauer, S.; Cai, J.; Amooie, M.A.; Qin, C. Local instabilities during capillary-dominated immiscible displacement in porous media. Capillarity 2019, 2, 1–7. [Google Scholar] [CrossRef]
- Sivanesapillai, R.; Falkner, N.; Hartmaier, A.; Steeb, H. A CSF-SPH method for simulating drainage and imbibition at pore-scale resolution while tracking interfacial areas. Adv. Water Resour. 2016, 95, 212–234. [Google Scholar] [CrossRef]
- Yang, H.; Yang, C.; Sun, S. Active-set reduced-space methods with nonlinear elimination for two-phase flow problems in porous media. SIAM J. Sci. Comput. 2016, 38, B593–B618. [Google Scholar] [CrossRef]
- Feng, X.; Chen, M.-H.; Wu, Y.; Sun, S. A fully explicit and unconditionally energy-stable scheme for Peng-Robinson VT flash calculation based on dynamic modeling. J. Comput. Phys. 2022, 463, 111275. [Google Scholar] [CrossRef]
- McCamy, C.S. Correlated color temperature as an explicit function of chromaticity coordinates. Color Res. Appl. 1992, 17, 142–144. [Google Scholar] [CrossRef]
- Chen, T.; Chiu, M.-S.; Weng, C.-N. Derivation of the generalized Young-Laplace equation of curved interfaces in nanoscaled solids. J. Appl. Phys. 2006, 100, 074308. [Google Scholar] [CrossRef]
- Yang, Y.; Che Ruslan, M.F.A.; Narayanan Nair, A.K.; Sun, S. Effect of ion valency on the properties of the carbon dioxide–methane–brine system. J. Phys. Chem. B 2019, 123, 2719–2727. [Google Scholar] [CrossRef]
- El-Amin, M.; Salama, A.; Sun, S. Numerical and dimensional analysis of nanoparticles transport with two-phase flow in porous media. J. Pet. Sci. Eng. 2015, 128, 53–64. [Google Scholar] [CrossRef]
- Li, Y.; Yang, H.; Sun, S. Fully implicit two-phase VT-flash compositional flow simulation enhanced by multilayer nonlinear elimination. J. Comput. Phys. 2022, 449, 110790. [Google Scholar] [CrossRef]
- Abdolahzadeh, M.; Tayebi, A.; Mansouri Mehryan, M. Numerical Simulation of Mixing in Active Micromixers Using SPH. Transp. Porous Media 2022, 1–18. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Meakin, P.; Scheibe, T.D.; Wood, B.D. A smoothed particle hydrodynamics model for reactive transport and mineral precipitation in porous and fractured porous media. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Bui, H.H.; Nguyen, G.D. A coupled fluid-solid SPH approach to modelling flow through deformable porous media. Int. J. Solids Struct. 2017, 125, 244–264. [Google Scholar] [CrossRef]
- Kazemi, E.; Luo, M. A comparative study on the accuracy and conservation properties of the SPH method for fluid flow interaction with porous media. Adv. Water Resour. 2022, 165, 104220. [Google Scholar] [CrossRef]
- Viccione, G.; Bovolin, V.; Carratelli, E.P. Defining and optimizing algorithms for neighbouring particle identification in SPH fluid simulations. Int. J. Numer. Methods Fluids 2008, 58, 625–638. [Google Scholar] [CrossRef]
- Yang, T.; Lin, M.; Martin, R.R.; Chang, J.; Hu, S. Versatile interactions at interfaces for SPH-based simulations. In Proceedings of the Eurographics/ACM SIGGRAPH Symposium on Computer Animation, Zurich, Switzerland, 11–13 July 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 57–66. [Google Scholar]
- He, X.; Luo, L.-S. Lattice Boltzmann model for the incompressible Navier–Stokes equation. J. Stat. Phys. 1997, 88, 927–944. [Google Scholar] [CrossRef]
- Mohd-Yusof, J. Combined immersed-boundary/B-spline methods for simulations of flow in complex geometries. Cent. Turbul. Res. Annu. Res. Briefs 1997, 161, 317–327. [Google Scholar]
- Tartakovsky, A.M.; Meakin, P. Pore scale modeling of immiscible and miscible fluid flows using smoothed particle hydrodynamics. Adv. Water Resour. 2006, 29, 1464–1478. [Google Scholar] [CrossRef]
- Zhu, Y.; Fox, P.J. Simulation of pore-scale dispersion in periodic porous media using smoothed particle hydrodynamics. J. Comput. Phys. 2002, 182, 622–645. [Google Scholar] [CrossRef]
- Price, D.J. Smoothed particle hydrodynamics and magnetohydrodynamics. J. Comput. Phys. 2012, 231, 759–794. [Google Scholar] [CrossRef] [Green Version]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Zhu, Y.; Fox, P.J.; Morris, J.P. A pore-scale numerical model for flow through porous media. Int. J. Numer. Anal. Methods Geomech. 1999, 23, 881–904. [Google Scholar] [CrossRef]
- Koschier, D.; Bender, J.; Solenthaler, B.; Teschner, M. Smoothed particle hydrodynamics techniques for the physics based simulation of fluids and solids. arXiv 2020, arXiv:2009.06944. [Google Scholar]
- Tartakovsky, A.M.; Trask, N.; Pan, K.; Jones, B.; Pan, W.; Williams, J.R. Smoothed particle hydrodynamics and its applications for multiphase flow and reactive transport in porous media. Comput. Geosci. 2016, 20, 807–834. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Panchenko, A. Pairwise force smoothed particle hydrodynamics model for multiphase flow: Surface tension and contact line dynamics. J. Comput. Phys. 2016, 305, 1119–1146. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R.; Piechor, K. Level set methods and dynamic implicit surfaces. Appl. Mech. Rev. 2004, 57, B15–B16. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R.P. Level set methods: An overview and some recent results. J. Comput. Phys. 2001, 169, 463–502. [Google Scholar] [CrossRef]
- Yang, Q.; Yao, J.; Huang, Z.; Asif, M. A comprehensive SPH model for three-dimensional multiphase interface simulation. Comput. Fluids 2019, 187, 98–106. [Google Scholar] [CrossRef]
- Yang, Q.; Yao, J.; Huang, Z.; Zhu, G.; Liu, L.; Song, W. Pore-scale investigation of petro-physical fluid behaviours based on multiphase SPH method. J. Pet. Sci. Eng. 2020, 192, 107238. [Google Scholar] [CrossRef]
- Zhang, C.; Rezavand, M.; Zhu, Y.; Yu, Y.; Wu, D.; Zhang, W.; Zhang, S.; Wang, J.; Hu, X. SPHinXsys: An open-source meshless, multi-resolution and multi-physics library. Softw. Impacts 2020, 6, 100033. [Google Scholar] [CrossRef]
- Zhang, C.; Rezavand, M.; Zhu, Y.; Yu, Y.; Wu, D.; Zhang, W.; Wang, J.; Hu, X. SPHinXsys: An open-source multi-physics and multi-resolution library based on smoothed particle hydrodynamics. Comput. Phys. Commun. 2021, 267, 108066. [Google Scholar] [CrossRef]
- He, M.; Szuchmacher Blum, A.; Aston, D.E.; Buenviaje, C.; Overney, R.M.; Luginbühl, R. Critical phenomena of water bridges in nanoasperity contacts. J. Chem. Phys. 2001, 114, 1355–1360. [Google Scholar] [CrossRef]
- Fang, G.; Amirfazli, A. Understanding the edge effect in wetting: A thermodynamic approach. Langmuir 2012, 28, 9421–9430. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wang, K.; Zhang, L.; Sun, H.; Zhang, K.; Ma, J. Pore-scale simulation of shale oil flow based on pore network model. Fuel 2019, 251, 683–692. [Google Scholar] [CrossRef]
- Meng, Q.; Cai, J. Recent advances in spontaneous imbibition with different boundary conditions. Capillarity 2018, 1, 19–26. [Google Scholar] [CrossRef]
- Cai, J.; Sun, S. Fractal analysis of fracture increasing spontaneous imbibition in porous media with gas-saturated. Int. J. Mod. Phys. C 2013, 24, 1350056. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Katterbauer, K.; Al Shehri, A.; Sun, S.; Hoteit, I. Phase equilibrium in the hydrogen energy chain. Fuel 2022, 328, 125324. [Google Scholar] [CrossRef]

| Phase | Density/(kg·m−3) | Viscosity/(mPa·s) |
|---|---|---|
| Gas | 1.225 | 0.019 |
| Liquid | 1000 | 0.925 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhang, T.; Sun, S. Study of the Imbibition Phenomenon in Porous Media by the Smoothed Particle Hydrodynamic (SPH) Method. Entropy 2022, 24, 1212. https://doi.org/10.3390/e24091212
Liu J, Zhang T, Sun S. Study of the Imbibition Phenomenon in Porous Media by the Smoothed Particle Hydrodynamic (SPH) Method. Entropy. 2022; 24(9):1212. https://doi.org/10.3390/e24091212
Chicago/Turabian StyleLiu, Jie, Tao Zhang, and Shuyu Sun. 2022. "Study of the Imbibition Phenomenon in Porous Media by the Smoothed Particle Hydrodynamic (SPH) Method" Entropy 24, no. 9: 1212. https://doi.org/10.3390/e24091212
APA StyleLiu, J., Zhang, T., & Sun, S. (2022). Study of the Imbibition Phenomenon in Porous Media by the Smoothed Particle Hydrodynamic (SPH) Method. Entropy, 24(9), 1212. https://doi.org/10.3390/e24091212









