An Algorithmic Approach to Emergence
Abstract
1. Introduction
1.1. Existing Notions of Emergence
The ability to reduce everything to simple fundamental laws does not imply the ability to start from those laws and reconstruct the universe. In fact, the more elementary particle physicists tell us about the nature of the fundamental laws, the less relevance they seem to have for the very real problems of the rest of science, much less to those of society.
The constructionist hypothesis breaks down when confronted with the twin difficulty of scale and complexity. […] at each level of complexity, entirely new properties appear, and the understanding of the new behaviours requires research which I think is as fundamental in its nature as any other. […] At each stage, entirely new laws, concepts, and generalizations are necessary, requiring inspiration and creativity to just as great a degree as the previous one. Psychology is not applied biology, nor biology is applied chemistry.
1.2. From Systems to Bit Strings
1.3. Outline
2. A Primer on Algorithmic Methods
2.1. Algorithmic Complexity
2.2. Non-Probabilistic Statistics
Kolmogorov’s Structure Function
2.3. Algorithmic Connections in Physics
3. Defining Emergence
3.1. Towards a Definition
3.1.1. Index Models
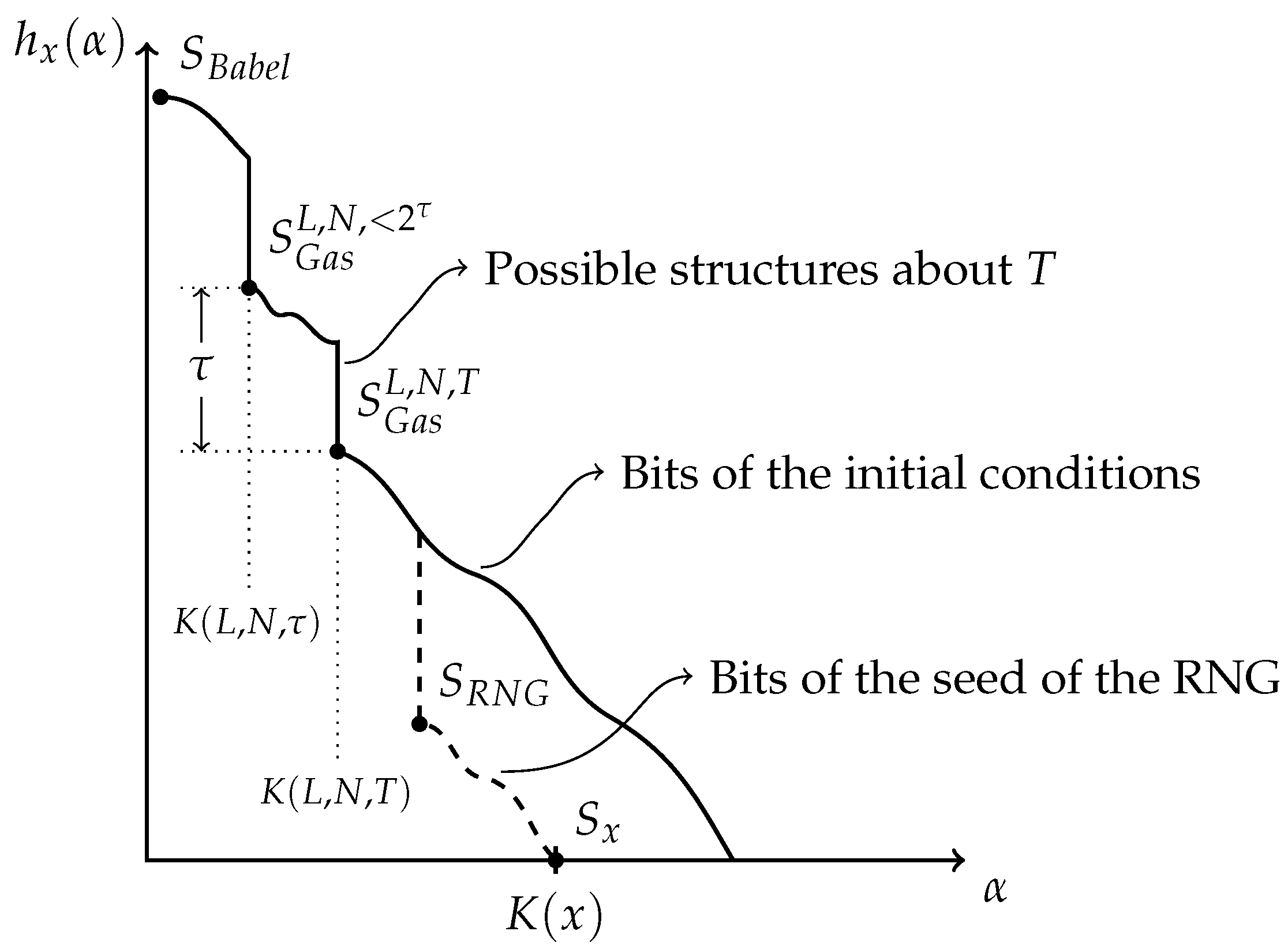
3.1.2. A Modified Structure Function
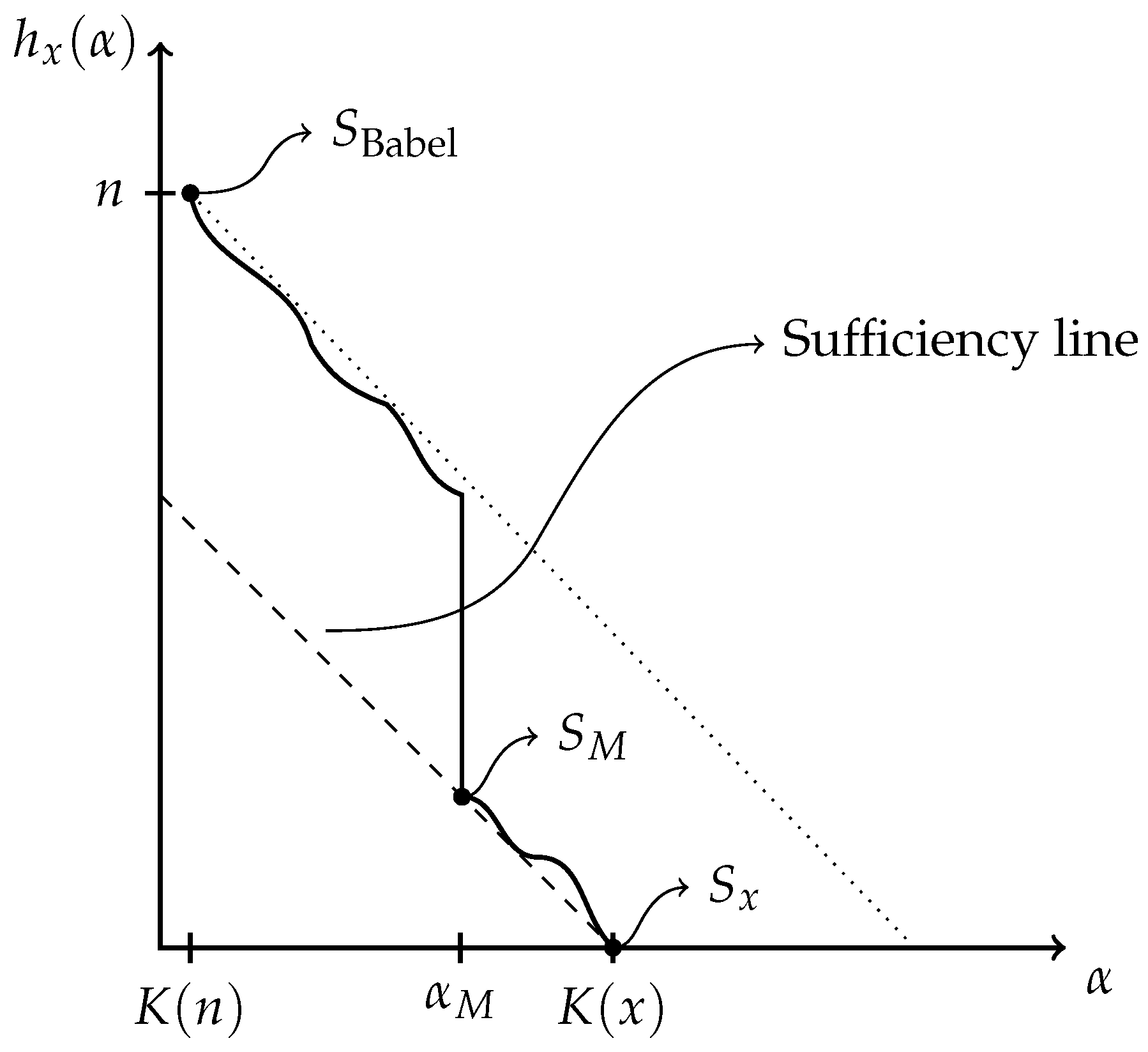
3.1.3. Minimal Partial Models as a Signature of Emergence
3.2. Quantifying Emergence
3.2.1. The Data Specifies the Minimal Partial Models
3.2.2. Partial Understanding
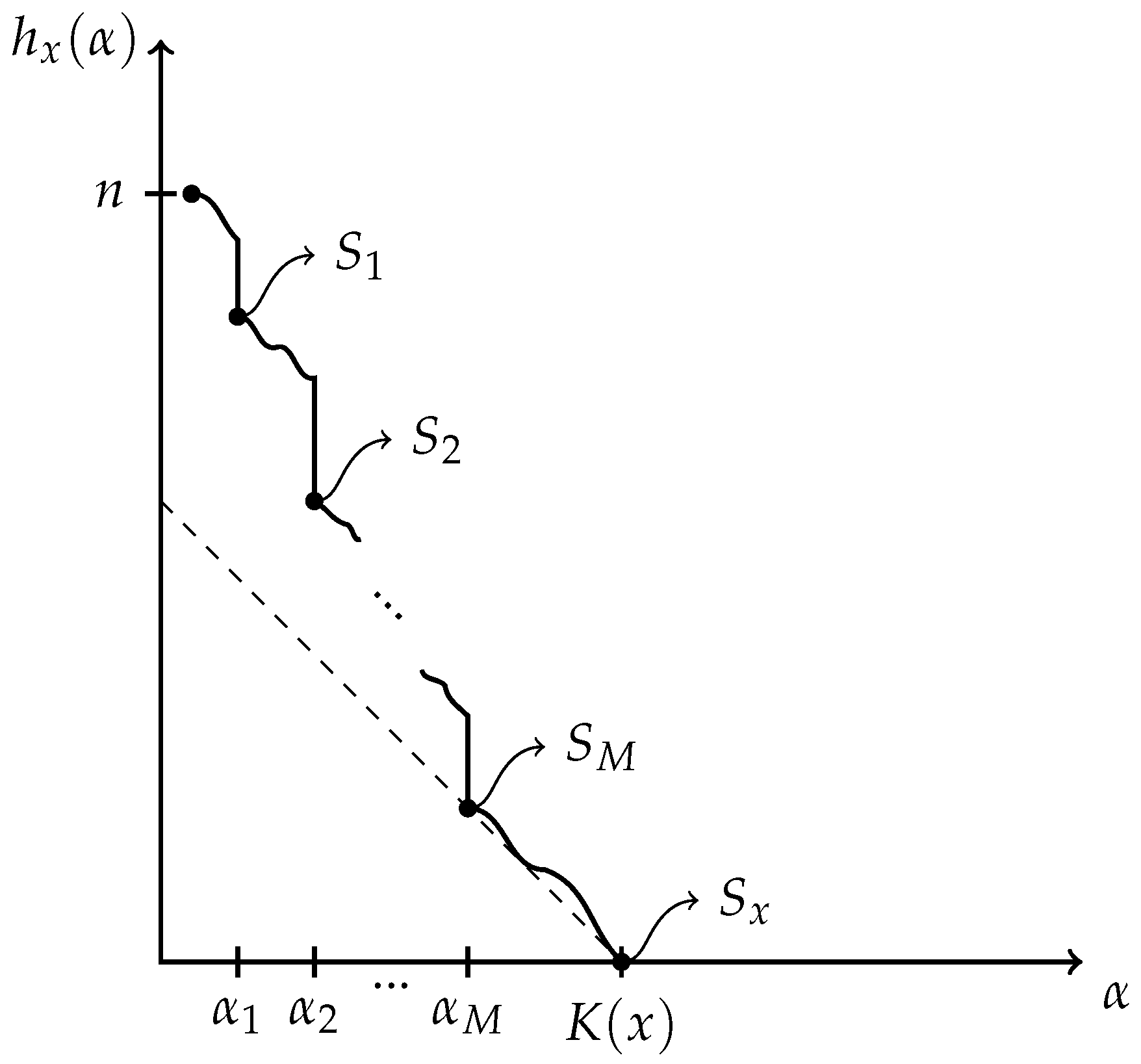
3.2.3. Hierarchy of Minimal Partial Models
3.3. Extending Concepts
3.3.1. A Notion of Coarse-Graining
3.3.2. Boundary Conditions
4. Applications
4.1. Simulation of a 2D Gas Toy Model
4.2. Dynamical Systems
4.2.1. From Integrability to Chaos
4.2.2. Thermodynamics and Statistical Mechanics
5. Conclusions
- The data specifies almost everything about the minimal partial models;
- The magnitude of the drop measures the amount of new understanding;
- More complex minimal partial models specify almost completely the simpler ones.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Technical Precisions
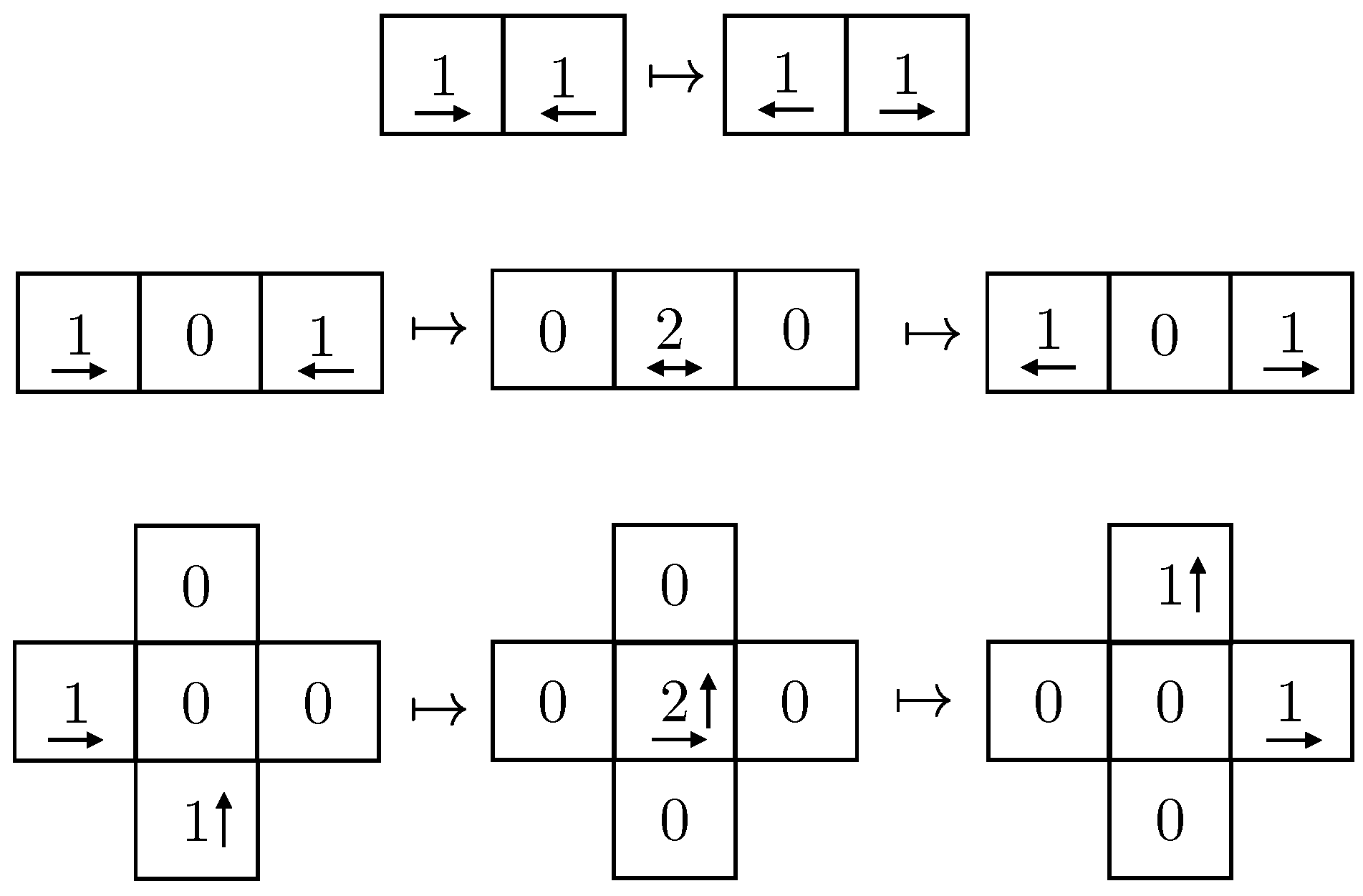
Appendix A.1. Precisions on the First Theorem
Appendix A.2. Precisions on the Second Theorem
Appendix A.3. Precisions on the Third Theorem and Its Proof
References
- Lewes, G.H. Problems of Life and Mind; Facsimile Publisher: London, UK, 1875. [Google Scholar]
- O’Connor, T.; Wong, H.Y. Emergent Properties; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2012. [Google Scholar]
- Bedau, M.A.; Humphreys, P.E. Emergence: Contemporary Readings in Philosophy and Science; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Available online: https://en.wikipedia.org/wiki/Emergence (accessed on 1 September 2021).
- Ross, W.D. Aristotle’s Metaphysics. A Revised Text with Introduction and Commentary; John Murray: London, UK, 1925. [Google Scholar]
- Anderson, P.W. More is different. Science 1972, 177, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Wallace, D. The Emergent Multiverse: Quantum Theory According to the Everett Interpretation; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Dennett, D.C. Real patterns. J. Philos. 1991, 88, 27–51. [Google Scholar] [CrossRef]
- Popper, K. The Logic of Scientific Discovery; Routledge: Thames, UK, 2005. [Google Scholar]
- Gell-Mann, M.; Lloyd, S. Information measures, effective complexity, and total information. Complexity 1996, 2, 44–52. [Google Scholar] [CrossRef]
- Li, M.; Vitányi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Chaitin, G.J. The halting probability omega: Irreducible complexity in pure mathematics. Milan J. Math. 2007, 75, 291–304. [Google Scholar] [CrossRef][Green Version]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Solomonoff, R.J. A formal theory of inductive inference. Part I. Inf. Control 1964, 7, 1–22. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Peredachi Inf. 1965, 1, 3–11. [Google Scholar] [CrossRef]
- Chaitin, G.J. On the length of programs for computing finite binary sequences. J. ACM 1966, 13, 547–569. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Turing, A.M. On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 1937, 2, 230–265. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Talk at the Information Theory Symposium in Tallinn. Estonia (then USSR). 1974. [Google Scholar]
- Vereshchagin, N.; Shen, A. Algorithmic statistics: Forty years later. In Computability and Complexity; Springer: Berlin/Heidelberg, Germany, 2017; pp. 669–737. [Google Scholar]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. A 1922, 222, 309–368. [Google Scholar]
- Antunes, L.; Bauwens, B.; Souto, A.; Teixeira, A. Sophistication vs. Logical Depth. Theory Comput. Syst. 2017, 60, 280–298. [Google Scholar] [CrossRef][Green Version]
- Koppel, M. Complexity, depth, and sophistication. Complex Syst. 1987, 1, 1087–1091. [Google Scholar]
- Vitányi, P.M. Meaningful information. IEEE Trans. Inf. Theory 2006, 52, 4617–4626. [Google Scholar] [CrossRef]
- Bennett, C.H. The thermodynamics of computation—A review. Int. J. Theor. Phys. 1982, 21, 905–940. [Google Scholar] [CrossRef]
- Zurek, W.H. Algorithmic randomness and physical entropy. Phys. Rev. A 1989, 40, 4731. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, J.C. Theory of Heat; Cambridge University Press: Cambridge, UK, 1871. [Google Scholar]
- Jaynes, E.T. The gibbs paradox. In Maximum Entropy and Bayesian Methods; Springer: Berlin/Heidelberg, Germany, 1992; pp. 1–21. [Google Scholar]
- Rosenkrantz, R.D. ET Jaynes: Papers on Probability, Statistics and Statistical Physics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 158. [Google Scholar]
- Baumeler, Ä.; Wolf, S. Causality–Complexity–Consistency: Can space-time be based on logic and computation? In Time in Physics; Springer: Berlin/Heidelberg, Germany, 2017; pp. 69–101. [Google Scholar]
- Ay, N.; Muller, M.; Szkola, A. Effective complexity and its relation to logical depth. IEEE Trans. Inf. Theory 2010, 56, 4593–4607. [Google Scholar] [CrossRef]
- Vereshchagin, N.; Vitányi, P. Kolmogorov’s structure functions with an application to the foundations of model selection. In Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, BC, Canada, 19 November 2002; pp. 751–760. [Google Scholar]
- Gács, P.; Tromp, J.T.; Vitányi, P.M. Algorithmic statistics. IEEE Trans. Inf. Theory 2001, 47, 2443–2463. [Google Scholar] [CrossRef]
- Callen, H.B.; Welton, T.A. Irreversibility and generalized noise. Phys. Rev. 1951, 83, 34. [Google Scholar] [CrossRef]
- Caux, J.S.; Mossel, J. Remarks on the notion of quantum integrability. J. Stat. Mech. Theory Exp. 2011, 2011, P02023. [Google Scholar] [CrossRef]
- Chaitin, G.J. Information-theoretic incompleteness. In Applied Mathematics and Computation; Elsevier: Amsterdam, The Netherlands, 1992; Volume 52, pp. 83–101. [Google Scholar]
- Chaitin, G.J. Meta Maths! The Quest for Omega; Pantheon Books: New York, NY, USA, 2005. [Google Scholar]
- Shen, A.; Uspensky, V.A.; Vereshchagin, N. Kolmogorov Complexity and Algorithmic Randomness; MCCME: Moscow, Russia, 2013. [Google Scholar]
- Bennett, C.H. Logical depth and physical complexity. In The Universal Turing Machine: A Half-Century Survey; Oxford University Press: New York, NY, USA, 1988; pp. 227–257. [Google Scholar]


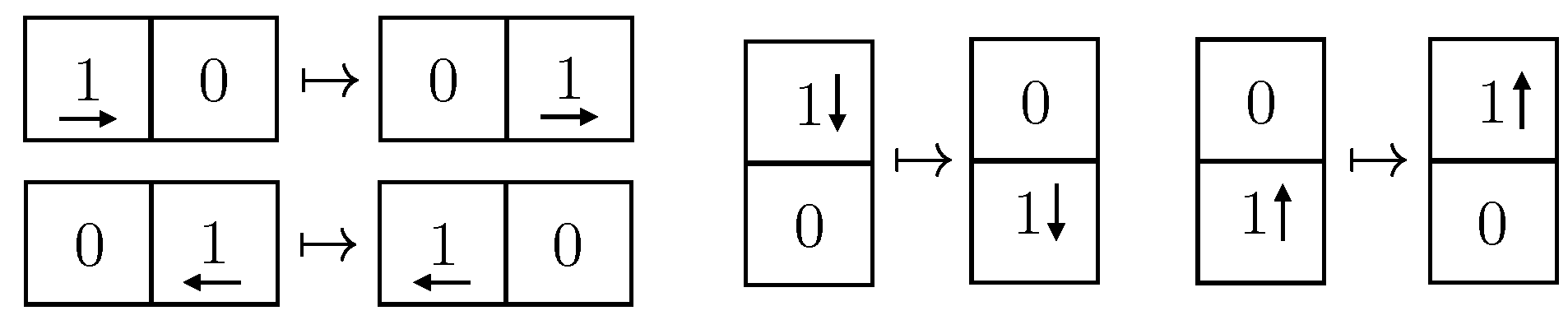




| Model S | Complexity | Cardinality | ||
|---|---|---|---|---|
| Small | Large | n | ||
| Large | Small | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bédard, C.A.; Bergeron, G. An Algorithmic Approach to Emergence. Entropy 2022, 24, 985. https://doi.org/10.3390/e24070985
Bédard CA, Bergeron G. An Algorithmic Approach to Emergence. Entropy. 2022; 24(7):985. https://doi.org/10.3390/e24070985
Chicago/Turabian StyleBédard, Charles Alexandre, and Geoffroy Bergeron. 2022. "An Algorithmic Approach to Emergence" Entropy 24, no. 7: 985. https://doi.org/10.3390/e24070985
APA StyleBédard, C. A., & Bergeron, G. (2022). An Algorithmic Approach to Emergence. Entropy, 24(7), 985. https://doi.org/10.3390/e24070985







