Domain Adaptation with Data Uncertainty Measure Based on Evidence Theory
Abstract
:1. Introduction
- Designing an evidence net based on evidence theory to measure the uncertainty of source domain data about a target domain classification task.
- Designing a general loss function with uncertainty measure for learning of the adaptive classifier.
- Extending the SVM by the general loss function with uncertainty measure for enhancing its transferred performance.
2. Related Work
2.1. Domain Adaptation with Metric Learning
2.2. Learning with Evidence Theory
2.2.1. Mass Function
2.2.2. Dempster’s Rule
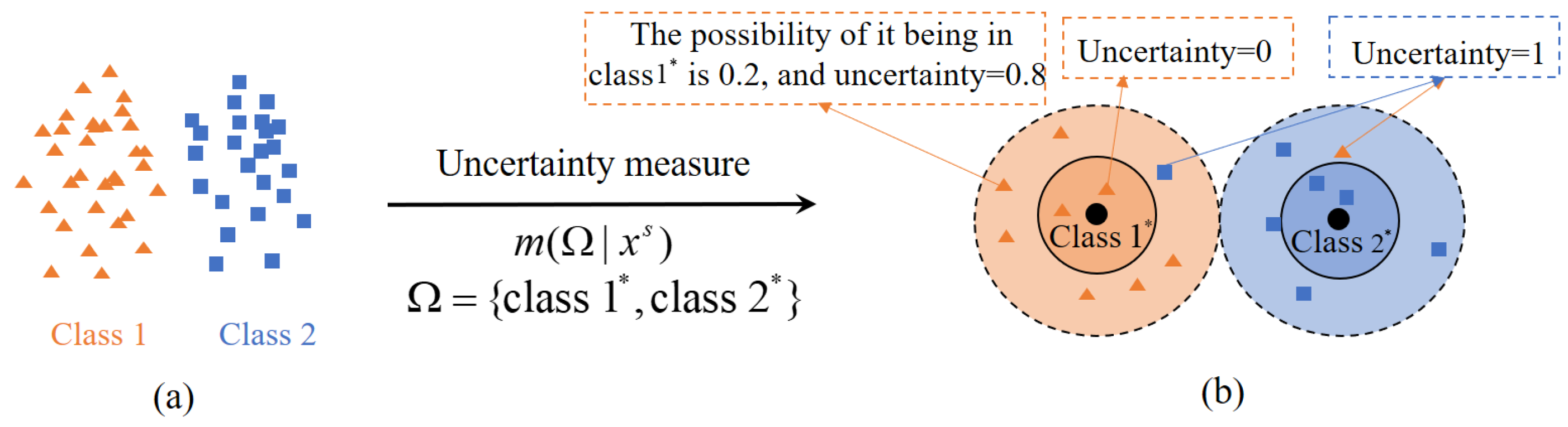
3. Uncertainty Measure in Domain Adaptation Based on Evidence Theory
3.1. Obtaining the Trusty Evidence Set
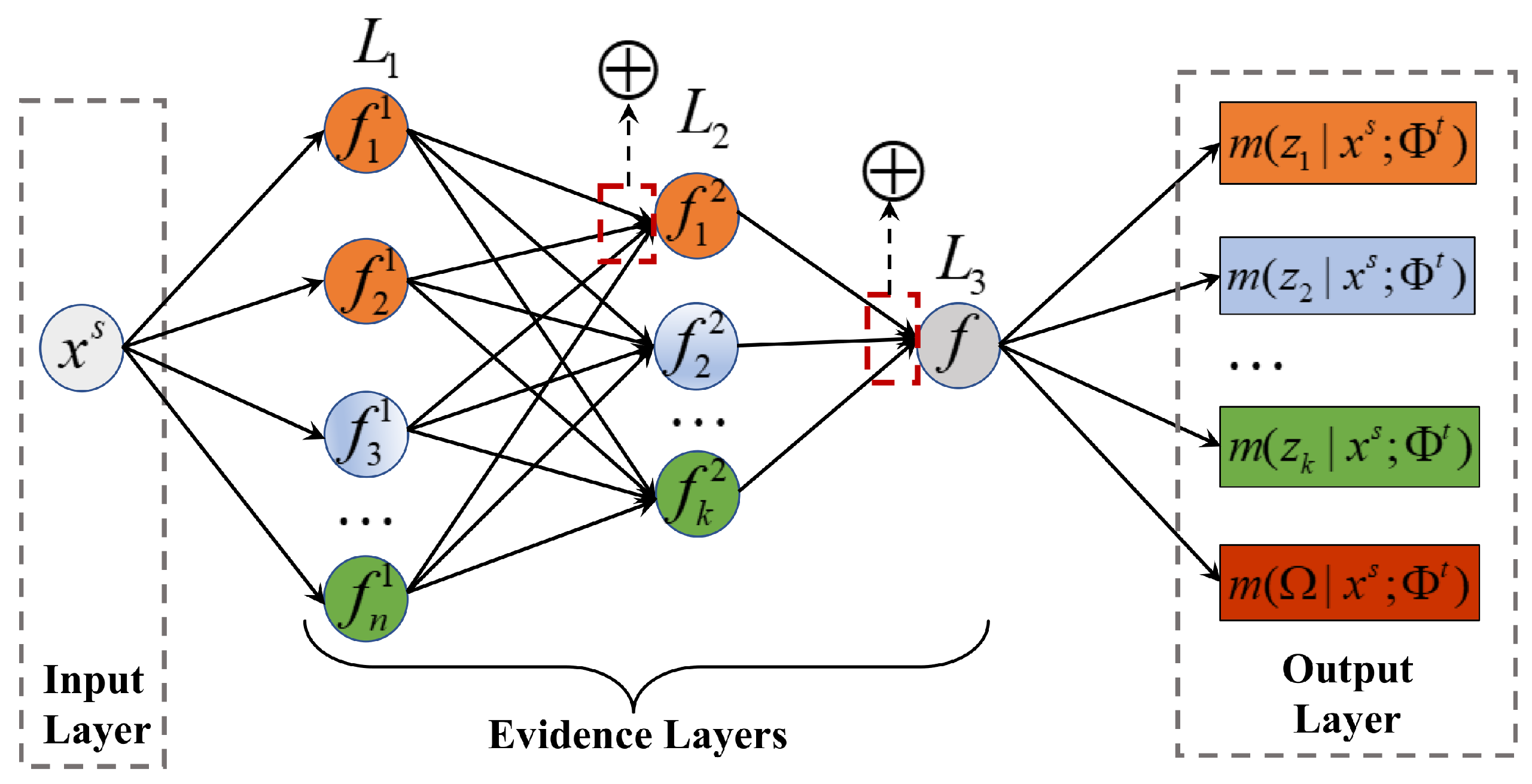
3.2. Constructing Evidence Net Based on Evidence Theory
| Algorithm 1 The uncertainty measure based on evidence net for source domain data |
| Input: source domain , labeled target domain . |
| Output: source domain with uncertainty . |
| 1: for all do |
| 2: Generate an evidence set for according to Equation (9). |
| 3: Estimate uncertainty of based on the evidence net . |
| 4: end for |
| 5: return with . |
4. Learning Algorithm of Adaptive Classifier with Uncertainty Measure
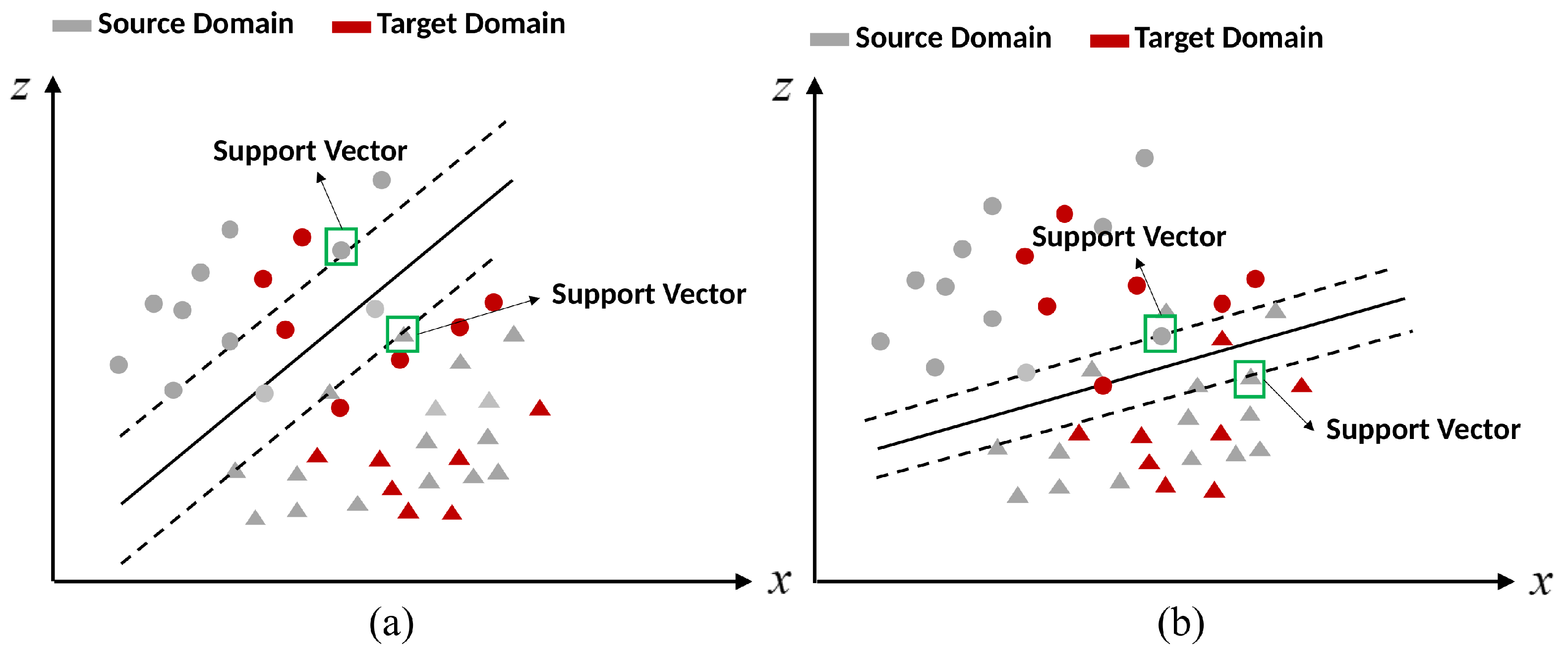
4.1. Support Vector Machine with Uncertainty Measure (SVMU)
5. Experiments
5.1. Comparative Studies
- (1)
- Testing on Amazon product reviews dataset
- (2)
- Testing on Office+Caltech datasets
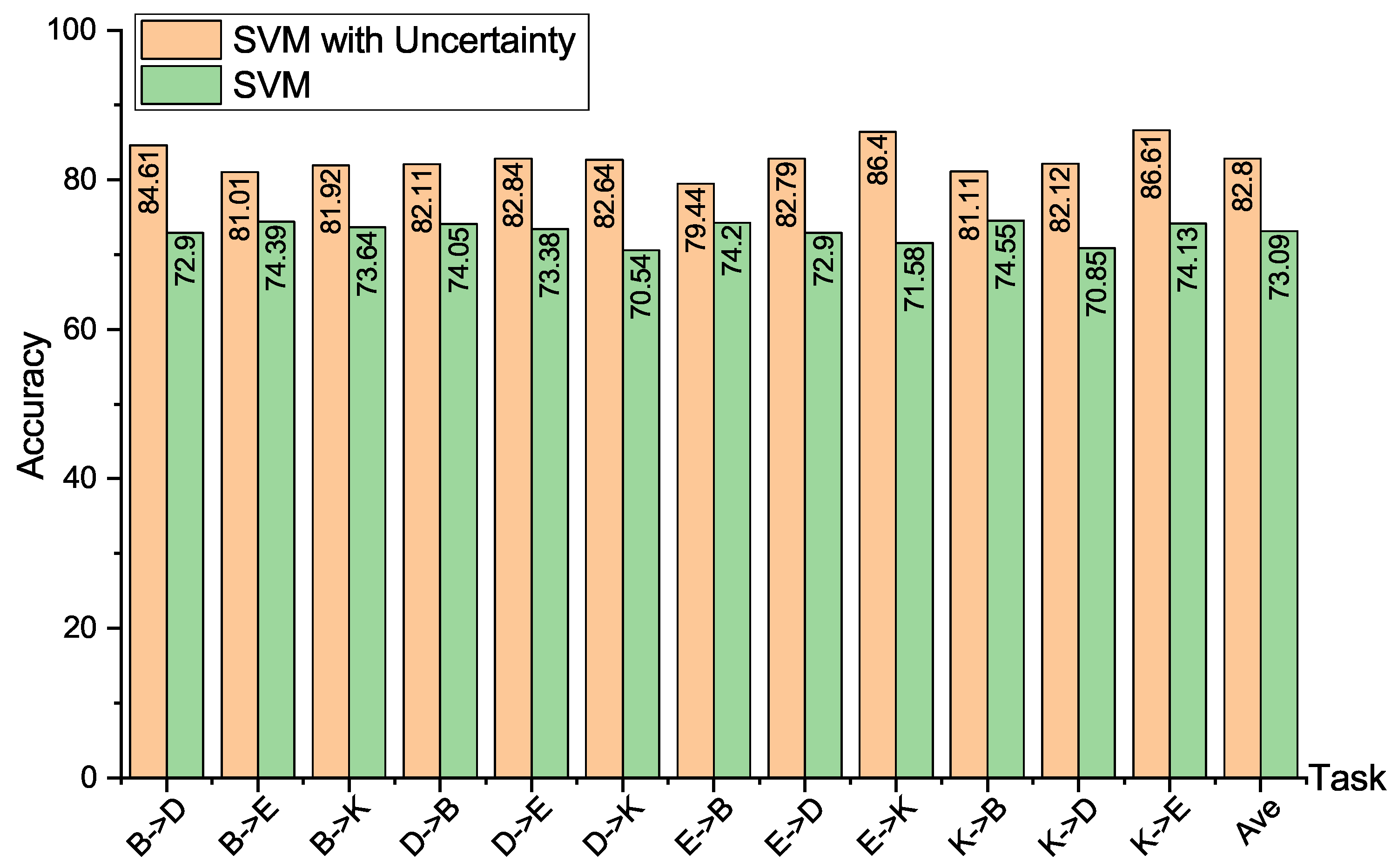
5.2. Effectiveness Verification of Uncertainty Measure
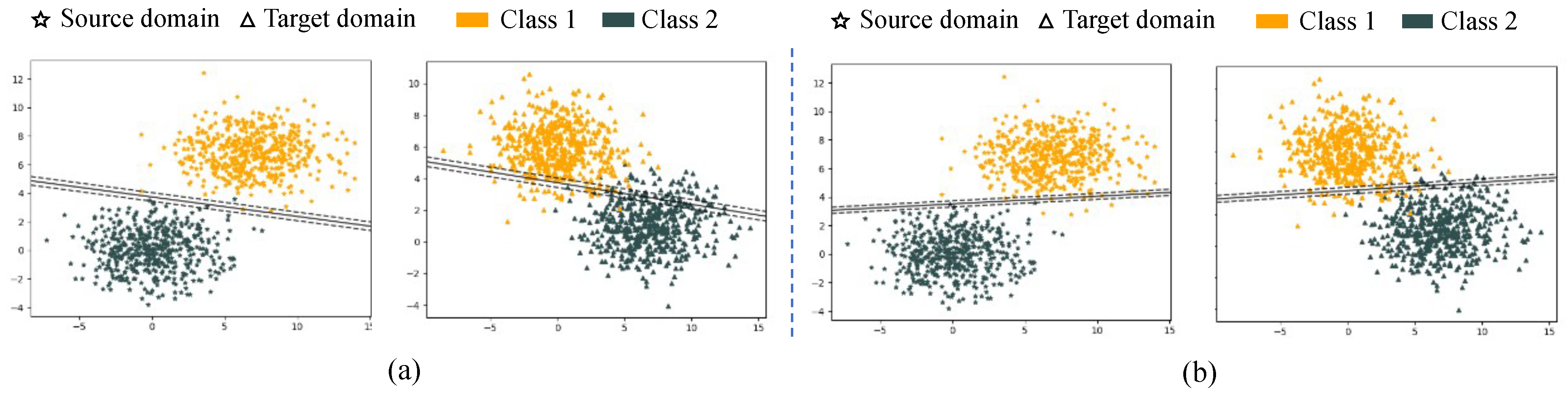
5.2.1. Testing on Synthetic Data
5.2.2. Testing on Real-World Datasets
5.2.3. Case Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Lu, J.; Behbood, V.; Hao, P.; Zuo, H.; Xue, S.; Zhang, G. Transfer learning using computational intelligence: A survey. Knowl.-Based Syst. 2015, 80, 14–23. [Google Scholar] [CrossRef]
- Zhang, L. Transfer adaptation learning: A decade survey. arXiv 2019, arXiv:1903.04687. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Chen, Y.; Li, W.; Sakaridis, C.; Dai, D.; Van Gool, L. Domain adaptive faster r-cnn for object detection in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3339–3348. [Google Scholar]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-fcn: Object detection via region-based fully convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 379–387. [Google Scholar]
- Ye, H.; Tan, Q.; He, R.; Li, J.; Ng, H.T.; Bing, L. Feature adaptation of pre-trained language models across languages and domains for text classification. arXiv 2020, arXiv:2009.11538. [Google Scholar]
- Guo, H.; Pasunuru, R.; Bansal, M. Multi-Source Domain Adaptation for Text Classification via DistanceNet-Bandits. In Proceedings of the AAAI, New York, NY, USA, 7–12 February 2020; pp. 7830–7838. [Google Scholar]
- Apostolopoulos, I.D.; Mpesiana, T.A. COVID-19: Automatic detection from x-ray images utilizing transfer learning with convolutional neural networks. Phys. Eng. Sci. Med. 2020, 43, 635–640. [Google Scholar] [CrossRef] [Green Version]
- Raghu, M.; Zhang, C.; Kleinberg, J.; Bengio, S. Transfusion: Understanding transfer learning for medical imaging. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 3347–3357. [Google Scholar]
- Zhao, H.; Hu, J.; Risteski, A. On learning language-invariant representations for universal machine translation. arXiv 2020, arXiv:2008.04510. [Google Scholar]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 2010, 22, 199–210. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Feng, J.; Saenko, K. Return of frustratingly easy domain adaptation. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Ghifary, M.; Balduzzi, D.; Kleijn, W.B.; Zhang, M. Scatter Component Analysis: A Unified Framework for Domain Adaptation and Domain Generalization. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1414–1430. [Google Scholar] [CrossRef] [Green Version]
- Long, M.; Zhu, H.; Wang, J.; Jordan, M.I. Deep transfer learning with joint adaptation networks. In Proceedings of the International Conference on Machine Learning. PMLR, Sydney, Australia, 6–11 August 2017; pp. 2208–2217. [Google Scholar]
- Wang, J.; Feng, W.; Chen, Y.; Yu, H.; Huang, M.; Yu, P.S. Visual domain adaptation with manifold embedded distribution alignment. In Proceedings of the 26th ACM international conference on Multimedia, Seoul, Korea, 22–26 October 2018; pp. 402–410. [Google Scholar]
- Zhu, Y.; Zhuang, F.; Wang, J.; Chen, J.; Shi, Z.; Wu, W.; He, Q. Multi-representation adaptation network for cross-domain image classification. Neural Netw. 2019, 119, 214–221. [Google Scholar] [CrossRef]
- Bielza, C.; Larranaga, P. Discrete Bayesian network classifiers: A survey. ACM Comput. Surv. (CSUR) 2014, 47, 1–43. [Google Scholar] [CrossRef]
- Shafer, G. A mathematical theory of evidence turns 40. Int. J. Approx. Reason. 2016, 79, 7–25. [Google Scholar] [CrossRef]
- Principe, J.C.; Xu, D.; Fisher, J.; Haykin, S. Information theoretic learning. Unsupervised Adapt. Filter. 2000, 1, 265–319. [Google Scholar]
- Zadeh, L.A.; Klir, G.J.; Yuan, B. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers; World Scientific: Singapore, 1996; Volume 6. [Google Scholar]
- Denoeux, T. A k-nearest neighbor classification rule based on Dempster-Shafer theory. In Classic Works of the Dempster-Shafer Theory of Belief Functions; Springer: Berlin/Heidelberg, Germany, 2008; pp. 737–760. [Google Scholar]
- Su, Z.; Hu, Q.; Denaeux, T. A distributed rough evidential K-NN classifier: Integrating feature reduction and classification. IEEE Trans. Fuzzy Syst. 2020, 29, 2322–2335. [Google Scholar] [CrossRef]
- Quost, B.; Denœux, T.; Li, S. Parametric classification with soft labels using the evidential EM algorithm: Linear discriminant analysis versus logistic regression. Adv. Data Anal. Classif. 2017, 11, 659–690. [Google Scholar] [CrossRef] [Green Version]
- Denoeux, T. Logistic regression, neural networks and Dempster–Shafer theory: A new perspective. Knowl.-Based Syst. 2019, 176, 54–67. [Google Scholar] [CrossRef] [Green Version]
- Denoeux, T.; Sriboonchitta, S.; Kanjanatarakul, O. Evidential clustering of large dissimilarity data. Knowl.-Based Syst. 2016, 106, 179–195. [Google Scholar] [CrossRef] [Green Version]
- Borgwardt, K.M.; Gretton, A.; Rasch, M.J.; Kriegel, H.P.; Schölkopf, B.; Smola, A.J. Integrating structured biological data by kernel maximum mean discrepancy. Bioinformatics 2006, 22, e49–e57. [Google Scholar] [CrossRef] [Green Version]
- Long, M.; Wang, J.; Ding, G.; Sun, J.; Yu, P.S. Transfer feature learning with joint distribution adaptation. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2200–2207. [Google Scholar]
- Ghifary, M.; Kleijn, W.B.; Zhang, M. Domain adaptive neural networks for object recognition. In Proceedings of the Pacific Rim International Conference on Artificial Intelligence, Gold Coast, QLD, Australia, 1–5 December 2014; pp. 898–904. [Google Scholar]
- Long, M.; Wang, J.; Ding, G.; Pan, S.J.; Philip, S.Y. Adaptation regularization: A general framework for transfer learning. IEEE Trans. Knowl. Data Eng. 2013, 26, 1076–1089. [Google Scholar] [CrossRef]
- Yan, H.; Ding, Y.; Li, P.; Wang, Q.; Xu, Y.; Zuo, W. Mind the class weight bias: Weighted maximum mean discrepancy for unsupervised domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2272–2281. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Dai, W.; Xue, G.R.; Yang, Q.; Yu, Y. Co-clustering based classification for out-of-domain documents. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, VA, USA; 2007; pp. 210–219. [Google Scholar]
- Dai, W.; Yang, Q.; Xue, G.R.; Yu, Y. Self-taught clustering. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 200–207. [Google Scholar]
- Zhuang, F.; Cheng, X.; Luo, P.; Pan, S.J.; He, Q. Supervised representation learning: Transfer learning with deep autoencoders. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Giles, J.; Ang, K.K.; Mihaylova, L.S.; Arvaneh, M. A Subject-to-subject Transfer Learning Framework Based on Jensen-shannon Divergence for Improving Brain-computer Interface. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 3087–3091. [Google Scholar]
- Dey, S.; Madikeri, S.; Motlicek, P. Information theoretic clustering for unsupervised domain-adaptation. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2016; pp. 5580–5584. [Google Scholar]
- Shen, J.; Qu, Y.; Zhang, W.; Yu, Y. Wasserstein Distance Guided Representation Learning for Domain Adaptation. In Proceedings of the AAAI, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Lee, C.Y.; Batra, T.; Baig, M.H.; Ulbricht, D. Sliced wasserstein discrepancy for unsupervised domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10285–10295. [Google Scholar]
- Dempster, A.P. Upper and lower probabilities generated by a random closed interval. Ann. Math. Stat. 1968, 39, 957–966. [Google Scholar] [CrossRef]
- Walley, P. Belief function representations of statistical evidence. Ann. Stat. 1987, 15, 1439–1465. [Google Scholar] [CrossRef]
- Denœux, T. Reasoning with imprecise belief structures. Int. J. Approx. Reason. 1999, 20, 79–111. [Google Scholar] [CrossRef]
- Blitzer, J.; Dredze, M.; Pereira, F. Biographies, bollywood, boom-boxes and blenders: Domain adaptation for sentiment classification. In Proceedings of the 45th Annual Meeting of the Association of Computational Linguistics, Prague, Czech Republic, 23–30 June 2007; pp. 440–447. [Google Scholar]
- Gong, B.; Shi, Y.; Sha, F.; Grauman, K. Geodesic flow kernel for unsupervised domain adaptation. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2066–2073. [Google Scholar]
- Huang, J.; Gretton, A.; Borgwardt, K.M.; Schölkopf, B.; Smola, A.J. Correcting Sample Selection Bias by Unlabeled Data. Adv. Neural Inf. Process. Syst. 2006, 19, 601–608. [Google Scholar]
- Xu, Y.; Pan, S.J.; Xiong, H.; Wu, Q.; Luo, R.; Min, H.; Song, H. A Unified Framework for Metric Transfer Learning. IEEE Trans. Knowl. Data Eng. 2017, 29, 1158–1171. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Yu, H.; Huang, M.; Yang, Q. Easy Transfer Learning By Exploiting Intra-Domain Structures. In Proceedings of the 2019 IEEE International Conference on Multimedia and Expo (ICME), Shanghai, China, 8–12 July 2019; pp. 1210–1215. [Google Scholar]

| Task | SVMU | TCA | CORAL | GFK | JDA | KMM | MTLF | SCA | EasyTL | WDGAL |
|---|---|---|---|---|---|---|---|---|---|---|
| 84.61 | 77.76 | 70.76 | 75.76 | 77.26 | 83.76 | 68.59 | 81.56 | 79.80 | 83.05 | |
| 81.01 | 75.54 | 66.21 | 72.00 | 75.93 | 79.02 | 69.63 | 78.08 | 79.70 | 80.09 | |
| 81.92 | 78.74 | 70.00 | 73.50 | 78.09 | 75.90 | 72.74 | 79.09 | 80.90 | 85.45 | |
| 82.11 | 76.05 | 73.05 | 71.85 | 77.65 | 80.50 | 70.70 | 82.35 | 79.90 | 80.72 | |
| 82.84 | 76.38 | 68.70 | 68.96 | 76.03 | 68.51 | 71.90 | 78.82 | 80.80 | 82.26 | |
| 82.64 | 79.34 | 71.96 | 75.70 | 78.29 | 76.45 | 74.18 | 80.39 | 82.00 | 85.23 | |
| 79.44 | 73.35 | 69.90 | 72.60 | 72.65 | 73.70 | 69.20 | 77.00 | 75.00 | 77.22 | |
| 82.79 | 73.66 | 65.71 | 71.11 | 72.16 | 77.86 | 70.73 | 77.26 | 75.30 | 78.28 | |
| 86.40 | 79.74 | 72.35 | 76.20 | 80.14 | 80.39 | 71.36 | 84.63 | 84.90 | 88.16 | |
| 81.11 | 73.05 | 67.45 | 73.75 | 75.05 | 74.25 | 66.04 | 78.90 | 76.50 | 77.16 | |
| 82.12 | 77.26 | 68.61 | 74.21 | 77.56 | 75.96 | 70.31 | 77.46 | 76.30 | 78.89 | |
| 86.61 | 78.74 | 75.68 | 76.58 | 80.32 | 85.00 | 68.58 | 85.65 | 82.50 | 86.29 | |
| Average | 82.80 | 76.63 | 70.03 | 73.52 | 76.76 | 77.61 | 70.33 | 80.10 | 79.47 | 81.90 |
| Task | SVMU | TCA | CORAL | GFK | JDA | KMM | MTLF | SCA | EasyTL |
|---|---|---|---|---|---|---|---|---|---|
| 51.55 | 47.76 | 45.37 | 40.25 | 49.36 | 45.41 | 45.37 | 48.29 | 43.01 | |
| 44.31 | 41.12 | 43.75 | 43.31 | 42.49 | 41.40 | 41.38 | 44.21 | 45.85 | |
| 47.28 | 44.63 | 44.78 | 43.98 | 45.97 | 42.85 | 42.59 | 43.90 | 40.68 | |
| 63.29 | 58.20 | 53.59 | 51.20 | 54.78 | 50.10 | 54.17 | 53.74 | 50.10 | |
| 44.00 | 41.40 | 46.22 | 42.85 | 43.22 | 43.58 | 40.69 | 39.49 | 48.41 | |
| 46.44 | 42.64 | 43.73 | 40.68 | 41.69 | 43.81 | 46.10 | 43.56 | 42.49 | |
| 63.29 | 52.15 | 58.81 | 52.05 | 53.09 | 58.60 | 59.92 | 57.72 | 61.94 | |
| 51.33 | 49.70 | 48.01 | 48.28 | 45.52 | 47.81 | 45.73 | 50.32 | 51.17 | |
| 46.44 | 46.10 | 44.40 | 45.59 | 43.49 | 44.45 | 43.50 | 42.81 | 44.49 | |
| 63.29 | 58.06 | 56.20 | 59.75 | 56.78 | 52.15 | 51.07 | 60.48 | 60.18 | |
| 51.22 | 45.30 | 42.08 | 48.72 | 49.17 | 49.81 | 49.38 | 50.63 | 49.65 | |
| 47.77 | 43.26 | 44.08 | 40.89 | 46.17 | 45.62 | 44.76 | 46.36 | 47.07 | |
| Average | 51.68 | 47.52 | 47.58 | 46.46 | 47.64 | 47.13 | 47.05 | 48.45 | 48.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Y.; Zhang, B.; Zou, G.; Yue, X.; Xu, Z.; Li, H. Domain Adaptation with Data Uncertainty Measure Based on Evidence Theory. Entropy 2022, 24, 966. https://doi.org/10.3390/e24070966
Lv Y, Zhang B, Zou G, Yue X, Xu Z, Li H. Domain Adaptation with Data Uncertainty Measure Based on Evidence Theory. Entropy. 2022; 24(7):966. https://doi.org/10.3390/e24070966
Chicago/Turabian StyleLv, Ying, Bofeng Zhang, Guobing Zou, Xiaodong Yue, Zhikang Xu, and Haiyan Li. 2022. "Domain Adaptation with Data Uncertainty Measure Based on Evidence Theory" Entropy 24, no. 7: 966. https://doi.org/10.3390/e24070966
APA StyleLv, Y., Zhang, B., Zou, G., Yue, X., Xu, Z., & Li, H. (2022). Domain Adaptation with Data Uncertainty Measure Based on Evidence Theory. Entropy, 24(7), 966. https://doi.org/10.3390/e24070966






