Nonlinear Analysis of Rotational Springs to Model Semi-Rigid Frames
Abstract
:1. Introduction
2. Materials and Methods
2.1. Problem-Solving Strategy
2.2. Obtaintion of the Vector of Internal Forces from Its Analytic Expression
- (1)
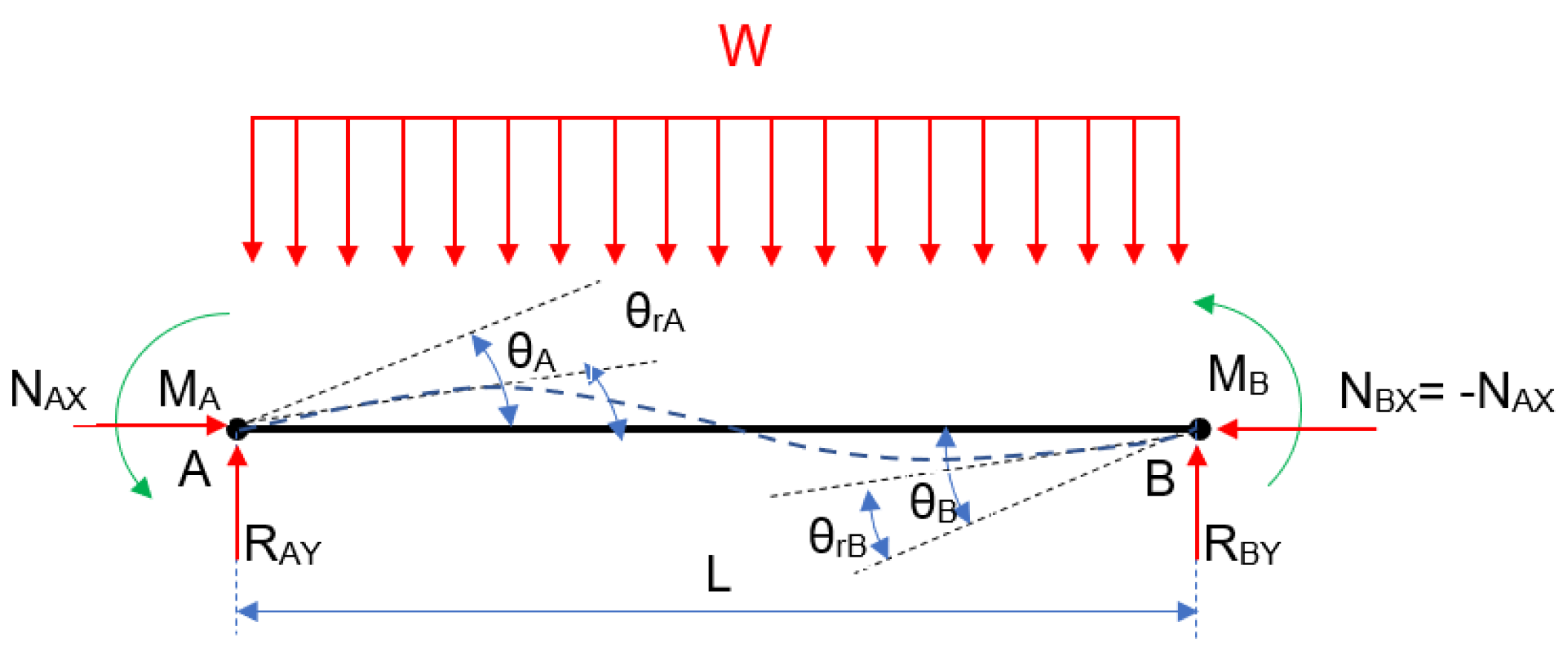
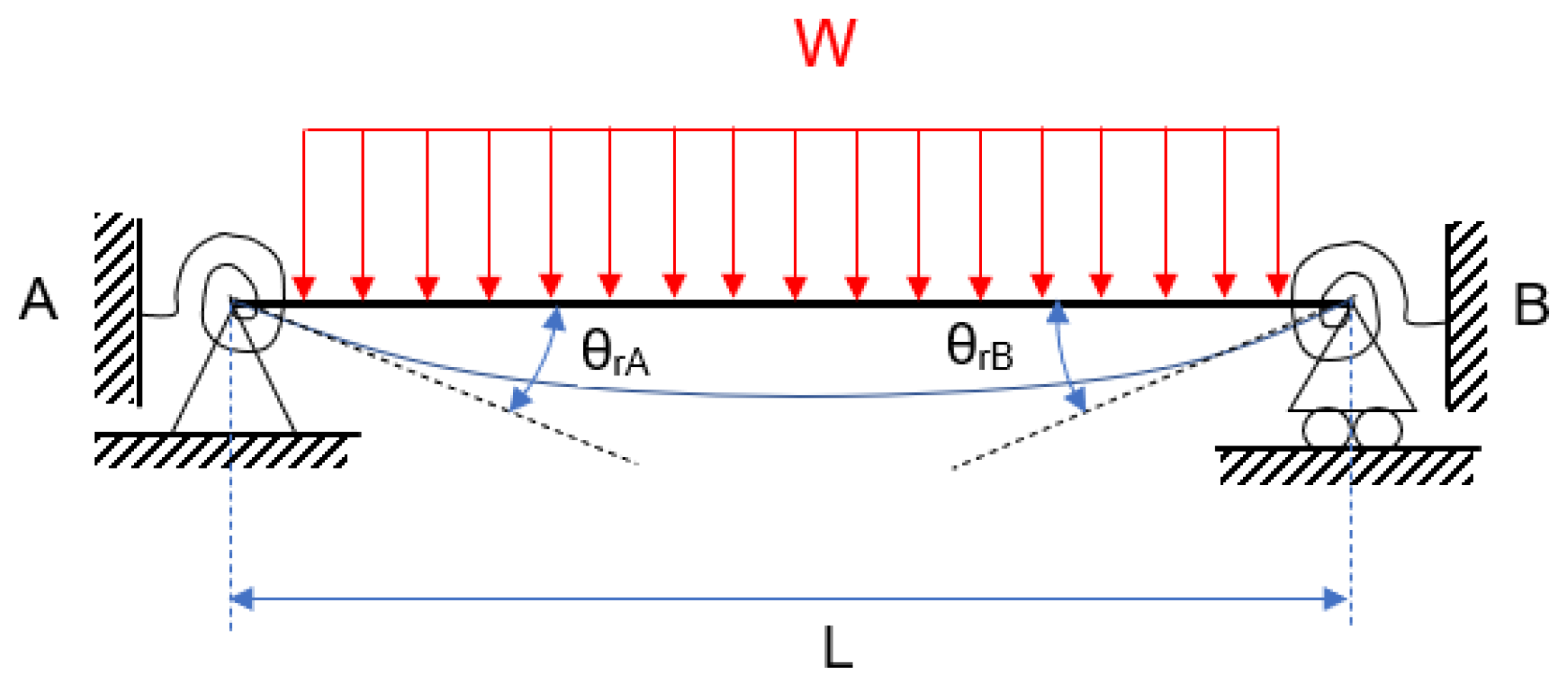
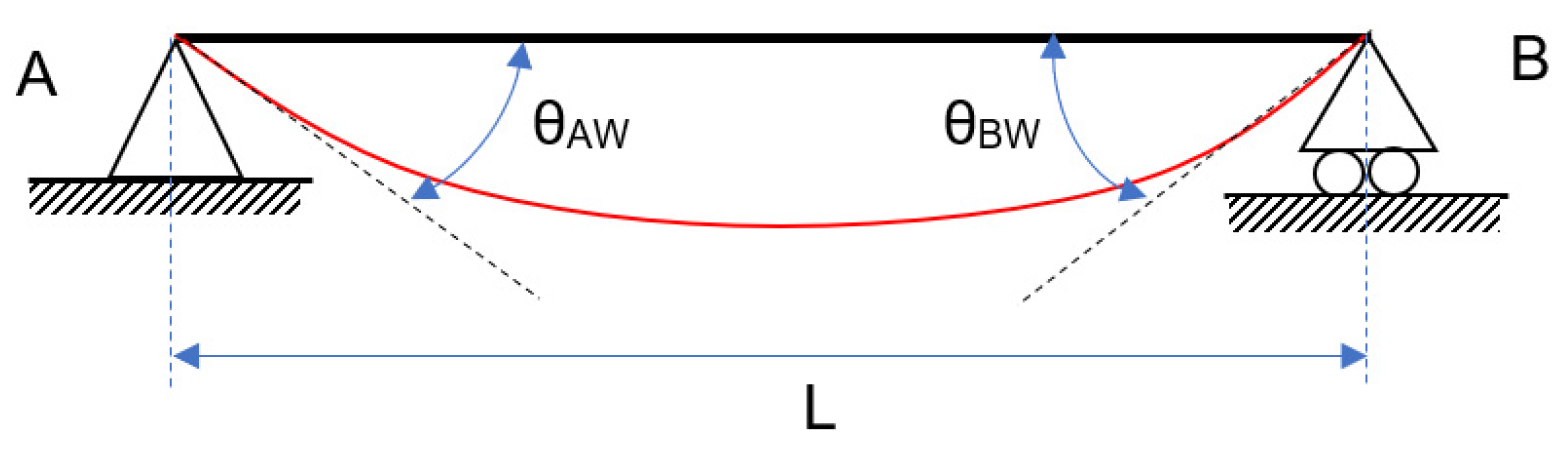
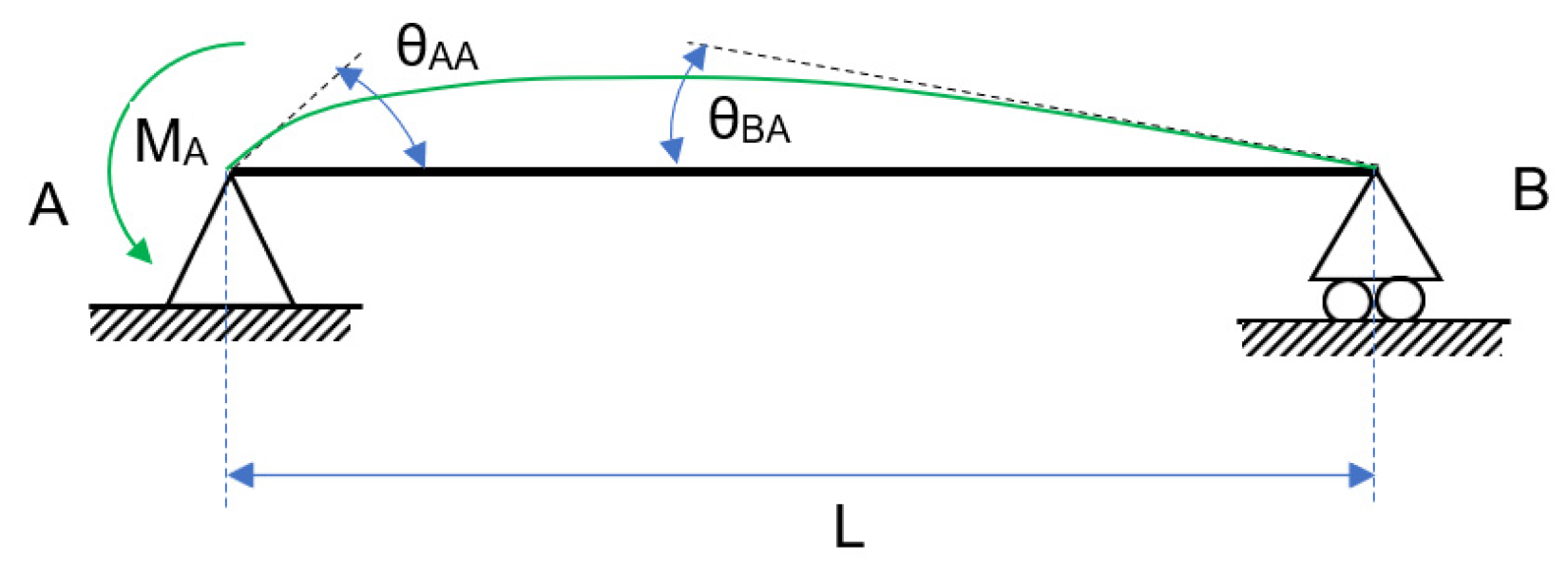
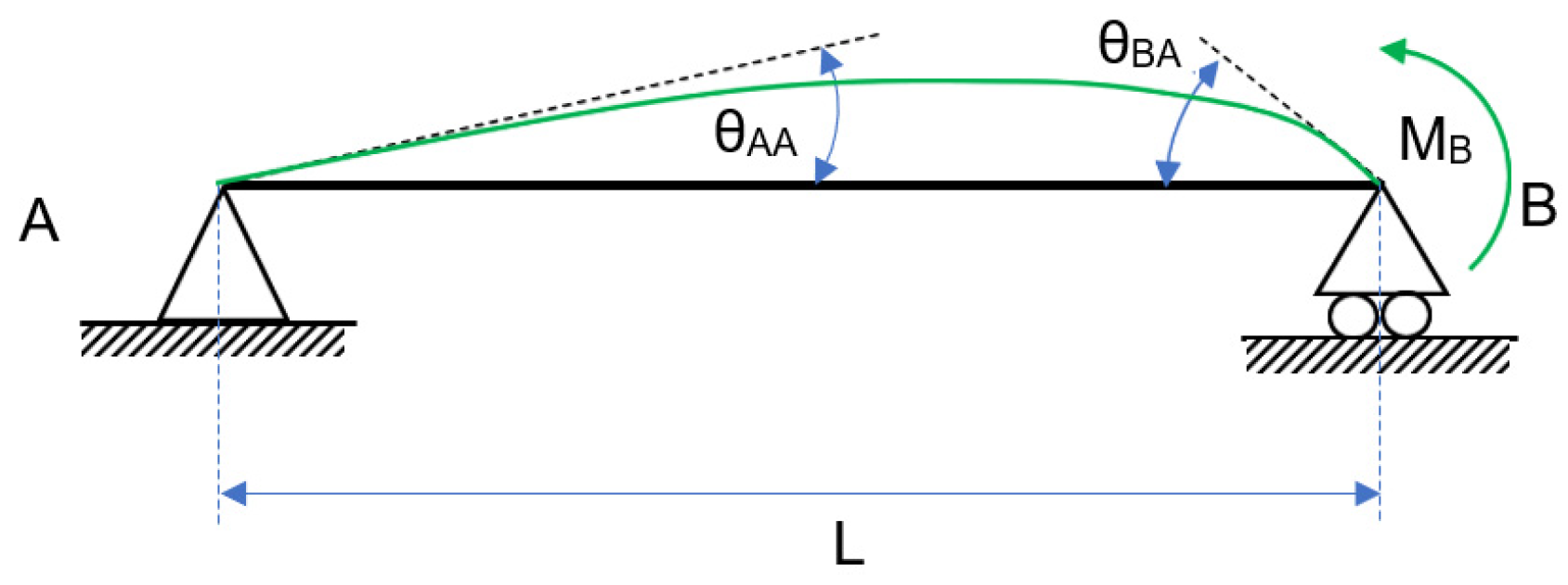
- Composition and resolution of the free-body diagram of a semi-rigid beam without the P effect, as well as the determination of bending moments and strains;
- (2)
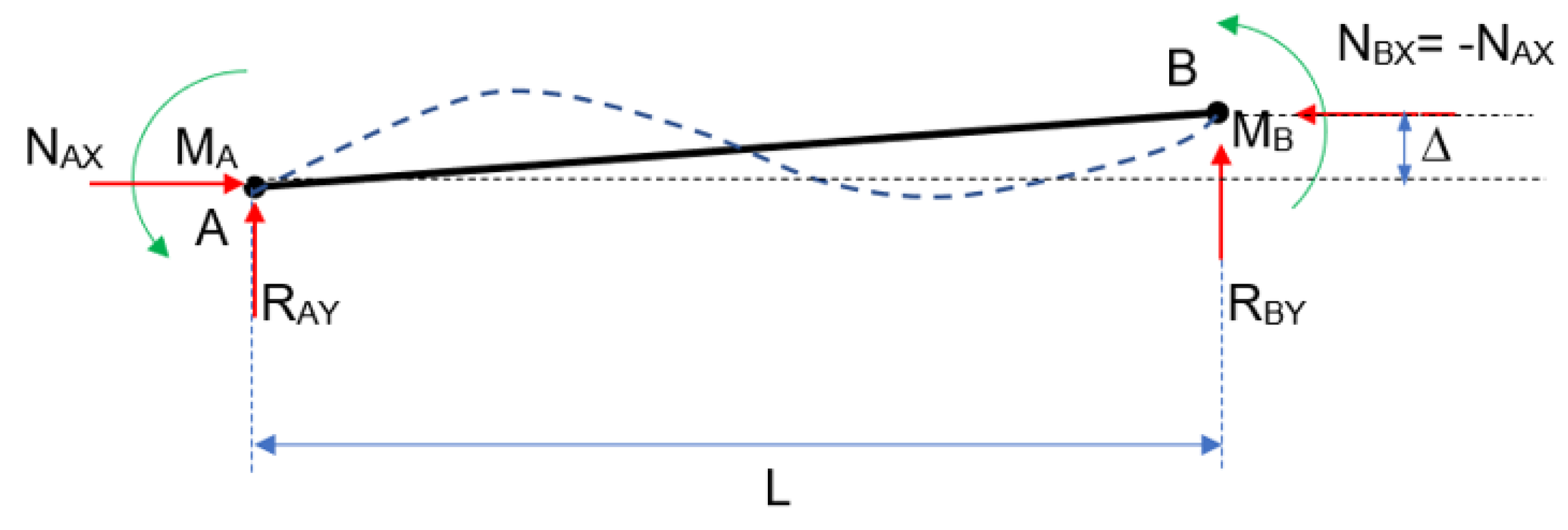
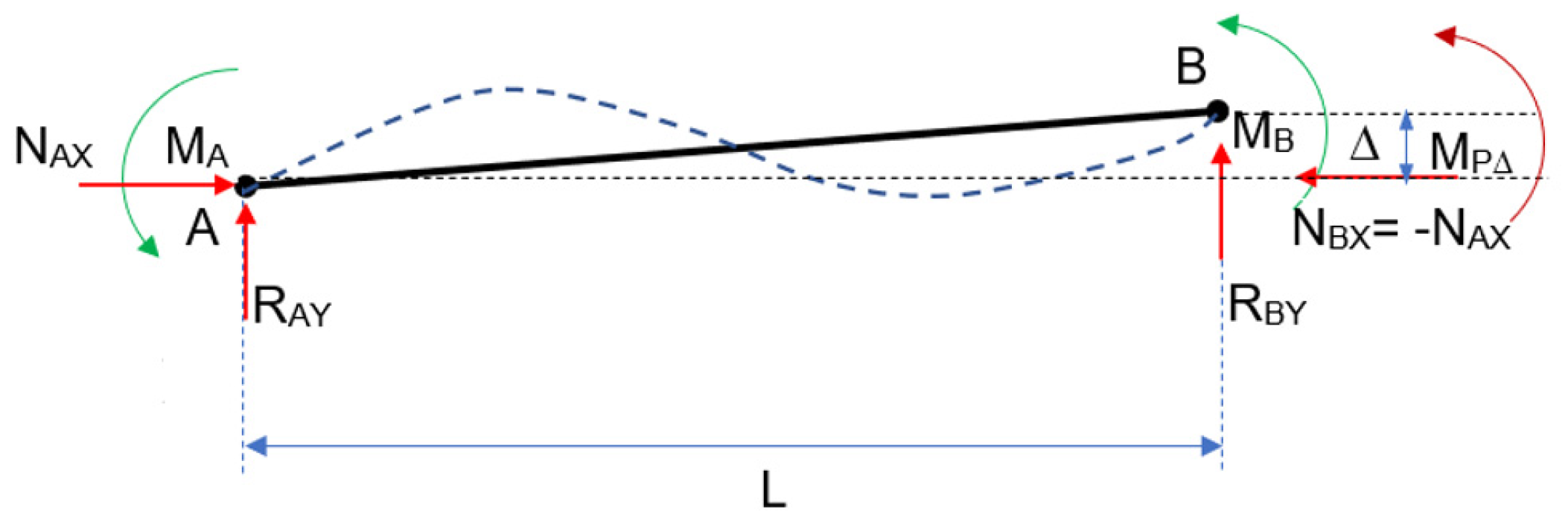
- Composition and resolution of the free-body diagram of a semi-rigid beam including the P effect, and the indirect methodology to include the strains in the forces vector from the stiffness matrix;
- (3)
- Define the vector of internal forces according to one or more element displacements and a recalculation of the vector of forces based on the results of point (2) using the elemental stiffness matrix.
2.3. Definition of the Tangent Stiffness Matrix
2.4. No-Linear Rotary Spring Adjustment
- (1)
- Identifying the relative rotation generated by the springs (theta_r_observada, ec. 3 a 5);
- (2)
- Obtaining the tangent stiffness matrix of each spring through derivation according to the increments in moment Mr(A) y Mr(B);
- (3)
- Define the reminder as the difference between the observed and the calculated rotation;
- (4)
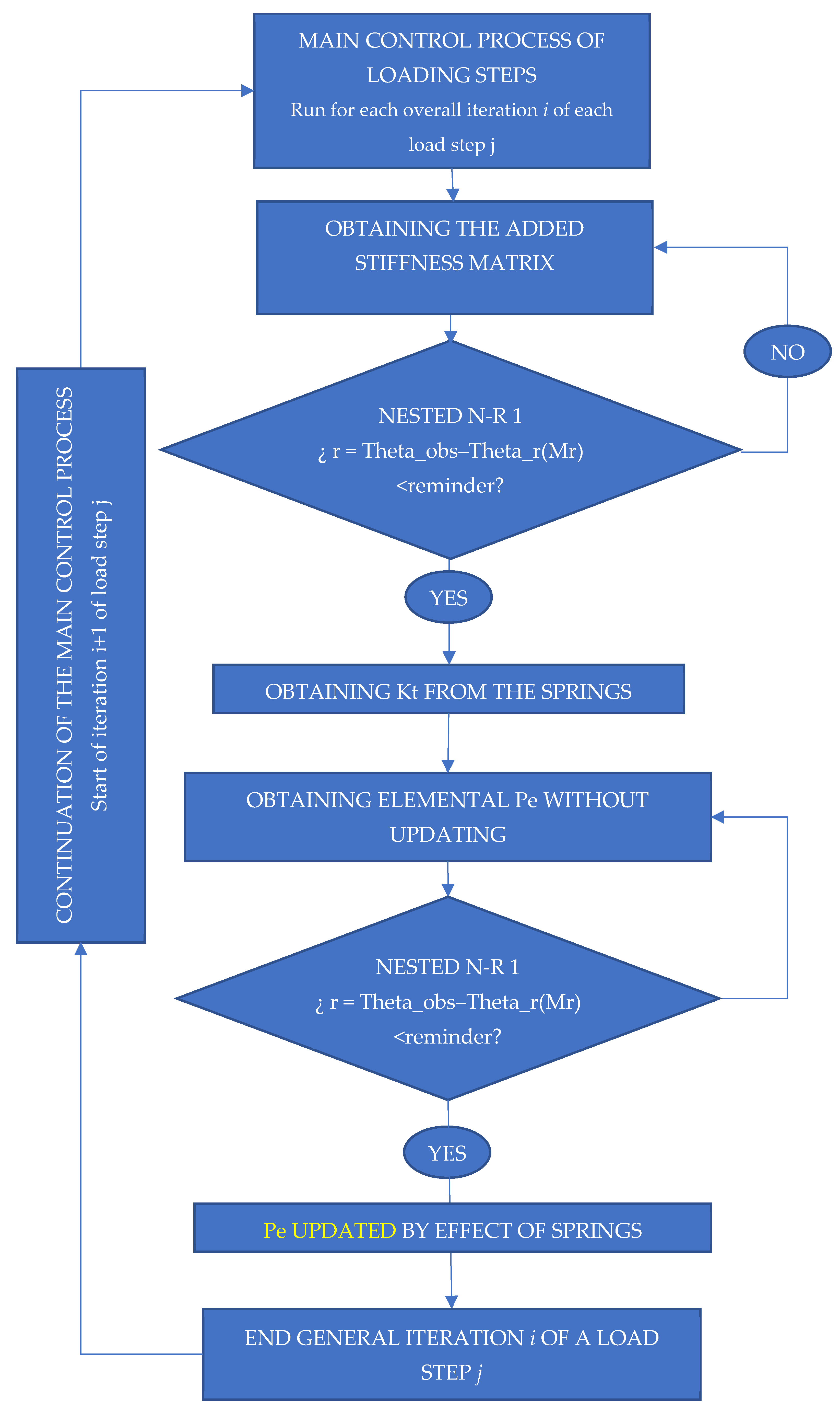
- The results of stiffness for the springs are obtained by several iterations, for a generic iteration i of the loading dock j. The primary control method that oversees the process specifies the loading steps;
- (5)
- Once the Kt of each spring has been determined, the elemental stiffness may be calculated. Without updating, a Pe is obtained. With this Kt, a vector of internal forces Pe is obtained, which has been updated due to the springs’ effect. This is now performed for each general iteration i of the loading process j.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rigi, A.; JavidSharifi, B.; Hadianfard, M.A.; Yang, T. Study of the seismic behavior of rigid and semi-rigid steel moment-resisting frames. J. Constr. Steel Res. 2021, 186, 106910. [Google Scholar] [CrossRef]
- Sharma, V.; Shrimali, M.K.; Bharti, S.D.; Datta, T.K. Behavior of semi-rigid steel frames under near-and far-field earthquakes. Steel Compos. Struct. Int. J. 2020, 34, 625–641. [Google Scholar]
- Azizinamini, A.; Radziminski, J.B. Static and Cyclic Performance of Semirigid Steel Beam-to-Column Connections. J. Struct. Eng. 1989, 115, 2979–2999. [Google Scholar] [CrossRef]
- Elnashai, A.S.; Elghazouli, A.Y.; Denesh-Ashtiani, F.A. Response of Semirigid Steel Frames to Cyclic and Earthquake Loads. J. Struct. Eng. 1998, 124, 857–867. [Google Scholar] [CrossRef]
- Nguyen, P.-C.; Kim, S.-E. Second-order spread-of-plasticity approach for nonlinear time-history analysis of space semi-rigid steel frames. Finite Elem. Anal. Des. 2015, 105, 1–15. [Google Scholar] [CrossRef]
- Soriano-Heras, E.; Rubio, H.; Bustos, A.; Castejon, C. Mathematical Analysis of the Process Forces Effect on Collet Chuck Holders. Mathematics 2021, 9, 492. [Google Scholar] [CrossRef]
- Bandyopadhyay, M.; Banik, A.K.; Datta, T.K. Numerical Modeling of Compound Element for Static Inelastic Analysis of Steel Frames with Semi-rigid Connections; Springer: New Delhi, India, 2014; pp. 543–558. [Google Scholar] [CrossRef]
- Faridmehr, I.; Tahir, M.; Lahmer, T. Classification System for Semi-Rigid Beam-to-Column Connections. Lat. Am. J. Solids Struct. 2016, 13, 2152–2175. [Google Scholar] [CrossRef] [Green Version]
- Chajes, A.; Churchill, J.E. Nonlinear Frame Analysis by Finite Element Methods. J. Struct. Eng. 1987, 113, 1221–1235. [Google Scholar] [CrossRef]
- Dhillon, B.S.; O’Malley, J.W., III. Interactive design of semirigid steel frames. J. Struct. Eng. 1999, 125, 556–564. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A. Analytical Solution of Sloshing in a Cylindrical Tank with an Elastic Cover. Mathematics 2019, 7, 1070. [Google Scholar] [CrossRef] [Green Version]
- Chan, S.L.; Chui, P.T. (Eds.) Non-Linear Static and Cyclic Analysis of Steel Frames with Semi-Rigid Connections; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Koriga, S.; Ihaddoudene, A.; Saidani, M. Numerical model for the non-linear dynamic analysis of multi-storey structures with semi-rigid joints with specific reference to the Algerian code. Structures 2019, 19, 184–192. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, H.; Liang, B.; Sun, Q. Semi-rigid beam element model for progressive collapse analysis of steel frame structures. Proc. Inst. Civ. Eng.-Struct. Build. 2019, 172, 113–126. [Google Scholar] [CrossRef]
- Hou, R.; Beck, J.L.; Zhou, X.; Xia, Y. Structural damage detection of space frame structures with semi-rigid connections. Eng. Struct. 2021, 235, 112029. [Google Scholar] [CrossRef]
- Frye, M.J.; Morris, G.A. Analysis of Flexibly Connected Steel Frames. Can. J. Civ. Eng. 1975, 2, 280–291. [Google Scholar] [CrossRef]
- Degertekin, S.O.; Hayalioglu, M.S. Design of non-linear semi-rigid steel frames with semi-rigid column bases. Electron. J. Struct. Eng. 2004, 4, 1–16. [Google Scholar]
- Sagiroglu, M.; Aydin, A.C. Design and analysis of non-linear space frames with semi-rigid connections. Steel Compos. Struct. 2015, 18, 1405–1421. [Google Scholar] [CrossRef]
- Kazemi, F.; Mohebi, B.; Yakhchalian, M. Evaluation the P-Delta Effect on Collapse Capacity of Adjacent Structures Subjected to Far-field Ground Motions. Civ. Eng. J. 2018, 4, 1066. [Google Scholar] [CrossRef] [Green Version]
- González, J.A.; Park, K. A simple explicit-implicit finite element tearing and interconnecting transient analysis algorithm. Int. J. Numer. Methods Eng. 2011, 89, 1203–1226. [Google Scholar] [CrossRef]
- González, J.A.; Park, K. Accelerating the convergence of AFETI partitioned analysis of heterogeneous structural dynamical systems. Comput. Methods Appl. Mech. Eng. 2019, 360, 112726. [Google Scholar] [CrossRef]
- Ritto-Corrêa, M.; Camotim, D. On the arc-length and other quadratic control methods: Established, less known and new implementation procedures. Comput. Struct. 2008, 86, 1353–1368. [Google Scholar] [CrossRef]
- Kolman, R.; Kopačka, J.; González, J.A.; Cho, S.; Park, K. Bi-penalty stabilized technique with predictor–corrector time scheme for contact-impact problems of elastic bars. Math. Comput. Simul. 2021, 189, 305–324. [Google Scholar] [CrossRef]
- Taşdemir, E.; Soykan, Y. Dynamical analysis of a non-linear difference equation. J. Comput. Anal. Appl. 2019, 26, 288–301. [Google Scholar]
- Zupan, E.; Zupan, D. Dynamic analysis of geometrically non-linear three-dimensional beams under moving mass. J. Sound Vib. 2018, 413, 354–367. [Google Scholar] [CrossRef]
- Gedig, M.H.; Stiemer, S.F. A Method for the Automatic Generation of Timber Connection Patterns. Electron. J. Struct. Eng. 2003, 3, 171–183. [Google Scholar]
- Han, Y.; Xu, B.; Liu, Y. An efficient 137-line MATLAB code for geometrically nonlinear topology optimization using bi-directional evolutionary structural optimization method. Struct. Multidiscip. Optim. 2021, 63, 2571–2588. [Google Scholar] [CrossRef]
- Benterkia, Z. End-Plate Connections and Analysis of Semi-Rigid Steel Frames. Ph.D. Thesis, University of Warwick, Coventry, UK, 1991. [Google Scholar]
- Díaz, C.; Martí, P.; Victoria, M.; Querin, O.M. Review on the modelling of joint behaviour in steel frames. J. Constr. Steel Res. 2011, 67, 741–758. [Google Scholar] [CrossRef]
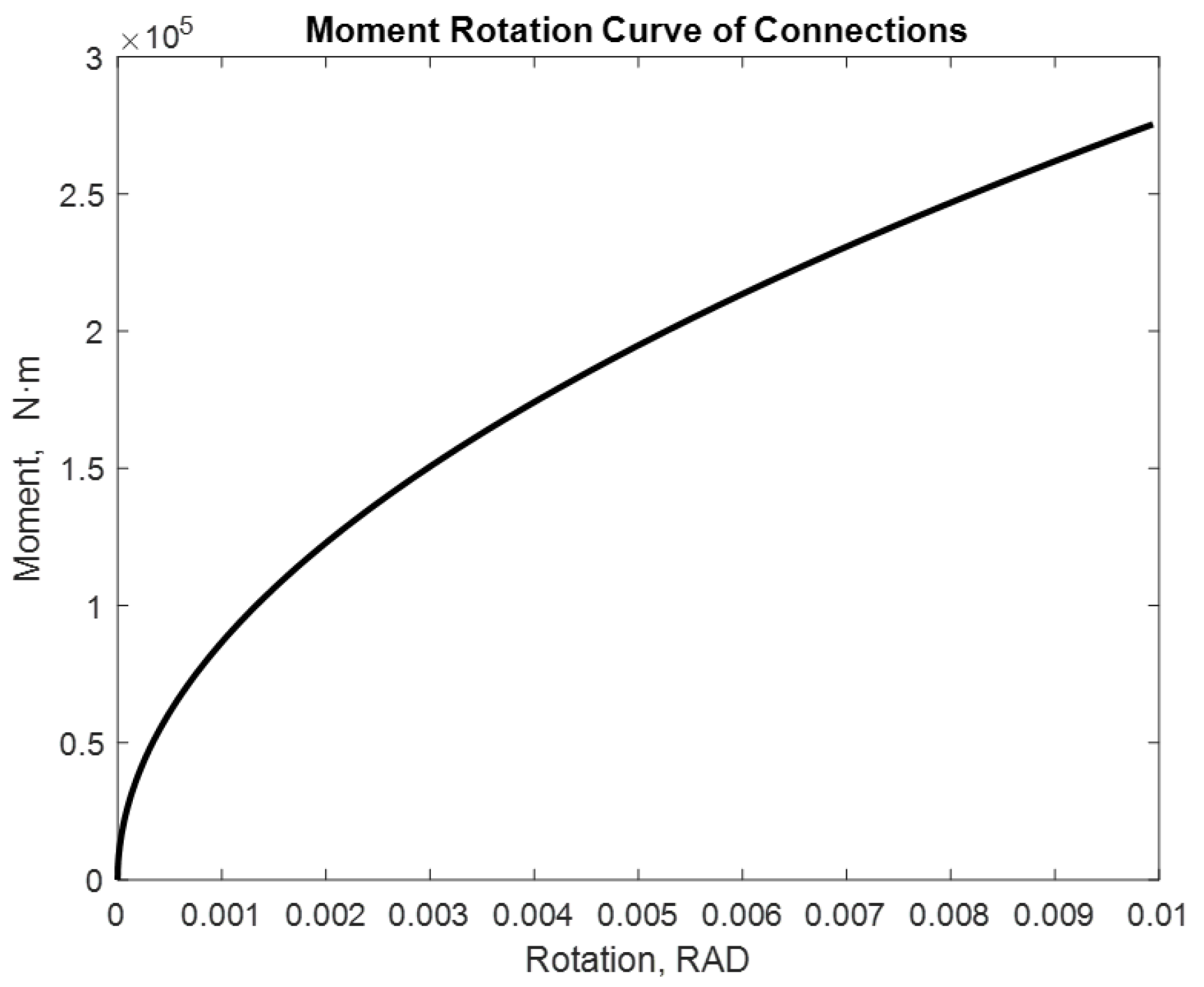
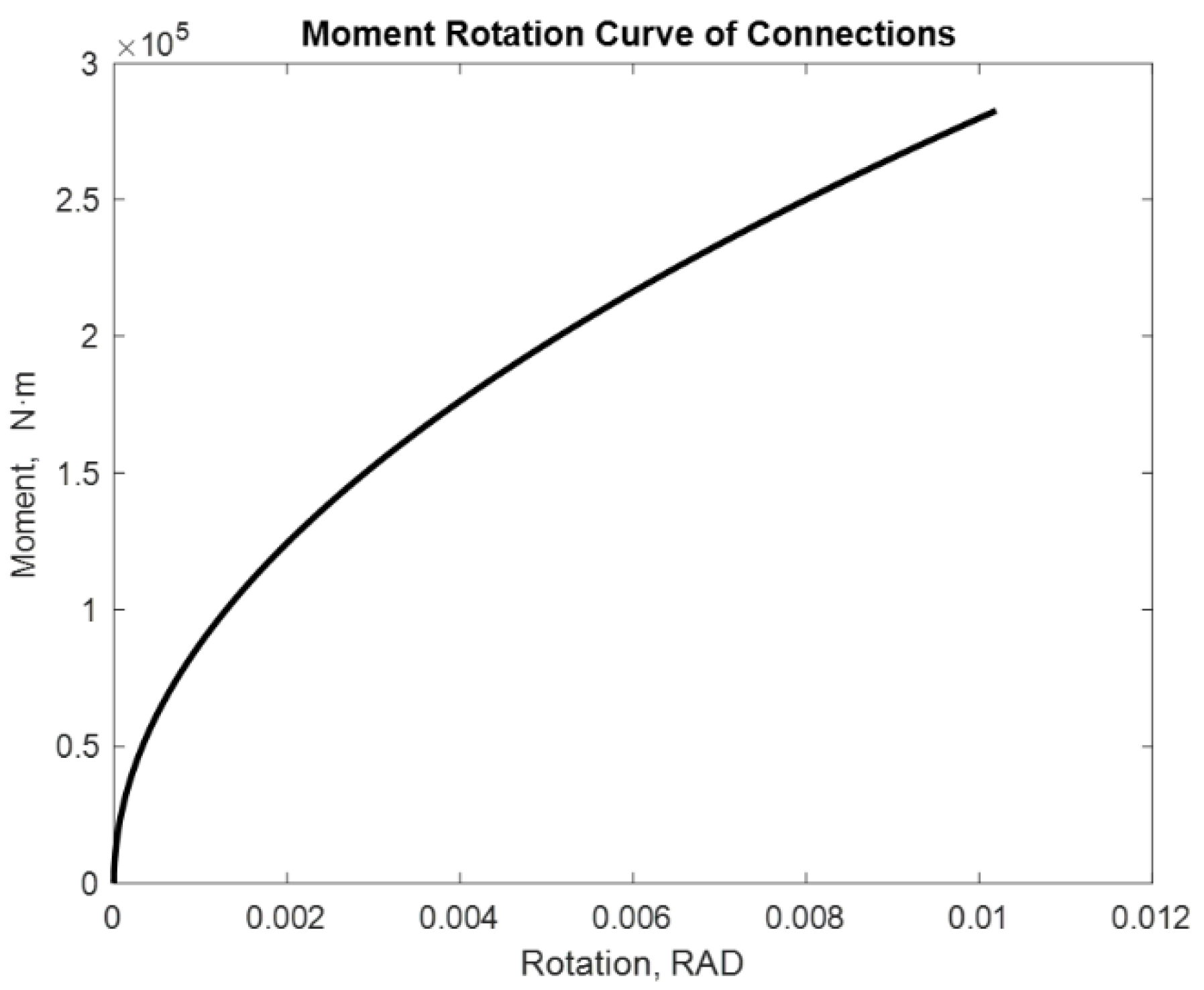

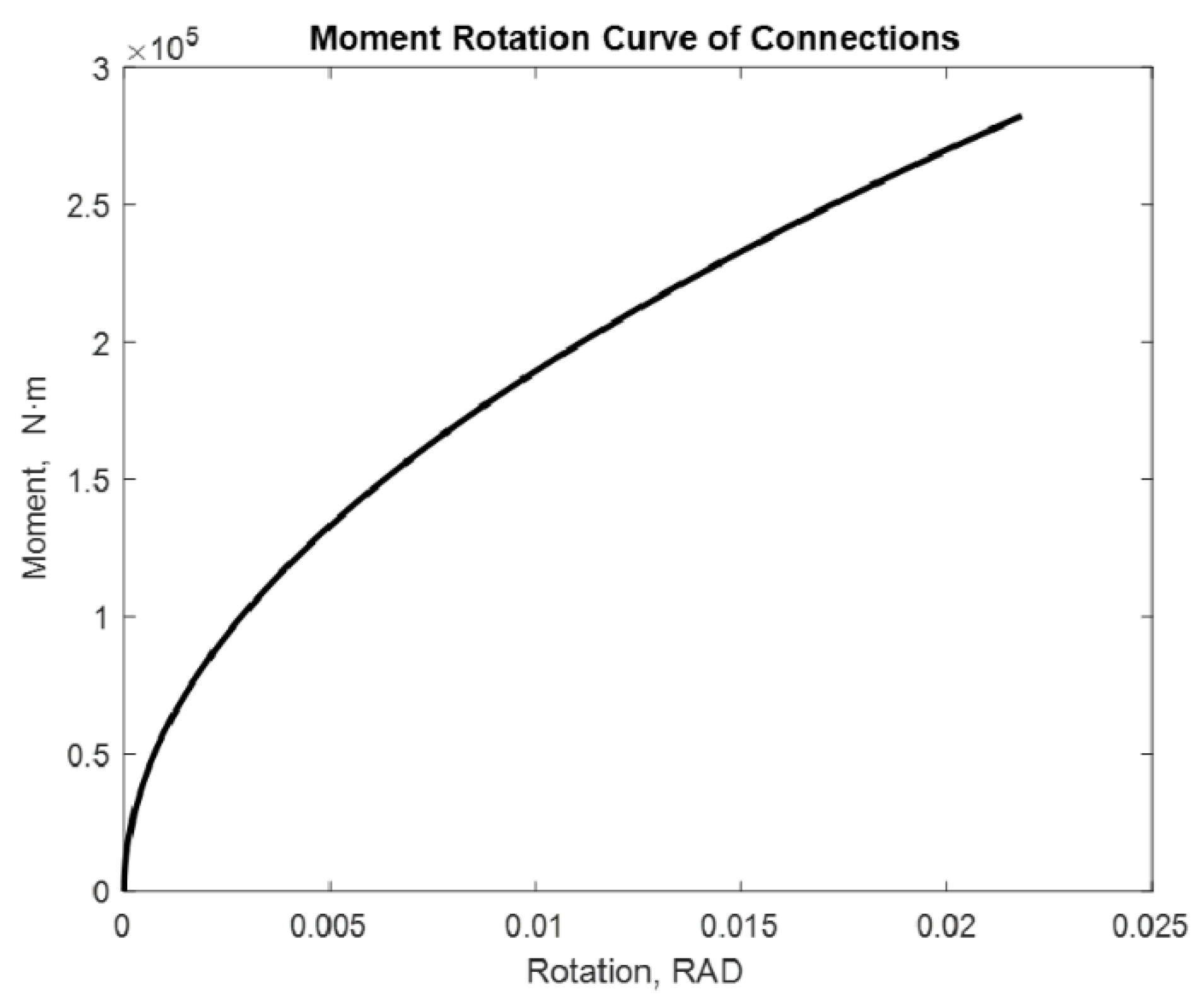


| Properties of the Materials and Joints | Connection Type End-Plate without Column Web Stiffeners |
|---|---|
| Section | W 12 × 72 |
| Plate thickness | tp = 2.54 |
| Bolt spacing | dg = 72.48 mm |
| Bolt diameter | db = 2.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez González, C.A.; Caparrós-Mancera, J.J.; Hernández-Torres, J.A.; Rodríguez-Pérez, Á.M. Nonlinear Analysis of Rotational Springs to Model Semi-Rigid Frames. Entropy 2022, 24, 953. https://doi.org/10.3390/e24070953
Rodríguez González CA, Caparrós-Mancera JJ, Hernández-Torres JA, Rodríguez-Pérez ÁM. Nonlinear Analysis of Rotational Springs to Model Semi-Rigid Frames. Entropy. 2022; 24(7):953. https://doi.org/10.3390/e24070953
Chicago/Turabian StyleRodríguez González, César Antonio, Julio José Caparrós-Mancera, José Antonio Hernández-Torres, and Ángel Mariano Rodríguez-Pérez. 2022. "Nonlinear Analysis of Rotational Springs to Model Semi-Rigid Frames" Entropy 24, no. 7: 953. https://doi.org/10.3390/e24070953
APA StyleRodríguez González, C. A., Caparrós-Mancera, J. J., Hernández-Torres, J. A., & Rodríguez-Pérez, Á. M. (2022). Nonlinear Analysis of Rotational Springs to Model Semi-Rigid Frames. Entropy, 24(7), 953. https://doi.org/10.3390/e24070953







