Quantum Linear System Algorithm for General Matrices in System Identification
Abstract
:1. Introduction
2. Quantum Algorithms for System Identification
2.1. The Classical System Identification Problem
2.2. The Quantum Linear System Algorithm for General Matrices
- Preparing the initial quantum state , which can be represented as:
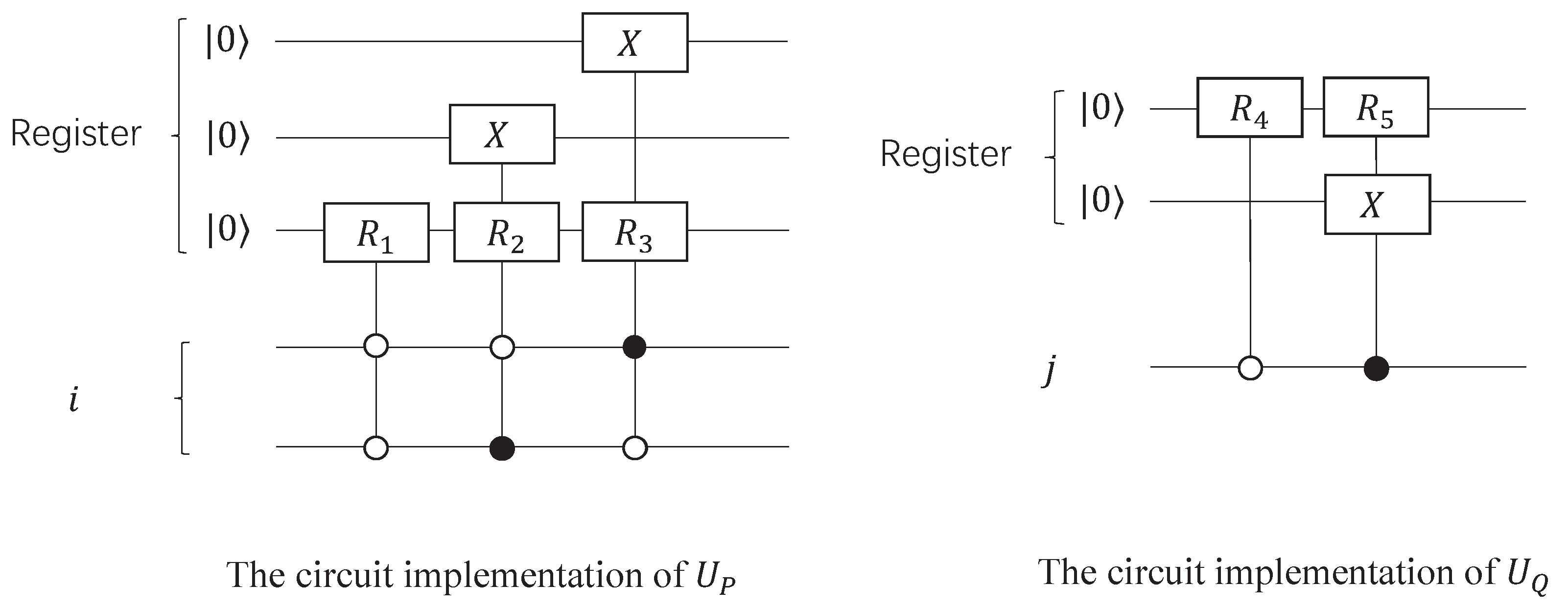
- Apply P in the initial state
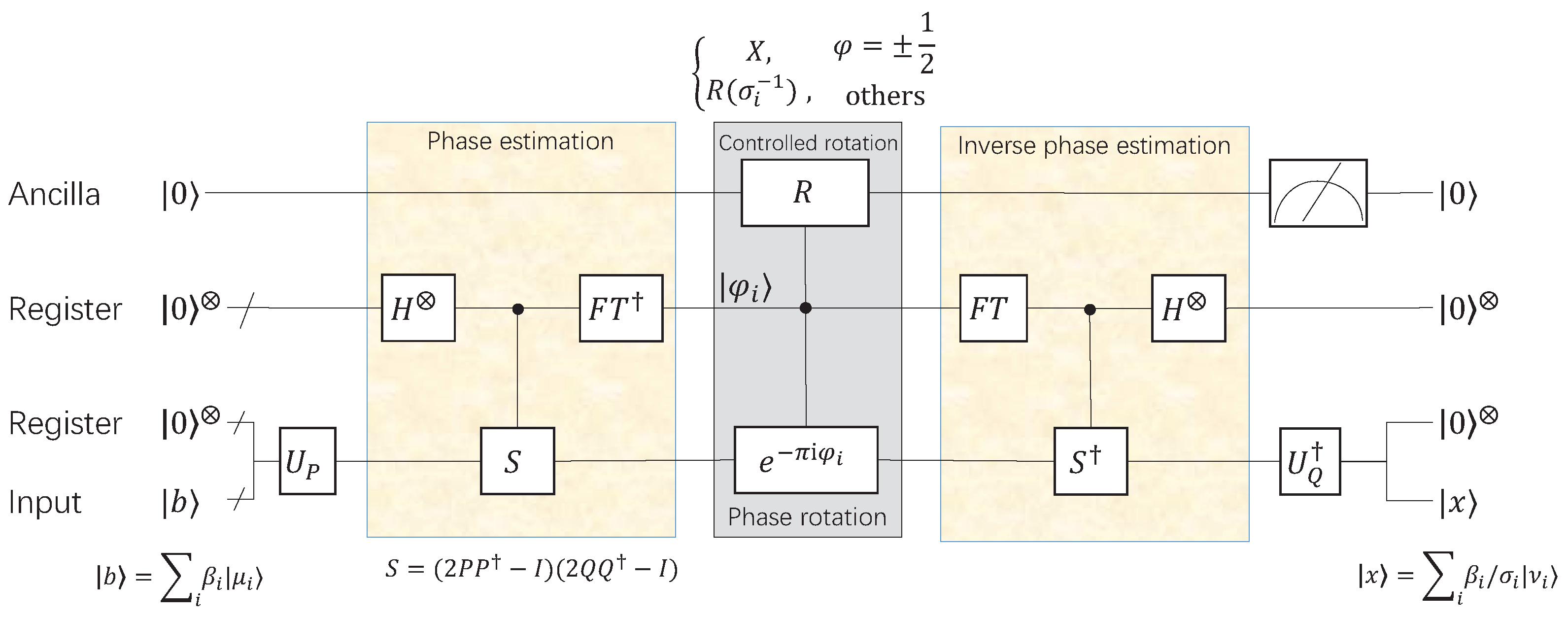
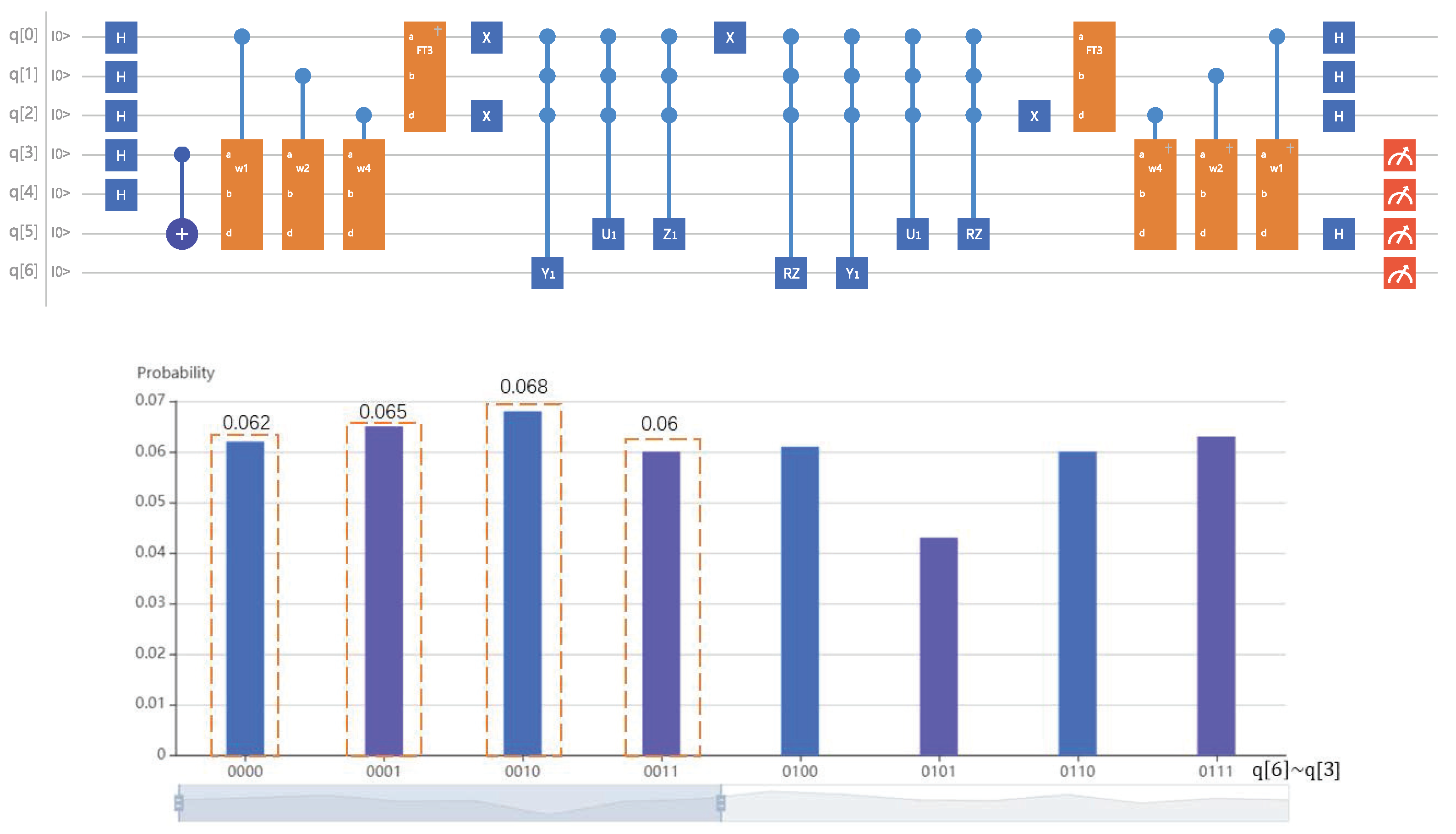
- Perform phase estimation on input for , as shown in Figure 1, then we obtain the following statewhere is the eigenvalue of S and .
- Apply a phase shift operator controlled by the phase , then we obtain
- Perform a controlled rotation on the ancillary qubit based on the register storing phase value and will obtainwhere and .
- Apply the inverse transformation of step 3 to obtain
- Measure the ancillary register. When the measurement result is , the quantum state will collapse to
- Apply the inverse of Q and we will obtain the desired statewhich is the particular solution of the equation , that is, the lowest energy solution state.
2.3. The Quantum Algorithm for Homogeneous Linear Equations
3. Algorithms Complexity Analysis
4. Numerical Simulation
- Preparing the initial state .
- Apply P in the initial state , .
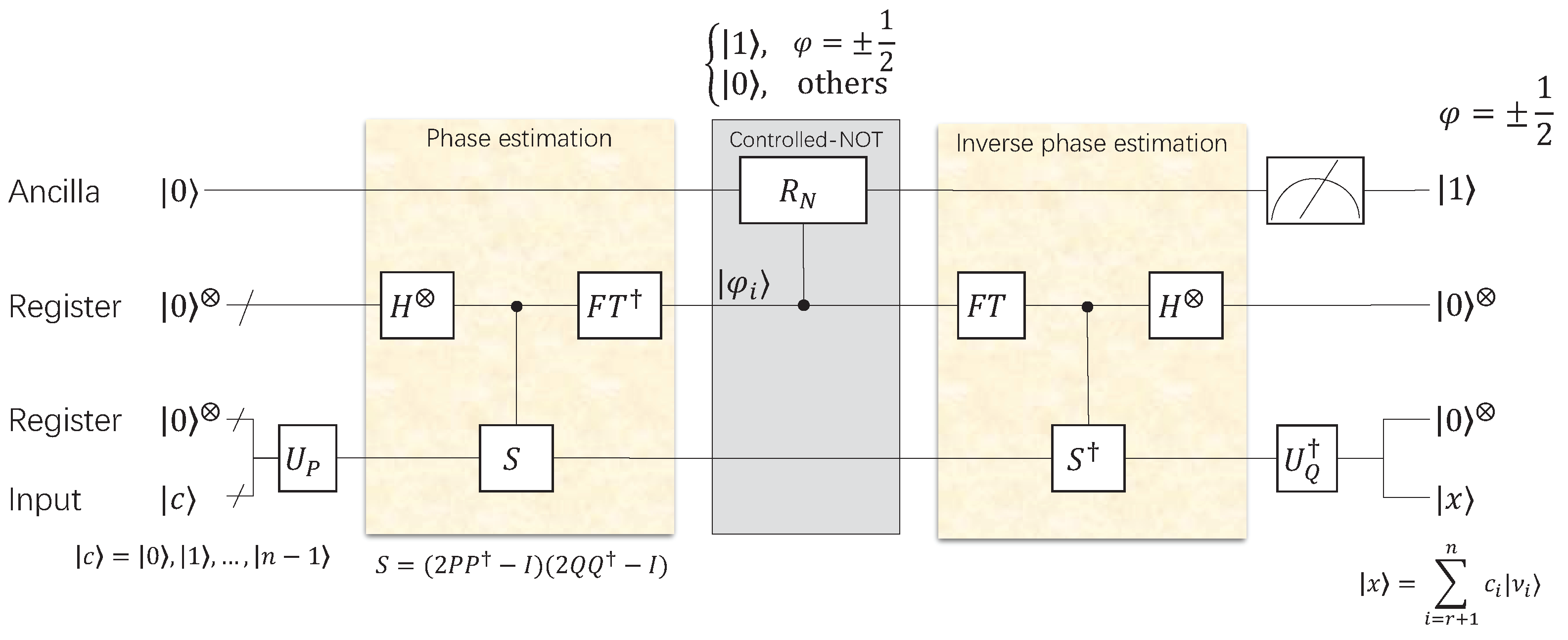
- Perform phase estimation on for , then we obtain the following statewhere the eigenvalues of S are , and is the corresponding eigenvector.
- Change the phase, then we obtain
- Perform a controlled rotation on the ancillary qubit based on the register storing phase value:where .
- Apply the inverse transformation of step 3 to obtain
- Apply the inverse of Q and we will obtain the desired state
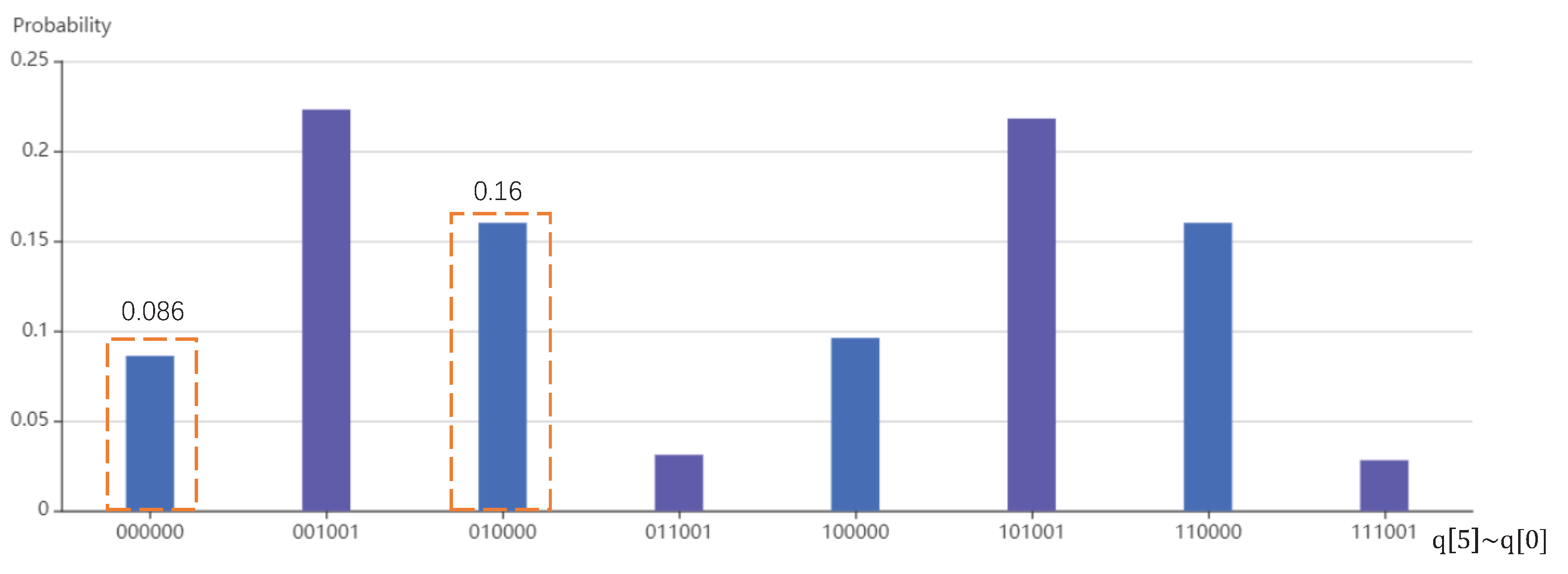
- Measure the ancillary register. When the result is , the quantum state will collapse tothat is proportional to the solution of the equation , so we obtain and . Substituting a and d into Equation (29), we obtain . So far, the first-order discrete identification model is:
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goodwin, G.; Payne, R. Dynamic System Identification; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Mehra, R.K.; Lainiotis, D.G. System Identification; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Ljung, L. System Identification: Theory for The User; Tsinghua University Press: Beijing, China, 2002. [Google Scholar]
- Marquardt, D. An algorithm for least-Squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Kohout, R.B. Hedged maximum likelihood quantum state estimation. Phys. Rev. Lett. 2010, 105, 200504. [Google Scholar] [CrossRef] [PubMed]
- Teo, Y.; Zhu, H.; Englert, B.; Rehacekand, J.; Hradil, Z. Quantum-state reconstruction by maximizing likelihood and entropy. Phys. Rev. Lett. 2011, 107, 020404. [Google Scholar] [CrossRef] [Green Version]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; p. 4. ISBN 9780387310732. [Google Scholar]
- Childs, A.M.; Liu, J.P.; Ostrander, A. High-precision quantum algorithms for partial differential equations. arXiv 2020, arXiv:2002.07868. [Google Scholar] [CrossRef]
- Magnus, J.; Neudecker, H. The elimination matrix: Some lemmas and applications. SIAM J. Algebr. Discret. Methods 1980, 1, 422–449. [Google Scholar] [CrossRef] [Green Version]
- Haddock, J.; Needell, D.; Rebrova, E.; Swartworth, W. Quantile-based iterative methods for corrupted systems of linear equations. arXiv 2020, arXiv:2107.05554. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambrige, MA, USA, 2000. [Google Scholar]
- Emily, G.; Mark, H. Quantum Computing: Progress and Prospects; The National Academy Press: Washington, DC, USA, 2018. [Google Scholar]
- Adedoyin, A.; Ambrosiano, J.; Anisimov, P.; Bärtschi, A.; Casper, W.; Chennupati, G.; Coffrin, C.; Djidjev, H.; Gunter, D.; Karra, S.; et al. Quantum algorithm implementations for beginners. arXiv 2018, arXiv:1804.03719. [Google Scholar]
- Wiebe, N.; Braun, D.; Lloyd, S. Quantum algorithm for data fitting. Phys. Rev. Lett. 2012, 109, 50505. [Google Scholar] [CrossRef] [Green Version]
- Shor, P. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the 28th ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Lloyd, S. Universal quantum simulators. Science 1996, 273, 1073–1078. [Google Scholar] [CrossRef] [PubMed]
- Berry, D.W.; Childs, A.M. Black-box Hamiltonian simulation and unitary implementation. Quantum Inf. Comput. 2012, 12, 29–62. [Google Scholar]
- Long, G.L. General quantum interference principle and duality computer. Commun. Theor. Phys. 2006, 45, 825–844. [Google Scholar]
- Long, G.L.; Liu, Y. Duality computing in quantum computers. Commun. Theor. Phys. 2009, 50, 1303. [Google Scholar]
- Long, G.L.; Liu, Y.; Wang, C. Allowable generalized quantum gates. Commun. Theor. Phys. 2009, 51, 65. [Google Scholar]
- Harrow, A.W.; Hassidim, A.; Lloyd, S. Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef]
- Kerenidis, I.; Prakash, A. Quantum recommendation system. Lipics Leibniz Int. Proc. Inform. 2017, 49, 1–21. [Google Scholar]
- Li, K.; Dai, H.; Jing, F.; Gao, M.; Xue, B.; Wang, P.; Zhang, M. Quantum algorithms for solving linear regression equation. J. Phys. Conf. Ser. 2021, 1738, 012063. [Google Scholar] [CrossRef]
- Shao, C.P. Quantum algorithms to matrix multiplication. arXiv 2018, arXiv:1803.01601. [Google Scholar]
- Li, K.; Dai, H.Y.; Zhang, M. Quantum algorithms of state estimators in classical control systems. Sci. China Inf. Sci. 2020, 63, 1–12. [Google Scholar] [CrossRef]
- Wossnig, L.; Zhao, Z.K.; Prakash, A. A quantum linear system algorithm for dense matrices. Phys. Rev. Lett. 2018, 120, 050502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shao, C.P.; Xiang, H. Quantum circulant preconditioner for a linear system of equations. Phys. Rev. A 2018, 98, 062321. [Google Scholar] [CrossRef] [Green Version]
- Childs, A.M.; Wiebe, N. Hamiltonian simulation using linear combinations of unitary operations. Quantum Inf. Comput. 2012, 12, 901–924. [Google Scholar] [CrossRef]
- Berry, D.W.; Ahokas, G.; Cleve, R. Efficient quantum algorithms for simulating sparse Hamiltonians. Commun. Math. Phys. 2007, 270, 359–371. [Google Scholar] [CrossRef] [Green Version]
- Cheng, D.Z. On semi-tensor product of matrices and its applications. Acta Math. Appl. Sin. 2003, 19, 219–228. [Google Scholar] [CrossRef]
- Kerenidis, I.; Prakash, A. Quantum Recommendation Systems. In Proceedings of the 8th Innovations in Theoretical Computer Science Conference, Berkeley, CA, USA, 9–11 January 2017; Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2017. [Google Scholar]
- Lin, L.; Tong, Y. Near-Optimal Ground State Preparation. Quantum 2020, 4, 372. [Google Scholar] [CrossRef]
- Buhrman, H.; Cleve, R.; Watrous, J.; Wolf, R. Quantum Fingerprinting. Phys. Rev. Lett. 2001, 87, 167902. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Zhang, M.; Liu, X.; Liu, Y.; Dai, H.; Zhang, Y.; Dong, C. Quantum Linear System Algorithm for General Matrices in System Identification. Entropy 2022, 24, 893. https://doi.org/10.3390/e24070893
Li K, Zhang M, Liu X, Liu Y, Dai H, Zhang Y, Dong C. Quantum Linear System Algorithm for General Matrices in System Identification. Entropy. 2022; 24(7):893. https://doi.org/10.3390/e24070893
Chicago/Turabian StyleLi, Kai, Ming Zhang, Xiaowen Liu, Yong Liu, Hongyi Dai, Yijun Zhang, and Chen Dong. 2022. "Quantum Linear System Algorithm for General Matrices in System Identification" Entropy 24, no. 7: 893. https://doi.org/10.3390/e24070893
APA StyleLi, K., Zhang, M., Liu, X., Liu, Y., Dai, H., Zhang, Y., & Dong, C. (2022). Quantum Linear System Algorithm for General Matrices in System Identification. Entropy, 24(7), 893. https://doi.org/10.3390/e24070893





