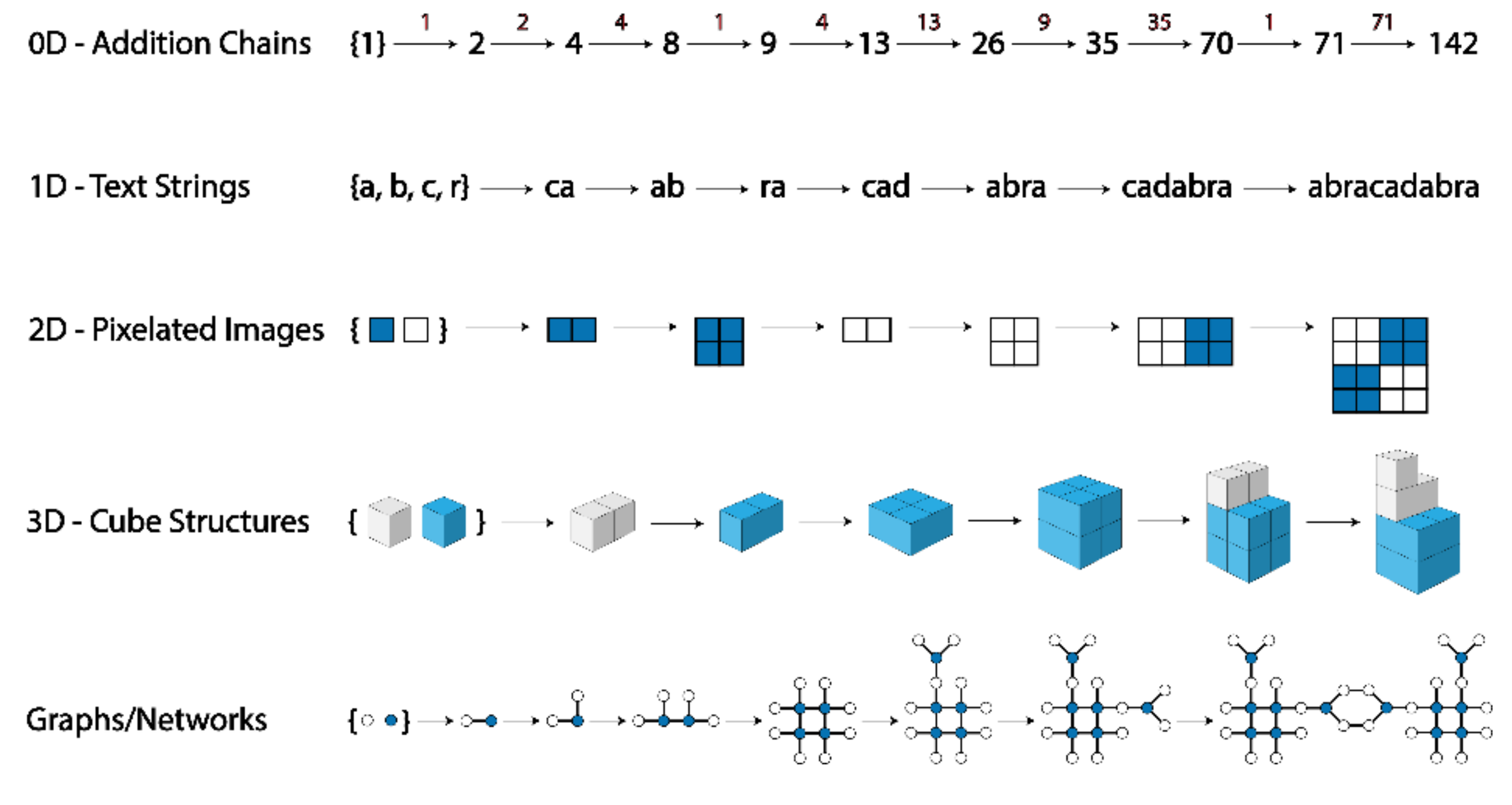
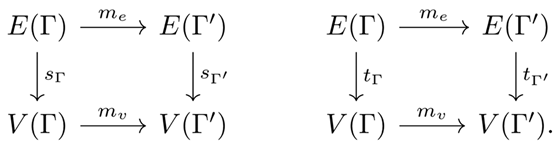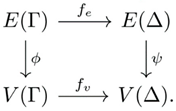2.1. Graph Theoretical Prerequisites
In constructing an assembly space, we consider a set of objects, possibly infinitely many objects, which can be combined in various ways to produce others. If an object can be combined with some other object to yield an object , we represent the relationship between a and b by drawing a directed edge or arrow from to . Altogether, this structure is a quiver, also called a directed multigraph, as we allow for the possibility that there is more than one way to produce from ; that is, there may be more than one edge from to .
Definition 1. A quiver Γ consists of
- 1.
A set of vertices ;
- 2.
A set of edges ;
- 3.
A pair of maps .
For an edge , is referred to as the source and the target of the edge, and we will often leave off the subscripts when the context is clear, e.g., and . We will often describe an edge with and as . This does not mean that e is a unique edge with endpoints a and b; it is possible that two edges have the same endpoints .
From here, we consider paths—that is, sequences of edges—that describe the process of sequentially combining objects to yield intermediate objects and ultimately some terminal object.
Definition 2. If is a quiver, a path in of lengthis a sequence of edges, such that for. The functions and can be extended to paths asand . We write to denote the length, or number of edges, in the path. Additionally, for each vertex there is a zero path, denoted , with length 0 and.
A natural point is that combining two objects should never yield something that can be used to create either of those objects. Essentially, there are no directed cycles—sequences of edges that form a closed cycle—within the quiver.
Definition 3. A path in a quiver is a directed cycle if with .
Definition 4. A quiveris acyclic if it has no directed cycles.
We can think of an object as being reachable from an object if there is a path from to , and this relationship forms a partial ordering on the quiver if the quiver is acyclic.
Definition 5. Let be an acyclic quiver and let . We sayis reachable from if there exists a path such that and, where .
Lemma 1. Letbe an acyclic quiver, and define a binary relationon the vertices of such that if and only if is reachable from . is a partially ordered set, and is referred to as the reachability relation on .
Proof. For to be a partial ordering on , we need to show that it is reflexive, transitive and antisymmetric. Reflexivity follows directly from the definition of reachability as is reachable from itself via the zero path . To show transitivity, let and . If or , then we are done. Otherwise, there are paths from to and from to . The composite path is a path from to ; thus is reachable from so that . Now consider antisymmetry and suppose that and . Then there exist paths and from a to b and to , respectively. Then is a path from to itself. Since is acyclic, this implies that , and consequently that . Thus, and is antisymmetric. □
The idea of reachability allows us to think of all objects that are reachable from (or above) a given object , the upper quiver of . Similarly, we can think of all objects that can reach , the lower quiver.
Definition 6. Letbe an acyclic quiver and letbe the reachability relation on it. The upper quiver of is with vertices, edges,, and. The lower quiver ofiswith vertices , edges,, and .
Similarly, the upper quiver of a subset in is with vertices , edges , , and . The lower quiver of a subset is defined dually.
Going further, we can consider those objects that cannot be reached as minimal and those that cannot reach anything as maximal. An object which can be reached by finitely many objects is called finite.
Definition 7. Letbe an acyclic quiver,be the reachability relation on it, and a vertex in . Then, is said to be maximal in if, wheneverin , we have . Dually, is maximal in if, whenever in , we have . The set of all maximal vertices of is denoted with defined dually.
Definition 8. A quiveris said to be finiteif its vertex and edge sets are both finite. Similarly, a vertex in a quiver is said to be finite ifin is a finite quiver.
With this idea of a quiver of objects defined, we can consider asking about subsets of objects and relations between them in the context of the quiver as a whole.
Definition 9. Letand be quivers. Then is a subquiver of if,, and. We will denote this relationship as .
Lemma 2. If,, and are quivers, such that and , then . That is, the binary relation on quivers is transitive.
Proof. Suppose , , and are quivers with and . Then, , so that . Similarly, . Next, since , and , . The same argument applies to show that . Thus , so that is transitive. □
Finally, we will need to consider how to map one quiver to another in a consistent fashion, maintaining the basic relational structure of the original quiver.
Definition 10. Letand be quivers. A quiver morphism, denoted, consists of a pair of functionsand such that and . That is, the following diagrams commute:
2.2. Assembly Spaces
The assembly process is the process of constructing some object, which can be decomposed into a finite set of basic objects, through a sequence of joining operations. During this process, objects already constructed can be used in subsequent steps. We formally define this in the context of an assembly space (see
Figure 3), as follows:
Definition 11. An assembly space is an acyclic quivertogether with an edge-labelling mapwhich satisfies the following axioms:
- 1.
is finite and non-empty;
- 2.
;
- 3.
is an edge from toin with , then there exists an edge from to with .
Definition 12. The set of minimal vertices of an assembly spaceis referred to as the basis of and is denoted . Elements of the basis are referred to as basic objects, basic vertices, or basic elements.
An assembly space as in definition 11 is denoted , or simply where appropriate. is taken to mean that is a vertex of the quiver. Within the assembly space, we can think of the vertices as objects and traversal along the directed edge as the construction of the target object from the source object, with the edge label determining the object that is combined with the source to construct the target. The assembly process starts from a set of basic objects (axiom 1) from which all other objects can be constructed (axiom 2). Axiom 3 requires that a symmetric edge exists for every edge within the assembly space wherein the roles of source and edge label are reversed. Intuitively, this can be thought of as saying: if you can combine with to construct , then you can also combine with to construct . Axiom 3 also formalises the requirement that both items in the construction lie below the target in the assembly tree, i.e., only objects already assembled can be used in further assembly steps (see Lemma 3).
Lemma 3. Let be an assembly space and let . If is an edge in with , then .
Proof. Since is an assembly space, we have where is the reachability relation on , since there is an arrow from to b by point 3 of Definition 11. By construction, so that . Therefore, . □
Within an assembly space, an assembly pathway is a sequence that respects the order of the reachability relation. We can think of an assembly pathway as being an order of construction for all the objects within the space, ensuring that the objects required for each step are available earlier in the sequence.
Definition 13. An assembly pathway of an assembly spaceis any topological ordering of the vertices of with respect to the reachability relation.
Definition 14. An assembly spacewith reachability relation is said to be split-branched if for all ,orwhenever .
In a split-branch assembly space, other than basic objects, when combining two different objects, neither of them can have an assembly pathway that uses objects created in the construction of the other. They may use objects that are considered identical (e.g., the same string) but these are separate objects within the space. Since we can define an assembly map to a new space where these separate but identical objects are mapped to the same object, the split-branched assembly index for a system is an upper bound for the assembly index on that system (see
Section 3.4). Calculations of the assembly index in a split-branch space can be less computationally intensive than in the corresponding non-split-branch space. A split-branch algorithm was used in our recent work on molecular assembly [
19].
2.3. Assembly Subspaces and the Assembly Index
We define an assembly subspace, and the rooted property, as follows:
Definition 15. Let andbe assembly spaces. Thenis anassembly subspaceofifis a subquiver ofand. This relationship is denoted as, or simply, when there is no ambiguity.
Definition 16. Letbe an assembly subspace of. Thenisrootedinifis non-empty, andas sets.
An assembly subspace of is simply an assembly space that contains a subset of the objects in and the relationships between them. It is rooted if its set of basic objects is a nonempty subset of the basic objects of . The assembly subspace relationship is transitive (see Lemma 4).
Lemma 4. Let , and be assembly spaces with and , then . Further, if is rooted in and is rooted in , then is rooted in .
Proof. Let , and be assembly spaces such that and . Since , and are quivers, by the transitivity of on quivers. Further, since , , and , we have . Thus, . That is, is transitive on assembly spaces. If is rooted in and is rooted in , then . That is, is rooted in . □
We can also show that for any object in an assembly space , the objects and relationships that lie below are a rooted assembly subspace of .
Lemma 5. Letbe an assembly space and let. Then,is a rooted assembly subspace of.
Proof. We first show that is an assembly space. Since is an assembly space, it is the upper set of its basis, . As such, is a non-empty subset of and , giving us axiom 1. The remaining axiom follows directly from Lemma 6. Additionally, we already have that , so is rooted in . □
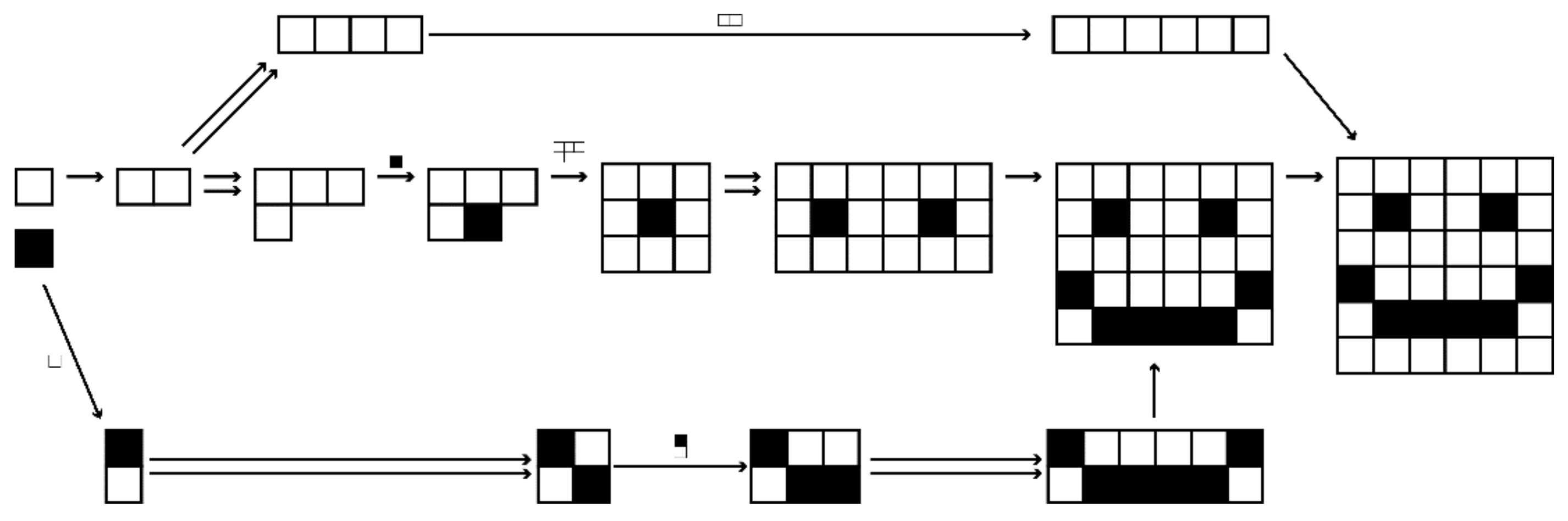
Figure 3.
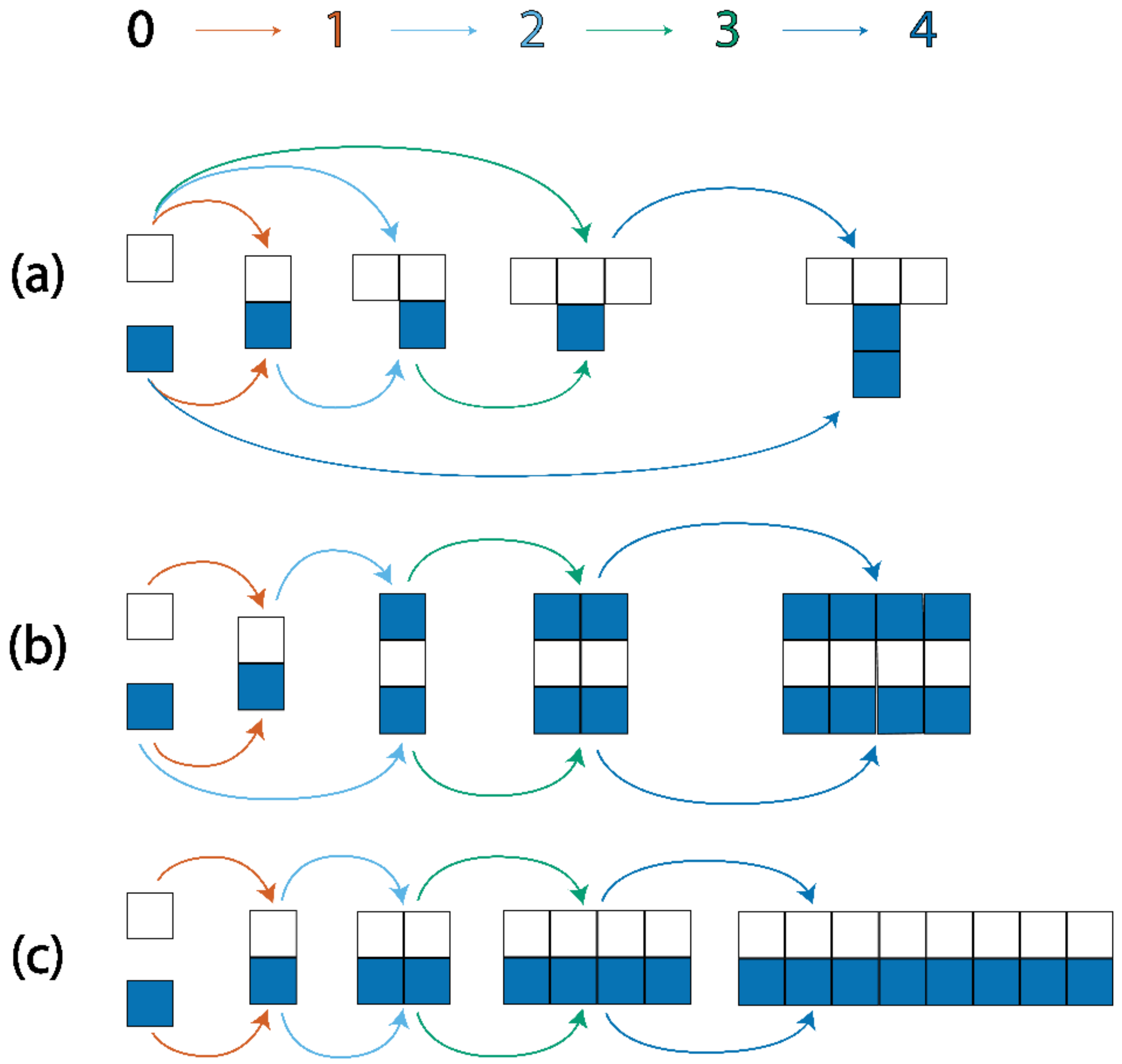
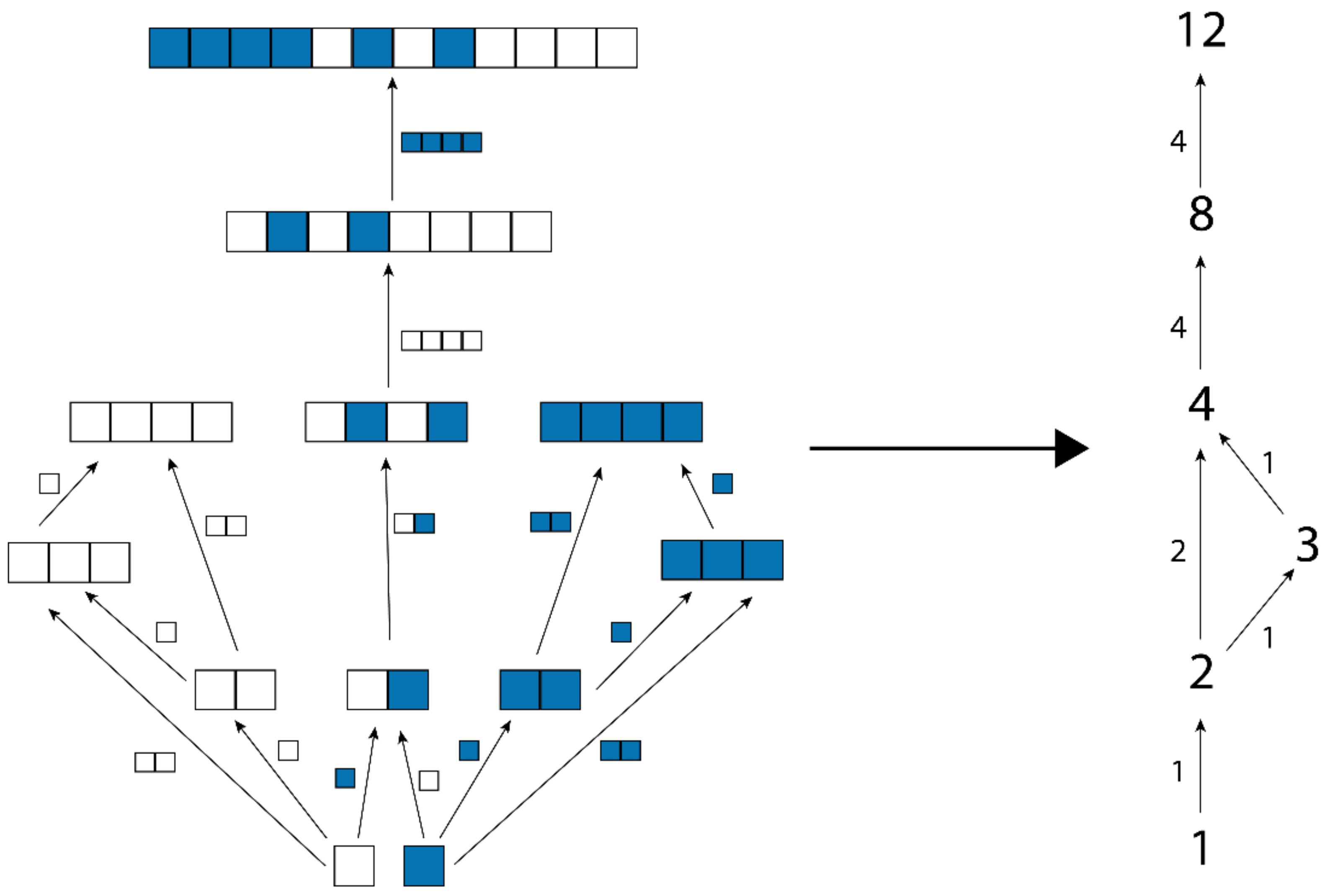
An assembly space comprised of objects formed by joining together white and blue blocks. Some of the arrows have been omitted for clarity. The dotted region is an assembly subspace, and the topological ordering of the objects in the subspace represents a minimal assembly pathway for any subspace containing the sequence of four blue boxes.
Figure 3.
An assembly space comprised of objects formed by joining together white and blue blocks. Some of the arrows have been omitted for clarity. The dotted region is an assembly subspace, and the topological ordering of the objects in the subspace represents a minimal assembly pathway for any subspace containing the sequence of four blue boxes.
We now move on to the assembly index, which is a measure of how directly an object can be constructed from basic objects.
Definition 17. The cardinality of an assembly spaceis the cardinality of the underlying quiver’s vertex set,. The augmented cardinality of an assembly spacewith basisis.
Definition 18. The assembly index of a finite objectis the minimal augmented cardinality of all rooted assembly subspaces containing. This can be writtenwhen the relevant assembly spaceis clear from the context.
The cardinality is the number of objects within the assembly space, and the augmented cardinality is the number of objects excluding basic objects. Thus, the assembly index of is the number of objects within the smallest rooted assembly subspace containing , not including the basic objects. We require the subspaces to be rooted, as otherwise, a space containing only would fit this criterion.
The assembly index can be thought of as how many construction steps we need to take at a minimum to create , starting from our set of basic objects. This is a key concept in assembly theory, as it allows us to place a lower bound on the number of joining operations required to make an object. The augmented cardinality is used as defining the assembly index without including basic objects in accord with this physical interpretation of joining objects in steps; however, the cardinality could instead be used if desired, and the difference in the measures for any structures with shared basic objects would be a constant.
2.5. Bounds on the Assembly Index
In this section, we look at some bounds on the assembly index. First, the assembly index of an object in an assembly space is always less than or equal to the assembly index of in any rooted assembly subspace of that contains x. Essentially, since the assembly subspace may have fewer edges, and cannot have more edges, there are fewer “shortcuts” for assembling a given object.
Lemma 6. Letbe an assembly space anda rooted assembly subspace of. For every finite, the assembly index ofinis greater than or equal to the assembly index ofin. That is,for all.
Proof .
Let and suppose . Then, there exists a rooted assembly subspace containing , such that . However, by the transitivity of rooted assembly subspaces (Lemma 4), is a rooted assembly subspace of —but if that is the case, there exists a rooted assembly subspace of with augmented cardinality less than , namely ; a contradiction. □
Since the lower quiver of an object is a rooted assembly subspace, we know the assembly index of the object in bounds the real assembly index of the object from above. However, we can show that these assembly indices are equal, i.e., . This result allows any computational approaches aiming to compute to focus only on the objects below .
Theorem 2. Let be an assembly space and let be finite. Then .
Proof. Since is finite, we need only consider finite, rooted assembly subspaces of . Let be such a subspace containing , and suppose that . Let such that , then is a rooted assembly subspace of containing with augmented cardinality strictly less than . As such . □
In other words, if is not a subspace of , then it cannot have the augmented cardinality . Thus, by contrapositive if , then . Since is rooted in , it must also be rooted in .
Therefore, if a rooted subspace of has the minimal augmented cardinality in , it must be a rooted assembly subspace of . This implies that . Additionally, by Lemma 6, . Then, . □
Finally, assembly maps allow us to place lower bounds on the assembly index – the assembly index of the image of an object bounds the object’s actual assembly index below. In other words, we can place lower bounds on the assembly index of an object by mapping the assembly space into a simpler space and computing the assembly index there.
Theorem 3. Ifis an assembly map, thenfor all finite .