Quantum Simulation of Pseudo-Hermitian-φ-Symmetric Two-Level Systems
Abstract
:1. Introduction
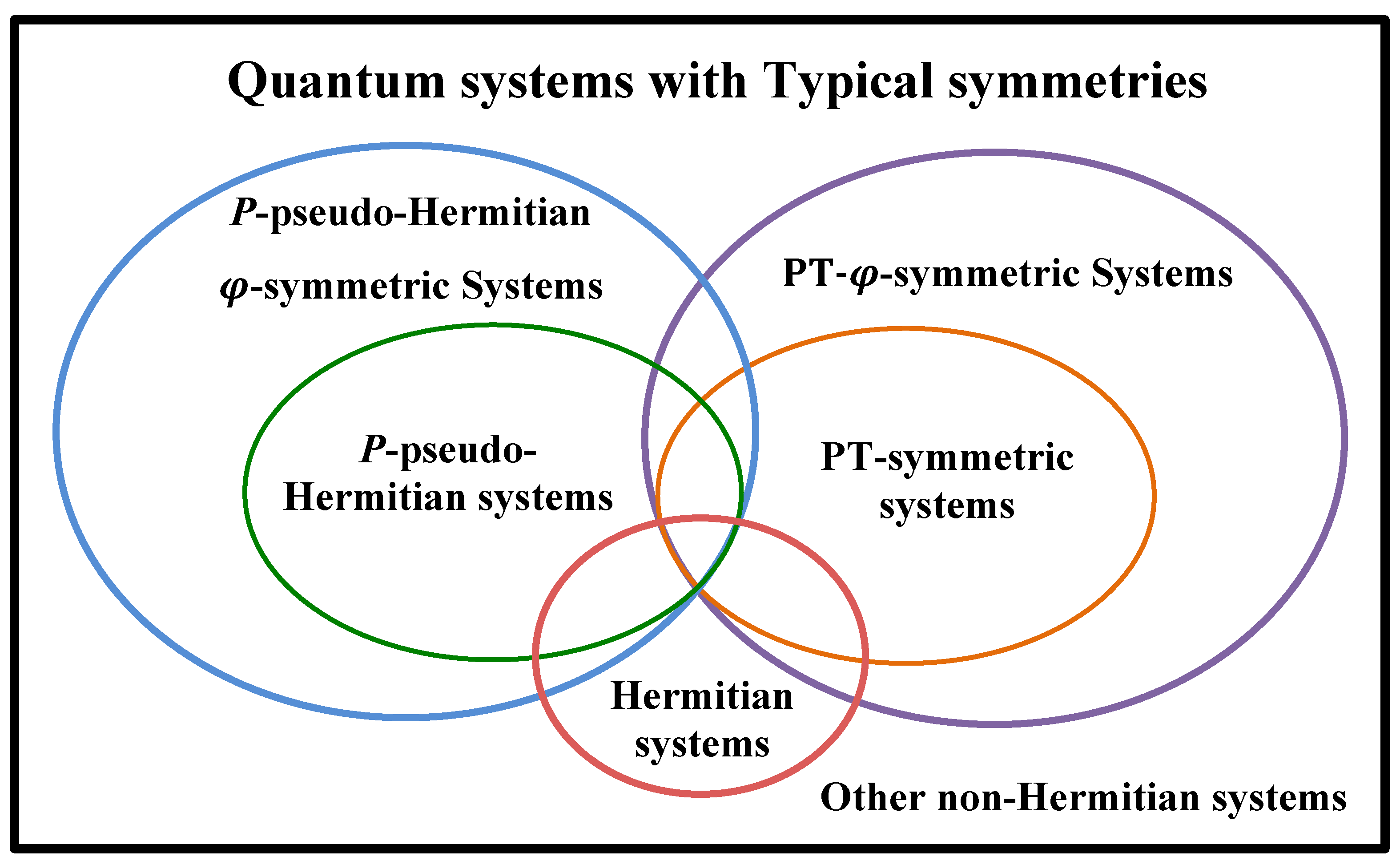
2. Complex Generalization of Pseudo-Hermitian Symmetry
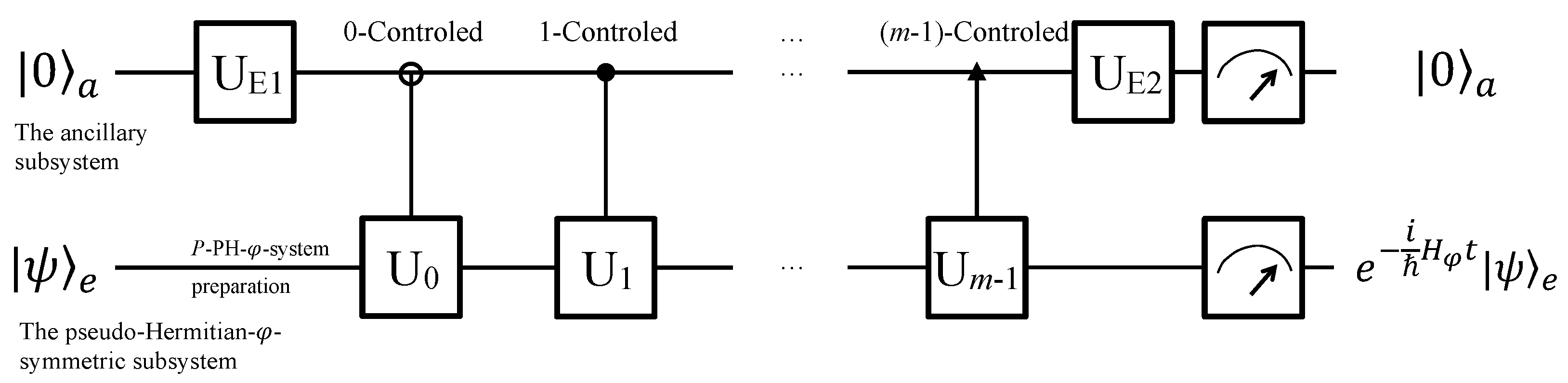
3. Quantum Simulation Using LCU by Duality Quantum Computing
4. Quantum Simulation of -Pseudo-Hermitian--Symmetric Two-Level Systems
4.1. P-PH- Two-Level Systems
4.2. UE of the Time-Evolutionary Operator
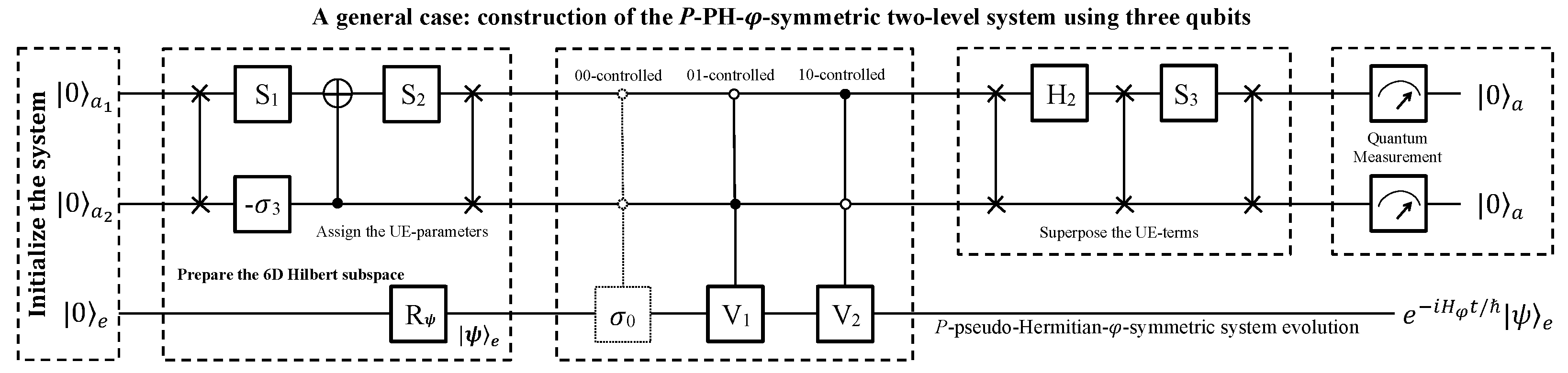
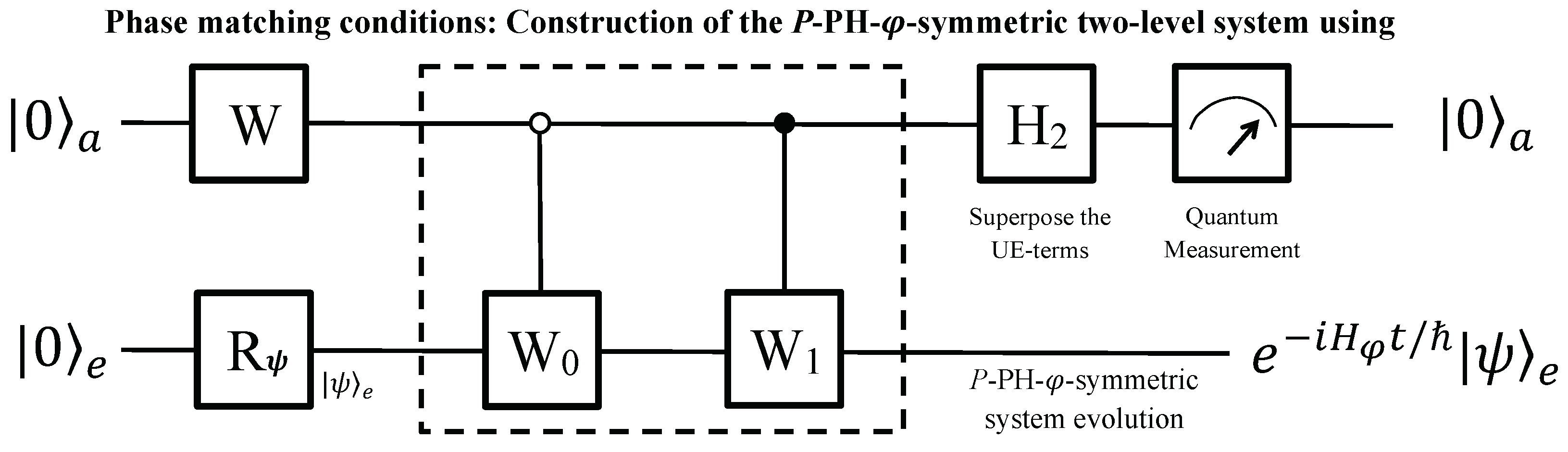
4.3. Qubit Simulation
5. Experimental Proposals
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NH | non-Hermitian |
| PT | parity-time-reversal |
| PH | pseudo-Hermitian |
| PHA | pseudo-Hermitian anti-symmetric |
| PH- | pseudo-Hermitian--symmetric |
| P | parity |
| EP | exceptional point |
| LCU | linear combination of unitaries |
| NMR | nuclear magnetic resonance |
Appendix A
References
- Gamow, G. Quantum Theory at Nucleus. Z. Phys. 1928, 51, 204. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems, 10th Anniversary ed.; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Barreiro, J.T.; Müller, M.; Schindler, P.; Nigg, D.; Monz, T.; Chwalla, M.; Hennrich, M.; Roos, C.F.; Zoller, P.; Blatt, R. An Open-system Quantum Simulator with Trapped Ions. Nature 2011, 470, 486–491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, Z.; Xia, R.; Kais, S. A Quantum Algorithm for Evolving Open Quantum Dynamics on Quantum Computing Devices. Sci. Rep. 2020, 10, 3301. [Google Scholar] [CrossRef]
- Del Re, L.; Rost, B.; Kemper, A.F.; Freericks, J.K. Driven-Dissipative Quantum Mechanics on a Lattice: Simulating a Fermionic Reservoir on a Quantum Computer. Phys. Rev. B 2020, 102, 125112. [Google Scholar] [CrossRef]
- Viyuela, O.; Rivas, A.; Gasparinetti, S.; Wallraff, A.; Filipp, S.; Martin-Delgado, M.A. Observation of Topological Uhlmann Phases with Superconducting Qubits. Njp Quantum Inf. 2018, 4, 10. [Google Scholar] [CrossRef] [Green Version]
- Zheng, C. Universal Quantum Simulation of Single-Qubit Nonunitary Operators using Duality Quantum Algorithm. Sci. Rep. 2021, 11, 3960. [Google Scholar] [CrossRef]
- Schlimgen, A.W.; Head-Marsden, K.; Sager, L.M.; Narang, P.; Mazziotti, D.A. Quantum Simulation of Open Quantum Systems Using a Unitary Decomposition of Operators. Phys. Rev. Lett. 2021, 127, 270503. [Google Scholar] [CrossRef]
- Del Re, L.; Rost, B.; Foss-Feig, M.; Kemper, A.F.; Freericks, J.K. Robust Measurements of N-Point Correlation Functions of Driven-Dissipative Quantum Systems on a Digital Quantum Computer. arXiv 2022, arXiv:2204.12400. [Google Scholar]
- Ding, P.Z.; Yi, W. Two-body exceptional points in open dissipative systems. Chin. Phys. B 2022, 31, 010309. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef] [Green Version]
- Bender, C.M.; Boettcher, S.; Meisinger, P.N. PT-Symmetric Quantum Mechanics. J. Math. Phys. 1999, 40, 2201–2229. [Google Scholar] [CrossRef] [Green Version]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Complex Extension of Quantum Mechanics. Phys. Rev. Lett. 2002, 89, 270401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bender, C.M.; Brody, D.C.; Jones, H.F. Must a Hamiltonian be Hermitian? Am. J. Phys. 2003, 71, 1095–1102. [Google Scholar] [CrossRef] [Green Version]
- Bender, C.M. PT-symmetric Quantum Theory. J. Phys. Conf. Ser. 2015, 631, 012002. [Google Scholar] [CrossRef]
- Zhang, S.; Jin, L.; Song, Z. Topology of a parity-time symmetric non-Hermitian rhombic lattice. Chin. Phys. B 2022, 31, 010312. [Google Scholar] [CrossRef]
- Hu, Z.; Jin, L.; Zeng, Z.-Y.; Tang, J.; Luo, X.-B. Quasi-parity-time symmetric dynamics in periodically driven two-level non-Hermitian system. Acta Phys. Sin. 2022, 71, 074207. [Google Scholar] [CrossRef]
- Wang, K.; Gao, Y.-P.; Jiao, R.; Wang, C. Recent progress on optomagnetic coupling and optical manipulation based on cavity-optomagnonics. Front. Phys. 2021, 14, 42201. [Google Scholar] [CrossRef]
- Xu, W.-L.; Liu, X.-F.; Sun, Y.; Gao, Y.-P.; Wang, T.-J.; Wang, C. Magnon-induced chaos in an optical PT-symmetric resonator. Phys. Rev. E 2020, 101, 012205. [Google Scholar] [CrossRef]
- Bender, C.M.; Brody, D.C.; Jones, H.F.; Meister, B.K. Faster than Hermitian Quantum Mechanics. Phys. Rev. Lett. 2007, 98, 040403. [Google Scholar] [CrossRef] [Green Version]
- Günther, U.; Samsonov, B.F. Naimark-dilated PT-Symmetric Brachistochrone. Phys. Rev. Lett. 2008, 101, 230404. [Google Scholar] [CrossRef] [Green Version]
- Zheng, C.; Hao, L.; Long, G.L. Observation of a Fast Evolution in a Parity-Time-Symmetric System. Philos. Trans. R. Soc. A 2013, 371, 20120053. [Google Scholar] [CrossRef] [PubMed]
- Zheng, C. Duality Quantum Simulation of a General Parity-Time-Symmetric Two-level System. EPL 2018, 123, 40002. [Google Scholar] [CrossRef]
- Wen, J.; Zheng, C.; Kong, X.; Wei, S.; Xin, T.; Long, G.L. Experimental Demonstration of a Digital Quantum Simulation of a General PT-symmetric System. Phys. Rev. A 2019, 99, 062122. [Google Scholar] [CrossRef]
- Gao, W.-C.; Zheng, C.; Liu, L.; Wang, T.-J.; Wang, C. Experimental simulation of the parity-time symmetric dynamics using photonic qubits. Opt. Exp. 2021, 29, 517–526. [Google Scholar] [CrossRef]
- Wen, J.; Zheng, C.; Ye, Z.; Xin, T.; Long, G.L. Stable states with nonzero entropy under broken PT-symmetry. Phys. Rev. Res. 2021, 3, 013256. [Google Scholar] [CrossRef]
- Zheng, C. Quantum simulation of PT-arbitrary-phase–symmetric systems. EPL 2021, 136, 30002. [Google Scholar] [CrossRef]
- Lee, T.D.; Wick, G.C. Negative Metric and the Unitarity of the S Matrix. Nucl. Phys. B 1969, 9, 209–243. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermiticity versus PT Symmetry: The Necessary Condition for the Reality of the Spectrum of a Non-Hermitian Hamiltonian. J. Math. Phys. 2002, 43, 205–243. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermiticity versus PT-symmetry. II. A complete characterization of non-Hermitian Hamiltonians with a real spectrum. J. Math. Phys. 2002, 43, 2814–2816. [Google Scholar] [CrossRef]
- Konotop, V.V.; Yang, Z.; Zezyulin, D.A. Nonlinear Waves in PT-Symmetric Systems. Rev. Mod. Phys. 2016, 88, 035002. [Google Scholar] [CrossRef] [Green Version]
- Mostafazadeh, A. Pseudo-Hermiticity versus PT-Symmetry III: Equivalence of Pseudo-Hermiticity and the Presence of Antilinear Symmetries. J. Math. Phys. 2002, 43, 3944–3951. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermiticity and generalized PT- and CPT-symmetries. J. Math. Phys. 2003, 44, 974–989. [Google Scholar] [CrossRef] [Green Version]
- Zheng, C.; Tian, J.; Li, D.; Wen, J.; Wei, S.; Li, Y.-S. Efficient quantum simulation of an anti-P-pseudo-Hermitian two-level system. Entropy 2020, 22, 812. [Google Scholar] [CrossRef] [PubMed]
- Solombrino, L. Weak Pseudo-Hermiticity and Antilinear Commutant. J. Math. Phys. 2002, 43, 5439–5445. [Google Scholar] [CrossRef] [Green Version]
- Nixon, S.; Yang, J. All-real spectra in optical systems with arbitrary gain-and-loss distributions. Phys. Rev. A 2016, 93, 031802(R). [Google Scholar] [CrossRef] [Green Version]
- Mostafazadeh, A. Time-Dependent Pseudo-Hermitian Hamiltonians and a Hidden Geometric Aspect of Quantum Mechanics. Entropy 2020, 22, 471. [Google Scholar] [CrossRef] [Green Version]
- Pinske, J.; Teuber, L.; Scheel, S. Holonomic Gates in Pseudo-Hermitian Quantum Systems. Phys. Rev. A 2019, 100, 042316. [Google Scholar] [CrossRef] [Green Version]
- Chu, Y.; Liu, Y.; Liu, H.; Cai, J. Quantum Sensing with a Single-Qubit Pseudo-Hermitian System. Phys. Rev. Lett. 2020, 124, 020501. [Google Scholar] [CrossRef] [Green Version]
- Jin, L. Unitary Scattering Protected by Pseudo-Hermiticity. Chin. Phys. Lett. 2022, 39, 037302. [Google Scholar] [CrossRef]
- Feynman, R. Simulating Physics with Computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Greiner, M.; Mandel, O.; Esslinger, T.; Hansch, T.W.; Bloch, I. Quantum Phase Transition from a Superfluid to a Mott Insulator in a Gas of Ultracold Atoms. Nature 2002, 415, 39–44. [Google Scholar] [CrossRef] [PubMed]
- Leibfried, D.; DeMarco, B.; Meyer, V.; Rowe, M.; Ben-Kish, A.; Britton, J.; Itano, W.M.; Jelenkovic, B.; Langer, C.; Rosenband, T.; et al. Trapped-Ion Quantum Simulator: Experimental Application to Nonlinear Interferometers. Phys. Rev. Lett. 2002, 89, 247901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedenauer, A.; Schmitz, H.; Glueckert, J.T.; Porras, D.; Schaetz, T. Simulating a Quantum Magnet with Trapped Ions. Nat. Phys. 2008, 4, 757–761. [Google Scholar] [CrossRef]
- Kim, K.; Chang, M.-S.; Korenblit, S.; Islam, R.; Edwards, E.E.; Freericks, J.K.; Lin, G.-D.; Duan, L.-M.; Monroe, C. Quantum Simulation of Frustrated Ising Spins with Trapped Ions. Nature 2010, 465, 590–593. [Google Scholar] [CrossRef] [PubMed]
- Lanyon, B.P.; Whitfield, J.D.; Gillett, G.G.; Goggin, M.E.; Almeida, M.P.; Kassal, I.; Biamonte, J.D.; Mohseni, M.; Powell, B.J.; Barbieri, M.; et al. Towards Quantum Chemistry on a Quantum Computer. Nat. Chem. 2010, 2, 106–111. [Google Scholar] [CrossRef] [Green Version]
- Gerritsma, R.; Kirchmair, G.; Zahringer, F.; Solano, E.; Blatt, R.; Roos, C.F. Quantum Simulation of the Dirac Equation. Nature 2010, 463, 68–71. [Google Scholar] [CrossRef] [Green Version]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum Simulation. Nature 2014, 86, 153–185. [Google Scholar] [CrossRef] [Green Version]
- Setia, K.; Bravyi, S.; Mezzacapo, A.; Whitfield, J.D. Superfast Encodings for Fermionic Quantum Simulation. Phys. Rev. Res. 2019, 1, 033033. [Google Scholar] [CrossRef] [Green Version]
- Aspuru-Guzik, A.; Walther, P. Photonic Quantum Simulators. Nat. Phys. 2012, 8, 285–291. [Google Scholar] [CrossRef] [Green Version]
- Sheng, Y.B.; Zhou, L. Distributed Secure Quantum Machine Learning. Sci. Bull. 2017, 62, 1025–1029. [Google Scholar] [CrossRef] [Green Version]
- Tranter, A.; Love, P.J.; Mintert, F.; Wiebe, N.; Coveney, P.V. Ordering of Trotterization: Impact on Errors in Quantum Simulation of Electronic Structure. Entropy 2019, 21, 1218. [Google Scholar] [CrossRef] [Green Version]
- Ge, L.; Tureci, H.E. Antisymmetric PT-Photonic Structures with Balanced Positive- and Negative-index Materials. Phys. Rev. A 2013, 88, 053810. [Google Scholar] [CrossRef] [Green Version]
- Hang, C.; Huang, G.; Konotop, V.V. PT Symmetry with a System of Three-Level Atoms. Phys. Rev. Lett. 2013, 110, 083604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antonosyan, D.A.; Solntsev, A.S.; Sukhorukov, A.A. Parity-time anti-symmetric parametric amplifier. Opt. Lett. 2015, 40, 4575–4582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, J.-H.; Artoni, M.; La Rocca, G.C. Parity-Time-Antisymmetric Atomic Lattices without Gain. Phys. Rev. A 2015, 91, 033811. [Google Scholar] [CrossRef] [Green Version]
- Peng, P.; Cao, W.; Shen, C.; Qu, W.; Wen, J.; Jiang, L.; Xiao, Y. Anti-Parity-Time Symmetry with Flying Atoms. Nat. Phys. 2016, 12, 1139–1145. [Google Scholar] [CrossRef]
- Yang, F.; Liu, Y.C.; You, L. Anti-PT Symmetry in Dissipatively Coupled Optical Systems. Phys. Rev. A 2017, 96, 053845. [Google Scholar] [CrossRef]
- Choi, Y.; Hahn, C.; Yoon, J.W.; Song, H.S. Observation of an Anti-PT-Symmetric Exceptional Point and Energy-Difference Conserving Dynamics in Electrical Circuit Resonators. Nat. Commun. 2018, 9, 2182. [Google Scholar] [CrossRef]
- Konotop, V.V.; Zezyulin, D.A. Odd-Time Reversal PT Symmetry Induced by an Anti-PT-Symmetric Medium. Phys. Rev. Lett. 2018, 120, 123902. [Google Scholar] [CrossRef] [Green Version]
- Chuang, Y.-L.; Ziauddin; Lee, R.-K. Realization of Simultaneously Parity-Time-Symmetric and Parity-Time-Antisymmetric Susceptibilities along the Longitudinal Direction in Atomic Systems with all Optical Controls. Opt. Express 2018, 26, 21969–21978. [Google Scholar] [CrossRef]
- Li, Y.; Peng, Y.-G.; Han, L.; Miri, M.-A.; Li, W.; Xiao, M.; Zhu, X.-F.; Zhao, J.; Alu, A.; Fan, S.; et al. Odd-Time Reversal PT Symmetry Induced by an Anti-PT-Symmetric Medium. Science 2019, 364, 170–173. [Google Scholar] [CrossRef] [PubMed]
- Zheng, C. Duality quantum simulation of a generalized anti-PT-symmetric two-level system. EPL 2019, 126, 30005. [Google Scholar] [CrossRef]
- Wen, J.; Qin, G.; Zheng, C.; Wei, S.; Kong, X.; Xin, T.; Long, G.L. Observation of information flow in the anti-PT-symmetric system with nuclear spins. Npj Quantum Inf. 2020, 6, 28. [Google Scholar] [CrossRef]
- Zhang, H.; Peng, M.; Xu, X.-W.; Jing, H. Anti-PT-symmetric Kerr gyroscope. Chin. Phys. B 2022, 31, 014215. [Google Scholar] [CrossRef]
- Long, G.-L. General Quantum Interference Principle and Duality Computer. Commun. Theor. Phys. 2006, 45, 825–843. [Google Scholar]
- Long, G.-L.; Liu, Y. Duality Quantum Computing. Front. Comput. Sci. 2008, 2, 167. [Google Scholar] [CrossRef]
- Long, G.-L.; Liu, Y.; Wang, C. Allowable Generalized Quantum Gates. Commun. Theor. Phys. 2009, 51, 65–67. [Google Scholar]
- Long, G.L. Duality Quantum Computing and Duality Quantum Information Processing. Int. J. Theor. Phys. 2011, 50, 1305–1318. [Google Scholar] [CrossRef]
- Cui, J.; Zhou, T.; Long, G.L. Density Matrix Formalism of Duality Quantum Computer and the Solution of Zero-Wave-Function Paradox. Quantum Inf. Process. 2012, 11, 317–323. [Google Scholar] [CrossRef]
- Qiang, X.; Zhou, X.; Wang, J.; Wilkes, C.M.; Loke, T.; O’Gara, S.; Kling, L.; Marshall, G.D.; Santagati, R.; Ralph, T.C.; et al. Large-Scale Silicon Quantum Photonics Implementing Arbitrary Two-Qubit Processing. Nat. Photon. 2018, 12, 534–539. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.-J.; Li, H.; Long, G.-L. A Full Quantum Eigensolver for Quantum Chemistry Simulations. Research 2020, 2020, 1486935. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shao, C.P.; Li, Y.; Li, H.B. Quantum Algorithm Design: Techniques and Applications. J. Syst. Sci. Complex. 2019, 32, 375–495. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin, Germany, 1966. [Google Scholar]
- Neeley, M.; Ansmann, M.; Bialczak, R.C.; Hofheinz, M.; Lucero, E.; O’Connell, A.D.; Sank, D.; Wang, H.; Wenner, J.; Cleland, A.N.; et al. Emulation of a Quantum Spin with a Superconducting Phase Qudit. Science 2009, 325, 722–725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information, 10th Anniversary ed.; Cambridge University Press: Cambridge, UK, 2010; pp. 217–226. [Google Scholar]
- Cory, D.G.; Price, M.D.; Havel, T.F. Nuclear Magnetic Resonance Spectroscopy: An Experimentally Accessible Paradigm for Quantum Computing. Physics D 2008, 120, 82–101. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.W.; Xue, K.; Ge, M.L. Optical Simulation of the Yang-Baxter Equation. Phys. Rev. A 2008, 78, 022319. [Google Scholar] [CrossRef] [Green Version]
- Knill, E.; Laflamme, R.; Milburn, G. A Scheme for Efficient Quantum Computation with Linear Optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef]
- Cerf, N.J.; Adami, C.; Kwiat, P.G. Optical Simulation of Quantum Logic. Phys. Rev. A 1998, 57, R1477(R). [Google Scholar] [CrossRef] [Green Version]
- Fan, C.-R.; Lu, B.; Feng, X.-T.; Gao, W.-C.; Wang, C. Efficient multi-qubit quantum data compression. Quantum Eng. 2021, 3, e67. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, C. Quantum Simulation of Pseudo-Hermitian-φ-Symmetric Two-Level Systems. Entropy 2022, 24, 867. https://doi.org/10.3390/e24070867
Zheng C. Quantum Simulation of Pseudo-Hermitian-φ-Symmetric Two-Level Systems. Entropy. 2022; 24(7):867. https://doi.org/10.3390/e24070867
Chicago/Turabian StyleZheng, Chao. 2022. "Quantum Simulation of Pseudo-Hermitian-φ-Symmetric Two-Level Systems" Entropy 24, no. 7: 867. https://doi.org/10.3390/e24070867
APA StyleZheng, C. (2022). Quantum Simulation of Pseudo-Hermitian-φ-Symmetric Two-Level Systems. Entropy, 24(7), 867. https://doi.org/10.3390/e24070867





