Competency in Navigating Arbitrary Spaces as an Invariant for Analyzing Cognition in Diverse Embodiments
Abstract
“Intelligence is a fixed goal with variable means of achieving it.”—William James
1. Introduction
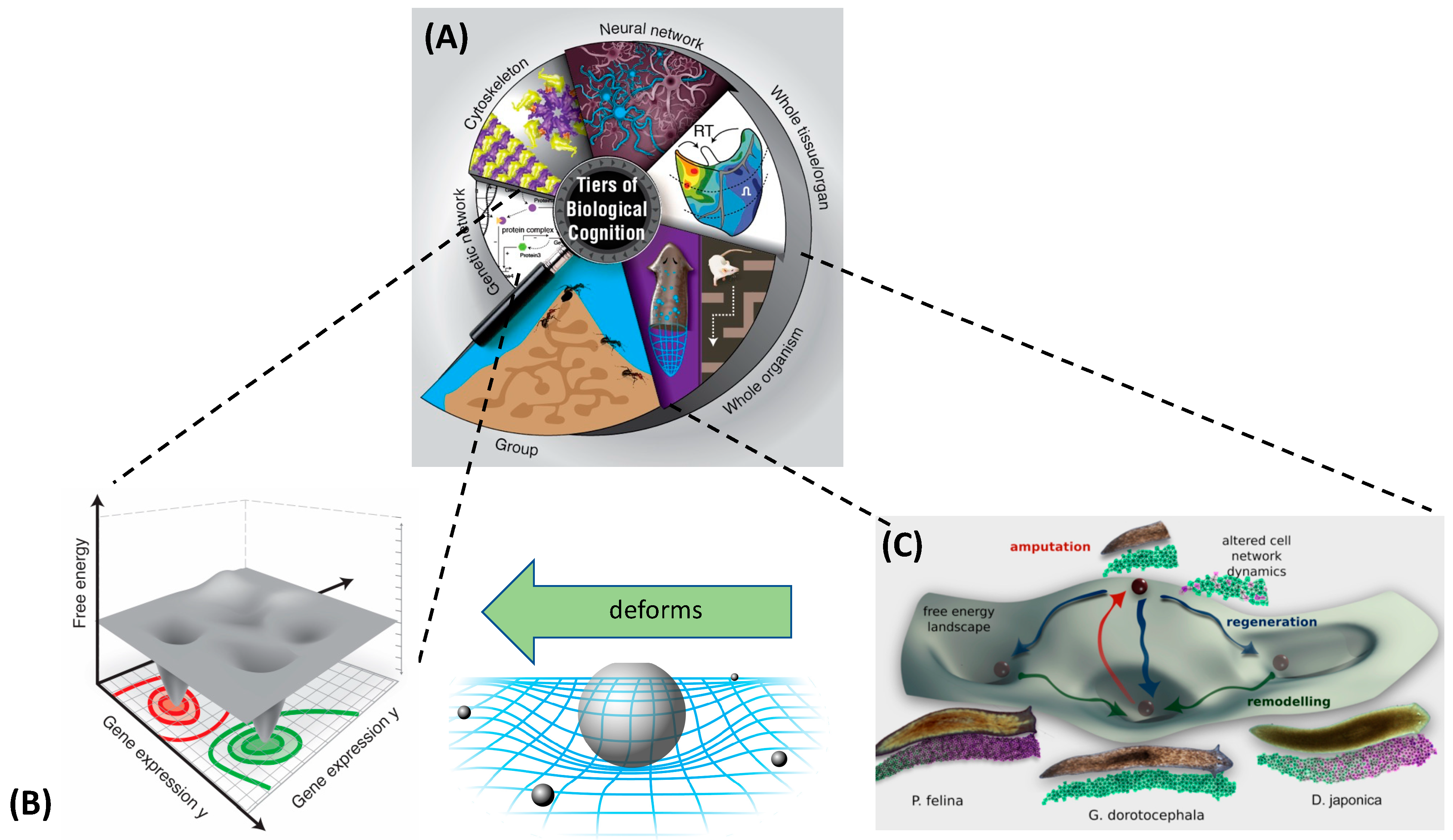
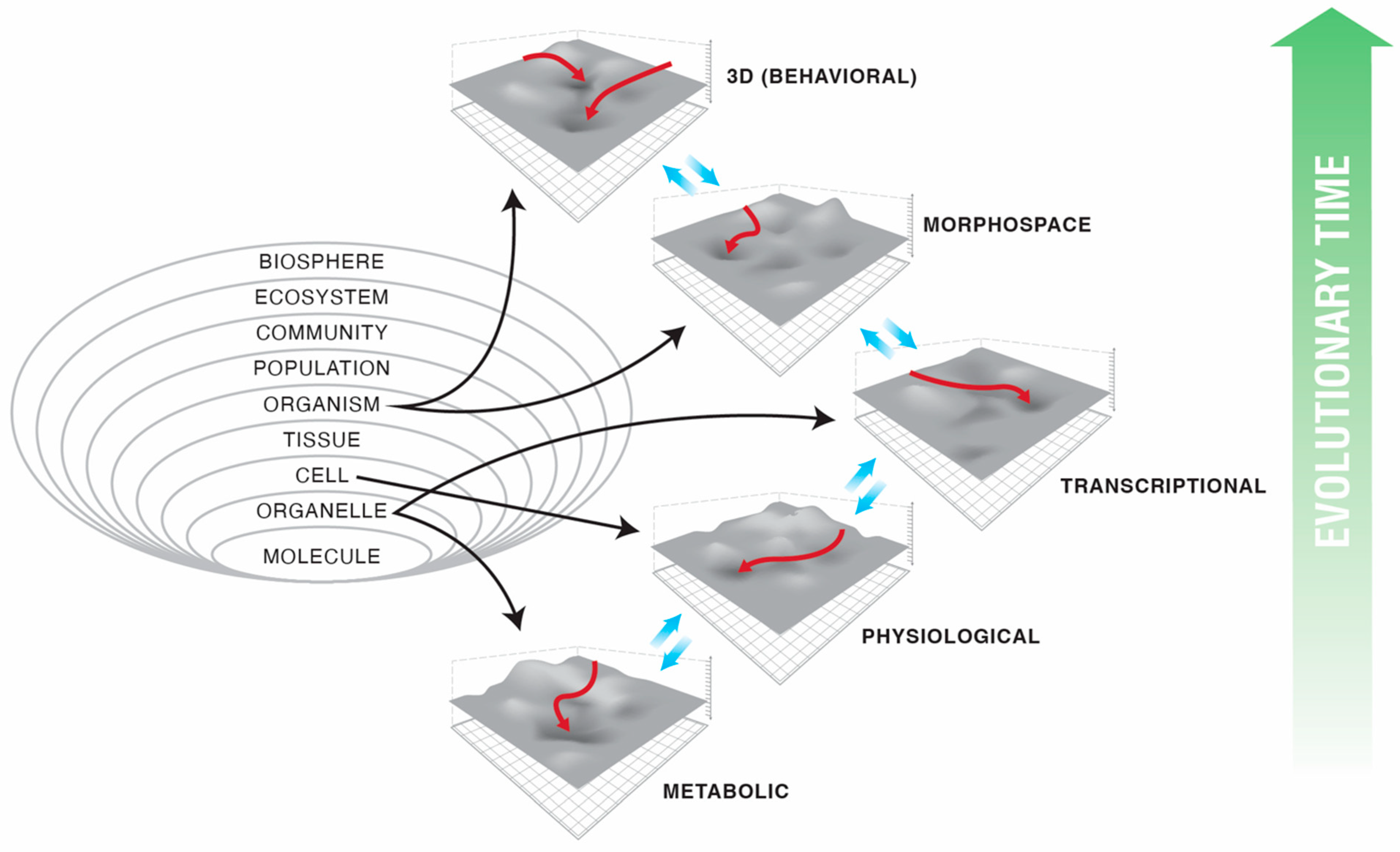
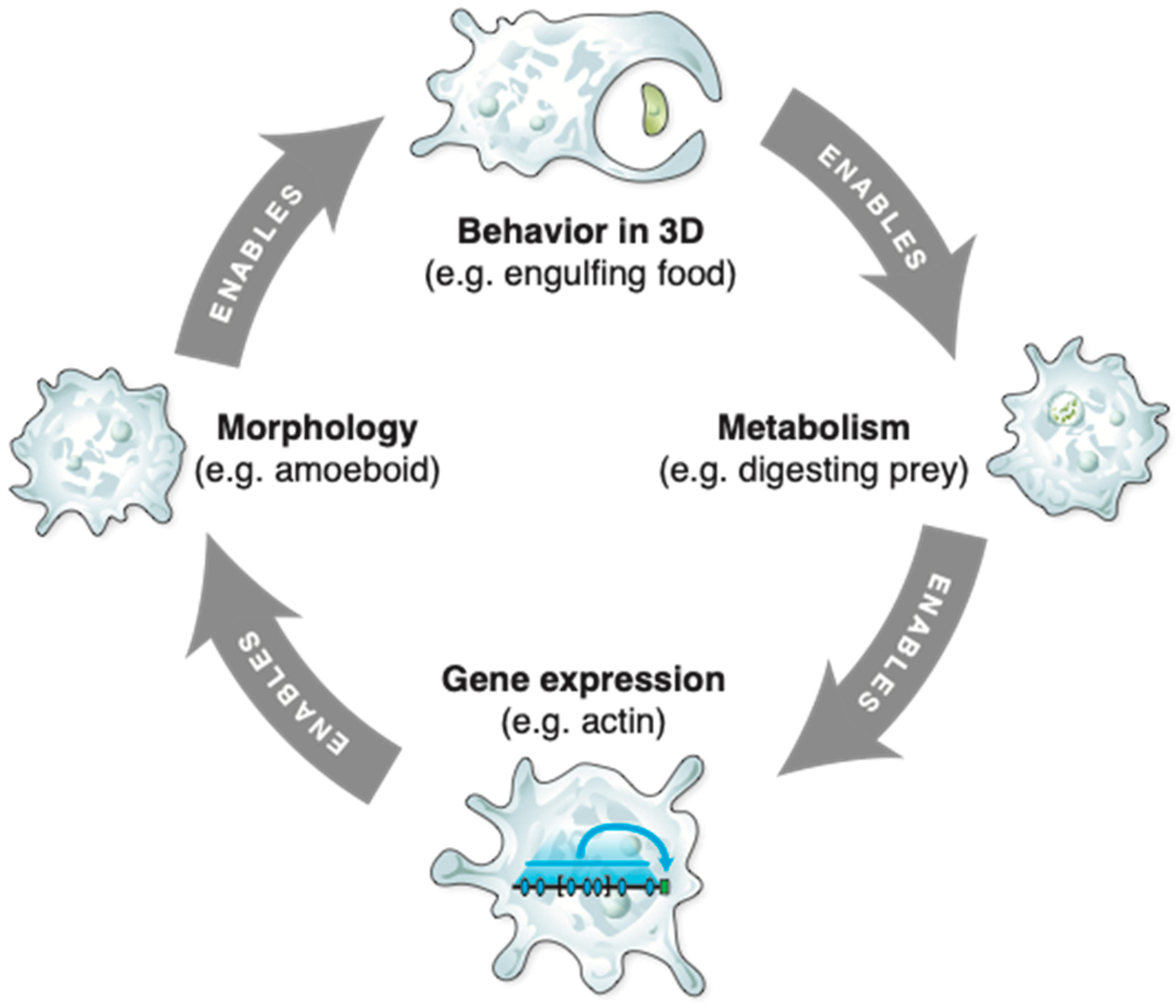
2. Abstract Spaces Reveal Behavior across Biology
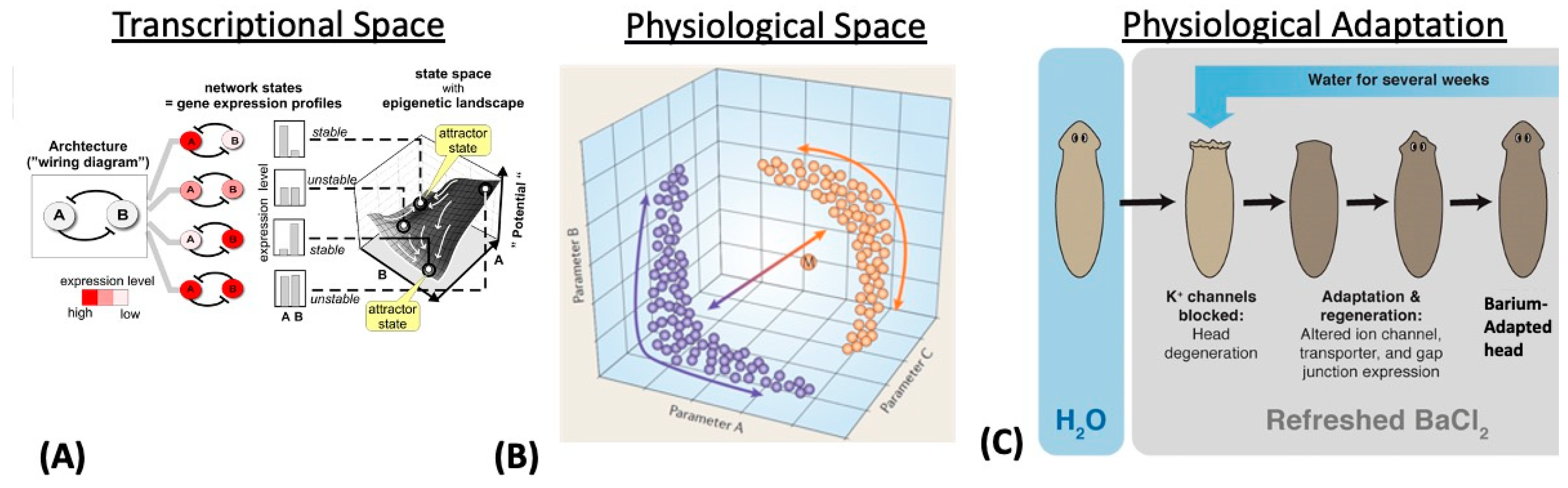
3. Transcriptional, Metabolic, and Physiological Spaces
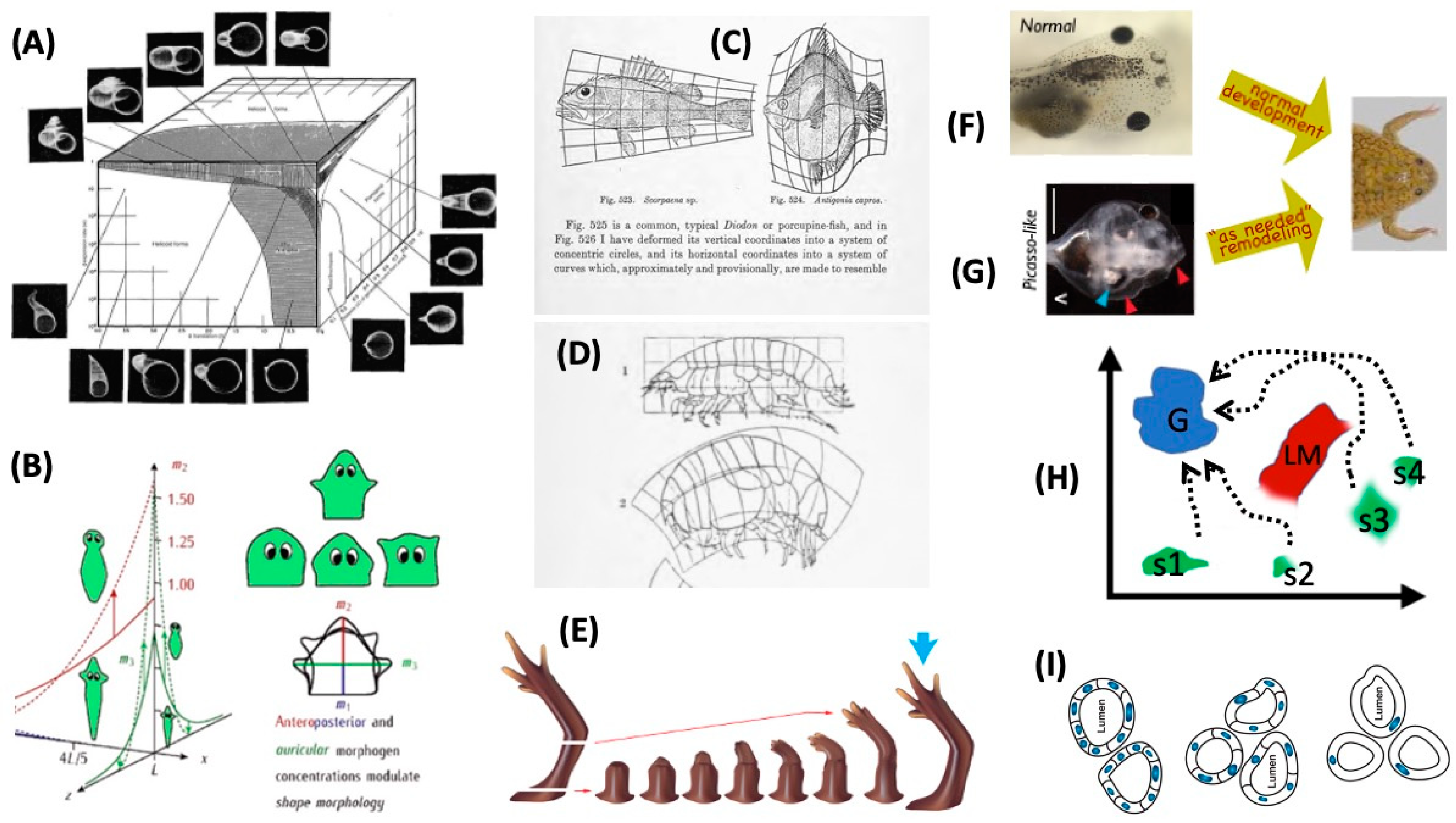
4. Morphospace: Control of Growth and Form as a Collective Intelligence
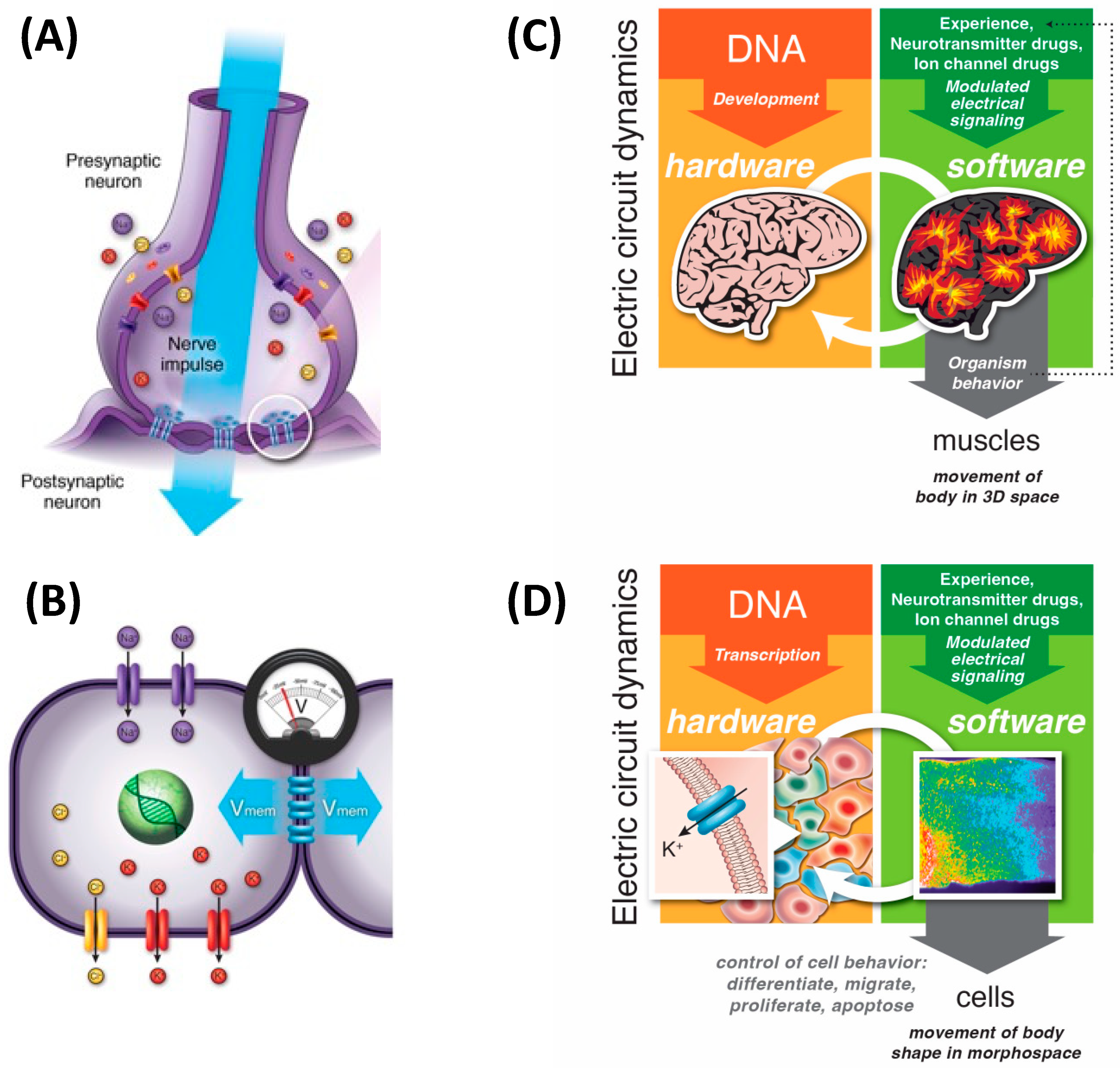
5. 3D Behavior: Movements in Space and Time
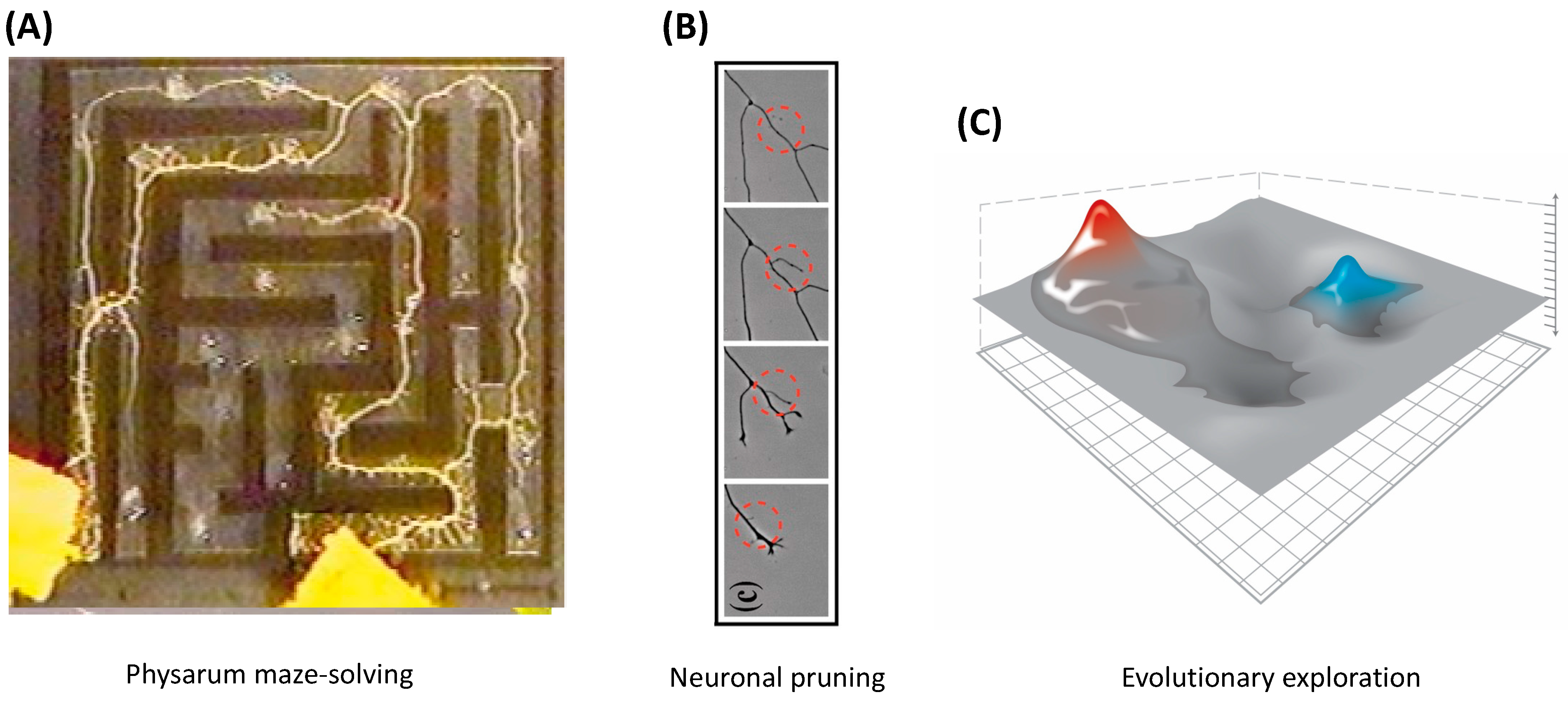
6. Navigating Arbitrary Spaces: A Powerful Invariant
7. Active Inference Generates Spaces
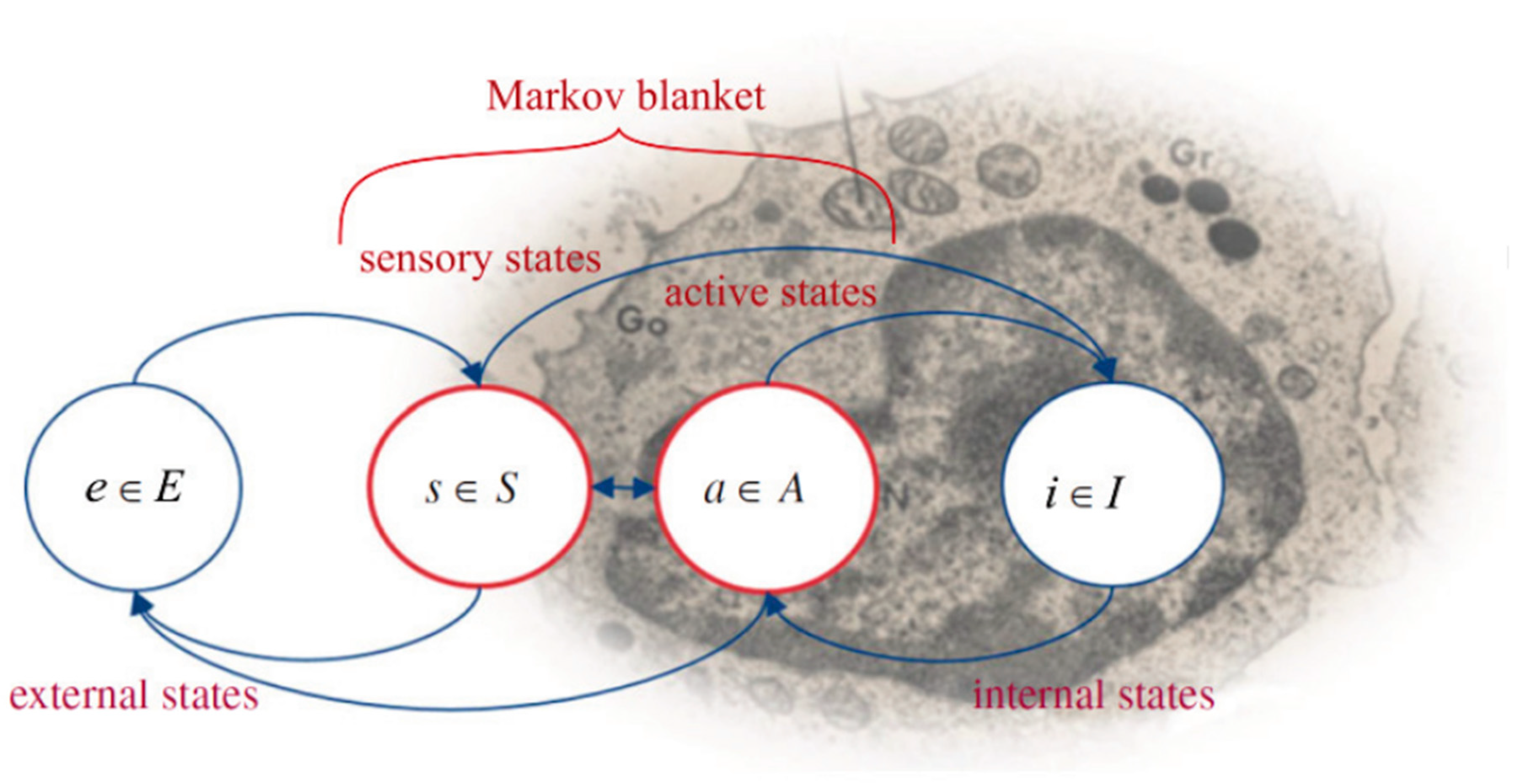
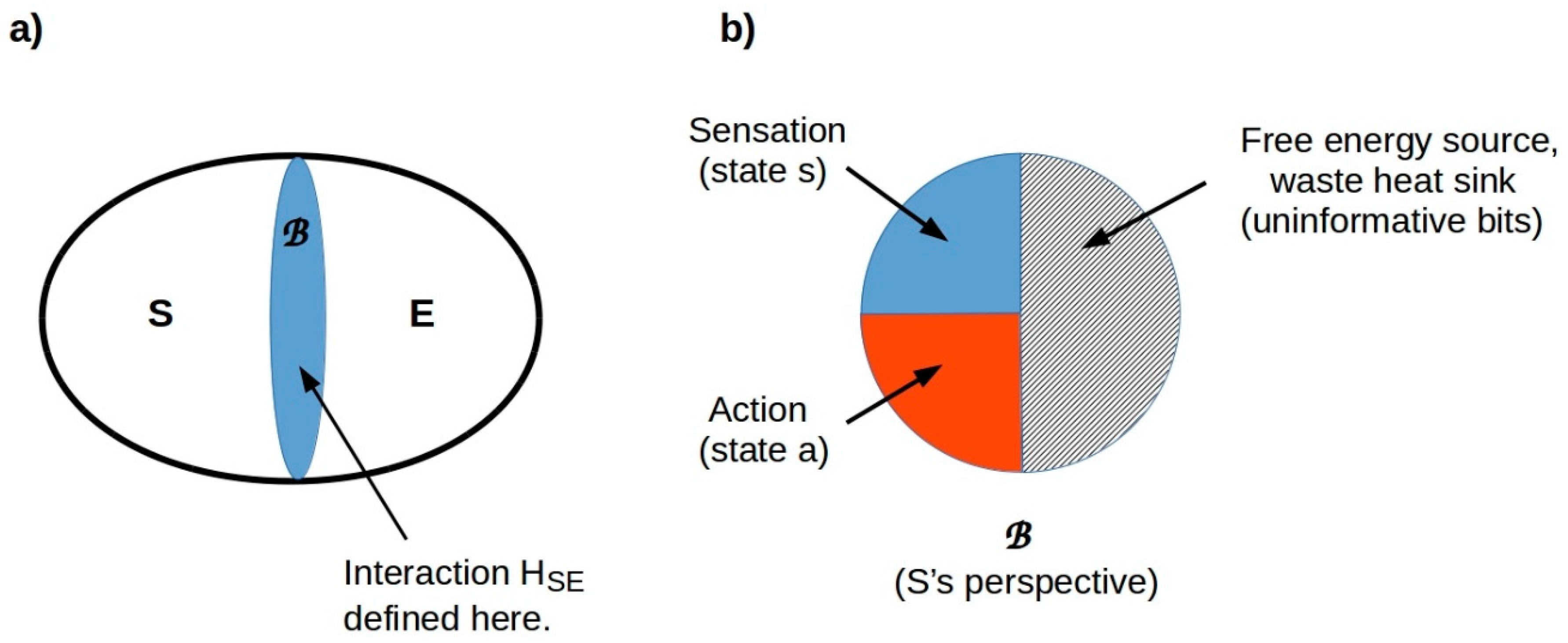
7.1. Organisms Interact with Their Environments via Markov Blankets
7.2. Behavioral “Spaces” Are Tractable Components of an Overall State Space
7.3. Problem Spaces Are Observer-Dependent
7.4. Tractable Spaces Correspond to Perception and Action Modules
7.5. Experimentally Probing a System’s QRFs
7.6. Common Inference Mechanisms Induce Symmetries between Spaces
8. Implications: A Research Program
8.1. Conceptual Questions and Further Links to Develop
- While higher-level systems bend action spaces for lower-level subsystems, it can be predicted that the higher level no longer needs to operate in a very rugged space of microstates. Instead, evolution can search a coarse-grained space of interventions, which also includes changing the resource availability landscapes at both the lower and higher levels (e.g., inventing a mouth and a specialized digestive system). Computational models can be created to quantify the efficiency gains of evolutionary search in such multi-scale competency systems.
- Links can be made to higher levels of cognitive activity and neuroscience. For example, yoga and biofeedback can be seen as ways for systems to forge new links between higher- and lower-level measurables. Gaining control over formerly autonomic system functions is akin to rerunning causal analysis functions on oneself to discover new axes in physiological spaces that the higher-level self did not previously have actuators for. Such processes clearly depend on interoception, a process for which active inference models are now well-developed [206,207], and being integrated with models of perception in a shared memory global workspace architecture [208].
- More broadly, models of space traversal help flesh out a true continuum of agency, placing simple systems that only know how to “roll down a hill” on the same overall spectrum as psychological systems that minimize complex cognitive stress states. Concepts related to free energy help provide a single framework that is required to explain how complex minds emerge from “just physics” without magical discontinuities in evolution or development. The capacity to traverse a space without getting caught in local optima can be developed into a formal definition of IQ for a system in that space. This links naturally to the work in morphological computation and embodied cognition because body shape determines the IQ of traversing a 3D behavioral space. How does this extend into other spaces? Many fascinating conceptual links can be developed to work on embodied premotor cognition in math, causal reasoning, general planning, etc. [209,210,211].
- How do cells, both native and after modification via synthetic biology tools, make internal models of their “body shape” in unconventional spaces, such as a transcriptional space? Cells in vitro can learn to control flight simulators [212], as can people with BCIs [213]. Brains can learn to control prosthetic limbs with new degrees of freedom [214]. What self- and world-modeling capacities are invariant across such problem spaces?
- The tight link we have developed between motion in spaces and degrees of cognition across scales suggests that it may be possible to develop models of evolutionary search itself as a kind of meta-agent searching the fitness space via active inference and other strategies [62,63,215,216]. In this light, evolution is still not claimed to be a complex meta-cognitive agent that is knowingly seeking specific ends, but on the other hand, it may not be completely blind either. It may be possible to develop models of minimal information processing that better explain the ability of the evolutionary process to solve problems, to choose which problems to solve, and to give rise to architectures that not only provide immediate fitness payoffs but also perform well in entirely new environments.
- A key opportunity for new theory concerns what tools could be developed for a system to detect that it is part of a larger system that is deforming its action space with nonzero agency. It may not be possible due to the Gödelian limits for a system to fathom the actual goals of the larger system, of which it forms a part, but how does an intelligent system gain evidence that it is part of an agent with some “grand design” versus living in a cold, mechanical universe that does not care what the parts do? The Lovecraftian horror of catching a glimpse of the fact that one is a cog in a grandiose intelligent system may be tempered by mathematical tools that enable us to have more agency over which aspects of the externally applied gradients we wish to fight against and which gradients we gladly roll down.
- We foresee great promise in the application of the mathematical framework of category theory [217,218], which provides the conceptual and formal tools needed to model the relationships between arbitrary spaces. Any of the spaces discussed here, together with the search operations acting within that space, can be considered a category. The theory provides, in this case, rigorous tools for determining whether multiple paths through the space yield the same outcome and, even more interestingly, whether paths through different spaces, such as a path in a morphological space or a path in a 3D behavioral space, yield the same outcome. We defer such analysis to future work. Some preliminary steps in this direction, characterizing arbitrary QRFs as category-theoretic constructs, can be found in [170,178].
- There are numerous analogies to be explored with respect to porting conceptual tools from relativity to study scale-free cognition. The use of cognitive geometry and infodesics [219] ties naturally to general relativity. Other examples include the following:
- ○
- Gravitational memory (permanent distortions of spacetime by gravitational waves [220]) to link the structure of action spaces to past experience;
- ○
- Inertia in terms of resilience to stress (anatomical homeostasis as a kind of inertia against movement in the morphospace and other spaces);
- ○
- Acceleration and force in a network space, where every connection in a network could be modeled via a “spring constant” or, even better, an LRC circuit. With feedback, interesting oscillations can appear, which can be harnessed as computations;
- ○
- The ability of one system to warp the action space for another, such as warping the morphospace for the embryonic head by specific organ movements, generates an analog of “mass”;
- ○
- Bioelectric circuits could be modeled as warping the morphospace in the same way wormholes warp physical space. The two points at opposite ends of a wire are, for informational purposes, the same point, even if they are on opposite sides of the embryo. Neal Stephenson stated, “The cyberspace-warping power of wires, therefore, changes the geometry of the world of commerce and politics and ideas that we live in’’ [221]. The gap junctions’ control of morphogenetic bioelectric communication deforms the physiological space to overcome distance in the anatomical space. Neurons do this too, as do mechanical stress in connective tissue and hormones;
- ○
- Links also could be made to concepts of special relativity. For example, doppler effects in morphogenesis have already been described [222]. Moreover, the limited speed at which information can propagate through tissue naturally defines a minimal “now” moment, a temporal thickness for the integrated agent below which only submodules exist, in effect illustrating the relatedness of space and time by the propagation speed of information signals within living systems.
8.2. Specific Empirical Research Directions
- Specific models of morphogenetic control (embryogenesis, regeneration, cancer, etc.) that rely on navigation policies with diverse levels of cognitive sophistication need to be created and empirically tested. Can craniofacial remodeling be understood as a “run and tumble” strategy? Can evolution of morphogenetic control circuits be understood as the evolution of abstract vehicle navigation skills, thus porting knowledge from evolutionary robotics and collective intelligence to developmental biology [157,223,224,225]?
- Similarly, such models need to be developed to understand allostasis in transcriptional, metabolic, and physiological spaces, modeling and then developing minimal Braitenberg vehicles [44,226,227,228,229] as real devices to implement biomedical interventions such as smart insulin and neurotransmitter delivery devices.
- Regenerative medicine needs to be moved beyond an exclusive focus on the micro-level hardware (genomic editing and protein pathway engineering) to include interventions at higher levels. Using tools from behavioral science such as training in various learning assays can manipulate the lower-dimensional and smoother space of tissue- and organ-level incentives (described in more detail in [35,36]). Much as evolution exploits multi-scale competency to maximize the adaptive gains per change made, bioengineers and workers in regenerative medicine can take advantage of behavior shaping of cellular agendas and plasticity, working in a reward space. Interestingly, this was well-appreciated by Pavlov, whose early work included training animals’ organs in addition to the animals themselves. He understood the physiological space, and his experiments on training the pancreas and other body systems can now be performed with much higher-resolution tools. More broadly, impacting and incentivizing decision-making modules at higher levels is much more likely to produce coordinated, coherent outcomes than interventions at lower levels [230], resulting in fewer side effects in pharmacology and avoiding unhappy monsters in synthetic bioengineering. The future of biomedicine will look much more like communication (with unconventional intelligences in the body) than mechanical control at the molecular pathway level. This includes signaling to exploit the control policies of cells in the morphospace for regenerative control of growth and form [35,36] and exploiting gene-regulatory networks’ abilities to learn from experience to modify how they move in the transcriptional space while healthy and in the case of disease [79,83,231,232,233,234,235].
- Computer engineering and robotics also afford many opportunities for testing and applying this framework. Incorporating biological concepts into a computing system design has been explored in the abstract [236,237], at the level of system design [238,239], and with neuromorphic hardware [240,241]. The present work suggests further directions, including developing frameworks for working with agential materials (like the cells that make up Xenobots), which requires distinct strategies from those used with passive materials or even active matter [242,243,244,245], creating evolutionary simulations and human use tools to explicitly address multiple scales of organization and problem solving.
- More broadly, artificial intelligence can benefit from enhancing current neuromorphic approaches with systems based on much more general, ancient intelligence, creating systems with motivation and agency from the ground up by taking embodiment seriously from an evolutionary perspective. The classic Dennett and Minsky debate about how much real-world embodiment matters for artificial intelligence can now be reframed in more general terms: embodiment is critical indeed, but it does not have to be in the classic 3D space. Embodiment in other action spaces can drive the same intelligence ratchet described above. New general AIs are likely to be developed gradually from minimal systems driven by the dynamics described above, which eventually scale homeostatic action into advanced metacognition. One specific strategy that can be suggested is the creation of an unsupervised agency estimator, which seeks to make models of its environment anywhere on the spectrum of persuadability [9]. This system will not only be useful for human scientists (freeing their hypothesis-making from the mindblindness [246] that limits imagination with respect to unconventional intelligences); it can also be used in an “adversarial” mode with evolving intelligences, a cycle that increasingly potentiates both the intelligence and the ability to detect it.
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- James, W. The Principles of Psychology; H. Holt and Company: New York, NY, USA, 1890. [Google Scholar]
- Rosenblueth, A.; Wiener, N.; Bigelow, J. Behavior, purpose, and teleology. Philos. Sci. 1943, 10, 18–24. [Google Scholar] [CrossRef]
- Krupenye, C.; Call, J. Theory of mind in animals: Current and future directions. Wiley Interdiscip. Rev. Cogn. Sci. 2019, 10, e1503. [Google Scholar] [CrossRef]
- Balázsi, G.; van Oudenaarden, A.; Collins, J.J. Cellular decision making and biological noise: From microbes to mammals. Cell 2011, 144, 910–925. [Google Scholar] [CrossRef] [PubMed]
- Baluška, F.; Levin, M. On Having No Head: Cognition throughout Biological Systems. Front. Psychol. 2016, 7, 902. [Google Scholar] [CrossRef]
- Keijzer, F.; van Duijn, M.; Lyon, P. What nervous systems do: Early evolution, input-output, and the skin brain thesis. Adapt. Behav. 2013, 21, 67–85. [Google Scholar] [CrossRef]
- Lyon, P. The biogenic approach to cognition. Cogn. Process. 2006, 7, 11–29. [Google Scholar] [CrossRef] [PubMed]
- Lyon, P. The cognitive cell: Bacterial behavior reconsidered. Front. Microbiol. 2015, 6, 264. [Google Scholar] [CrossRef] [PubMed]
- Levin, M. Technological Approach to Mind Everywhere: An Experimentally-Grounded Framework for Understanding Diverse Bodies and Minds. Front. Syst. Neurosci. 2022, 16, 768201. [Google Scholar] [CrossRef]
- Westerhoff, H.V.; Brooks, A.N.; Simeonidis, E.; Garcia-Contreras, R.; He, F.; Boogerd, F.C.; Jackson, V.J.; Goncharuk, V.; Kolodkin, A. Macromolecular networks and intelligence in microorganisms. Front. Microbiol. 2014, 5, 379. [Google Scholar] [CrossRef]
- Ando, N.; Kanzaki, R. Insect-machine hybrid robot. Curr. Opin. Insect Sci. 2020, 42, 61–69. [Google Scholar] [CrossRef]
- Dong, X.; Kheiri, S.; Lu, Y.; Xu, Z.; Zhen, M.; Liu, X. Toward a living soft microrobot through optogenetic locomotion control of Caenorhabditis elegans. Sci. Robot. 2021, 6, eabe3950. [Google Scholar] [CrossRef] [PubMed]
- Saha, D.; Mehta, D.; Altan, E.; Chandak, R.; Traner, M.; Lo, R.; Gupta, P.; Singamaneni, S.; Chakrabartty, S.; Raman, B. Explosive sensing with insect-based biorobots. Biosens. Bioelectron. X 2020, 6, 100050. [Google Scholar] [CrossRef]
- Bakkum, D.J.; Chao, Z.C.; Gamblen, P.; Ben-Ary, G.; Shkolnik, A.G.; DeMarse, T.B.; Potter, S.M. Embodying cultured networks with a robotic drawing arm. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 2996–2999. [Google Scholar]
- Bakkum, D.J.; Gamblen, P.M.; Ben-Ary, G.; Chao, Z.C.; Potter, S.M. MEART: The Semi-Living Artist. Front. Neurorobot. 2007, 1, 5. [Google Scholar] [CrossRef] [PubMed]
- DeMarse, T.B.; Wagenaar, D.A.; Blau, A.W.; Potter, S.M. The Neurally Controlled Animat: Biological Brains Acting with Simulated Bodies. Auton. Robot. 2001, 11, 305–310. [Google Scholar] [CrossRef]
- Ebrahimkhani, M.R.; Levin, M. Synthetic living machines: A new window on life. iScience 2021, 24, 102505. [Google Scholar] [CrossRef] [PubMed]
- Merritt, T.; Hamidi, F.; Alistar, M.; DeMenezes, M. Living media interfaces: A multi-perspective analysis of biological materials for interaction. Digit. Creat. 2020, 31, 1–21. [Google Scholar] [CrossRef]
- Potter, S.M.; Wagenaar, D.A.; Madhavan, R.; DeMarse, T.B. Long-term bidirectional neuron interfaces for robotic control, and in vitro learning studies. In Proceedings of the 25th Annual International Conference of the Ieee Engineering in Medicine and Biology Society, Cancun, Mexico, 17–21 September 2003; pp. 3690–3693. [Google Scholar]
- Ricotti, L.; Trimmer, B.; Feinberg, A.W.; Raman, R.; Parker, K.K.; Bashir, R.; Sitti, M.; Martel, S.; Dario, P.; Menciassi, A. Biohybrid actuators for robotics: A review of devices actuated by living cells. Sci. Robot. 2017, 2, aaq0495. [Google Scholar] [CrossRef]
- Tsuda, S.; Artmann, S.; Zauner, K.-P. The Phi-Bot: A Robot Controlled by a Slime Mould. In Artificial Life Models in Hardware; Adamatzky, A., Komosinski, M., Eds.; Springer: London, UK, 2009; pp. 213–232. [Google Scholar]
- Warwick, K.; Nasuto, S.J.; Becerra, V.M.; Whalley, B.J. Experiments with an In-Vitro Robot Brain. In Computing with Instinct: Rediscovering Artificial Intelligence; Cai, Y., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; pp. 1–15. [Google Scholar]
- Bongard, J.; Levin, M. Living Things Are Not (20th Century) Machines: Updating Mechanism Metaphors in Light of the Modern Science of Machine Behavior. Front. Ecol. Evol. 2021, 9, 650726. [Google Scholar] [CrossRef]
- Davies, J.A.; Glykofrydis, F. Engineering pattern formation and morphogenesis. Biochem. Soc. Trans. 2020, 48, 1177–1185. [Google Scholar] [CrossRef]
- Kriegman, S.; Blackiston, D.; Levin, M.; Bongard, J. A scalable pipeline for designing reconfigurable organisms. Proc. Natl. Acad. Sci. USA 2020, 117, 1853–1859. [Google Scholar] [CrossRef]
- Constant, A.; Ramstead, M.J.D.; Veissiere, S.P.L.; Campbell, J.O.; Friston, K.J. A variational approach to niche construction. J. R. Soc. Interface 2018, 15, 20170685. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. Life as we know it. J. R. Soc. Interface 2013, 10, 20130475. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. Active inference and free energy. Behav. Brain Sci. 2013, 36, 212–213. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J.; Daunizeau, J.; Kilner, J.; Kiebel, S.J. Action and behavior: A free-energy formulation. Biol. Cybern 2010, 102, 227–260. [Google Scholar] [CrossRef]
- Sengupta, B.; Stemmler, M.B.; Friston, K.J. Information and efficiency in the nervous system—A synthesis. PLoS Comput. Biol. 2013, 9, e1003157. [Google Scholar] [CrossRef]
- Emmons-Bell, M.; Durant, F.; Hammelman, J.; Bessonov, N.; Volpert, V.; Morokuma, J.; Pinet, K.; Adams, D.S.; Pietak, A.; Lobo, D.; et al. Gap Junctional Blockade Stochastically Induces Different Species-Specific Head Anatomies in Genetically Wild-Type Girardia dorotocephala Flatworms. Int. J. Mol. Sci. 2015, 16, 27865–27896. [Google Scholar] [CrossRef]
- Gerhart, J.; Kirschner, M. The theory of facilitated variation. Proc. Natl. Acad. Sci. USA 2007, 104 (Suppl. S1), 8582–8589. [Google Scholar] [CrossRef]
- Wagner, A. Arrival of the Fittest: Solving Evolution’s Greatest Puzzle; Penguin Group: New York, NY, USA, 2014. [Google Scholar]
- Levin, M. The wisdom of the body: Future techniques and approaches to morphogenetic fields in regenerative medicine, developmental biology and cancer. Regen. Med. 2011, 6, 667–673. [Google Scholar] [CrossRef]
- Pezzulo, G.; Levin, M. Re-membering the body: Applications of computational neuroscience to the top-down control of regeneration of limbs and other complex organs. Integr. Biol. 2015, 7, 1487–1517. [Google Scholar] [CrossRef]
- Pezzulo, G.; Levin, M. Top-down models in biology: Explanation and control of complex living systems above the molecular level. J. R. Soc. Interface 2016, 13, 20160555. [Google Scholar] [CrossRef]
- Lobo, D.; Solano, M.; Bubenik, G.A.; Levin, M. A linear-encoding model explains the variability of the target morphology in regeneration. J. R. Soc. Interface 2014, 11, 20130918. [Google Scholar] [CrossRef] [PubMed]
- Mathews, J.; Levin, M. The body electric 2.0: Recent advances in developmental bioelectricity for regenerative and synthetic bioengineering. Curr. Opin. Biotechnol. 2018, 52, 134–144. [Google Scholar] [CrossRef] [PubMed]
- Ashby, W.R. Design for a Brain: The Origin of Adaptive Behavior; Chapman & Hall: London, UK, 1952. [Google Scholar]
- Maturana, H.R.; Varela, F.J. Autopoiesis and Cognition: The Realization of the Living; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1980. [Google Scholar]
- Pattee, H.H. Cell Psychology: An Evolutionary Approach to the Symbol-Matter Problem. Cogn. Brain Theory 1982, 5, 325–341. [Google Scholar]
- Rosen, R. Anticipatory Systems: Philosophical, Mathematical, and Methodological Foundations, 1st ed.; Pergamon Press: Oxford, UK; New York, NY, USA, 1985. [Google Scholar]
- Rosen, R. On Information and Complexity. In Complexity, Language, and Life: Mathematical Approaches; Casti, J.L., Karlqvist, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; Volume 16, pp. 174–196. [Google Scholar]
- Braitenberg, V. Vehicles, Experiments in Synthetic Psychology; MIT Press: Cambridge, MA, USA, 1984; 152p. [Google Scholar]
- Klyubin, A.S.; Polani, D.; Nehaniv, C.L. Empowerment: A universal agent-centric measure of control. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–4 September 2005; pp. 128–135. [Google Scholar]
- Vernon, D.; Thill, S.; Ziemke, T. The Role of Intention in Cognitive Robotics. In Toward Robotic Socially Believable Behaving Systems; Esposito, A., Jain, L., Eds.; Intelligent Systems Reference Library; Springer: Cham, Switzerland, 2016; Volume 1, pp. 15–27. [Google Scholar]
- Vernon, D.; Lowe, R.; Thill, S.; Ziemke, T. Embodied cognition and circular causality: On the role of constitutive autonomy in the reciprocal coupling of perception and action. Front. Psychol. 2015, 6, 1660. [Google Scholar] [CrossRef] [PubMed]
- Ziemke, T.; Thill, S. Robots are not Embodied! Conceptions of Embodiment and their Implications for Social Human-Robot Interaction. Front. Artif. Intell. Appl. 2014, 273, 49–53. [Google Scholar] [CrossRef]
- Ziemke, T. On the role of emotion in biological and robotic autonomy. Biosystems 2008, 91, 401–408. [Google Scholar] [CrossRef]
- Ziemke, T. The embodied self—Theories, hunches and robot models. J. Conscious. Stud. 2007, 14, 167–179. [Google Scholar]
- Ziemke, T. Cybernetics and embodied cognition: On the construction of realities in organisms and robots. Kybernetes 2005, 34, 118–128. [Google Scholar] [CrossRef]
- Sharkey, N.; Ziemke, T. Life, mind, and robots—The ins and outs of embodied cognition. In Hybrid Neural Systems; Wermter, S., Sun, R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1778, pp. 313–332. [Google Scholar]
- Toro, J.; Kiverstein, J.; Rietveld, E. The Ecological-Enactive Model of Disability: Why Disability Does Not Entail Pathological Embodiment. Front. Psychol. 2020, 11, 1162. [Google Scholar] [CrossRef]
- Kiverstein, J. The meaning of embodiment. Top Cogn. Sci. 2012, 4, 740–758. [Google Scholar] [CrossRef]
- Altschul, S.F. Amino acid substitution matrices from an information theoretic perspective. J. Mol. Biol. 1991, 219, 555–565. [Google Scholar] [CrossRef]
- Kaneko, K. Characterization of stem cells and cancer cells on the basis of gene expression profile stability, plasticity, and robustness: Dynamical systems theory of gene expressions under cell-cell interaction explains mutational robustness of differentiated cells and suggests how cancer cells emerge. Bioessays 2011, 33, 403–413. [Google Scholar] [PubMed]
- Morgan, C.L. Other minds than ours. In Review of An Introduction to Comparative Psychology, New ed.; Morgan, C.L., Ed.; Walter Scott Publishing Company: London, UK, 1903; pp. 36–59. [Google Scholar]
- Bui, T.T.; Selvarajoo, K. Attractor Concepts to Evaluate the Transcriptome-wide Dynamics Guiding Anaerobic to Aerobic State Transition in Escherichia coli. Sci. Rep. 2020, 10, 5878. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Ernberg, I.; Kauffman, S. Cancer attractors: A systems view of tumors from a gene network dynamics and developmental perspective. Semin. Cell Dev. Biol. 2009, 20, 869–876. [Google Scholar] [CrossRef]
- Li, Q.; Wennborg, A.; Aurell, E.; Dekel, E.; Zou, J.Z.; Xu, Y.; Huang, S.; Ernberg, I. Dynamics inside the cancer cell attractor reveal cell heterogeneity, limits of stability, and escape. Proc. Natl. Acad. Sci. USA 2016, 113, 2672–2677. [Google Scholar] [CrossRef]
- Zhou, P.J.; Wang, S.X.; Li, T.J.; Nie, Q. Dissecting transition cells from single-cell transcriptome data through multiscale stochastic dynamics. Nat. Commun. 2021, 12, 5609. [Google Scholar] [CrossRef]
- Fields, C.; Levin, M. Does Evolution Have a Target Morphology? Org. J. Biol. Sci. 2020, 4, 57–76. [Google Scholar] [CrossRef]
- Fields, C.; Levin, M. Scale-Free Biology: Integrating Evolutionary and Developmental Thinking. Bioessays 2020, 42, e1900228. [Google Scholar] [CrossRef]
- Hamood, A.W.; Marder, E. Animal-to-Animal Variability in Neuromodulation and Circuit Function. Cold Spring Harb. Symp. Quant. Biol. 2014, 79, 21–28. [Google Scholar] [CrossRef][Green Version]
- O’Leary, T.; Williams, A.H.; Franci, A.; Marder, E. Cell types, network homeostasis, and pathological compensation from a biologically plausible ion channel expression model. Neuron 2014, 82, 809–821. [Google Scholar] [CrossRef]
- Ori, H.; Marder, E.; Marom, S. Cellular function given parametric variation in the Hodgkin and Huxley model of excitability. Proc. Natl. Acad. Sci. USA 2018, 115, E8211–E8218. [Google Scholar] [CrossRef] [PubMed]
- Barkai, N.; Leibler, S. Robustness in simple biochemical networks. Nature 1997, 387, 913–917. [Google Scholar] [CrossRef] [PubMed]
- Kochanowski, K.; Okano, H.; Patsalo, V.; Williamson, J.; Sauer, U.; Hwa, T. Global coordination of metabolic pathways in Escherichia coli by active and passive regulation. Mol. Syst. Biol. 2021, 17, e10064. [Google Scholar] [CrossRef]
- Mosteiro, L.; Hariri, H.; van den Ameele, J. Metabolic decisions in development and disease. Development 2021, 148, dev199609. [Google Scholar] [CrossRef] [PubMed]
- Marder, E.; Goaillard, J.M. Variability, compensation and homeostasis in neuron and network function. Nat. Rev. Neurosci. 2006, 7, 563–574. [Google Scholar] [CrossRef]
- Emmons-Bell, M.; Durant, F.; Tung, A.; Pietak, A.; Miller, K.; Kane, A.; Martyniuk, C.J.; Davidian, D.; Morokuma, J.; Levin, M. Regenerative Adaptation to Electrochemical Perturbation in Planaria: A Molecular Analysis of Physiological Plasticity. iScience 2019, 22, 147–165. [Google Scholar] [CrossRef]
- Bassel, G.W. Information Processing and Distributed Computation in Plant Organs. Trends Plant Sci. 2018, 23, 994–1005. [Google Scholar] [CrossRef]
- Elgart, M.; Snir, O.; Soen, Y. Stress-mediated tuning of developmental robustness and plasticity in flies. Biochim. Biophys. Acta 2015, 1849, 462–466. [Google Scholar] [CrossRef]
- Schreier, H.I.; Soen, Y.; Brenner, N. Exploratory adaptation in large random networks. Nat. Commun. 2017, 8, 14826. [Google Scholar] [CrossRef]
- Soen, Y.; Knafo, M.; Elgart, M. A principle of organization which facilitates broad Lamarckian-like adaptations by improvisation. Biol. Direct 2015, 10, 68. [Google Scholar] [CrossRef]
- Millard, P.; Smallbone, K.; Mendes, P. Metabolic regulation is sufficient for global and robust coordination of glucose uptake, catabolism, energy production and growth in Escherichia coli. PLoS Comput. Biol. 2017, 13, e1005396. [Google Scholar] [CrossRef] [PubMed]
- Ledezma-Tejeida, D.; Schastnaya, E.; Sauer, U. Metabolism as a signal generator in bacteria. Curr. Opin. Syst. Biol. 2021, 28, 100404. [Google Scholar] [CrossRef]
- Kuchling, F.; Fields, C.; Levin, M. Metacognition as a Consequence of Competing Evolutionary Time Scales. Entropy 2022, 24, 601. [Google Scholar] [CrossRef] [PubMed]
- Biswas, S.; Manicka, S.; Hoel, E.; Levin, M. Gene regulatory networks exhibit several kinds of memory: Quantification of memory in biological and random transcriptional networks. iScience 2021, 24, 102131. [Google Scholar] [CrossRef] [PubMed]
- Fernando, C.T.; Liekens, A.M.; Bingle, L.E.; Beck, C.; Lenser, T.; Stekel, D.J.; Rowe, J.E. Molecular circuits for associative learning in single-celled organisms. J. R. Soc. Interface 2009, 6, 463–469. [Google Scholar] [CrossRef]
- McGregor, S.; Vasas, V.; Husbands, P.; Fernando, C. Evolution of associative learning in chemical networks. PLoS Comput. Biol. 2012, 8, e1002739. [Google Scholar] [CrossRef]
- Vey, G. Gene Coexpression as Hebbian Learning in Prokaryotic Genomes. Bull. Math. Biol. 2013, 75, 2431–2449. [Google Scholar] [CrossRef]
- Watson, R.A.; Buckley, C.L.; Mills, R.; Davies, A.P. Associative memory in gene regulation networks. In Proceedings of the 12th International Conference on the Synthesis and Simulation of Living Systems, Odense, Denmark, 19–23 August 2010; pp. 194–202. [Google Scholar]
- Abzhanov, A. The old and new faces of morphology: The legacy of D’Arcy Thompson’s ‘theory of transformations’ and ‘laws of growth’. Development 2017, 144, 4284–4297. [Google Scholar] [CrossRef]
- Avena-Koenigsberger, A.; Goni, J.; Sole, R.; Sporns, O. Network morphospace. J. R. Soc. Interface 2015, 12, 20140881. [Google Scholar] [CrossRef]
- Stone, J.R. The spirit of D’arcy Thompson dwells in empirical morphospace. Math. Biosci. 1997, 142, 13–30. [Google Scholar] [CrossRef]
- Raup, D.M.; Michelson, A. Theoretical Morphology of the Coiled Shell. Science 1965, 147, 1294–1295. [Google Scholar] [CrossRef] [PubMed]
- Cervera, J.; Levin, M.; Mafe, S. Morphology changes induced by intercellular gap junction blocking: A reaction-diffusion mechanism. Biosystems 2021, 209, 104511. [Google Scholar] [CrossRef] [PubMed]
- Thompson, D.A.W.; Whyte, L.L. On Growth and Form, A New ed.; The University Press: Cambridge, UK, 1942; pp. 1055–1064. [Google Scholar]
- Vandenberg, L.N.; Adams, D.S.; Levin, M. Normalized shape and location of perturbed craniofacial structures in the Xenopus tadpole reveal an innate ability to achieve correct morphology. Dev. Dyn. 2012, 241, 863–878. [Google Scholar] [CrossRef] [PubMed]
- Fankhauser, G. The Effects of Changes in Chromosome Number on Amphibian Development. Q. Rev. Biol. 1945, 20, 20–78. [Google Scholar] [CrossRef]
- Fankhauser, G. Maintenance of normal structure in heteroploid salamander larvae, through compensation of changes in cell size by adjustment of cell number and cell shape. J. Exp. Zool. 1945, 100, 445–455. [Google Scholar] [CrossRef]
- Abzhanov, A.; Kuo, W.P.; Hartmann, C.; Grant, B.R.; Grant, P.R.; Tabin, C.J. The calmodulin pathway and evolution of elongated beak morphology in Darwin’s finches. Nature 2006, 442, 563–567. [Google Scholar] [CrossRef]
- Abzhanov, A.; Protas, M.; Grant, B.R.; Grant, P.R.; Tabin, C.J. Bmp4 and morphological variation of beaks in Darwin’s finches. Science 2004, 305, 1462–1465. [Google Scholar] [CrossRef]
- Cervera, J.; Pietak, A.; Levin, M.; Mafe, S. Bioelectrical coupling in multicellular domains regulated by gap junctions: A conceptual approach. Bioelectrochemistry 2018, 123, 45–61. [Google Scholar] [CrossRef]
- Cervera, J.; Ramirez, P.; Levin, M.; Mafe, S. Community effects allow bioelectrical reprogramming of cell membrane potentials in multicellular aggregates: Model simulations. Phys. Rev. E 2020, 102, 052412. [Google Scholar] [CrossRef]
- Niehrs, C. On growth and form: A Cartesian coordinate system of Wnt and BMP signaling specifies bilaterian body axes. Development 2010, 137, 845–857. [Google Scholar] [CrossRef]
- Riol, A.; Cervera, J.; Levin, M.; Mafe, S. Cell Systems Bioelectricity: How Different Intercellular Gap Junctions Could Regionalize a Multicellular Aggregate. Cancers 2021, 13, 5300. [Google Scholar] [CrossRef] [PubMed]
- Shi, R.; Borgens, R.B. Three-dimensional gradients of voltage during development of the nervous system as invisible coordinates for the establishment of embryonic pattern. Dev. Dyn. 1995, 202, 101–114. [Google Scholar] [CrossRef] [PubMed]
- Marnik, E.A.; Updike, D.L. Membraneless organelles: P granules in Caenorhabditis elegans. Traffic 2019, 20, 373–379. [Google Scholar] [CrossRef]
- Adams, D.S.; Robinson, K.R.; Fukumoto, T.; Yuan, S.; Albertson, R.C.; Yelick, P.; Kuo, L.; McSweeney, M.; Levin, M. Early, H+-V-ATPase-dependent proton flux is necessary for consistent left-right patterning of non-mammalian vertebrates. Development 2006, 133, 1657–1671. [Google Scholar] [CrossRef] [PubMed]
- Levin, M.; Thorlin, T.; Robinson, K.R.; Nogi, T.; Mercola, M. Asymmetries in H+/K+-ATPase and cell membrane potentials comprise a very early step in left-right patterning. Cell 2002, 111, 77–89. [Google Scholar] [CrossRef]
- Fields, C.; Levin, M. Somatic multicellularity as a satisficing solution to the prediction-error minimization problem. Commun. Integr. Biol. 2019, 12, 119–132. [Google Scholar] [CrossRef]
- Fields, C.; Bischof, J.; Levin, M. Morphological Coordination: A Common Ancestral Function Unifying Neural and Non-Neural Signaling. Physiology 2020, 35, 16–30. [Google Scholar] [CrossRef]
- Fields, C.; Levin, M. Why isn’t sex optional? Stem-cell competition, loss of regenerative capacity, and cancer in metazoan evolution. Commun. Integr. Biol. 2020, 13, 170–183. [Google Scholar] [CrossRef]
- Prager, I.; Watzl, C. Mechanisms of natural killer cell-mediated cellular cytotoxicity. J. Leukoc. Biol. 2019, 105, 1319–1329. [Google Scholar] [CrossRef]
- Casas-Tinto, S.; Torres, M.; Moreno, E. The flower code and cancer development. Clin. Transl. Oncol. 2011, 13, 5–9. [Google Scholar] [CrossRef]
- Rhiner, C.; Lopez-Gay, J.M.; Soldini, D.; Casas-Tinto, S.; Martin, F.A.; Lombardia, L.; Moreno, E. Flower forms an extracellular code that reveals the fitness of a cell to its neighbors in Drosophila. Dev. Cell 2010, 18, 985–998. [Google Scholar] [CrossRef] [PubMed]
- Gawne, R.; McKenna, K.Z.; Levin, M. Competitive and Coordinative Interactions between Body Parts Produce Adaptive Developmental Outcomes. Bioessays 2020, 42, e1900245. [Google Scholar] [CrossRef] [PubMed]
- Rubenstein, M.; Cornejo, A.; Nagpal, R. Robotics. Programmable self-assembly in a thousand-robot swarm. Science 2014, 345, 795–799. [Google Scholar] [CrossRef] [PubMed]
- Couzin, I. Collective minds. Nature 2007, 445, 715. [Google Scholar] [CrossRef] [PubMed]
- Couzin, I.D. Collective cognition in animal groups. Trends Cogn. Sci. 2009, 13, 36–43. [Google Scholar] [CrossRef]
- Birnbaum, K.D.; Sanchez Alvarado, A. Slicing across kingdoms: Regeneration in plants and animals. Cell 2008, 132, 697–710. [Google Scholar] [CrossRef]
- Levin, M. The Computational Boundary of a “Self”: Developmental Bioelectricity Drives Multicellularity and Scale-Free Cognition. Front. Psychol. 2019, 10, 2688. [Google Scholar] [CrossRef]
- Levin, M. Bioelectrical approaches to cancer as a problem of the scaling of the cellular self. Prog. Biophys. Mol. Biol. 2021, 165, 102–113. [Google Scholar] [CrossRef]
- Durant, F.; Morokuma, J.; Fields, C.; Williams, K.; Adams, D.S.; Levin, M. Long-Term, Stochastic Editing of Regenerative Anatomy via Targeting Endogenous Bioelectric Gradients. Biophys. J. 2017, 112, 2231–2243. [Google Scholar] [CrossRef]
- Pezzulo, G.; LaPalme, J.; Durant, F.; Levin, M. Bistability of somatic pattern memories: Stochastic outcomes in bioelectric circuits underlying regeneration. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2021, 376, 20190765. [Google Scholar] [CrossRef]
- Sullivan, K.G.; Emmons-Bell, M.; Levin, M. Physiological inputs regulate species-specific anatomy during embryogenesis and regeneration. Commun. Integr. Biol. 2016, 9, e1192733. [Google Scholar] [CrossRef] [PubMed]
- Cooke, J. Cell number in relation to primary pattern formation in the embryo of Xenopus laevis. I: The cell cycle during new pattern formation in response to implanted organisers. J. Embryol. Exp. Morph. 1979, 51, 165–182. [Google Scholar]
- Cooke, J. Scale of body pattern adjusts to available cell number in amphibian embryos. Nature 1981, 290, 775–778. [Google Scholar] [CrossRef] [PubMed]
- Pinet, K.; Deolankar, M.; Leung, B.; McLaughlin, K.A. Adaptive correction of craniofacial defects in pre-metamorphic Xenopus laevis tadpoles involves thyroid hormone-independent tissue remodeling. Development 2019, 146, dev175893. [Google Scholar] [CrossRef] [PubMed]
- Pinet, K.; McLaughlin, K.A. Mechanisms of physiological tissue remodeling in animals: Manipulating tissue, organ, and organism morphology. Dev. Biol. 2019, 451, 134–145. [Google Scholar] [CrossRef] [PubMed]
- Blackiston, D.; Lederer, E.; Kriegman, S.; Garnier, S.; Bongard, J.; Levin, M. A cellular platform for the development of synthetic living machines. Sci. Robot. 2021, 6, eabf1571. [Google Scholar] [CrossRef]
- Kriegman, S.; Blackiston, D.; Levin, M.; Bongard, J. Kinematic self-replication in reconfigurable organisms. Proc. Natl. Acad. Sci. USA 2021, 118, e2112672118. [Google Scholar] [CrossRef]
- McEwen, B.S. Stress, adaptation, and disease. Allostasis and allostatic load. Ann. N. Y. Acad. Sci. 1998, 840, 33–44. [Google Scholar] [CrossRef]
- Schulkin, J.; Sterling, P. Allostasis: A Brain-Centered, Predictive Mode of Physiological Regulation. Trends Neurosci. 2019, 42, 740–752. [Google Scholar] [CrossRef]
- Ziemke, T. The body of knowledge: On the role of the living body in grounding embodied cognition. Biosystems 2016, 148, 4–11. [Google Scholar] [CrossRef]
- Turing, A.M. Computing machinery and intelligence. Mind 1950, 59, 433–460. [Google Scholar] [CrossRef]
- Turing, A.M. The Chemical Basis of Morphogenesis. Philos. Trans. R. Soc. Lond. Ser. B-Biol. Sci. 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Keijzer, F.; Arnellos, A. The animal sensorimotor organization: A challenge for the environmental complexity thesis. Biol. Philos. 2017, 32, 421–441. [Google Scholar] [CrossRef]
- Keijzer, F. Moving and sensing without input and output: Early nervous systems and the origins of the animal sensorimotor organization. Biol. Philos. 2015, 30, 311–331. [Google Scholar] [CrossRef] [PubMed]
- Adamatzky, A.; Costello, B.D.L.; Shirakawa, T. Universal Computation with Limited Resources: Belousov-Zhabotinsky and Physarum Computers. Int. J. Bifurc. Chaos 2008, 18, 2373–2389. [Google Scholar] [CrossRef]
- Beekman, M.; Latty, T. Brainless but Multi-Headed: Decision Making by the Acellular Slime Mould Physarum polycephalum. J. Mol. Biol. 2015, 427, 3734–3743. [Google Scholar] [CrossRef]
- Mori, Y.; Koaze, A. Cognition of different length by Physarum polycephalum: Weber’s law in an amoeboid organism. Mycoscience 2013, 54, 426–428. [Google Scholar] [CrossRef]
- Nakagaki, T.; Kobayashi, R.; Nishiura, Y.; Ueda, T. Obtaining multiple separate food sources: Behavioural intelligence in the Physarum plasmodium. Proc. Biol. Sci. 2004, 271, 2305–2310. [Google Scholar] [CrossRef]
- Vogel, D.; Dussutour, A. Direct transfer of learned behaviour via cell fusion in non-neural organisms. Proc. Biol. Sci. 2016, 283, 20162382. [Google Scholar] [CrossRef]
- Levin, M. Bioelectric signaling: Reprogrammable circuits underlying embryogenesis, regeneration, and cancer. Cell 2021, 184, 1971–1989. [Google Scholar] [CrossRef]
- Benitez, M.; Hernandez-Hernandez, V.; Newman, S.A.; Niklas, K.J. Dynamical Patterning Modules, Biogeneric Materials, and the Evolution of Multicellular Plants. Front. Plant Sci. 2018, 9, 871. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.A. The Origins of Order: Self Organization and Selection in Evolution; Oxford University Press: New York, NY, USA, 1993; pp. 18, 709. [Google Scholar]
- Kauffman, S.A.; Johnsen, S. Coevolution to the edge of chaos: Coupled fitness landscapes, poised states, and coevolutionary avalanches. J. Biol. 1991, 149, 467–505. [Google Scholar] [CrossRef]
- Powers, W.T. Behavior: The Control of Perception; Aldine Pub. Co.: Chicago, IL, USA, 1973; pp. 11, 296. [Google Scholar]
- Ramstead, M.J.D.; Badcock, P.B.; Friston, K.J. Answering Schrodinger’s question: A free-energy formulation. Phys. Life Rev. 2018, 24, 1–16. [Google Scholar] [CrossRef]
- Sengupta, B.; Tozzi, A.; Cooray, G.K.; Douglas, P.K.; Friston, K.J. Towards a Neuronal Gauge Theory. PLoS Biol. 2016, 14, e1002400. [Google Scholar] [CrossRef]
- Nakagaki, T.; Yamada, H.; Toth, A. Maze-solving by an amoeboid organism. Nature 2000, 407, 470. [Google Scholar] [CrossRef] [PubMed]
- Osan, R.; Su, E.; Shinbrot, T. The interplay between branching and pruning on neuronal target search during developmental growth: Functional role and implications. PLoS ONE 2011, 6, e25135. [Google Scholar] [CrossRef][Green Version]
- Katz, Y.; Springer, M. Probabilistic adaptation in changing microbial environments. PeerJ 2016, 4, e2716. [Google Scholar] [CrossRef]
- Katz, Y.; Springer, M.; Fontana, W. Embodying probabilistic inference in biochemical circuits. arXiv 2018, arXiv:1806.10161. [Google Scholar] [CrossRef]
- Whittington, J.C.R.; Muller, T.H.; Mark, S.; Chen, G.; Barry, C.; Burgess, N.; Behrens, T.E.J. The Tolman-Eichenbaum Machine: Unifying Space and Relational Memory through Generalization in the Hippocampal Formation. Cell 2020, 183, 1249–1263.e23. [Google Scholar] [CrossRef]
- George, D.; Rikhye, R.V.; Gothoskar, N.; Guntupalli, J.S.; Dedieu, A.; Lazaro-Gredilla, M. Clone-structured graph representations enable flexible learning and vicarious evaluation of cognitive maps. Nat. Commun. 2021, 12, 2392. [Google Scholar] [CrossRef]
- Merchant, H.; Harrington, D.L.; Meck, W.H. Neural basis of the perception and estimation of time. Annu. Rev. Neurosci 2013, 36, 313–336. [Google Scholar] [CrossRef] [PubMed]
- Jeffery, K.J.; Wilson, J.J.; Casali, G.; Hayman, R.M. Neural encoding of large-scale three-dimensional space-properties and constraints. Front. Psychol. 2015, 6, 927. [Google Scholar] [CrossRef] [PubMed]
- Schuster, M.; Sexton, D.J.; Diggle, S.P.; Greenberg, E.P. Acyl-homoserine lactone quorum sensing: From evolution to application. Annu. Rev. Microbiol. 2013, 67, 43–63. [Google Scholar] [CrossRef]
- Monds, R.D.; O’Toole, G.A. The developmental model of microbial biofilms: Ten years of a paradigm up for review. Trends Microbiol. 2009, 17, 73–87. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, L. Brains, innovations, tools and cultural transmission in birds, non-human primates, and fossil hominins. Front. Hum. Neurosci. 2013, 7, 245. [Google Scholar] [CrossRef]
- Harari, Y.N. Sapiens: A Brief History of Humankind; Harvill Secker: London, UK, 2014. [Google Scholar]
- Blackmore, S. Dangerous memes; or, What the Pandorans let loose. In Cosmos & Culture: Culture Evolution in a Cosmic Context; Dick, S.J., Lupisdella, M.L., Eds.; National Aeronautics and Space Administration, Office of External Relations, History Division: Washington, DC, USA, 2009; pp. 297–317. [Google Scholar]
- Friston, K.; Levin, M.; Sengupta, B.; Pezzulo, G. Knowing one’s place: A free-energy approach to pattern regulation. J. R. Soc. Interface 2015, 12, 20141383. [Google Scholar] [CrossRef]
- Kashiwagi, A.; Urabe, I.; Kaneko, K.; Yomo, T. Adaptive response of a gene network to environmental changes by fitness-induced attractor selection. PLoS ONE 2006, 1, e49. [Google Scholar] [CrossRef]
- Conway, J.; Kochen, S. The Free Will Theorem. Found. Phys. 2006, 36, 1441–1473. [Google Scholar] [CrossRef]
- Kahneman, D. Thinking, Fast and Slow; Farrar, Straus and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Chater, N. The Mind Is Flat: The Remarkable Shallowness of the Improvising Brain; Yale University Press: New Haven, CT, USA, 2018. [Google Scholar]
- Ashby, W.R. Design for a Brain; Chapman & Hall: London, UK, 1952; p. 259. [Google Scholar]
- Friston, K. A theory of cortical responses. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2005, 360, 815–836. [Google Scholar] [CrossRef]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef]
- Friston, K.J.; Stephan, K.E. Free-energy and the brain. Synthese 2007, 159, 417–458. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; FitzGerald, T.; Rigoli, F.; Schwartenbeck, P.; Pezzulo, G. Active Inference: A Process Theory. Neural Comput. 2017, 29, 1–49. [Google Scholar] [CrossRef] [PubMed]
- Ramstead, M.J.D.; Constant, A.; Badcock, P.B.; Friston, K.J. Variational ecology and the physics of sentient systems. Phys. Life Rev. 2019, 31, 188–205. [Google Scholar] [CrossRef]
- Kuchling, F.; Friston, K.; Georgiev, G.; Levin, M. Morphogenesis as Bayesian inference: A variational approach to pattern formation and control in complex biological systems. Phys. Life Rev. 2020, 33, 88–108. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. A free energy principle for a particular physics. arXiv 2019, arXiv:1906.10184. [Google Scholar] [CrossRef]
- Fields, C.; Friston, K.; Glazebrook, J.F.; Levin, M. A free energy principle for generic quantum systems. arXiv 2021, arXiv:2112.15242. [Google Scholar] [CrossRef] [PubMed]
- Jeffery, K.; Pollack, R.; Rovelli, C. On the Statistical Mechanics of Life: Schrödinger Revisited. Entropy 2019, 21, 1211. [Google Scholar] [CrossRef]
- Clark, A. How to knit your own Markov blanket: Resisting the Second Law with metamorphic minds. In Philosophy and Predictive Processing 3; Metzinger, T., Wiese, W., Eds.; MIND Group: Frankfurt am Main, Germany, 2017. [Google Scholar]
- Hoffman, D.D. The Case Against Reality: Why Evolution Hid the Truth from Our Eyes; W. W. Norton & Company: New York, NY, USA, 2019. [Google Scholar]
- Fields, C. Building the Observer into the System: Toward a Realistic Description of Human Interaction with the World. Systems 2016, 4, 32. [Google Scholar] [CrossRef]
- Fields, C. Sciences of Observation. Philosophies 2018, 3, 29. [Google Scholar] [CrossRef]
- Conant, R.C.; Ross Ashby, W. Every good regulator of a system must be a model of that system†. Int. J. Syst. Sci. 1970, 1, 89–97. [Google Scholar] [CrossRef]
- Rubin, S.; Parr, T.; Da Costa, L.; Friston, K. Future climates: Markov blankets and active inference in the biosphere. J. R. Soc. Interface 2020, 17, 20200503. [Google Scholar] [CrossRef] [PubMed]
- Fields, C.; Glazebrook, J.F.; Marcianò, A. Reference Frame Induced Symmetry Breaking on Holographic Screens. Symmetry 2021, 13, 408. [Google Scholar] [CrossRef]
- Robbins, R.J.; Krishtalka, L.; Wooley, J.C. Advances in biodiversity: Metagenomics and the unveiling of biological dark matter. Stand. Genom. Sci. 2016, 11, 69. [Google Scholar] [CrossRef]
- Addazi, A.; Chen, P.S.; Fabrocini, F.; Fields, C.; Greco, E.; Lulli, M.; Marcianò, A.; Pasechnik, R. Generalized Holographic Principle, Gauge Invariance and the Emergence of Gravity a la Wilczek. Front. Astron. Space Sci. 2021, 8, 563450. [Google Scholar] [CrossRef]
- Fields, C.; Hoffman, D.D.; Prakash, C.; Prentner, R. Eigenforms, Interfaces and Holographic Encoding toward an Evolutionary Account of Objects and Spacetime. Constr. Found. 2017, 12, 265–274. [Google Scholar]
- Law, J.; Shaw, P.; Earland, K.; Sheldon, M.; Lee, M. A psychology based approach for longitudinal development in cognitive robotics. Front. Neurorobot. 2014, 8, 1. [Google Scholar] [CrossRef]
- Hoffman, D.D.; Singh, M.; Prakash, C. The Interface Theory of Perception. Psychon. Bull. Rev. 2015, 22, 1480–1506. [Google Scholar] [CrossRef]
- Bongard, J.; Zykov, V.; Lipson, H. Resilient machines through continuous self-modeling. Science 2006, 314, 1118–1121. [Google Scholar] [CrossRef]
- Griffiths, T.L.; Chater, N.; Kemp, C.; Perfors, A.; Tenenbaum, J.B. Probabilistic models of cognition: Exploring representations and inductive biases. Trends Cogn. Sci. 2010, 14, 357–364. [Google Scholar] [CrossRef]
- Conway, M.A.; Pleydell-Pearce, C.W. The construction of autobiographical memories in the self-memory system. Psychol. Rev. 2000, 107, 261–288. [Google Scholar] [CrossRef]
- Simons, J.S.; Ritchey, M.; Fernyhough, C. Brain Mechanisms Underlying the Subjective Experience of Remembering. Annu. Rev. Psychol. 2022, 73, 159–186. [Google Scholar] [CrossRef] [PubMed]
- Prentner, R. Consciousness and topologically structured phenomenal spaces. Conscious. Cogn. 2019, 70, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Ter Haar, S.M.; Fernandez, A.A.; Gratier, M.; Knornschild, M.; Levelt, C.; Moore, R.K.; Vellema, M.; Wang, X.; Oller, D.K. Cross-species parallels in babbling: Animals and algorithms. Philos. Trans R. Soc. Lond. B Biol. Sci. 2021, 376, 20200239. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.; Chinn, L.K.; Somogyi, G.; Heed, T.; Fagard, J.; Lockman, J.J.; O’Regan, J.K. Development of reaching to the body in early infancy: From experiments to robotic models. In Proceedings of the 7th Joint IEEE International Conference on Development and Learning and Epigenetic Robotics (ICDL-EpiRob), Lisbon, Portugal, 18–21 September 2017; pp. 112–119. [Google Scholar]
- Dietrich, E.; Fields, C.; Hoffman, D.D.; Prentner, R. Editorial: Epistemic Feelings: Phenomenology, Implementation, and Role in Cognition. Front. Psychol. 2020, 11, 606046. [Google Scholar] [CrossRef] [PubMed]
- Prakash, C.; Fields, C.; Hoffman, D.D.; Prentner, R.; Singh, M. Fact, Fiction, and Fitness. Entropy 2020, 22, 514. [Google Scholar] [CrossRef]
- Busse, S.M.; McMillen, P.T.; Levin, M. Cross-limb communication during Xenopus hindlimb regenerative response: Non-local bioelectric injury signals. Development 2018, 145, dev164210. [Google Scholar] [CrossRef]
- McMillen, P.; Novak, R.; Levin, M. Toward Decoding Bioelectric Events in Xenopus Embryogenesis: New Methodology for Tracking Interplay Between Calcium and Resting Potentials In Vivo. J. Mol. Biol. 2020, 432, 605–620. [Google Scholar] [CrossRef]
- Farinella-Ferruzza, N. Risultati di trapianti di bottone codale di urodeli su anuri e vice versa. Riv. Biol. 1953, 45, 523–527. [Google Scholar]
- Farinella-Ferruzza, N. The transformation of a tail into a limb after xenoplastic transformation. Experientia 1956, 15, 304–305. [Google Scholar] [CrossRef]
- Rijntjes, M.; Buechel, C.; Kiebel, S.; Weiller, C. Multiple somatotopic representations in the human cerebellum. Neuroreport 1999, 10, 3653–3658. [Google Scholar] [CrossRef]
- Bartlett, S.D.; Rudolph, T.; Spekkens, R.W. Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 2007, 79, 555–609. [Google Scholar] [CrossRef]
- Fields, C.; Glazebrook, J.F.; Levin, M. Minimal physicalism as a scale-free substrate for cognition and consciousness. Neurosci. Conscious. 2021, 7, niab013. [Google Scholar] [CrossRef] [PubMed]
- Fields, C.; Levin, M. How Do Living Systems Create Meaning? Philosophies 2020, 5, 36. [Google Scholar] [CrossRef]
- Dzhafarov, E.N.; Cervantes, V.H.; Kujala, J.V. Contextuality in canonical systems of random variables. Philos. Trans. A Math. Phys. Eng. Sci. 2017, 375. [Google Scholar] [CrossRef]
- Fields, C.; Glazebrook, J.F. Information flow in context-dependent hierarchical Bayesian inference. J. Exp. Artif. Intell. 2022, 34, 111–142. [Google Scholar] [CrossRef]
- Fields, C.; Marcianò, A. Sharing Nonfungible Information Requires Shared Nonfungible Information. Quantum Rep. 2019, 1, 252–259. [Google Scholar] [CrossRef]
- Buzsaki, G.; Tingley, D. Space and Time: The Hippocampus as a Sequence Generator. Trends Cogn. Sci. 2018, 22, 853–869. [Google Scholar] [CrossRef]
- Taylor, J.E.T.; Taylor, G.W. Artificial cognition: How experimental psychology can help generate explainable artificial intelligence. Psychon. Bull. Rev. 2021, 28, 454–475. [Google Scholar] [CrossRef]
- Seth, A.K.; Friston, K.J. Active interoceptive inference and the emotional brain. Philos. Trans R. Soc. Lond. B Biol. Sci. 2016, 371, 20160007. [Google Scholar] [CrossRef]
- Seth, A.K.; Tsakiris, M. Being a Beast Machine: The Somatic Basis of Selfhood. Trends Cogn. Sci. 2018, 22, 969–981. [Google Scholar] [CrossRef]
- Fields, C.; Glazebrook, J.F. Do Process-1 simulations generate the epistemic feelings that drive Process-2 decision making? Cogn. Process. 2020, 21, 533–553. [Google Scholar] [CrossRef]
- Lakoff, G.; Núñez, R.E. Where Mathematics Comes from: How the Embodied Mind Brings Mathematics into Being; Basic Books: New York, NY, USA, 2000. [Google Scholar]
- Bubic, A.; von Cramon, D.Y.; Schubotz, R.I. Prediction, cognition and the brain. Front. Hum. Neurosci. 2010, 4, 25. [Google Scholar] [CrossRef]
- Fields, C. Metaphorical motion in mathematical reasoning: Further evidence for pre-motor implementation of structure mapping in abstract domains. Cogn. Process. 2013, 14, 217–229. [Google Scholar] [CrossRef]
- DeMarse, T.B.; Dockendorf, K.P. Adaptive flight control with living neuronal networks on microelectrode arrays. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Montreal, QC, Canada, 31 July–4 August 2005; Volume 1–5, pp. 1548–1551. [Google Scholar]
- Kryger, M.; Wester, B.; Pohlmeyer, E.A.; Rich, M.; John, B.; Beaty, J.; McLoughlin, M.; Boninger, M.; Tyler-Kabara, E.C. Flight simulation using a Brain-Computer Interface: A pilot, pilot study. Exp. Neurol. 2017, 287, 473–478. [Google Scholar] [CrossRef]
- Collinger, J.L.; Wodlinger, B.; Downey, J.E.; Wang, W.; Tyler-Kabara, E.C.; Weber, D.J.; McMorland, A.J.; Velliste, M.; Boninger, M.L.; Schwartz, A.B. High-performance neuroprosthetic control by an individual with tetraplegia. Lancet 2013, 381, 557–564. [Google Scholar] [CrossRef]
- Hesp, C.; Ramstead, M.; Constant, A.; Badcock, P.; Kirchhoff, M.; Friston, K. A Multi-scale View of the Emergent Complexity of Life: A Free-Energy Proposal. In Evolution, Development and Complexity; Georgiev, G.Y., Smart, J.M., Flores Martinez, C.L., Price, M.E., Eds.; Springer Proceedings in Complexity; Springer: Cham, Switzerland, 2019; pp. 195–227. [Google Scholar]
- Xue, B.; Sartori, P.; Leibler, S. Environment-to-phenotype mapping and adaptation strategies in varying environments. Proc. Natl. Acad. Sci. USA 2019, 116, 13847–13855. [Google Scholar] [CrossRef]
- Adámek, J.; Herrlich, H.; Strecker, G.E. Abstract and Concrete Categories: The Joy of Cats; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Awodey, S. Category Theory. In Oxford Logic Guides, 2nd ed.; Oxford University Press: Oxford, UK, 2010; Volume 52. [Google Scholar]
- Archer, K.; Catenacci Volpi, N.; Bröker, F.; Polani, D. A space of goals: The cognitive geometry of informationally bounded agents. arXiv 2021, arXiv:2111.03699. [Google Scholar] [CrossRef]
- Barrow, J.D. Gravitational Memory. Ann. N. Y. Acad. Sci. 1993, 688, 686–689. [Google Scholar] [CrossRef]
- Vazquez, A.; Pastor-Satorras, R.; Vespignani, A. Large-scale topological and dynamical properties of the Internet. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002, 65, 066130. [Google Scholar] [CrossRef]
- Soroldoni, D.; Jorg, D.J.; Morelli, L.G.; Richmond, D.L.; Schindelin, J.; Julicher, F.; Oates, A.C. Genetic oscillations. A Doppler effect in embryonic pattern formation. Science 2014, 345, 222–225. [Google Scholar] [CrossRef]
- Hills, T.T.; Todd, P.M.; Lazer, D.; Redish, A.D.; Couzin, I.D.; Cognitive Search Research, G. Exploration versus exploitation in space, mind, and society. Trends Cogn. Sci. 2015, 19, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Valentini, G.; Moore, D.G.; Hanson, J.R.; Pavlic, T.P.; Pratt, S.C.; Walker, S.I. Transfer of Information in Collective Decisions by Artificial Agents. In Proceedings of the 2018 Conference on Artificial Life (Alife 2018), Tokyo, Japan, 22–28 July 2018; pp. 641–648. [Google Scholar]
- Serlin, Z.; Rife, J.; Levin, M. A Level Set Approach to Simulating Xenopus laevis Tail Regeneration. In Proceedings of the Fifteenth International Conference on the Synthesis and Simulation of Living Systems (ALIFE XV), Cancun, Mexico, 4–8 July 2016; pp. 528–535. [Google Scholar]
- Beer, R.D. Autopoiesis and cognition in the game of life. Artif. Life 2004, 10, 309–326. [Google Scholar] [CrossRef]
- Beer, R.D. The cognitive domain of a glider in the game of life. Artif. Life 2014, 20, 183–206. [Google Scholar] [CrossRef]
- Beer, R.D. Characterizing autopoiesis in the game of life. Artif. Life 2015, 21, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Beer, R.D.; Williams, P.L. Information processing and dynamics in minimally cognitive agents. Cogn. Sci. 2015, 39, 1–38. [Google Scholar] [CrossRef] [PubMed]
- Durant, F.; Bischof, J.; Fields, C.; Morokuma, J.; LaPalme, J.; Hoi, A.; Levin, M. The Role of Early Bioelectric Signals in the Regeneration of Planarian Anterior/Posterior Polarity. Biophys. J. 2019, 116, 948–961. [Google Scholar] [CrossRef]
- Szilagyi, A.; Szabo, P.; Santos, M.; Szathmary, E. Phenotypes to remember: Evolutionary developmental memory capacity and robustness. PLoS Comput. Biol. 2020, 16, e1008425. [Google Scholar] [CrossRef]
- Watson, R.A.; Wagner, G.P.; Pavlicev, M.; Weinreich, D.M.; Mills, R. The evolution of phenotypic correlations and “developmental memory”. Evolution 2014, 68, 1124–1138. [Google Scholar] [CrossRef]
- Sorek, M.; Balaban, N.Q.; Loewenstein, Y. Stochasticity, bistability and the wisdom of crowds: A model for associative learning in genetic regulatory networks. PLoS Comput. Biol. 2013, 9, e1003179. [Google Scholar] [CrossRef]
- Emmert-Streib, F.; Dehmer, M. Information processing in the transcriptional regulatory network of yeast: Functional robustness. BMC Syst. Biol. 2009, 3, 35. [Google Scholar] [CrossRef]
- Tagkopoulos, I.; Liu, Y.C.; Tavazoie, S. Predictive behavior within microbial genetic networks. Science 2008, 320, 1313–1317. [Google Scholar] [CrossRef] [PubMed]
- Mikkilineni, R. Infusing Autopoietic and Cognitive Behaviors into Digital Automata to Improve Their Sentience, Resilience, and Intelligence. Big Data Cogn. Comput. 2022, 6, 7. [Google Scholar] [CrossRef]
- Mikkilineni, R. A New Class of Autopoietic and Cognitive Machines. Information 2022, 13, 24. [Google Scholar] [CrossRef]
- Darwish, A. Bio-inspired computing: Algorithms review, deep analysis, and the scope of applications. Future Comput. Inform. J. 2018, 3, 231–246. [Google Scholar] [CrossRef]
- Kar, A.K. Bio inspired computing—A review of algorithms and scope of applications. Expert Syst. Appl. 2016, 59, 20–32. [Google Scholar] [CrossRef]
- Indiveri, G.; Chicca, E.; Douglas, R.J. Artificial Cognitive Systems: From VLSI Networks of Spiking Neurons to Neuromorphic Cognition. Cogn. Comput. 2009, 1, 119–127. [Google Scholar] [CrossRef]
- Schuman, C.D.; Potok, T.E.; Patton, R.M.; Birdwell, J.D.; Dean, M.E.; Rose, G.S.; Plank, J.S. A Survey of Neuromorphic Computing and Neural Networks in Hardware. arXiv 2017, arXiv:1705.06963. [Google Scholar]
- Adamatzky, A.; Holley, J.; Dittrich, P.; Gorecki, J.; De Lacy Costello, B.; Zauner, K.P.; Bull, L. On architectures of circuits implemented in simulated Belousov-Zhabotinsky droplets. Biosystems 2012, 109, 72–77. [Google Scholar] [CrossRef]
- Cejkova, J.; Banno, T.; Hanczyc, M.M.; Stepanek, F. Droplets As Liquid Robots. Artif. Life 2017, 23, 528–549. [Google Scholar] [CrossRef]
- Peng, C.; Turiv, T.; Guo, Y.; Wei, Q.H.; Lavrentovich, O.D. Command of active matter by topological defects and patterns. Science 2016, 354, 882–885. [Google Scholar] [CrossRef]
- Wang, A.L.; Gold, J.M.; Tompkins, N.; Heymann, M.; Harrington, K.I.; Fraden, S. Configurable NOR gate arrays from Belousov-Zhabotinsky micro-droplets. Eur. Phys. J. Spec. Top. 2016, 225, 211–227. [Google Scholar] [CrossRef] [PubMed]
- Frith, U. Mind blindness and the brain in autism. Neuron 2001, 32, 969–979. [Google Scholar] [CrossRef]
- Sultan, S.E.; Moczek, A.P.; Walsh, D. Bridging the explanatory gaps: What can we learn from a biological agency perspective? Bioessays 2022, 44, e2100185. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fields, C.; Levin, M. Competency in Navigating Arbitrary Spaces as an Invariant for Analyzing Cognition in Diverse Embodiments. Entropy 2022, 24, 819. https://doi.org/10.3390/e24060819
Fields C, Levin M. Competency in Navigating Arbitrary Spaces as an Invariant for Analyzing Cognition in Diverse Embodiments. Entropy. 2022; 24(6):819. https://doi.org/10.3390/e24060819
Chicago/Turabian StyleFields, Chris, and Michael Levin. 2022. "Competency in Navigating Arbitrary Spaces as an Invariant for Analyzing Cognition in Diverse Embodiments" Entropy 24, no. 6: 819. https://doi.org/10.3390/e24060819
APA StyleFields, C., & Levin, M. (2022). Competency in Navigating Arbitrary Spaces as an Invariant for Analyzing Cognition in Diverse Embodiments. Entropy, 24(6), 819. https://doi.org/10.3390/e24060819






