1. Introduction
The impossibility of simultaneous realizations of two quantum operations is one of the fundamental features of quantum theory [
1,
2]. Two of the most famous incarnations of this principle are the
Heisenberg uncertainty principle (the position and momentum of a quantum particle can not be measured simultaneously [
1]) and the
no-cloning theorem (there is no physical operation producing two identical copies of an unknown, arbitrary, quantum state [
3,
4]). In general, two (or more) quantum operations, such as measurements, channels, or instruments, are called
compatible if they can be seen as marginals of a common operation; if there is no physical operation having the original ones as marginals, they are called
incompatible. As quantum theory is built on Hilbert space, general quantum measurements are considered the positive operator-valued measures (POVMs). In quantum information theory, there are many applications of the notion of incompatibility, such as the robustness of entanglement [
5,
6], the robustness of measurement incompatibility [
7,
8,
9], quantum non-locality [
10,
11], quantum steering [
7,
12], quantum state discrimination [
13,
14,
15], quantum resource theory [
16], and quantum cryptography [
17].
In the modern formalism of quantum theory, the most general description of physical transformations of quantum states is in terms of
quantum channels [
18,
19]. The concept of incompatibility of quantum channels has been proposed in terms of the input–output devices [
20,
21]. In [
21], the authors show that the definition of the
incompatibility of quantum channels is a natural generalization of joint measurability of quantum observables. There exists a large body of work dealing with this notion from various points of view [
15,
22,
23,
24]. Generally speaking, deciding whether a given family of quantum operations is compatible can be formulated as a
semidefinite program [
25]. However, the size of the program grows
exponentially with the number of operations considered. Hence, this method can be computationally prohibitive even for small system sizes (such as qubits) when the number of systems is moderately large. To cope with this dimensionality problem, (in-)compatibility criteria have been introduced; these are conditions that are only necessary, or sufficient, for the compatibility of the given tuple of channels. As is the case with quantum measurements [
20], there exist much more compatibility criteria [
26] than incompatibility criteria.
In this work, we introduce a new
incompatibility criterion for quantum channels based on the notion of (quantum) Fisher information. Our criterion is based on a similar condition put forward by H. Zhu [
27,
28] in the case of quantum measurements.
After introducing the necessary background on Fisher information and quantum channel compatibility (
Section 2 and
Section 3), we put forward the new incompatibility criterion in
Section 4. The statement of the main result of the paper can be found in Theorem 1. We then apply this result to study, for the first time, the incompatibility of Schur channels, an important class of quantum operations with wide-ranging applications; see
Section 5. In the final two sections of the paper, we introduce different compatibility structures for assemblages of quantum channels (
Section 6), and we study them in the case of generalized depolarizing channels (
Section 7).
2. Classical and Quantum Fisher Information
Consider a family of probability distributions
parametrized by
. A central research direction in statistics is to estimate the accuracy of the value of parameter
by observing
x outcomes sampled from the distributions. Recall that the (classical)
Fisher information of the model is defined as
when an estimator
of the parameter
is unbiased, the inverse of the classical Fisher information gives a lower bound on the
mean square error (MSE) of the estimator, which is the well-known
Cramér-Rao bound [
29,
30]. The notion of the classical Fisher information plays a significant role in the geometrical approach to statistics [
31,
32] and the information theory approach to physics [
33].
In the multiple-parameter scenario, when
is a vector, the classical Fisher information is considered as a matrix form, which is a real symmetric matrix with matrix elements [
34,
35,
36]:
In a quantum parameter estimation scenario, we may perform the quantum positive operator-valued measurement (POVM) on a quantum state that depends on a parameter to extract the parameter information. Consider a quantum measurement
acting on the states
. The parameterized probability of outcomes
x of the measurement is
. The corresponding measurement-induced Fisher information
is then given by
The
quantum Fisher information of the model
is defined as [
37]
where the symmetric logarithmic derivative (SLD) operators
for the parameter
are determined implicitly by
In contrast with the classical Cramér-Rao bound, the inverse of quantum Fisher information is also a lower bound for the MSE of an unbiased estimator, which is called the
quantum Cramér-Rao bound [
37].
In quantum multiple-parameter estimation scenarios, both the measure-induced Fisher information and quantum Fisher information are matrices
where
is the SLD operator corresponding with
. The measurement-induced Fisher information resembles the classical correlations, while the quantum Fisher information resembles the quantum mutual information. From the Braunstein–Caves theorem [
36], the quantum Fisher information, independent of measurement, is an upper bound of the measurement-induced Fisher information in the positive semidefinite order for matrices:
In this work, we shall consider another relationship proposed by Gill and Massar [
38] for any
—dimensional quantum system:
This inequality was the main ingredient in the incompatibility criterion invented by Zhu [
27], which lies at the foundation of our incompatibility criterion for quantum channels.
3. Compatibility of Quantum Channels
In this section, we review the basic definitions of quantum channel compatibility.
Let and be Hilbert spaces, and denote the family of linear operators on . In the Schrödinger picture, a quantum channel is defined as a linear map having the following two properties:
complete positivity: for any dimension , the linear map is a positive operator;
trace-preservation: for all operators , .
We say that quantum channels are trace-preserving, completely positive (TPCP) maps. In this paper, we shall also consider the Heisenberg picture of quantum mechanics, where channels are seen as acting on observables instead of states. This amounts to considering the adjoint map
, where the adjoint is taken with respect to the Hilbert–Schmidt scalar product on the corresponding matrix spaces [
21]:
where
,
, and
.
We now recall the definition of the compatibility of quantum channels and refer the reader to the review [
20] for further properties.
Definition 1. Consider two quantum channels and having the same input space. The pair is said to be compatible,
if there exists a joint channel
such that are the marginals
of Λ
:where denote the partial trace operations in . In the Heisenberg (dual) picture, the condition above readsThe (in-)compatibility of more than two channels is defined in a similar manner. As an example, let us consider the partially depolarizing channel, which is defined as:
with
and
for any operator
A; these quantum channels will be discussed at length in
Section 7. From the
no-cloning theorem [
3,
4], it follows that two copies of the identity channel
, are incompatible. On the other hand, the completely depolarizing channel
is compatible with any other channel. A question is the self-incompatibility of
. It is well known that the channel
is self-compatible if
[
26,
39]. The necessary and sufficient condition for the compatibility of two different depolarizing channels
and
were shown in [
40,
41,
42]:
As previously discussed, quantum channel incompatibility is a key phenomenon in quantum theory, being at the heart of fundamental results in quantum information, such as the
no-cloning theorem. In order to measure the degree of incompatibility of a given set of quantum channels, several definitions of the
robustness of incompatibility have been considered in the literature [
8,
26,
43]. In this section, we introduce a new such measure for a tuple of channels, which has the merit of taking into consideration the asymmetry between the channels considered. A similar definition was considered in the case of POVMs in [
44,
45]. We shall consider only channels acting on
, and we recall that
denotes the fully depolarizing channel
.
Definition 2. Given an N-tuple of quantum channels , define the compatibility region
of Φ as Note that the definition is a relevant event in the case where the channels are identical: for all , in which case we call the self-compatibility region (note that the dependence in N is still present since we are consider N copies of the channel ).
The following result is a simple exercise.
Proposition 1. For any N-tuple of quantum channels , the set is convex and closed (i.e., a convex body). We have , and, for all , 4. Channel Incompatibility via POVM Incompatibility
This is the main section of our paper, where we put forward a new incompatibility criterion for quantum channels in Theorem 1. Our criterion is based on an incompatibility criterion for quantum measurements (POVMs) introduced by H. Zhu and his collaborators [
27,
28].
Let us start by recalling the definition of compatibility (or joint measurability) of quantum measurements. First, recall that a quantum measurement (or POVM) is a k-tuple of operators , having the following two properties:
positivity: the operators are positive semidefinite;
normalization: .
A POVM gives the most general form of a physical process that produces the probabilities given by the
Born rule: when measuring a quantum system described by a density matrix
, one obtains the result
with probability
Naturally, one can see a POVM
as a quantum-to-classical channel
where
denotes the canonical basis of
corresponding to the pointer states of the measurement apparatus.
Whether two (or more) quantum measurements can be performed simultaneously is one of the crucial questions lying at the foundations of quantum theory [
1,
2]. Mathematically, we have the following important definition (compare with Definition 1).
Definition 3. Two POVMs and are said to be compatible
(or jointly measurable
) if there exists a third POVM , called joint measurement,
such thatOtherwise, the measurements and are called incompatible [46]. The compatibility of more than two measurements is defined similarly. Quantum measurement (in-)compatibility has received a lot of attention in the literature, see, e.g., the excellent reviews [
20,
47], or the recent perspective on the problem focusing on the post-processing partial order [
48]. Importantly for us, in [
27], H. Zhu proposed a family of universal
POVM incompatibility criteria based on the classical Fisher information matrix. Assume a measurement
is the joint measurement of
. According to the Fisher information data-processing inequality, the measurement-induced Fisher information matrix of
should not exceed that of
, that is to say
for all quantum states
(
is omitted in the formula above for convenience); the Fisher information matrix
I was defined in Equation (
1). Define
as the metric-adjusted Fisher information. The following inequality holds for compatible measurements based on the Gill–Massar inequality (
3):
Otherwise, the
N-tuple of measurements
is incompatible. When the parameter
(the state around which we compute the Fisher information) corresponds to the maximally mixed state
, inequality (
6) can be rephrased as the following proposition [
27,
28].
Proposition 2. For a set of N measurements on , define the operatorswhere are the (non-zero) effects of the POVM , having outcomes. Consider now the quantity If , then the N-tuple of POVMs is incompatible.
Remark 1. Note that the function satisfies two basic requirements for a good measure of (in-)compatibility: monotonicity under coarse-graining and global unitary invariance.
Remark 2. For any POVM , the associated matrix is larger, in the positive semidefinite order, than the maximally entangled stateThis fact is a consequence of the important observation that the is an order morphism for the post-processing order of quantum measurements [48], and . A natural question is how to capture the incompatibility of quantum channels using measurements. Let
and
be any sets of the basis of Hilbert spaces
and
, respectively. Motivated by the definition of incompatibility of quantum channels, we dedicate to research properties of the induced sets
and
. As we consider the quantum channel is trace-preserving, thus
and
can be regarded as POVMs [
23], that is to say,
Lemma 1. [21] If N quantum channels are compatible, then, for all orthonormal bases of , the corresponding POVMsare compatible. Proof. Let
be a joint channel for the compatible
N-tuple
. Clearly,
thus its adjoint is an unital, completely positive map
Define operators
From the fact that
is a completely positive, unital map, we infer that
is a POVM (with
outcomes). Let us now compute the marginals of this POVM. For some fixed
and
, we have
showing that the
s-th marginal of
is
. Thus
is a joint measurement of
, proving the claim. □
We leave open the reciprocal question, which we formulate as a conjecture (below for two channels, although the general version, for a N-tuple, can be easily stated).
Conjecture 1. Consider two quantum channelssuch that, for all orthonormal bases,of, the POVMsare compatible. Then,andare compatible channels. We now turn to the main theoretical result of our paper: a criterion for quantum channel incompatibility. Informally, one can formulate it as follows: given an
N-tuple of quantum channels, if one can find an
N-tuple of orthonormal bases such that the corresponding quantum measurements are incompatible, then the original
N-tuple of channels must also be incompatible. Our criterion is important since there are very few useful incompatibility criteria for channel incompatibility. On the other hand, there exist quite numerous incompatibility criteria for quantum measurements, so one can turn those into criteria for channels using Lemma 1. We introduce the following important notation: to a quantum channel
and an orthonormal basis
of
, we associate the
G matrix
which corresponds to the
G matrix associated to the POVM
Theorem 1. Let be N quantum channels. If there exists orthonormal bases of such that the value of the semidefinite programis strictly larger than d, then the n-tuple of channels is incompatible. Proof. The theorem follows directly from Proposition 2 and Lemma 1. □
Remark 3. If the quantum channel Φ is unital
, that is to say, , the formula (10) simplifies, in the sense that the denominator is trivial: This will be the case for most of the examples we shall discuss in what follows.
It is important at this point to note that the incompatibility criterion we put forward in the result above is formulated as an SDP (semidefinite program). The usual way of formulating the compatibility of a tuple of quantum channels is also an SDP: one looks for a joint channel, a problem that can be formulated as an SDP thanks to the Choi formalism. However, let us compare the size of the SDPs:
Note also that one has, in both cases, N constraints of size . Therefore, we obtain a dramatic reduction in the size of the SDP at the price of having only a necessary compatibility condition (i.e., an incompatibility criterion).
There is, however, a situation when SDP (
11) simplifies and can be analytically solved. This is when the matrices
G corresponding to the channel are orthogonal (up to the maximally entangled state
). We formalize this observation below.
Proposition 3. Consider N quantum channels and orthonormal bases such that, for all , , Then, the value of SDP (11) is Proof. Taking into consideration Remark 2, one can rewrite SDP (
11) by subtracting
everywhere:
where
. Using the hypothesis and noting that the matrices
are all positive semidefinite, any feasible
must satisfy
Hence, the optimal
achieves equality above, and the conclusion follows. □
This idea will be used in
Section 5 and
Section 7 to obtain (analytical) incompatibility criteria for important classes of quantum channels.
As an example, let us work out the
G matrix for the identity channel
.
The matrix
will play an important role in what follows. We gather some useful facts about it below. Recall that two orthonormal bases
of
are called
unbiased if
Lemma 2. For any orthonormal basis , we have Moreover, if and are unbiased
orthonormal bases, then Let us close this section by mentioning how the matrices G behave when mixing noise into a quantum channel . This property will be very useful in what follows when investigating the compatibility robustness of some classes of quantum channels.
Lemma 3. Given a quantum channel , consider its noisy versionwhere is the completely depolarizing channel, and is some parameter. Then, for any orthonormal basis ,where ω is the maximally entangled state (note that ). Proof. This can either be proven directly using formula (
10) or by using the corresponding result for POVMs, see, e.g., ([
48] Proposition 5.3). □
5. Incompatibility of Two Schur Channels
As the first application of our newly introduced incompatibility criterion for quantum channels, we consider
Schur channels. A Schur map is a linear map of the form
where
B is a
complex matrix and ∘ denotes the Hadamard product. The map
is completely positive if and only if matrix
B is positive semidefinite, and it is trace-preserving if the diagonal of
B is the identity:
for all
i. If both conditions are satisfied, we call map
a Schur channel (sometimes also called a Schur multiplier), see [
49,
50,
51,
52]. Schur channels have received a lot of attention in operator algebra and quantum information theory, and they contain the identity channel
, where
J is the all 1s matrix, and the dephasing channel (the conditional expectation on the diagonal sub-algebra)
as examples.
For Schur channel
, we have
for any orthonormal basis
(recall the form of the matrix
Z from (
14)). If
e is the canonical basis, we have
Consider now a basis
that is unbiased with respect to the canonical basis; in other works, the elements of
form the columns of a Hadamard matrix
U:
for all
j. An important example of such a basis is the
Fourier basis:
Lemma 4. If B and C are two positive semidefinite matrices with unit diagonal, and and are unbiased, then Proof. Expanding the scalar product and using Lemma 2, we need to show that
Let us work out the left-hand-side:
where we have used Lemma 2 and the fact that
, which follows from the fact that
C has unit diagonal. The right-hand-side can be dealt with in the same manner. □
For a
matrix
B with unit diagonal, define the real parameter
as follows:
Recall that the torus is the set of vectors with for all .
Lemma 5. If B is a positive semidefinite matrix with unit diagonal, thenwith iff and iff for a vector . Proof. The non-negativity of
, as well as the equality case, follows directly from definition (
15). For the upper bound, use the ordering of the
-Schatten norms of
B to write
proving the inequality. Equality holds if
B is rank one, which, together with the condition on the diagonal, proves that
for some vector
. □
We can now, using Theorem 1, provide a new incompatibility criterion for Schur channels.
Theorem 2. Consider two positive semidefinite matrices B and C with unit diagonal, and the corresponding depolarized Schur channels If , then the channels and are incompatible. We have, thus, an upper bound for the compatibility region from Definition 2:where and . Proof. The proof is an application of Theorem 1. To start, let us compute the
G matrices associated with these channels, taking, respectively, the canonical basis
, and any unbiased base
(e.g., the Fourier basis); this choice is inspired by Lemma 4 and Proposition 3. Applying these results, as well as the scaling Lemma 3, we have
Hence, the value of SDP (
11) is given by (see Proposition 3)
We can evaluate
and, using parameter
from (
15), the incompatibility criterion reads
which is the first claim. The second claim follows by swapping the roles of the unbiased bases
and
. □
Remark 4. One can not easily generalize the result above to more than two Schur channels. This is due to the fact that one has to fix one of the bases in Theorem 1 to be the canonical basis. This is due to the fact that the Hadamard product used to define Schur channels is adapted to the canonical basis. We leave the generalization of the result (and method) above for three or more Schur channels open.
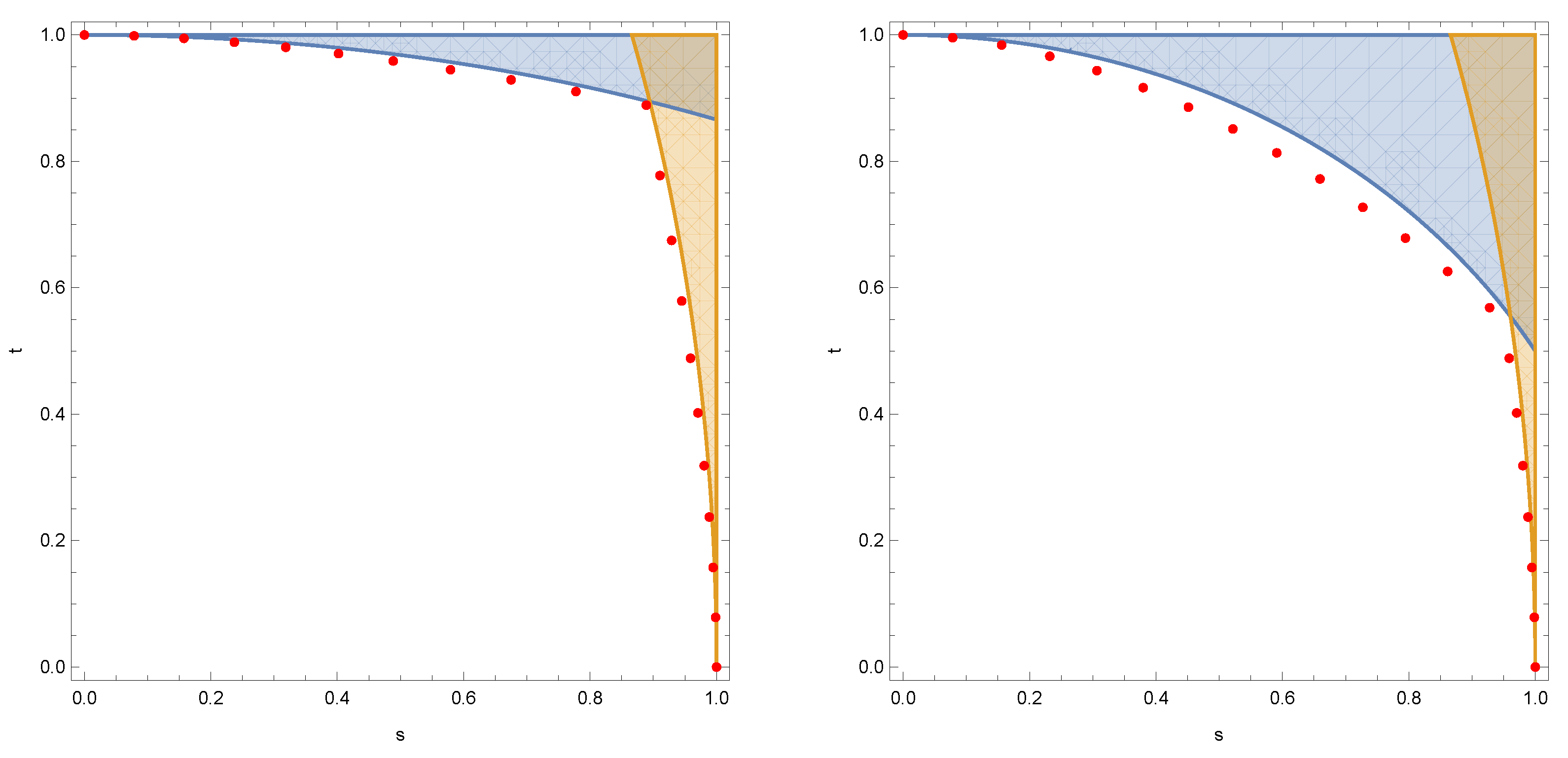
We compare, in
Figure 1, the criterion from the theorem above with the actual incompatibility thresholds for some particular Schur channels, concluding that the incompatibility criterion is close to being exact.
6. Channel Assemblages
The way in which several quantum measurement and quantum channels can be incompatible has been studied extensively in the literature [
53,
54,
55,
56]. The kind of (in-)compatibility structures that can be found in nature, and their relation to other important manifestations of non-locality (such as Bell inequality violations), is clearly a crucial question at the foundation of quantum theory.
Let
be a
channel assemblage that is an
N-tuple of quantum channels. If
are incompatible, there does not exist a joint quantum channel for
all the
N channels. However, a joint channel may exist when we consider a certain subset of
. In other words, some subsets of
may be compatible, even though the whole set is incompatible. Obviously, if the whole set of
N channels is compatible, then so is any subset: if
is a joint channel for the
N-tuple. Then, for any subset
of the channels,
, the marginal of
corresponding to the output indices in
S
is a joint channel for
; above, we identify the different copies of the output space
by a superscript. Therefore, it is significant to classify the incompatibility of subsets for a given quantum channel assemblage. A
K-subset of
is simply a subset
of cardinality
.
Definition 4. Consider a quantum channel assemblage and an integer. The N-tuple Φ is called:
-compatible if all K-subsets of Φ are compatible.
-incompatible if at least one K-subset of Φ is incompatible.
-strong incompatible if all K-subsets of Φ are incompatible.
-genuinely incompatible if it is -compatible and -incompatible.
-genuinely strong incompatible if it is -compatible and -strong incompatible.
Note that the assemblage
is compatible if and only if it is
-compatible. The previous definition is strongly inspired by the one from ([
56]
Section 2) in the case of POVMs. The incompatibility criterion from Theorem 1 can be readily adapted to the previous definition by considering subsets of the PSD constraints in (
11). We restate it here for the convenience of the reader. We shall apply it in the next section for assemblages of depolarizing channels.
Theorem 3. Consider an assemblage of quantum channels acting on . For a K-subset S of , and K orthonormal bases of , define the value of the following semidefinite program If there exists at least one and a K-tuple of orthonormal bases such that , then the assemblage Φ is -incompatible. Moreover, if for all K-subsets , there exists a K-tuple of bases such that , the assemblage Φ is -strong incompatible.
7. Assemblages of Depolarizing Channels
In this section, we address the (in-)compatibility properties of an
N-tuple of partially depolarizing channels, using the Fisher information-based criterion from Theorem 1. Recall that the
partially depolarizing channel is the linear map
given by
where
is the identity channel
and
is the fully depolarizing channel
. The parameter
interpolates between the identity channel and the fully depolarizing channel.
In this section, we shall study the incompatibility of
N partially depolarizing channels {
, for some fixed parameters
, with the help of the criterion from Theorem 1. To do so, let us first compute the
G matrices of depolarizing channels, which are just noisy versions of the identity channel. Recall from Equation (
14) that, for the identity channel, we have, for an arbitrary basis
,
where
denotes the (entrywise) complex conjugate of the vector
. Hence, by Lemma 3, we have
As in
Section 5, we are going to use the orthogonality of the
G matrices in order to put forward analytical incompatibility criteria for depolarizing channels (see Proposition 3). To do so, recall that the
matrices have tractable scalar products for unbiased bases. As it turns out, mutually unbiased bases [
57] will play an important role in what follows. Let
be the maximal cardinality of a set of mutually unbiased bases of
. It is known that
[
58,
59,
60]. The upper bounds are attained for all dimensions
d, which are prime powers; whether it is always attained is an important open problem in quantum information theory, even the case
being undecided.
We now state the main result of this section, an incompatibility criterion for depolarizing channels.
Proposition 4. Let N be an integer such that , the maximal number of mutually unbiased bases of . Consider N depolarizing channels , where are noise parameters. Ifthen the N depolarizing channels are incompatible. Proof. Since the number of channels we consider is smaller than
, we can choose
N mutually unbiased bases
. SDP (
11) reads
Proposition 3 applies, so the value of the SDP above is
Hence, if condition (
19) holds, by Theorem 1, the
N quantum depolarizing channels
are incompatible. □
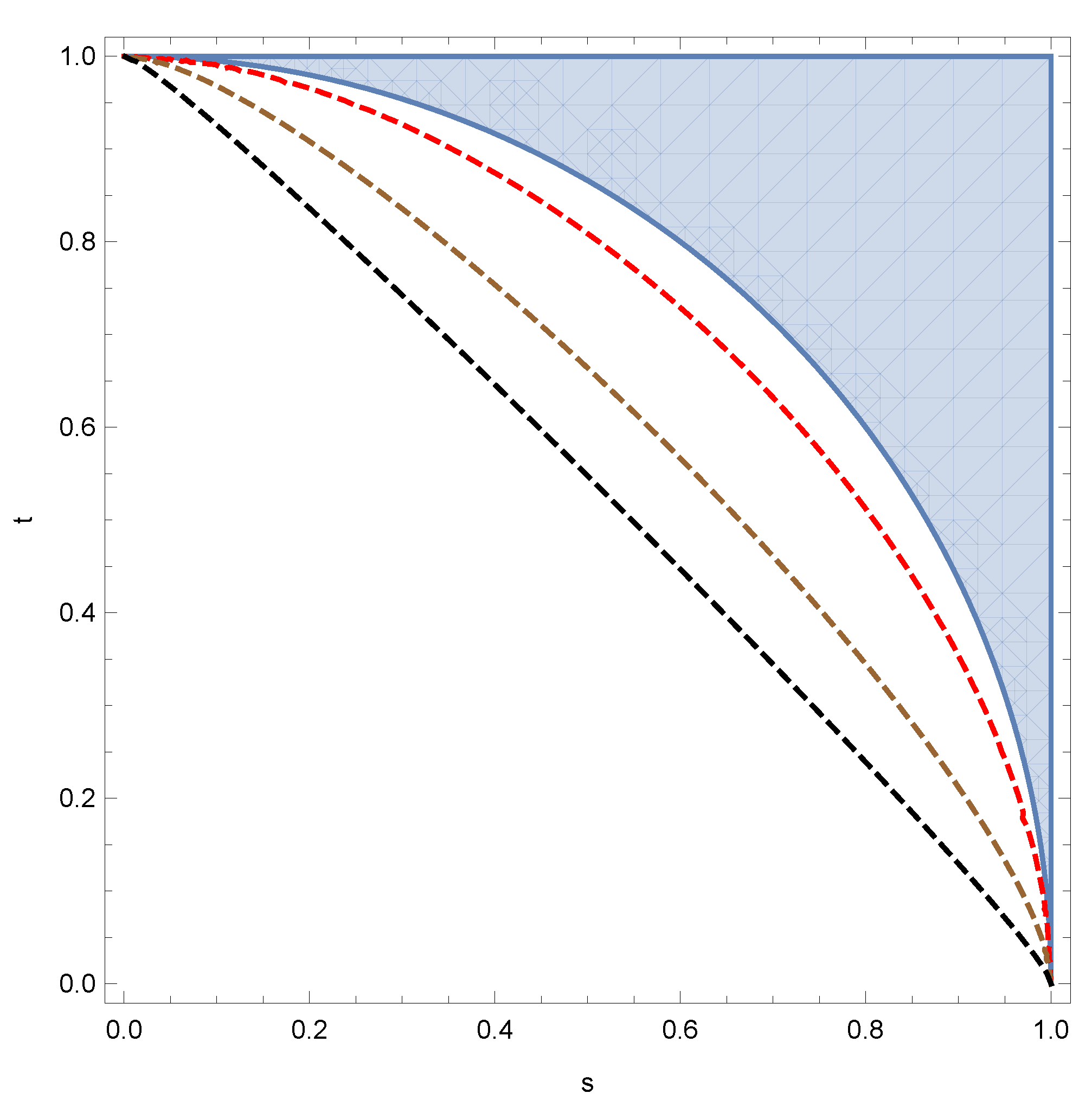
As mentioned in the introduction, the compatibility of depolarizing channels is equivalent to approximate quantum cloning: how much noise one needs to add to
N copies of the identity channel to render them compatible. In
Figure 2, we present the relative performance of the criterion from Proposition 4, with the true values of the noise parameters for
asymmetric approximate quantum clonings from Equation (
5).
We can specialize the result above to assemblages of depolarizing channels in the spirit of Definition 4.
Corollary 1. Consider N partially depolarizing channels { acting on and let be an integer. If there exists a subset of cardinality K such thatthen the channels are -incompatible. Moreover, if for every
subset of cardinality K the condition above holds, the channels are -strongly incompatible. Note that in the statement above, we do not require that the number N of channels must be smaller than the number of mutually unbiased bases in the corresponding Hilbert space; this is required only of the parameter K. This criterion might thus be useful in situations where one has a large number of channels.
We end this section by a similar corollary, in the setting where the channels are identical.
Corollary 2. If are integers such that , then the partially depolarizing channel from Equation (18) is -self-(strong) incompatible as soon as .