Finite-Time Stochastic Stability Analysis of Permanent Magnet Synchronous Motors with Noise Perturbation
Abstract
:1. Introduction
- (1)
- The effect of noise perturbation on the finite-time stability of PMSMs is considered for the first time.
- (2)
- Combining the advantages of the adaptive method and finite-time control technology, the designed controllers can realize the stochastic stability of the PMSM system within a finite time.
- (3)
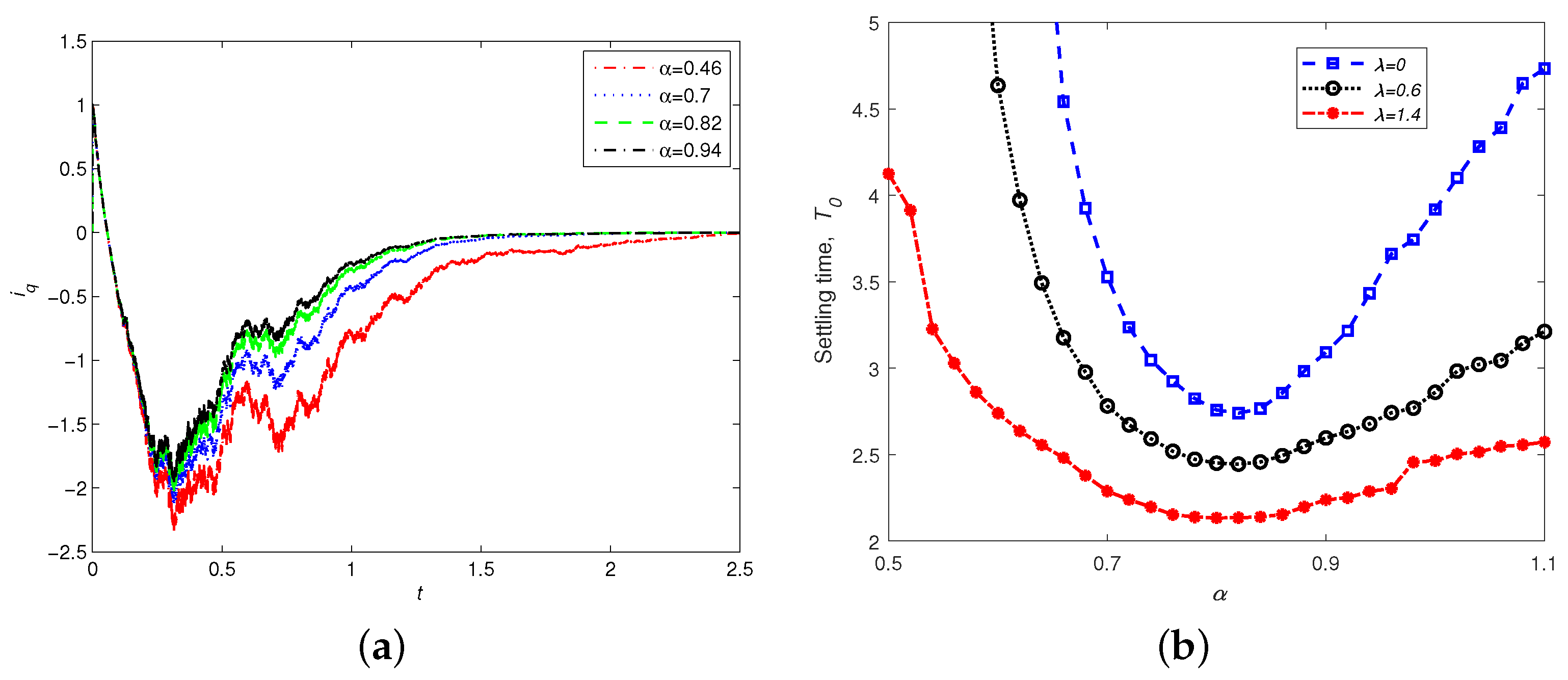
- We consider the effect of a control parameter and noise on the stability, and find that there is an optimal parameter such that the convergence time is shortest.
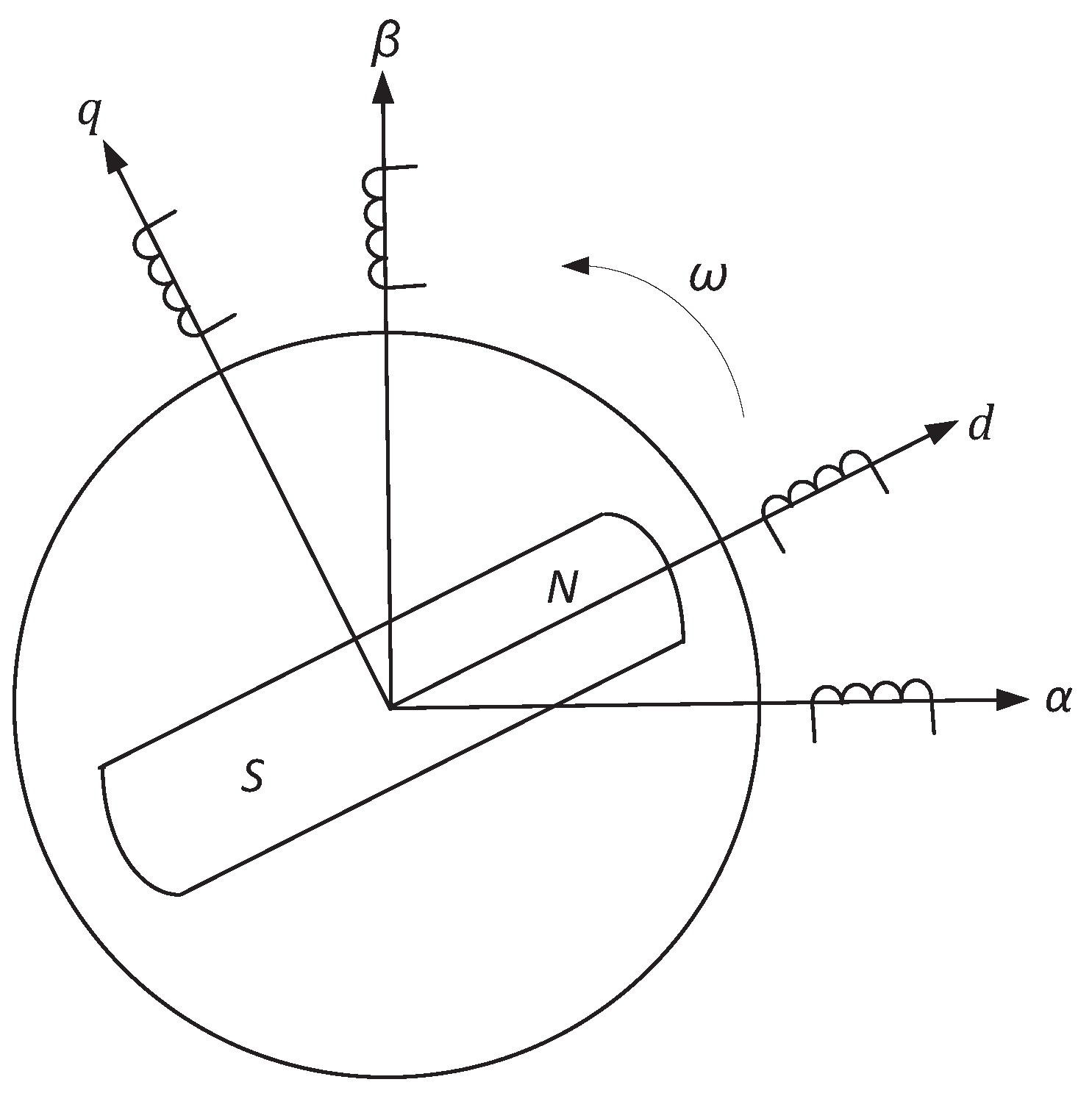
2. Model Description and Problem Formulation
3. Main Results
- Step 1
- The initial state of the PMSM system and the input parameters of the noise intensity are determined, and the appropriate control parameter for the controllers (7) is selected to speed up the convergence process.
- Step 2
- Calculate the tuning parameters according to the updated Equation (8) for the terminal attractor and the current state of the PMSM.
- Step 3
- The values of and are substituted into the controllers (7), and thus the values of and from the adaptive controller can be calculated.
- Step 4
- Substituting the values of , and into the Equation (6), the state values of , , and can be obtained.
- Step 5
- Determine the accuracy parameter . If , the PMSM system is considered to have achieved a stable state, then quit, or else return to Step 2.
4. Numerical Simulation
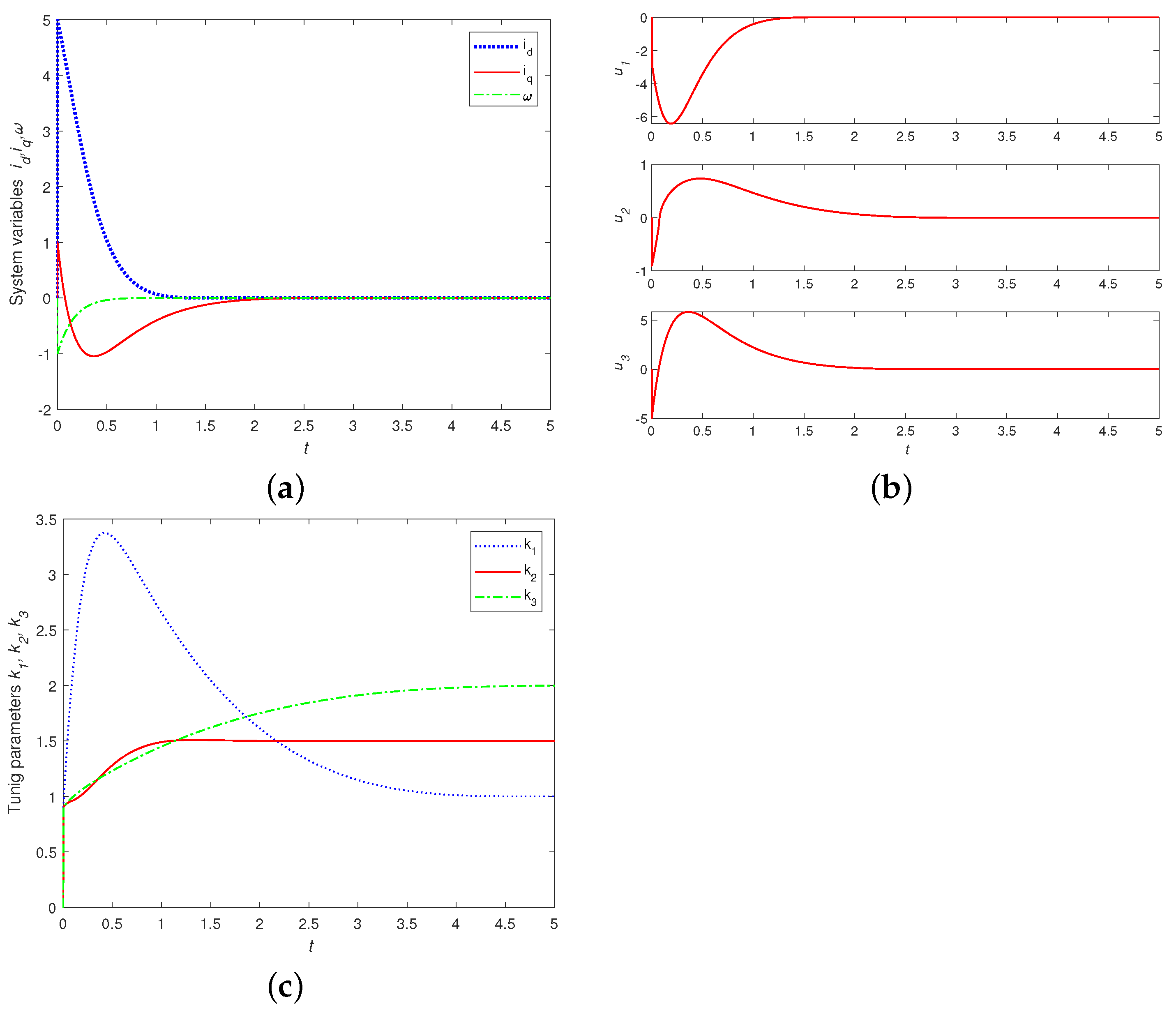
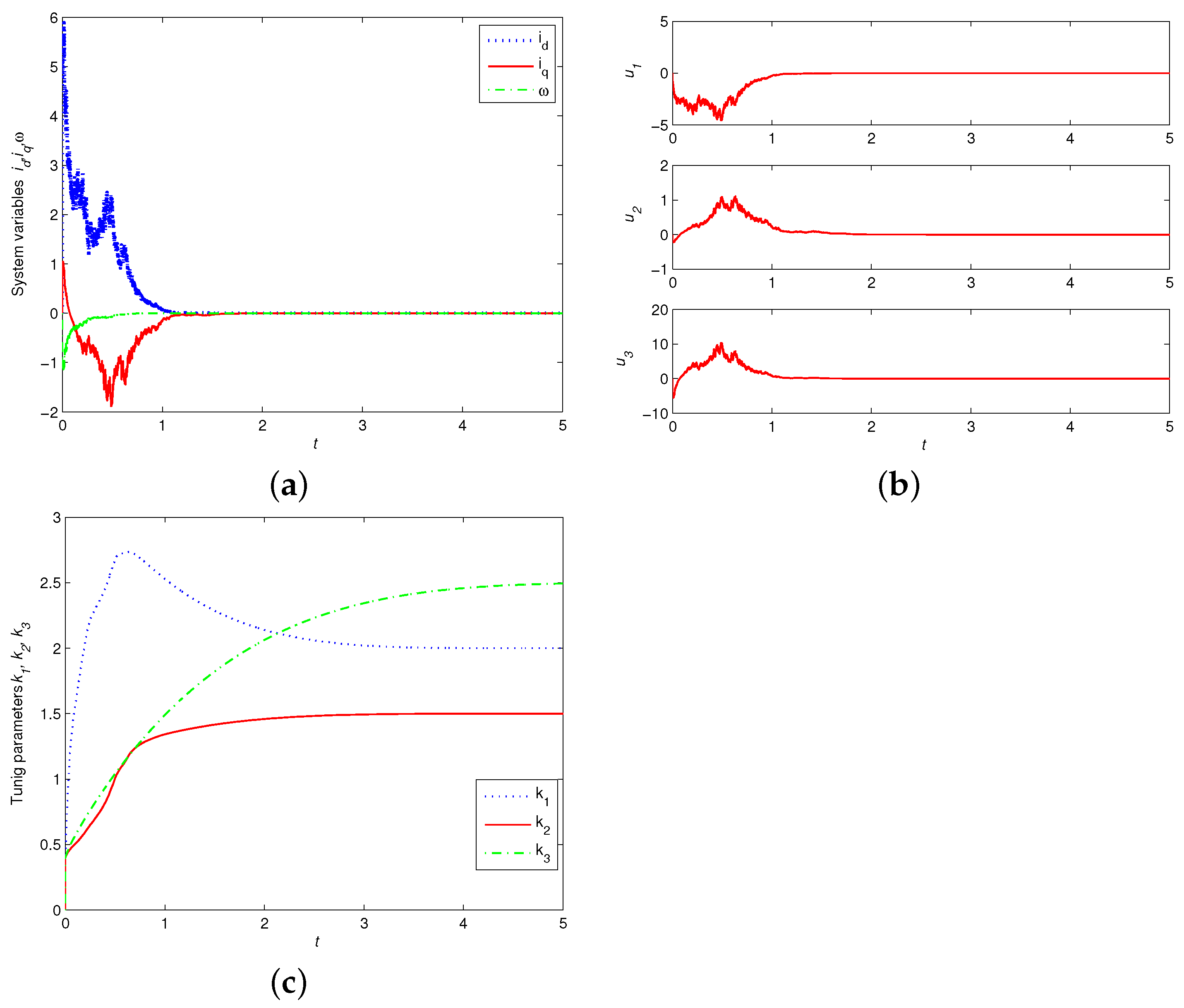
4.1. Finite-Time Control of PMSM with Noise Perturbation
4.2. Robust Finite-Time Synchronization and Parameters Identification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| PMSM | Permanent Magnet Synchronous Motors |
References
- Lorenz, N. Deterministic nonperiodic flow. J. Atmos. Sci. 1962, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Pennacchi, P. Nonlinear effects due to electromechanical interaction in generators with smooth poles. Nonlinear Dyn. 2009, 57, 607–622. [Google Scholar] [CrossRef]
- Skufca, J.D.; Yorke, J.A.; Eckhardt, B. Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 2006, 96, 174101. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.G.; Shi, P.H.; Su, Y.; Chu, J. Local synchronization of chaotic neural networks with sampled-data and saturating actuators. IEEE Trans. Cybern. 2014, 44, 2635–2645. [Google Scholar]
- Sun, Y.H.; Wei, Z.N.; Sun, G.Q.; Ju, P.; Wei, Y.F. Stochastic synchronization of nonlinear energy resource system via partial feedback control. Nonlinear Dyn. 2012, 70, 2269–2278. [Google Scholar] [CrossRef]
- Cheng, Z.S.; Cao, J.D. Synchronization of a growing chaotic network model. Appl. Math. Comput. 2011, 218, 2122–2127. [Google Scholar] [CrossRef]
- Yang, X.S.; Cao, J.D. Exponential synchronization of delayed neural networks with discontinuous activations. IEEE Trans. Circuits Syst. I-Regul. Pap. 2013, 60, 2431–2439. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef]
- Wu, J.; Cai, Z.; Sun, Y.; Liu, F. Finite-time synchronization of chaotic system with noise perturbation. Kybernetika 2015, 54, 137–149. [Google Scholar] [CrossRef] [Green Version]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.L.; Zhou, C.S. The synchronization of chaotic systems. Phys. Rep.-Rev. Sec. Phys. Lett. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Shi, H.; Miao, L.; Sun, Y. Fixed-time outer synchronization of complex networks with noise coupling. Commun. Theor. Phys. 2018, 69, 271–279. [Google Scholar] [CrossRef]
- Zhang, W.W.; Cao, J.D.; Wu, R.C.; Alsaedi, A.; Alsaadi, F.E. Projective synchronization of fractional-order delayed neural networks based on the comparison principle. Adv. Differ. Equ. 2018, 1, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Shen, Z.; Yang, F.; Chen, J.; Zhang, J.X.A.; Hu, H.; Hu, M.F. Adaptive event-triggered synchronization of uncertain fractional order neural networks with double deception attacks and time-varying delay. Entropy 2021, 23, 1291. [Google Scholar] [CrossRef] [PubMed]
- Azar, A.T.; Serrano, F.E.; Zhu, Q.; Bettayeb, M.; Fusco, G.; Na, J.; Zhang, W.; Kamal, N.A. Robust stabilization and synchronization of a novel chaotic system with input saturation constraints. Entropy 2021, 23, 1110. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.M.; Volos, C.; Serrano, F.E.; Jafari, S.; Kengne, J.; Rajagopal, K. Stabilization and synchronization of a complex hidden attractor chaotic system by backstepping technique. Entropy 2021, 23, 921. [Google Scholar] [CrossRef]
- Wen, G.H.; Wan, Y.; Cao, J.D.; Huang, T.W.; Yu, W.W. Master-slave synchronization of heterogeneous systems under scheduling communication. IEEE Trans. Syst. Man Cybern.-Syst. 2018, 48, 473–484. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, J.; Lu, J.A.; Lu, J.H. On applicability of auxiliary system approach to detect generalized synchronization in complex network. IEEE Trans. Autom. Control 2017, 62, 3468–3473. [Google Scholar] [CrossRef]
- Erban, R.; Haskovec, J.; Sun, Y. A Cucker-smale model with noise and delay. SIAM J. Appl. Math. 2016, 76, 1535–1557. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.S.; Lu, J.Q.; Ho, D.W.C.; Song, Q. Synchronization of uncertain hybrid switching and impulsive complex networks. Appl. Math. Model. 2018, 59, 379–392. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, W.L.; Yang, X.S.; Xu, C.; Feng, J.W. Finite-time synchronization of complex-valued neural networks with mixed delays and uncertain perturbations. Neural Process. Lett. 2017, 46, 271–291. [Google Scholar] [CrossRef]
- Yu, W.W.; Wang, H.; Cheng, F.; Yu, X.H.; Wen, G.H. Second-order consensus in multiagent systems via distributed sliding mode control. IEEE Trans. Cybern. 2017, 47, 1872–1881. [Google Scholar] [CrossRef] [PubMed]
- Hemati, N. Strange attractors in brushless DC motors. IEEE Trans. Syst. Man Cybern.-Syst. 1994, 41, 40–45. [Google Scholar] [CrossRef]
- Gao, J.S.; Shi, L.L.; Deng, L.W. Finite-time adaptive chaos control for permanent magnet synchronous motor. J. Comput. Appl. 2017, 37, 597–601. [Google Scholar]
- Choi, H.H. Adaptive control of a chaotic permanent magnet synchronous motor. Nonlinear Dyn. 2012, 69, 1311–1322. [Google Scholar] [CrossRef]
- Harb, A.M. Nonlinear chaos control in a permanent magnet reluctance machine. Chaos Solitons Fractals 2004, 19, 1217–1224. [Google Scholar] [CrossRef]
- Maeng, G.; Choi, H.H. Adaptive sliding mode control of a chaotic nonsmooth-air-gap permanent magnet synchronous motor with uncertainties. Nonlinear Dyn. 2013, 74, 571–580. [Google Scholar] [CrossRef]
- Loria, A. Robust linear control of (chaotic) permanent-magnet synchronous motors with uncertainties. IEEE Trans. Circuits Syst. I-Regul. Pap. 2009, 56, 2109–2122. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.X.; Wu, J.; Sun, Y.Z. Fixed-time stability analysis of permanent magnet synchronous motors with novel adaptive control. Math. Probl. Eng. 2017, 2017, 4903863. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Cao, J.D. Finite-time synchronization of coupled networks with one single time-varying delay coupling. Neurocomputing 2015, 166, 265–270. [Google Scholar] [CrossRef]
- Zhang, W.L.; Yang, X.S.; Xu, C.; Feng, J.W.; Li, C.D. Finite-time synchronization of discontinuous neural networks with delays and mismatched parameters. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3761–3771. [Google Scholar]
- Yang, X.S.; Cao, J.D.; Xu, C.; Feng, J.W. Finite-time stabilization of switched dynamical networks with quantized couplings via quantized controller. Sci. China Technol. Sci. 2018, 61, 299–308. [Google Scholar] [CrossRef]
- Hou, Y.-Y. Finite-time chaos suppression of permanent magnent synchronous motor systems. Entropy 2014, 16, 1099–4300. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Ren, X.M.; Na, J. Robust finite-time chaos synchronization of uncertain permanent magnet synchronous motors. IEEE Trans. Circuits Syst. I-Regul. Pap. 2015, 58, 262–269. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Park, J.B.; Joo, Y.H.; Zhang, B.; Chen, G.R. Bifurcations and chaos in a permanent-magnet synchronous motor. IEEE Trans. Syst. Man Cybern.-Syst. 2002, 49, 383–387. [Google Scholar]
- Haimo, V. Finite time controllers. Soc. Ind. Appl. Math. 1986, 24, 760–770. [Google Scholar] [CrossRef]
- Sun, Y.Z.; Li, W.; Zhao, D.H. Finite-time stochastic outer synchronization between two complex dynamical networks with different topologies. Chaos 2012, 22, 440. [Google Scholar] [CrossRef]
- Khalil, H.K.; Grizzle, J.W. Nonlinear System; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Sun, Y.H.; Wu, X.P.; Bai, L.Q.; Wei, Z.N.; Sun, G.Q. Finite-time synchronization control and parameter identification of uncertain permanent magnet synchronous motor. Neurocomputing 2016, 207, 511–518. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Shi, H.; Nie, P.; Wu, J. Finite-Time Stochastic Stability Analysis of Permanent Magnet Synchronous Motors with Noise Perturbation. Entropy 2022, 24, 791. https://doi.org/10.3390/e24060791
Ma C, Shi H, Nie P, Wu J. Finite-Time Stochastic Stability Analysis of Permanent Magnet Synchronous Motors with Noise Perturbation. Entropy. 2022; 24(6):791. https://doi.org/10.3390/e24060791
Chicago/Turabian StyleMa, Caoyuan, Hongjun Shi, Pingping Nie, and Jiaming Wu. 2022. "Finite-Time Stochastic Stability Analysis of Permanent Magnet Synchronous Motors with Noise Perturbation" Entropy 24, no. 6: 791. https://doi.org/10.3390/e24060791
APA StyleMa, C., Shi, H., Nie, P., & Wu, J. (2022). Finite-Time Stochastic Stability Analysis of Permanent Magnet Synchronous Motors with Noise Perturbation. Entropy, 24(6), 791. https://doi.org/10.3390/e24060791





