1. Introduction
The emergence of objective, classical information from quantum systems is due to amplification: Many pieces of the environment—e.g., many photons—each interact with a quantum system and acquire an imprint of certain states, the pointer states. This is the process by which select information becomes redundant and accessible to many different observers. The framework, where the environment decoheres systems and acts as a communication channel for the resulting information, is known as quantum Darwinism [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. It is the pointer states that survive the interaction with the environment and create “copies” of themselves from which observers can infer the pointer state of the system. This process has been seen experimentally in both natural [
21] and engineered [
22,
23] settings, and both theory and practical calculations are steadily progressing [
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38].
Within this framework, one primary question concerns the information available within an environment fragment as its size increases. This allows one to quantify redundancy: If small fragments
of the environment
all contain the same information about the system
, then that information is available to many observers. Given a global state,
, the accessible information
can quantify the amount of information an observer learns about
(a positive operator-valued measure, a POVM, on
) by making a measurement
on only
. The quantity
is the classical mutual information computed from the joint probability distribution from outcomes of
and
. The POVM
has elements
that generate an ensemble
of outcomes
s with probability
and conditional states
on
(i.e., assuming the POVM acts on only
and an auxiliary system but
is not directly affected). Allowing
to be arbitrary, the accessible information, Equation (
1), depicts a situation where some auxiliary system
, perhaps a special observer or another part of the environment, has access directly only to
, makes a measurement
, and holds a record of the outcome
s, leaving a joint state (after tracing out the now irrelevant
)
An observer
then wants to predict the outcome
s by making measurements only on
, e.g., correlations are generated between
and
but indirectly from separate measurements on
and
, for which Equation (
1) quantifies this capability. One could then maximize the accessible information over all
to see what quantity the observer can learn most about. This allows one to quantify the structure of correlations between
and
induced by, e.g., a decohering interaction between them.
Within the context of physical processes that give rise to quantum Darwinism,
is not arbitrary, however. For redundant information to be present, there must be at least two records of some information, which, when decoherence is the main interaction, will be the pointer information. Hence, there must be an
that almost, to a degree we want to quantify, makes a measurement of the pointer states. At the same time, the remaining part of the environment,
, has already made an effective measurement for all intents and purposes, to a degree that we can retroactively validate. This entails that the correlations are effectively of the form of Equation (
2) but with
or
and
(the pointer observable),
where
labels the pointer states (see Refs. [
39,
40] for a discussion of pointer states). This form is a consequence of “branching” [
3] and appears in the good decoherence limit of purely decohering models, which will be extensively discussed below. Here, it is sufficient to note that the state, Equation (
3), is the most relevant to quantum Darwinism. It makes little difference if one treats the
as
or as just the fully decohered, or directly measured,
, even when
is extremely large in absolute terms. Only for “global” questions, where
is some sizable fraction of the environment, does it matter. Since the environment is huge for most problems of everyday interest, such as photon scattering,
can be very large—even asymptotically large—without concern for this. However, Equation (
3) does drop exponentially small corrections in the size of
and one can not formally take the asymptotic limit of
without first doing so in
. The degree to which asymptotic approximations work thus relies on the balance sheet—how well records are kept in the environment components compared to
’s absolute size. Ref. [
14] has dealt with retaining corrections to Equation (
3). Hereon, I treat the auxiliary system
as if it were
.
2. Results
With states of the form in Equation (
3), the mutual information between
and
is the Holevo quantity
where
is the von Neumann entropy for the state
. This quantity upper bounds the capacity of
to transmit pointer state information (the variable
is encoded in the conditional states
). Moreover, for an important class of interactions—purely decohering Hamiltonians with independent environment components—the quantum Chernoff bound determines the behavior of the optimal measurement on
to extract
and, thus, is related to the accessible information, Equation (
1) with
. One can generalize Equation (
4) by allowing one to maximize over measurements on the system,
where, when good decoherence has taken place,
maximizes the Holevo quantity [
14]. The good decoherence limit is when
is sufficient to decohere the system and, thus, the
state is exactly of the form in Equation (
3) [
10,
14]. Here, I employ the notation
of Touil et al. [
38] to indicate that the Holevo quantity is maximized over measurements on
, see also the next equation.
Touil et al. [
38] examined an alternative Holevo quantity with the measurement on the fragment side,
where the maximization is over all POVMs
and
f labels the outcomes of
and
their probabilities. In that work, they compute the quantum mutual information, the Holevo quantity in Equation (
4), and the alternative Holevo quantity in Equation (
6) for a “
c-maybe” model of decoherence of
by
, a model that falls into the class of purely decohering models (see below). They analytically found
by making use of the Koashi–Winter monogamy relation [
41] and showed all the mutual information quantities above that approach the missing information,
, with a similar dependence on
.
If one were to interpret this alternative Holevo quantity, Equation (
6), in the typical way, then it would bound the channel capacity of
to transmit information about (the optimal)
. One important observation, however, is that, in the good decoherence limit—when the
state is of the form in Equation (
3)—
lower bounds
for any
by the data processing inequality since
is already measured on
by
. In this limit,
is the actual accessible pointer information.
For an arbitrary
state, however, there is no strict relation of
or
with
or
. In that case, the Holevo quantities with measurements on the
side can not upper or lower bound quantities with
side measurements. For a particular state with a given inequality between
and
side measurements, one can swap
and
in the state
—it is arbitrary after all—and reverse the inequality. Instead, the inequality
holds for any
. The measurement on the two sides of the inequality is generically different—the measurement that maximizes
is not the measurement,
, that maximizes
to get the accessible information, Equation (
1). The proof of Equation (
7) is straightforward,
where the system
is adjoined in a product state with
and a unitary on
makes a measurement
. The fourth line follows from data processing.
Equation (
7) is an accessibility bound. Any information about
(i.e., that can be extracted by a direct POVM on
) can, at best, have
amount of shared information with
. Then, as already noted, if the good decoherence limit is reached, that bound becomes equality,
for the pointer information. This follows from the form of the state in Equation (
3). To determine
for this state, an apparatus makes a measurement
and records the outcome, leaving a joint system-apparatus state
. This is a classical-classical state that yields, after maximizing over
, both
, Equation (
6), and the accessible information, Equation (
1). This makes
desirable in the context of quantum Darwinism: It not only is a better bound on the accessible information in the good decoherence limit—the main limit of interest for quantum Darwinism—but it is the actual accessible information.
To proceed further—to compute the accessible information and the associated redundancy—we need to specify a model or class of models that provide the global states of interest. The everyday photon environment has a particular structure where independent environment components (photons) scatter off objects, acquire an imprint of the state, and transmit that information onward, interacting little with each other in the process [
11,
12,
16,
42,
43,
44]. This structure is captured by purely decohering Hamiltonians by independent environment components. I will consider this general class here. Under this evolution, the quantum Chernoff bound (QCB) provides a universal lower bound to the accessible information and the associated redundancy. The quantum Chernoff result is also meaningful on its own as a single-shot result, quantifying how well an individual observer (with the best measurement apparatus) can learn the pointer state of
indirectly from
.
Pure decoherence occurs when environments select, but do not perturb, the pointer states of
. When the environment components do so independently, the Hamiltonian is of the form
with
and the initial state
Here,
k specifies a component of the environment
of size
. The operators,
and
, are arbitrary. This class of models contains the
c-maybe model of Touil et al. [
38]. That model has
and
for all
k, where
a is the angle of rotation of the “target” environment bit after a time
t. Note that all the coupling frequencies (i.e., the energy scales divided by the reduced Planck’s constant) are absorbed into the definition of the operators
,
, and
, while
is dimensionless. All other operators are 0. The collection of operators act similarly to those in the controlled NOT gate. They only swap as well, only a bit more lazily, as here
a is any number, so it is called
c-maybe.
Starting from the initial product state, Equation (
10), and evolving for some time under the Hamiltonian, Equation (
9), one can obtain the conditional states that appear in the Holevo quantity, Equation (
4),
Due to the structure of the evolution, these are product states over the components of the environment fragment. However, they need not be identically distributed (that is, they need not be fully
i.i.d.—independently and identically distributed—states).
The structure, Equation (
11), is a manifestation of amplification. The pointer states
leave an imprint on the environment components, of which there are many. Observers intercepting those environment components can then make a measurement to infer the pointer state. This is the setting of quantum hypothesis testing. For instance, in the binary case with two pointer states
or 1, one wants to decide whether the fragment state is
or
with a minimum average probability of error,
. This is based on a POVM measurement,
, composed of two positive operators
and
(with
) that indicate the occurrence of “0” or “1”, respectively. The first contribution to this average error is when the actual state is
, with
a priori probability of occurring
(where I explicitly show
to connect to Equation (
3)) but the measurement yielded the incorrect outcome
. Similarly for the second contribution. Moreover, when amplification occurs, i.e., the conditional states are of the form in Equation (
11), one is specifically interested in how the error probability behaves as the fragment size grows. This is the setting of the QCB.
To employ the QCB, one makes use of a two-sided measurement. The first is on
, putting it into its pointer states (i.e.,
now provides the mutual information between
and
). This reflects the action of
and is the good decoherence limit—, i.e.,
provided
and
have interacted for some finite time under the evolution given by Equations (
9) and (
10). This also requires that the coupling strength to the environment components do not depend on
. The second is on
to access the pointer state. By Fano’s inequality [
45,
46],
where
is the error probability for extracting information about a (sub)space of pointer states (of dimension
D) from a measurement on
. One could replace the left hand side of this inequality with
. Here, I use the binary entropy,
. The QCB upper bound,
, gives a second inequality
which is partway to the final QCB result [
16,
19].
The QCB upper bounds the error probability,
, for both the
case [
47,
48,
49] or the
cases [
50]. There is no fundamental difference between these cases, it is only the closest two states that determine the asymptotic decay of
when
. I will restrict to
from hereon to make a correspondence with Touil et al. [
38]. The error probability (bound) is
For pure
states in the purely decohering scenario, Equations (
9) and (
10),
c can be any value between 0 and 1 within the generalized overlap contribution,
, and it will give the exact overlap
(which is also the decoherence factor
squared for this case of pure states). Touil et al. [
38] consider the homogeneous case where
for all
k, which I will also consider (see Refs. [
16,
19] for inhomogeneous results).
For pure states, therefore, only the prefactor needs optimizing over
c as the generalized overlap gives
for all
and with
the number of components in
. The prefactor is optimal at one of the two boundaries (
or
), giving
I use a slightly different notation here than Ref. [
38] to keep the correspondence with prior work. Opposed to pure states, for mixed
states within the pure decohering scenario, Equations (
9) and (
10), the error probability (bound) is
for both spin and photon models [
16,
19] (i.e.,
is optimal). Either prefactor,
or
, will give a bound for the pure state case. Letting the prefactor to be just some
C, the QCB result for pure, homogeneous
is
where I stress that this is a classical-classical information about random variable
(pointer states on
) with measurement outcomes on
. If we want general
states, but still the pure decoherence model, Equations (
9) and (
10), we have exactly the same form as Equation (
16) but the decoherence factor (the pure state overlap) is replaced by the generalized measure of overlap,
, see Ref. [
19] for these expressions in terms of generic angles (between conditional states) and lengths on the Bloch sphere for spins and Ref. [
16] for photons.
The QCB is a universal result. The bound Equation (
14) is true for all models of pure decoherence by independent spins or the standard photon model, all dimensions in between (qutrits, qudits, etc.), inhomogeneous models, pure and mixed
states, and ones with individual self-Hamiltonians on
. The only stipulation for Equation (
14) and the lower bound
is that one is distinguishing within a two-dimensional subspace of
pointer states. For higher dimensional subspaces, the number of pointer states,
D, appears in Equation (
13) and the exponent in the decay of
requires a pair-wise minimization of the generalized overlap over conditional states (as well as a different prefactor outside of the exponential).
The most important aspect of the compact form, Equation (
16), and its generalization to higher
D, is that the right hand side reflects actual, inferable information about the pointer states that the observer can retrieve by interaction with just
in a single shot. Moreover, while the QCB is traditionally cast as an asymptotic result, we have not actually used any asymptotic limits to obtain Equation (
16). Both of these aspects—single shot and finite
—provide a natural setting for our world, where observers are “agents” within these regimes. One can then ask questions about resources of observers (for instance, global versus local measurements on
subcomponents [
51] or the ability to perform coherent measurements [
52]) that further refine the results but do not change the fundamental framework of single-shot, finite
inference.
Let us return to the
c-maybe model and the Holevo quantities. Touil et al. [
38] present results for the quantum mutual information,
, and
. In the good decoherence limit, the latter two are
and
in the form as they appear in their main text but using the notation here (Equations (17) and (20) in Ref. [
38]). Rewriting these in terms of binary entropy gives
corresponding to the good decoherence expressions in Ref. [
10], and
We see that Equations (
16) and (
20) have a similar structure. Indeed, in the good decoherence limit and for pure conditional states, the accessible information, which is equivalent to Equation (
18) or Equation (
20), is equal to
. Here,
is the optimal error probability, which is given by the Helstrom measurement [
53], for single shot state discrimination of the conditional fragment states [
54,
55,
56]. This is not true for mixed or for higher dimensional pointer subspaces [
57,
58,
59,
60]. It can be verified in this case by a direct computation of the error probability from the optimal measurement for the pure conditional states. For
pure, the trace distance in the Helstrom expression just requires diagonalizing an operator in a two-dimensional subspace, giving
(this readily generalizes to the inhomogeneous case: The factor
just needs to be replaced by
). This result makes no use of the fact that the environment components were spins, and thus it is directly applicable to (pure state) photon scattering off an object in a two dimensional superposition, more directly supporting the connection discussed in Touil et al. [
38] and extending it to
in the good decoherence limit. Moreover, as with the QCB result, the form of the accessible information for pure
states,
, with the optimal
from Equation (
21) holds regardless of the environment components. They can be spins, qudits, or photons. Furthermore, the connection with hypothesis testing allows for even more general statements about models that are not purely decohering. For instance, for projection-valued measurements and pure
states, one obtains the same accessible information,
, but the error probability just has the overlap between the conditional fragment states, which can behave in a manner that is not exponentially decaying with
.
While specific to the case of
and pure
states evolving under Equations (
9) and (
10), the connection provides a window into the behavior of different ways to quantify correlations. The alternate Holevo quantity,
, becomes the inferable information in this specific setting. However, inferable information has a universal form that goes beyond this specific setting of dimensionality and purity.
Redundancy. The decay to the classical plateau—the missing information
about the system—for the quantities in Equations (
16), (
19) and (
20), all are controlled by the
-induced decoherence factor,
. Ultimately, though, we are interested in the redundancy of information. This requires introducing a control, the information deficit
, which reflects the fact that one can not generally obtain perfect knowledge from a finite-size fragment
. This is typically taken as
where
is some mutual information (quantum mutual information, Holevo, accessible information, etc.). This is the form I will employ here. However, both the form of the QCB and the form of
(in the good decoherence limit) suggest employing the information deficit as an entropic quantity when thresholding entropic measures of information,
This allows
to be a factor reflecting distinguishability of conditional states and allows for non-asymptotic computations to proceed for the redundancy (it removes the transcendental form of the equations). I will not use this in what follows.
The approach to the plateau and the redundancy (to within
) have simple asymptotic results regardless of quantity used to compute them. The decay exponent to the plateau,
, of some information theoretic quantity
, such as Equations (
19) and (
20), or Equation (
16), is
For the pure, homogeneous
c-maybe model, all three decay to the plateau with exponent
That is universality in a nutshell. Moreover, the exponent is the leading order of the redundancy,
This is the essence of the QCB: The exponent—the quantum Chernoff information,
, or its inhomogeneous counterpart,
—controls the redundancy, see Refs. [
16,
19] for additional discussion and results. For the pure
c-maybe model, this exponent is the same whether using Equations (
19) and (
20), or Equation (
16). The quantum mutual information also yields the same decay and redundancy in the good decoherence limit, as it is the same as
from Equation (
19). In order to apply Equation (
24) for the quantum mutual information, one needs
. As already mentioned previously, though, this will entail good decoherence provided some finite interaction between
and
components has taken place. In the end, all the information theoretic quantities provide the same decay and redundancy, which the asymptotic calculation, Equation (
24), makes apparent in a non-empirical manner.
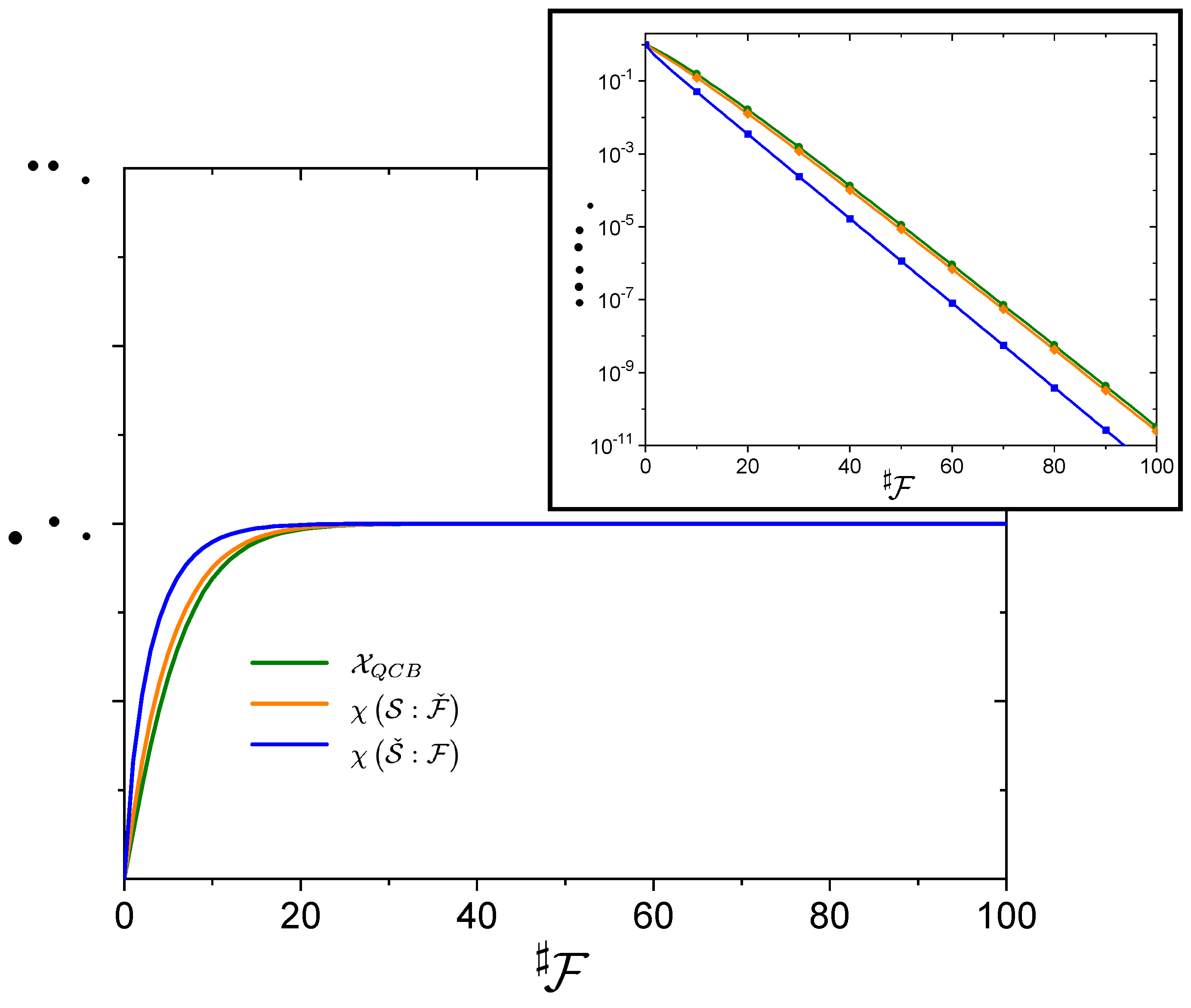
Figure 1 shows the approach to the plateau for the three information measures. The quantity
is a weaker bound to the accessible information. Yet, the separation between the decay curves is unimportant for passing the threshold in Equation (
22):
passes it sooner than the other quantities, but this only gives a relative correction to Equation (
26) that goes to zero asymptotically (
and
have to simultaneously go to infinity), albeit weakly as
. To clarify this statement, let
, with
from the right hand side of Equation (
26) and
the corrections. The relative correction,
decays as
for
and as
for
and
as
. In other words,
asymptotically. The very weak prefactor,
, for the latter two cases is due to the presence of
in the prefactor in Equations (
28) and (
29). The leading order contribution to the decay for
is
or with a prefactor of
when
. For
, the decay is
and, for the QCB result,
with
or
depending on whether we take the pure state result or generically take the mixed state bound. These forms show the same exponential decay but the latter two have a weak dependence of the prefactor on
.