Coherence and Anticoherence Induced by Thermal Fields
Abstract
:1. Introduction
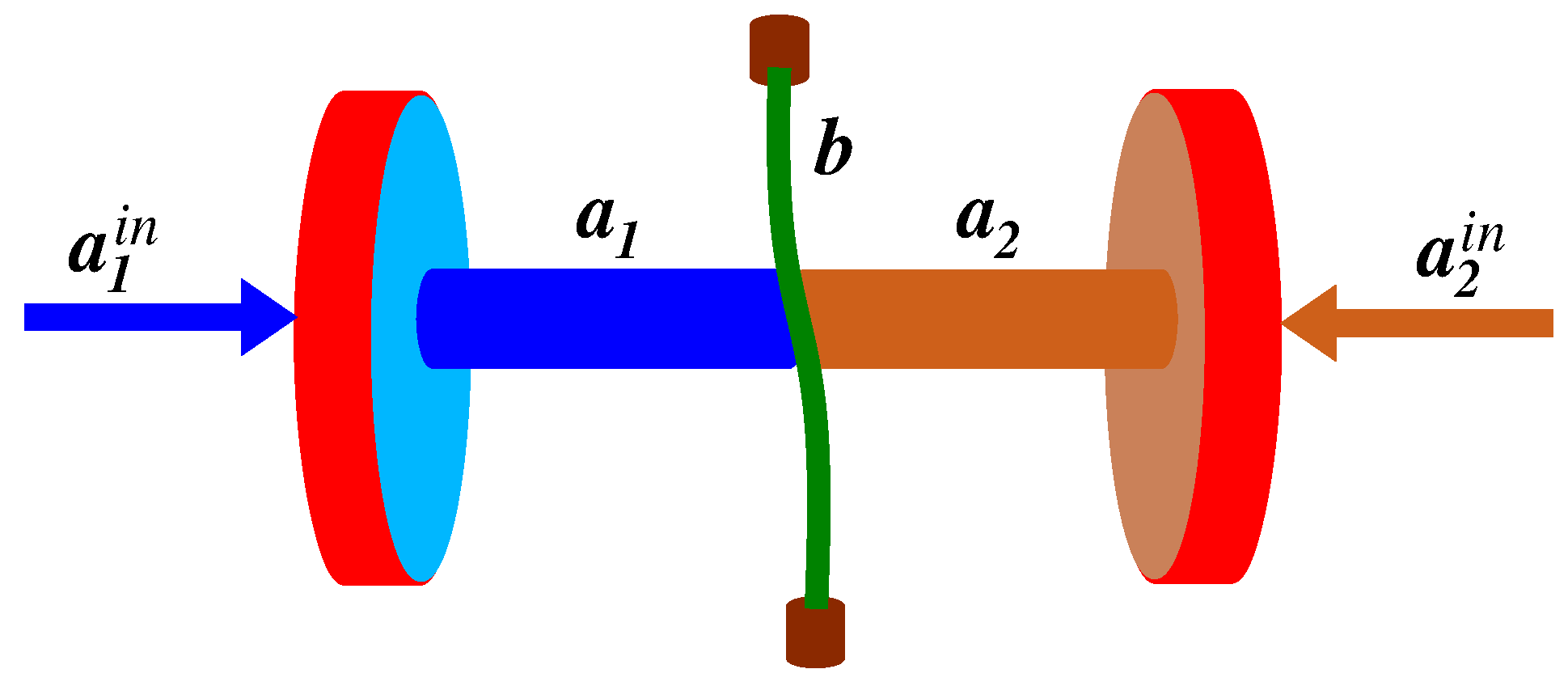
2. Three-Mode System
2.1. Time Evolution of the Modes
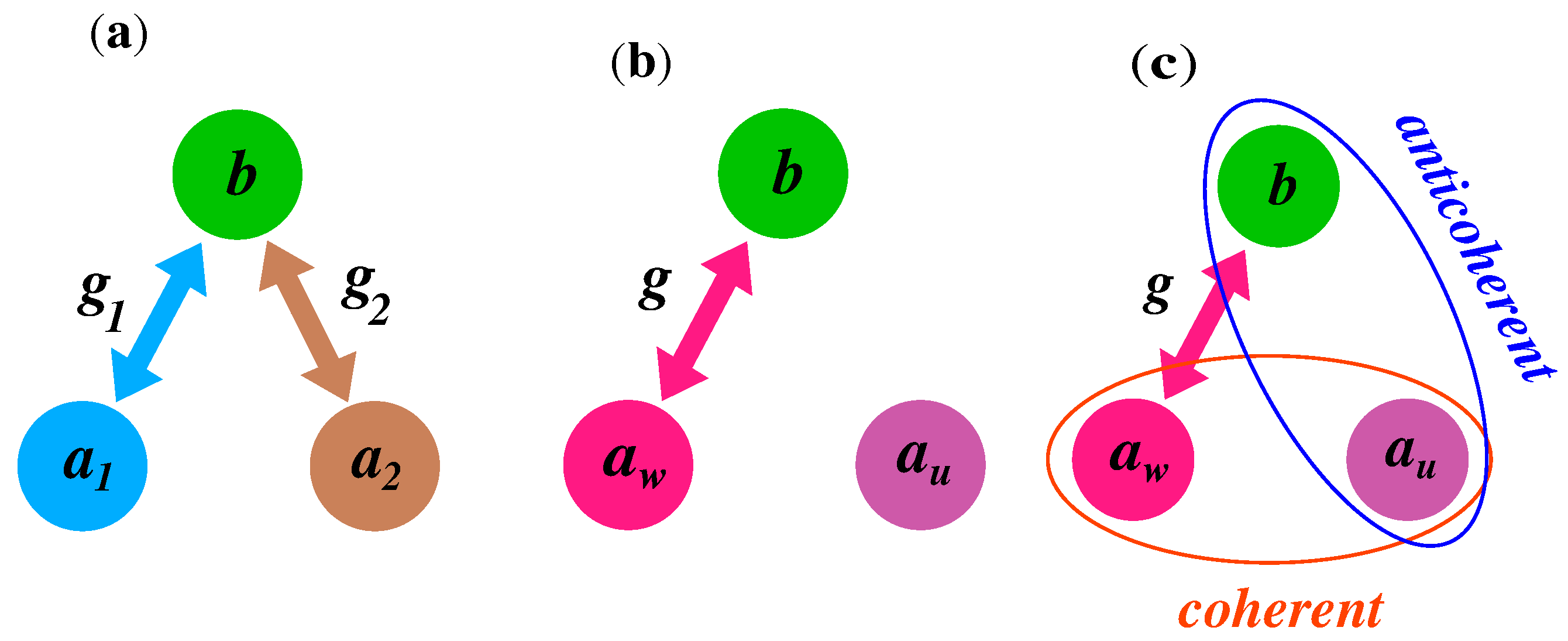
2.2. Linear Superpositions of the Modes
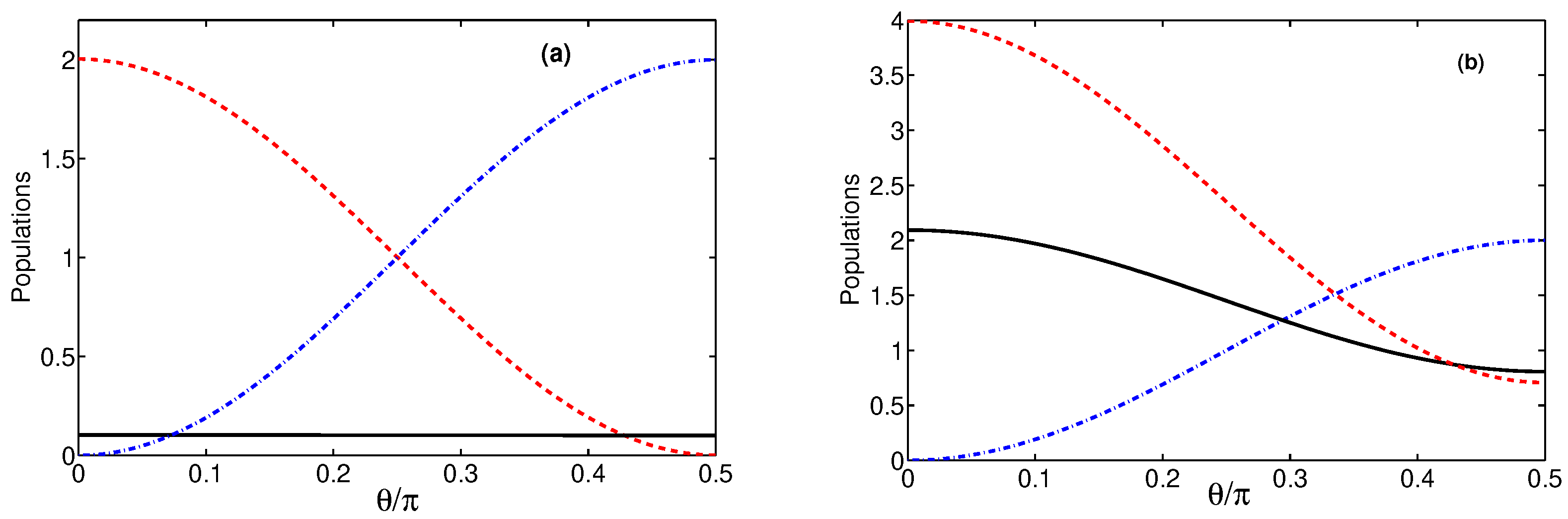
3. Populations of the Modes
4. Correlations between the Modes
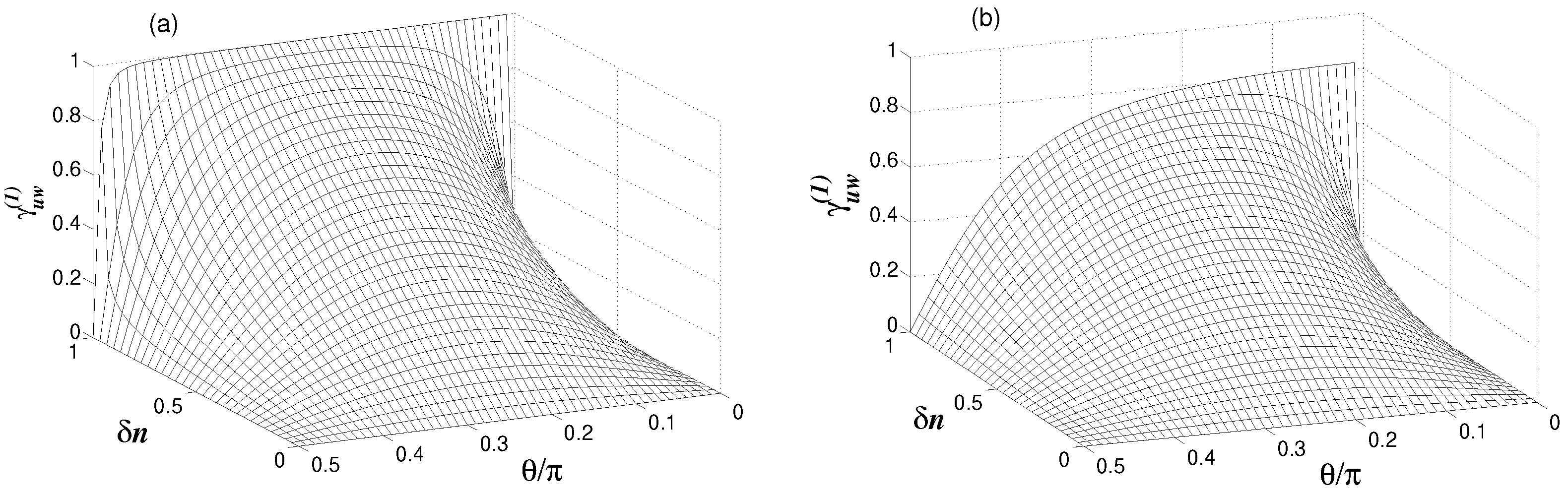
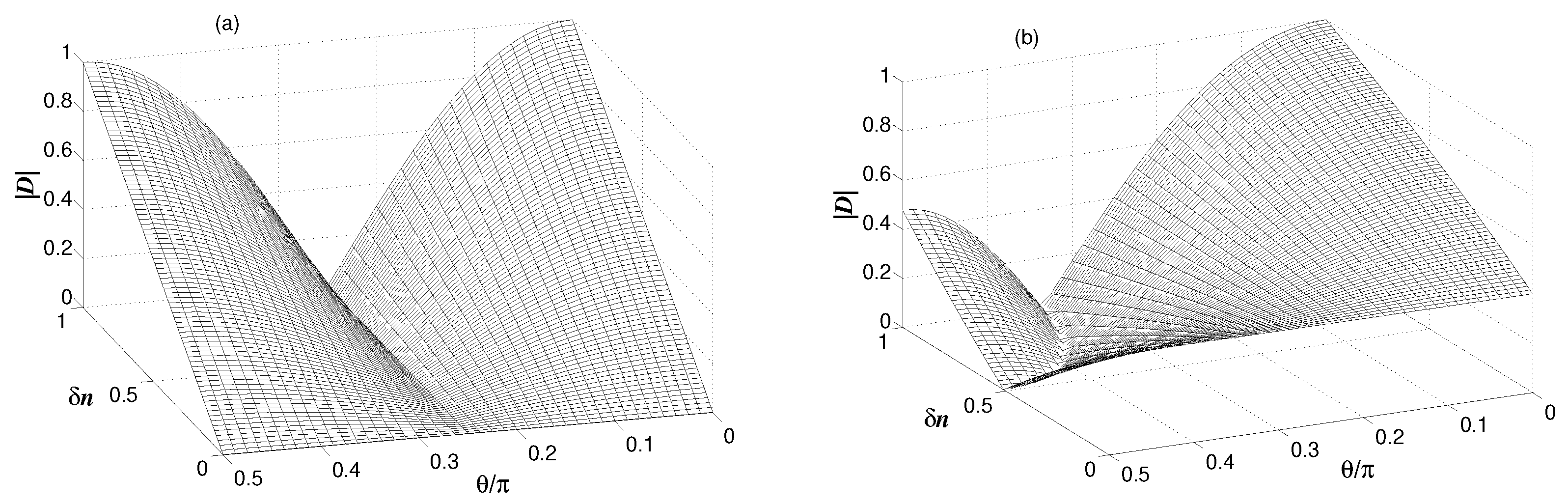
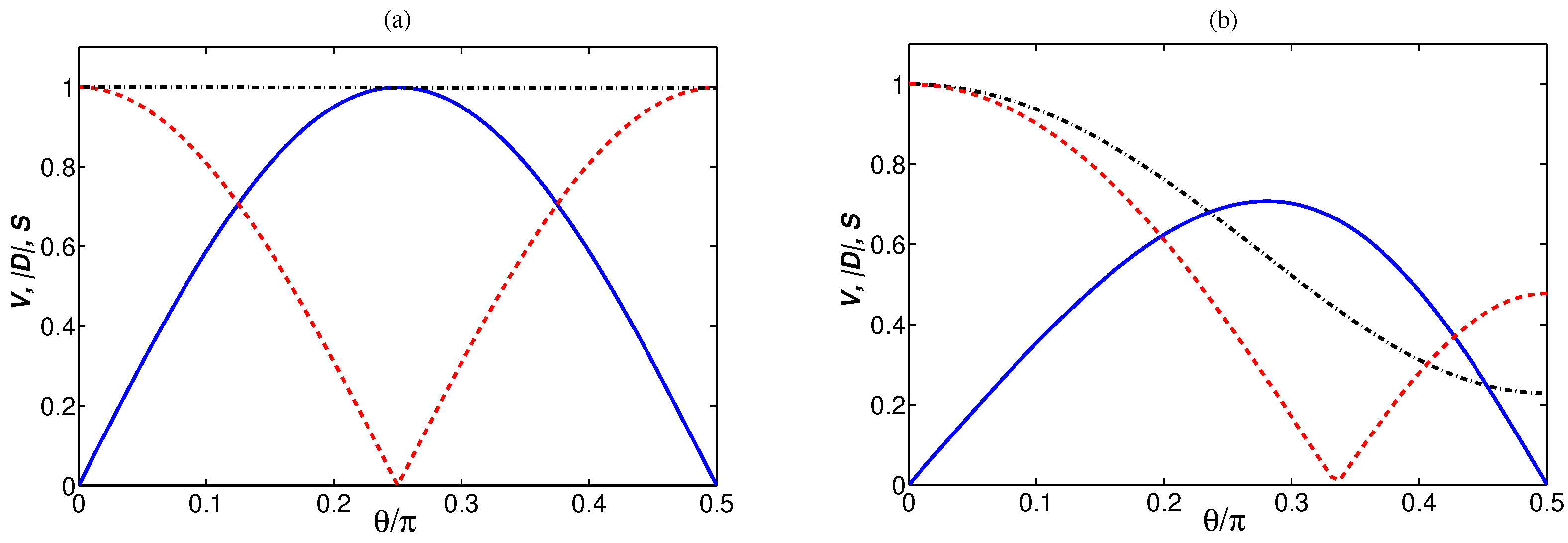
4.1. Degree of Coherence and Visibility
4.2. Degree of Anticoherence and Entanglement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Evaluation of the Steady-State Population of the Membrane Mode
References
- Glauber, R.J. Photon correlations. Phys. Rev. Lett. 1963, 10, 84. [Google Scholar] [CrossRef] [Green Version]
- Glauber, R.J. The quantum theory of optical coherence. Phys. Rev. 1963, 130, 2529. [Google Scholar] [CrossRef] [Green Version]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Ficek, Z.; Swain, S. Quantum Interference and Coherence: Theory and Experiments; Springer: New York, NY, USA, 2004. [Google Scholar]
- Agarwal, G.S. Anomalous coherence functions of the radiation fields. Phys. Rev. A 1986, 33, 11584. [Google Scholar] [CrossRef] [PubMed]
- Heidmann, A.; Reynaud, S. Squeezing and antibunching in phase-matched many-atom resonance fluorescence. J. Mod. Opt. 1987, 34, 923. [Google Scholar] [CrossRef]
- Wolf, S.; Wechs, J.; von Zanthier, J.; Schmidt-Kaler, F. Visibility of Young’s interference fringes: Scattered light from small ion crystals. Phys. Rev. Lett. 2016, 116, 183002. [Google Scholar] [CrossRef] [Green Version]
- Obsil, P.; Lesundák, A.; Pham, T.; Araneda, G.; Cizek, M.; Cip, O.; Filip, R.; Slodicka, L. Multipath interference from large trapped ion chains. New J. Phys. 2019, 21, 093039. [Google Scholar] [CrossRef] [Green Version]
- Mandel, L. Photon interference and correlation effects produced by independent quantum sources. Phys. Rev. A 1983, 28, 929. [Google Scholar] [CrossRef]
- Ghosh, R.; Hong, C.K.; Ou, Z.Y.; Mandel, L. Interference of two photons in parametric down conversion. Phys. Rev. A 1986, 34, 3962. [Google Scholar] [CrossRef] [Green Version]
- Silverstone, J.W.; Bonneau, D.; Ohira, K.; Suzuki, N.; Yoshida, H.; Iizuka, N.; Ezaki, M.; Natarajan, C.M.; Tanner, M.G.; Hadfield, R.H.; et al. On-chip quantum interference between silicon photon-pair sources. Nat. Photonics 2014, 8, 104. [Google Scholar] [CrossRef]
- Preble, S.F.; Fanto, M.L.; Steidle, J.A.; Tison, C.C.; Howland, G.A.; Wang, Z.; Alsing, P.M. On-chip quantum interference from a single silicon ring-resonator source. Phys. Rev. Appl. 2015, 4, 021001. [Google Scholar] [CrossRef]
- Barnett, S.M.; Knight, P.L. Squeezing in correlated quantum systems. J. Mod. Opt. 1987, 34, 841. [Google Scholar] [CrossRef]
- Ficek, Z.; Tanaś, R. Quantum-Limit Spectroscopy; Springer: New York, NY, USA, 2017. [Google Scholar]
- Wang, L.J.; Zou, X.Y.; Mandel, L. Induced coherence without induced emission. Phys. Rev. A 1991, 44, 4614. [Google Scholar] [CrossRef] [PubMed]
- Heuer, A.; Menzel, R.; Milonni, P.W. Induced coherence, vacumm fields, and complementatity in biphoton generation. Phys. Rev. Lett. 2015, 114, 053601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ou, Z.Y.; Mandel, L. Further evidence of nonclassical behavior in optical interference. Phys. Rev. Lett. 1989, 62, 2941. [Google Scholar] [CrossRef]
- Rubin, M.H.; Klyshko, D.N.; Shih, Y.H.; Sergienko, A.V. Theory of two-photon entanglement in type-II optical parametric down-conversion. Phys. Rev. A 1994, 50, 5122. [Google Scholar] [CrossRef]
- Mandel, L. Anticoherence. Pure Appl. Opt. 1998, 7, 927. [Google Scholar] [CrossRef]
- Armstrong, S.; Wang, M.; Teh, R.Y.; Gong, Q.H.; He, Q.Y.; Janousek, J.; Bachor, H.A.; Reid, M.D.; Lam, P.K. Multipartite Einstein-Podolsky-Rosen steering and genuine tripartite entanglement with optical networks. Nat. Phys. 2015, 11, 167. [Google Scholar] [CrossRef] [Green Version]
- Parkins, A.S.; Solano, E.; Cirac, J.I. Unconditional two-mode squeezing of separated atomic ensembles. Phys. Rev. Lett. 2006, 96, 053602. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.H.; Li, G.X.; Gu, W.J.; Ficek, Z. Generating coherence and entanglement with a finite-size atomic ensemble in a ring cavity. New J. Phys. 2011, 13, 093019. [Google Scholar] [CrossRef]
- Paternostro, M.; Vitali, D.; Gigan, S.; Kim, M.S.; Brukner, C.; Eisert, J.; Aspelmeyer, M. Creating and probing multipartite macroscopic entanglement with light. Phys. Rev. Lett. 2007, 99, 250401. [Google Scholar] [CrossRef]
- Shkarin, A.B.; Flowers-Jacobs, N.E.; Hoch, S.W.; Kashkanova, A.D.; Deutsch, C.; Reichel, J.; Harris, J.G.E. Optically mediated hybridization between two mechanical modes. Phys. Rev. Lett. 2014, 112, 013602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, H.H.; Jiang, L.; Clerk, A.A.; Harris, J.G.E. Nonreciprocal control and cooling of phonon modes in an optomechanical system. Nature 2019, 568, 65. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heinrich, G.; Ludwig, M.; Wu, H.; Hammerer, K.; Marquardt, F. Dynamics of coupled multimode and hybrid optomechanical systems. C. R. Phys. 2011, 12, 837. [Google Scholar] [CrossRef] [Green Version]
- Genes, C.; Mari, A.; Vitali, D.; Tombesi, P. Quantum effects in optomechanical systems. Adv. At. Mol. Opt. Phys. 2009, 57, 33. [Google Scholar]
- Meystre, P. A short walk through quantum optomechanics. Ann. Phys. 2013, 525, 215. [Google Scholar] [CrossRef] [Green Version]
- Aspelmeyer, M.; Kippenberg, T.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Vitali, D.; Tombesi, P.; Woolley, M.J.; Doherty, A.C.; Milburn, G.J. Entangling a nanomechanical resonator and a superconducting microwave cavity. Phys. Rev. A 2007, 76, 042336. [Google Scholar] [CrossRef] [Green Version]
- Aspelmeyer, M.; Gröblacher, S.; Hammerer, K.; Kiesel, N. Quantum optomechanics—Throwing a glance. J. Opt. Soc. Am. B 2010, 27, A189–A197. [Google Scholar] [CrossRef] [Green Version]
- Hofer, S.G.; Wieczorek, W.; Aspelmeyer, M.; Hammerer, K. Quantum entanglement and teleportation in pulsed cavity optomechanics. Phys. Rev. A 2011, 84, 052327. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.H.; Li, G.X.; Ficek, Z. First-order coherence versus entanglement in a nanomechanical cavity. Phys. Rev. A 2012, 85, 022327. [Google Scholar] [CrossRef] [Green Version]
- Sun, F.X.; Mao, D.; Dai, Y.T.; Ficek, Z.; He, Q.Y.; Gong, Q.H. Phase control of entanglement and quantum steering in a three-mode optomechanical system. New J. Phys. 2017, 19, 123039. [Google Scholar] [CrossRef]
- de Lépinay, L.M.; Ockeloen-Korppi, C.F.; Woolley, M.J.; Sillanpää, M.A. Quantum mechanics–free subsystem with mechanical oscillators. Science 2021, 372, 625. [Google Scholar] [CrossRef] [PubMed]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products; Academic Press: Orlando, FL, USA, 1980; p. 1119. [Google Scholar]
- Heuer, A.; Menzel, R.; Milonni, P.W. Complementarity in biphoton generation with stimulated or induced coherence. Phys. Rev. A 2015, 92, 033834. [Google Scholar] [CrossRef] [Green Version]
- Menzel, R.; Heuer, A.; Milonni, P.W. Entanglement, complementarity, and vacuum fields in spontaneous parametric down-conversion. Atoms 2019, 7, 27. [Google Scholar] [CrossRef] [Green Version]
- Lahiri, M.; Hochrainer, A.; Lapkiewicz, R.; Lemos, G.B.; Zeilinger, A. Nonclassicality of induced coherence without induced emission. Phys. Rev. A 2019, 100, 053839. [Google Scholar] [CrossRef] [Green Version]
- Wiseman, H.M.; Molmer, K. Induced coherence with and without induced emission. Phys. Lett. A 2000, 270, 245. [Google Scholar] [CrossRef] [Green Version]
- Gardiner, C.W.; Zoller, P. Quantum Noise; Springer: New York, NY, USA, 2000; p. 122. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Liu, Y.; Li, C.; Zhang, K.; Yang, W.; Ficek, Z. Coherence and Anticoherence Induced by Thermal Fields. Entropy 2022, 24, 692. https://doi.org/10.3390/e24050692
Sun L, Liu Y, Li C, Zhang K, Yang W, Ficek Z. Coherence and Anticoherence Induced by Thermal Fields. Entropy. 2022; 24(5):692. https://doi.org/10.3390/e24050692
Chicago/Turabian StyleSun, Lihui, Ya Liu, Chen Li, Kaikai Zhang, Wenxing Yang, and Zbigniew Ficek. 2022. "Coherence and Anticoherence Induced by Thermal Fields" Entropy 24, no. 5: 692. https://doi.org/10.3390/e24050692
APA StyleSun, L., Liu, Y., Li, C., Zhang, K., Yang, W., & Ficek, Z. (2022). Coherence and Anticoherence Induced by Thermal Fields. Entropy, 24(5), 692. https://doi.org/10.3390/e24050692





