2.1. Background
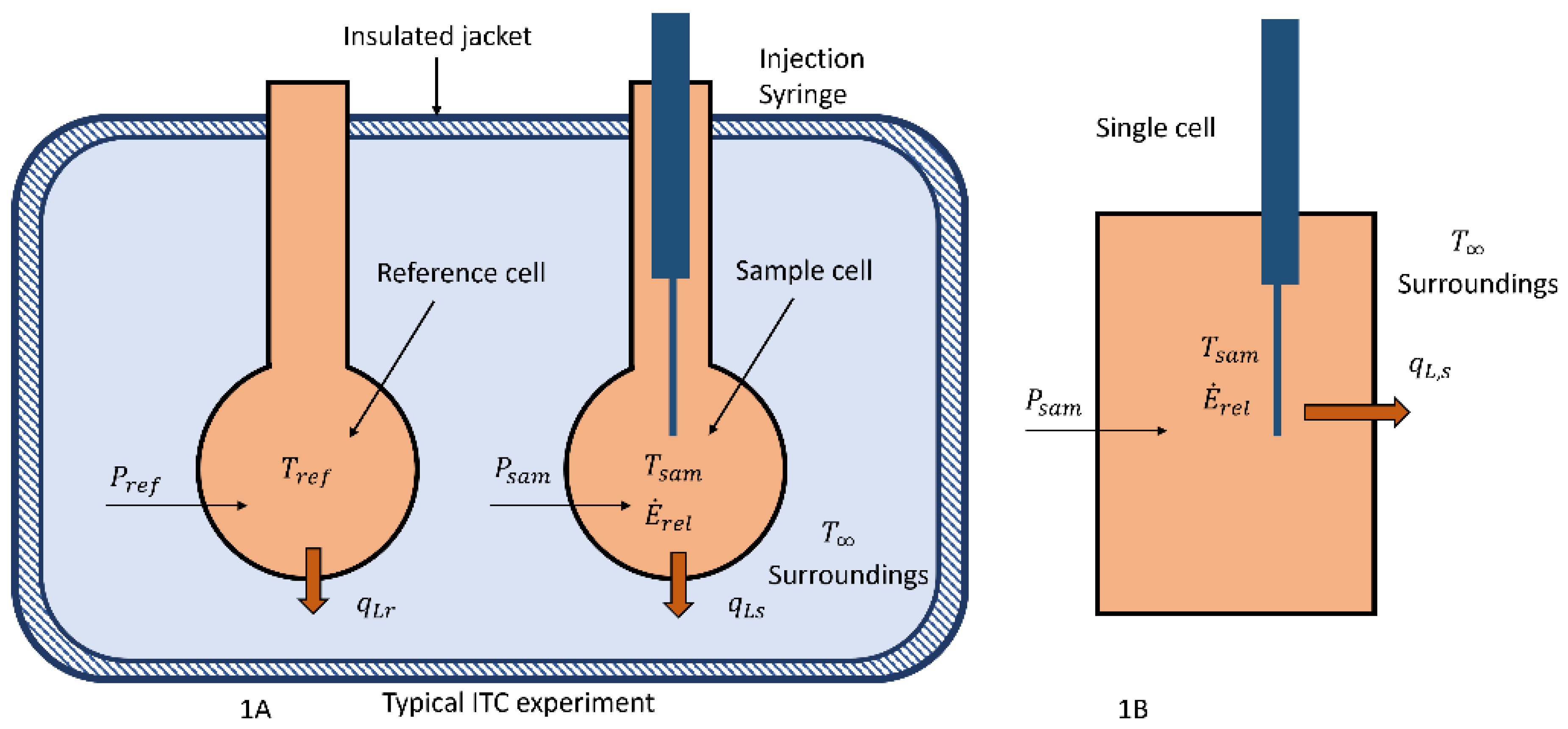
Two different configurations of a calorimeter that could be used to measure the energy released by microbes, phages, and virus, their interactions, or drug-related chemical reactions are shown in
Figure 1.
In
Figure 1A, a typical isothermal titration calorimeter (ITC) or two cell configuration that has been involved in the previously cited papers [
3] is illustrated. This configuration is usually operated at a constant temperature and in biological situations is not operated in a titration mode [
2,
10], but the operating principle is similar to that described below. In this device the two cells, reference and sample cells, are similarly constructed so that the heat transfer between them and the surroundings can be considered to be the same if they are maintained at the same temperature using electric heaters. The heaters are controlled by varying the power to them to maintain the same temperature in each cell where the respective cell temperatures are measured by either thermopiles or other accurate devices.
The rate of energy released by the observed reaction in the sample cell; for example, a microbe community with a food source, will cause the temperature of the sample cell to change unless the power to it is adjusted to maintain a constant temperature. The observed variable in these measurements is the difference between the reference and sample power, Δ
P, which is stated to be equal to the rate of energy released during this process. The rate of energy released ultimately is transferred as heat to the surrounding large thermal reservoir. The energy released associated with the process under the assumption of constant temperature in each cell and that the cells are similarly constructed lead to a simple relationship, Equation (1).
where
PREF and
PSAM are the power to the reference and sample cell, respectively.
equals the rate of energy released by the reactions occurring in the sample cell. The energy balance on the sample cell provides additional insights into these assumptions and the mechanisms that occur during the reaction, Equation (2).
In Equation (2)
is the internal energy change in the materials in the sample cell,
t is time and
is the rate of heat transfer between the sample cell and the surrounding bath. While in most of these devices, there is an injection to the test sample to add food or duplicate injections requiring a transient form of the energy balance to simulate the process. It should be noted that the rate of change of the internal energy depends on the temperature change in the sample, as well as the changes in its mass. In these calorimeters the temperatures of the reference and sample cells are controlled to be equal and set to a constant value. For these conditions, the derivative of the internal energy term will be zero; if the mass of the sample cell remains constant during the measurement, at steady state conditions, or when a balance of the interacting group of various species is reached, the transient term on the RHS of Equation (2) will approach zero. Assuming that the working fluid in the device is an incompressible material yields Equation (5). The time dependence of the mass in the sample cell is related to the mass flow rate of the injection, Equation (3) and the expanded form of the internal energy, Equation (4) is included in the transient energy balance, Equation (5), to emphasize the above assumptions.
In Equation (4),
mSAM and
cs equal the mass of material and the specific heat of the material in the sample cell,
Ts is the temperature of the sample cell at any time and
TR is the reference temperature for the internal energy. The mass of material,
, in a typical titration experiment is related to the injection rate, concentration, and injecting time.
is the injection of the syringe in Equation (4). A similar energy balance can be written for the reference cell where there is no rate of energy released term. Since the temperature of both cells is controlled to be equal in the theory of two-cells ITC and they are geometrically similar, the heat loss from both cells will be the same at any time. The internal energy balance in the reference cell is constant as its mass does not vary with time. Since the temperature of each cell is controlled to a constant value, the temperature time derivatives are also zero. The implications of these assumptions will be discussed later. Combining these energy balances of sample and reference cell under these conditions yields the following relationship:
The derivative term in Equation (6) was left to illustrate that even if the temperatures are controlled to be equal and constant, a part of the internal energy change will remain if the mass changes. Equation (2) assumes that the preceding condition is satisfied. If it is not, then the result summarized in Equation (2) is not valid.
Commercial ITC/sample and reference cell calorimeters are designed and manufactured to satisfy these conditions for chemical reaction processes. When these calorimeters are used to measure the rate of energy release from the microbe community, as in [
1,
2,
10], the effects of injecting fluids at a different temperature need to be taken into account. As that of the cells, the effects include the changes in mass from gas exchange with the surroundings, separating the growth of the microbes, significant changes in the metabolic rate based on the community dynamics and potential interactions between the microbes and phages or viruses. If sufficient time is taken one can reach a near steady state condition, which avoids the initial injection region and the growth of the community phases. In standard ITC practice, the power difference which equals the energy release is integrated over the time of reaction to obtain the thermodynamic property of the enthalpy of reaction, Δ
H, and is usually expressed per number of microbes or mole of injectant. In the case of the microbial community, this change in power is related to energy released by the microbes and has also been reported [
1,
2,
10]. The heat transfer rate from each cell in these types of measurements is not usually reported, although the difference in the power between the reference and sample as a function of time is as reported in [
2].
To understand what is measured by the change in power, the single-cell calorimeter as shown in
Figure 1B is analyzed and it is essentially one of the cells from the ITC/ sample and reference cell device. In this case, the energy released,
, is determined from the observed temperature response, the heat input,
Psam, if any, and the heat transfer characteristics of the cell,
. A calibration relation is required to determine these heat transfer characteristics. The energy balance on this device is similar to that of Equation (2) and can be solved for energy released,
. The integration of the energy release term over the time of the process can be used to determine the enthalpy of reaction as stated above.
If the energy released by the community or the enthalpy of reaction was the only variable of interest and not the entropy flows in the system, the above experimental protocols would be sufficient [
1,
2]. In this case, the internal energy of the community is assumed to be a function of the temperature and mass of the fluid containing the microbes and other biological materials. Additional experiments to determine these parameters can be easily designed. The heat transfer from the cell is described in Equation (8) by the temperature difference between it and the surroundings and the overall heat transfer coefficient, (
uHTA).
What is not obvious in both Equations (2) and (7) is that the heat transfer from the cell also would transport any irreversibility associated with the processes being observed which are convoluted with the heat flowrate from the sample cell. The details of this process are discussed in
Section 2.1. The steady-state results stated in Equation (1) do not provide information on the irreversibility directly when a reaction is occurring and only the energy leaving the sample cell can be used to determine the rate of entropy flow from the sample cell. Other means are needed to provide information on the irreversibility or process efficiencies. For example, in (ITC) experiments, one performs the experiments sequentially to observe the reaction as the concentrations change in a prescribed manner in order to develop a relationship between the extents of the reaction and to determine the reaction’s equilibrium constant,
kD. The equilibrium constant allows the introduction of second law parameters such as the Gibbs free energy change of the reaction, which then allows the entropy of the system during the reaction to be determined. A second law analysis of the calorimeter is then used to calculate the entropy production rate, which is related to the irreversibility of the reaction (
Section 2.3). Procedures and hypotheses concerning the relationships for energy stored in growth, growth rate, and generation times would need to be applied to possibly formulate entropy statements for these processes, similar to that carried out in the ITC analysis [
10].
2.2. Case 1: Spatially Uniform System Heating without Reaction
Consider a simple system such as the single-cell,
Figure 1B, that corresponds to an incompressible material, water, that is excited using microwave heating. This problem, while simple, provides the base solution to illustrate the determination of the rate of energy released, entropy flow, entropy property changes and the rate of entropy production from a calorimeter device. Assume that the single cell is a closed system, there is no expansion work nor mass exchange with the surroundings. A steady-state heat source,
that represents the microwave or Joule heating per volume is active in the closed system,
, and there is heat exchange,
with the surroundings through convection (Equation (9)). The internal energy,
u, is determined from the equation of state for the material in the cell.
is the surface area for heat transfer of the closed system of the test cell and the temperature of the surroundings is
T∞. The energy balance is developed as in Equation (5).
The initial conditions for this problem are:
The material in the single-cell system is water with constant properties of specific heat,
cS = 4180 kJ/(kg K), thermal conductivity = 0.6 W/(m K), and density of 997 kg/m
3.
PSAM is set to zero in this simulation. The volume of the liquid is fixed at 80 µL and the (
uHTA) product is 0.0356 W/K. The value of the power into the cell is zero in this experiment. Equation (9) was solved numerically using the code developed by Modaresifar and Kowalski [
11] for reactingmixtures in microchambers, which simulates an injection experiment and analyzes its thermal process in a microscale calorimeter. This is a straightforward problem that is easily solved. This code was found to spatially converge to an accurate solution with three nodes for this small volume and uniform heat generation rate. It predicts the temperature time response, as shown in
Figure 2, until the steady state is reached, approximately
tf = 130 s. In
Figure 2 the temperatures of the three spatial nodes are shown. They are not distinguishable from one another, which confirms that the numerical simulation satisfies the uniformly spatial assumption. Tests at a higher number of nodes, providing more precise resolution in the simulation, confirm that the solution has converged.
This case provides a baseline solution of what is measured in a calorimetric type of device and allows one to investigate the entropy flow from the sample cell, the rate of change of the entropy property of the material within it, and the rate of entropy production for this process involving a single material phase with known properties. To illustrate the above statement, one must view
Figure 2 not as an end result of a simulation, but as the observed variable in the calorimetric device. As described in the background section, what one observes in the calorimeter is either the temperature response or the result of a small change in temperature that alters the power into the cell. For this discussion,
Figure 2 is not the outcome, but the starting point to determine the heat generation term,
qg, in Equation (9). This calculation is accomplished by integrating Equation (9) with respect to time under the assumption that
qg is constant. In this step, note that one is specifying the function form of the internal heat generation, a constant, that is occurring in the sample, i.e., a mechanism. The integrated form of Equation (9) is:
The heat generation term, the LHS of Equation (12), is usually the primary measurement sought, since it can be related to the energy released by the microbe community or a chemical reaction. Further analysis is performed to determine the irreversibility associated with this heating process, using relationships with the entropy flow.
The heat loss,
qL,s, in Equation (12) is the heat transfer rate and is summarized in
Figure 3 as a function of time using Equation (10). As expected, the heat transfer rate starts at zero and increases to its steady value. The difference between the heat transfer rate and the rate of energy released from the heat generation term is the internal energy storage rate, the first term on the RHS of Equation (12).
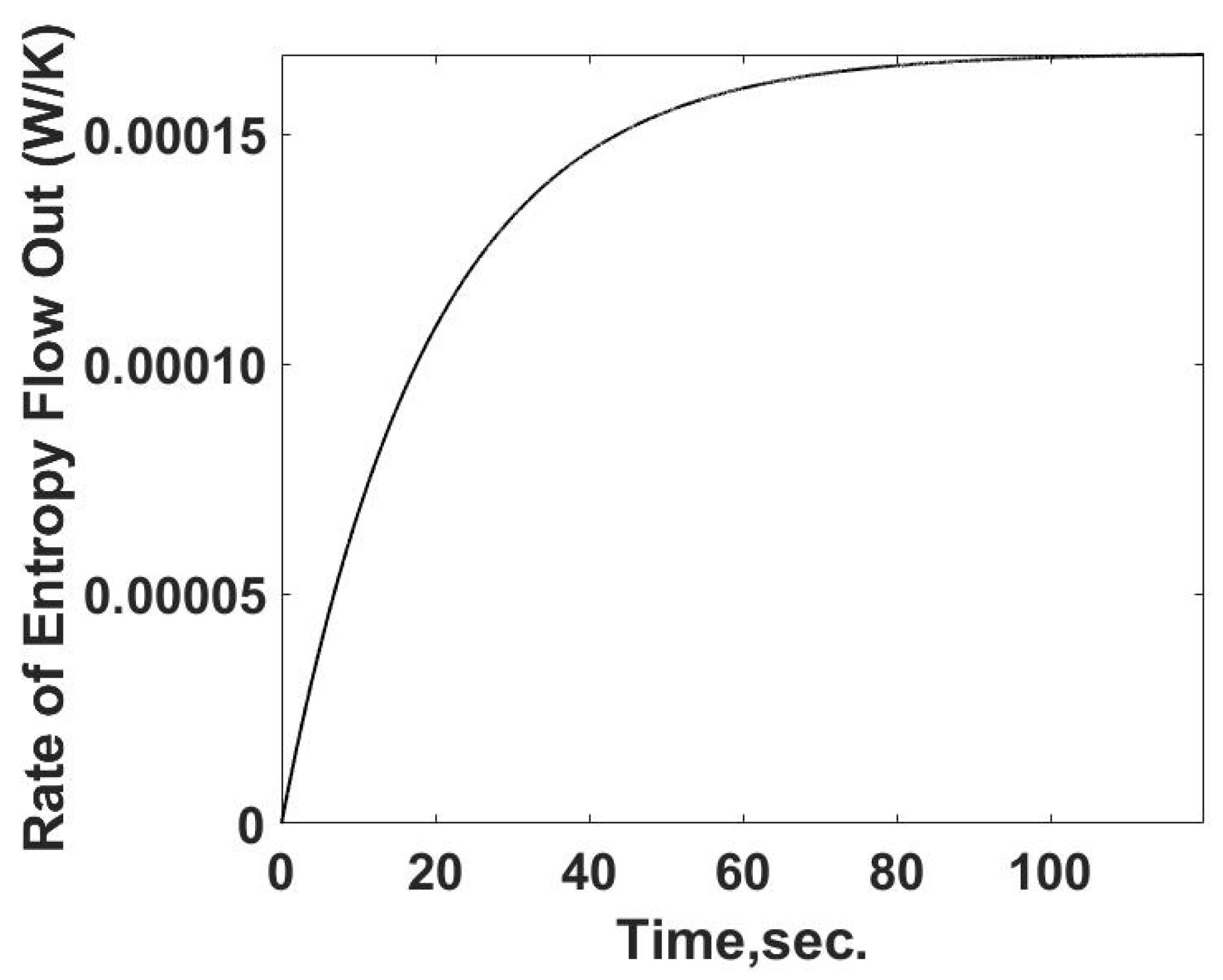
The flow of entropy from the sample cell is determined from the calculated heat flow and the temperature of the sample cell. This relationship is summarized in
Figure 4. The rate of entropy flow out of the sample cell can be determined from the calorimetric measurements of the temperature and heat transfer information, as demonstrated below. The entropy flow out follows the behavior of the heat transfer rate as expected.
The entropy property change is determined by the temperature, as observed in
Figure 2, and the Gibbs equation. Water at moderate temperatures and pressures is used in this simulation and is treated as an incompressible material
The rate of entropy property changes at each observed time,
Figure 5. This simulation case can be determined because one is using a pure material with a known equation of state. The temperature terms can be calculated for this case from the calorimetric observations. One feature of
Figure 5 is the rapid increase in the rate of entropy property changes at the start of the process and then a steady decline until it reaches zero. During this response, the rate of entropy flow from the sample cell is increasing to its steady-state value,
Figure 4.
The preceding calculations and graphs illustrate the different entropy components that are obtained from calorimetric measurements. The entropy balance is used to determine the rate of entropy production, which is related to the irreversibility observed for the constant heating process in this case.
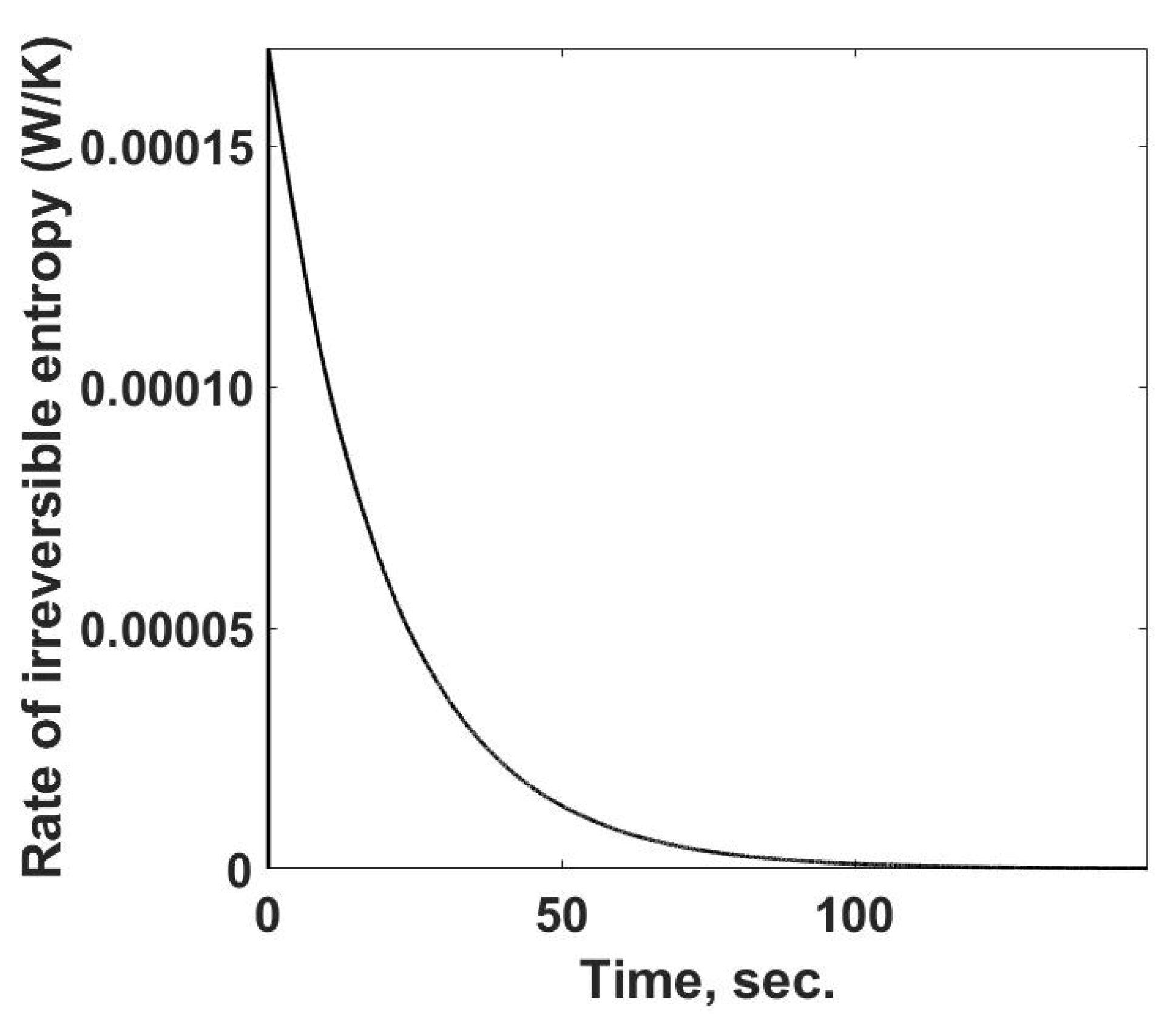
The rate of entropy production as a function of time is determined from the previously calculated values using Equation (15) and is summarized in
Figure 6. One interesting feature is that the rate of entropy production increases rapidly and then slightly decreases, reaching a near-constant value, similar to that of the entropy flow out of the system.
For the heat generation process in this case, the rate of entropy production has a direct link to the irreversibility of this process. If this were a microbe community with a constant energy release rate, the results in
Figure 6 would be a measure of the irreversibility and possibly would be related to the efficiency with which the community is using its resources. Such a case of near-constant energy release rates has been reported for
E. coli during the stationary phase [
10].
The above case is simplistic and a direct application of thermodynamics to a calorimetric type device. The results are expected and are presented here to establish; 1. what information could be obtained from a calorimetric type device and, 2. an approach to provide a baseline measure of the irreversibility. It neglects the complications of inter species competition for food sources, different phases such as exponential growth or declining, as well as changes in the immediate surroundings that one species may cause. These complications go directly to the assumption that the property relationships for calculating the entropy property solely on the observed temperature in an active community are possible. Without these key relationships, other means are needed to describe the interactions. Some of these complications are introduced in the second case, that of a sample cell containing a reacting mixture or interacting group of various species.
2.3. Case 2: Spatially Uniform System with Reaction Limited by an Equilibrium Constant
Case 2 considers the same sample cell as shown in
Figure 1B and that was discussed in detail for case 1 for the constant heat generation case. In case 2, the sample cell is initially filled with two reacting solutions, where these solutions could reflect chemical reactions or two interacting species; for example,
E. coli and phages or ligands. From an experimental viewpoint, the same observed property, the temperature, is measured. The reacting solutions will normally be low concentrations of the reacting species in a buffer or low concentrations of microbes in water that contains a food source. From a calorimetric viewpoint, the key rates of energy exchanges are the rate of change in internal energy of the buffer/water and the rate of heat transfer from the sample cell. The driving thermodynamic potential is the reaction that will be characterized in terms of reaction equation, equilibrium constant, growth rate constant, degree of reduction, or equivalent, and the rate of reaction. The reacting compound case will be used as a starting point to illustrate these relationships and what information we can obtain from a calorimeter experiment. The role of the equilibrium constant on the resulting energy release rate is similar to the biological interaction restrictions that determine how fast and to what extent two biological species react with one another. This reaction constraint has direct implications on the flow of entropy and entropy production in these systems. Consider a concentration of compound [
], which reacts with a concentration of [
], where both are in the same buffer of [
] and produce a concentration [
], the product. A similar development can be found in [
3]
The reaction summarized in Equation (16) is constrained by the equilibrium constant,
kB and the products are as shown in Equation (17), which assumes a complete reaction.
The correct form of Equation (16) that includes the equilibrium composition of the products is:
The energy and entropy balances for the described reaction can be written using absolute thermodynamic properties and are simar to that of Equations (8), (9) and (13). The transient energy balance, Equation (8), with
PSAM = 0 is:
where
In this experiment, the compound [
X] is injected into the sample cell that contains a fixed amount of [
Y] = [
YTOT]. During this injection, the rate of reaction is considered to be very fast and the rate of energy released per volume,
qg2, is not a constant and is determined from the equilibrium constant
kB and the enthalpy of reaction per mol of the injected compound, Δ
H. The rate of energy release between two specified times is:
Differentiating Equation (21) with respect to time determines the rate of energy released per volume:
To determine the derivative in Equation (22), the equilibrium constant, Equation (17), is used to obtain a quadratic expression for the product [
XY] by combining it with the species/mass balance of the species:
where the molar rate of injection is
and
t is the time from the start of the injection. The resulting relationship is
It is observed from Equation (26) that the energy release rate for the reacting compound example is time dependent, unlike that in case 1. Equations (26) and (22) are used to determine the rate of energy release during the injection of compound [
X] into the chamber filled with compound [
Y]. The initial concentration of compound [
Y],
YTOT, is known at the start and the injection rate of compound [
X] is held constant. Unlike case 1, the rate of energy added to the chamber is not constant but is a function of time that starts at a maximum value and then decreases to zero, or a constant value as the number of reaction sites or available food goes towards zero,
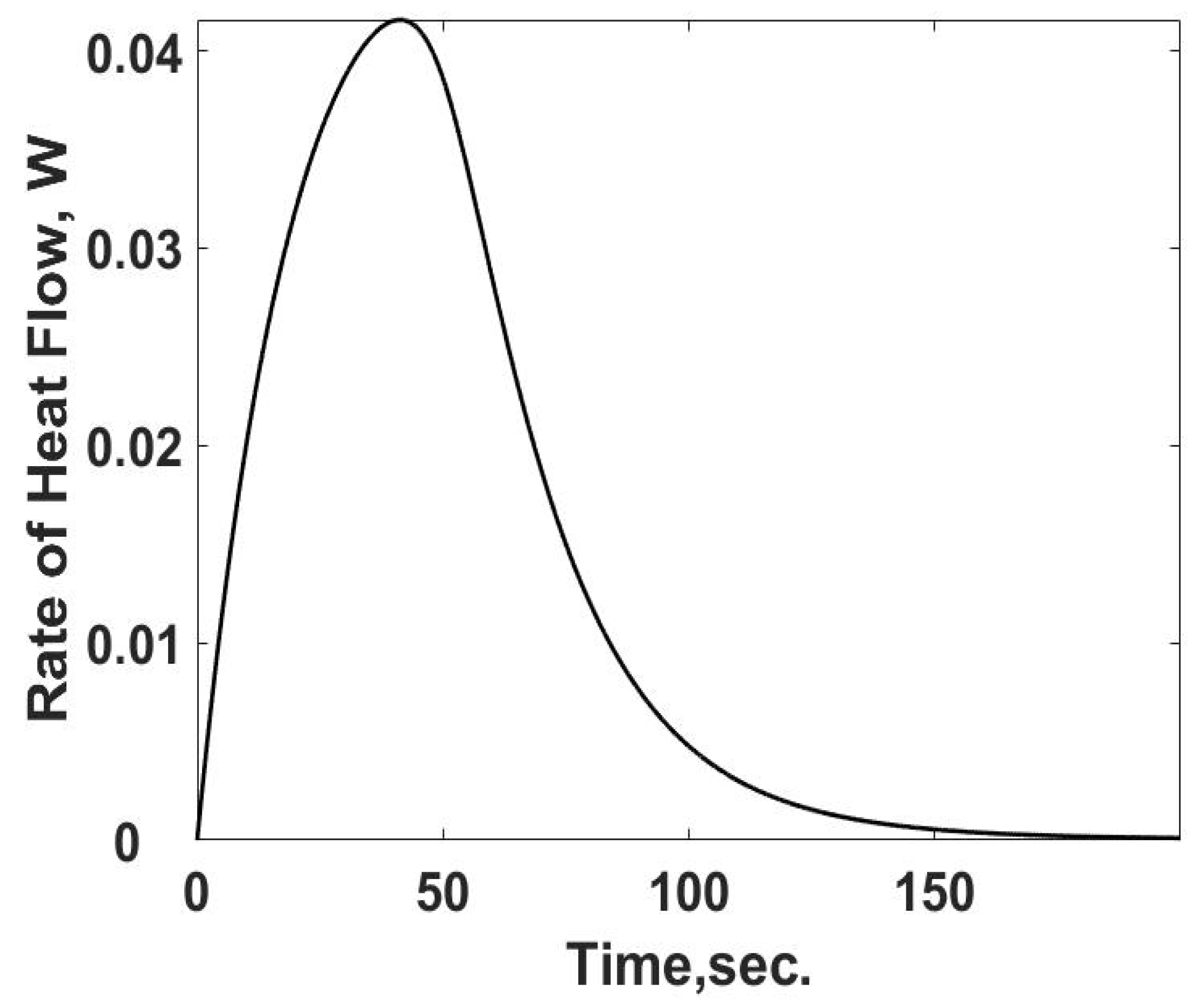
Figure 7.
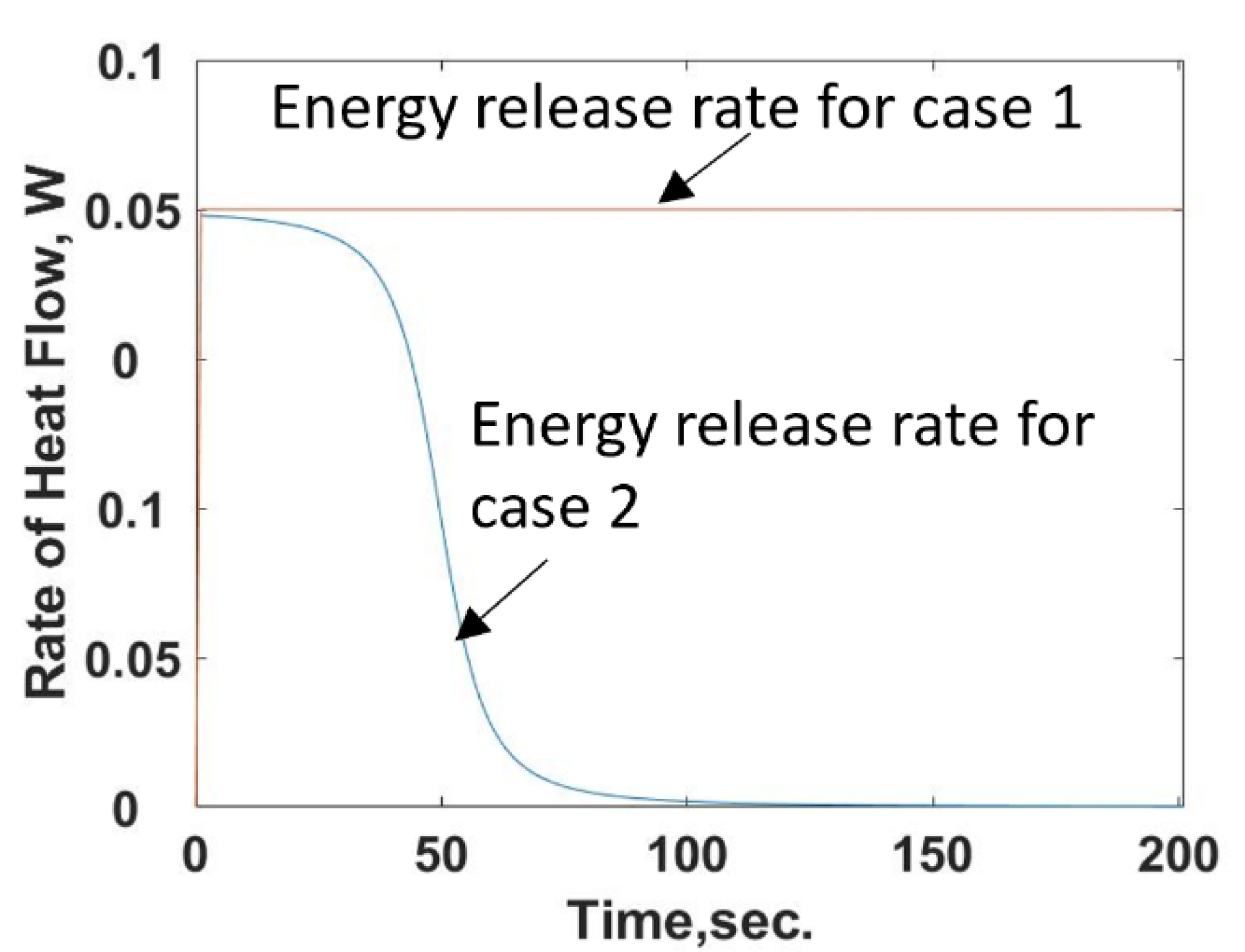
The shape of this curve reflects the trends discussed in [
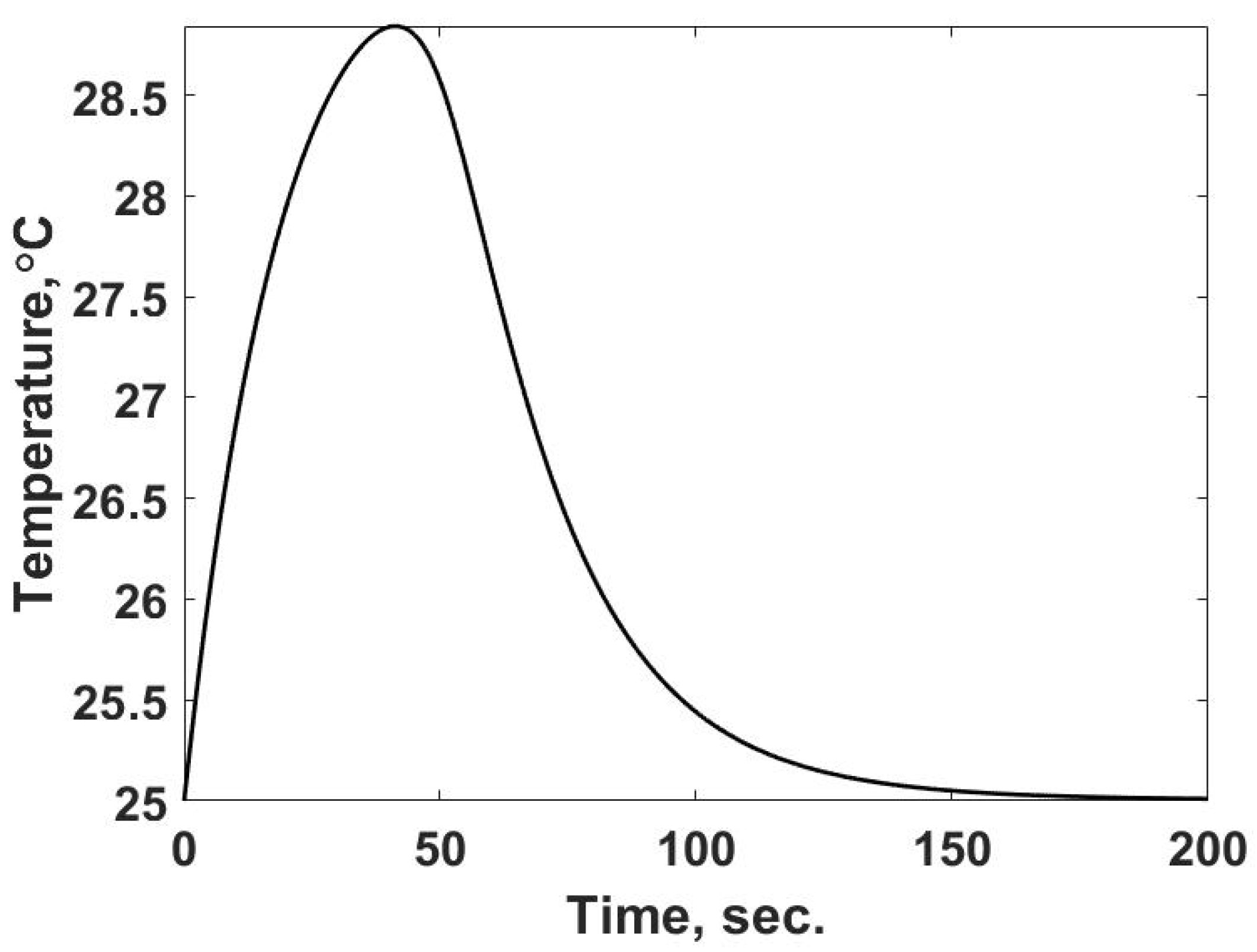
3], which is shown inverted since it is measuring the change in power in the two-cell calorimeter. Numerically solving Equation (19) using the energy release rate given by Equation (22) predicts the temperature response shown in
Figure 8. The temperature response corresponds to the observed property in the single-cell calorimeter.
The results in
Figure 8 are expected: a rise in temperature to the maximum value due to the thermal capacitance of the system, while the rate of energy release is greater than the heat transfer rate. Once the heat transfer rate overcomes the rate of energy, the temperature decreases in the system. The system returns to the temperature of the surroundings at the end of the process as expected. In terms of determining the entropy flows in this case, the observed temperature is shown in
Figure 8: the heat transfer characteristics of the cell, and the thermodynamic properties of the buffer and each reactant are needed. Due to the reaction between the reactants, the absolute entropy for the products is unknown for a test case and, unlike case 1, the case of a single, non-reacting material, there are no equations of state to determine the entropy property change from the calorimeter experiment. What can be determined is the entropy flow from the chamber, since the rate of heat flow is determined in the simulation, Equation (21) (
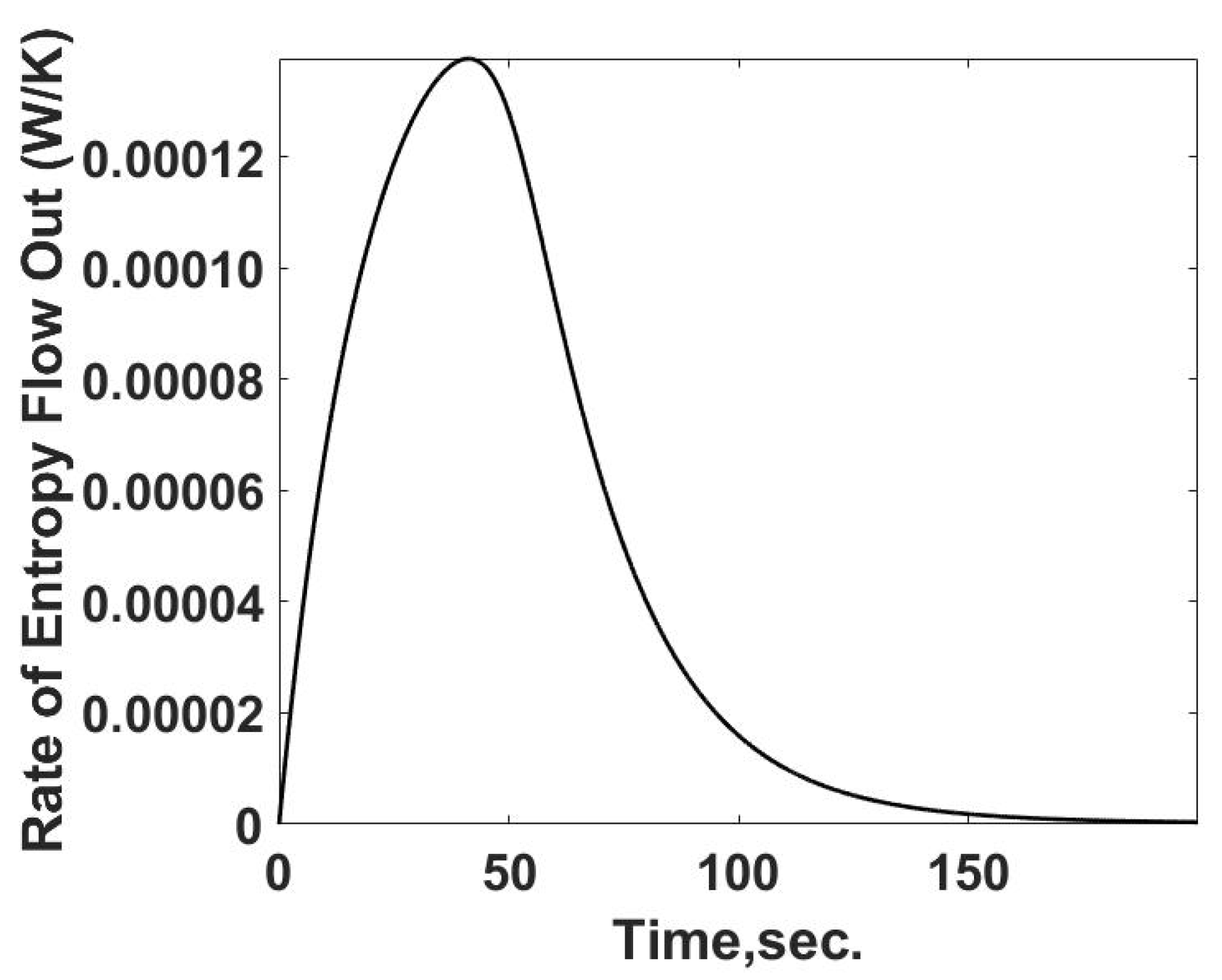
Figure 9).
Since the temperature at the system boundary is known as a function of time the rate of entropy flow from the cell can be calculated by Equation (27) and is summarized in
Figure 10.
From the entropy balance on the test cell:
where
The rate of entropy flow out of the system can be determined from the observed experimental parameters. In this case, the rate of change in the entropy property cannot be determined, unless this is a known reaction and the absolute entropy values of the reactants and products are known, Equations (28) and (29). This is not usually the case when testing reacting compounds in a calorimeter because that is the purpose of the experiments. As a result, the only statement that can be made is the calculated value of the confusing parameters of the rate of entropy property change and the entropy production rate. This calculation does not allow the irreversibility of the reaction or interactions,, in the biological communities to be determined for possible use in better understanding the dynamics of the community, the efficient use of food sources or evolutionary trends.
In 1999, Battley [
12] developed an empirical statistic model to calculate the standard molar entropy
with accuracy at 2%. However, the method to calculate the information of
from the experiment is still limited. The Gibbs free energy is defined as the maximum amount of non-expansion work in a thermodynamic system and is related to enthalpy, temperature, and entropy. The definition equation can be written as Equation (29) at thermodynamic standard states for the absolute entropy property changes [
8].
In the case of drug and protein reactions, there is an additional procedural step that can be used to determine the equilibrium constant, which can then be related to the change in the Gibbs energy from which the rate of entropy property change can be calculated. This step is best illustrated from the ITC version of the calorimeter, in which a series of titrations are performed and the energy released at each step is determined as a function of the mole fraction of the product [
3]. This leads to a graph that is similar to that of
Figure 8 for the reacting case and the slope of the curve equals the equilibrium constant,
kB. The thermodynamics of the equilibrium composition
KB is related to the change in the Gibbs energy.
For the case of the single injection experiment described in this section, a similar curve as that developed in the ITC experiment can be determined by calculating the energy release rate within a finite time interval from the observed temperature–time response and the energy balance. The determined value of kB would then be used in Equation (30) to determine the change in the Gibbs Energy and the change in the absolute entropy property change. These results, together with Equation (26), would allow one to isolate the rate of entropy productions and measure the irreversibility of the reaction.
While the above procedure applies to a reacting system, it does not directly relate to the activities of biological microorganisms due to the lack of a clear definition of what would be the corresponding equilibrium constant. A similar parameter to the equilibrium constant for monotypic microorganisms interacting with their surroundings using a calorimeter-based measurement needs to be defined in order to separate the entropy property changes from the entropy production changes. Using probabilistic methods as described by [
7] to identify a constant that characterizes the energy releasing interactions is one approach and is beyond the scope of this paper. From the comparison of case 1 and 2, it is demonstrated that the calorimeter measurement can identify the combined values of the entropy property changes and entropy production, but without further analysis or observed information, it cannot separate these parameters.