Changes in the Complexity of Limb Movements during the First Year of Life across Different Tasks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Equipment
2.3. Procedure
2.4. Data Pre-Processing
2.5. Complexity Analysis
- Entropy (Ent): it is the Shannon entropy of the distribution of the diagonal lines on the recurrence plot, capturing repeating movement patterns;
- Recurrence Rate (RR): it is the density of recurrence points in a recurrence plot, and it corresponds to the probability that a specific state will recur;
- Mean Line (ML): it is the average length of repeating patterns in the system, which can be understood as a measure of overall system’s stability.
2.6. Statistical Analysis
3. Results
3.1. Complexity Measures
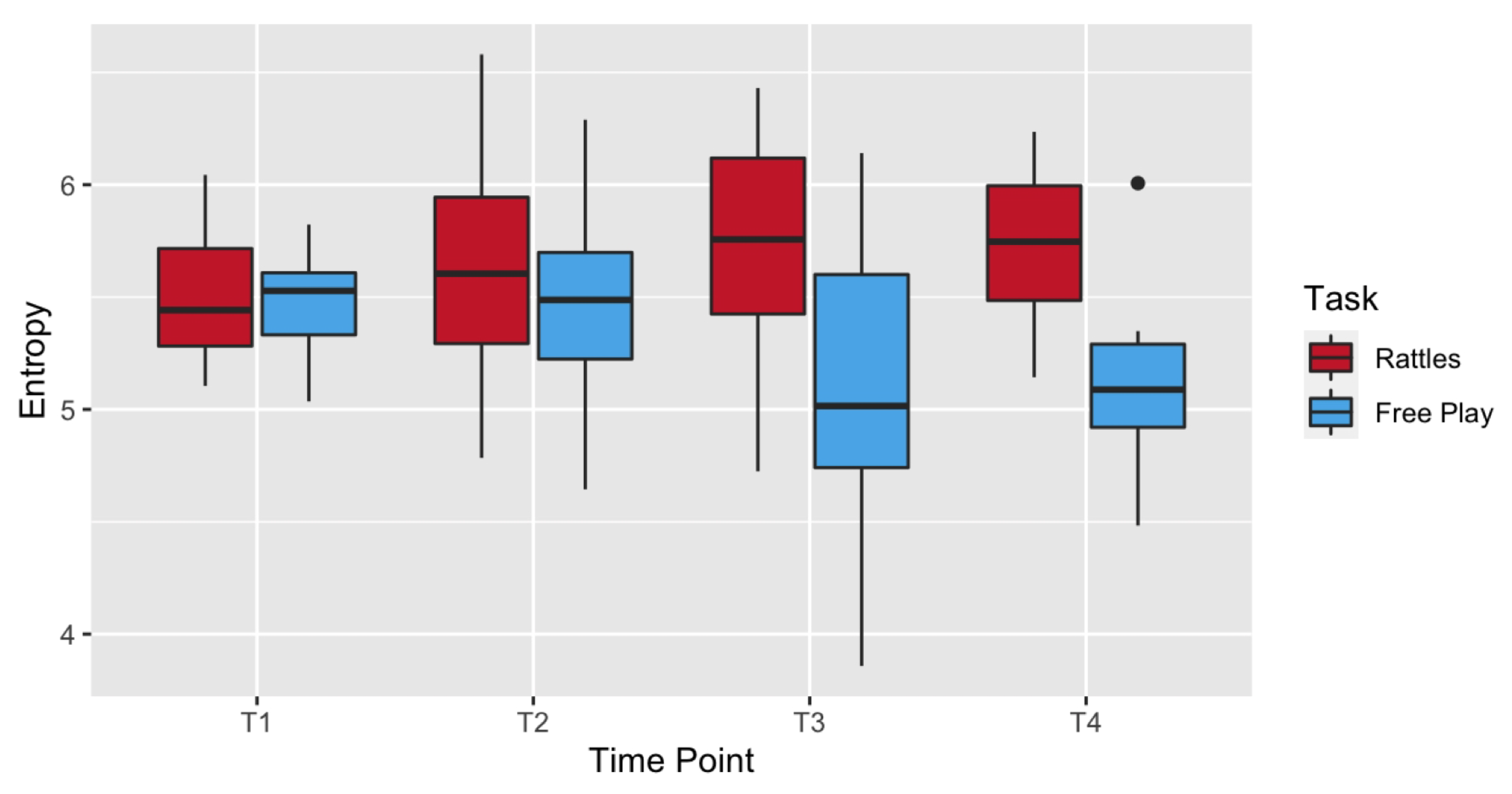
3.1.1. Entropy
3.1.2. Recurrence Rate
3.1.3. Mean Line
3.2. Control Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thelen, E.; Smith, L.B. A Dynamic Systems Approach to the Development of Cognition and Action; The MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Kobesova, A.; Kolar, P. Developmental kinesiology: Three levels of motor control in the assessment and treatment of the motor system. J. Bodyw. Mov. Ther. 2014, 18, 23–33. [Google Scholar] [CrossRef] [PubMed]
- Dusing, S.C.; Harbourne, R.T. Variability in Postural Control During Infancy: Implications for Development, Assessment, and Intervention. Phys. Ther. 2010, 90, 1838–1849. [Google Scholar] [CrossRef]
- Westcott, S.L.; Lowes, L.P.; Richardson, P.K. Evaluation of postural stability in children: Current theories and assessment tools. Phys. Ther. 1997, 77, 629–645. [Google Scholar] [CrossRef] [PubMed]
- Piek, J.P.; Gasson, N. Spontaneous kicking in fullterm and preterm infants: Are there leg asymmetries? Hum. Mov. Sci. 1999, 18, 377–395. [Google Scholar] [CrossRef]
- Piek, J.P.; Gasson, N.; Barrett, N.; Case, I. Limb and gender differences in the development of coordination in early infancy. Hum. Mov. Sci. 2002, 21, 621–639. [Google Scholar] [CrossRef]
- Kanemaru, N.; Watanabe, H.; Taga, G. Increasing selectivity of interlimb coordination during spontaneous movements in 2- to 4-month-old infants. Exp. Brain Res. 2012, 218, 49–61. [Google Scholar] [CrossRef]
- Watanabe, H.; Taga, G. Flexibility in infant actions during arm- and leg-based learning in a mobile paradigm. Infant Behav. Dev. 2009, 32, 79–90. [Google Scholar] [CrossRef]
- Abney, D.H.; Warlaumont, A.S.; Haussman, A.; Ross, J.M.; Wallot, S. Using nonlinear methods to quantify changes in infant limb movements and vocalizations. Front. Psychol. 2014, 5, 771. [Google Scholar] [CrossRef] [Green Version]
- Greco, A.L.R.; da Costa, C.S.N.; Tudella, E. Identifying the level of trunk control of healthy term infants aged from 6 to 9 months. Infant Behav. Dev. 2018, 50, 207–212. [Google Scholar] [CrossRef]
- Rachwani, J.; Santamaria, V.; Saavedra, S.L.; Wood, S.; Porter, F.; Woollacott, M.H. Segmental trunk control acquisition and reaching in typically developing infants. Exp. Brain Res. 2013, 228, 131–139. [Google Scholar] [CrossRef] [Green Version]
- Hadders-Algra, M. Development of Postural Control During the First 18 Months of Life. Neural Plast. 2005, 12, 99–108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adolph, K.E.; Hoch, J.E. Motor Development: Embodied, Embedded, Enculturated, and Enabling. Annu. Rev. Psychol. 2019, 70, 141–164. [Google Scholar] [CrossRef] [PubMed]
- Rocha, S.; Southgate, V.; Mareschal, D. Infant Spontaneous Motor Tempo. Dev. Sci. 2021, 24, e13032. [Google Scholar] [CrossRef] [PubMed]
- Hoehl, S.; Fairhurst, M.; Schirmer, A. Interactional synchrony: Signals, mechanisms and benefits. Soc. Cogn. Affect. Neurosci. 2021, 16, 5–18. [Google Scholar] [CrossRef] [Green Version]
- Trujillo-Priego, I.A.; Smith, B.A. Kinematic characteristics of infant leg movements produced across a full day. J. Rehabil. Assist. Technol. Eng. 2017, 4, 205566831771746. [Google Scholar] [CrossRef]
- Deng, W.; Trujillo-Priego, I.A.; Smith, B.A. How Many Days Are Necessary to Represent an Infant’s Typical Daily Leg Movement Behavior Using Wearable Sensors? Phys. Ther. 2019, 99, 730–738. [Google Scholar] [CrossRef]
- Patel, P.; Shi, Y.; Hajiaghajani, F.; Biswas, S.; Lee, M.H. A novel two-body sensor system to study spontaneous movements in infants during caregiver physical contact. Infant Behav. Dev. 2019, 57, 101383. [Google Scholar] [CrossRef]
- Zhou, J.; Schaefer, S.Y.; Smith, B.A. Quantifying Caregiver Movement when Measuring Infant Movement across a Full Day: A Case Report. Sensors 2019, 19, 2886. [Google Scholar] [CrossRef] [Green Version]
- Airaksinen, M.; Räsänen, O.; Ilén, E.; Häyrinen, T.; Kivi, A.; Marchi, V.; Gallen, A.; Blom, S.; Varhe, A.; Kaartinen, N.; et al. Automatic Posture and Movement Tracking of Infants with Wearable Movement Sensors. Sci. Rep. 2020, 10, 169. [Google Scholar] [CrossRef]
- Franchak, J.M.; Scott, V.; Luo, C. A Contactless Method for Measuring Full-Day, Naturalistic Motor Behavior Using Wearable Inertial Sensors. Front. Psychol. 2021, 12, 701343. [Google Scholar] [CrossRef]
- Khan, M.H.; Helsper, J.; Boukhers, Z.; Grzegorzek, M. Automatic recognition of movement patterns in the vojta-therapy using RGB-D data. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 1235–1239. [Google Scholar] [CrossRef]
- Jiang, C.; Lane, C.J.; Perkins, E.; Schiesel, D.; Smith, B.A. Determining if wearable sensors affect infant leg movement frequency. Dev. Neurorehabilit. 2018, 21, 133–136. [Google Scholar] [CrossRef] [PubMed]
- López Pérez, D.; Leonardi, G.; Niedźwiecka, A.; Radkowska, A.; Rączaszek-Leonardi, J.; Tomalski, P. Combining Recurrence Analysis and Automatic Movement Extraction from Video Recordings to Study Behavioral Coupling in Face-to-Face Parent-Child Interactions. Front. Psychol. 2017, 8, 2228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- López Pérez, D.; Laudańska, Z.; Radkowska, A.; Babis, K.; Kozioł, A.; Tomalski, P. Do we need expensive equipment to quantify infants’ movement? A cross-validation study between computer vision methods and sensor data. In Proceedings of the 2021 IEEE International Conference on Development and Learning (ICDL), Beijing, China, 23–26 August 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Khan, M.H.; Schneider, M.; Farid, M.S.; Grzegorzek, M. Detection of Infantile Movement Disorders in Video Data Using Deformable Part-Based Model. Sensors 2018, 18, 3202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, M.H.; Zöller, M.; Farid, M.S.; Grzegorzek, M. Marker-Based Movement Analysis of Human Body Parts in Therapeutic Procedure. Sensors 2020, 20, 3312. [Google Scholar] [CrossRef] [PubMed]
- Baccinelli, W.; Bulgheroni, M.; Simonetti, V.; Fulceri, F.; Caruso, A.; Gila, L.; Scattoni, M.L. Movidea: A Software Package for Automatic Video Analysis of Movements in Infants at Risk for Neurodevelopmental Disorders. Brain Sci. 2020, 10, 203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wallot, S.; Roepstorff, A.; Mønster, D. Multidimensional Recurrence Quantification Analysis (MdRQA) for the Analysis of Multidimensional Time-Series: A Software Implementation in MATLAB and Its Application to Group-Level Data in Joint Action. Front. Psychol. 2016, 7, 1835. [Google Scholar] [CrossRef]
- Roetenberg, D.; Luinge, H.J.; Baten, C.T.; Veltink, P.H. Compensation of magnetic disturbances improves inertial and magnetic sensing of human body segment orientation. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 395–405. [Google Scholar] [CrossRef] [Green Version]
- Gordon, I.; Wallot, S.; Berson, Y. Group-level physiological synchrony and individual-level anxiety predict positive affective behaviors during a group decision-making task. J. Psychophysiol. 2021, 9, 58. [Google Scholar] [CrossRef]
- Ossmy, O.; Adolph, K.E. Real-Time Assembly of Coordination Patterns in Human Infants. Curr. Biol. 2020, 30, 4553–4562.e4. [Google Scholar] [CrossRef]
- Kello, C.T.; Beltz, B.C.; Holden, J.G.; Van Orden, G.C. The Emergent Coordination of Cognitive Function. J. Exp. Psychol. Gen. 2007, 136, 551–568. [Google Scholar] [CrossRef] [Green Version]
- Ihlen, E.A.; Vereijken, B. Interaction-dominant dynamics in human cognition: Beyond 1/f αfluctuation. J. Exp. Psychol. Gen. 2010, 139, 436–463. [Google Scholar] [CrossRef] [PubMed]
- Wijnants, M.L.; Hasselman, F.; Cox, R.F.; Bosman, A.M.; van Orden, G. An interaction-dominant perspective on reading fluency and dyslexia. Ann. Dyslexia 2012, 62, 100–119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wallot, S.; Mønster, D. Calculation of Average Mutual Information (AMI) and false-nearest neighbors (FNN) for the estimation of embedding parameters of multidimensional time series in matlab. Front. Psychol. 2018, 9, 1679. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marwan, N.; Webber, C.L. Recurrence Quantification Analysis. Understanding Complex Systems; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Marwan, N.; Wessel, N.; Meyerfeldt, U.; Schirdewan, A.; Kurths, J. Recurrence-plot-based measures of complexity and their application to heart-rate-variability data. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2002, 66, 026702. [Google Scholar] [CrossRef] [Green Version]
- Richardson, D.C.; Dale, R. Looking to understand: The coupling between speakers’ and listeners’ eye movements and its relationship to discourse comprehension. Cogn. Sci. 2005, 29, 1045–1060. [Google Scholar] [CrossRef] [Green Version]
- Twisk, J.; de Vente, W. Attrition in longitudinal studies: How to deal with missing data. J. Clin. Epidemiol. 2002, 55, 329–337. [Google Scholar] [CrossRef]
- Diggle, P.; Diggle, D.; Allgemeine Tierzucht, F.; Press, O.U.; Diggle, P.; Heagerty, P.; Liang, K.; Zeger, S.; Zeger, B. Analysis of Longitudinal Data; Oxford Statistical Science Series; OUP: Oxford, UK, 2002. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- RStudio Team. RStudio: Integrated Development Environment for R; RStudio, PBC.: Boston, MA, USA, 2020. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Goldfield, E.C. Emergent forms: Origins and Early Development of Human Action and Perception; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Soska, K.C.; Galeon, M.A.; Adolph, K.E. On the other hand: Overflow movements of infants’ hands and legs during unimanual object exploration. Dev. Psychobiol. 2012, 54, 372–382. [Google Scholar] [CrossRef] [Green Version]
- D’Souza, H.; Cowie, D.; Karmiloff-Smith, A.; Bremner, A.J. Specialization of the motor system in infancy: From broad tuning to selectively specialized purposeful actions. Dev. Sci. 2017, 20, e12409. [Google Scholar] [CrossRef] [Green Version]
- Wallot, S. Multidimensional Cross-Recurrence Quantification Analysis (MdCRQA)—A Method for Quantifying Correlation between Multivariate Time-Series. Multivar. Behav. Res. 2019, 54, 173–191. [Google Scholar] [CrossRef]
- De Jonge-Hoekstra, L.; Van der Steen, S.; Van Geert, P.; Cox, R.F.A. Asymmetric Dynamic Attunement of Speech and Gestures in the Construction of Children’s Understanding. Front. Psychol. 2016, 7, 473. [Google Scholar] [CrossRef] [Green Version]
- Adolph, K.E.; Robinson, S.R.; Young, J.W.; Gill-Alvarez, F. What is the shape of developmental change? Psychol. Rev. 2008, 115, 527–543. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borghi, A.M.; Binkofski, F. Words as Social Tools: An Embodied View on Abstract Concepts; SpringerBriefs in Psychology; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Wilson, R.B.; Vangala, S.; Elashoff, D.; Safari, T.; Smith, B.A. Using wearable sensor technology to measure motion complexity in infants at high familial risk for autism spectrum disorder. Sensors 2021, 21, 616. [Google Scholar] [CrossRef] [PubMed]
- Abrishami, M.S.; Nocera, L.; Mert, M.; Trujillo-Priego, I.A.; Purushotham, S.; Shahabi, C.; Smith, B.A. Identification of developmental delay in infants using wearable sensors: Full-day leg movement statistical feature analysis. IEEE J. Transl. Eng. Health Med. 2019, 7, 2800207. [Google Scholar] [CrossRef] [PubMed]


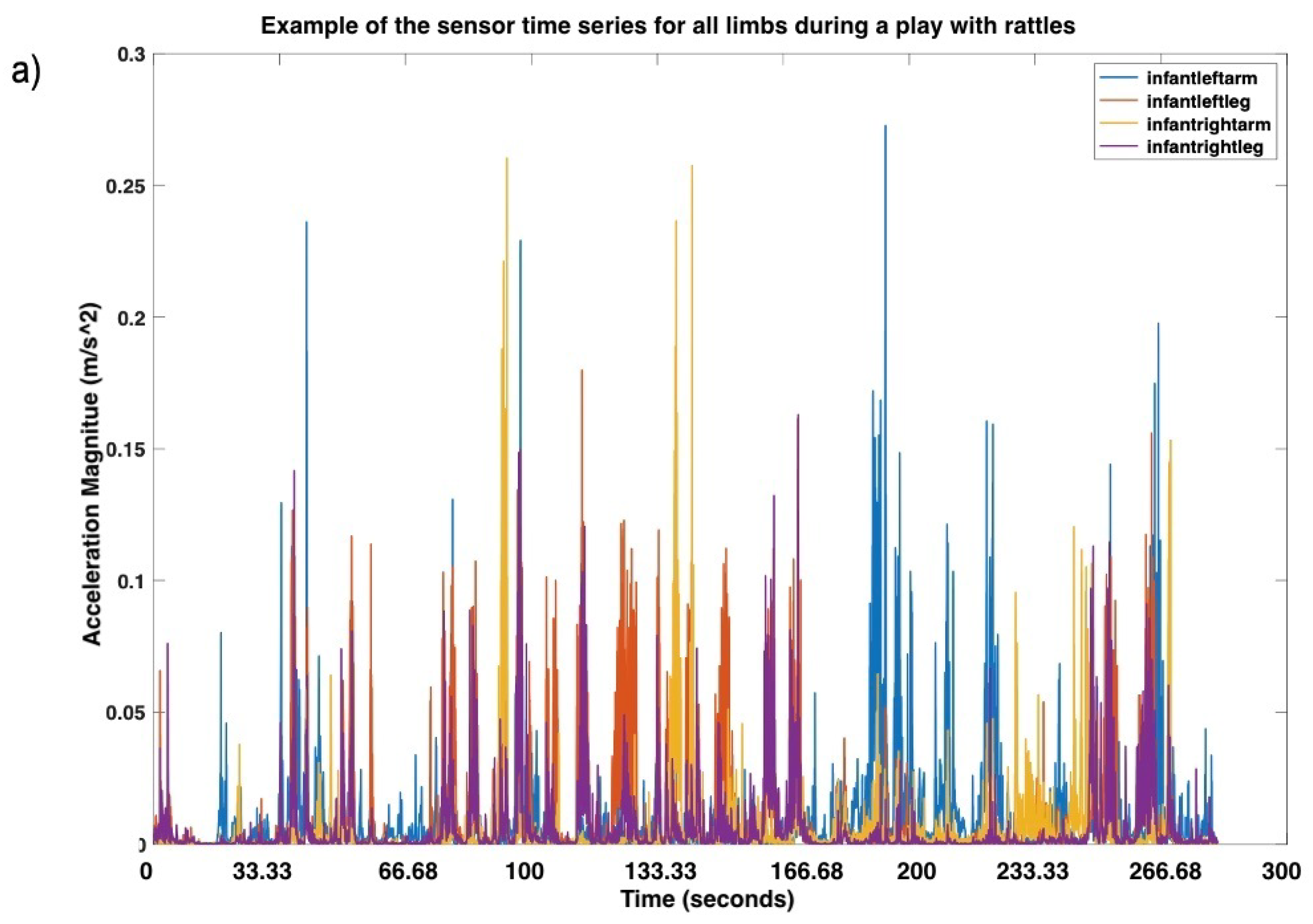
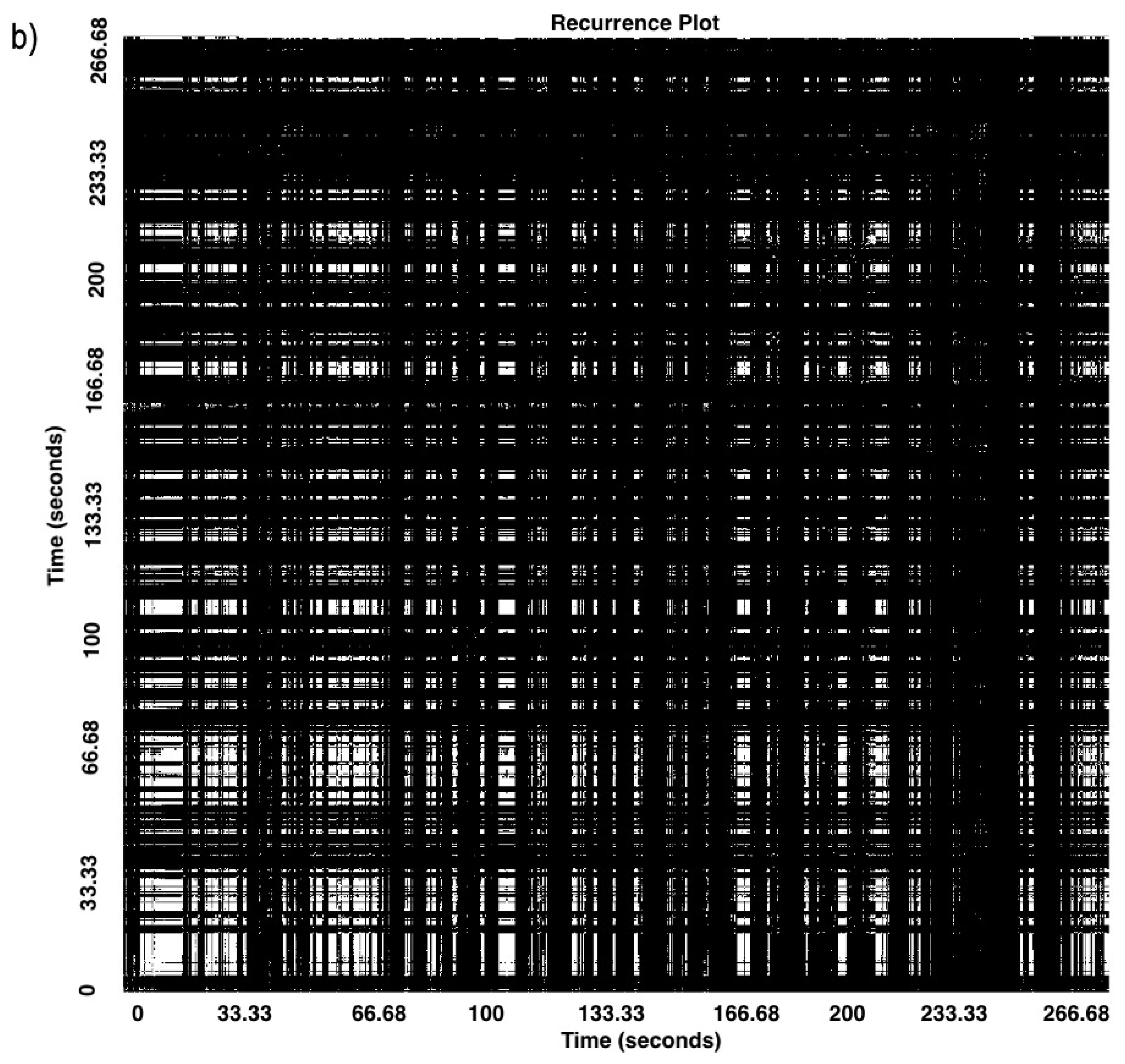
| Time Point | N | Mean Age in Months (SD) | Min Age in Months | Max Age in Months |
|---|---|---|---|---|
| T1 | 19 | 4.41 (0.30) | 4.00 | 5.20 |
| T2 | 21 | 6.57 (0.36) | 6.00 | 7.20 |
| T3 | 26 | 9.14 (0.41) | 8.60 | 10.20 |
| T3 | 17 | 12.14 (0.46) | 11.60 | 13.10 |
| T1 | T2 | T3 | T4 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean (SD) | Min | Max | Mean (SD) | Min | Max | Mean (SD) | Min | Max | Mean (SD) | Min | Max | ||
| Rattles | Ent | 5.51 (0.30) | 5.10 | 6.04 | 5.62 (0.44) | 4.78 | 6.58 | 5.72 (0.45) | 4.72 | 6.43 | 5.73 (0.37) | 5.14 | 6.24 |
| RR | 5.03 (0.05) | 4.93 | 5.09 | 7.28 (5.13) | 2.07 | 19.14 | 9.17 (7.19) | 0.69 | 27.55 | 7.78 (5.01) | 0.95 | 15.60 | |
| ML | 19.48 (6.61) | 5.07 | 35.20 | 23.06 (8.59) | 11.96 | 50.95 | 23.55 (9.02) | 1.66 | 41.79 | 23.79 (5.78) | 15.13 | 32.19 | |
| Free Play | Ent | 5.46 (0.20) | 5.04 | 5.82 | 5.48 (0.42) | 4.64 | 6.29 | 5.10 (0.59) | 3.86 | 6.14 | 5.08 (0.42) | 4.48 | 6.01 |
| RR | 5.05 (0.04) | 4.98 | 5.09 | 5.47 (3.84) | 0.14 | 14.54 | 4.51 (4.79) | 0.02 | 16.26 | 2.99 (3.52) | 0.17 | 13.28 | |
| ML | 18.96 (2.75) | 14.17 | 23.79 | 21.04 (7.36) | 10.96 | 39.05 | 16.15 (6.28) | 7.44 | 30.03 | 15.39 (4.53) | 9.92 | 26.78 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laudańska, Z.; López Pérez, D.; Radkowska, A.; Babis, K.; Malinowska-Korczak, A.; Wallot, S.; Tomalski, P. Changes in the Complexity of Limb Movements during the First Year of Life across Different Tasks. Entropy 2022, 24, 552. https://doi.org/10.3390/e24040552
Laudańska Z, López Pérez D, Radkowska A, Babis K, Malinowska-Korczak A, Wallot S, Tomalski P. Changes in the Complexity of Limb Movements during the First Year of Life across Different Tasks. Entropy. 2022; 24(4):552. https://doi.org/10.3390/e24040552
Chicago/Turabian StyleLaudańska, Zuzanna, David López Pérez, Alicja Radkowska, Karolina Babis, Anna Malinowska-Korczak, Sebastian Wallot, and Przemysław Tomalski. 2022. "Changes in the Complexity of Limb Movements during the First Year of Life across Different Tasks" Entropy 24, no. 4: 552. https://doi.org/10.3390/e24040552
APA StyleLaudańska, Z., López Pérez, D., Radkowska, A., Babis, K., Malinowska-Korczak, A., Wallot, S., & Tomalski, P. (2022). Changes in the Complexity of Limb Movements during the First Year of Life across Different Tasks. Entropy, 24(4), 552. https://doi.org/10.3390/e24040552






