A Bayesian Approach to Predict Football Matches with Changed Home Advantage in Spectator-Free Matches after the COVID-19 Break
Abstract
:1. Introduction
2. Statistical Analysis
3. Proposed Method
3.1. Bayesian Hierarchical Poisson Model
3.1.1. Model Structure
3.1.2. Model Fitting
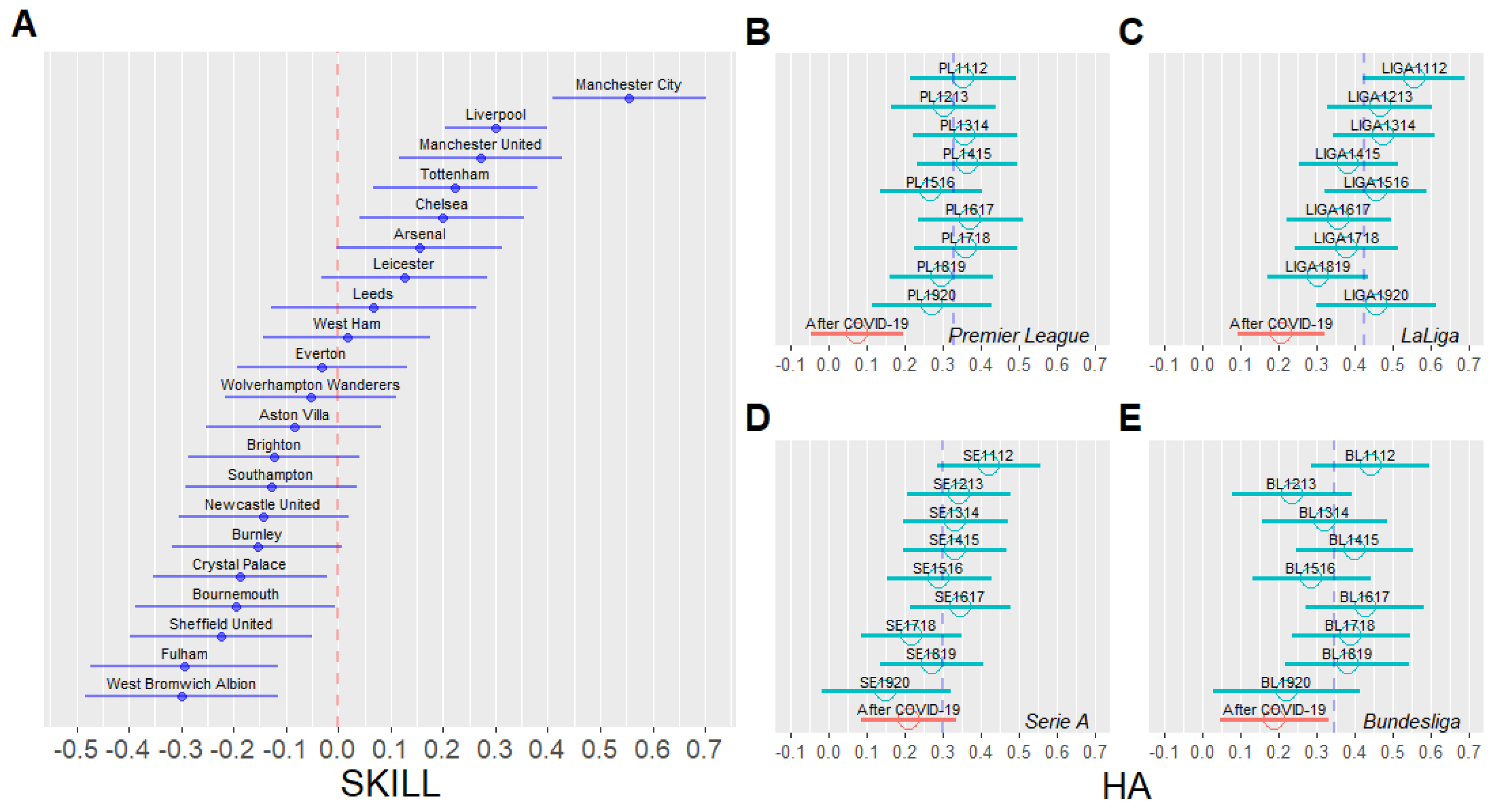
3.2. Home Advantage
3.3. Additional Features for Prediction
4. Experiments
4.1. Dataset
4.2. Visualization of Parameters
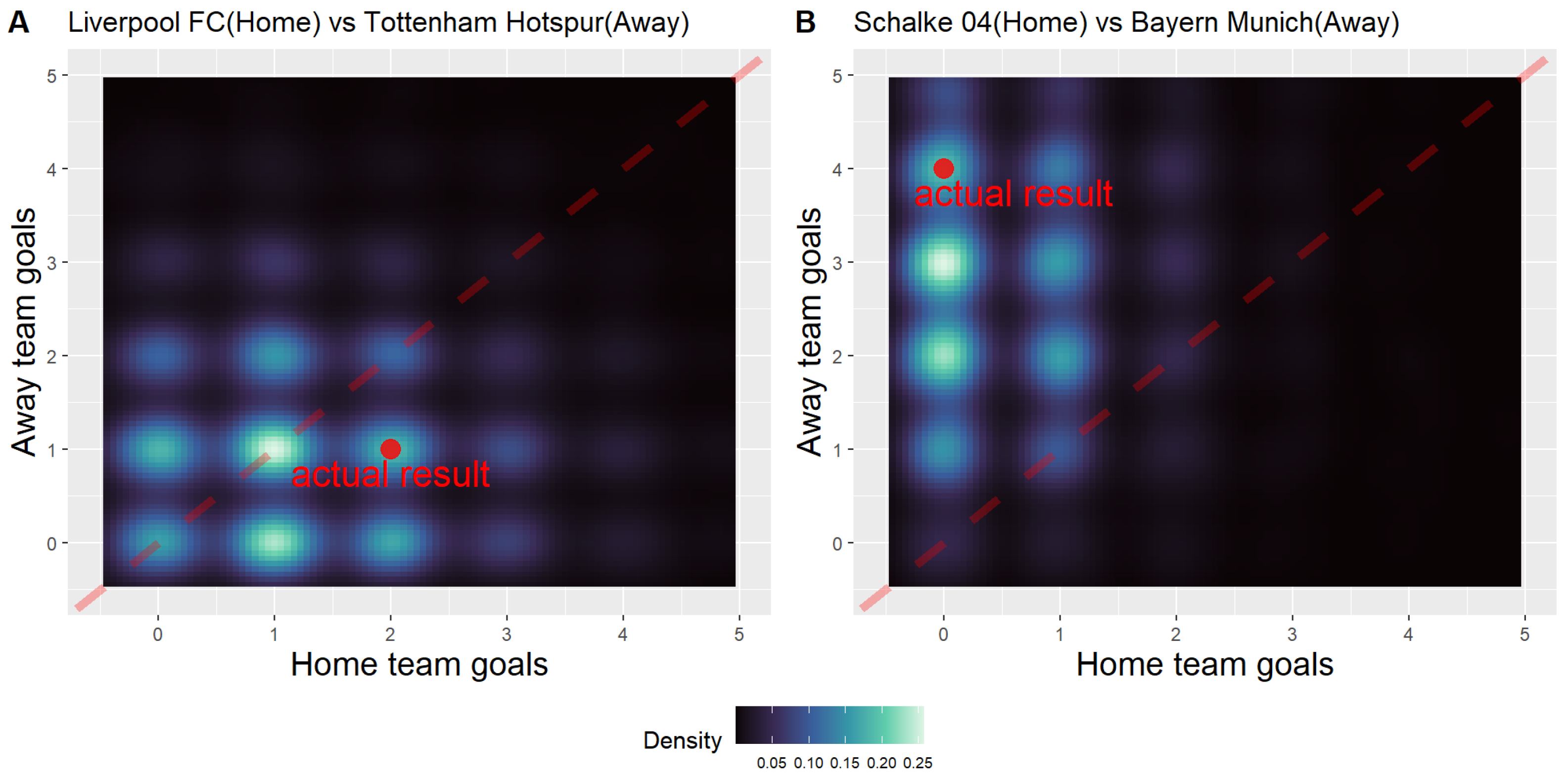
4.3. Score Prediction by Sampling
4.4. Match Prediction Model with Additional Features
- Win: Number of matches won in the last season;
- Draw: Number of matches drawn in the last season;
- Loss: Number of matches lost in the last season;
- Goals_scored: Number of goals scored in the last season;
- Goals_conceded: Number of goals conceded in the last season;
- Points: Final points in the last season;
- Promoted: Recently promoted to the league in the last season.
- OTHERS(fixed): Mean of sampled OTHERS parameters from the uniform HA model;
- SKILL(fixed): Mean of sampled SKILL parameters from the uniform HA model;
- HA(fixed): HA value from the uniform HA model.
- OTHERS: Mean of sampled OTHERS parameters from the changed HA model;
- SKILL: Mean of sampled SKILL parameters from the changed HA model;
- HA: HA value from the changed HA model.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| COVID-19 | coronavirus disease 2019 |
| HA | home advantage |
| MLP | multilayer perception |
| SVM | support vector machine |
References
- Drewes, M.; Daumann, F.; Follert, F. Exploring the sports economic impact of COVID-19 on professional soccer. Soccer Soc. 2021, 22, 125–137. [Google Scholar] [CrossRef]
- McGrath, M. ‘Anfield Is Only Anfield When It Is Full,’ Marcelo Bielsa Says ahead of Liverpool vs. Leeds Game. 2020. Available online: https://www.telegraph.co.uk/football/2020/09/11/anfield-anfield-full-marcelo-bielsa-says-ahead-liverpool-vs/ (accessed on 2 March 2022).
- Deloitte Touche Tohmatsu Limited. Annual Review of Football Finance 2020. Available online: https://www2.deloitte.com/uk/en/pages/sports-business-group/articles/annual-review-of-football-finance.html (accessed on 2 March 2022).
- Grand View Research. Online Gambling Market Size, Share & Trends Analysis Report by Type (Sports Betting, Casinos, Poker, Bingo), by Device (Desktop, Mobile), by Region (North America, Europe, APAC, Latin America, MEA), and Segment Forecasts, 2020–2027. Available online: https://www.grandviewresearch.com/industry-analysis/online-gambling-market (accessed on 2 March 2022).
- Nevill, A.M.; Balmer, N.J.; Williams, A.M. The influence of crowd noise and experience upon refereeing decisions in football. Psychol. Sport Exerc. 2002, 3, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Boyko, R.H.; Boyko, A.R.; Boyko, M.G. Referee bias contributes to home advantage in English Premiership football. J. Sport. Sci. 2007, 25, 1185–1194. [Google Scholar] [CrossRef] [PubMed]
- Buraimo, B.; Forrest, D.; Simmons, R. The 12th man?: Refereeing bias in English and German soccer. J. R. Stat. Soc. Ser. (Stat. Soc.) 2010, 173, 431–449. [Google Scholar] [CrossRef] [Green Version]
- Dohmen, T.; Sauermann, J. Referee Bias. J. Econ. Surv. 2015, 30, 679–695. [Google Scholar] [CrossRef]
- Fischer, K.; Haucap, J. Does Crowd Support Drive the Home Advantage in Professional Football? Evidence from German Ghost Games during the COVID-19 Pandemic. J. Sport. Econ. 2021, 22, 982–1008. [Google Scholar] [CrossRef]
- Tilp, M.; Thaller, S. Covid-19 Has Turned Home Advantage Into Home Disadvantage in the German Soccer Bundesliga. Front. Sport. Act. Living 2020, 2, 165. [Google Scholar] [CrossRef]
- Reade, J.; Schreyer, D.; Singleton, C. Eliminating Supportive Crowds Reduces Referee Bias. Econ. Inq. 2021. [Google Scholar] [CrossRef]
- Bryson, A.; Dolton, P.; Reade, J.J.; Schreyer, D.; Singleton, C. Causal effects of an absent crowd on performances and refereeing decisions during Covid-19. Econ. Lett. 2021, 198, 109664. [Google Scholar] [CrossRef]
- Hill, Y.; Van Yperen, N.W. Losing the Home Field Advantage When Playing Behind Closed Doors During COVID-19: Change or Chance? Front. Psychol. 2021, 12, 1321. [Google Scholar] [CrossRef]
- Benz, L.S.; Lopez, M.J. Estimating the change in soccer’s home advantage during the Covid-19 pandemic using bivariate Poisson regression. Asta Adv. Stat. Anal. 2021, 2021, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Higgs, N.; Stavness, I. Bayesian analysis of home advantage in North American professional sports before and during COVID-19. Sci. Rep. 2021, 11, 14521. [Google Scholar] [CrossRef] [PubMed]
- McCarrick, D.; Bilalic, M.; Neave, N.; Wolfson, S. Home advantage during the COVID-19 pandemic: Analyses of European football leagues. Psychol. Sport Exerc. 2021, 56, 102013. [Google Scholar] [CrossRef] [PubMed]
- Azhari, H.R.; Widyaningsih, Y.; Lestari, D. Predicting Final Result of Football Match Using Poisson Regression Model. J. Phys. Conf. Ser. 2018, 1108, 012066. [Google Scholar] [CrossRef]
- Aslan, B.G.; Inceoglu, M.M. A Comparative Study on Neural Network based Soccer Result Prediction. In Proceedings of the Seventh International Conference on Intelligent Systems Design and Applications, Rio de Janeiro, Brazil, 20–24 October 2007; pp. 545–550. [Google Scholar] [CrossRef] [Green Version]
- Cho, Y.; Yoon, J.; Lee, S. Using social network analysis and gradient boosting to develop a soccer win–lose prediction model. Eng. Appl. Artif. Intell. 2018, 72, 228–240. [Google Scholar] [CrossRef]
- Saricaoğlu, A.E.; Aksoy, A.; Kaya, T. Prediction of Turkish Super League Match Results Using Supervised Machine Learning Techniques. In Intelligent and Fuzzy Techniques in Big Data Analytics and Decision Making; Springer: Cham, Switzerland, 2019; Volume 1029, pp. 273–280. [Google Scholar] [CrossRef]
- Brooks, J.; Kerr, M.; Guttag, J. Using machine learning to draw inferences from pass location data in soccer. Stat. Anal. Data Mining Asa Data Sci. J. 2016, 9, 338–349. [Google Scholar] [CrossRef]
- Berrar, D.; Lopes, P.; Dubitzky, W. Incorporating domain knowledge in machine learning for soccer outcome prediction. Mach. Learn. 2018, 108, 97–126. [Google Scholar] [CrossRef] [Green Version]
- Gorgi, P.; Koopman, S.J.; Lit, R. Estimation of final standings in football competitions with a premature ending: The case of COVID-19. Asta Adv. Stat. Anal. 2021, 1–18. [Google Scholar] [CrossRef]
- Price, M.; Yan, J. The Effects of the NBA COVID Bubble on the NBA Playoffs: A Case Study for Home-Court Advantage. arXiv 2021, arXiv:2103.02832. [Google Scholar]
- Szabó, D.V.; Pérez, D.A. Does home advantage without crowd exist in American football? arXiv 2021, arXiv:2104.11595. [Google Scholar]
- Welch, B.L. The Generalization of ‘Student’s’ Problem when Several Different Population Variances Are Involved. Biometrika 1947, 34, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Routledge: London, UK, 1988. [Google Scholar]
- Lee, A.J. Modeling Scores in the Premier League: Is Manchester United Really the Best? CHANCE 1997, 10, 15–19. [Google Scholar] [CrossRef]
- Albert, J.H. Bayesian selection of log-linear models. Can. J. Stat. 1996, 24, 327–347. [Google Scholar] [CrossRef]
- Baio, G.; Blangiardo, M. Bayesian hierarchical model for the prediction of football results. J. Appl. Stat. 2010, 37, 253–264. [Google Scholar] [CrossRef] [Green Version]
- Karlis, D.; Ntzoufras, I. Bayesian modelling of football outcomes: Using the Skellam’s distribution for the goal difference. Ima J. Manag. Math. 2009, 20, 133–145. [Google Scholar] [CrossRef] [Green Version]
- Baath, R. Modeling Match Results in Soccer Using a Hierarchical Bayesian Poisson Model. 2015. Available online: http://sumsar.net/papers/baath_2015_modeling_match_resluts_in_soccer.pdf (accessed on 2 March 2022).
- Plummer, M. JAGS: A Program for Analysis of Bayesian Graphical Models Using Gibbs Sampling. 2003. Available online: https://www.r-project.org/conferences/DSC-2003/Proceedings/Plummer.pdf (accessed on 2 March 2022).
- Plummer, M. Rjags: Bayesian Graphical Models Using MCMC; R Package Version 4-10; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Geman, S.; Geman, D. Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 721–741. [Google Scholar] [CrossRef]
- Groot, L. Economics, Uncertainty and European Football: Trends in Competitive Balance; Edward Elgar: Cheltenham, UK, 2008. [Google Scholar]
- Swanson, B. Premier League Restart Depends on 8–10 Neutral Venues; Clubs Still Committed to Finishing Season. 2020. Available online: https://www.skysports.com/football/news/11095/11981803/premier-league-restart-depends-on-neutral-venues-clubs-still-committed-to-finishing-season (accessed on 20 February 2022).
- Andrieu, C.; De Freitas, N.; Doucet, A.; Jordan, M.I. An introduction to MCMC for machine learning. Mach. Learn. 2003, 50, 5–43. [Google Scholar] [CrossRef] [Green Version]
- Plummer, M.; Best, N.; Cowles, K.; Vines, K. CODA: Convergence Diagnosis and Output Analysis for MCMC. 2006. Available online: https://cran.r-project.org/doc/Rnews/Rnews_2006-1.pdf#page=7 (accessed on 2 March 2022).
- Epstein, E.S. A scoring system for probability forecasts of ranked categories. J. Appl. Meteorol. 1969, 8, 985–987. [Google Scholar] [CrossRef] [Green Version]
- Constantinou, A.C.; Fenton, N.E. Solving the problem of inadequate scoring rules for assessing probabilistic football forecast models. J. Quant. Anal. Sport. 2012, 8, 1–12. [Google Scholar] [CrossRef]
- Tsokos, A.; Narayanan, S.; Kosmidis, I.; Baio, G.; Cucuringu, M.; Whitaker, G.; Király, F. Modeling outcomes of soccer matches. Mach. Learn. 2019, 108, 77–95. [Google Scholar] [CrossRef] [Green Version]

| Test Statistic | Expected Points | Goal Difference |
|---|---|---|
| t | 2.3451 | 2.3049 |
| df | 7.6454 | 7.7808 |
| p-value | 0.0485 | 0.0510 |
| 95% confidence interval | [0.0011, 0.2730] | [−0.0009, 0.3371] |
| mean_before_COVID-19 | 1.6214 | 0.3671 |
| mean_after_COVID-19 | 1.4843 | 0.1990 |
| effect size (Cohen’s d) | −1.4612 | −1.3731 |
| Home/Away | Team Name | Parameters | Simulated Results | Most Frequent Score | Actual Outcome | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean_SKILL | Mean_OTHERS | Win | Draw | Loss | ||||||
| Match1 | Home | Liverpool FC | 0.301 | 0.272 | 1.42 | 0.425 | 0.273 | 0.302 | 1 | 2 |
| Away | Tottenham Hotspur | 0.224 | 0.212 | 1.14 | 0.302 | 0.273 | 0.425 | 1 | 1 | |
| Match2 | Home | Schalke 04 | −0.314 | 0.432 | 0.64 | 0.039 | 0.091 | 0.870 | 0 | 0 |
| Away | Bayern Munich | 0.561 | 0.300 | 3.23 | 0.870 | 0.091 | 0.039 | 3 | 4 | |
| Classifier | Feature Set 1 | Feature Set 2 | Feature Set 3 | Hyperparameter | |||
|---|---|---|---|---|---|---|---|
| Test Accuracy | Test Accuracy | Test Accuracy | |||||
| Logistic regression | 0.5062 | 0.2011 | 0.5208 | 0.2008 | 0.5229 | 0.1999 | C = 10 (L2 regularization) |
| MLP | 0.5076 | 0.2003 | 0.5145 | 0.2010 | 0.5186 | 0.2009 | hidden layer = 2, hidden node = (3, 3) |
| Random forest | 0.4695 | 0.2123 | 0.4889 | 0.2100 | 0.5020 | 0.2073 | max features = 5, n tree = 100 |
| Linear SVM | 0.4951 | 0.2050 | 0.5159 | 0.2023 | 0.5193 | 0.2015 | C = 1 (L2 regularization) |
| Naïve Bayes | 0.4792 | 0.1165 | 0.4819 | 0.1175 | 0.4778 | 0.1177 | prior = (0.3, 0.24, 0.46) |
| Score sampling | N/A | N/A | 0.5214 | 0.2997 | 0.5249 | 0.2998 | simulated 10,000 times |
| Average (except score sampling) | 0.4915 | 0.1870 | 0.5044 | 0.1863 | 0.5081 | 0.1855 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Kim, J.; Kim, H.; Lee, J.-S. A Bayesian Approach to Predict Football Matches with Changed Home Advantage in Spectator-Free Matches after the COVID-19 Break. Entropy 2022, 24, 366. https://doi.org/10.3390/e24030366
Lee J, Kim J, Kim H, Lee J-S. A Bayesian Approach to Predict Football Matches with Changed Home Advantage in Spectator-Free Matches after the COVID-19 Break. Entropy. 2022; 24(3):366. https://doi.org/10.3390/e24030366
Chicago/Turabian StyleLee, Jaemin, Juhuhn Kim, Hyunho Kim, and Jong-Seok Lee. 2022. "A Bayesian Approach to Predict Football Matches with Changed Home Advantage in Spectator-Free Matches after the COVID-19 Break" Entropy 24, no. 3: 366. https://doi.org/10.3390/e24030366
APA StyleLee, J., Kim, J., Kim, H., & Lee, J.-S. (2022). A Bayesian Approach to Predict Football Matches with Changed Home Advantage in Spectator-Free Matches after the COVID-19 Break. Entropy, 24(3), 366. https://doi.org/10.3390/e24030366







