Coupled Transport Effects in Solid Oxide Fuel Cell Modeling
Abstract
:1. Introduction
2. Materials and Methods
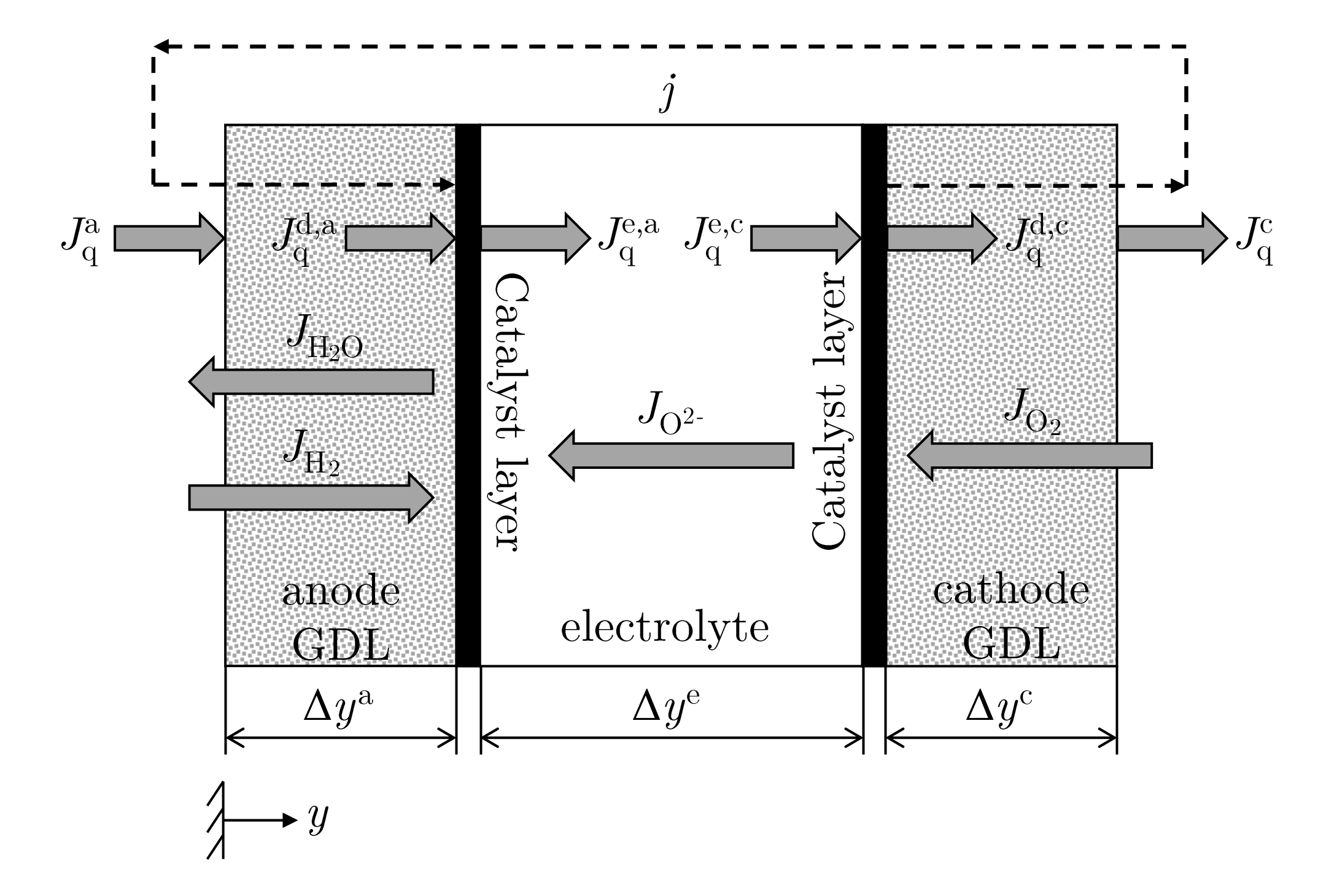
2.1. The Thermodynamic System—Solid Oxide Fuel Cell (SOFC)
2.2. Theory
2.2.1. Mass and Energy Balance Equations for the Gas Diffusion Layers (GDL)
2.2.2. Transport Equations for the Homogeneous Phase
2.2.3. Modeling of the Gas Diffusion Layers (GDL)
2.2.4. Mass Transport by Stefan–Maxwell Diffusion (1)
2.2.5. Extension by Knudsen Diffusion (2)
2.2.6. Extension by Convection (3)
2.2.7. Extension through Thermal Diffusion (4)
2.2.8. Mass Transfer Approach According to NET
2.2.9. Modeling of the Reaction Layers
2.2.10. Modeling of the Electrolyte
2.2.11. Exergy Analysis
2.3. Simulation
2.3.1. General Parameters
2.3.2. Parameters for Mass Transport
3. Results and Discussion
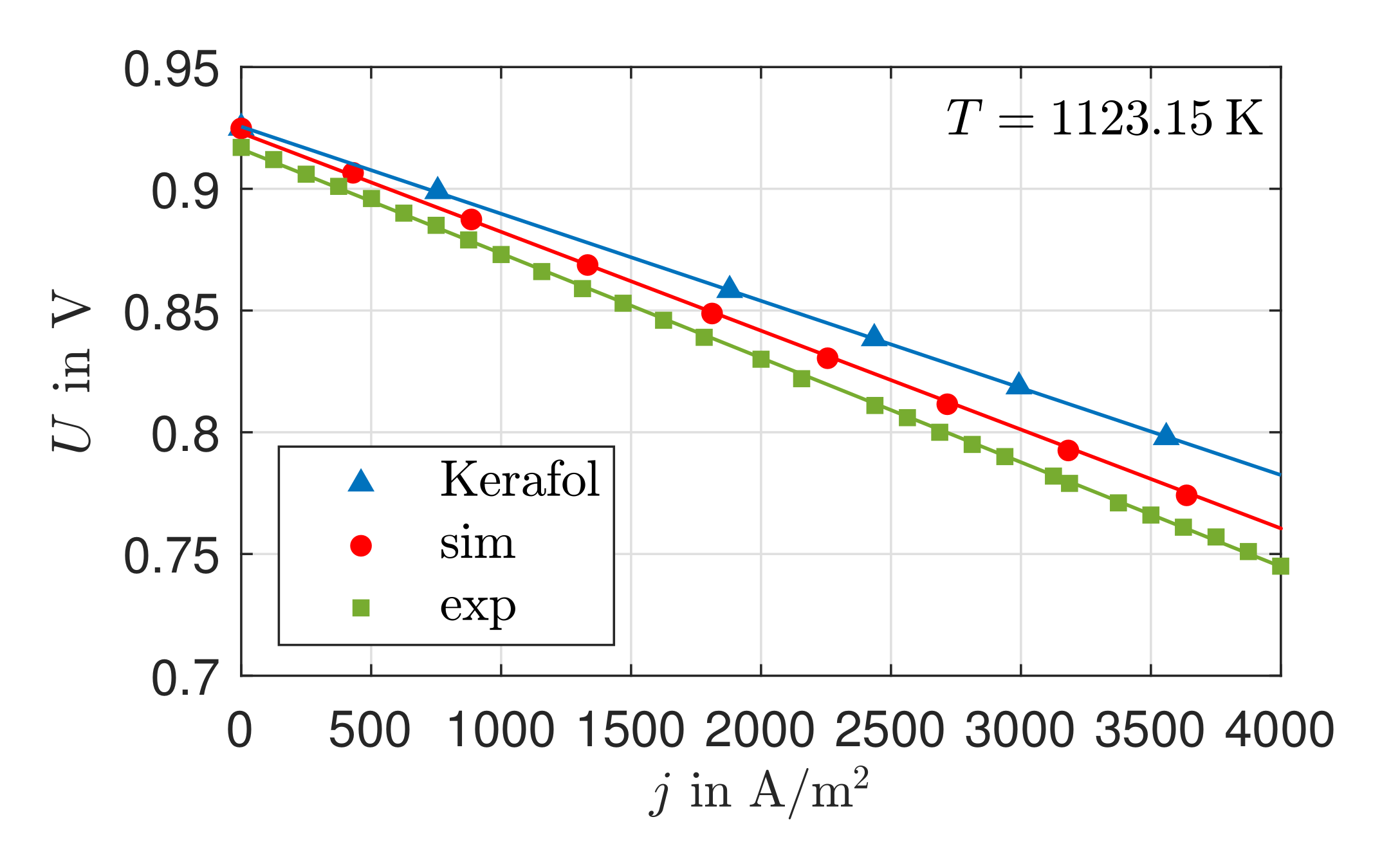
3.1. Validation
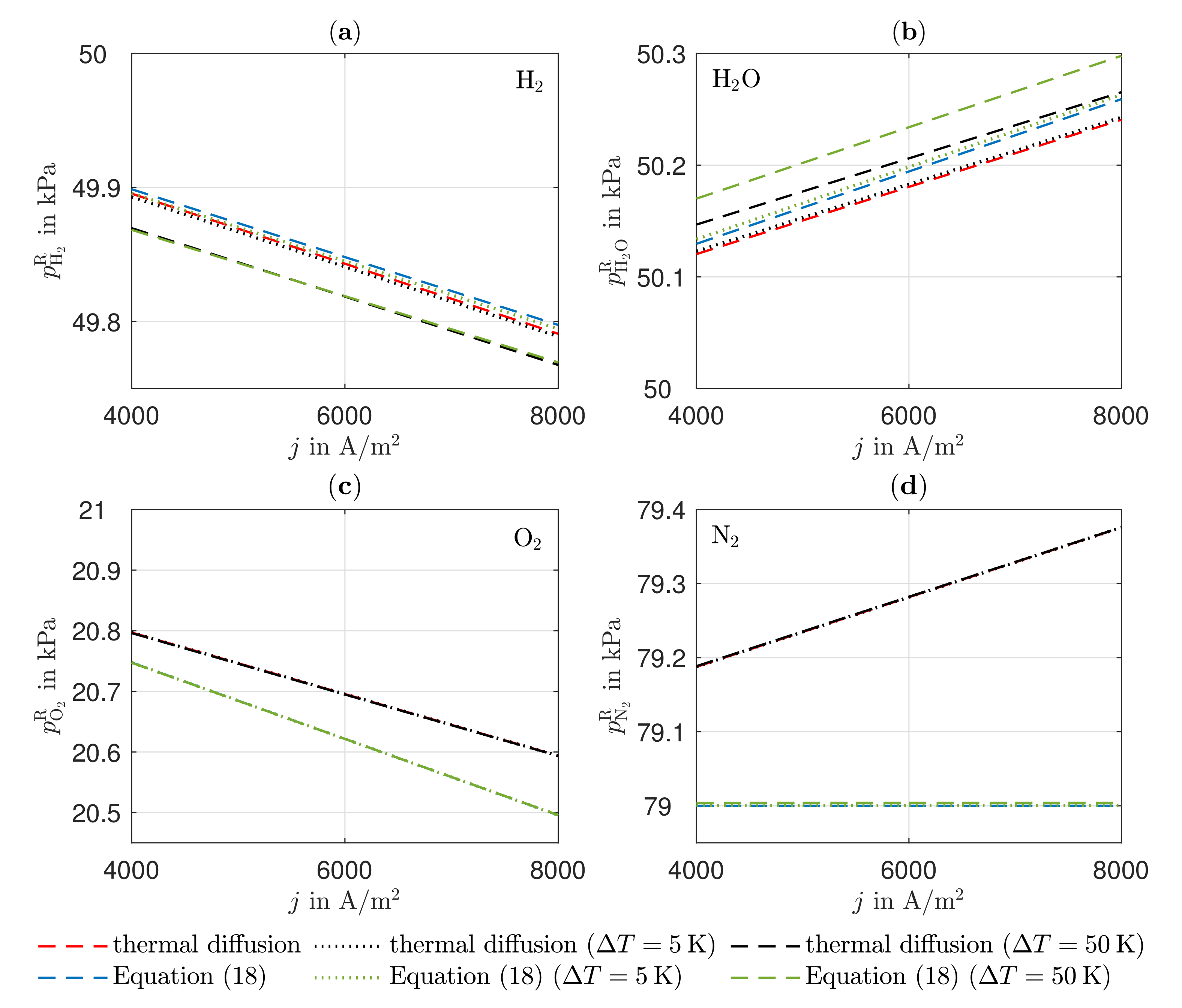
3.2. Partial Pressures
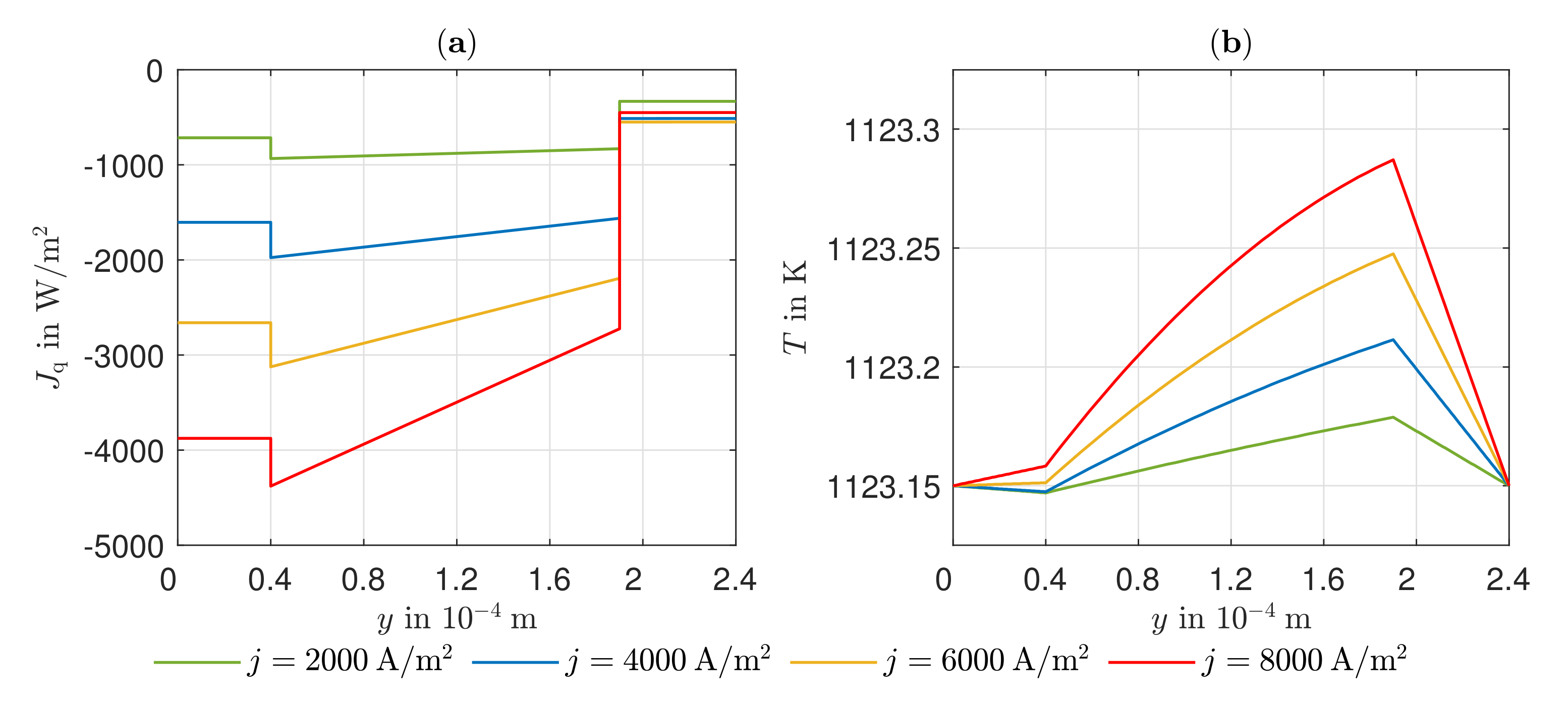
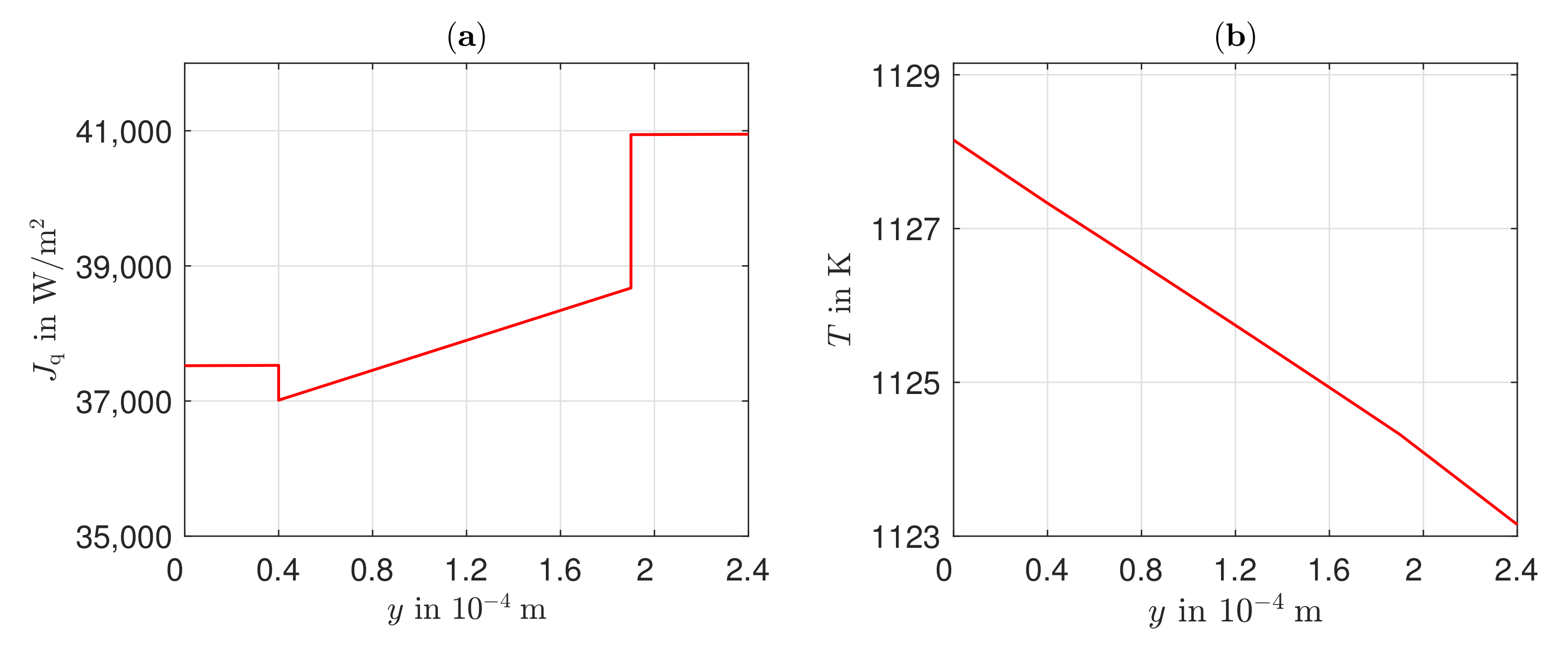
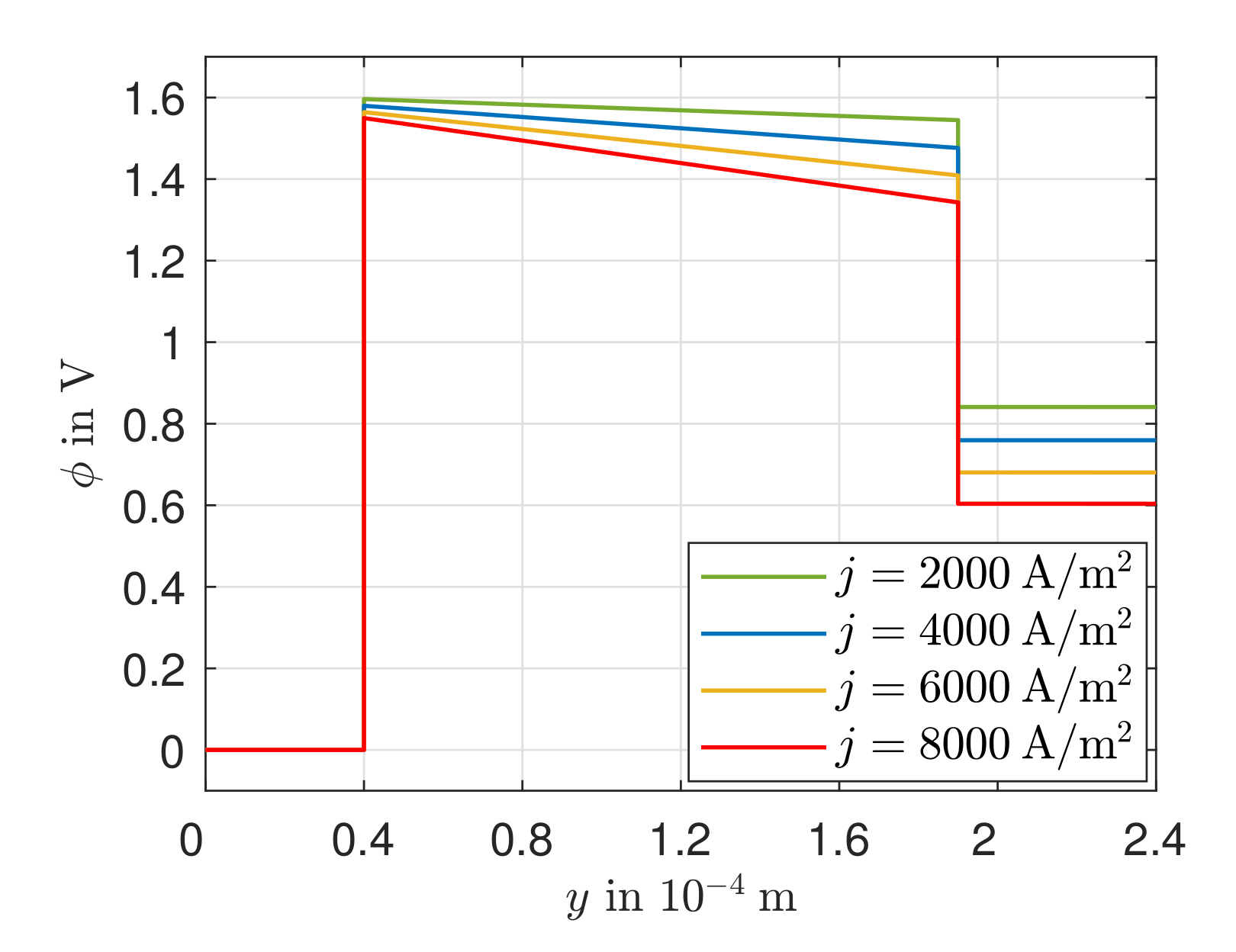
3.3. Heat Transport, Temperature Gradient, and Potential Field
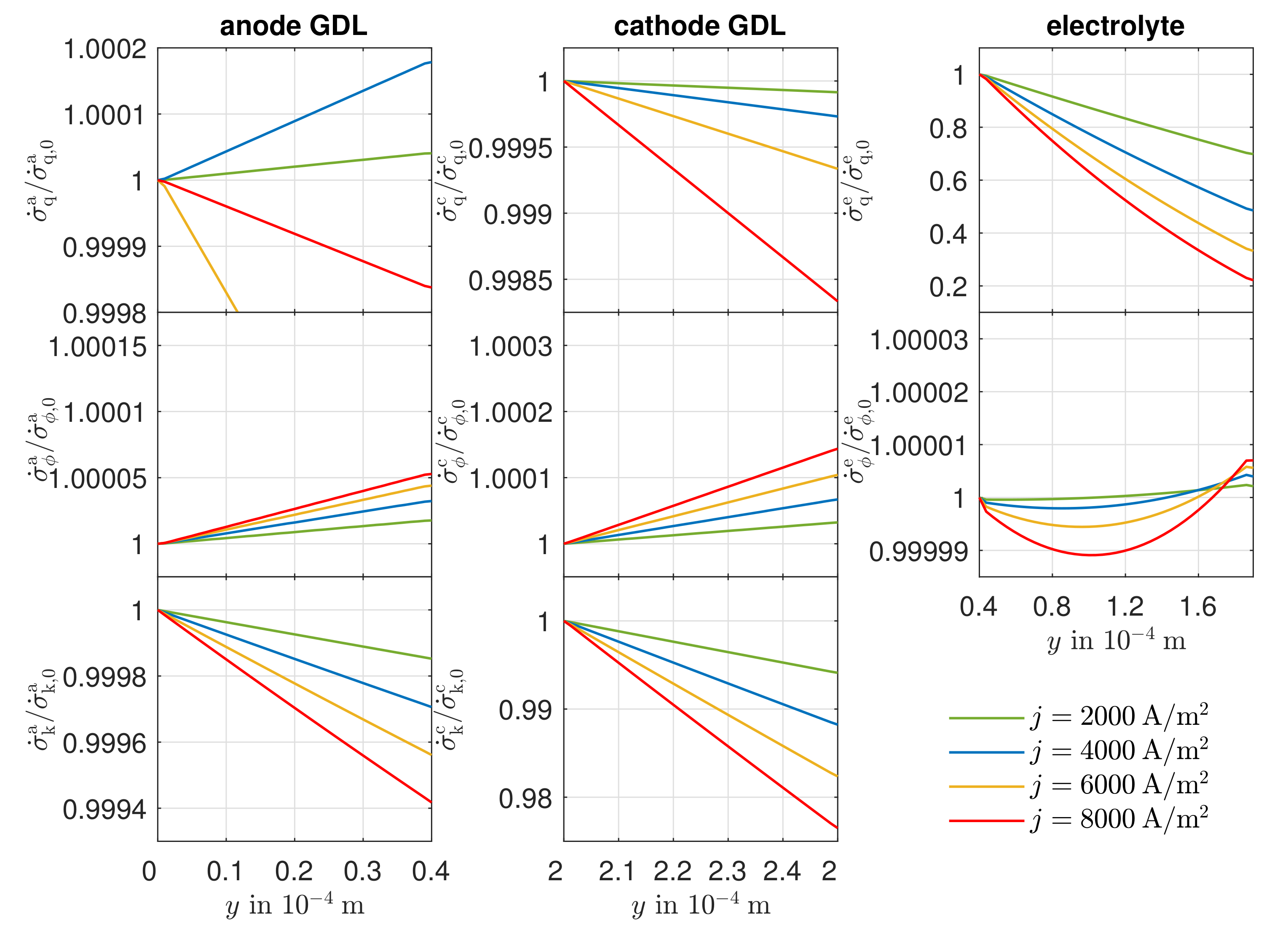
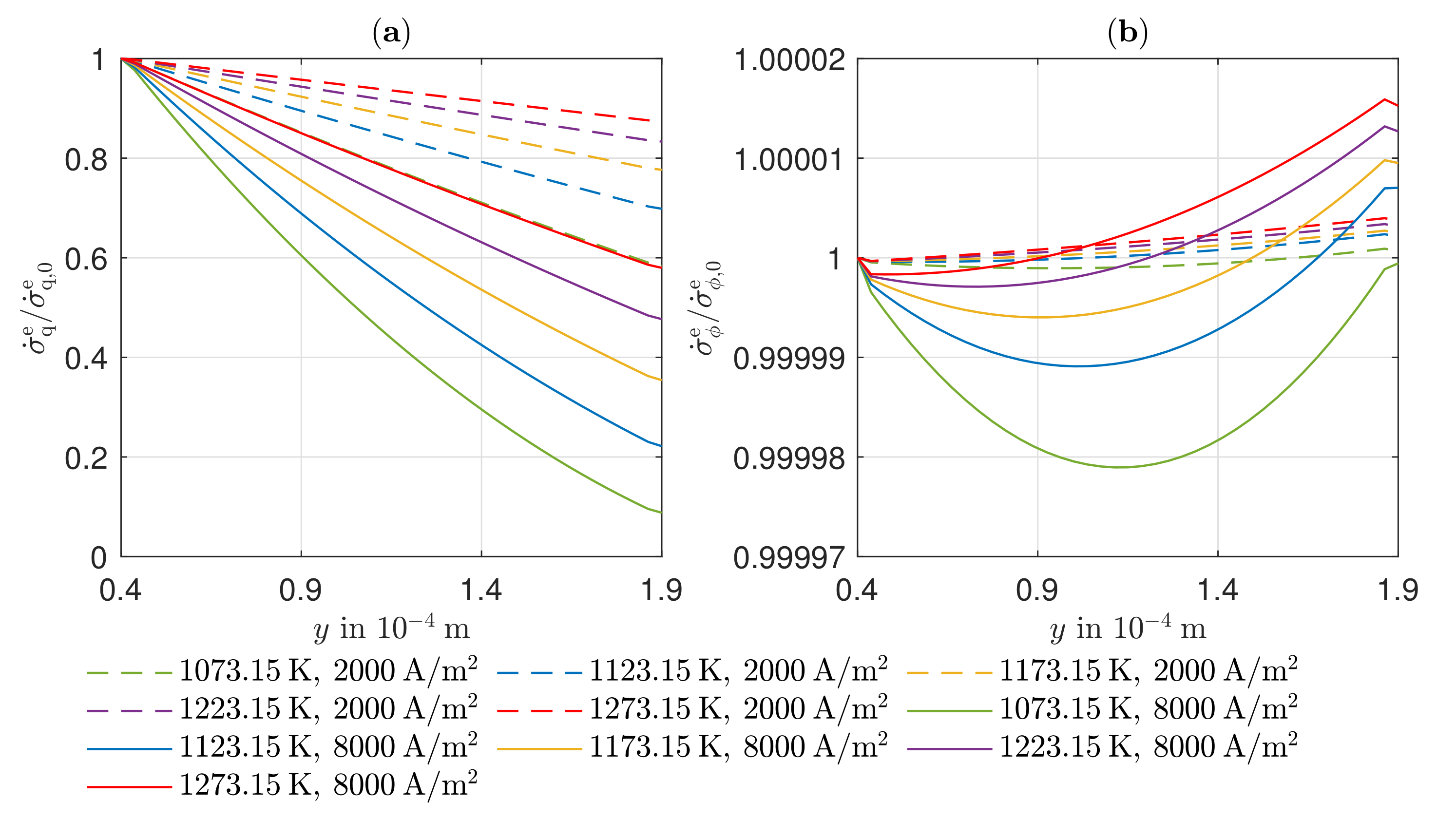
3.4. Entropy Production Rate
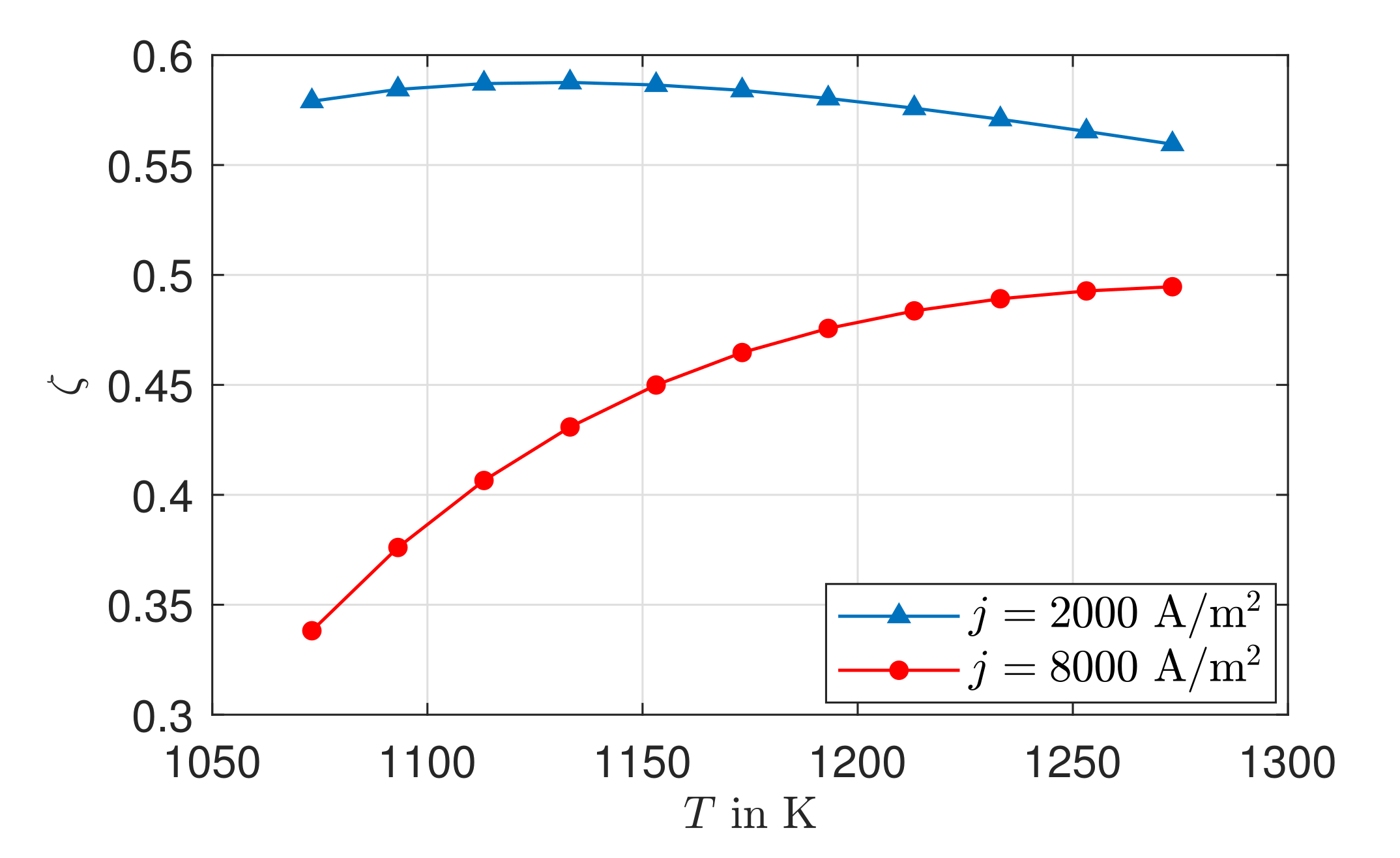
3.5. Exergy Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DGM | Dusty-Gas model |
| GDL | Gas diffusion layer |
| HOR | Hydrogen oxidation reaction |
| NET | Non-equilibrium thermodynamics |
| ORR | Oxygen reduction reaction |
| PEMFC | Proton exchange membrane fuel cell |
| SOFC | Solid oxide fuel cell |
| SOEC | Solid oxide electrolyzer cell |
References
- Kurzweil, P. Brennstoffzellentechnik: Grundlagen, Komponenten, Systeme, Anwendungen, 2nd ed.; Vieweg + Teubner: Wiesbaden, Germany, 2013. [Google Scholar]
- Andersson, M.; Yuan, J.; Sunden, B. Three-Dimensional Design Optimization of an Anode-Supported SOFC Using FEM. J. Electrochem. Soc. 2013, 57, 2485–2494. [Google Scholar] [CrossRef] [Green Version]
- Mauro, A.; Arpino, F.; Massarotti, N. Three-dimensional simulation of heat and mass transport phenomena in planar SOFCs. Int. J. Hydrog. Energy 2011, 36, 10288–10301. [Google Scholar] [CrossRef]
- Yakabe, H.; Ogiwara, T.; Hishinuma, M.; Yasuda, I. 3-D model calculation for planar SOFC. J. Power Sources 2001, 102, 144–154. [Google Scholar] [CrossRef]
- Peksen, M.; Al-Masri, A.; Peters, R.; Blum, L.; Stolten, D. Recent Developments of 3D Coupled Multiphysics SOFC Modelling At Forschungszentrum Julich. J. Electrochem. Soc. 2013, 57, 2537–2541. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Dang, Z. Numerical investigation of coupled mass transport and electrochemical reactions in porous SOFC anode microstructure. Int. J. Heat Mass Transf. 2017, 109, 1252–1260. [Google Scholar] [CrossRef] [Green Version]
- Niu, Y.; Lv, W.; Chen, D.; Han, J.; He, W. A model study on correlation between microstructure-gas diffusion and Cr deposition in porous LSM/YSZ cathodes of solid oxide fuel cells. Int. J. Hydrog. Energy 2019, 44, 18319–18329. [Google Scholar] [CrossRef]
- Joos, J. Microstructural Characterisation, Modelling and Simulation of Solid Oxide Fuel Cell Cathodes. Ph.D. Thesis, Karlsruher Institut für Technologie, Karlsruhe, Germany, 2015. [Google Scholar] [CrossRef]
- Zeng, Z.; Qian, Y.; Zhang, Y.; Hao, C.; Dan, D.; Zhuge, W. A review of heat transfer and thermal management methods for temperature gradient reduction in solid oxide fuel cell (SOFC) stacks. Appl. Energy 2020, 280, 115899. [Google Scholar] [CrossRef]
- Aguiar, P.; Adjiman, C.S.; Brandon, N.P. Anode-supported intermediate-temperature direct internal reforming solid oxide fuel cell. J. Power Sources 2005, 147, 136–147. [Google Scholar] [CrossRef]
- Sauermoser, M.; Kjelstrup, S.; Pollet, B.G. The Impact of Peltier and Dufour Coefficients on Heat Fluxes and Temperature Profiles in the Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2020, 167, 144503. [Google Scholar] [CrossRef]
- Huerta, G.V.; Flasbart, V.; Marquardt, T.; Radici, P.; Kabelac, S. Impact of multi-causal transport mechanisms in an electrolyte supported planar SOFC with (ZrO2)x-1(Y2O3)x electrolyte. Entropy 2018, 20, 469. [Google Scholar] [CrossRef] [Green Version]
- Ratkje, S.K.; Førland, K.S. The Transported Entropy of Oxygen Ion in Yttria–Stabilized Zirconia. J. Electrochem. Soc. 1991, 138, 2374–2376. [Google Scholar] [CrossRef]
- Ratkje, S.K.; Tomii, Y. Transported Entropy in Zirconia with 3 to 12 Mole Percent Yttria. J. Electrochem. Soc. 1993, 140, 59–66. [Google Scholar] [CrossRef]
- Costamagna, P.; Selimovic, A.; Del Borghi, M.; Agnew, G. Electrochemical model of the integrated planar solid oxide fuel cell (IP-SOFC). Chem. Eng. J. 2004, 102, 61–69. [Google Scholar] [CrossRef]
- Suwanwarangkul, R.; Croiset, E.; Fowler, M.W.; Douglas, P.L.; Entchev, E.; Douglas, M.A. Performance comparison of Fick’s, dusty-gas and Stefan–Maxwell models to predict the concentration overpotential of a SOFC anode. J. Power Sources 2003, 122, 9–18. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Bedeaux, D. Jumps in electric potential and in temperature at the electrode surfaces of the solid oxide fuel cell. Phys. A Stat. Mech. Its Appl. 1997, 244, 213–226. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Bedeaux, D.; Johannessen, E.; Gross, J. Non-Equilibrium Thermodynamics for Engineers; World Scientific: Singapore, 2010. [Google Scholar]
- Höpfner, A. Irreversible Thermodynamik für Chemiker; Sammlung Göschen, Walter de Gruyter: Berlin/Heidelberg, Germany, 1977; Volume 2611. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D. Non-Equilibrium Thermodynamics of Heterogeneous Systems; Series on Advances in Statistical Mechanics; World Scientific: Hackensack, NJ, USA, 2008; Volume 16. [Google Scholar]
- Kabelac, S.; Siemer, M.; Ahrendts, J. Thermodynamische Stoffdaten für Biogase. Forschung im Ingenieurwesen 2005, 70, 46–55. [Google Scholar] [CrossRef]
- Hajimolana, S.A.; Hussain, M.A.; Daud, W.A.W.; Soroush, M.; Shamiri, A. Mathematical modeling of solid oxide fuel cells: A review. Renew. Sustain. Energy Rev. 2011, 15, 1893–1917. [Google Scholar] [CrossRef]
- Gunnarshaug, A.F.; Kjelstrup, S.; Bedeaux, D. The heat of transfer and the Peltier coefficient of electrolytes. Chem. Phys. Lett. X 2020, 5, 100040. [Google Scholar] [CrossRef]
- Moore, J.P.; Graves, R.S. Absolute Seebeck coefficient of platinum from 80 to 340 K and the thermal and electrical conductivities of lead from 80 to 400 K. J. Appl. Phys. 1973, 44, 1174–1178. [Google Scholar] [CrossRef]
- Abadlia, L.; Gasser, F.; Khalouk, K.; Mayoufi, M.; Gasser, J.G. New experimental methodology, setup and LabView program for accurate absolute thermoelectric power and electrical resistivity measurements between 25 and 1600 K: Application to pure copper, platinum, tungsten, and nickel at very high temperatures. Rev. Sci. Instrum. 2014, 85, 095121. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. Investigating the validity of the Bosanquet formula for estimation of diffusivities in mesopores. Chem. Eng. Sci. 2012, 69, 684–688. [Google Scholar] [CrossRef]
- Krishna, R.; Wesselingh, J.A. The Maxwell-Stefan approach to mass transfer. Chem. Eng. Sci. 1997, 52, 861–911. [Google Scholar] [CrossRef]
- Todd, B.; Young, J.B. Thermodynamic and transport properties of gases for use in solid oxide fuel cell modelling. J. Power Sources 2002, 110, 186–200. [Google Scholar] [CrossRef]
- VDI-Wärmeatlas: Fachlicher Träger VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen, 12th ed.; Stephan, P.; Kabelac, S.; Kind, M.; Mewes, D.; Schaber, K.; Wetzel, T. (Eds.) Springer Reference Technik VDI Springer Reference; Springer Vieweg: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Siemer, M. Lokale Entropieproduktionsratenin der Polymerelektrolyt-Membran-Brennstoffzelle; Helmut-Schmidt-Universität, Universität der Bundeswehr Hamburg: Hamburg, Germany, 2007. [Google Scholar]
- Mason, E.A.; Malinauskas, A.P. Gas Transport in Porous Media: The Dusty-Gas model; Chemical Engineering Monographs Book Series; Elsevier: Amsterdam, The Netherlands; New York, NY, USA, 1983; Volume 17. [Google Scholar]
- Wilke, C.R. A Viscosity Equation for Gas Mixtures. J. Chem. Phys. 1950, 18, 517–519. [Google Scholar] [CrossRef]
- Văsaru, G. Thermal Diffusion in Isotopic Gaseous Mixtures. Fortschritte der Physik 1967, 15, 1–111. [Google Scholar] [CrossRef]
- Davarzani, H.; Marcoux, M.; Costeseque, P.; Quintard, M. Experimental measurement of the effective diffusion and thermodiffusion coefficients for binary gas mixture in porous media. Chem. Eng. Sci. 2010, 65, 5092–5104. [Google Scholar] [CrossRef]
- Klein, M.; Smith, F.J. Tables of Collision Integrals for the (m,6) Potential Function for 10 Values of m. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1968, 72A, 359–423. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Saxena, S.C. On the Two Schemes of Approximating the Transport Coefficients (Chapman–Cowling and Kihara). J. Phys. Soc. Jpn. 1956, 11, 367–369. [Google Scholar] [CrossRef]
- Kihara, T. The Chapman-Enskog and Kihara approximations for isotopic thermal diffusion in gases. J. Stat. Phys. 1975, 13, 137–143. [Google Scholar] [CrossRef]
- Yonekura, T.; Tachikawa, Y.; Yoshizumi, T.; Shiratori, Y.; Ito, K.; Sasaki, K. Exchange Current Density of Solid Oxide Fuel Cell Electrodes. ECS Trans. 2011, 35, 1007–1014. [Google Scholar] [CrossRef]
- Guggenheim, E.A. The Conceptions of Electrical Potential Difference between Two Phases and the Individual Activities of Ions. J. Phys. Chem. 1929, 33, 842–849. [Google Scholar] [CrossRef]
- Radici, P.; Valadez Huerta, G.; Geesmann, N.; Kabelac, S. A novel method to determine the transport coefficients of an YSZ electrolyte based on impedance spectroscopy. Solid State Ionics 2021, 363, 115591. [Google Scholar] [CrossRef]
- Baehr, H.D.; Kabelac, S. Thermodynamik; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Rivero, R.; Garfias, M. Standard chemical exergy of elements updated. Energy 2006, 31, 3310–3326. [Google Scholar] [CrossRef]
- KERAFOL® - Keramische Folien GmbH & Co. KG: KeraCell III: Electrolyte Supported Cells: Data Sheet. 2014. Available online: https://www.kerafol.com/sofc/downloads-datenblaetter (accessed on 1 January 2022).
- Schlichting, K.W.; Padture, N.P.; Klemens, P.G. Thermal conductivity of dense and porous yttria-stabilized zirconia. J. Mater. Sci. 2001, 36, 3003–3010. [Google Scholar] [CrossRef]
- Sasaki, K.; Terai, T.; Suzuki, A.; Akasaka, N. Effect of the Y2O3 Concentration in YSZ on the Thermophysical Property as a Thermal Shielding Material. Int. J. Appl. Ceram. Technol. 2010, 4, 518–527. [Google Scholar] [CrossRef]
- Radovic, M.; Lara-Curzio, E.; Trejo, R.M.; Wang, H.; Porter, W.D. Thermophysical Properties of YSZ and Ni-YSZ as a Function of Temperature and Porosity. In Advances in Solid Oxide Fuel Cells II: Ceramic Engineering and Science Proceedings, Volume 27, Issue 4; Bansal, N.P., Wereszczak, A., Lara-Curzio, E., Eds.; Ceramic Engineering and Science Proceedings; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2006; pp. 79–85. [Google Scholar] [CrossRef]
- Gibson, I.R.; Irvine, J.T.S. Study of the order–disorder transition in yttria-stabilised zirconia by neutron diffraction. J. Mater. Chem. 1996, 6, 895–898. [Google Scholar] [CrossRef]
- Antunes, F.C.; Goulart, C.A.; Andreeta, M.R.; de Souza, D.P. YSZ/Al2O3 multilayer thick films deposited by spin coating using ceramic suspensions on Al2O3 polycrystalline substrate. Mater. Sci. Eng. B 2018, 228, 60–66. [Google Scholar] [CrossRef]
- Artemov, V.G.; Kuritsyna, I.E.; Lebedev, S.P.; Komandin, G.A.; Kapralov, P.O.; Spektor, I.E.; Kharton, V.V.; Bredikhin, S.I.; Volkov, A.A. Analysis of electric properties of ZrO2-Y2O3 single crystals using teraherz IR and impedance spectroscopy techniques. Russ. J. Electrochem. 2014, 50, 690–693. [Google Scholar] [CrossRef]
- Brus, G.; Miyawaki, K.; Iwai, H.; Saito, M.; Yoshida, H. Tortuosity of an SOFC anode estimated from saturation currents and a mass transport model in comparison with a real micro-structure. Solid State Ionics 2014, 265, 13–21. [Google Scholar] [CrossRef]
- Zouhri, K.; Shinneeb, M.; Chikhalsouk, M.; Cress, J. Solid oxide fuel cell cathode diffusion polarization: Materials and exergy study. Energy Convers. Manag. 2021, 231, 113865. [Google Scholar] [CrossRef]
- Zouhri, K.; Lee, S.Y. Exergy study on the effect of material parameters and operating conditions on the anode diffusion polarization of the SOFC. Int. J. Energy Environ. Eng. 2016, 7, 211–224. [Google Scholar] [CrossRef] [Green Version]
- Midilli, A.; Akbulut, U.; Dincer, I. A parametric study on exergetic performance of a YSZ electrolyte supported SOFC stack. Int. J. Exergy 2017, 24, 173. [Google Scholar] [CrossRef]

| Parameter | Value | Reference |
|---|---|---|
| Dimensions | m | [44] |
| m | [44] | |
| m | [44] | |
| Thermal conductivity | W/m·K | [17] |
| W/m·K | [17] | |
| W/m·K | [45] | |
| Entropy of the electrons | J/K·mol | [24] |
| J/K·mol | [25] | |
| Entropy of the ions | calculated | [14] |
| Peltier coefficient | calculated with Equation (23) | |
| calculated with Equation (24) | ||
| calculated with Equation (66) | ||
| Ionic conductivity | Wm·K | [17] |
| Pre-exponential factors | mK | [22] |
| for electrical resistances | mK | [22] |
| Activation energy | · R K | [22] |
| · R K | [22] | |
| J/mol | [12] | |
| J/mol | [12] | |
| Pre-exponential factors | A/m | [12] |
| for exchange current densities | A/m | [12] |
| Penetration coefficients | [15] | |
| [15] |
| Parameter | Value | Reference |
|---|---|---|
| Diffusion volume | [29] | |
| Lennard-Jones | Å, | [36] |
| parameter | Å, | |
| Å, | ||
| Å, | ||
| Pore diameter for GDL | m | [1] |
| Porosity for GDL | [1] | |
| [51] | ||
| Tortuosity for GDL | [52] |
| Diffusion coefficients | Value |
|---|---|
| m/s | |
| m/s | |
| m/s | |
| m/s | |
| m/s | |
| m/s | |
| m/s | |
| m/s | |
| m/s | |
| m/s | |
| m/Ks | |
| m/Ks | |
| m/Ks | |
| m/Ks |
| Anode GDL | Electrolyte | Cathode GDL | |
|---|---|---|---|
| j in | in | in | in |
| 2000 | |||
| 8000 |
| j in | T in | in | in |
|---|---|---|---|
| 2000 | 1073.15 | 0.19 | 933.10 |
| 2000 | 1273.15 | 0.16 | 233.78 |
| 8000 | 1073.15 | 5.70 | 14,928.61 |
| 8000 | 1273.15 | 3.06 | 3740.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gedik, A.; Lubos, N.; Kabelac, S. Coupled Transport Effects in Solid Oxide Fuel Cell Modeling. Entropy 2022, 24, 224. https://doi.org/10.3390/e24020224
Gedik A, Lubos N, Kabelac S. Coupled Transport Effects in Solid Oxide Fuel Cell Modeling. Entropy. 2022; 24(2):224. https://doi.org/10.3390/e24020224
Chicago/Turabian StyleGedik, Aydan, Nico Lubos, and Stephan Kabelac. 2022. "Coupled Transport Effects in Solid Oxide Fuel Cell Modeling" Entropy 24, no. 2: 224. https://doi.org/10.3390/e24020224
APA StyleGedik, A., Lubos, N., & Kabelac, S. (2022). Coupled Transport Effects in Solid Oxide Fuel Cell Modeling. Entropy, 24(2), 224. https://doi.org/10.3390/e24020224







