Spectral Properties of Stochastic Processes Possessing Finite Propagation Velocity
Abstract
1. Introduction
2. One-Velocity GPK Processes
3. Lévy Walks
3.1. Gamma-Distributed Transition Times
3.2. Superdiffusive Lévy Walk
3.3. Power-Law Distributed Transition Times
4. GPK Process with a Continuum of States
4.1. Spectral Properties
5. Quantum Mechanical Extension
Spectral Properties and Dispersion Relations
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SEO | Statistical evolution operator |
| GPK | Generalized Poisson–Kac |
| LW | Lévy Walk |
References
- Klages, R.; Just, W.; Jarzynski, C. Nonequilibrium Statistical Physics of Small Systems: Fluctuation Relations and Beyond; Wiley-VCH: Berlin, Germany, 2013. [Google Scholar]
- Bechinger, C.; di Leonardo, R.; Löwen, H.; Reichhardt, C.; Volpe, G.; Volpe, G. Active particles in complex and crowded environments. Rev. Mod. Phys. 2016, 88, 045006. [Google Scholar] [CrossRef]
- Marchetti, M.C.; Joanny, J.F.; Ramaswamy, S.; Liverpool, T.B.; Prost, J.; Rao, M.; Simha, R.A. Hydrodynamics of soft active matter. Rev. Mod. Phys. 2013, 85, 1143. [Google Scholar] [CrossRef]
- Klages, R.; Radons, G.; Sokolov, I.M. (Eds.) Anomalous Transport: Foundations and Applications; Wiley-VCH: Berlin, Germany, 2008. [Google Scholar]
- Krapivsky, P.L.; Redner, S.; Ben-Naim, E. A Kinetic View of Statistical Physics; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Ebeling, W.; Sokolov, I.M. Statistical Thermodynamics and Stochastic Theory of Nonequilibrium Systems; World Scientific: Singapore, 2005. [Google Scholar]
- Viswanathan, G.M.; da Luz, M.G.E.; Raposo, E.P.; Stanley, H.E. The Physics of Foraging; Cambridge University Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Müller, I. Speeds of propagation in classical and relativistic extended thermodynamics. Living Rev. Relativ. 1999, 2, 1–32. [Google Scholar] [CrossRef] [PubMed]
- Giona, M. Relativistic analysis of stochastic kinematics. Phys. Rev. E 2017, 96, 042133. [Google Scholar] [CrossRef] [PubMed]
- Wolschin, G. Diffusion in relativistic systems. Prog. Particle Nucl. Phys. 2007, 59, 374–382. [Google Scholar] [CrossRef]
- Muniz, C.R.; Cunha, M.S.; Filho, R.N.C.; Berezza, V.B. Some remarks on relativistic diffusion and the spectral dimension criterion. Phys. Rev. D 2015, 91, 027501. [Google Scholar] [CrossRef]
- Müller, I.; Ruggeri, T. Extended Thermodynamics; Springer: New York, NY, USA, 1993. [Google Scholar]
- Ferreira, J.A.; Grassi, M.; Gudino, E.; de Oliveira, P. A new look to non-Fickian diffusion. Appl. Math. Model 2015, 39, 194–204. [Google Scholar] [CrossRef]
- Jou, D.; Cimmelli, V.A. Constitutive equations for heat conduction in nanosystems and nonequilibrium processes: An overview. Comm. Appl. Ind. Math. 2016, 7, 196–222. [Google Scholar] [CrossRef]
- Kac, M. A stochastic model related to the telegrapher’s equation. Rocky Mount. J. Math. 1974, 4, 497–509. [Google Scholar] [CrossRef]
- Pinsky, M.A. Lectures on Random Evolutions; World Scientific: Singapore, 1991. [Google Scholar]
- Kolesnik, A.D. A note on planar random motion at finite speed. J. Appl. Prob. 2007, 44, 838–842. [Google Scholar] [CrossRef]
- Giona, M.; Crescitelli, S.; Brasiello, A. Stochastic foundations of undulatory transport phenomena: Generalized Poisson–Kac processes—Part I basic theory. J. Phys. A 2017, 50, 335002. [Google Scholar] [CrossRef]
- Shlesinger, M.F.; Klafter, J.; Wong, Y.M. Random walks with infinite spatial and temporal moments. J. Stat. Phys. 1982, 3, 499–512. [Google Scholar] [CrossRef]
- Shlesinger, M.F.; Klafter, J.; West, B.J. Lévy walks with applications to turbulence and chaos. Physica A 1986, 140, 212–218. [Google Scholar] [CrossRef]
- Klafter, J.; Blumen, A.; Shlesinger, M.F. Stochastic pathway to anomalous diffusion. Phys. Rev. A 1987, 7, 3081–3085. [Google Scholar] [CrossRef] [PubMed]
- Zaburdaev, V.; Denisov, S.; Klafter, J. Lévy walks. Rev. Mod. Phys. 2015, 87, 483–530. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vazquez, J.; Lebon, G. Extended Irreversible Thermodynamics; Springer: Berlin, Germany, 2001. [Google Scholar]
- Hänggi, P.; Jung, P. Colored noise in dynamical systems. Adv. Chem. Phys. 1995, 39, 239–326. [Google Scholar]
- Weiss, G.H. Aspects and Applications of the Random Walk; North-Holland: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Horsthemke, W.; Lefever, R. Noise-Induced Transitions; Springer: Berlin, Germany, 1984. [Google Scholar]
- Bena, I. Dichotomous Markov noise: Exact results for out-of-equilibrium systems. Int. J. Mod, Phys. B 2006, 20, 2825–2888. [Google Scholar] [CrossRef]
- d’Onofrio, A. (Ed.) Bounded Noises in Physics, Biology and Engineering; Springer: New York, NY, USA, 2013. [Google Scholar]
- Fedotov, S. Single integrodifferential wave equation for a Lévy walk. Phys. Rev. E 2016, 93, 020101. [Google Scholar] [CrossRef]
- Fedotov, S.; Korabel, N. Emergence of Lévy walks in systems of interacting individuals. Phys. Rev. E 2017, 95, 030107. [Google Scholar] [CrossRef]
- Stage, H. Aging in mortal superdiffusive Lévy walkers. Phys. Rev. E 2017, 96, 062150. [Google Scholar] [CrossRef]
- Shkilev, V.P. Subordinated stochastic processes with aged operational time. Phys. Rev. E 2018, 97, 012102. [Google Scholar] [CrossRef] [PubMed]
- Giona, M.; D’Ovidio, M.; Cocco, M.; Cairoli, A.; Klages, R. Age representation of Lévy walks: Partial density waves, relaxation and first passage time statistics. J. Phys. A 2019, 52, 384001. [Google Scholar] [CrossRef]
- Giona, M.; Cairoli, A.; Klages, R. Extended Poisson-Kac theory: A unifying framework for stochastic processes with finite propagation velocity. arXiv 2020, arXiv:2009.13434. [Google Scholar]
- Oxenius, J. Kinetic Theory of Particles and Photons; Springer: Berlin, Germany, 1986. [Google Scholar]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin, Germany, 1995. [Google Scholar]
- Gaveau, B.; Jacobson, T.; Kac, M.; Schulman, L.S. Relativistic Extension of the Analogy between Quantum Mechanics and Brownian Motion. Phys. Rev. Lett. 1984, 53, 419–422. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. The Undivided Universe; Routledge: London, UK, 1993. [Google Scholar]
- Bohm, D. Wholeness and the Implicate Order; Routledge: London, UK, 1980. [Google Scholar]
- Kolesnik, A.D.; Ratanov, N. Telegraph Processes and Option Pricing; Springer: Berlin, Germany, 2013. [Google Scholar]
- Kolesnik, A.D. Markov Random Flights; Chapman & Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Giona, M.; Pucci, L. Hyperbolic heat/mass transport and stochastic modelling—Three simple problems. Math. Eng. 2019, 1, 224–251. [Google Scholar] [CrossRef]
- Politi, M.; Kaizoj, T.; Scalas, E. Full characterization of the fractional Poisson process. Europhys. Lett. 2011, 96, 20004. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Y.; Qiu, T. Fractional Processes and Fractional-Order Signal Processing: Techniques and Applications; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Martino Publ.: Mansfield Centre, CT, USA, 2014. [Google Scholar]
- Zaburdaev, V.; Fouxon, I.; Denisov, S.; Barkai, E. Superdiffusive Dispersals Impart the Geometry of Underlying Random Walks. Phys. Rev. Lett. 2016, 117, 270601. [Google Scholar] [CrossRef]
- Giona, M.; Brasiello, A.; Crescitelli, S. Stochastic foundations of undulatory transport phenomena: Generalized Poisson–Kac processes—Part III extensions and applications to kinetic theory and transport. J. Phys. A 2017, 50, 335004. [Google Scholar] [CrossRef]
- Giona, M.; Brasiello, A.; Crescitelli, S. Stochastic foundations of undulatory transport phenomena: Generalized Poisson–Kac processes—Part II Irreversibility, norms and entropies. J. Phys. A 2017, 50, 335003. [Google Scholar] [CrossRef]
- Nelson, E. Derivation of the Schrödinger equation from Newtonian mechanics. Phys. Rev. 1966, 150, 1079. [Google Scholar] [CrossRef]
- Nelson, E. Quantum Fluctuations; Princeton Univ. Press: Princeton, NJ, USA, 1985. [Google Scholar]
- Gudder, S.P. Stochastic Methods in Quantum Mechanics; Dover Publications Inc.: Mineola, NY, USA, 2005. [Google Scholar]
- Nagasawa, M. Schrödinger Equations and Diffusion Theory; Birkhäuser: Basel, Switzerland, 1993. [Google Scholar]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Inregrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Thaller, B. The Dirac Equation; Springer: Berlin, Germany, 1992. [Google Scholar]
- de Angelis, G.F.; Jona-Lasinio, G.; Serva, M.; Zanghi, N. Stochastic mechanics of a Dirac particle in two spacetime dimensions. J. Phys. A 1986, 19, 865–871. [Google Scholar] [CrossRef]
- McKeon, D.G.C.; Ord, G.N. Time Reversal in Stochastic Processes and the Dirac Equation. Phys. Rev. Lett. 1992, 69, 3–4. [Google Scholar] [CrossRef] [PubMed]
- Bialynicki-Birula, I. Weyl, Dirac, and Maxwell equations on a lattice as unitary cellular automata. Phys. Rev. D 1994, 49, 6920–6927. [Google Scholar] [CrossRef] [PubMed]
- Strauch, F.W. Relativistic quantum walks. Phys. Rev. A 2006, 73, 054302. [Google Scholar] [CrossRef]
- Balakrishnan, V.; Lakshmibala, S. On the connection between biased dichotomous diffusion and the one-dimensional Dirac equation. New J. Phys. 2005, 7, 11. [Google Scholar] [CrossRef]
- Mackey, M.C. Time’s Arrow—The Origins of Thermodynamic Behavior; Dover Publications Inc.: Mineola, NY, USA, 2003. [Google Scholar]
- Giona, M. Variational principles and Lagrangian functions for stochastic processes and their dissipative statistical descriptions. Physica A 2017, 473, 561–577. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Blumen, A.; Klafter, J. Linear response in complex systems: CTRW and the fractional Fokker–Planck equations. Physica A 2001, 302, 268–278. [Google Scholar] [CrossRef][Green Version]
- Allegrini, P.; Aquino, G.; Grigolini, P.; Palatella, L.; Rosa, A.; West, B.J. Correlation function and generalized master equation of arbitrary age. Phys. Rev. E 2005, 71, 066109. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Klafter, J. Field-Induced Dispersion in Subdiffusion. Phys. Rev. Lett. 2006, 97, 140602. [Google Scholar] [CrossRef]
- Aquino, G.; Grigolini, P.; West, B.J. Linear response and Fluctuation-Dissipation Theorem for non-Poissonian renewal processes. Europhys. Lett. 2007, 80, 10002. [Google Scholar] [CrossRef][Green Version]
- Aquino, G.; Bologna, M.; Grigolini, P.; West, B.J. Beyond the Death of Linear Response: 1/f Optimal Information Transport. Phys. Rev. Lett. 2010, 105, 040601. [Google Scholar] [CrossRef] [PubMed]
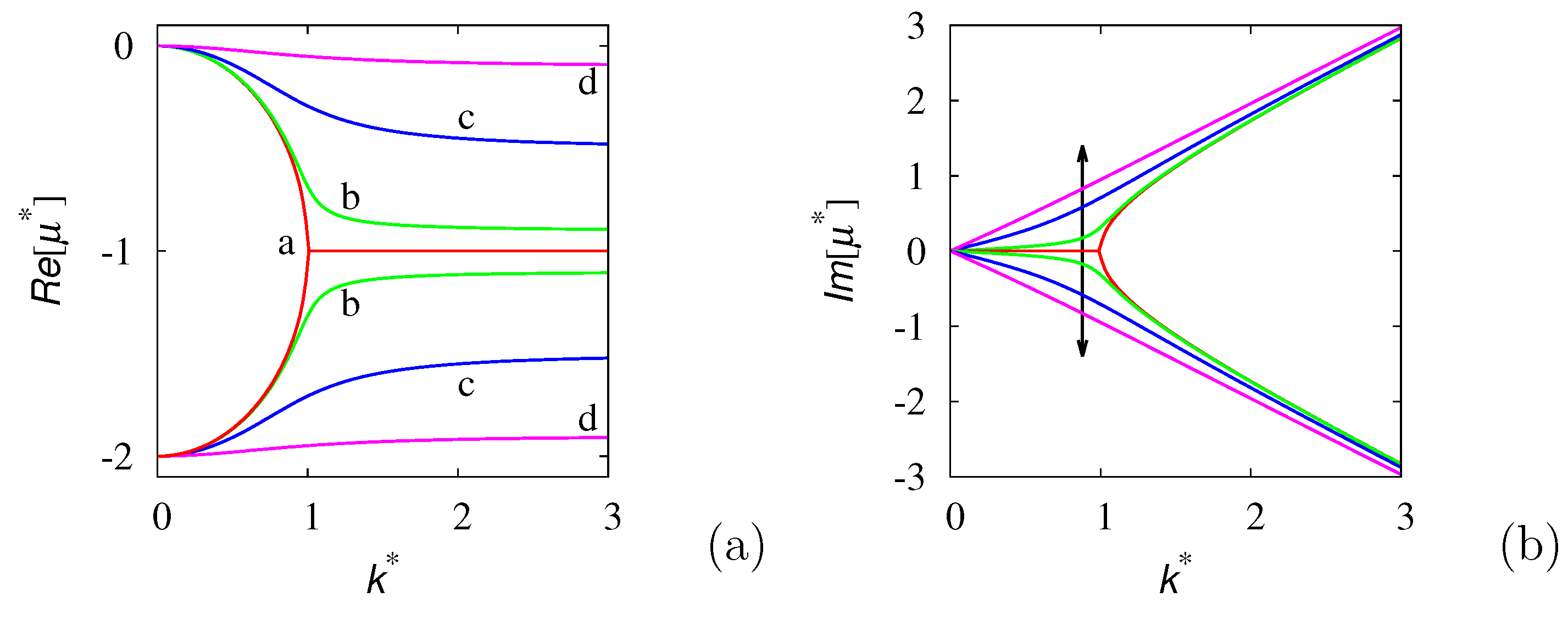
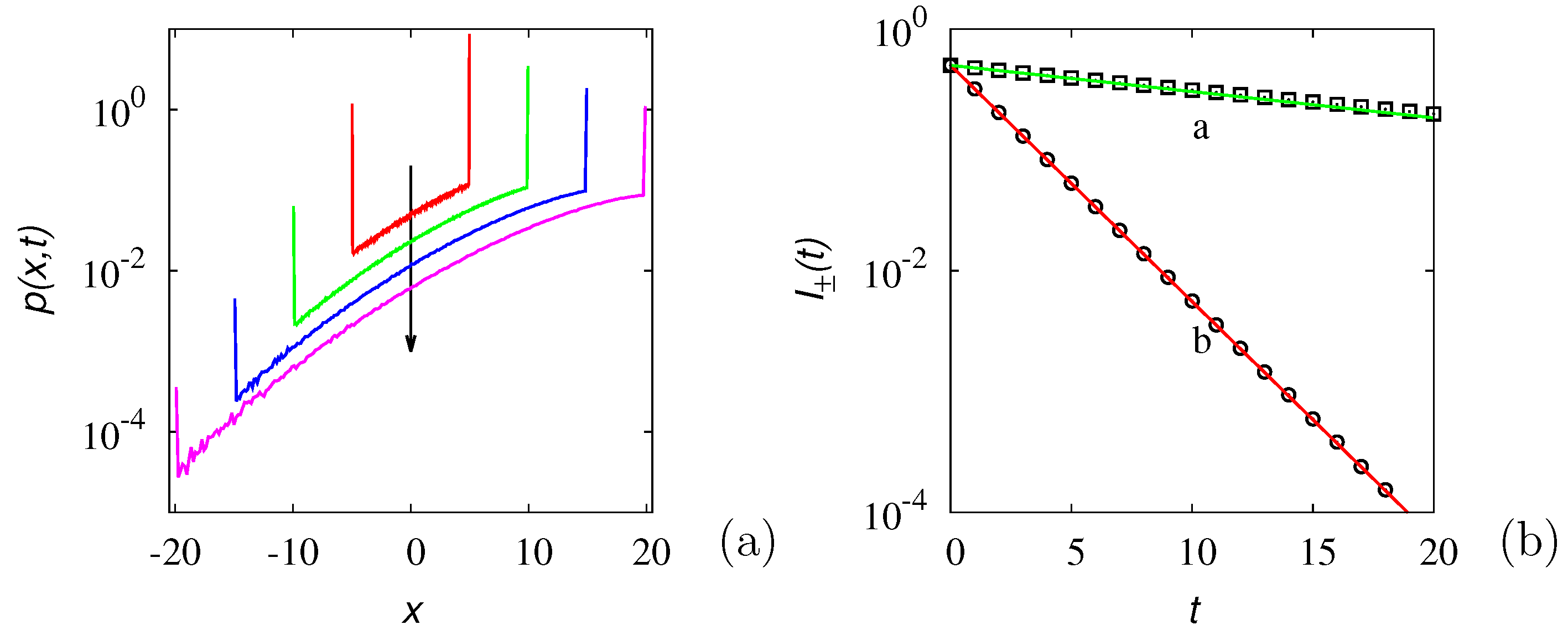


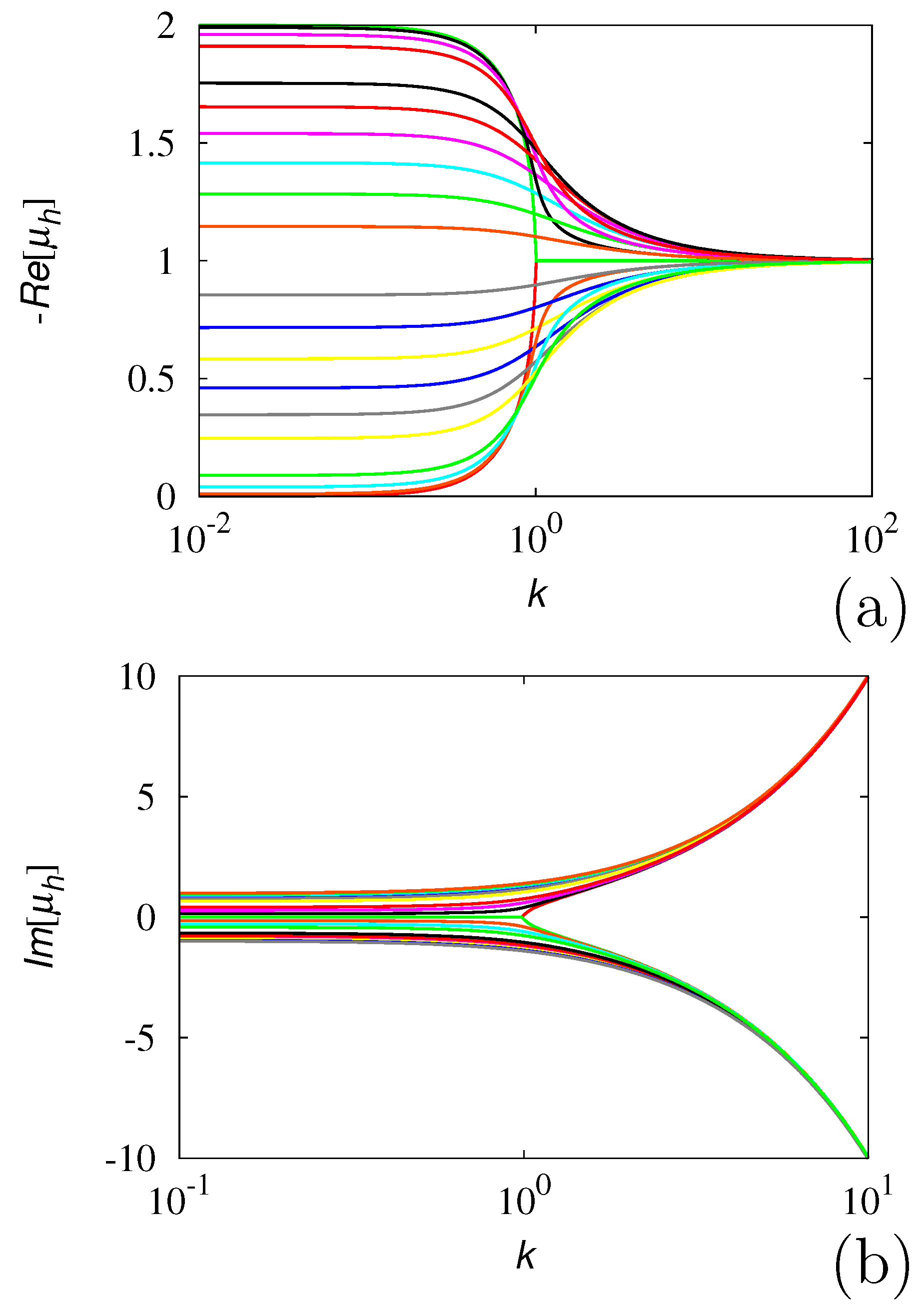
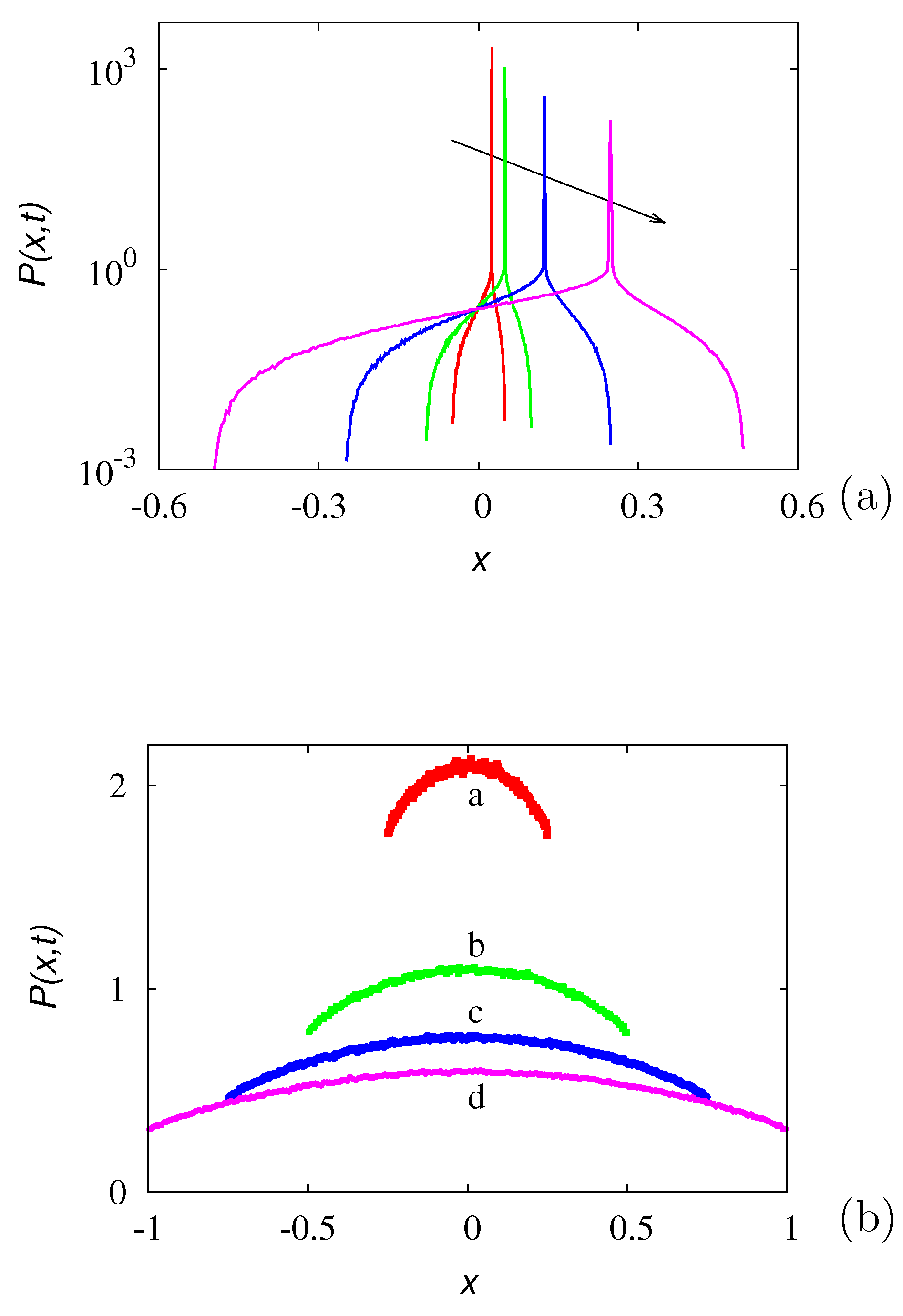
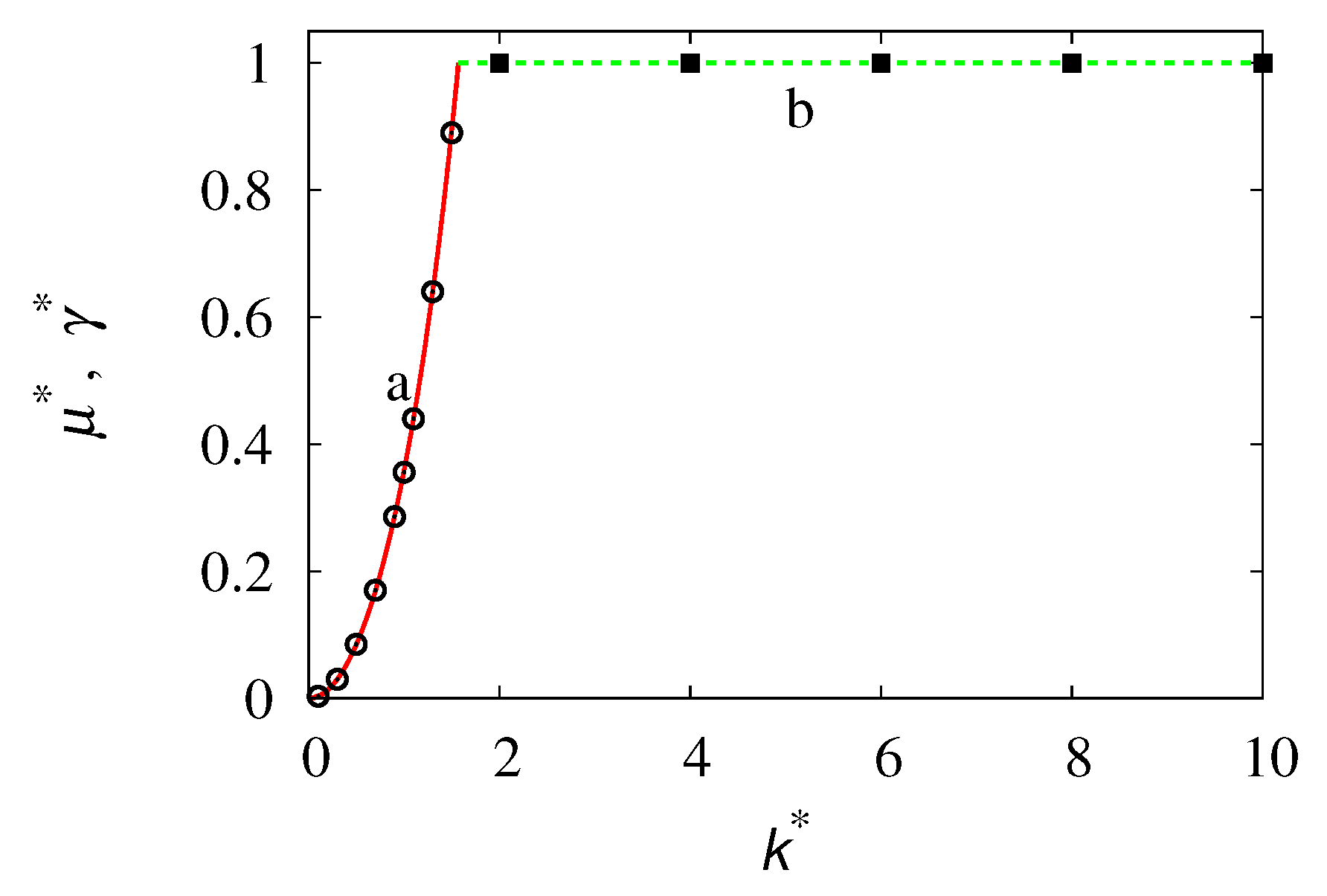


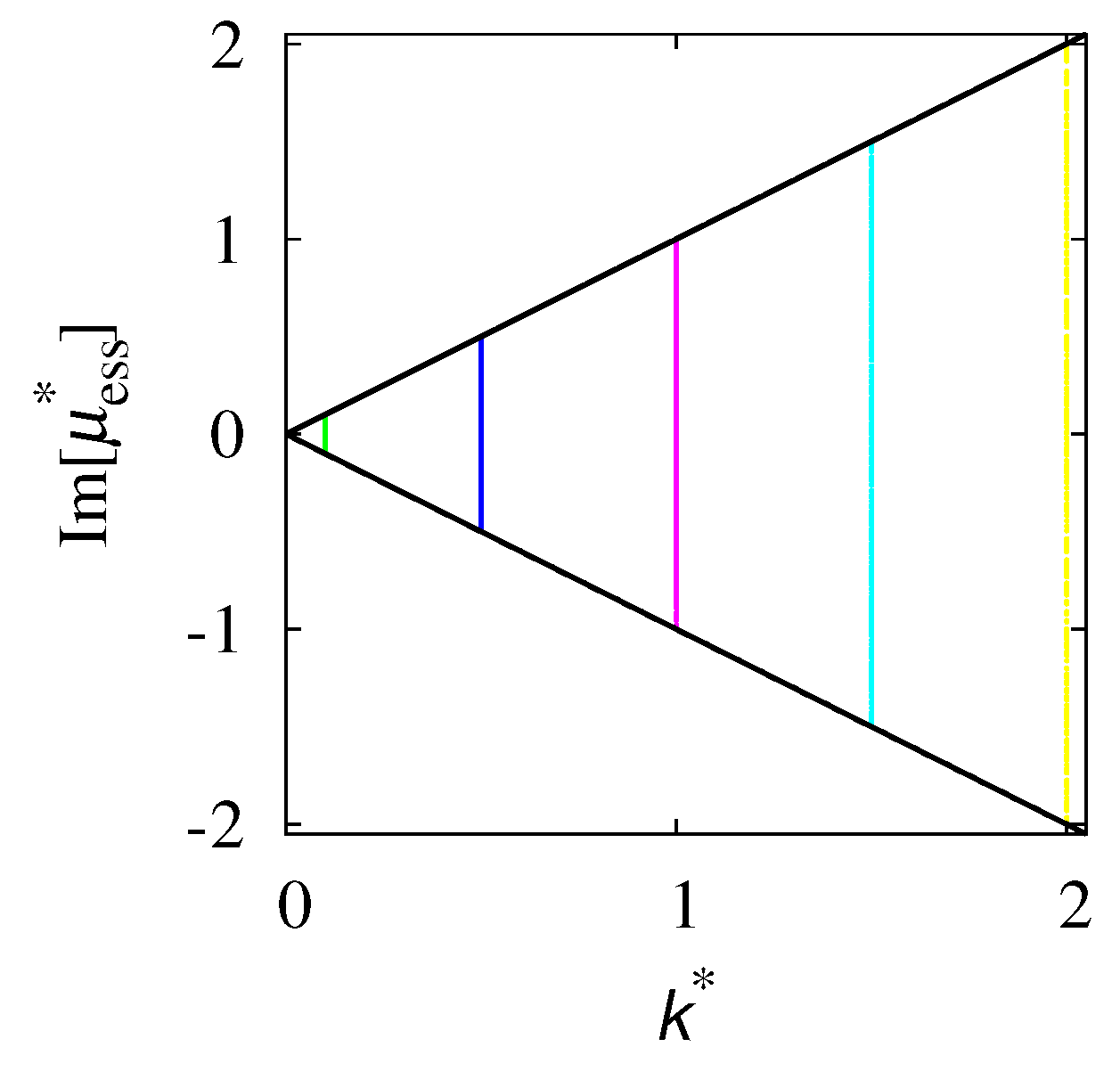
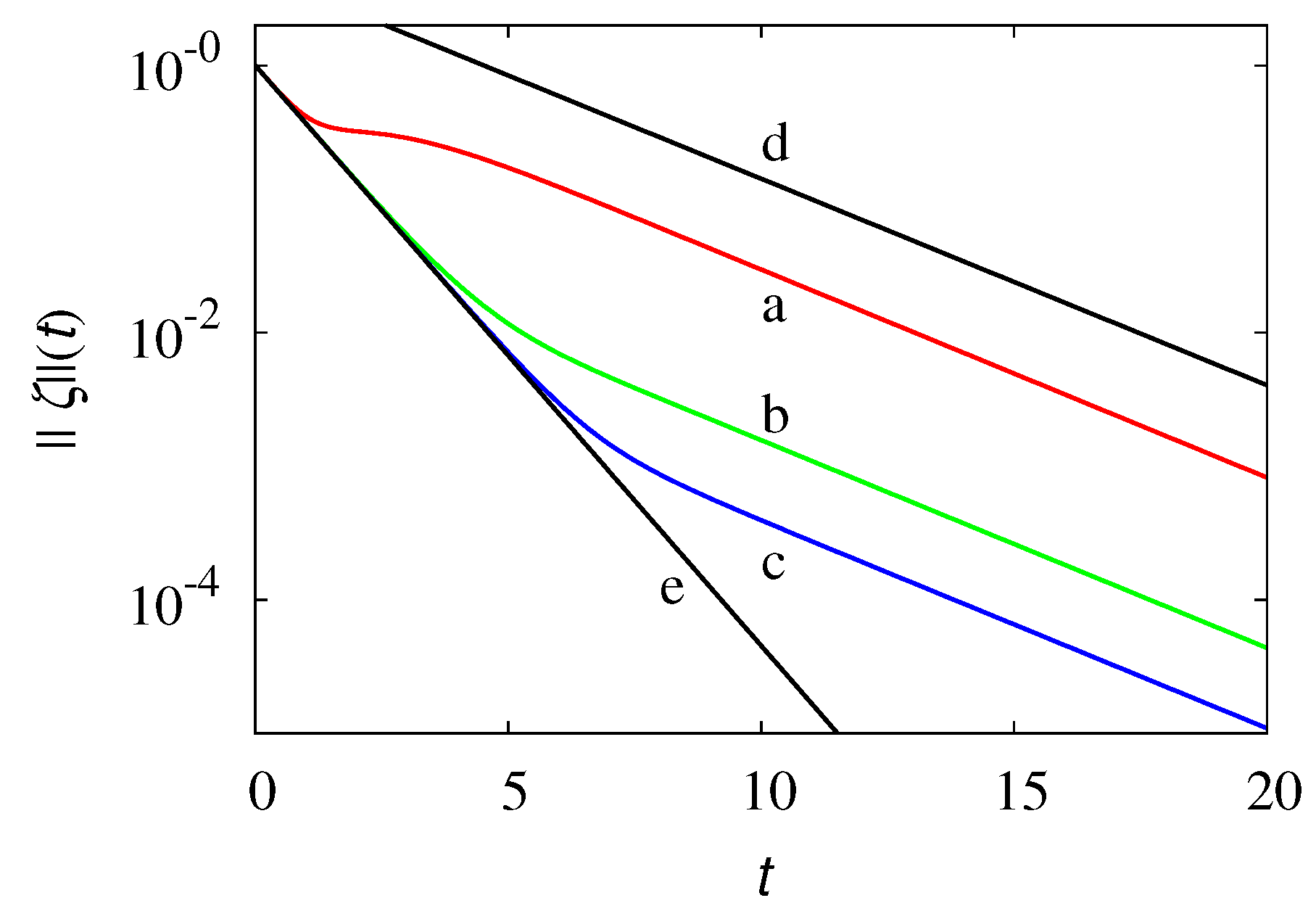

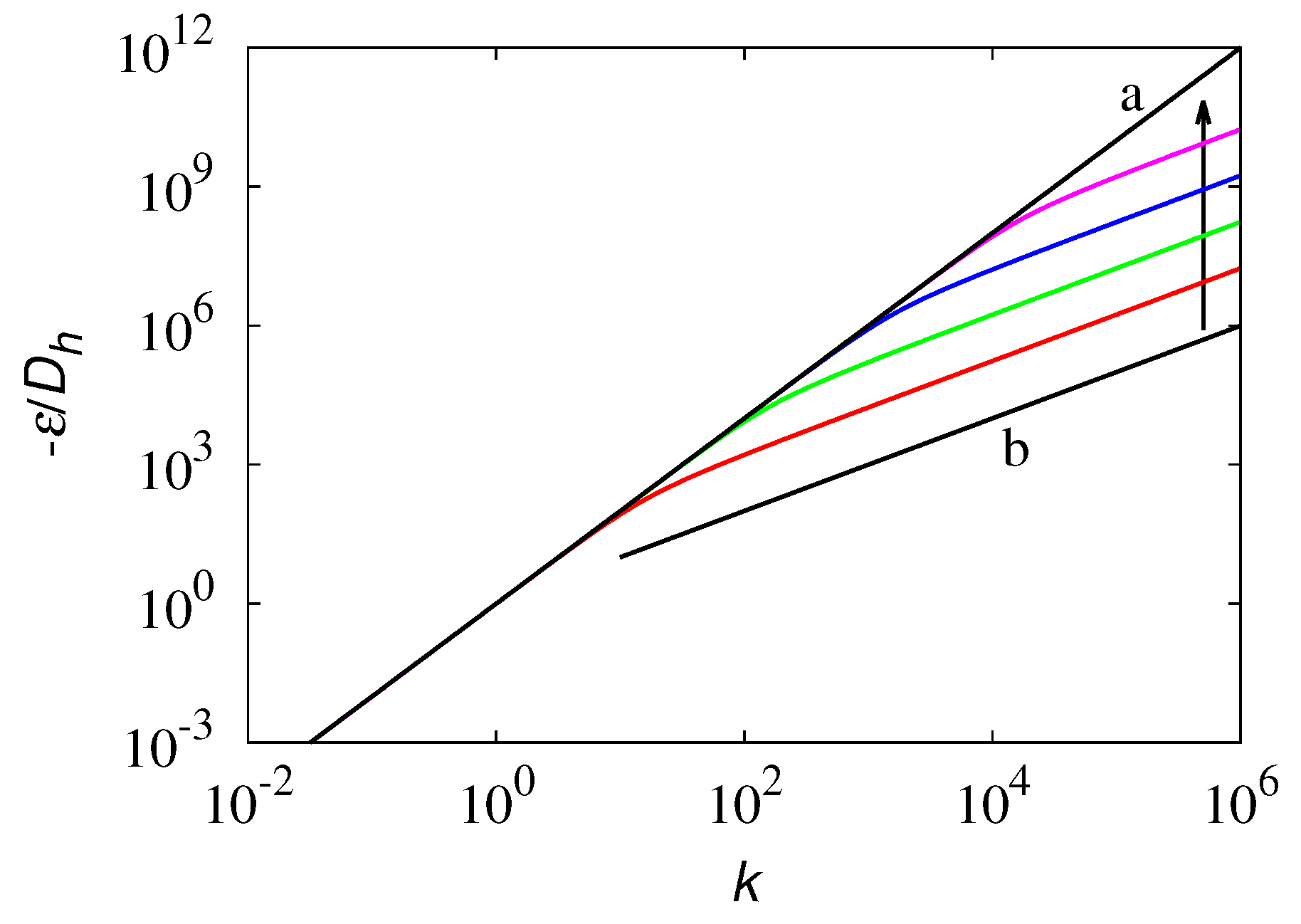
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giona, M.; Cairoli, A.; Cocco, D.; Klages, R. Spectral Properties of Stochastic Processes Possessing Finite Propagation Velocity. Entropy 2022, 24, 201. https://doi.org/10.3390/e24020201
Giona M, Cairoli A, Cocco D, Klages R. Spectral Properties of Stochastic Processes Possessing Finite Propagation Velocity. Entropy. 2022; 24(2):201. https://doi.org/10.3390/e24020201
Chicago/Turabian StyleGiona, Massimiliano, Andrea Cairoli, Davide Cocco, and Rainer Klages. 2022. "Spectral Properties of Stochastic Processes Possessing Finite Propagation Velocity" Entropy 24, no. 2: 201. https://doi.org/10.3390/e24020201
APA StyleGiona, M., Cairoli, A., Cocco, D., & Klages, R. (2022). Spectral Properties of Stochastic Processes Possessing Finite Propagation Velocity. Entropy, 24(2), 201. https://doi.org/10.3390/e24020201






