Efficient System for Delimitation of Benign and Malignant Breast Masses
Abstract
1. Introduction
- 1.
- A competent system capable of delimiting breast benign and malignant masses, which consists of a simple pipeline processing, with a denoising stage, as well as local and global clustering procedures.
- 2.
- A system with a reduced number of internal parameters, most of them required for the Intuitionistic Fuzzy stage. Specifically, they are transformation factor , fuzzifier factor , and the superpixels number K, which can be set to a specific value (see Section 2.2). It is an important advantage over all methods mentioned in the state-of-the-art review.
- 3.
- Superpixels are generated and processed in the Intuitionistic Fuzzy domain, which has an advantage compared to superpixels processed in the crisp domain (by SLIC), since a better adhesion to the edges can be guaranteed.
- 4.
- The DBSCAN is adjusted in order to cluster superpixels instead conventional pixels.
- 5.
- The system does not require processing special features, since it works only with the pixels’ intensity.
2. Materials and Methods
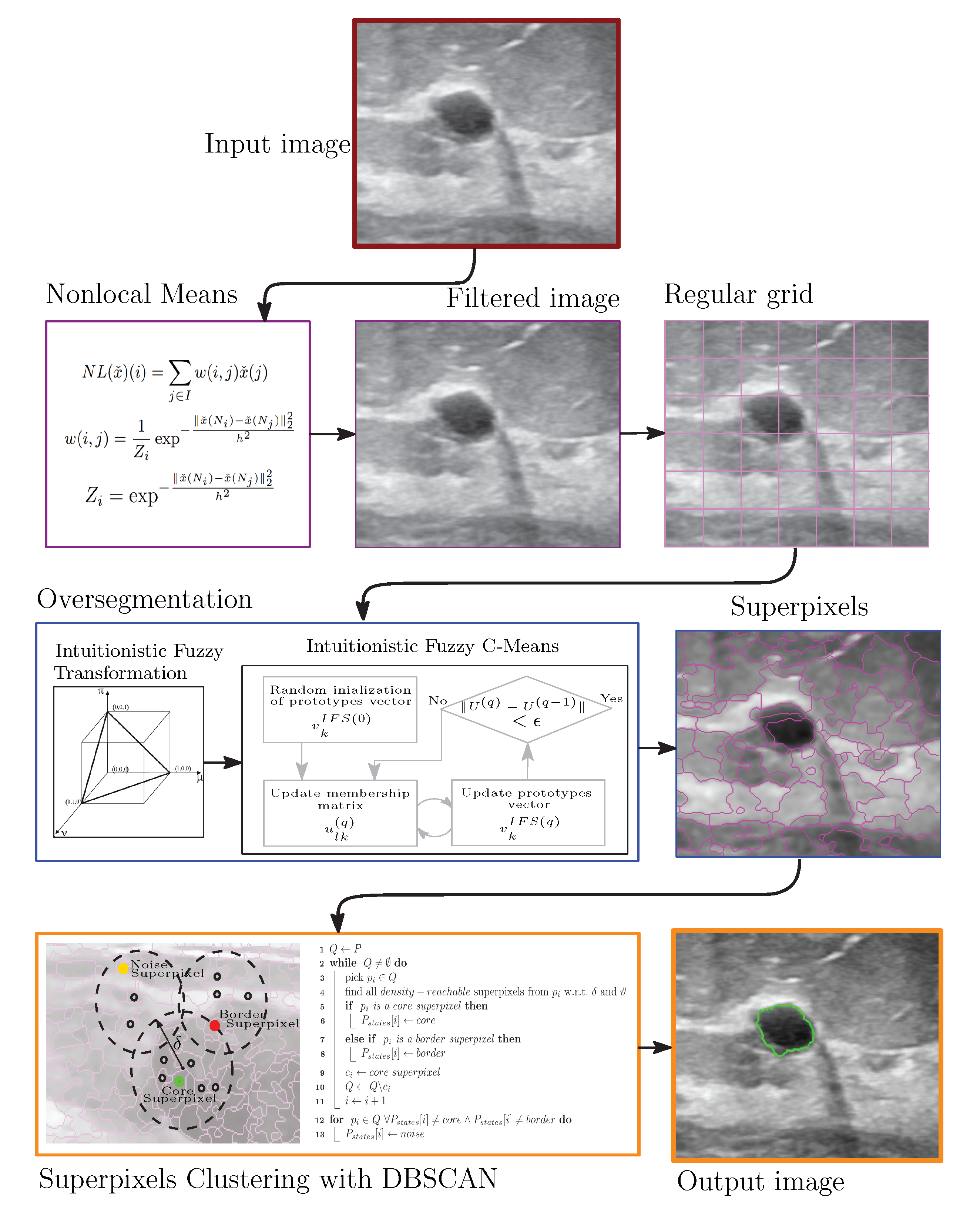
2.1. Ultrasound Image Denoising
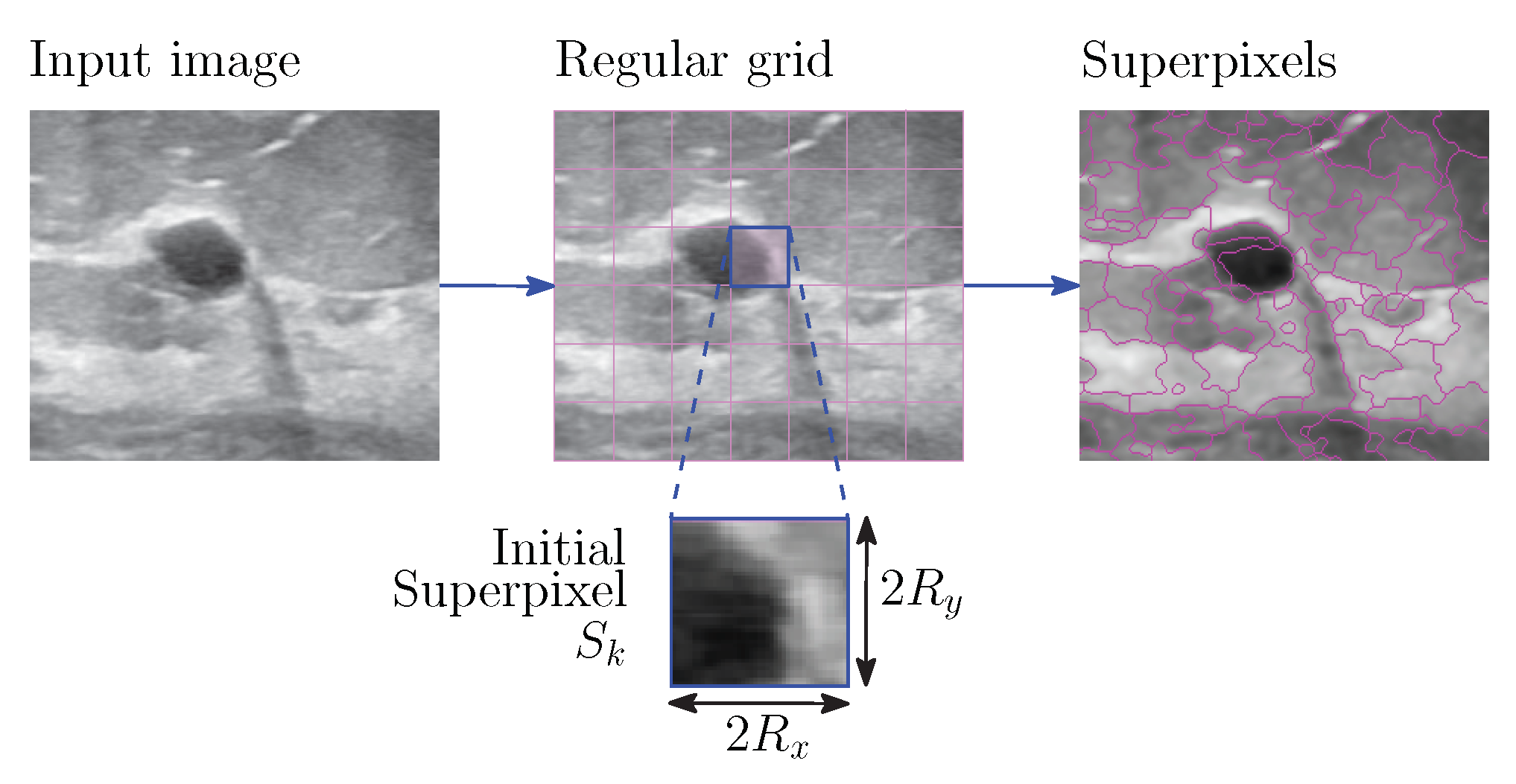
2.2. Grayscale Image Oversegmentation Using Intuitionistic Fuzzy Theory
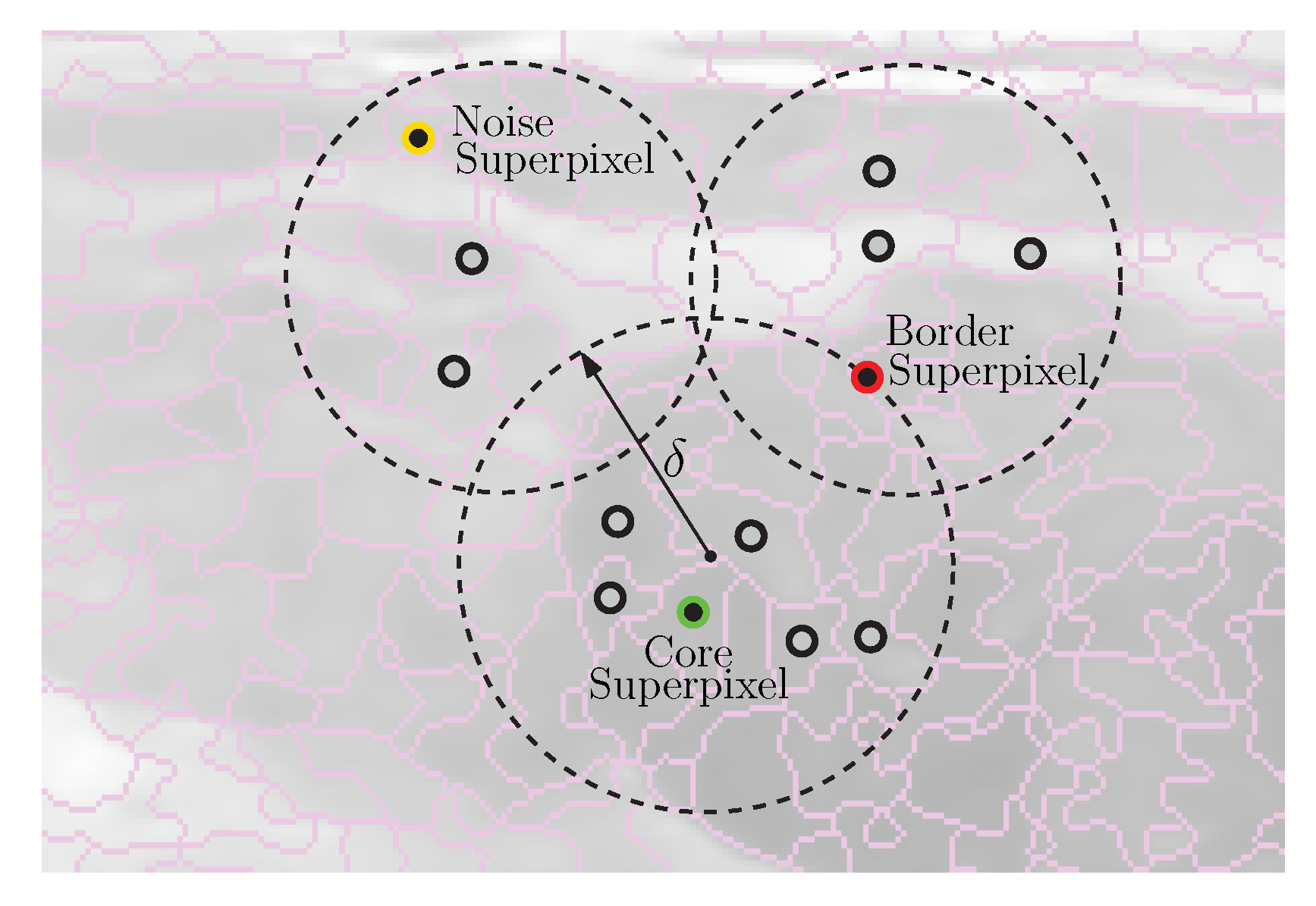
2.3. Clustering of Intuitionistic Fuzzy Superpixels
3. Proposed Scheme
| Algorithm 1: Intuitionistic Fuzzy Superpixels-DBSCAN |
 |
4. Experimental Results
4.1. Metrics
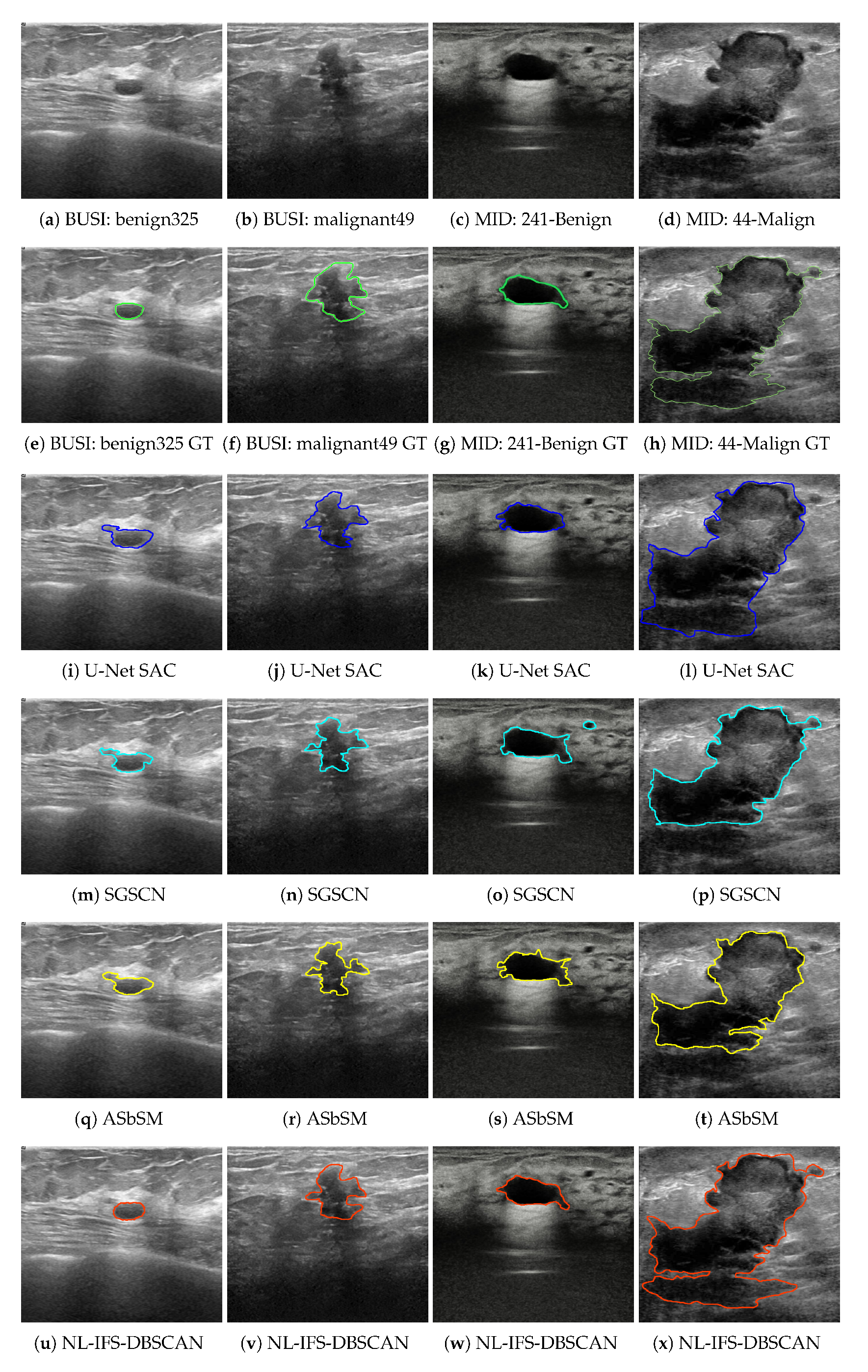
4.2. Experiment 1: BUSI Dataset
4.3. Experiment 2: MID Dataset
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.Y.; Chang, T.F.; Chou, Y.H.; Yang, K.C. Fully automated lesion segmentation and visualization in automated whole breast ultrasound (ABUS) images. Quant. Imaging Med. Surg. 2020, 10, 568. [Google Scholar] [CrossRef] [PubMed]
- Lai, X.; Yang, W.; Li, R. DBT masses automatic segmentation using U-net neural networks. Comput. Math. Methods Med. 2020, 2020, 7156165. [Google Scholar] [CrossRef]
- Bhateja, V.; Misra, M.; Urooj, S. Non-Linear Filters for Mammogram Enhancement; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Byra, M.; Jarosik, P.; Szubert, A.; Galperin, M.; Ojeda-Fournier, H.; Olson, L.; O’Boyle, M.; Comstock, C.; Andre, M. Breast mass segmentation in ultrasound with selective kernel U-Net convolutional neural network. Biomed. Signal Process. Control 2020, 61, 102027. [Google Scholar] [CrossRef]
- Byra, M.; Jarosik, P.; Dobruch-Sobczak, K.; Klimonda, Z.; Piotrzkowska-Wróblewska, H.; Litniewski, J.; Nowicki, A. Breast mass segmentation based on ultrasonic entropy maps and attention gated U-Net. arXiv 2020, arXiv:2001.10061. [Google Scholar]
- Kumar, V.; Webb, J.M.; Gregory, A.; Denis, M.; Meixner, D.D.; Bayat, M.; Whaley, D.H.; Fatemi, M.; Alizad, A. Automated and real-time segmentation of suspicious breast masses using convolutional neural network. PLoS ONE 2018, 13, e0195816. [Google Scholar] [CrossRef]
- Ilesanmi, A.E.; Chaumrattanakul, U.; Makhanov, S.S. A method for segmentation of tumors in breast ultrasound images using the variant enhanced deep learning. Biocybern. Biomed. Eng. 2021, 41, 802–818. [Google Scholar] [CrossRef]
- Pi, J.; Qi, Y.; Lou, M.; Li, X.; Wang, Y.; Xu, C.; Ma, Y. FS-UNet: Mass segmentation in mammograms using an encoder-decoder architecture with feature strengthening. Comput. Biol. Med. 2021, 137, 104800. [Google Scholar] [CrossRef]
- Cao, X.; Chen, H.; Li, Y.; Peng, Y.; Wang, S.; Cheng, L. Dilated densely connected U-Net with uncertainty focus loss for 3D ABUS mass segmentation. Comput. Methods Programs Biomed. 2021, 209, 106313. [Google Scholar] [CrossRef]
- Vakanski, A.; Xian, M.; Freer, P.E. Attention-Enriched Deep Learning Model for Breast Tumor Segmentation in Ultrasound Images. Ultrasound Med. Biol. 2020, 46, 2819–2833. [Google Scholar] [CrossRef]
- Jiao, H.; Jiang, X.; Pang, Z.; Lin, X.; Huang, Y.; Li, L. Deep convolutional neural networks-based automatic breast segmentation and mass detection in DCE-MRI. Comput. Math. Methods Med. 2020, 2020, 2413706. [Google Scholar] [CrossRef] [PubMed]
- Yap, M.H.; Goyal, M.; Osman, F.; Martí, R.; Denton, E.; Juette, A.; Zwiggelaar, R. Breast ultrasound region of interest detection and lesion localisation. Artif. Intell. Med. 2020, 107, 101880. [Google Scholar] [CrossRef] [PubMed]
- An, J.; Yu, H.; Bai, R.; Li, J.; Wang, Y.; Cao, R. Detection and Segmentation of Breast Masses Based on Multi-Layer Feature Fusion. Methods 2022, 202, 54–61. [Google Scholar] [CrossRef] [PubMed]
- Webb, J.M.; Adusei, S.A.; Wang, Y.; Samreen, N.; Adler, K.; Meixner, D.D.; Fazzio, R.T.; Fatemi, M.; Alizad, A. Comparing deep learning-based automatic segmentation of breast masses to expert interobserver variability in ultrasound imaging. Comput. Biol. Med. 2021, 139, 104966. [Google Scholar] [CrossRef]
- Irfan, R.; Almazroi, A.A.; Rauf, H.T.; Damaševičius, R.; Nasr, E.A.; Abdelgawad, A.E. Dilated semantic segmentation for breast ultrasonic lesion detection using parallel feature fusion. Diagnostics 2021, 11, 1212. [Google Scholar] [CrossRef]
- Yan, Y.; Conze, P.H.; Quellec, G.; Lamard, M.; Cochener, B.; Coatrieux, G. Two-stage multi-scale breast mass segmentation for full mammogram analysis without user intervention. Biocybern. Biomed. Eng. 2021, 41, 746–757. [Google Scholar] [CrossRef]
- Pan, P.; Chen, H.; Li, Y.; Cai, N.; Cheng, L.; Wang, S. Tumor segmentation in automated whole breast ultrasound using bidirectional LSTM neural network and attention mechanism. Ultrasonics 2021, 110, 106271. [Google Scholar] [CrossRef]
- Ahn, E.; Feng, D.; Kim, J. A Spatial Guided Self-supervised Clustering Network for Medical Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Panigrahi, L.; Verma, K.; Singh, B.K. Ultrasound image segmentation using a novel multi-scale Gaussian kernel fuzzy clustering and multi-scale vector field convolution. Expert Syst. Appl. 2019, 115, 486–498. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, Y.; Luo, Y.; Yuan, F.; Li, X. Segmentation of breast ultrasound image with semantic classification of superpixels. Med. Image Anal. 2020, 61, 101657. [Google Scholar] [CrossRef]
- Daoud, M.I.; Atallah, A.A.; Awwad, F.; Al-Najjar, M.; Alazrai, R. Automatic superpixel-based segmentation method for breast ultrasound images. Expert Syst. Appl. 2019, 121, 78–96. [Google Scholar] [CrossRef]
- Militello, C.; Rundo, L.; Dimarco, M.; Orlando, A.; Conti, V.; Woitek, R.; D’Angelo, I.; Bartolotta, T.V.; Russo, G. Semi-automated and interactive segmentation of contrast-enhancing masses on breast DCE-MRI using spatial fuzzy clustering. Biomed. Signal Process. Control 2022, 71, 103113. [Google Scholar] [CrossRef]
- Keatmanee, C.; Chaumrattanakul, U.; Kotani, K.; Makhanov, S.S. Initialization of active contours for segmentation of breast cancer via fusion of ultrasound, Doppler, and elasticity images. Ultrasonics 2019, 94, 438–453. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Xie, F.; Liu, L.; Peng, Y.; Cai, H.; Li, L. Discrimination of malignant and benign breast masses using automatic segmentation and features extracted from dynamic contrast-enhanced and diffusion-weighted MRI. Oncol. Lett. 2018, 16, 1521–1528. [Google Scholar] [CrossRef]
- Bechar, M.E.A.; Settouti, N.; Domingues, I. Deep Learning vs. Super Pixel Classification for Breast Masses Segmentation. In Deep Learning for Biomedical Applications; CRC Press: Boca Raton, FL, USA, 2021; pp. 121–156. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A review of image denoising algorithms, with a new one. Multiscale Model. Simul. 2005, 4, 490–530. [Google Scholar] [CrossRef]
- Mújica-Vargas, D. Superpixels extraction by an Intuitionistic fuzzy clustering algorithm. J. Appl. Res. Technol. 2021, 19, 140–152. [Google Scholar] [CrossRef]
- Zhu, Q.; Tang, X.; Elahi, A. Application of the novel harmony search optimization algorithm for DBSCAN clustering. Expert Syst. Appl. 2021, 178, 115054. [Google Scholar] [CrossRef]
- Hiremath, P.; Akkasaligar, P.T.; Badiger, S.; Gunarathne, G. Speckle noise reduction in medical ultrasound images. Adv. Break. Ultrasound Imaging 2013, 1, 1–8. [Google Scholar]
- Balodi, A. Despeckling in echocardiographic images using a hybrid fuzzy filter. In Image Processing for Automated Diagnosis of Cardiac Diseases; Elsevier: Amsterdam, The Netherlands, 2021; pp. 77–97. [Google Scholar]
- Mao, Y.M.; Mwakapesa, D.S.; Li, Y.C.; Xu, K.B.; Nanehkaran, Y.A.; Zhang, M.S. Assessment of landslide susceptibility using DBSCAN-AHD and LD-EV methods. J. Mt. Sci. 2022, 19, 184–197. [Google Scholar] [CrossRef]
- Al-Dhabyani, W.; Gomaa, M.; Khaled, H.; Fahmy, A. Dataset of breast ultrasound images. Data Brief 2020, 28, 104863. [Google Scholar] [CrossRef]
- Rodtook, A.; Kirimasthong, K.; Lohitvisate, W.; Makhanov, S.S. Automatic initialization of active contours and level set method in ultrasound images of breast abnormalities. Pattern Recognit. 2018, 79, 172–182. [Google Scholar] [CrossRef]
- Jiang, L.; Yang, W. A modified fuzzy c-means algorithm for segmentation of magnetic resonance images. In Proceedings of the VIIth Digital Image Computing: Techniques and Applications, Sydney, Australia, 10–12 December 2003. [Google Scholar]
| Algorithm | Masses | JSC | DM | HD | MCR |
|---|---|---|---|---|---|
| SAC U-Net | Benign | 0.871 ± 0.073 | 0.896 ± 0.083 | 7.342 ± 1.801 | 7.029 ± 1.253 |
| SGSCN | Benign | 0.864 ± 0.108 | 0.878 ± 0.110 | 8.290 ± 2.347 | 8.590 ± 2.032 |
| ASbSM | Benign | 0.892 ± 0.088 | 0.905 ± 0.085 | 7.756 ± 2.103 | 7.167 ± 1.747 |
| NL-IFS-DBSCAN | Benign | 0.907 ± 0.064 | 0.913 ± 0.083 | 7.025 ± 1.274 | 6.431 ± 0.913 |
| SAC U-Net | Malignant | 0.848 ± 0.089 | 0.866 ± 0.092 | 10.160 ± 3.192 | 9.033 ± 2.418 |
| SGSCN | Malignant | 0.831 ± 0.127 | 0.859 ± 0.152 | 11.048 ± 3.211 | 10.065 ± 2.841 |
| ASbSM | Malignant | 0.851 ± 0.112 | 0.872 ± 0.108 | 9.139 ± 2.879 | 8.693 ± 2.032 |
| NL-IFS-DBSCAN | Malignant | 0.879 ± 0.082 | 0.900 ± 0.087 | 8.666 ± 1.545 | 8.016 ± 1.268 |
| Algorithm | Masses | JSC | DM | HD | MCR |
|---|---|---|---|---|---|
| SAC U-Net | Benign | 0.847 ± 0.086 | 0.883 ± 0.098 | 9.822 ± 2.120 | 8.262 ± 1.580 |
| SGSCN | Benign | 0.817 ± 0.136 | 0.853 ± 0.119 | 10.983 ± 2.986 | 9.041 ± 2.963 |
| ASbSM | Benign | 0.870 ± 0.115 | 0.882 ± 0.107 | 9.139 ± 2.654 | 7.797 ± 2.121 |
| NL-IFS-DBSCAN | Benign | 0.890 ± 0.071 | 0.905 ± 0.081 | 8.370 ± 1.663 | 7.241 ± 1.240 |
| SAC U-Net | Malignant | 0.791 ± 0.109 | 0.834 ± 0.090 | 10.882 ± 2.011 | 8.573 ± 1.805 |
| SGSCN | Malignant | 0.753 ± 0.172 | 0.808 ± 0.157 | 11.292 ± 2.693 | 9.743 ± 2.759 |
| ASbSM | Malignant | 0.818 ± 0.148 | 0.869 ± 0.139 | 9.946 ± 2.129 | 8.428 ± 1.792 |
| NL-IFS-DBSCAN | Malignant | 0.881 ± 0.080 | 0.898 ± 0.073 | 8.865 ± 1.799 | 7.808 ± 1.441 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mújica-Vargas, D.; Matuz-Cruz, M.; García-Aquino, C.; Ramos-Palencia, C. Efficient System for Delimitation of Benign and Malignant Breast Masses. Entropy 2022, 24, 1775. https://doi.org/10.3390/e24121775
Mújica-Vargas D, Matuz-Cruz M, García-Aquino C, Ramos-Palencia C. Efficient System for Delimitation of Benign and Malignant Breast Masses. Entropy. 2022; 24(12):1775. https://doi.org/10.3390/e24121775
Chicago/Turabian StyleMújica-Vargas, Dante, Manuel Matuz-Cruz, Christian García-Aquino, and Celia Ramos-Palencia. 2022. "Efficient System for Delimitation of Benign and Malignant Breast Masses" Entropy 24, no. 12: 1775. https://doi.org/10.3390/e24121775
APA StyleMújica-Vargas, D., Matuz-Cruz, M., García-Aquino, C., & Ramos-Palencia, C. (2022). Efficient System for Delimitation of Benign and Malignant Breast Masses. Entropy, 24(12), 1775. https://doi.org/10.3390/e24121775






