Sparse Regularized Optimal Transport with Deformed q-Entropy
Abstract
1. Introduction
2. Background
2.1. Preliminaries
2.2. Optimal Transport
2.3. Entropic Regularization and Sinkhorn Algorithm
3. Deformed q-Entropy and q-Regularized Optimal Transport
3.1. Regularized Optimal Transport and Its Dual
3.2. q Algebra and Deformed Entropy
4. Optimization and Convergence Analysis
4.1. Optimization Algorithm

4.2. Convergence Analysis
4.3. Proofs
5. Numerical Experiments
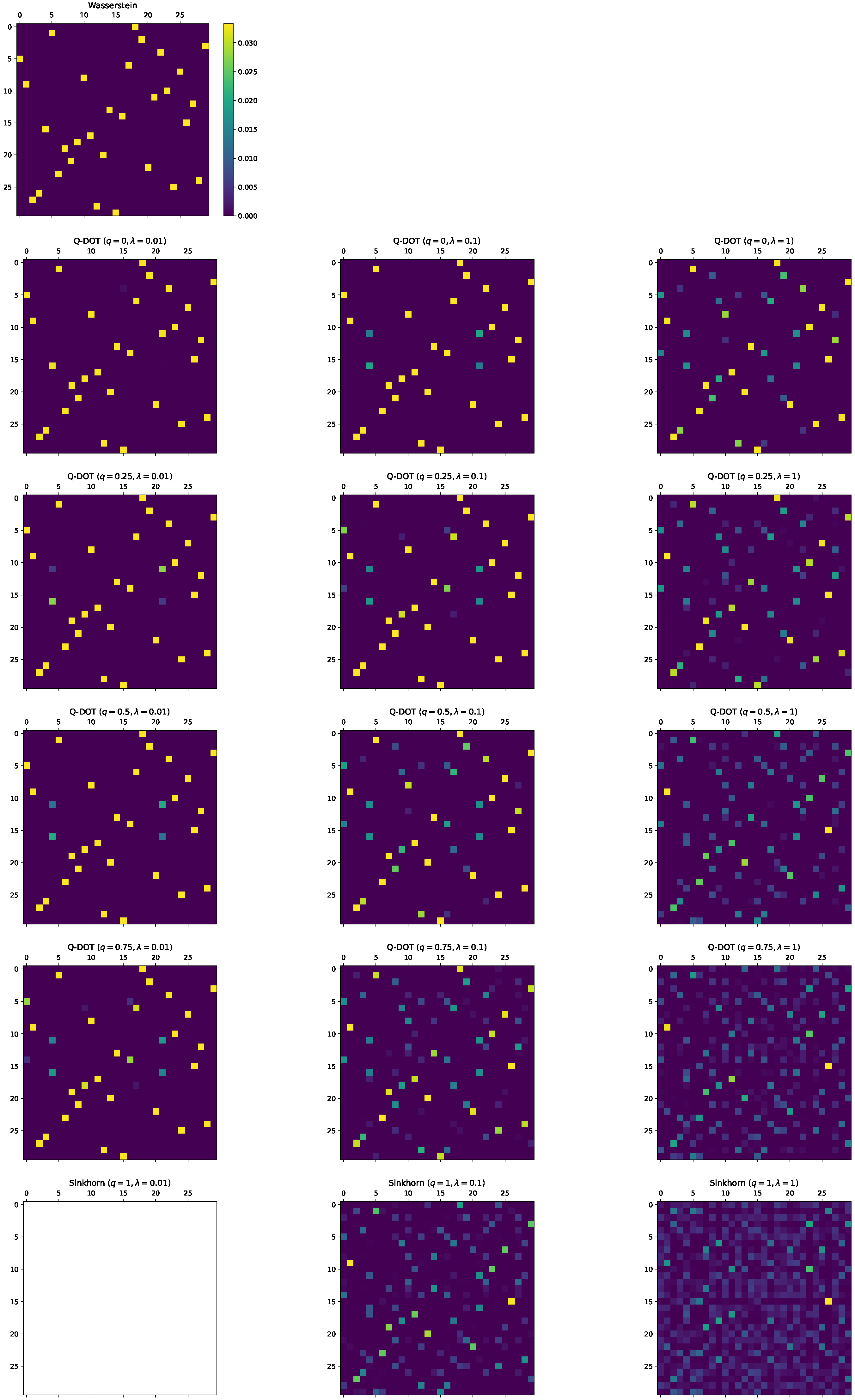
5.1. Sparsity
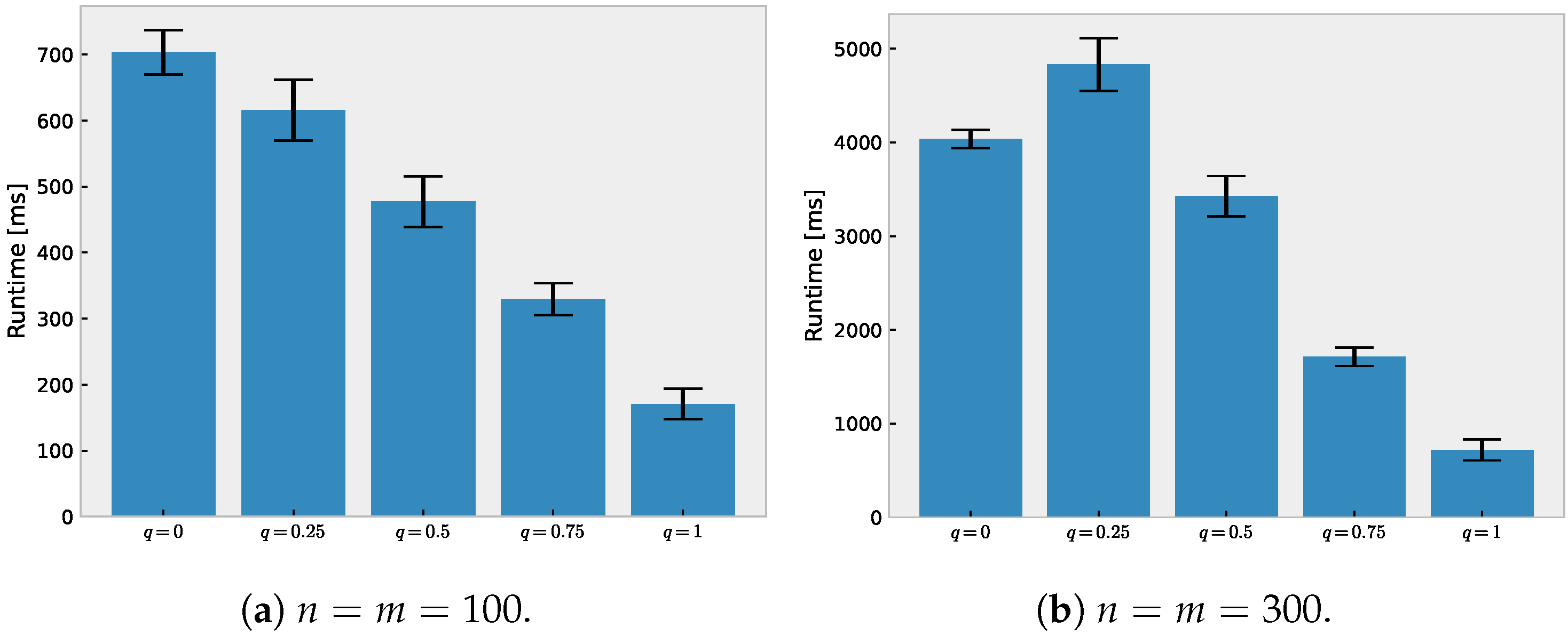
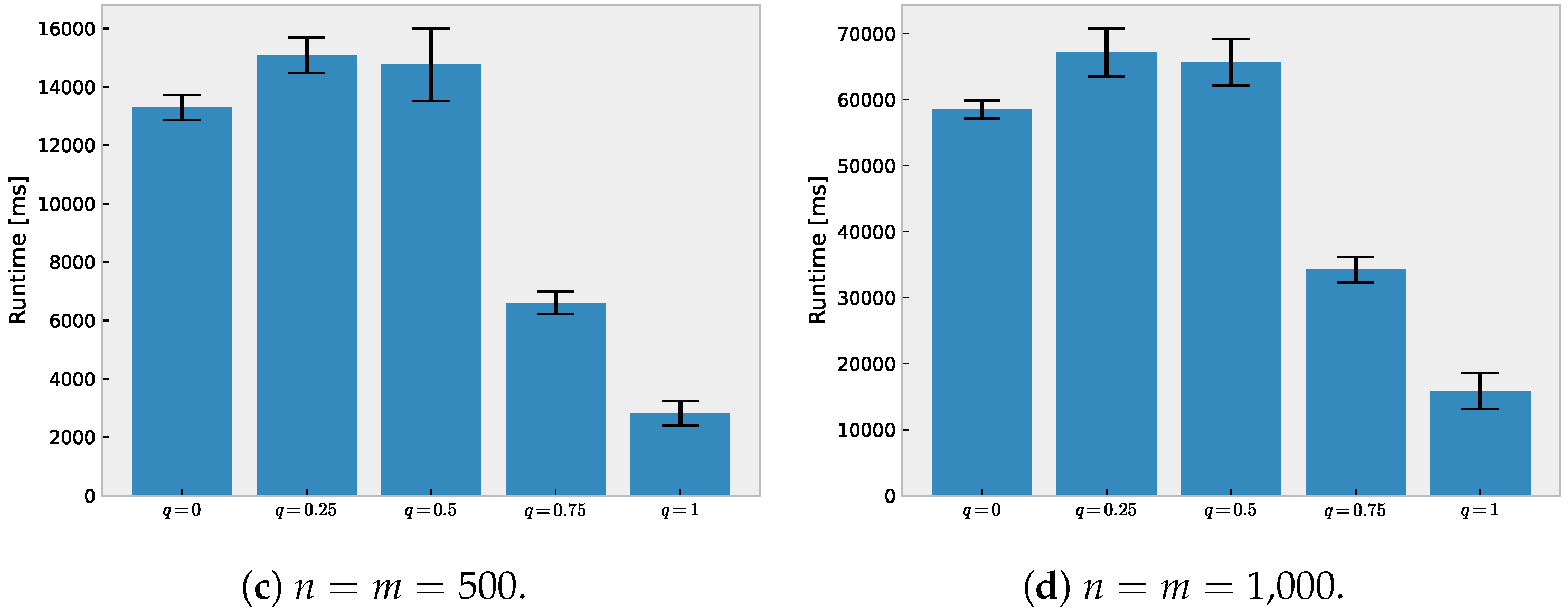
5.2. Runtime Comparison
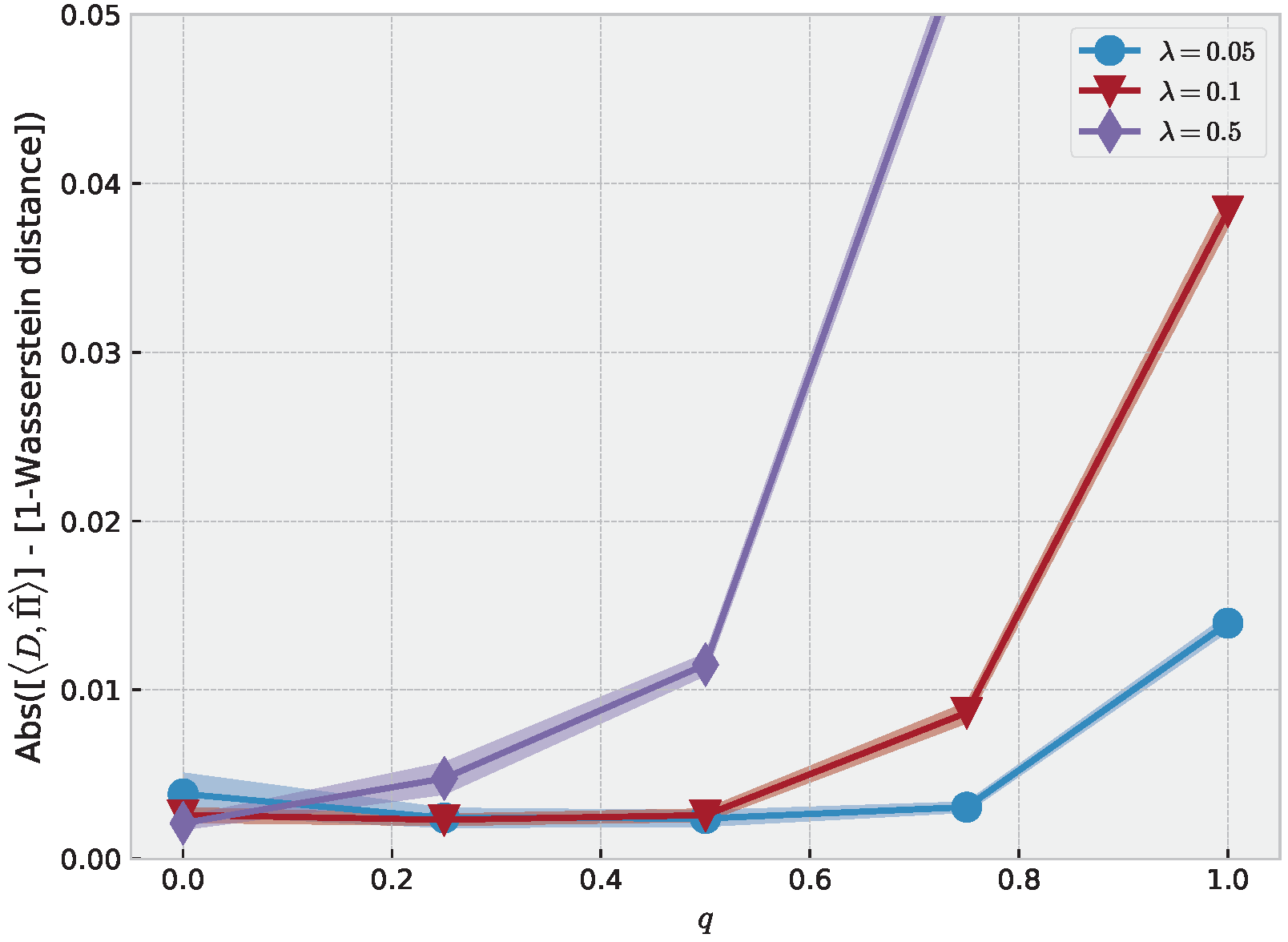
5.3. Approximation of 1-Wasserstein Distance
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BFGS | Broyden–Fletcher–Goldfarb–Shannon |
| q-DOT | Deformed q-optimal transport |
| L-BFGS | Limited-memory BFGS |
| OT | Optimal transport |
Appendix A. Derivation of Deformed q Entropy
Appendix B. Additional Lemmas
Appendix C. Deferred Proofs
Appendix C.1. Proof of Lemma 1
Appendix C.2. Proof of Lemma 2
Appendix C.3. Proof of Lemma 3
Appendix D. Additional Experiments
Appendix D.1. Comparison with Tsallis Entropy
| Sparsity (q-DOT) | Abs. Error (q-DOT) | Sparsity (Tsallis) | Abs. Error (Tsallis) | |
|---|---|---|---|---|
| 0.984 | 0.001 | — | — | |
| 0.981 | 0.011 | — | — | |
| 0.977 | 0.008 | 0.000 | 3.362 | |
| 0.973 | 0.010 | 0.000 | 3.388 | |
| 0.959 | 0.015 | 0.000 | 3.153 | |
| 0.944 | 0.022 | 0.000 | 3.283 | |
| 0.861 | 0.052 | 0.000 | 1.962 | |
| 0.776 | 0.099 | 0.000 | 2.582 |
Appendix D.2. Hyperparameter Sensitivity
| () | Sparsity | Abs. Error | Runtime [ms] | () | Sparsity | Abs. Error | Runtime [ms] |
|---|---|---|---|---|---|---|---|
| 0.990 | 2.28× 10 | 4366.142 | 0.997 | 1.30× 10 | 33,592.026 | ||
| 0.988 | 3.63 × 10 | 1236.346 | 0.996 | 2.15× 10 | 14,641.740 | ||
| 0.982 | 6.20× 10 | 842.253 | 0.994 | 2.03× 10 | 7749.233 | ||
| 0.989 | 8.18× 10 | 3182.535 | 0.996 | 7.07× 10 | 36,167.445 | ||
| 0.986 | 5.54× 10 | 1131.784 | 0.994 | 1.83× 10 | 15,176.970 | ||
| 0.973 | 1.16× 10 | 668.734 | 0.990 | 2.69× 10 | 5848.561 | ||
| 0.987 | 9.91× 10 | 2388.176 | 0.994 | 1.99× 10 | 25,940.619 | ||
| 0.977 | 7.66× 10 | 1040.818 | 0.991 | 2.41× 10 | 8304.774 | ||
| 0.946 | 2.40× 10 | 339.978 | 0.976 | 3.52× 10 | 2713.598 | ||
| 0.979 | 1.16× 10 | 2396.353 | 0.991 | 2.97× 10 | 18,820.365 | ||
| 0.950 | 1.31× 10 | 731.564 | 0.973 | 3.34× 10 | 4823.098 | ||
| 0.786 | 1.02× 10 | 200.654 | 0.864 | 9.57× 10 | 1654.697 | ||
| — | — | — | — | — | — | ||
| 0.000 | 5.83× 10 | 1132.516 | 0.000 | 7.39× 10 | 2014.341 | ||
| 0.000 | 7.51× 10 | 31.284 | 0.000 | 8.15× 10 | 207.094 | ||
| () | Sparsity | Abs. error | Runtime [ms] | () | Sparsity | Abs. error | Runtime [s] |
| 0.999 | 2.48× 10 | 86,046.395 | 1.000 | 6.39× 10 | 336.207 | ||
| 0.997 | 3.91× 10 | 49,523.995 | 0.999 | 8.76× 10 | 286.879 | ||
| 0.996 | 4.10× 10 | 27,357.659 | 0.998 | 8.22× 10 | 133.223 | ||
| 0.998 | 2.36× 10 | 104,346.641 | 0.999 | 4.27× 10 | 413.775 | ||
| 0.996 | 5.12× 10 | 41,810.473 | 0.998 | 1.01× 10 | 221.787 | ||
| 0.994 | 4.22× 10 | 18,415.400 | 0.997 | 9.01× 10 | 87.945 | ||
| 0.996 | 4.52× 10 | 78,618.996 | 0.998 | 8.61× 10 | 374.123 | ||
| 0.994 | 4.50× 10 | 25,512.371 | 0.997 | 9.37× 10 | 120.605 | ||
| 0.984 | 4.92× 10 | 8266.048 | 0.990 | 9.49× 10 | 41.435 | ||
| 0.994 | 4.55× 10 | 57,839.639 | 0.996 | 1.05× 10 | 275.101 | ||
| 0.979 | 5.07× 10 | 14,257.452 | 0.985 | 1.02× 10 | 67.301 | ||
| 0.890 | 1.00× 10 | 4362.478 | 0.917 | 1.34× 10 | 21.536 | ||
| — | — | — | — | — | — | ||
| 0.000 | 7.92× 10 | 5731.333 | 0.000 | 8.62× 10 | 57.739 | ||
| 0.000 | 8.35× 10 | 562.722 | 0.000 | 8.51× 10 | 2.215 | ||
| () | Sparsity | Abs. error | Runtime [s] | () | Sparsity | Abs. error | Runtime [s] |
| 1.000 | 3.59× 10 | 1386.554 | 1.000 | 4.09× 10 | 3257.314 | ||
| 0.999 | 2.25× 10 | 1245.867 | 1.000 | 8.56× 10 | 3108.889 | ||
| 0.999 | 1.85× 10 | 823.011 | 0.999 | 2.68× 10 | 2355.733 | ||
| 1.000 | 5.88× 10 | 1555.064 | 1.000 | 3.78× 10 | 3821.319 | ||
| 0.999 | 1.86× 10 | 1201.656 | 0.999 | 2.94× 10 | 3532.833 | ||
| 0.998 | 1.86× 10 | 492.324 | 0.999 | 2.76× 10 | 1530.838 | ||
| 0.999 | 6.66× 10 | 1494.270 | 1.000 | 1.85× 10 | 3669.894 | ||
| 0.998 | 1.97× 10 | 589.379 | 0.999 | 2.93× 10 | 1637.985 | ||
| 0.994 | 1.85× 10 | 210.008 | 0.995 | 2.71× 10 | 644.164 | ||
| 0.998 | 2.00× 10 | 1300.517 | 0.998 | 2.98× 10 | 3560.379 | ||
| 0.989 | 2.00× 10 | 321.221 | 0.991 | 2.91× 10 | 853.451 | ||
| 0.937 | 2.08× 10 | 106.334 | 0.946 | 2.83× 10 | 270.046 | ||
| — | — | — | — | — | — | ||
| 0.000 | 9.06× 10 | 147.372 | 0.000 | 8.94× 10 | 272.210 | ||
| 0.000 | 8.62× 10 | 8.575 | 0.000 | 8.62× 10 | 20.120 |
References
- Villani, C. Optimal Transport: Old and New; Springer: Berlin/Heidelberg, Germany, 2009; Volume 338. [Google Scholar]
- Shafieezadeh-Abadeh, S.; Mohajerin Esfahani, P.M.; Kuhn, D. Distributionally robust logistic regression. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar]
- Courty, N.; Flamary, R.; Habrard, A.; Rakotomamonjy, A. Joint distribution optimal transportation for domain adaptation. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; PMLR. pp. 214–223. [Google Scholar]
- Kusner, M.; Sun, Y.; Kolkin, N.; Weinberger, K. From word embeddings to document distances. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015; PMLR. pp. 957–966. [Google Scholar]
- Swanson, K.; Yu, L.; Lei, T. Rationalizing text matching: Learning sparse alignments via optimal transport. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 5609–5626. [Google Scholar]
- Otani, M.; Togashi, R.; Nakashima, Y.; Rahtu, E.; Heikkilä, J.; Satoh, S. Optimal correction cost for object detection evaluation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21–24 June 2022; pp. 21107–21115. [Google Scholar]
- Pele, O.; Werman, M. Fast and robust Earth Mover’s Distances. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; IEEE: New York, NY, USA, 2009; pp. 460–467. [Google Scholar]
- Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. Adv. Neural Inf. Process. Syst. 2013, 26, 2292–2300. [Google Scholar]
- Dessein, A.; Papadakis, N.; Rouas, J.L. Regularized optimal transport and the rot mover’s distance. J. Mach. Learn. Res. 2018, 19, 590–642. [Google Scholar]
- Dvurechensky, P.; Gasnikov, A.; Kroshnin, A. Computational optimal transport: Complexity by accelerated gradient descent is better than by Sinkhorn’s algorithm. In Proceedings of the 36th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR. pp. 1367–1376. [Google Scholar]
- Le, T.; Yamada, M.; Fukumizu, K.; Cuturi, M. Tree-sliced variants of Wasserstein distances. Adv. Neural Inf. Process. Syst. 2019, 32, 12304–12315. [Google Scholar]
- Le, T.; Nguyen, T.; Phung, D.; Nguyen, V.A. Sobolev transport: A scalable metric for probability measures with graph metrics. In Proceedings of the 25th International Conference on Artificial Intelligence and Statistics, Online, 28–30 March 2022; PMLR. pp. 9844–9868. [Google Scholar]
- Frogner, C.; Zhang, C.; Mobahi, H.; Araya, M.; Poggio, T.A. Learning with a Wasserstein loss. Adv. Neural Inf. Process. Syst. 2015, 28, 2053–2061. [Google Scholar]
- Cuturi, M.; Teboul, O.; Vert, J.P. Differentiable ranking and sorting using optimal transport. Adv. Neural Inf. Process. Syst. 2019, 32, 6861–6871. [Google Scholar]
- Blondel, M.; Martins, A.F.; Niculae, V. Learning with Fenchel-Young losses. J. Mach. Learn. Res. 2020, 21, 1–69. [Google Scholar]
- Birkhoff, G. Tres observaciones sobre el algebra lineal. Univ. Nac. Tucum’an Rev. Ser. A 1946, 5, 147–154. [Google Scholar]
- Brualdi, R.A. Combinatorial Matrix Classes; Cambridge University Press: Cambridge, UK, 2006; Volume 13. [Google Scholar]
- Alvarez-Melis, D.; Jaakkola, T. Gromov–Wasserstein alignment of word embedding spaces. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 1881–1890. [Google Scholar]
- Blondel, M.; Seguy, V.; Rolet, A. Smooth and sparse optimal transport. In Proceedings of the 21st International Conference on Artificial Intelligence and Statistics, Canary Islands, Spain, 9–11 April 2018; PMLR. pp. 880–889. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Amari, S.i.; Ohara, A. Geometry of q-exponential family of probability distributions. Entropy 2011, 13, 1170–1185. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Powell, M.J.D. Some global convergence properties of a variable metric algorithm for minimization without exact line searches. In Proceedings of the Nonlinear Programming, SIAM-AMS Proceedings, New York, NY, USA, 1 January 1976; Volume 9. [Google Scholar]
- Altschuler, J.; Niles-Weed, J.; Rigollet, P. Near-linear time approximation algorithms for optimal transport via Sinkhorn iteration. Adv. Neural Inf. Process. Syst. 2017, 30, 1961–1971. [Google Scholar]
- Sinkhorn, R.; Knopp, P. Concerning nonnegative matrices and doubly stochastic matrices. Pac. J. Math. 1967, 21, 343–348. [Google Scholar] [CrossRef]
- Danskin, J.M. The theory of max-min, with applications. SIAM J. Appl. Math. 1966, 14, 641–664. [Google Scholar] [CrossRef]
- Bao, H.; Sugiyama, M. Fenchel-Young losses with skewed entropies for class-posterior probability estimation. In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics, San Diego, CA, USA, 13–15 April 2021; pp. 1648–1656. [Google Scholar]
- Naudts, J. Deformed exponentials and logarithms in generalized thermostatistics. Phys. A Stat. Mech. Its Appl. 2002, 316, 323–334. [Google Scholar] [CrossRef]
- Suyari, H. The unique non self-referential q-canonical distribution and the physical temperature derived from the maximum entropy principle in Tsallis statistics. Prog. Theor. Phys. Suppl. 2006, 162, 79–86. [Google Scholar] [CrossRef]
- Ding, N.; Vishwanathan, S. t-Logistic regression. Adv. Neural Inf. Process. Syst. 2010, 23, 514–522. [Google Scholar]
- Futami, F.; Sato, I.; Sugiyama, M. Expectation propagation for t-exponential family using q-algebra. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Amid, E.; Warmuth, M.K.; Anil, R.; Koren, T. Robust bi-tempered logistic loss based on bregman divergences. Adv. Neural Inf. Process. Syst. 2019, 32, 15013–15022. [Google Scholar]
- Martins, A.F.; Figueiredo, M.A.; Aguiar, P.M.; Smith, N.A.; Xing, E.P. Nonextensive entropic kernels. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 640–647. [Google Scholar]
- Muzellec, B.; Nock, R.; Patrini, G.; Nielsen, F. Tsallis regularized optimal transport and ecological inference. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Byrd, R.H.; Nocedal, J.; Yuan, Y.X. Global convergence of a cass of quasi-Newton methods on convex problems. SIAM J. Numer. Anal. 1987, 24, 1171–1190. [Google Scholar] [CrossRef]
- Schmitzer, B. Stabilized sparse scaling algorithms for entropy regularized transport problems. SIAM J. Sci. Comput. 2019, 41, A1443–A1481. [Google Scholar] [CrossRef]
- Flamary, R.; Courty, N.; Gramfort, A.; Alaya, M.Z.; Boisbunon, A.; Chambon, S.; Chapel, L.; Corenflos, A.; Fatras, K.; Fournier, N.; et al. POT: Python optimal transport. J. Mach. Learn. Res. 2021, 22, 1–8. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Weed, J. An explicit analysis of the entropic penalty in linear programming. In Proceedings of the the 31st Conference on Learning Theory, Stockholm, Sweden, 5–9 July 2018; PMLR. pp. 1841–1855. [Google Scholar]
- Golub, G.H.; van Loan, C.F. Matrix Computations; The Johns Hopkins University Press: Baltimore, MA, USA, 2013. [Google Scholar]
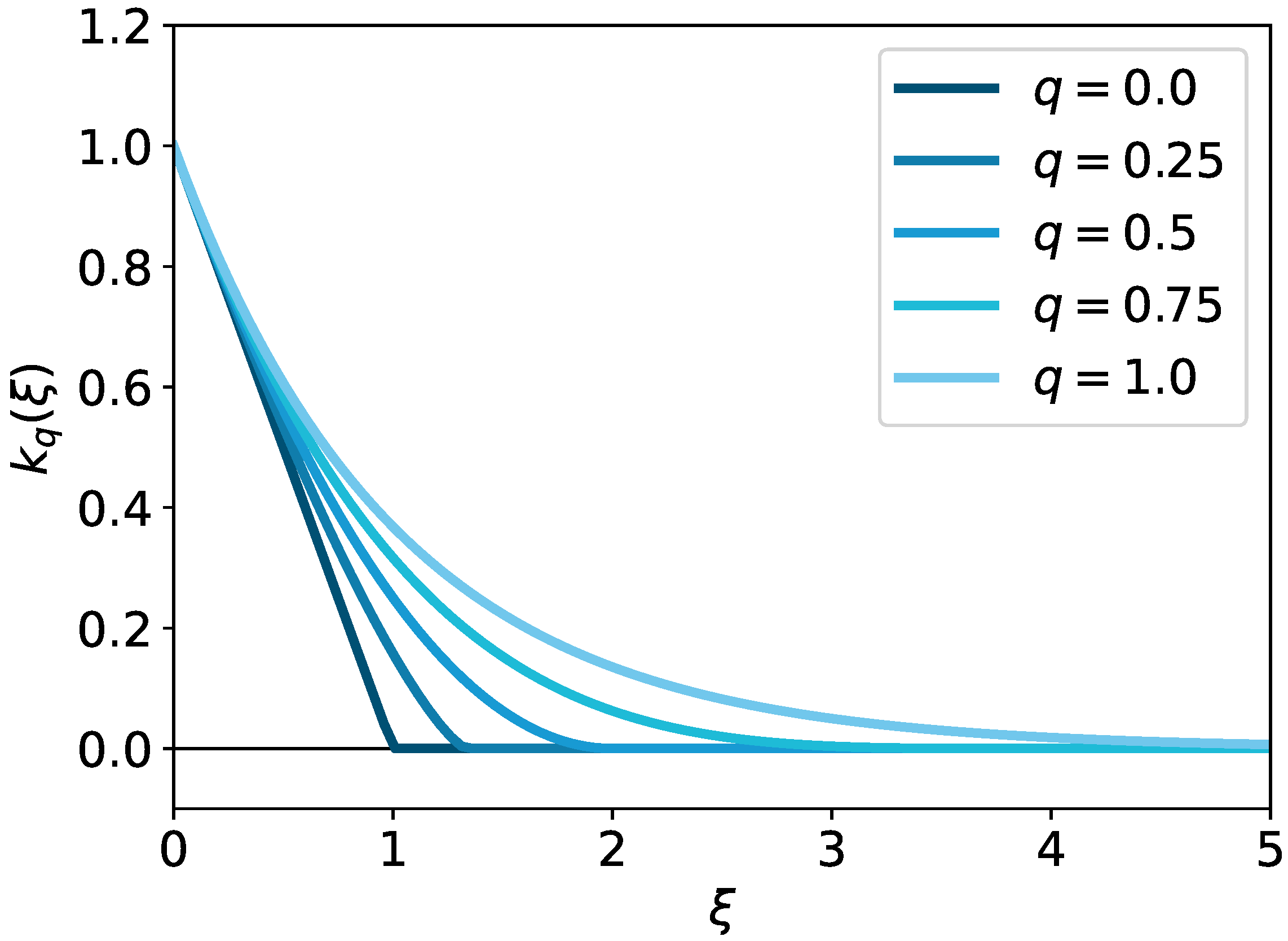
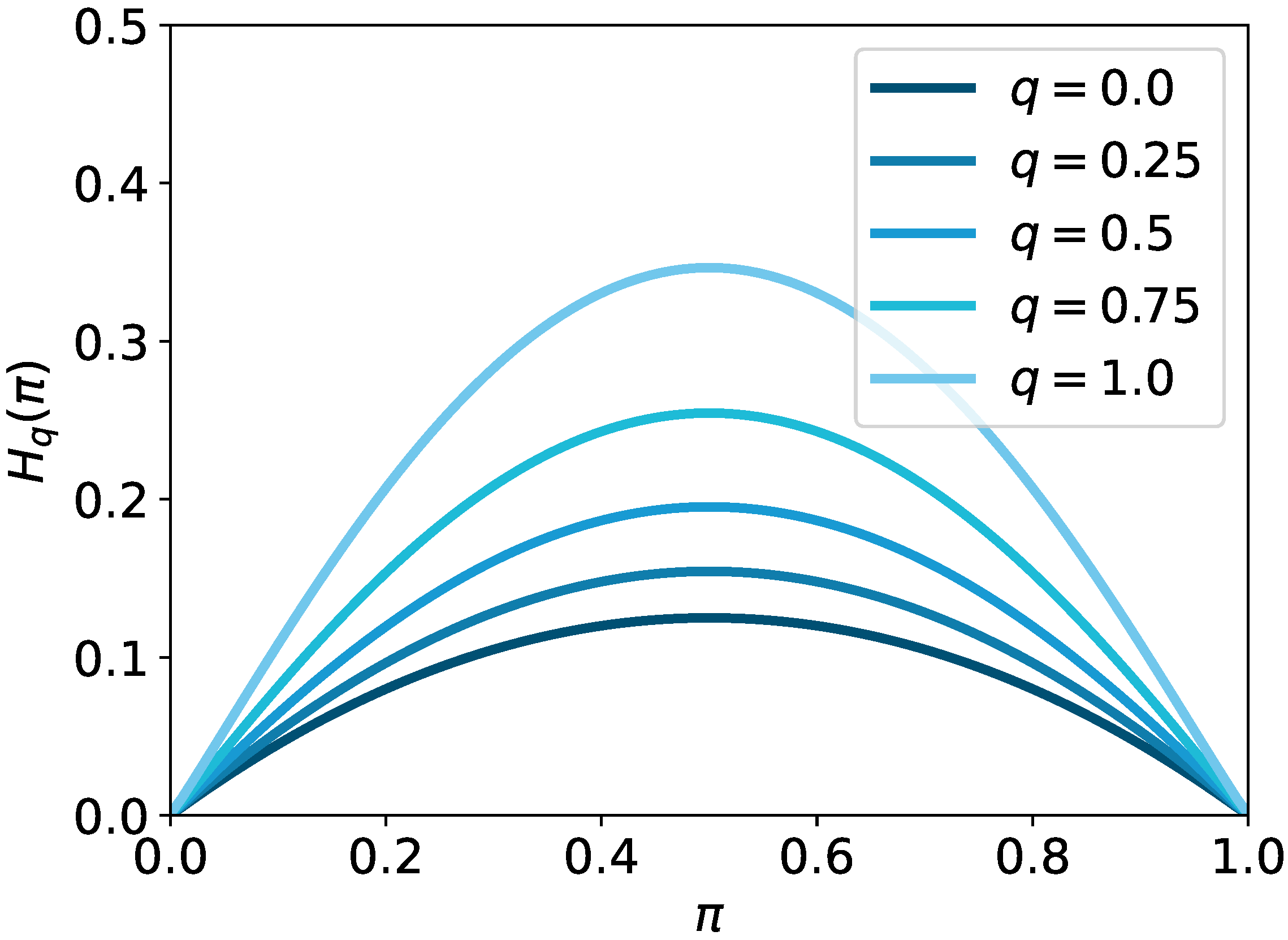
| Negative entropy | |||
| Squared 2-norm | |||
| Deformed q entropy |
| Sinkhorn | q-DOT |
|---|---|
| Sparsity | Cost | |
|---|---|---|
| Wasserstein (unregularized) | 0.967 | 7.126 |
| q-DOT () | 0.962 | 7.129 |
| q-DOT () | 0.961 | 7.126 |
| q-DOT () | 0.950 | 7.144 |
| q-DOT () | 0.963 | 7.129 |
| q-DOT () | 0.959 | 7.126 |
| q-DOT () | 0.912 | 7.133 |
| q-DOT () | 0.963 | 7.136 |
| q-DOT () | 0.946 | 7.127 |
| q-DOT () | 0.879 | 7.155 |
| q-DOT () | 0.948 | 7.127 |
| q-DOT () | 0.897 | 7.136 |
| q-DOT () | 0.647 | 7.245 |
| Sinkhorn () | — | — |
| Sinkhorn () | 0.000 | 7.164 |
| Sinkhorn () | 0.000 | 7.788 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, H.; Sakaue, S. Sparse Regularized Optimal Transport with Deformed q-Entropy. Entropy 2022, 24, 1634. https://doi.org/10.3390/e24111634
Bao H, Sakaue S. Sparse Regularized Optimal Transport with Deformed q-Entropy. Entropy. 2022; 24(11):1634. https://doi.org/10.3390/e24111634
Chicago/Turabian StyleBao, Han, and Shinsaku Sakaue. 2022. "Sparse Regularized Optimal Transport with Deformed q-Entropy" Entropy 24, no. 11: 1634. https://doi.org/10.3390/e24111634
APA StyleBao, H., & Sakaue, S. (2022). Sparse Regularized Optimal Transport with Deformed q-Entropy. Entropy, 24(11), 1634. https://doi.org/10.3390/e24111634






