Localization in Two-Dimensional Quasicrystalline Lattices
Abstract
1. Introduction
2. Model
Energy Scale and Length Units
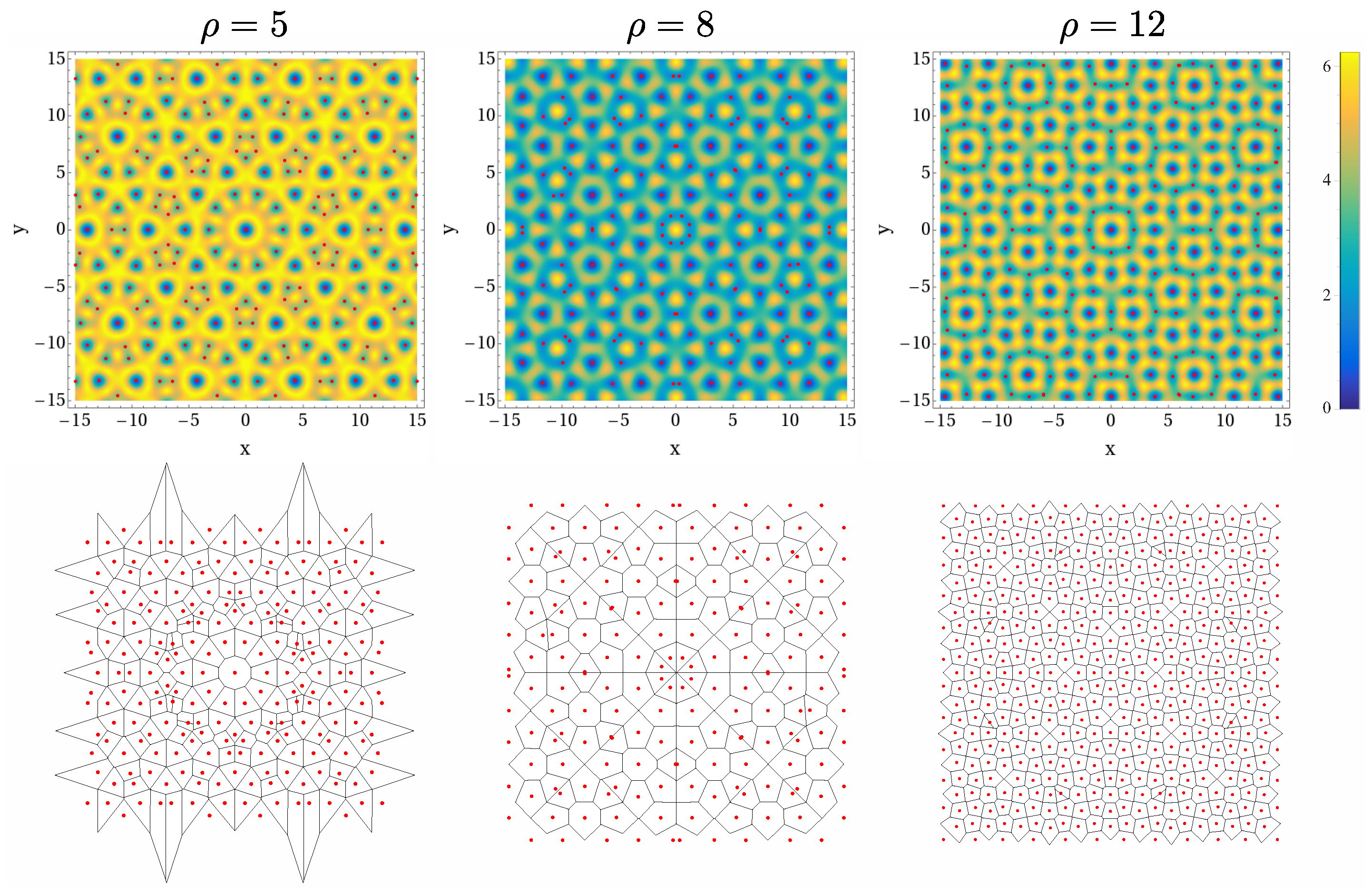
3. Localization in Quasicrystalline Lattices
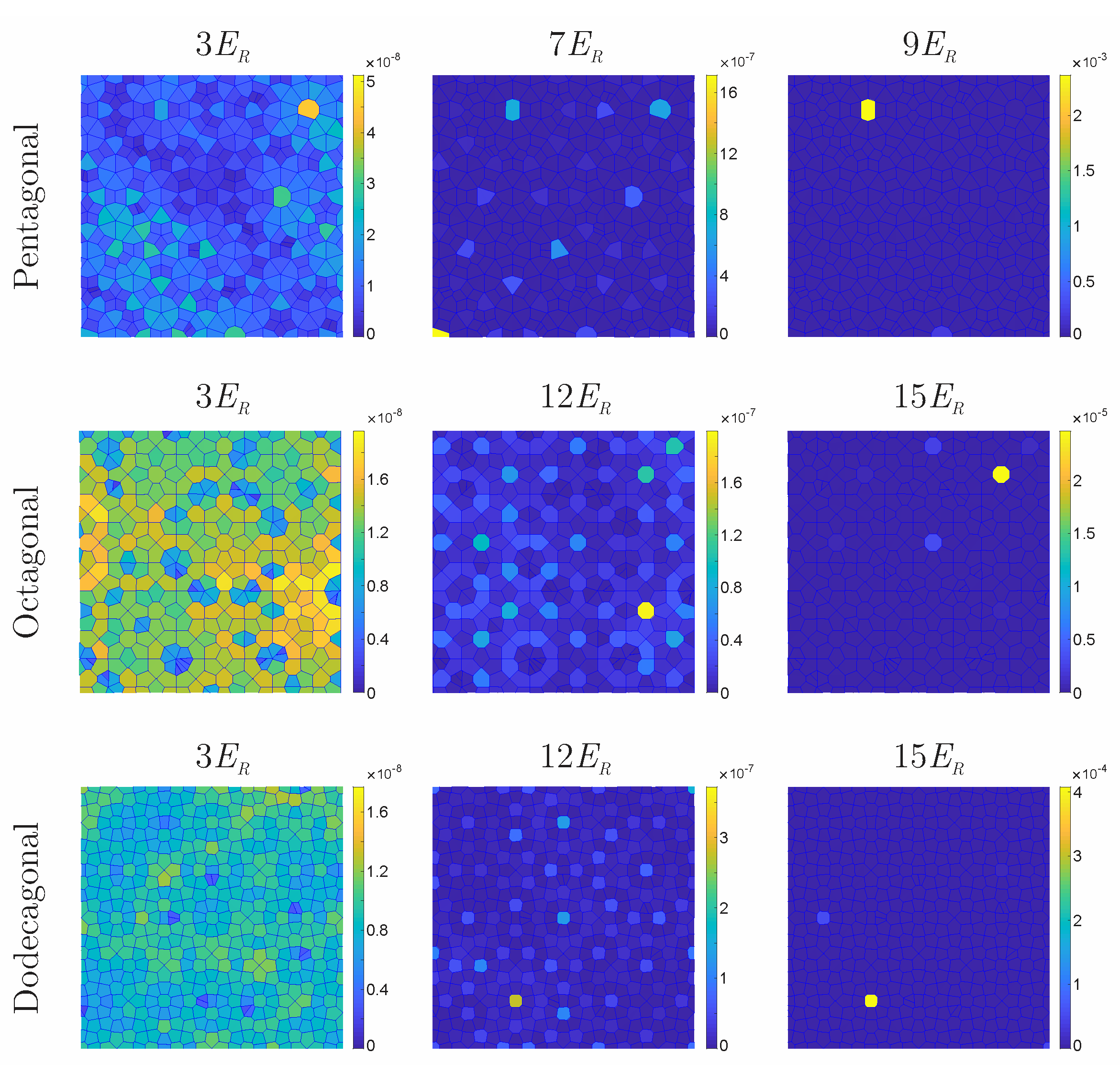
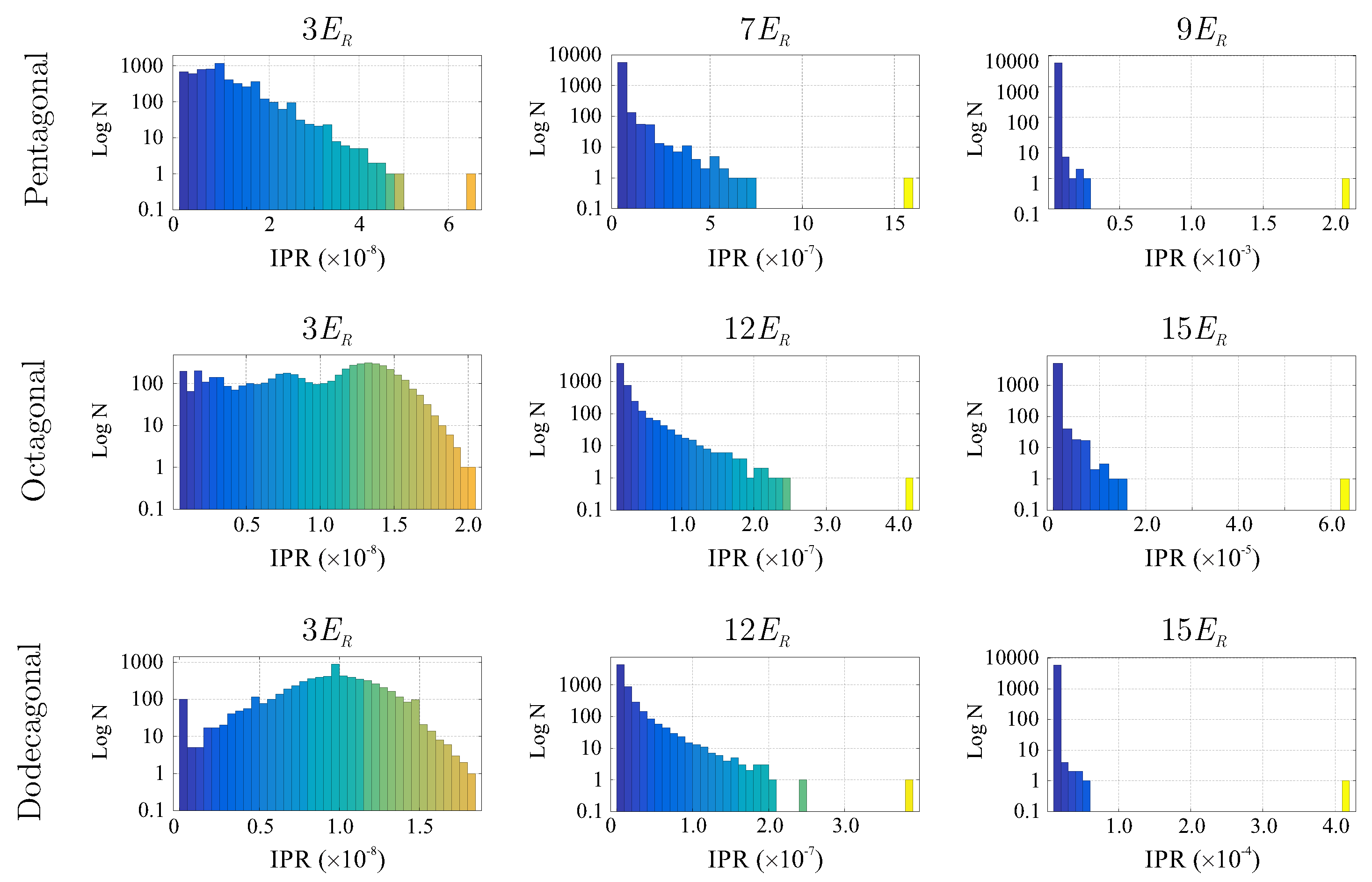
Inverse Participation Ratio
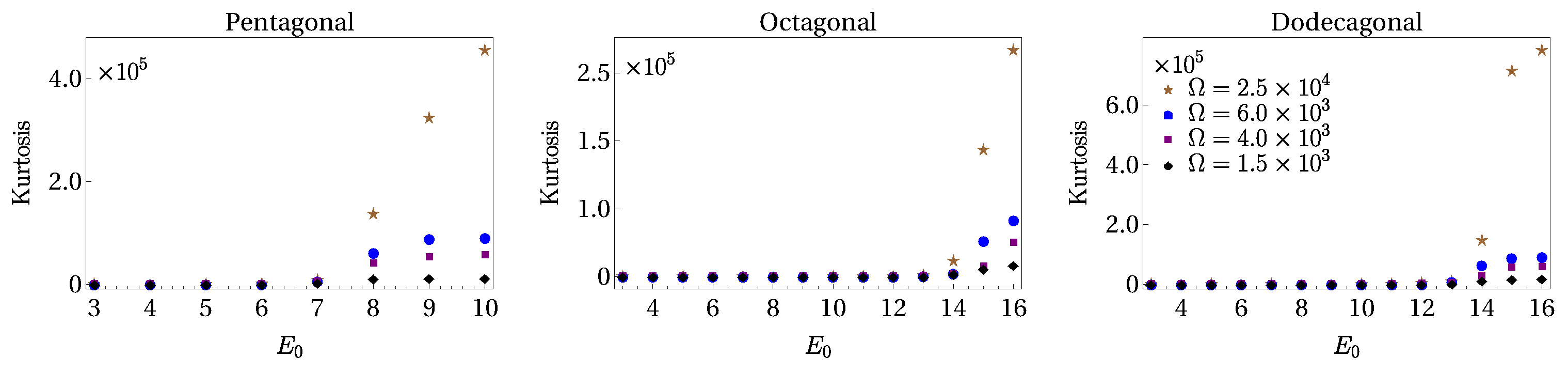
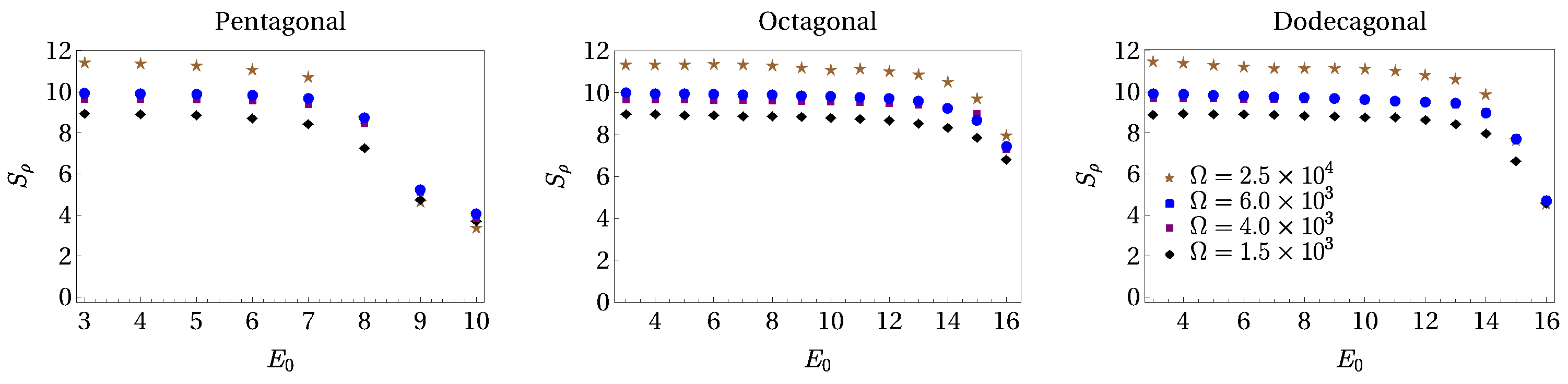
4. Shannon Entropy of BEC Matter Waves
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References and Note
- Shechtman, D.; Blech, I.; Gratias, D. Metallic Phase with Long-Range Orientational Order and No Translational Symmetry. Phys. Rev. Lett. 1984, 53, 1951. [Google Scholar] [CrossRef]
- Bendersky, L. Quasicrystal with One-Dimensional Translational Symmetry and a Tenfold Rotation Axis. Phys. Rev. Lett. 1985, 55, 1461. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Chen, H.; Kuo, K.H. Two-Dimensional Quasicrystal with Eightfold Rotational Symmetry. Phys. Rev. Lett. 1987, 59, 1010. [Google Scholar] [CrossRef] [PubMed]
- Pierce, F.S.; Poon, S.J.; Guo, Q. Electron Localization in Metallic Quasicrystals. Science 1993, 261, 737. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Poon, S.J. Metal-insulator transition and localization in quasicrystalline Al70.5Pd21Re8.5−xMnx alloys. Phys. Rev. B 1996, 54, 12793. [Google Scholar] [CrossRef]
- Samavat, F.; Tavakoli, M.H.; Habibi, S.; Jaleh, B.; Ahmad, P.T. Quasicrystals. Open J. Phys. Chem. 2012, 2, 2. [Google Scholar] [CrossRef]
- Banerjee, S.; Goswami, R.; Chattopadhyay, K.; Raychaudhuri, A.K. Structural and electrical transport properties of Al-Cu-Cr quasicrystals. Phys. Rev. B 1995, 52, 3220. [Google Scholar] [CrossRef]
- Dolinsek, J. Electrical and thermal transport properties of icosahedral and decagonal quasicrystals. Chem. Soc. Rev. 2012, 41, 6730. [Google Scholar] [CrossRef]
- Mivehvar, F.; Ritsch, H.; Piazza, F. Emergent Quasicrystalline Symmetry in Light-Induced Quantum Phase Transitions. Phys. Rev. Lett. 2019, 123, 210604. [Google Scholar] [CrossRef]
- Viebahn, K.; Sbroscia, M.; Carter, E.; Yu, J.-C.; Schneider, U. Matter-wave diffraction from a quasicrystalline optical lattice. Phys. Rev. Lett. 2019, 122, 110404. [Google Scholar] [CrossRef]
- Sbroscia, M.; Viebahn, K.; Carter, E.; Yu, C., Jr.; Gaunt, A.; Schneider, U. Observing Localization in a 2D Quasicrystalline Optical Lattice. Phys. Rev. Lett. 2020, 125, 200604. [Google Scholar] [CrossRef]
- Viebahn, K.G.H. Quasicrystalline Optical Lattices for Ultracold Atoms. Ph.D. Thesis, Cavendish Laboratory, University of Cambridge, Cambridge, UK, 2018. [Google Scholar]
- Corcovilos, T.A.; Mittal, J. Two-dimensional optical quasicrystal potentials for ultracold atom experiments. Appl. Opt. 2019, 58, 2256. [Google Scholar] [CrossRef]
- Roux, G.; Barthel, T.; McCulloch, I.P.; Kollath, C.; Schollwöck, U.; Giamarchi, T. Quasiperiodic Bose-Hubbard model and localization in one-dimensional cold atomic gases. Phys. Rev. A 2008, 78, 023628. [Google Scholar] [CrossRef]
- Ghadimi, R.; Sugimoto, T.; Tohyama, T. Mean-field study of the Bose-Hubbard model in Penrose lattice. Phys. Rev. B 2020, 102, 224201. [Google Scholar] [CrossRef]
- Zhang, Y.-C.; Maucher, F.; Pohl, T. Supersolidity around a Critical Point in Dipolar Bose-Einstein Condensates. Phys. Rev. Lett. 2019, 123, 015301. [Google Scholar] [CrossRef]
- Camacho-Guardian, A.; Paredes, R. Supersolid phases of dipolar fermions in a 2D lattices bilayer array. Phys. Rev. A 2016, 94, 043638. [Google Scholar] [CrossRef]
- Camacho-Guardian, A.; Paredes, R.; Caballero-Benítez, S.F. Quantum simulation of competing orders with fermions in quantum optical lattices. Phys. Rev. A 2017, 96, 051602R. [Google Scholar] [CrossRef]
- Johnstone, D.; Öhberg, P.; Duncan, C.W. Mean-field phases of an ultracold gas in a quasicrystalline potential. Phys. Rev. A 2019, 100, 053609. [Google Scholar] [CrossRef]
- Domínguez-Castro, G.A.; Paredes, R. The Aubry-André model as the hobbyhorse for understanding localization phenomenon. Eur. J. Phys. 2019, 40, 045403. [Google Scholar] [CrossRef]
- Domínguez-Castro, G.A.; Paredes, R. Enhanced transport of two interacting quantum walkers in a one- dimensional quasicrystal with power-law hopping. Phys. Rev. A 2021, 104, 033306. [Google Scholar] [CrossRef]
- This coupling constant is related to the standard 3D coupling interaction g3D, as g2D ≈ , with g3D being the usual coupling interaction written in terms of the s-wave scattering length asc, g3D = , and lz being the natural length of the ground state harmonic oscillator of a condensate originally confined in 3D and then squeezed along z direction, thus resulting into a disk shape condensate confined in the x − y plane.
- Posazhennikov, A. Colloquium: Weakly interacting, dilute Bose gases in 2D. Rev. Mod. Phys. 2006, 78, 1111. [Google Scholar] [CrossRef]
- Petrov, D.S.; Holzmann, M.; Shlyapnikov, G.V. Bose-Einstein condensation in quasi-2D trapped gases. Phys. Rev. Lett. 2000, 84, 2551. [Google Scholar] [CrossRef] [PubMed]
- Salasnich, L.; Parola, A.; Reatto, L. Effective wave equations for the dynamics of cigar-shaped and disk-shaped Bose condensates. Phys. Rev. A 2002, 65, 043614. [Google Scholar] [CrossRef]
- Muñoz Mateo, A.; Delgado, V. Effective mean-field equations for cigar-shaped and disk-shaped Bose-Einstein condensates. Phys. Rev. A 2008, 77, 013617. [Google Scholar]
- Bao, W.; Jaksch, D.; Markowich, P.A. Numerical Solution of the Gross–Pitaevskii Equation for Bose-Einstein Condensation. J. of Comput. Phys. 2003, 187, 318. [Google Scholar]
- Trallero-Giner, C.; Cipolattu, R.; Liew, T.C.H. One-dimensional cubic-quintic Gross–Pitaevskii equation for Bose-Einstein condensates in a trap potential. Eur. Phys. J. D 2013, 67, 143. [Google Scholar] [CrossRef]
- Sanchez-Palencia, L.; Santos, L. Bose-Einstein condensates in optical quasicrystal lattices. Phys. Rev. A 2005, 72, 053607. [Google Scholar] [CrossRef]
- Steurer, W. Twenty years of structure research on quasicrystals. Part I. Pentagonal, octagonal, decagonal and dodecagonal quasicrystals. Z. Kristallogr. 2004, 219, 391. [Google Scholar] [CrossRef]
- Gäler, F. Crystallography of dodecagonal quasicrystals. In Proceedings of the I.L.L./Codest Workshop, Grenoble, France, 21–25 March 1988; World Scientific: Singapore, 1988. [Google Scholar]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492. [Google Scholar] [CrossRef]
- Teichmann, N.; Hinrichis, D.; Holthaus, M. Reference data for phase diagrams of triangular and hexagonal bosonic lattices. Eur. Phys. Lett. 2010, 91, 10004. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379. [Google Scholar] [CrossRef]
- Nesi, F.; Modugno, M. Loss and revival of phase coherence in a Bose-Einstein condensate moving through an optical lattice. J. Phys. B: At. Mol. Opt. Phys. 2004, 37, S101. [Google Scholar] [CrossRef]
- González-García, L.A.; Caballero-Benítez, S.F.; Paredes, R. Localisation of weakly interacting bosons in two dimensions: Disorder vs lattice geometry effects. Sci. Rep. 2019, 9, 11049. [Google Scholar] [CrossRef]
- Bell, R.J.; Dean, P. Atomic Vibrations in Vitreous Silica. Dhcuss. Faraday Soc. 1970, 50, 55. [Google Scholar] [CrossRef]
- Aoki, H. Critical behaviour of extended states in disordered systems. J. Phys. C: Solid State Phys. 1983, 16, L205. [Google Scholar] [CrossRef]
- Aurenhammer, F. Voronoi diagrams a survey of a fundamental geometric data structure. Acm Comput. Surv. 1991, 23, 345–405. [Google Scholar] [CrossRef]
- MATLAB, Version 9.6.0.; (R2019a); The MathWorks Inc.: Natick, MA, USA, 2019.
- Gong, L.; Zhang, J.; Ma, K.; Zhou, X.; Zhai, X.; Cheng, W.; Zhao, S. A novel quantum Shannon entropy as a sensitivity of Anderson transitions: It simultaneously relates to periodic and antiperiodic boundary conditions. EPL 2018, 122, 37002. [Google Scholar] [CrossRef]
- Dey, K.; Das, S.; Sekh, G.A. On the information entropy of matter-waves in quasi-periodic lattice potentials. Eur. Phys. J. D 2019, 73, 18. [Google Scholar] [CrossRef]
- Sriraman, T.; Chakrabarti, B.; Trombettoni, A.; Muruganandam, P. Characteristic features of the Shannon information entropy of dipolar Bose-Einstein condensates. J. Chem. Phys. 2017, 147, 044304. [Google Scholar] [CrossRef]
- Gong, L.; Feng, Y.; Ding, Y. Anderson localization in one-dimensional quasiperiodic lattice models with nearest- and next-nearest-neighbor hopping. Phys. Lett. A 2017, 381, 588. [Google Scholar] [CrossRef]
- Subramanian, P.; Archer, A.J.; Knobloch, E.; Rucklidge, A.M. Spatially localized quasicrystalline structures. New J. Phys. 2018, 20, 122002. [Google Scholar] [CrossRef]
- Romera, E.; de los Santos, F. Identifying Wave-Packet Fractional Revivals by Means of Information Entropy. Phys. Rev. Lett. 2007, 99, 263601. [Google Scholar] [CrossRef] [PubMed]
- Gong, L.; Wei, L.; Zhao, S.; Cheng, W. Comparison of Shannon information entropies in position and momentum space for an electron in one-dimensional nonuniform systems. Phys. Rev. E 2012, 86, 061122. [Google Scholar] [CrossRef] [PubMed]
- Niederle, A.E.; Rieger, H. Superfluid clusters, percolation and phase transitions in the disordered, two-dimensional Bose–Hubbard model. New J. Phys. 2013, 15, 075029. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-García, L.A.; Alva-Sánchez, H.; Paredes, R. Localization in Two-Dimensional Quasicrystalline Lattices. Entropy 2022, 24, 1628. https://doi.org/10.3390/e24111628
González-García LA, Alva-Sánchez H, Paredes R. Localization in Two-Dimensional Quasicrystalline Lattices. Entropy. 2022; 24(11):1628. https://doi.org/10.3390/e24111628
Chicago/Turabian StyleGonzález-García, Luis Antonio, Héctor Alva-Sánchez, and Rosario Paredes. 2022. "Localization in Two-Dimensional Quasicrystalline Lattices" Entropy 24, no. 11: 1628. https://doi.org/10.3390/e24111628
APA StyleGonzález-García, L. A., Alva-Sánchez, H., & Paredes, R. (2022). Localization in Two-Dimensional Quasicrystalline Lattices. Entropy, 24(11), 1628. https://doi.org/10.3390/e24111628





