Generation of Schrödinger Cat States in a Hybrid Cavity Optomechanical System
Abstract
1. Introduction
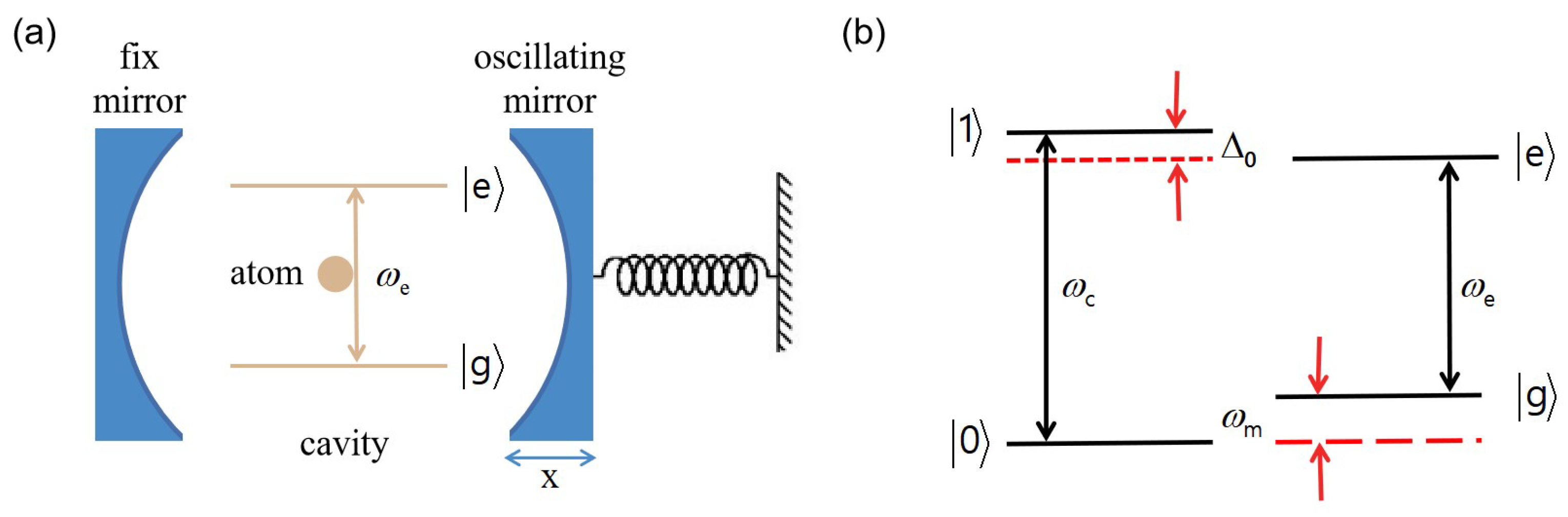
2. Model and Hamiltonian
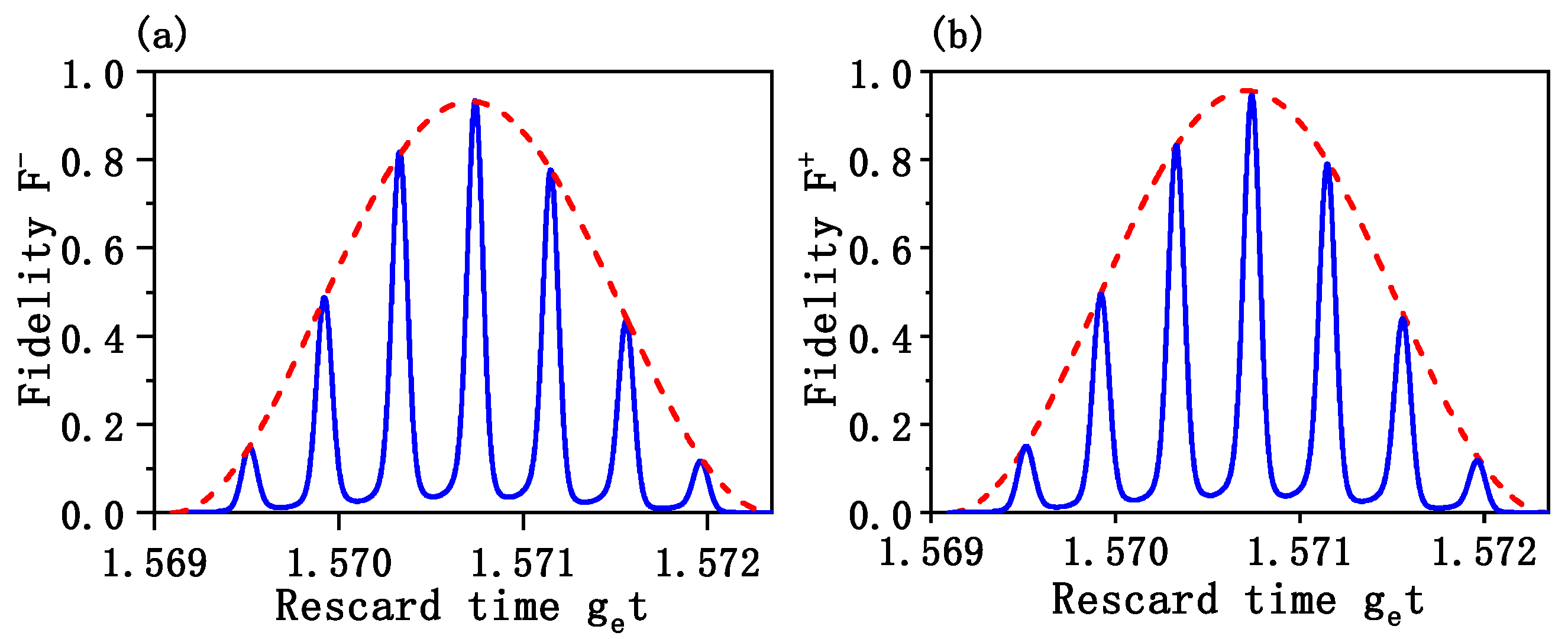
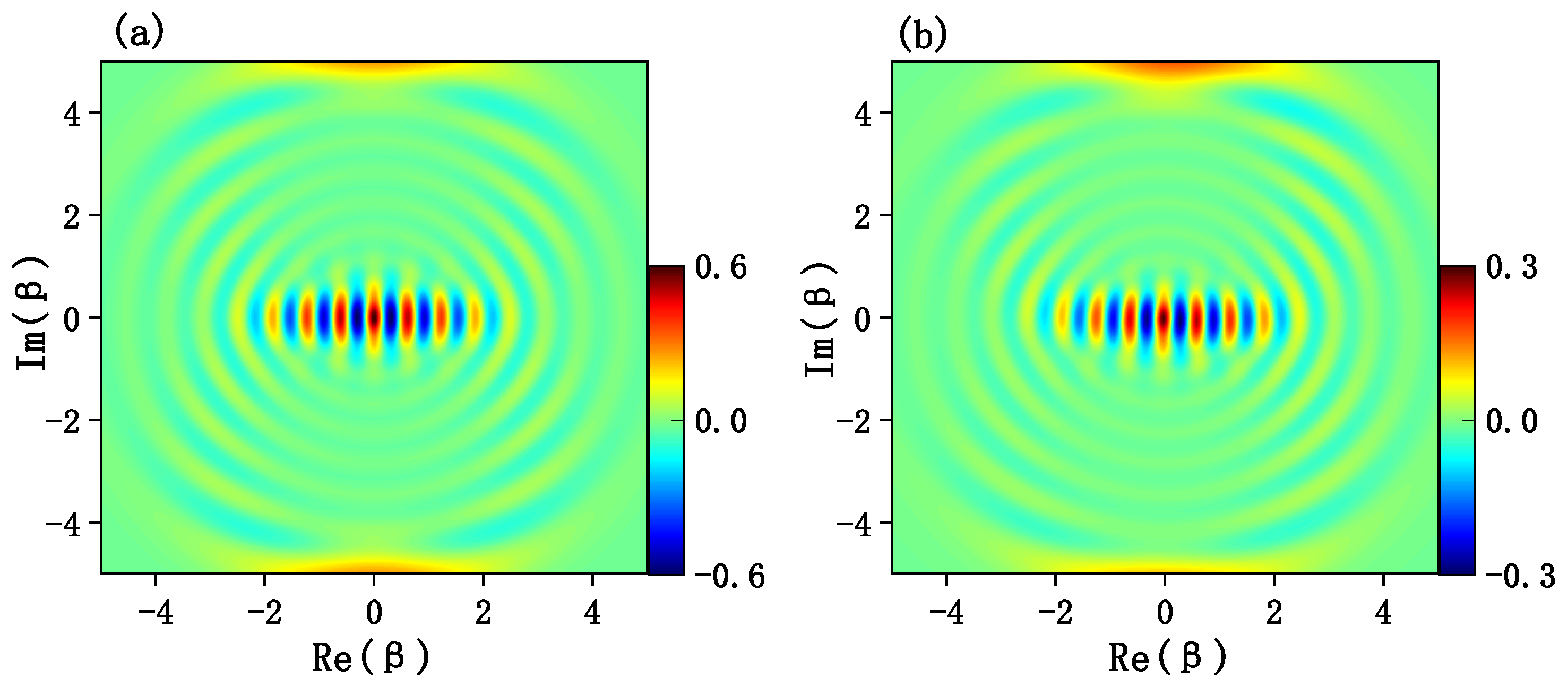
3. Numerical Simulations
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schrödinger, E. Quantisierung als eigenwertproblem. Ann. Phys. 1926, 385, 437–490. [Google Scholar] [CrossRef]
- Deleglise, S.; Dotsenko, I.; Sayrin, C.; Bernu, J.; Brune, M.; Raimond, J.M.; Haroche, S. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 2008, 455, 510–514. [Google Scholar] [CrossRef] [PubMed]
- Solano, E.; Agarwal, G.S.; Walther, H. Strong-driving-assisted multipartite entanglement in cavity QED. Phys. Rev. Lett. 2002, 90, 027903. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Xiong, H. Macroscopical entangled coherent state generator in a V configuration atom system. J. Phys. B 2007, 41, 025501. [Google Scholar] [CrossRef]
- Ma, S.L.; Xie, J.K.; Li, F.L. Generation of superposition coherent states of microwave fields via dissipation of a superconducting qubit with broken inversion symmetry. Phys. Rev. A 2019, 99, 022302. [Google Scholar] [CrossRef]
- Cosacchi, M.; Seidelmann, T.; Wiercinski, J.; Cygorek, M.; Vagov, A.; Reiter, D.E.; Axt, V.M. Schrödinger cat states in quantum-dot-cavity systems. Phys. Rev. Res. 2021, 3, 023088. [Google Scholar] [CrossRef]
- Yang, C.P.; Zheng, Z.F. Deterministic generation of Greenberger-Horne-Zeilinger entangled states of cat state qubits in circuit QED. Opt. Lett. 2018, 43, 5126–5129. [Google Scholar] [CrossRef]
- Van Der Wal, C.H.; Ter Haar, A.; Wilhelm, F.; Schouten, R.; Harmans, C.; Orlando, T.; Lloyd, S.; Mooij, J. Quantum superposition of macroscopic persistent-current states. Science 2000, 290, 773–777. [Google Scholar] [CrossRef]
- Brune, M.; Hagley, E.; Dreyer, J.; Maitre, X.; Maali, A.; Wunderlich, C.; Raimond, J.; Haroche, S. Observing the progressive decoherence of the “meter” in a quantum measurement. Phys. Rev. Lett. 1997, 77, 4887. [Google Scholar] [CrossRef]
- Ourjoumtsev, A.; Jeong, H.; Tualle-Brouri, R.; Grangier, P. Generation of optical ‘Schrödinger cats’ from photon number states. Nature 2007, 448, 784–786. [Google Scholar] [CrossRef]
- Ning, W.; Huang, X.J.; Han, P.R.; Li, H.; Deng, H.; Yang, Z.B.; Zhong, Z.R.; Xia, Y.; Xu, K.; Zheng, D.; et al. Deterministic entanglement swapping in a superconducting circuit. Phys. Rev. Lett. 2019, 123, 060502. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.W.; Pan, X.X.; Cai, W.Z.; Mu, X.H.; Xu, Y.; Hu, L.; Wang, W.T.; Wang, H.Y.; Song, Y.P.; Yang, Z.B.; et al. Manipulating complex hybrid entanglement and testing multipartite Bell inequalities in a superconducting circuit. Phys. Rev. Lett. 2020, 125, 180503. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Vahala, K.J. Cavity Optomechanics: Back-Action at the Mesoscale. Science 2008, 321, 1172–1176. [Google Scholar] [CrossRef]
- Marquardt, F.; Girvin, S.M. Optomechanics. Physics 2009, 2, 40. [Google Scholar] [CrossRef]
- Favero, I.; Karrai, K. Optomechanics of deformable optical cavities. Nat. Photon. 2009, 3, 201–205. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Yang, Y.T.; Callegari, C.; Feng, X.; Ekinci, K.L.; Roukes, M.L. Zeptogram-scale nanomechanical mass sensing. Nano Lett. 2006, 6, 583–586. [Google Scholar] [CrossRef]
- Corbitt, T.; Chen, Y.; Innerhofer, E.; Müller-Ebhardt, H.; Ottaway, D.; Rehbein, H.; Sigg, D.; Whitcomb, S.; Wipf, C.; Mavalvala, N. An all-optical trap for a gram-scale mirror. Phys. Rev. Lett. 2007, 98, 150802. [Google Scholar] [CrossRef]
- Courty, J.M.; Heidmann, A.; Pinard, M. Quantum locking of mirrors in interferometers. Phys. Rev. Lett. 2003, 90, 083601. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Meystre, P.; Schwab, K. Quantum optomechanics. Phys. Today 2012, 65, 29–35. [Google Scholar] [CrossRef]
- Ai, Q.; Li, P.B.; Qin, W.; Zhao, J.X.; Sun, C.P.; Nori, F. The NV metamaterial: Tunable quantum hyperbolic metamaterial using nitrogen vacancy centers in diamond. Phys. Rev. B 2021, 104, 014109. [Google Scholar] [CrossRef]
- Li, B.B.; Ou, L.; Lei, Y.; Liu, Y.C. Cavity optomechanical sensing. Nanophotonics 2021, 10, 2799–2832. [Google Scholar] [CrossRef]
- Lin, Q.; He, B.; Ghobadi, R.; Simon, C. Fully quantum approach to optomechanical entanglement. Phys. Rev. A 2014, 90, 022309. [Google Scholar] [CrossRef]
- Verhagen, E.; Deléglise, S.; Weis, S.; Schliesser, A.; Kippenberg, T.J. Quantum-coherent coupling of a mechanical oscillator to an optical cavity mode. Nature 2012, 482, 63–67. [Google Scholar] [CrossRef]
- Palomaki, T.; Teufel, J.; Simmonds, R.; Lehnert, K.W. Entangling mechanical motion with microwave fields. Science 2013, 342, 710–713. [Google Scholar] [CrossRef]
- Xue, F.; Liu, Y.X.; Sun, C.P.; Nori, F. Two-mode squeezed states and entangled states of two mechanical resonators. Phys. Rev. B 2007, 76, 064305. [Google Scholar] [CrossRef]
- Wu, Y.X.; Guan, Z.Y.; Li, S.; Xue, Z.Y. Fast quantum state transfer and entanglement for cavity-coupled many qubits via dark pathways. Front. Phys. 2022, 17, 42507. [Google Scholar] [CrossRef]
- Paz, J.P.; Roncaglia, A.J. Dynamics of the entanglement between two oscillators in the same environment. Phys. Rev. Lett. 2008, 100, 220401. [Google Scholar] [CrossRef]
- Hartmann, M.J.; Plenio, M.B. Steady state entanglement in the mechanical vibrations of two dielectric membranes. Phys. Rev. Lett. 2008, 101, 200503. [Google Scholar] [CrossRef]
- Vacanti, G.; Paternostro, M.; Palma, G.M.; Vedral, V. Optomechanical to mechanical entanglement transformation. New J. Phys. 2008, 10, 095014. [Google Scholar] [CrossRef]
- Jost, J.D.; Home, J.; Amini, J.M.; Hanneke, D.; Ozeri, R.; Langer, C.; Bollinger, J.J.; Leibfried, D.; Wineland, D.J. Entangled mechanical oscillators. Nature 2009, 459, 683–685. [Google Scholar] [CrossRef]
- Huang, S.; Agarwal, G. Entangling nanomechanical oscillators in a ring cavity by feeding squeezed light. New J. Phys. 2009, 11, 103044. [Google Scholar] [CrossRef]
- Liao, J.Q.; Tian, L. Macroscopic quantum superposition in cavity optomechanics. Phys. Rev. Lett. 2016, 116, 163602. [Google Scholar] [CrossRef]
- Marshall, W.; Simon, C.; Penrose, R.; Bouwmeester, D. Towards quantum superpositions of a mirror. Phys. Rev. Lett. 2003, 91, 130401. [Google Scholar] [CrossRef]
- Zheng, S.B. Scheme for Entangling Two Distant Cavity Mirrors. Commun. Theor. Phys. 2008, 49, 925. [Google Scholar] [CrossRef]
- Liao, J.Q.; Huang, J.F.; Tian, L. Generation of macroscopic Schrödinger-cat states in qubit-oscillator systems. Phys. Rev. A 2016, 93, 033853. [Google Scholar] [CrossRef]
- Abari, N.E.; Naderi, M.H. Generation of the mechanical Schrödinger cat state in a hybrid atom-optomechanical system. J. Opt. Soc. Am. B 2020, 37, 2146–2156. [Google Scholar] [CrossRef]
- Su, Q.P.; Liu, T.; Zhang, Y.; Yang, C.P. Construction of a qudit using Schrödinger cat states and generation of hybrid entanglement between a discrete-variable qudit and a continuous-variable qudit. Phys. Rev. A 2021, 104, 032412. [Google Scholar] [CrossRef]
- Sun, F.X.; Zheng, S.S.; Xiao, Y.; Gong, Q.; He, Q.; Xia, K. Remote generation of magnon Schrödinger cat state via magnon-photon entanglement. Phys. Rev. Lett. 2021, 127, 087203. [Google Scholar] [CrossRef]
- Kienzler, D.; Flühmann, C.; Negnevitsky, V.; Lo, H.Y.; Marinelli, M.; Nadlinger, D.; Home, J.P. Observation of quantum interference between separated mechanical oscillator wave packets. Phys. Rev. Lett. 2016, 116, 140402. [Google Scholar] [CrossRef] [PubMed]
- Safavi Naeini, A.H.; Alegre, T.; Chan, J.; Eichenfield, M.; Winger, M.; Lin, Q.; Hill, J.T.; Chang, D.E.; Painter, O. Electromagnetically induced transparency and slow light with optomechanics. Nature 2011, 472, 69–73. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wu, J.L.; Han, J.X.; Xia, Y.; Jiang, Y.Y.; Song, J. Enhanced Phonon Blockade in a Weakly Coupled Hybrid System via Mechanical Parametric Amplification. Phys. Rev. A 2022, 17, 024009. [Google Scholar] [CrossRef]
- Ran, D.; Shan, W.J.; Shi, Z.C.; Yang, Z.B.; Song, J.; Xia, Y. Generation of nonclassical states in nonlinear oscillators via Lyapunov control. Phys. Rev. A 2020, 102, 022603. [Google Scholar] [CrossRef]
- Qin, W.; Macrì, V.; Miranowicz, A.; Savasta, S.; Nori, F. Emission of photon pairs by mechanical stimulation of the squeezed vacuum. Phys. Rev. A 2019, 100, 062501. [Google Scholar] [CrossRef]
- Zhong, Z.R.; Chen, L.; Sheng, J.Q.; Shen, L.T.; Zheng, S.B. Multiphonon resonance quantum Rabi model and adiabatic passage in a cavity optomechanical system. Front. Phys. 2022, 17, 12501. [Google Scholar] [CrossRef]
- Chen, L.; An, X.W.; Deng, T.H.; Zhong, Z.R. Toward multimode quantum Rabi model in a strong-coupling cavity optomechanical system. Quantum Inf. Process. 2022, 21, 232. [Google Scholar] [CrossRef]
- Pirkkalainen, J.M.; Cho, S.U.; Massel, F.; Tuorila, J.; Heikkilä, T.T.; Hakonen, P.J.; Sillanpää, M. Cavity optomechanics mediated by a quantum two-level system. Nat. Commun. 2015, 6, 6981. [Google Scholar] [CrossRef]
- Zhong, Z.R.; Wang, X.; Qin, W. Towards quantum entanglement of micromirrors via a two level atom and radiation pressure. Front. Phys. 2018, 13, 130319. [Google Scholar] [CrossRef]
- Cotrufo, M.; Fiore, A.; Verhagen, E. Coherent atom-phonon interaction through mode field coupling in hybrid optomechanical systems. Phys. Rev. Lett. 2017, 118, 133603. [Google Scholar] [CrossRef]
- Xiong, B.; Li, X.; Chao, S.L.; Yang, Z.; Zhang, W.Z.; Zhou, L. Generation of entangled Schrödinger cat state of two macroscopic mirrors. Opt. Express 2019, 27, 13547–13558. [Google Scholar] [CrossRef]
- Zeng, Y.X.; Shen, J.; Ding, M.S.; Li, C. Macroscopic Schrödinger cat state swapping in optomechanical system. Opt. Express 2020, 28, 9587–9602. [Google Scholar] [CrossRef] [PubMed]
- Chao, S.L.; Xiong, B.; Zhou, L. Generating a Squeezed-Coherent-Cat State in a Double-Cavity Optomechanical System. Ann. Phys. 2019, 531, 1900196. [Google Scholar] [CrossRef]
- Leibfried, D.; Blatt, R.; Monroe, C.; Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 2003, 75, 281. [Google Scholar] [CrossRef]
- Mahmoudi, Z.; Shakeri, S.; Hamidi, O.; Zandi, M.; Bahrampour, A. Generation of motional entangled coherent state in an optomechanical system in the single photon strong coupling regime. J. Mod. Opt. 2015, 62, 1685–1691. [Google Scholar] [CrossRef]
- Blockley, C.; Walls, D.; Risken, H. Quantum collapses and revivals in a quantized trap. Europhys. Lett. 1992, 17, 509. [Google Scholar] [CrossRef]
- Gerry, C.C. Generation of Schrödinger cats and entangled coherent states in the motion of a trapped ionby a dispersive interaction. Phys. Rev. A 1997, 55, 2478. [Google Scholar] [CrossRef]
- Hood, C.J.; Lynn, T.W.; Doherty, A.C.; Parkins, A.S.; Kimble, H.J. The atom-cavity microscope: Single atoms bound in orbit by single photons. Science 2000, 287, 1447–1453. [Google Scholar] [CrossRef]
- Mabuchi, H.; Ye, J.; Kimble, H.J. Full observation of single-atom dynamics in cavity QED. Appl. Phys. B 1999, 68, 1095–1108. [Google Scholar] [CrossRef]
- Ye, J.; Vernooy, D.W.; Kimble, H.J. Trapping of single atoms in cavity QED. Phys. Rev. Lett. 1999, 83, 4987. [Google Scholar] [CrossRef]
- Rabl, P. Photon blockade effect in optomechanical systems. Phys. Rev. Lett. 2011, 107, 063601. [Google Scholar] [CrossRef]
- Arcizet, O.; Cohadon, P.F.; Briant, T.; Pinard, M.; Heidmann, A. Radiation-pressure cooling and optomechanical instability of a micromirror. Nature 2006, 444, 71–74. [Google Scholar] [CrossRef] [PubMed]
- Gigan, S.; Böhm, H.R.; Paternostro, M.; Blaser, F.; Langer, G.; Hertzberg, J.B.; Schwab, K.C.; Bäuerle, D.; Aspelmeyer, M.; Zeilinger, A. Self-cooling of a micromirror by radiation pressure. Nature 2006, 444, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Brune, M.; Haroche, S.; Raimond, J.M.; Davidovich, L.; Zagury, N. Manipulation of photons in a cavity by dispersive atom field coupling: Quantum nondemolition measurements and generation of “Schrödinger cat”states. Phys. Rev. A 1992, 45, 5193. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, X.; Deng, T.; Chen, L.; Ye, S.; Zhong, Z. Generation of Schrödinger Cat States in a Hybrid Cavity Optomechanical System. Entropy 2022, 24, 1554. https://doi.org/10.3390/e24111554
An X, Deng T, Chen L, Ye S, Zhong Z. Generation of Schrödinger Cat States in a Hybrid Cavity Optomechanical System. Entropy. 2022; 24(11):1554. https://doi.org/10.3390/e24111554
Chicago/Turabian StyleAn, Xingwei, Tonghui Deng, Lei Chen, Saiyun Ye, and Zhirong Zhong. 2022. "Generation of Schrödinger Cat States in a Hybrid Cavity Optomechanical System" Entropy 24, no. 11: 1554. https://doi.org/10.3390/e24111554
APA StyleAn, X., Deng, T., Chen, L., Ye, S., & Zhong, Z. (2022). Generation of Schrödinger Cat States in a Hybrid Cavity Optomechanical System. Entropy, 24(11), 1554. https://doi.org/10.3390/e24111554




