Abstract
Recently, an image encryption scheme based on a 2D hyperchaotic map is proposed. It adopts the permutation–diffusion architecture and consists of three steps, which are permutation, forward diffusion, and backward diffusion. In this paper, we break this cipher with both the chosen-plaintext attack (CPA) and the chosen-ciphertext attack (CCA). According to our analysis, we found the two complex diffusion processes could be simplified into two simple diffusions and a modular addition operation. Based on this, the equivalent key can be obtained with CPA and CCA. Detailed theoretical derivations and the results of experiments confirmed the feasibility of our attack methods. When the image size was , the running time of the attacks was less than 2 hours on a laptop with a 2.59 GHz Intel Core i7 and 16 GB DDR3 memory. Other sizes of images were also tested, and some rules were found. In addition, the probability of other attacks has also been discussed, and some suggestions for improvements are given. The source codes are publicly available and can be found online.
Keywords:
image encryption; permutation; diffusion; chosen-plaintext attack; chosen-ciphertext attack MSC:
37N99
1. Introduction
With the dramatic developments of communication technology, we have witnessed in recent years increasing popularity of secure transmission of multimedia data. The image is a common data model, and cryptographic methods are of critical importance for information sharing. Unfortunately, images are different from text in terms of their inherent properties, such as the large data volume and high redundancy [1,2,3]. If we use the traditional textual encryption methods such as 3DES and AES to encrypt images, it tends to lead to low efficiency and cannot fulfill the requirement of real-time transmission. Therefore, many encryption methods specifically for images have been proposed [4,5].
Due to the features of initial value sensitivity, ergodicity, and random similarity [6,7], chaotic systems are able to meet the needs of encryption processes. Many encryption schemes based on chaos have been proposed [8,9,10,11,12]. Fridrich proposed the first permutation–diffusion architecture image encryption scheme in 1998 [1], which became a paradigm adopted by other people. Some encryption schemes combined various mathematical theories of interesting problems [13,14]; for example, Josephus Problem was employed in [13] for designing a secure and efficient image encryption scheme. Some encryption schemes combine DNA coding technologies to acquire the confusion effect similarly to S-box [15,16,17]. Most schemes encrypt the image as a whole, but a few methods divide the image into several small blocks for encryption; e.g., Zhang et al. [18] decomposed the plaintext image into two components, achieving faster encryption speed and higher security. Most of these methods are a combination of permutation and diffusion operations, but there exist a few permutation-only methods, such as [19].
Although many image encryption schemes, to the best of our knowledge, have been proposed in the past few decades, so far no one has matched the security and applicability of AES, which is a widely accepted approach. In fact, many of them fail to meet actual encryption requirements and have been proven to be less secure than was thought when they were proposed [20]. A typical image encryption method [21] based on chaos which consists of two rounds of permutation–diffusion operations was cryptanalyzed by Chen et al. [22]. They found the relationship between the plaintext images and ciphertext images and proposed a chosen-plaintext attack. Some algorithms combined with DNA operations were attacked not long after they were proposed, e.g., [23]. The opponent used the chosen-plaintext attack [24] which regarded the complex DNA operations as the S-box and got the equivalent encryption elements. We can see a similar idea in [25,26]. More similar works can be seen in [27,28,29,30,31].
Permutation and diffusion are two operations that are commonly used in image encryption schemes [32]. The permutation process only scrambles the position of the plaintext pixels, whereas the diffusion changes the value of pixels to obtain an avalanche effect. In 2010, Fridrich’s premutation was cryptanalyzed by Solak et al. [33]. From then on, a series of studies have proven that most of the proposed permutation-only encryption algorithms are insecure against plaintext attacks. Zhang et al. [34] proposed an attack method making the tradeoffs between time and memory. Jolfaei et al. [2] minimized the required conditions by taking advantage of the pigeon nest principle. Accordingly, the diffusion operation was also analyzed in [35,36]. Chen et al. [37] further improved the efficiency of the attack. The general cryptanalysis of permutation–diffusion architecture image algorithm can be found in [38,39]. In addition, there can be different attacks for different encryption schemes. As it turns out, it is not enough to evaluate the security level of an image cipher by the number of pixels change rate (NPCR) and the unified average changing intensity (UACI), etc.
Recently, a novel image encryption algorithm based on 2D hyperchaotic map was proposed by Gao et al. [40]. The authors introduced a new 2D hyperchaotic map which had more complex chaotic behaviors than other chaotic systems. NPCR and UACI were tested to value the security level of the scheme. The encryption scheme consists of three steps, which are permutation, forward diffusion, and backward diffusion. However, according to our analysis, the two complex diffusion processes could be regarded as the combinations of two simple diffusion processes and a modular addition operation. Considering the diffusion processes, only a plaintext–ciphertext pair is sufficient to obtain the equivalent key. Based on this, we found it is vulnerable to both chosen-plaintext attacks and chosen-ciphertext attacks. Theoretical deductions and the results of experiment confirmed the feasibility of our attacks.
Our contributions are summarized as follows.
- An image encryption scheme was broken by both CCA and CPA.
- The equivalent process of original encryption algorithm is given.
- Detailed theoretical derivations and experimental results are given to confirm the feasibility of our approaches.
- The probabilities of other attack methods and some suggestions for improvements are also given.
The remainder of this paper is organized as follows. The second section briefly introduces the original image encryption scheme. Section 3 shows the theoretical analysis and derivation. Section 4 presents the equivalent process of the original image encryption scheme and the details of attacks. Experimental results are provided in Section 5. The possibility of other attacks and some suggestions for improvements are also discussed in Section 5. Finally, the last section concludes this work.
2. The Original Image Encryption Scheme
We briefly summarize the encryption scheme, and interested readers can find more details in [40].
2.1. Notation
Most of the notation adopted is listed in Table 1. Complementary descriptions are described as follows:

Table 1.
Summary of the notation.
- Generally, P and C denote the plaintext and ciphertext in an encryption scheme, respectively, and S refers to the intermediate result in a process. The plaintext image P is assumed to have a size of .
- The modular subtraction of two plaintext images is defined as their differential, denoted as .
- The notation T represents the equivalent key matrix of the diffusion process. The notation represents the intermediate result of the target plaintext image and ciphertext image.
2.2. The Encryption Procedures
The encryption scheme under study is a permutation–diffusion architecture. It consists of four steps: row shifting, column shifting, forward diffusion and backward diffusion. The row and column shifting can be considered as permutation operations, and the subsequent operations are diffusion. Figure 1 is an overall flowchart of the encryption scheme. The function max() returns the greater number of x and y. The secret key generates encryption elements through the chaotic system for the encryption process.
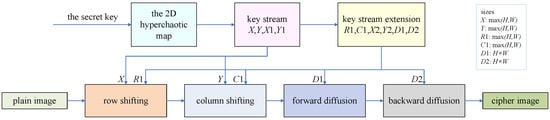
Figure 1.
Diagram of the encryption process.
- Generation of the key stream.
- (a)
- Iterate the following 2D hyperchaotic system, i.e., Equation (1), times to obtain the secret key flow sequence X and Y of the permutation process, where N is the greater number of H and W. The sequences X and Y discarded the first m values to get the more stable chaotic sequences. The parameters and initial values of the 2D hyperchaotic map, which include and , are the secret keys of the encryption scheme, where and . In the original encryption paper, the author used and Y(0) = Interested readers can find more information about the 2D hyperchaotic map in [40,41,42].
- (b)
- Vectors and for permutation are generated by X and Y through Equation (2). The function floor() rounds the original number to the nearest integer less than or equal to it.
- (c)
- Iterate the same chaotic system, i.e., Equation (1), () times to obtain the secret key flow sequence and . The sequences and discard the first n values to get the more stable chaotic sequences. The sequences and are then obtained by Equation (3). The function round() rounds the original number to the nearest integer.
- (d)
- Finally, we can get the matrixes and for forward and backward diffusion from and by Equation (4). The function reshape() is used to change the size of a matrix. If the input is a matrix of size and the output is a matrix of size , then it must satisfy . The elements of the matrix are read by column and stored by column. The function reshape returns the M-by-N matrix whose elements are taken column-wise from X.
- Row shiftingThe image P is row-permuted with chaotic sequences X and . The permutation principles are shown in Figure 2. For the input image with size , , when , the principle is shown in Figure 2a; for , the process is shown in Figure 2b.
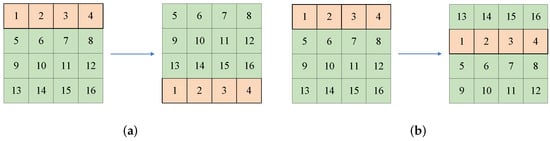 Figure 2. The permutation principle of rows: (a) the permutation principle of the image when and ; (b) the permutation principle of image when and .
Figure 2. The permutation principle of rows: (a) the permutation principle of the image when and ; (b) the permutation principle of image when and . - Column shifting Similarly, the column-permuted result is obtained by chaotic sequences Y and . The permutation principles are shown in Figure 3. For the input image with size , , when , the principle is shown in Figure 3a; when , the process is shown in Figure 3b.
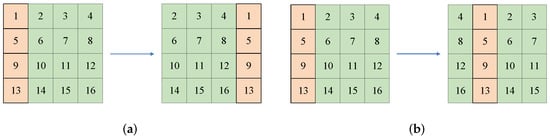 Figure 3. The permutation principle of columns: (a) the permutation principle of the image when and ; (b) the permutation principle of image when and .
Figure 3. The permutation principle of columns: (a) the permutation principle of the image when and ; (b) the permutation principle of image when and . - Forward diffusionWith the help of generated before, the forward diffusion is implemented according to Equation (5), in which is the forward diffusion result and represents the input image after row and column shifting, ; .
- Backward diffusion Similarly, the backward diffusion process is performed with the matrix , which is generated before. The diffusion operation is described in Equation (6), where C is the final encryption result; ; .
3. Security Analysis
The original encryption scheme has two main steps, which are permutation and diffusion. The secret key generates the key stream at each step through a novel chaotic system. For the permutation phase, we use a permutation matrix as the equivalent key. For the diffusion phase, the equivalent keys are two matrices. According to our analysis, it is enough to use only one matrix as the equivalent key in the diffusion phase.
Before describing the attack method, we give some necessary conclusions and prove them.
Theorem 1.
If we only consider the diffusion phase of the encryption scheme, each pixel value of the ciphertext is the sum of the pixel values of the plaintext and the corresponding location value of the equivalent key matrix, which is given by
where represents a variable that is related to the values of plaintext and its location and represents the corresponding value of the equivalent key matrix T which is dependent on the secret key.
Proof of Theorem 1.
We prove the forward diffusion process, which has four diffusion principles. The backward diffusion is symmetric with the forward diffusion and has the same theorem.
- For the first formula of the forward diffusion phase, i.e., the first subformula of Equation (5), we are able to obtain
- For the second formula of the forward diffusion phase, it is derived by:If we add both sides of this equation, we get
- The derivation of the third part is very similar to that of the second stage. For the third formula of forward diffusion, it is deduced from:Similarly, we can conclude
- In this section, we use a method which is similar to mathematical induction. As shown in Figure 4, if we assume that both pixel values, a and b, satisfy Equation (7), which is able to deduce that the value c also satisfies Equation (7), then if both the pixels of the first row and first column satisfy Equation (7), we can deduce that all the pixels satisfy Equation (7). It seems that this theorem will be transferred from the left and upper pixels to the middle pixels.
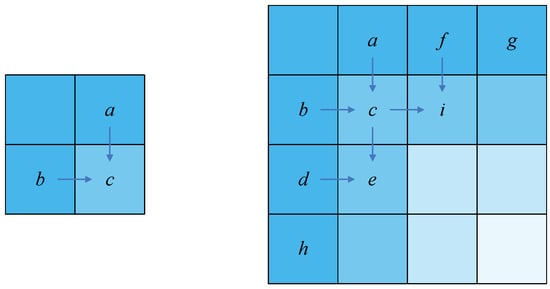 Figure 4. Schematic diagram of induction.If we suppose Equations (12) and (13) are correct and substitute Equations (12) and (13) into the last formula of forward diffusion, we can obtain Equation (14).
Figure 4. Schematic diagram of induction.If we suppose Equations (12) and (13) are correct and substitute Equations (12) and (13) into the last formula of forward diffusion, we can obtain Equation (14).
□
Theorem 2.
If we only consider the diffusion phase, the differential of ciphertexts is related to the differential of plaintexts. More specifically, the module subtraction of the pixel value of the ciphertext images is the module subtraction of the plaintext images after the diffusion process without encryption parameters.
Proof of Theorem 2.
From the conclusion in Theorem 1, we can obtain
□
4. The Proposed Attack
4.1. The Equivalent Processes
According to our analysis, the original encryption algorithm is equivalent to the combination of some simple processes, in which the encryption elements consist of a permutation matrix and an equivalent diffusion matrix.
4.1.1. The Equivalent Encryption Process
The equivalent encryption process comprises four phases, i.e., permutation, simple forward diffusion, simple backward diffusion, and modular addition with the equivalent key matrix.
- PermutationThe plaintext image permutes its pixels with the permutation matrix through Equation (16). An illustration is shown in Figure 5.
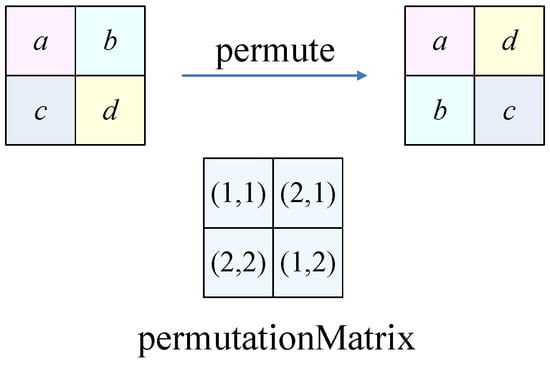 Figure 5. The equivalent permutation.
Figure 5. The equivalent permutation. - Simple forward diffusionThe simple forward diffusion is implemented according to Equation (17), where is the simple forward diffusion result, S represents the input image after permutation, and ; .
- Simple backward diffusionSimilarly, the simple backward diffusion operation is described in Equation (18), where is the diffusion result; ; .
- Modular addition with the equivalent keyThe final ciphertext image C will be generated using the diffusion result and the equivalent key matrix T through Equation (19).
4.1.2. The Decryption Process
Corresponding to the equivalent encryption process, the decryption process consists of four steps. They are modular subtraction, inverse backward diffusion, inverse forward diffusion, and inverse permutation.
- Modular subtraction with an equivalent key matrixThe immediate result S2 will be obtained from Equation (20), where C represents the final ciphertext image and T represents the equivalent key matrix.
- Inverse backward diffusion
- Inverse forward diffusion
- Inverse permutationThe plaintext image P will be obtained using the intermediate result S and permutation matrix from Equation (23). An illustration is shown in Figure 6.
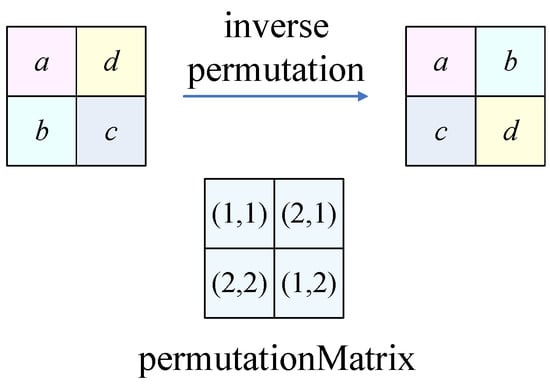 Figure 6. The inverse permutation.
Figure 6. The inverse permutation.
4.2. The Proposed Chosen-Plaintext Attack
In a chosen-plaintext attack scenario, the attackers can freely select a set of plaintexts and get the corresponding ciphertexts. Then, the information of secret key or encryption elements will be derived by these known plaintext–ciphertext pairs. The attackers use them to recover the target plaintext.
When we take an all-zero image as input, the permutation result is also an all-zero image. Then, we use the images before and after diffusion to obtain the equivalent key at this stage. When encryption elements in the diffusion stage are acquired, the encryption algorithm is simplified into a permutation process. The special plaintext–ciphertext pairs are then constructed to obtain the equivalent permutation matrix. Finally, we recover the plaintext using the previously obtained equivalent key.
Algorithm 1 reveals the process of the proposed chosen-plaintext attack. The details of Algorithm 1 are described below.
| Algorithm 1 The proposed chosen-plaintext attack |
|
- Construct an all-zero matrix and obtain the equivalent key T.
- The permutation process has no effect on an all-zero image, so we can get one pair of input and output of the diffusion phase.
- According to Theorem 1, i.e., , when , then .
- Initialize matrices and get the corresponding ciphertexts
- The function JolfaeiAlgorithmGeneration() is used to generate specially designed plaintexts of JolfaeiAlgorithm(). The function JolfaeiAlgorithmAdd() takes the specially designed plaintext–ciphertext pairs as input to the JolfaeiAlgorithm(). Readers can find more information in Appendix A.
- Obtain middle results with the diffusion matrix T.
- Obtain the equivalent permutation matrix
- The function JolfaeiAlgorithm(), i.e., Jolfaei’s algorithm [2], is a chosen-plaintext attack method for permutation-only image encryption algorithms. Interested readers can find more details in Appendix A.
- Recover the plaintext
- The function inversePermute() refers to the process of Equation (23).
4.3. The Proposed Chosen-Ciphertext Attack
In cryptanalysis, in contrast to chosen-plaintext attack, chosen-ciphertext attackers are able to obtain the plaintexts of the ciphertexts which they specially designed. After that, attackers acquire secret encryption elements or equivalent key streams. The plaintext that attackers wish to recover is retrieved after easily obtaining the necessary information.
For the current encryption algorithm under study, we found that making a differential of the ciphertexts eliminates the equivalent key stream of the diffusion phase. With this property, we can simplify the encryption algorithm to a permutation-only process. We can use the existing algorithm to obtain the equivalent permutation matrix. After obtaining the middle results, we can also obtain the equivalent key of diffusion. When all the necessary information has been collected, we then recover the plaintext as we did in chosen-plaintext method.
Algorithm 2 discloses the process of the proposed chosen-ciphertext attack. The details of Algorithm 2 are described below.
| Algorithm 2 The proposed chosen-ciphertext attack |
|
- Construct ciphertext–plaintext pairs and compute the differentials.
- Get the equivalent permutation matrix
- The differential of plaintexts and the differential of ciphertexts follow the same permutation principle. Thus, we can use these differentials to obtain the permutation matrix by Jolfaei’s algorithm.
- Obtain an intermediate result with the permutation matrix.
- The function permute() is the process of Equation (16).
- Obtain the equivalent key stream matrix of the diffusion process
- According to Theorem 1, i.e., , when and , then .
- Recover the plaintext
5. Experiments and Discussions
5.1. Experimental Results
This section presents the experiment results, which well validate the feasibility of our attack (The test images. Available online: https://sipi.usc.edu/database/database.php?volume=misc (accessed on 20 October 2022)). The proposed attacks and the studied encrytption schemes were implemented by simulations using matlab 2021a on a laptop with specifications of 2.59 GHz Intel Core i7 and 16 GB DDR3 memory, and the source code is openly accessible (The source code. Available online: https://github.com/F-cook/attack_test.git (accessed on 20 October 2022)).
The experimental results show the plaintext image was recovered successfully. The recovered image is exactly same as the plaintext image. Both CCA and CPA recovered the image without any error. When the image size was , the running time of CPA was 6776.714213s, and that of CCA was 6754.676951s. The original image is shown in Figure 7a, and the encrypted is shown in Figure 7b. Figure 7c shows the image recovered by CPA, and Figure 7d shows the image recovered by CCA.

Figure 7.
Numerical simulation results: (a) the original pepper image of size and pixel gray values vary from 0 to 255; (b) the encrypted ciphertext image; (c) the recovered image using the chosen-plaintext attack; (d) the recovered image using the chosen-ciphertext attack.
In addition, other sizes of images were also tested in our experiments. The running times of our attacks on different sizes of images are shown in Figure 8. All the images which were tested in our experiments are gray images. The original encryption scheme was designed for gray images and regards a color image as three gray images. Therefore, our methods are also applicable to color images, and the attack time on a color image is three times as long as that on a gray image of the same size.
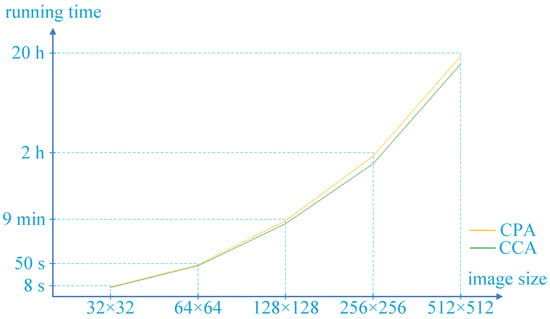
Figure 8.
The running times of the CPA and CCA.
It is worth mentioning that all the experimental results were obtained in our computing environment, which was a laptop with computing specifications of 2.59 GHz Intel Core i7 and 16 GB DDR3 memory. The running time of attack methods varied greatly in different environments.
It is found that as the image size becomes greater, the running time of the CPA and CCA increases rapidly. The CPA is a little faster than CCA. This is because the CCA needs to build more complex inputs to obtain the equivalent secret key.
5.2. The Probabilities of Other Attacks
As mentioned above, chosen-plaintext and chosen-ciphertext attacks are effective against the original encryption algorithm, and both attack methods exploit the weaknesses of the scheme. Below we briefly discuss the feasibility of known-plaintext and ciphertext-only attacks.
In the scenario of a known-plaintext attack, the attacker has a set of ciphertexts to which they know the corresponding plaintexts. The attacker cannot control the plaintext–ciphertexts pairs. In this case, random plain-ciphertext pairs often bring redundant information that is helpful in attacking the secret key system. If only the scrambling process is considered, in order to obtain a complete equivalent key stream, an extremely large number of random plaintext and ciphertext pairs are required, which makes it impossible to implement an attack in reality.
If an encryption system is resistant to known-plaintext attacks, then it must be resistant to ciphertext-only attacks. In the scenario of a ciphertext-only attack, the cryptanalyst has access only to a collection of ciphertexts. Attackers can generally guess the ciphertext corresponding to some plaintexts based on some plaintext format information, etc., and infer the secret key information based on the correspondence between very few plaintext ciphertexts. However, for the encryption system analyzed in this article, it is difficult to obtain a small amount of guessed information, and it is impossible to crack the entire encryption system.
5.3. Some Suggestions for Improvements
The original encryption scheme is vulnerable to both chosen-plaintext and chosen-ciphertext attacks. The complex encryption can be equivalent to simple processes, and the equivalent key can be obtained by CCA or CPA. In order to improve the security of the original encryption algorithm, some potentially useful suggestions are given below.
- It is suggested that the secret key includes plaintext-related information. The plaintext-dependent ciphers are highly resistant to plaintext attacks. Hash value and the hamming distance are common technologies which have high security.
- Multiple rounds of encryption are recommended. Multiple rounds of encryption help ciphers to achieve a high level of security. Different keys can be used in different rounds, but there should not be too many rounds so as not to affect the encryption efficiency.
- Some random information can be added to the encryption process. Random encryption elements cannot be obtained by various attacks and are very helpful to improve the security level of the encryption scheme.
5.4. Limitations and Future Works
Our proposed attack methods, which include CPA and CCA, are special for the original encryption scheme. In other words, they are not universal and cannot be applied to other different image ciphers. However, the idea of obtaining the equivalent key and eliminating the diffusion process may be applied to future cryptanalysis works. In addition, the original encryption scheme may have other flaws which can be used to break it. The permutation process is line by line, which will lead to unrandom results. There may be a more simple way to break the scheme. We only demonstrated the feasibility of our approaches in this paper.
We will explore the more general method to break a family of image encryption schemes. These schemes may have similar encryption processes or common weaknesses. We will use the weaknesses to obtain the equivalent key to break the scheme. More effective attack methods will be proposed. The corresponding suggestions will be also given to resist similar attacks. We believe that better image encryption schemes will be designed in the future.
6. Conclusions
In this paper, a permutation–diffusion image encryption based on a 2D hyperchaotic cap was cryptanalyzed, and two attacks, CPA and CCA, were proposed. The equivalent key of the original encryption was obtained, and the transformed process was also described in detail. The theory of the attack method was given by the detailed formula derivation. Different sizes of images were tested in the experiments to demonstrate the feasibility of the two attacks. The other attacks were discussed, and some suggestions for improvements were given. We believe that the ideas of this paper will provide an example of similar cryptanalysis works and give suggestions for the design of image schemes in the future.
Author Contributions
C.Z. carried out numerical simulation and analysis; J.C. and D.C. studied the proofs of relevant theories; C.Z. wrote the paper; J.C. and D.C. revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (number 62171114), the Key Technologies Research and Development Program of Liaoning Province in China (number 2021JH1/10400079) and the Fundamental Research Funds for the Central Universities under grant 2217002.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The image data are available in: https://sipi.usc.edu/database/database.php?volume=misc (accessed on 20 October 2022). The source codes are open and can be found in: https://github.com/F-cook/attack_test.git (accessed on 20 October 2022).
Acknowledgments
Special thanks to ABDULHAMID VICTOR IBRAHIM for his editing and modification of the paper.
Conflicts of Interest
The authors declare that they have no conflict of interest.
Appendix A. The introduction of Jolfaei’s Algorithm
Jolfaei’s algorithm [2] is a chosen-plaintext attack for permutation-only ciphers. When the size of plaintext image is , the required plaintext–ciphertext pairs are .
Permutation processes change the positions of pixels of the input image. An image which is of size with L different color intensities has locations and at most L different pixel values. Thus, one plaintext–ciphertext image pair determines at most L positions of an image. The number n of plaintext–ciphertext image pairs required to break the permutation-only image cipher must satisfy Equation (A1).
Furthermore, we get Equation (A2).
Based on Equation (A2), we found that the number n is at least log. To minimize the amount of chosen plain images required, we designed the plaintext with specific rules.
To illustrate the special plaintext design rule, consider a image. If the , then the permutation can be determined by plaintext–ciphertext image pairs. The three special plaintext images are shown in Figure A1. The chosen-plaintext images are obtained by splitting the first image into three. The complete permutation rules are obtained by these chosen-plaintext images and their ciphertext images.
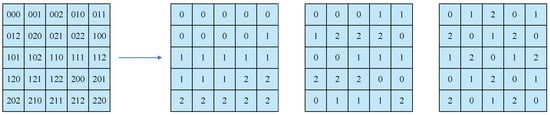
Figure A1.
The chosen plaintext images.
Lastly, we utilize an example to illustrate the complete attack procedure. We propose a permutation principle, which is shown in Figure A2, and . The complete attack process for obtaining the permutation matrix is shown in Figure A3. Firstly, we construct the chosen plaintexts from the plaintext image. Then we obtain the ciphertexts corresponding to the chosen plaintexts. After that, we find all possible cases based on the obtained plaintext–ciphertext pairs. Finally, we obtain the correct scrambling rule by taking the intersection of all possible outcomes.

Figure A2.
The supposed premutation principle.
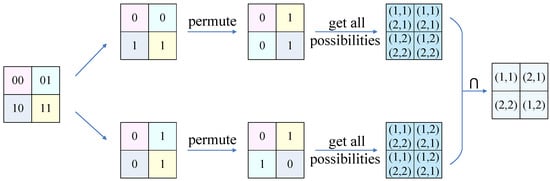
Figure A3.
The complete attack process.
References
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Jolfaei, A.; Wu, X.W.; Muthukkumarasamy, V. On the security of permutation-only image encryption schemes. IEEE Trans. Inf. Forensics Secur. 2015, 11, 235–246. [Google Scholar] [CrossRef]
- Wang, W.; Yu, X.; Fang, B.; Zhao, D.Y.; Chen, Y.; Wei, W.; Chen, J. Cross-modality LGE-CMR Segmentation using Image-to-Image Translation based Data Augmentation. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022. [Google Scholar] [CrossRef] [PubMed]
- Laiphrakpam, D.S.; Thingbaijam, R.; Singh, K.M.; Al Awida, M. Encrypting Multiple Images With an Enhanced Chaotic Map. IEEE Access 2022, 10, 87844–87859. [Google Scholar] [CrossRef]
- Alawida, M.; Teh, J.S.; Mehmood, A.; Shoufan, A. A chaos-based block cipher based on an enhanced logistic map and simultaneous confusion-diffusion operations. J. King Saud-Univ.-Comput. Inf. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Zhang, L.Y.; Pareschi, F.; Setti, G.; Chen, G. From Chaos to Pseudorandomness: A Case Study on the 2-D Coupled Map Lattice. IEEE Trans. Cybern. 2021, 1–11. [Google Scholar] [CrossRef]
- Alawida, M.; Teh, J.S.; Oyinloye, D.P.; Ahmad, M.; Alkhawaldeh, R.S. A new hash function based on chaotic maps and deterministic finite state automata. IEEE Access 2020, 8, 113163–113174. [Google Scholar] [CrossRef]
- Huang, X.; Nia, M.; Ding, Q. Research on image encryption based on hyperchaotic system. J. Netw. Intell. 2020, 5, 10–22. [Google Scholar]
- Suryanto, Y.; Suryadi, M.; Ramli, K. A Secure and Robust Image Encryption Based on Chaotic Permutation Multiple Circular Shrinking and Expanding. J. Inf. Hiding Multim. Signal Process. 2016, 7, 697–713. [Google Scholar]
- Feng, W.; Zhao, X.; Zhang, J.; Qin, Z.; Zhang, J.; He, Y. Image encryption algorithm based on plane-level image filtering and discrete logarithmic transform. Mathematics 2022, 10, 2751. [Google Scholar] [CrossRef]
- Cassal-Quiroga, B.B.; Campos-Cantón, E. Generation of dynamical S-boxes for block ciphers via extended logistic map. Math. Probl. Eng. 2020, 2020, 2702653. [Google Scholar] [CrossRef]
- García-Martínez, M.; Ontañón-García, L.; Campos-Cantón, E.; Čelikovskỳ, S. Hyperchaotic encryption based on multi-scroll piecewise linear systems. Appl. Math. Comput. 2015, 270, 413–424. [Google Scholar] [CrossRef]
- Hua, Z.; Xu, B.; Jin, F.; Huang, H. Image encryption using Josephus problem and filtering diffusion. IEEE Access 2019, 7, 8660–8674. [Google Scholar] [CrossRef]
- Chen, J.; Sun, S.; Zhang, L.b.; Yang, B.; Wang, W. Compressed sensing framework for heart sound acquisition in internet of medical things. IEEE Trans. Ind. Inform. 2022, 18, 2000–2009. [Google Scholar] [CrossRef]
- Wang, S.; Peng, Q.; Du, B. Chaotic color image encryption based on 4D chaotic maps and DNA sequence. Opt. Laser Technol. 2022, 148, 107753. [Google Scholar] [CrossRef]
- Qian, K.; Feng, W.; Qin, Z.; Zhang, J.; Luo, X.; Zhu, Z. A novel image encryption scheme based on memristive chaotic system and combining bidirectional bit-level cyclic shift and dynamic DNA-level diffusion. Front. Phys. 2022, 718. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z.L.; Zhang, L.B.; Zhang, Y.; Yang, B.Q. Exploiting self-adaptive permutation–diffusion and DNA random encoding for secure and efficient image encryption. Signal Process. 2018, 142, 340–353. [Google Scholar] [CrossRef]
- Zhang, Y. The fast image encryption algorithm based on lifting scheme and chaos. Inf. Sci. 2020, 520, 177–194. [Google Scholar] [CrossRef]
- Ye, G. Image scrambling encryption algorithm of pixel bit based on chaos map. Pattern Recognit. Lett. 2010, 31, 347–354. [Google Scholar] [CrossRef]
- Alawida, M.; Omolara, A.E.; Abiodun, O.I.; Al-Rajab, M. A deeper look into cybersecurity issues in the wake of Covid-19: A survey. J. King Saud-Univ.-Comput. Inf. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Hua, Z.; Yi, S.; Zhou, Y. Medical image encryption using high-speed scrambling and pixel adaptive diffusion. Signal Process. 2018, 144, 134–144. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, C.; Ye, R. Cryptanalysis and improvement of medical image encryption using high-speed scrambling and pixel adaptive diffusion. Signal Process. 2020, 167, 107286. [Google Scholar] [CrossRef]
- Wu, J.; Liao, X.; Yang, B. Image encryption using 2D Hénon-Sine map and DNA approach. Signal Process. 2018, 153, 11–23. [Google Scholar] [CrossRef]
- Chen, J.; Chen, L.; Zhou, Y. Cryptanalysis of a DNA-based image encryption scheme. Inf. Sci. 2020, 520, 130–141. [Google Scholar] [CrossRef]
- Feng, W.; Qin, Z.; Zhang, J.; Ahmad, M. Cryptanalysis and improvement of the image encryption scheme based on Feistel network and dynamic DNA encoding. IEEE Access 2021, 9, 145459–145470. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J. Cryptanalzing a novel hyper-chaotic image encryption scheme based on pixel-level filtering and DNA-level diffusion. IEEE Access 2020, 8, 209471–209482. [Google Scholar] [CrossRef]
- Munir, N.; Khan, M.; Jamal, S.S.; Hazzazi, M.M.; Hussain, I. Cryptanalysis of hybrid secure image encryption based on Julia set fractals and three-dimensional Lorenz chaotic map. Math. Comput. Simul. 2021, 190, 826–836. [Google Scholar] [CrossRef]
- Munir, N.; Khan, M.; Al Karim Haj Ismail, A.; Hussain, I. Cryptanalysis and Improvement of Novel Image Encryption Technique Using Hybrid Method of Discrete Dynamical Chaotic Maps and Brownian Motion. Multimed. Tools Appl. 2022, 81, 6571–6584. [Google Scholar] [CrossRef]
- Wu, T.Y.; Fan, X.; Wang, K.H.; Pan, J.S.; Chen, C.M.; Wu, J.M.T. Security Analysis and Improvement of An Image Encryption Scheme Based on Chaotic Tent Map. J. Inf. Hiding Multim. Signal Process. 2018, 9, 1050–1057. [Google Scholar]
- Arora, A.; Sharma, R.K. Cryptanalysis and enhancement of image encryption scheme based on word-oriented feed back shift register. Multimed. Tools Appl. 2022, 81, 16679–16705. [Google Scholar] [CrossRef]
- Feng, W.; He, Y.G.; Li, H.M.; Li, C.L. Cryptanalysis of the integrated chaotic systems based image encryption algorithm. Optik 2019, 186, 449–457. [Google Scholar] [CrossRef]
- Li, H.; Li, T.; Feng, W.; Zhang, J.; Zhang, J.; Gan, L.; Li, C. A novel image encryption scheme based on non-adjacent parallelable permutation and dynamic DNA-level two-way diffusion. J. Inf. Secur. Appl. 2021, 61, 102844. [Google Scholar] [CrossRef]
- Solak, E.; Cokal, C.; Yildiz, O.T.; Biyikoğlu, T. Cryptanalysis of Fridrich’s chaotic image encryption. Int. J. Bifurc. Chaos 2010, 20, 1405–1413. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Liu, Y.; Wang, C.; Zhou, J.; Zhang, Y.; Chen, G. Improved known-plaintext attack to permutation-only multimedia ciphers. Inf. Sci. 2018, 430, 228–239. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Liu, Y.; Pareschi, F.; Zhang, Y.; Wong, K.W.; Rovatti, R.; Setti, G. On the security of a class of diffusion mechanisms for image encryption. IEEE Trans. Cybern. 2017, 48, 1163–1175. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhang, Y.; Liu, Y.; Yang, A.; Chen, G. Security analysis of some diffusion mechanisms used in chaotic ciphers. Int. J. Bifurc. Chaos 2017, 27, 1750155. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, L.Y.; Zhou, Y. Re-evaluation of the security of a family of image diffusion mechanisms. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4747–4758. [Google Scholar] [CrossRef]
- Chen, J.; Chen, L.; Zhou, Y. Cryptanalysis of image ciphers with permutation-substitution network and chaos. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 2494–2508. [Google Scholar] [CrossRef]
- Chen, J.; Chen, L.; Zhou, Y. Universal chosen-ciphertext attack for a family of image encryption schemes. IEEE Trans. Multimed. 2020, 23, 2372–2385. [Google Scholar] [CrossRef]
- Gao, X. Image encryption algorithm based on 2D hyperchaotic map. Opt. Laser Technol. 2021, 142, 107252. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Pun, C.M.; Chen, C.P. 2D Sine Logistic modulation map for image encryption. Inf. Sci. 2015, 297, 80–94. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine-transform-based chaotic system with FPGA implementation. IEEE Trans. Ind. Electron. 2017, 65, 2557–2566. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).