Quantum Chaos in the Extended Dicke Model
Abstract
1. Introduction
2. Extended Dicke Model
3. Energy Spectrum Statistics
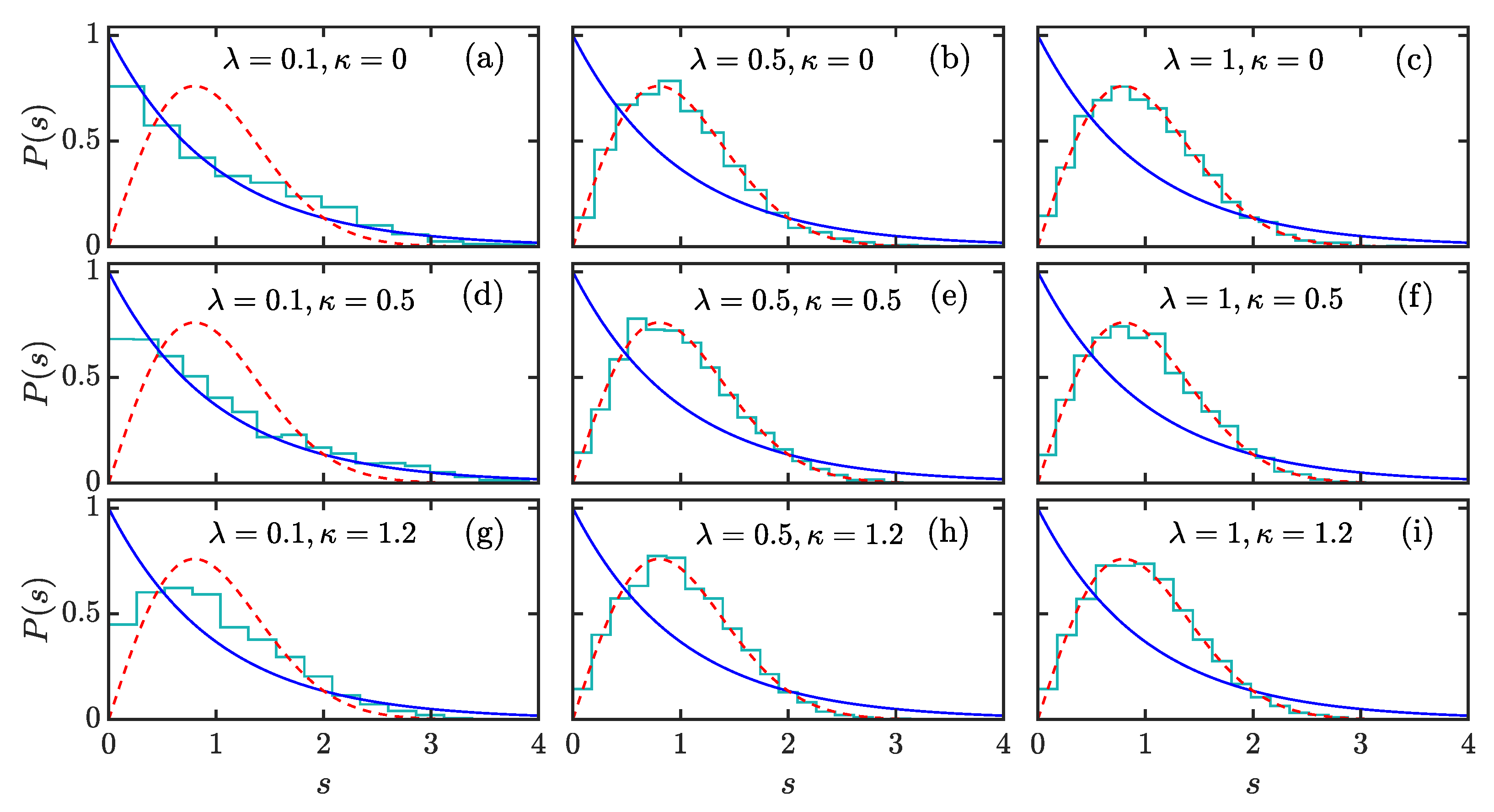
3.1. Level Spacing Statistics
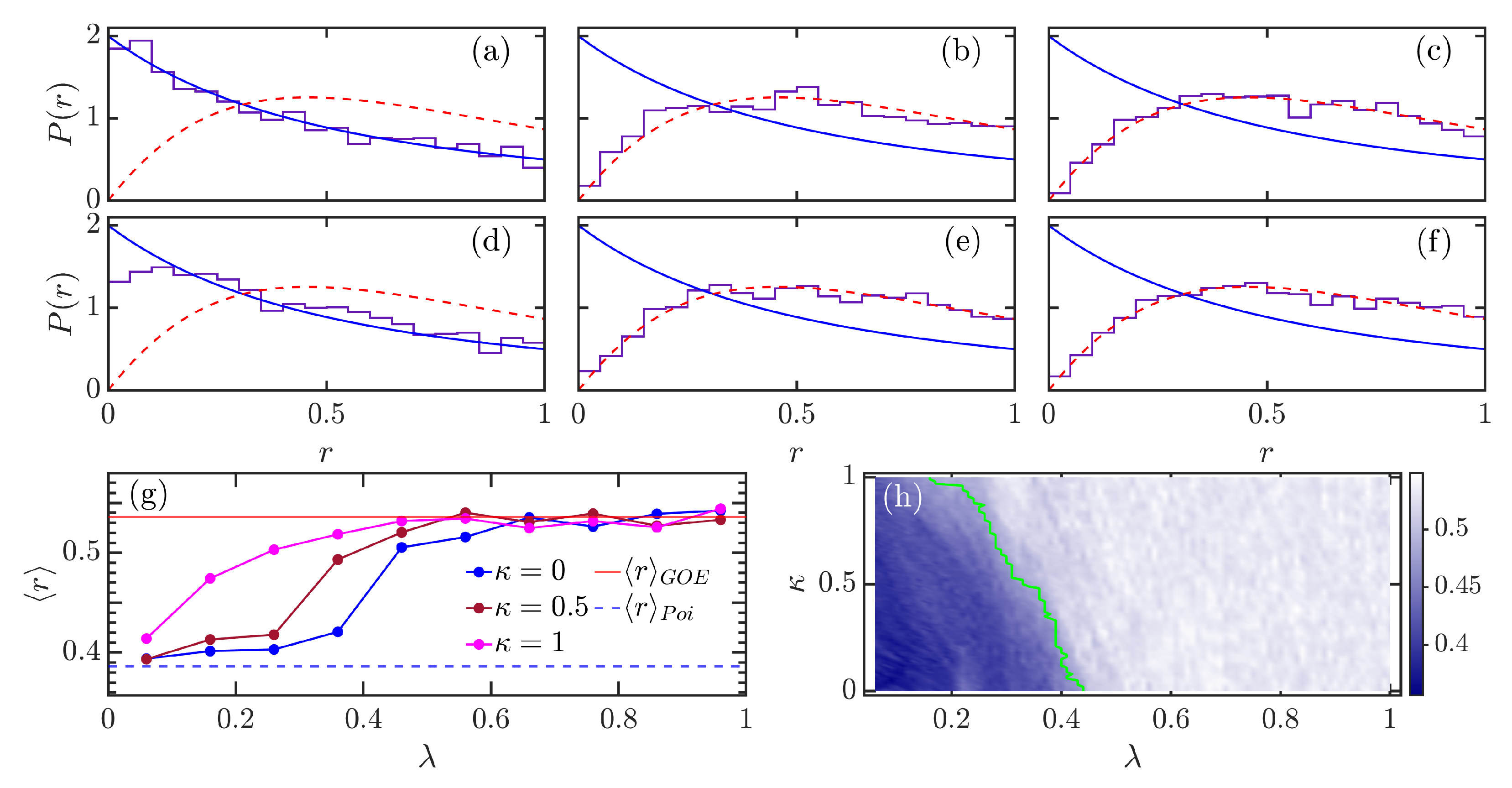
3.2. Level Spacing Ratio
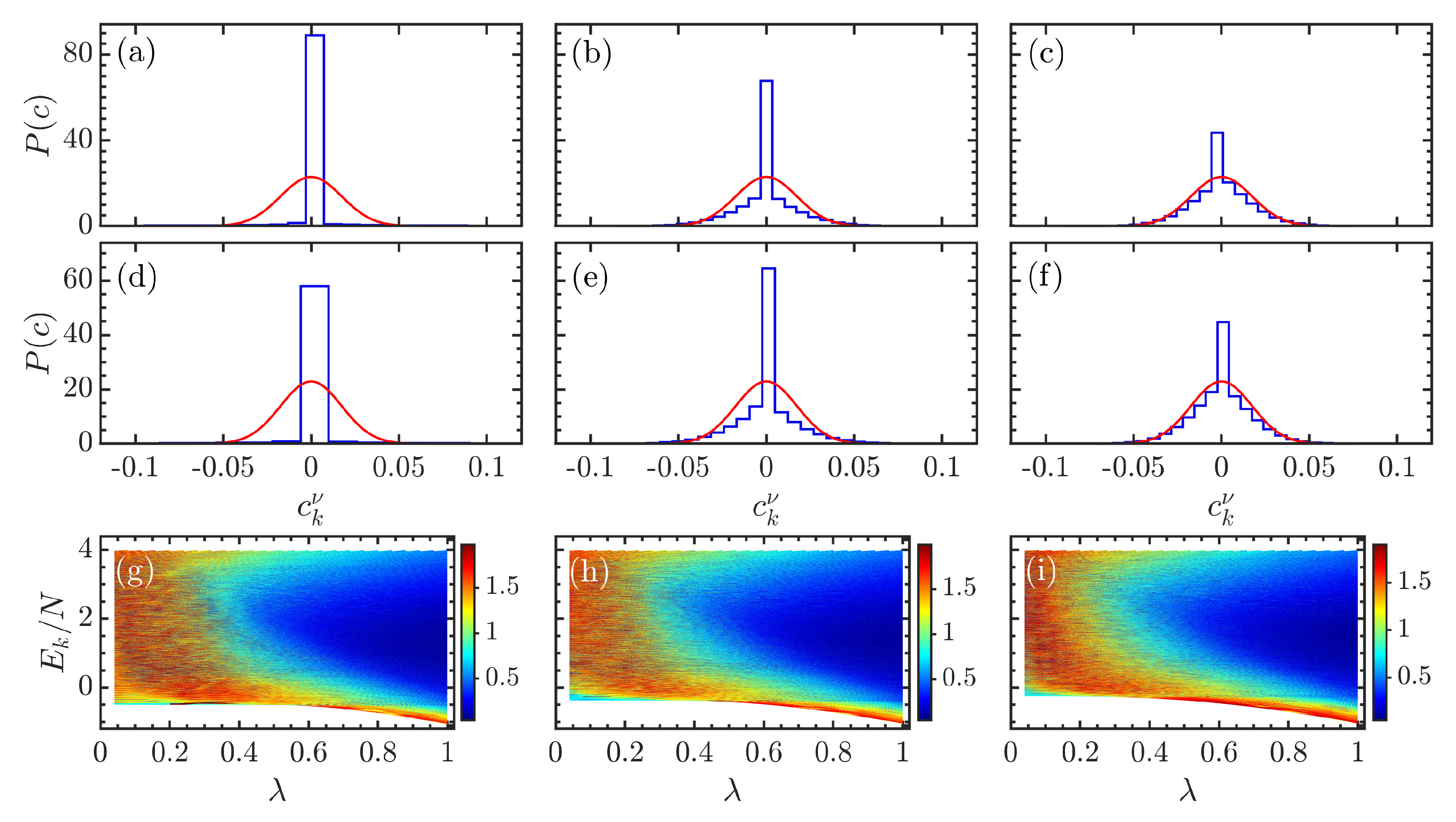
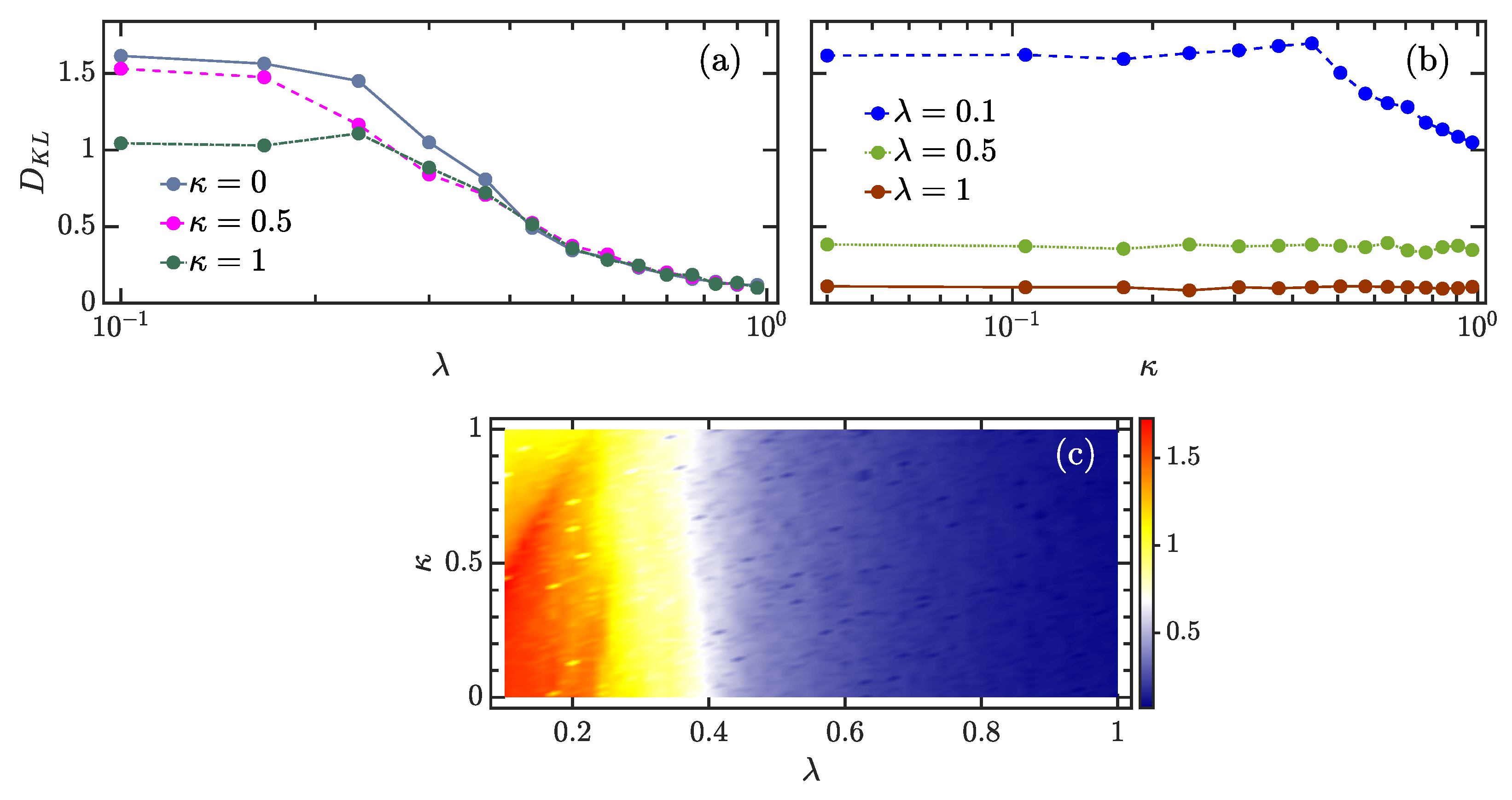
4. Structure of Eigenstates
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Altland, A.; Haake, F. Quantum Chaos and Effective Thermalization. Phys. Rev. Lett. 2012, 108, 073601. [Google Scholar] [CrossRef] [PubMed]
- D’Alessio, L.; Kafri, Y.; Polkovnikov, A.; Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 2016, 65, 239–362. [Google Scholar] [CrossRef]
- Borgonovi, F.; Izrailev, F.; Santos, L.; Zelevinsky, V. Quantum chaos and thermalization in isolated systems of interacting particles. Phys. Rep. 2016, 626, 1–58. [Google Scholar] [CrossRef]
- Nandkishore, R.; Huse, D.A. Many-Body Localization and Thermalization in Quantum Statistical Mechanics. Ann. Rev. Condens. Matter Phys. 2015, 6, 15–38. [Google Scholar] [CrossRef]
- Deutsch, J.M. Eigenstate thermalization hypothesis. Rep. Prog. Phys. 2018, 81, 082001. [Google Scholar] [CrossRef]
- Chan, A.; De Luca, A.; Chalker, J.T. Solution of a Minimal Model for Many-Body Quantum Chaos. Phys. Rev. X 2018, 8, 041019. [Google Scholar] [CrossRef]
- Garcia-March, M.A.; van Frank, S.; Bonneau, M.; Schmiedmayer, J.; Lewenstein, M.; Santos, L.F. Relaxation, chaos, and thermalization in a three-mode model of a Bose–Einstein condensate. New J. Phys. 2018, 20, 113039. [Google Scholar] [CrossRef]
- Friedman, A.J.; Chan, A.; De Luca, A.; Chalker, J.T. Spectral Statistics and Many-Body Quantum Chaos with Conserved Charge. Phys. Rev. Lett. 2019, 123, 210603. [Google Scholar] [CrossRef]
- Ray, S.; Cohen, D.; Vardi, A. Chaos-induced breakdown of Bose-Hubbard modeling. Phys. Rev. A 2020, 101, 013624. [Google Scholar] [CrossRef]
- Rautenberg, M.; Gärttner, M. Classical and quantum chaos in a three-mode bosonic system. Phys. Rev. A 2020, 101, 053604. [Google Scholar] [CrossRef]
- Kobrin, B.; Yang, Z.; Kahanamoku-Meyer, G.D.; Olund, C.T.; Moore, J.E.; Stanford, D.; Yao, N.Y. Many-Body Chaos in the Sachdev-Ye-Kitaev Model. Phys. Rev. Lett. 2021, 126, 030602. [Google Scholar] [CrossRef] [PubMed]
- Fogarty, T.; García-March, M.Á.; Santos, L.F.; Harshman, N.L. Probing the edge between integrability and quantum chaos in interacting few-atom systems. Quantum 2021, 5, 486. [Google Scholar] [CrossRef]
- Wittmann W., K.; Castro, E.R.; Foerster, A.; Santos, L.F. Interacting bosons in a triple well: Preface of many-body quantum chaos. Phys. Rev. E 2022, 105, 034204. [Google Scholar] [CrossRef] [PubMed]
- Maldacena, J.; Shenker, S.H.; Stanford, D. A bound on chaos. J. High Energy Phys. 2016, 2016, 106. [Google Scholar] [CrossRef]
- Stanford, D. Many-body chaos at weak coupling. J. High Energy Phys. 2016, 2016, 9. [Google Scholar] [CrossRef]
- Magán, J.M. Black holes, complexity and quantum chaos. J. High Energy Phys. 2018, 2018, 43. [Google Scholar] [CrossRef]
- Jahnke, V. Recent Developments in the Holographic Description of Quantum Chaos. Adv. High Energy Phys. 2019, 2019, 9632708. [Google Scholar] [CrossRef]
- Ali, T.; Bhattacharyya, A.; Haque, S.S.; Kim, E.H.; Moynihan, N.; Murugan, J. Chaos and complexity in quantum mechanics. Phys. Rev. D 2020, 101, 026021. [Google Scholar] [CrossRef]
- Rabinovici, E.; Sánchez-Garrido, A.; Shir, R.; Sonner, J. Operator complexity: A journey to the edge of Krylov space. J. High Energy Phys. 2021, 2021, 62. [Google Scholar] [CrossRef]
- Schack, R.; Caves, C.M. Information-theoretic characterization of quantum chaos. Phys. Rev. E 1996, 53, 3257–3270. [Google Scholar] [CrossRef] [PubMed]
- Vidmar, L.; Rigol, M. Entanglement Entropy of Eigenstates of Quantum Chaotic Hamiltonians. Phys. Rev. Lett. 2017, 119, 220603. [Google Scholar] [CrossRef] [PubMed]
- Piga, A.; Lewenstein, M.; Quach, J.Q. Quantum chaos and entanglement in ergodic and nonergodic systems. Phys. Rev. E 2019, 99, 032213. [Google Scholar] [CrossRef] [PubMed]
- Bertini, B.; Kos, P.; Prosen, T. Entanglement Spreading in a Minimal Model of Maximal Many-Body Quantum Chaos. Phys. Rev. X 2019, 9, 021033. [Google Scholar] [CrossRef]
- Lerose, A.; Pappalardi, S. Bridging entanglement dynamics and chaos in semiclassical systems. Phys. Rev. A 2020, 102, 032404. [Google Scholar] [CrossRef]
- Lantagne-Hurtubise, E.; Plugge, S.; Can, O.; Franz, M. Diagnosing quantum chaos in many-body systems using entanglement as a resource. Phys. Rev. Res. 2020, 2, 013254. [Google Scholar] [CrossRef]
- Anand, N.; Styliaris, G.; Kumari, M.; Zanardi, P. Quantum coherence as a signature of chaos. Phys. Rev. Res. 2021, 3, 023214. [Google Scholar] [CrossRef]
- Hosur, P.; Qi, X.L.; Roberts, D.A.; Yoshida, B. Chaos in quantum channels. J. High Energy Phys. 2016, 2016, 4. [Google Scholar] [CrossRef]
- Chenu, A.; Molina-Vilaplana, J.; del Campo, A. Work Statistics, Loschmidt Echo and Information Scrambling in Chaotic Quantum Systems. Quantum 2019, 3, 127. [Google Scholar] [CrossRef]
- Prakash, R.; Lakshminarayan, A. Scrambling in strongly chaotic weakly coupled bipartite systems: Universality beyond the Ehrenfest timescale. Phys. Rev. B 2020, 101, 121108. [Google Scholar] [CrossRef]
- Balasubramanian, V.; DeCross, M.; Kar, A.; Parrikar, O. Quantum complexity of time evolution with chaotic Hamiltonians. J. High Energy Phys. 2020, 2020, 134. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Haque, S.S.; Kim, E.H. Complexity from the reduced density matrix: A new diagnostic for chaos. J. High Energy Phys. 2021, 2021, 28. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Chemissany, W.; Haque, S.S.; Murugan, J.; Yan, B. The Multi-faceted Inverted Harmonic Oscillator: Chaos and Complexity. SciPost Phys. Core 2021, 4, 2. [Google Scholar] [CrossRef]
- Parker, D.E.; Cao, X.; Avdoshkin, A.; Scaffidi, T.; Altman, E. A Universal Operator Growth Hypothesis. Phys. Rev. X 2019, 9, 041017. [Google Scholar] [CrossRef]
- Dymarsky, A.; Gorsky, A. Quantum chaos as delocalization in Krylov space. Phys. Rev. B 2020, 102, 085137. [Google Scholar] [CrossRef]
- Caputa, P.; Magan, J.M.; Patramanis, D. Geometry of Krylov complexity. Phys. Rev. Res. 2022, 4, 013041. [Google Scholar] [CrossRef]
- Bertini, B.; Heidrich-Meisner, F.; Karrasch, C.; Prosen, T.; Steinigeweg, R.; Žnidarič, M. Finite-temperature transport in one-dimensional quantum lattice models. Rev. Mod. Phys. 2021, 93, 025003. [Google Scholar] [CrossRef]
- Cvitanovic, P.; Artuso, R.; Mainieri, R.; Tanner, G.; Vattay, G.; Whelan, N.; Wirzba, A. Chaos: Classical and quantum. In ChaosBook. Org; Niels Bohr Institute: Copenhagen, Denmark, 2005; Volume 69, p. 25. [Google Scholar]
- Schuster, H.G.; Just, W. Deterministic Chaos: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Bohigas, O.; Giannoni, M.J.; Schmit, C. Characterization of Chaotic Quantum Spectra and Universality of Level Fluctuation Laws. Phys. Rev. Lett. 1984, 52, 1–4. [Google Scholar] [CrossRef]
- Stöckmann, H.J. Quantum Chaos: An Introduction; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Haake, F. Quantum Signatures of Chaos; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zyczkowski, K. Indicators of quantum chaos based on eigenvector statistics. J. Phys. A 1990, 23, 4427. [Google Scholar] [CrossRef]
- Emerson, J.; Weinstein, Y.S.; Lloyd, S.; Cory, D.G. Fidelity Decay as an Efficient Indicator of Quantum Chaos. Phys. Rev. Lett. 2002, 89, 284102. [Google Scholar] [CrossRef] [PubMed]
- Rozenbaum, E.B.; Ganeshan, S.; Galitski, V. Lyapunov Exponent and Out-of-Time-Ordered Correlator’s Growth Rate in a Chaotic System. Phys. Rev. Lett. 2017, 118, 086801. [Google Scholar] [CrossRef] [PubMed]
- García-Mata, I.; Saraceno, M.; Jalabert, R.A.; Roncaglia, A.J.; Wisniacki, D.A. Chaos Signatures in the Short and Long Time Behavior of the Out-of-Time Ordered Correlator. Phys. Rev. Lett. 2018, 121, 210601. [Google Scholar] [CrossRef]
- Chen, X.; Ludwig, A.W.W. Universal spectral correlations in the chaotic wave function and the development of quantum chaos. Phys. Rev. B 2018, 98, 064309. [Google Scholar] [CrossRef]
- Kos, P.; Ljubotina, M.; Prosen, T. Many-Body Quantum Chaos: Analytic Connection to Random Matrix Theory. Phys. Rev. X 2018, 8, 021062. [Google Scholar] [CrossRef]
- Bertini, B.; Kos, P.; Prosen, T. Exact Spectral Form Factor in a Minimal Model of Many-Body Quantum Chaos. Phys. Rev. Lett. 2018, 121, 264101. [Google Scholar] [CrossRef]
- Gietka, K.; Chwedeńczuk, J.; Wasak, T.; Piazza, F. Multipartite entanglement dynamics in a regular-to-ergodic transition: Quantum Fisher information approach. Phys. Rev. B 2019, 99, 064303. [Google Scholar] [CrossRef]
- Xu, T.; Scaffidi, T.; Cao, X. Does Scrambling Equal Chaos? Phys. Rev. Lett. 2020, 124, 140602. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Xu, Z.; del Campo, A. Probing quantum chaos in multipartite systems. Phys. Rev. Res. 2022, 4, 033093. [Google Scholar] [CrossRef]
- Zonnios, M.; Levinsen, J.; Parish, M.M.; Pollock, F.A.; Modi, K. Signatures of Quantum Chaos in an Out-of-Time-Order Tensor. Phys. Rev. Lett. 2022, 128, 150601. [Google Scholar] [CrossRef]
- Raúl González Alonso, J.; Shammah, N.; Ahmed, S.; Nori, F.; Dressel, J. Diagnosing quantum chaos with out-of-time-ordered-correlator quasiprobability in the kicked-top model. arXiv 2022, arXiv:2201.08175. [Google Scholar]
- Joshi, L.K.; Elben, A.; Vikram, A.; Vermersch, B.; Galitski, V.; Zoller, P. Probing Many-Body Quantum Chaos with Quantum Simulators. Phys. Rev. X 2022, 12, 011018. [Google Scholar] [CrossRef]
- Lozej, Č.; Lukman, D.; Robnik, M. Phenomenology of quantum eigenstates in mixed-type systems: Lemon billiards with complex phase space structure. arXiv 2022, arXiv:2207.07197. [Google Scholar]
- Abanin, D.A.; Altman, E.; Bloch, I.; Serbyn, M. Colloquium: Many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 2019, 91, 021001. [Google Scholar] [CrossRef]
- Turner, C.J.; Michailidis, A.A.; Abanin, D.A.; Serbyn, M.; Papić, Z. Weak ergodicity breaking from quantum many-body scars. Nat. Phys. 2018, 14, 745–749. [Google Scholar] [CrossRef]
- Sinha, S.; Sinha, S. Chaos and Quantum Scars in Bose-Josephson Junction Coupled to a Bosonic Mode. Phys. Rev. Lett. 2020, 125, 134101. [Google Scholar] [CrossRef]
- Turner, C.J.; Desaules, J.Y.; Bull, K.; Papić, Z. Correspondence Principle for Many-Body Scars in Ultracold Rydberg Atoms. Phys. Rev. X 2021, 11, 021021. [Google Scholar] [CrossRef]
- Mondragon-Shem, I.; Vavilov, M.G.; Martin, I. Fate of Quantum Many-Body Scars in the Presence of Disorder. PRX Quantum 2021, 2, 030349. [Google Scholar] [CrossRef]
- Serbyn, M.; Abanin, D.A.; Papić, Z. Quantum many-body scars and weak breaking of ergodicity. Nat. Phys. 2021, 17, 675–685. [Google Scholar] [CrossRef]
- Kloc, M.; Stránský, P.; Cejnar, P. Quantum phases and entanglement properties of an extended Dicke model. Ann. Phys. 2017, 382, 85–111. [Google Scholar] [CrossRef]
- Rodriguez, J.P.J.; Chilingaryan, S.A.; Rodríguez-Lara, B.M. Critical phenomena in an extended Dicke model. Phys. Rev. A 2018, 98, 043805. [Google Scholar] [CrossRef]
- Guerra, C.A.E.; Mahecha-Gómez, J.; Hirsch, J.G. Quantum phase transition and Berry phase in an extended Dicke model. Eur. Phys. J. D 2020, 74, 200. [Google Scholar] [CrossRef]
- Herrera Romero, R.; Bastarrachea-Magnani, M.A.; Linares, R. Critical Phenomena in Light-Matter Systems with Collective Matter Interactions. Entropy 2022, 24, 1198. [Google Scholar] [CrossRef] [PubMed]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Emary, C.; Brandes, T. Chaos and the quantum phase transition in the Dicke model. Phys. Rev. E 2003, 67, 066203. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Robnik, M. Statistical properties of the localization measure of chaotic eigenstates in the Dicke model. Phys. Rev. E 2020, 102, 032212. [Google Scholar] [CrossRef]
- Bastarrachea-Magnani, M.A.; del Carpio, B.L.; Lerma-Hernández, S.; Hirsch, J.G. Chaos in the Dicke model: Quantum and semiclassical analysis. Phys. Scr. 2015, 90, 068015. [Google Scholar] [CrossRef]
- Bastarrachea-Magnani, M.A.; López-del Carpio, B.; Chávez-Carlos, J.; Lerma-Hernández, S.; Hirsch, J.G. Delocalization and quantum chaos in atom-field systems. Phys. Rev. E 2016, 93, 022215. [Google Scholar] [CrossRef]
- Robles Robles, R.A.; Chilingaryan, S.A.; Rodríguez-Lara, B.M.; Lee, R.K. Ground state in the finite Dicke model for interacting qubits. Phys. Rev. A 2015, 91, 033819. [Google Scholar] [CrossRef]
- Cejnar, P.; Stránský, P.; Macek, M. Regular and Chaotic Collective Modes in Nuclei. Nucl. Phys. News 2011, 21, 22–27. [Google Scholar] [CrossRef]
- Chávez-Carlos, J.; López-del Carpio, B.; Bastarrachea-Magnani, M.A.; Stránský, P.; Lerma-Hernández, S.; Santos, L.F.; Hirsch, J.G. Quantum and Classical Lyapunov Exponents in Atom-Field Interaction Systems. Phys. Rev. Lett. 2019, 122, 024101. [Google Scholar] [CrossRef]
- Rodríguez-Lara, B.M.; Lee, R.K. Classical dynamics of a two-species condensate driven by a quantum field. Phys. Rev. E 2011, 84, 016225. [Google Scholar] [CrossRef]
- Berry, M.V.; Tabor, M. Level clustering in the regular spectrum. Proc. R. Soc. A 1977, 356, 375–394. [Google Scholar] [CrossRef]
- Jacquod, P.; Shepelyansky, D.L. Emergence of Quantum Chaos in Finite Interacting Fermi Systems. Phys. Rev. Lett. 1997, 79, 1837–1840. [Google Scholar] [CrossRef]
- Brody, T.A.; Flores, J.; French, J.B.; Mello, P.A.; Pandey, A.; Wong, S.S.M. Random-matrix physics: Spectrum and strength fluctuations. Rev. Mod. Phys. 1981, 53, 385–479. [Google Scholar] [CrossRef]
- Guhr, T.; Müller-Groeling, A.; Weidenmüller, H.A. Random-matrix theories in quantum physics: Common concepts. Phys. Rep. 1998, 299, 189–425. [Google Scholar] [CrossRef]
- Oganesyan, V.; Huse, D.A. Localization of interacting fermions at high temperature. Phys. Rev. B 2007, 75, 155111. [Google Scholar] [CrossRef]
- Atas, Y.Y.; Bogomolny, E.; Giraud, O.; Roux, G. Distribution of the Ratio of Consecutive Level Spacings in Random Matrix Ensembles. Phys. Rev. Lett. 2013, 110, 084101. [Google Scholar] [CrossRef] [PubMed]
- Atas, Y.Y.; Bogomolny, E.; Giraud, O.; Vivo, P.; Vivo, E. Joint probability densities of level spacing ratios in random matrices. J. Phys. A Math. Theor. 2013, 46, 355204. [Google Scholar] [CrossRef]
- Giraud, O.; Macé, N.; Vernier, E.; Alet, F. Probing Symmetries of Quantum Many-Body Systems through Gap Ratio Statistics. Phys. Rev. X 2022, 12, 011006. [Google Scholar] [CrossRef]
- Berry, M.V. Regular and irregular semiclassical wavefunctions. J. Phys. A 1977, 10, 2083–2091. [Google Scholar] [CrossRef]
- Porter, C.E.; Thomas, R.G. Fluctuations of Nuclear Reaction Widths. Phys. Rev. 1956, 104, 483–491. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Izrailev, F.M. Simple models of quantum chaos: Spectrum and eigenfunctions. Phys. Rep. 1990, 196, 299–392. [Google Scholar] [CrossRef]
- Haake, F.; Życzkowski, K. Random-matrix theory and eigenmodes of dynamical systems. Phys. Rev. A 1990, 42, 1013–1016. [Google Scholar] [CrossRef]
- Leboeuf, P.; Voros, A. Chaos-revealing multiplicative representation of quantum eigenstates. J. Phys. A Math. Gen. 1990, 23, 1765–1774. [Google Scholar] [CrossRef]
- Wang, Q.; Robnik, M. Multifractality in Quasienergy Space of Coherent States as a Signature of Quantum Chaos. Entropy 2021, 23, 1347. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Karp, J.; Távora, M.; Santos, L.F. Realistic Many-Body Quantum Systems vs. Full Random Matrices: Static and Dynamical Properties. Entropy 2016, 18, 359. [Google Scholar] [CrossRef]
- Bäcker, A.; Haque, M.; Khaymovich, I.M. Multifractal dimensions for random matrices, chaotic quantum maps, and many-body systems. Phys. Rev. E 2019, 100, 032117. [Google Scholar] [CrossRef] [PubMed]
- Nakerst, G.; Haque, M. Chaos in the three-site Bose-Hubbard model—Classical vs. quantum. arXiv 2022, arXiv:2203.09953. [Google Scholar]
- Khaymovich, I.M.; Haque, M.; McClarty, P.A. Eigenstate Thermalization, Random Matrix Theory, and Behemoths. Phys. Rev. Lett. 2019, 122, 070601. [Google Scholar] [CrossRef] [PubMed]
- Pausch, L.; Carnio, E.G.; Rodríguez, A.; Buchleitner, A. Chaos and Ergodicity across the Energy Spectrum of Interacting Bosons. Phys. Rev. Lett. 2021, 126, 150601. [Google Scholar] [CrossRef]
- Beugeling, W.; Bäcker, A.; Moessner, R.; Haque, M. Statistical properties of eigenstate amplitudes in complex quantum systems. Phys. Rev. E 2018, 98, 022204. [Google Scholar] [CrossRef] [PubMed]
- Luitz, D.J.; Bar Lev, Y. Anomalous Thermalization in Ergodic Systems. Phys. Rev. Lett. 2016, 117, 170404. [Google Scholar] [CrossRef] [PubMed]
- Luitz, D.J.; Khaymovich, I.M.; Lev, Y.B. Multifractality and its role in anomalous transport in the disordered XXZ spin-chain. SciPost Phys. Core 2020, 2, 6. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Frisch, A.; Mark, M.; Aikawa, K.; Ferlaino, F.; Bohn, J.L.; Makrides, C.; Petrov, A.; Kotochigova, S. Quantum chaos in ultracold collisions of gas-phase erbium atoms. Nature 2014, 507, 475–479. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q. Quantum Chaos in the Extended Dicke Model. Entropy 2022, 24, 1415. https://doi.org/10.3390/e24101415
Wang Q. Quantum Chaos in the Extended Dicke Model. Entropy. 2022; 24(10):1415. https://doi.org/10.3390/e24101415
Chicago/Turabian StyleWang, Qian. 2022. "Quantum Chaos in the Extended Dicke Model" Entropy 24, no. 10: 1415. https://doi.org/10.3390/e24101415
APA StyleWang, Q. (2022). Quantum Chaos in the Extended Dicke Model. Entropy, 24(10), 1415. https://doi.org/10.3390/e24101415




