Quantum Energy Current Induced Coherence in a Spin Chain under Non-Markovian Environments
Abstract
1. Introduction
2. Formalism
2.1. Non-Markovian Quantum State Diffusion
2.2. Spin Chain
2.3. Energy Current
2.4. Quantum Coherence
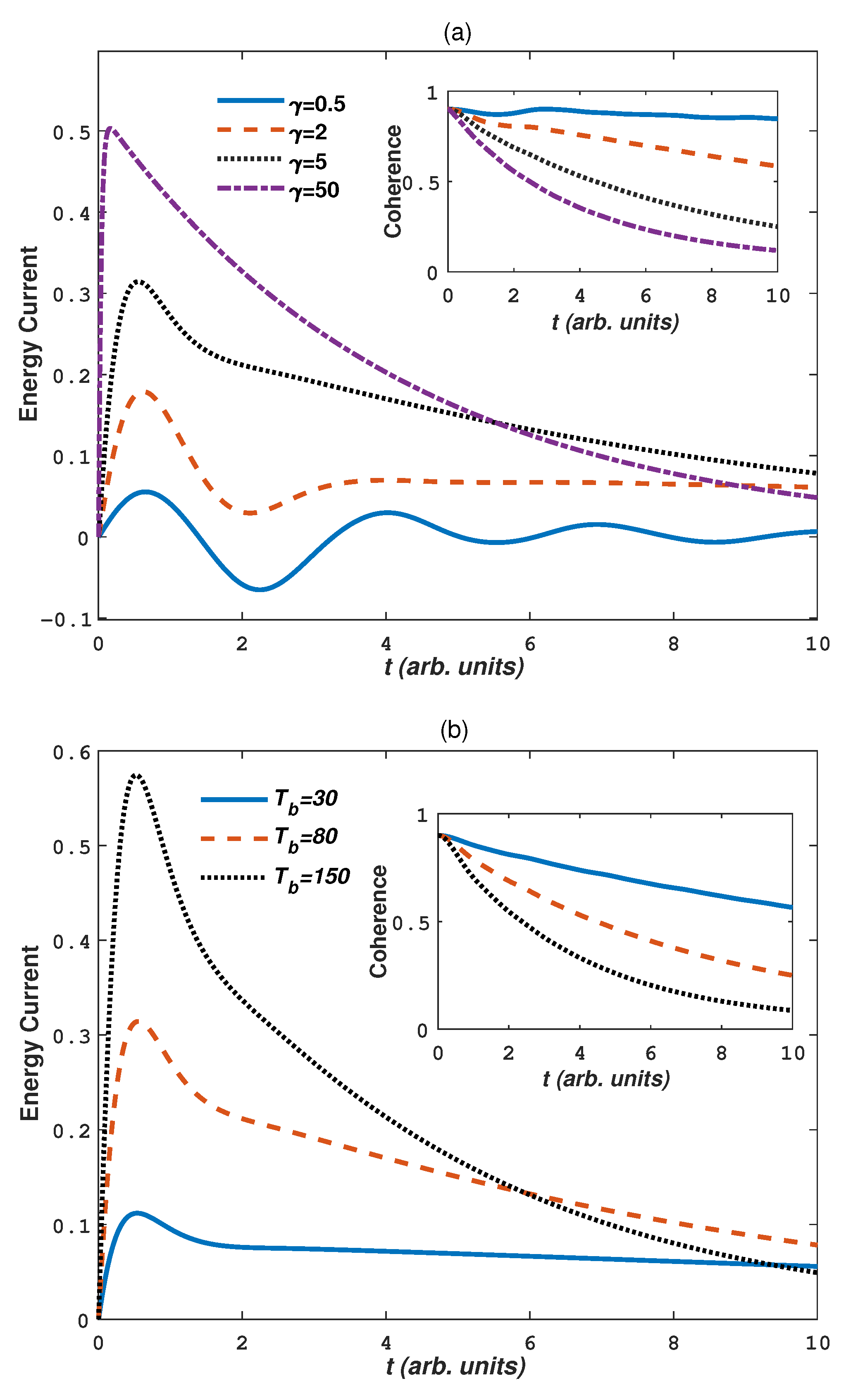
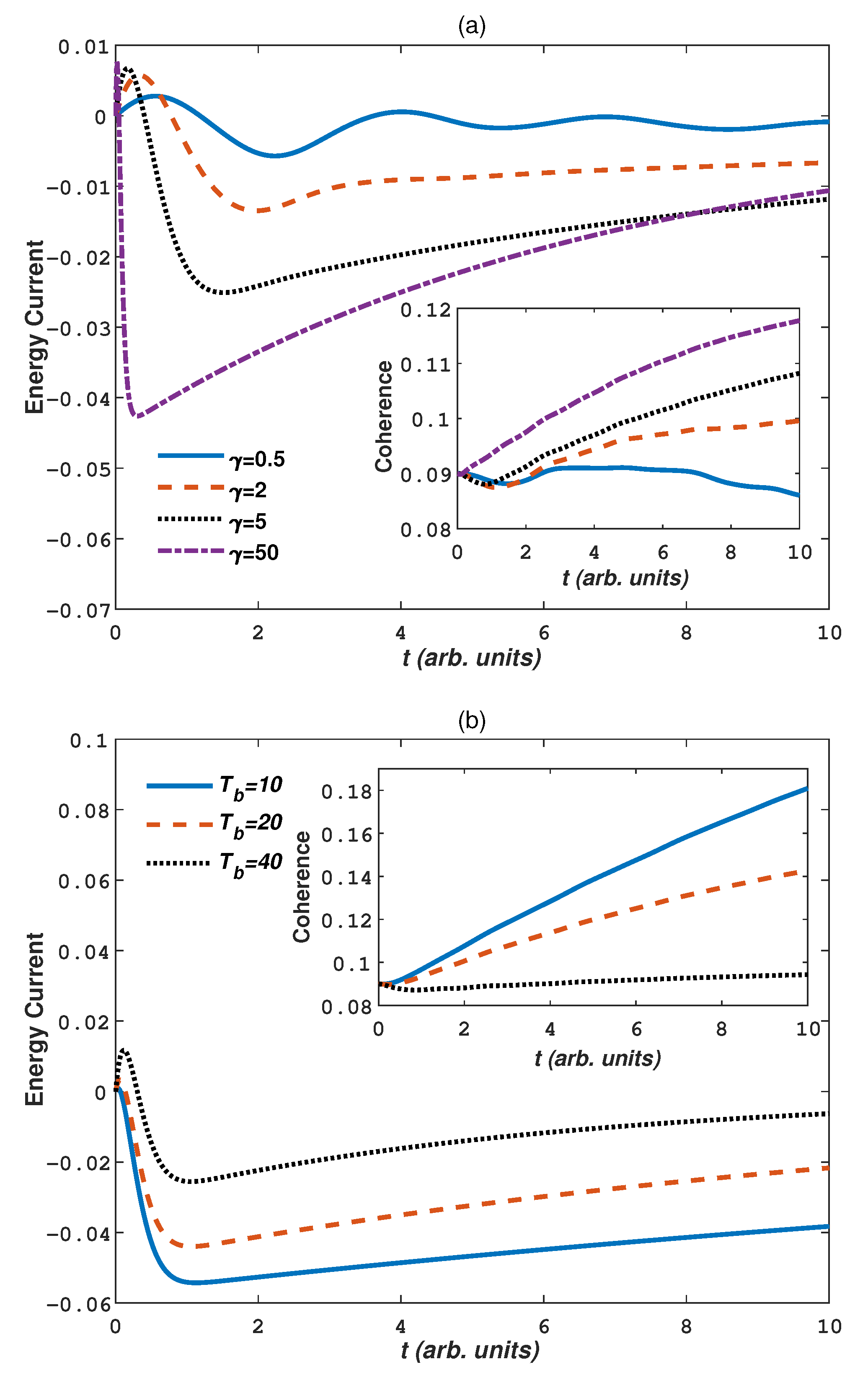
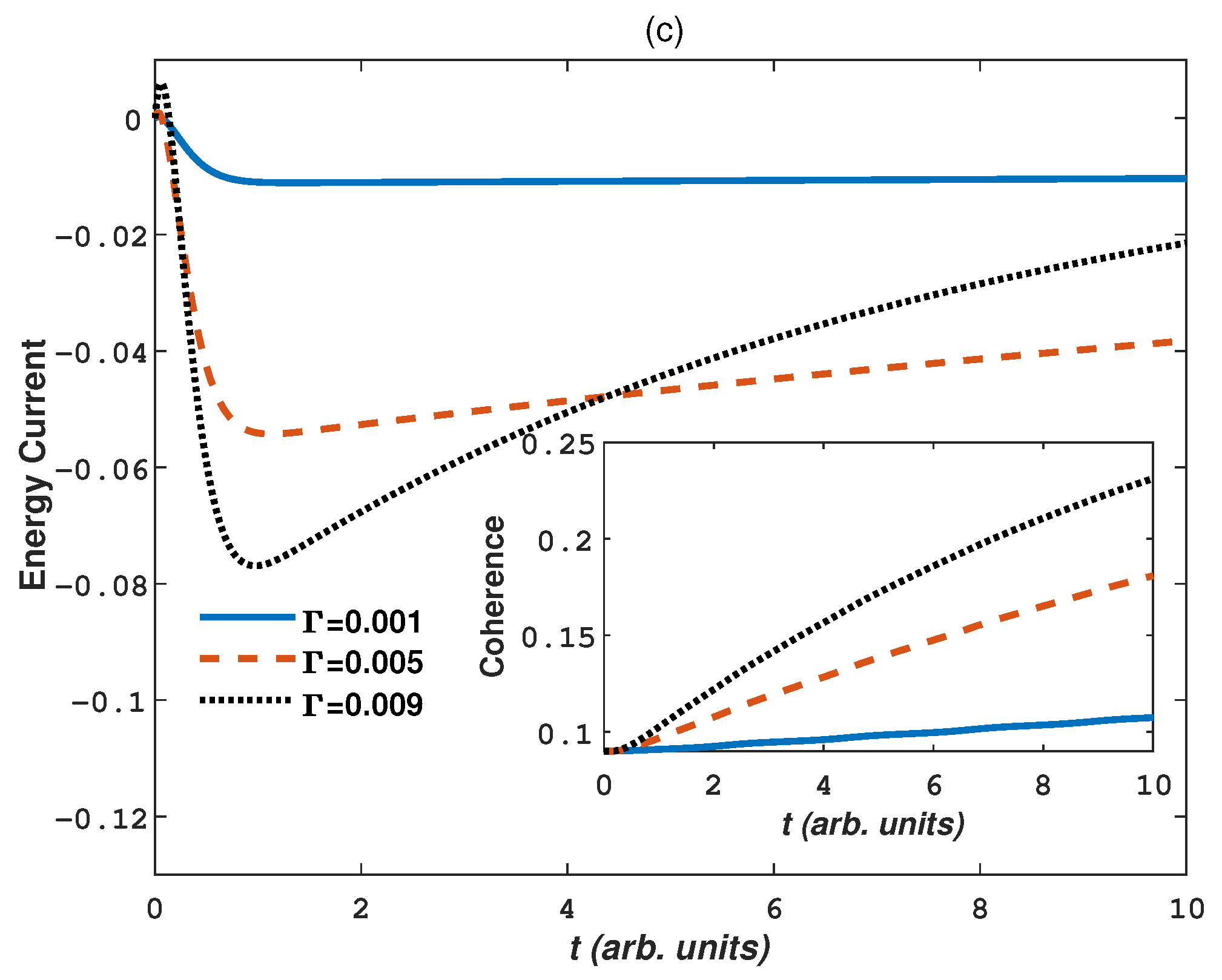
3. Numerical Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NMQSD | Non-Markovian Quantum State Diffusion |
| DM | Dzyaloshinskii–Moriya |
References
- Woggon, U.; Gindele, F.; Langbein, W.; Hvam, J.M. Quantum kinetic exciton–LO-phonon interaction in CdSe. Phys. Rev. B. 2000, 61, 1935–1940. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J.; Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef]
- Piilo, J.; Härkönen, K.; Maniscalco, S.; Suominen, K.A. Open system dynamics with non-Markovian quantum jumps. Phys. Rev. A 2009, 79, 062112. [Google Scholar] [CrossRef]
- Tarasov, V.E. General non-Markovian quantum dynamics. Entropy 2021, 23, 1006. [Google Scholar] [CrossRef] [PubMed]
- Czerwinski, A. Dynamics of open quantum systems—Markovian semigroups and beyond. Symmetry 2022, 14, 1752. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J. Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Helm, J.; Strunz, W.T. Decoherence and entanglement dynamics in fluctuating fields. Phys. Rev. A 2010, 81, 042314. [Google Scholar] [CrossRef]
- Guarnieri, G.; Uchiyama, C.; Vacchini, B. Energy backflow and non-Markovian dynamics. Phys. Rev. A 2016, 93, 012118. [Google Scholar] [CrossRef]
- Guarnieri, G.; Nokkala, J.; Schmidt, R.; Maniscalco, S.; Vacchini, B. Energy backflow in strongly coupled non-Markovian continuous-variable systems. Phys. Rev. A 2016, 94, 062101. [Google Scholar] [CrossRef]
- Wu, J.; Ren, F.H.; He, R.H.; Nie, S.S.; Wang, Z.M. Adiabatic speedup and quantum heat current in an open system. Eur. Phys. Lett. 2022, 139, 48001. [Google Scholar] [CrossRef]
- Schmidt, R.; Maniscalco, S.; Ala-Nissila, T. Heat flux and information backflow in cold environments. Phys. Rev. A 2016, 94, 010101. [Google Scholar] [CrossRef]
- Wittemer, M.; Clos, G.; Breuer, H.P.; Warring, U.; Schaetz, T. Measurement of quantum memory effects and its fundamental limitations. Phys. Rev. A 2018, 97, 020102. [Google Scholar] [CrossRef]
- Passos, M.; Obando, P.C.; Balthazar, W.; Paula, F.; Huguenin, J.; Sarandy, M. Non-Markovianity through quantum coherence in an all-optical setup. Opt. Lett. 2019, 44, 2478–2481. [Google Scholar] [CrossRef]
- Khurana, D.; Agarwalla, B.K.; Mahesh, T.S. Experimental emulation of quantum non-Markovian dynamics and coherence protection in the presence of information backflow. Phys. Rev. A 2019, 99, 022107. [Google Scholar] [CrossRef]
- Yan, Y.A.; Yang, F.; Liu, Y.; Shao, J. Hierarchical approach based on stochastic decoupling to dissipative systems. Chem. Phys. Lett. 2004, 395, 216–221. [Google Scholar] [CrossRef]
- Bundgaard-Nielsen, M.; Mørk, J.; Denning, E.V. Non-Markovian perturbation theories for phonon effects in strong-coupling cavity quantum electrodynamics. Phys. Rev. B 2021, 103, 235309. [Google Scholar] [CrossRef]
- Ricottone, A.; Rudner, M.S.; Coish, W.A. Topological transition of a non-Markovian dissipative quantum walk. Phys. Rev. A 2020, 102, 012215. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Entanglement and non-Markovianity of quantum evolutions. Phys. Rev. Lett. 2010, 105, 050403. [Google Scholar] [CrossRef]
- Chruściński, D.; Kossakowski, A.; Rivas, A. Measures of non-Markovianity: Divisibility versus backflow of information. Phys. Rev. A 2011, 83, 052128. [Google Scholar] [CrossRef]
- Chen, X.Y.; Zhang, N.N.; He, W.T.; Kong, X.Y.; Tao, M.J.; Deng, F.G.; Ai, Q.; Long, G.L. Global correlation and local information flows in controllable non-Markovian open quantum dynamics. Npj Quantum Inform. 2022, 8, 22. [Google Scholar] [CrossRef]
- Strathearn, A.; Lovett, B.W.; Kirton, P. Efficient real-time path integrals for non-Markovian spin-boson models. New J. Phys. 2017, 19, 093009. [Google Scholar] [CrossRef]
- Wang, Z.M.; Ren, F.H.; Luo, D.W.; Yan, Z.Y.; Wu, L.A. Quantum state transmission through a spin chain in finite-temperature heat baths. J. Phys. A Math. Theor. 2021, 54, 155303. [Google Scholar] [CrossRef]
- Wang, Z.M.; Luo, D.W.; Byrd, M.S.; Wu, L.A.; Yu, T.; Shao, B. Adiabatic speedup in a non-Markovian quantum open system. Phys. Rev. A 2018, 98, 062118. [Google Scholar] [CrossRef]
- Laine, E.M.; Breuer, H.P.; Piilo, J. Nonlocal memory effects allow perfect teleportation with mixed states. Sci. Rep. 2014, 4, 1–5. [Google Scholar] [CrossRef]
- Fahmy, A.F.; Marx, R.; Bermel, W.; Glaser, S.J. Thermal equilibrium as an initial state for quantum computation by NMR. Phys. Rev. A 2008, 78, 022317. [Google Scholar] [CrossRef]
- Genway, S.; Ho, A.F.; Lee, D.K.K. Dynamics of thermalization in small Hubbard-model systems. Phys. Rev. Lett. 2010, 105, 260402. [Google Scholar] [CrossRef]
- Ponomarev, A.V.; Denisov, S.; Hänggi, P. Thermal equilibration between Two quantum systems. Phys. Rev. Lett. 2011, 106, 010405. [Google Scholar] [CrossRef]
- Wu, S.X.; Yu, C.S. Quantum speed limit for a mixed initial state. Phys. Rev. A 2018, 98, 042132. [Google Scholar] [CrossRef]
- Jing, J.; Yu, T.; Lam, C.H.; You, J.Q.; Wu, L.A. Control relaxation via dephasing: A quantum-state-diffusion study. Phys. Rev. A 2018, 97, 012104. [Google Scholar] [CrossRef]
- Jing, J.; Yu, T. Non-Markovian relaxation of a three-level system: Quantum trajectory approach. Phys. Rev. Lett. 2010, 105, 240403. [Google Scholar] [CrossRef]
- Wang, Z.M.; Ren, F.H.; Luo, D.W.; Yan, Z.Y.; Wu, L.A. Almost-exact state transfer by leakage-elimination-operator control in a non-Markovian environment. Phys. Rev. A 2020, 102, 042406. [Google Scholar] [CrossRef]
- Link, V.; Strunz, W.T.; Luoma, K. Non-Markovian quantum dynamics in a squeezed reservoir. Entropy 2022, 24, 352. [Google Scholar] [CrossRef] [PubMed]
- Diósi, L.; Gisin, N.; Strunz, W.T. Non-Markovian quantum state diffusion. Phys. Rev. A 1998, 58, 1699–1712. [Google Scholar] [CrossRef]
- Flannigan, S.; Damanet, F.; Daley, A.J. Many-body quantum state diffusion for non-Markovian dynamics in strongly interacting systems. Phys. Rev. Lett. 2022, 128, 063601. [Google Scholar] [CrossRef]
- Chen, Y.; You, J.Q.; Yu, T. Exact non-Markovian master equations for multiple qubit systems: Quantum-trajectory approach. Phys. Rev. A 2014, 90, 052104. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, X.; Jing, J.; Wu, L.A.; Yu, T. Perturbation methods for the non-Markovian quantum state diffusion equation. J. Phys. A Math. Theor. 2014, 47, 435301. [Google Scholar] [CrossRef]
- Wang, H.; Thoss, M. From coherent motion to localization: II. Dynamics of the spin-boson model with sub-Ohmic spectral density at zero temperature. Chem. Phys. 2010, 370, 78–86. [Google Scholar] [CrossRef]
- Ritschel, G.; Eisfeld, A. Analytic representations of bath correlation functions for ohmic and superohmic spectral densities using simple poles. J. Chem. Phys. 2014, 141, 3365. [Google Scholar] [CrossRef]
- Meier, C.; Tannor, D.J. Non-Markovian evolution of the density operator in the presence of strong laser fields. J. Chem. Phys. 1999, 111, 3365. [Google Scholar] [CrossRef]
- Nie, S.S.; Ren, F.H.; He, R.H.; Wu, J.; Wang, Z.M. Control cost and quantum speed limit time in controlled almost-exact state transmission in open systems. Phys. Rev. A 2021, 104, 052424. [Google Scholar] [CrossRef]
- Ren, F.H.; Wang, Z.M.; Wu, L.A. Accelerated adiabatic quantum search algorithm via pulse control in a non-Markovian environment. Phys. Rev. A 2020, 102, 062603. [Google Scholar] [CrossRef]
- Marchukov, O.V.; Volosniev, A.G.; Valiente, M.; Petrosyan, D.; Zinner, N. Quantum spin transistor with a Heisenberg spin chain. Nat. Commun. 2016, 7, 13070. [Google Scholar] [CrossRef]
- Van-Diepen, C.J.; Hsiao, T.K.; Mukhopadhyay, U.; Reichl, C.; Wegscheider, W.; Vandersypen, L.M.K. Quantum simulation of antiferromagnetic Heisenberg chain with gate-defined quantum dots. Phys. Rev. X 2021, 11, 041025. [Google Scholar] [CrossRef]
- Dyszel, P.; Haraldsen, J.T. Thermodynamics of general Heisenberg spin tetramers composed of coupled quantum dimers. Magnetochemistry 2021, 7, 29. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; Botmart, T.; El-Morshedy, M. Wiener process effects on the solutions of the fractional (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation. Mathematics 2022, 10, 2043. [Google Scholar] [CrossRef]
- Lebrun, R.; Ross, A.; Bender, S.; Qaiumzadeh, A.; Baldrati, L.; Cramer, J.; Brataas, A.; Duine, R.; Kläui, M. Tunable long-distance spin transport in a crystalline antiferromagnetic iron oxide. Nature 2018, 561, 222–225. [Google Scholar] [CrossRef]
- Wadley, P.; Howells, B.; Železn‘y, J.; Andrews, C.; Hills, V.; Campion, R.P.; Novák, V.; Olejník, K.; Maccherozzi, F.; Dhesi, S.; et al. Electrical switching of an antiferromagnet. Science 2016, 351, 6273. [Google Scholar] [CrossRef]
- Olejník, K.; Seifert, T.; Kašpar, Z.; Novák, V.; Wadley, P.; Campion, R.P.; Baumgartner, M.; Gambardella, P.; Nemec, P.; Wunderlich, J.; et al. Terahertz electrical writing speed in an antiferromagnetic memory. Sci. Adv. 2018, 4, 3. [Google Scholar] [CrossRef]
- Wei, D.; Chang, Y.; Glaser, S.J.; Yang, X. Cooperative pulses for pseudo-pure state preparation. Appl. Phys. Lett. 2014, 104, 242409. [Google Scholar] [CrossRef]
- Peng, X.; Zhu, X.; Fang, X.; Feng, M.; Gao, K.; Yang, X.; Liu, M. Preparation of pseudo-pure states by line-selective pulses in nuclear magnetic resonance. Chem. Phys. Lett. 2001, 340, 5–6. [Google Scholar] [CrossRef]
- Cory, D.G.; Fahmy, A.F.; Havel, T.F. Ensemble quantum computing by NMR spectroscopy. Proc. Natl. Acad. Sci. USA 1997, 94, 1634–1639. [Google Scholar] [CrossRef]
- Warren, W.S. The usefulness of NMR quantum computing. Science 1997, 277, 1688–1690. [Google Scholar] [CrossRef]
- Wang, Z.M.; Luo, D.W.; Li, B.; Wu, L.A. Quantum energy transfer between a nonlinearly coupled bosonic bath and a fermionic chain: An exactly solvable model. Phys. Rev. A 2020, 101, 042130. [Google Scholar] [CrossRef]
- Wang, Z.M.; Ren, F.H.; Sarandy, M.S.; Byrd, M.S. Nonequilibrium quantum thermodynamics in non-Markovian adiabatic speedup. Physica A 2022, 603, 127861. [Google Scholar] [CrossRef]
- Whitney, R.S. Non-Markovian quantum thermodynamics: Laws and fluctuation theorems. Phys. Rev. B 2018, 98, 085415. [Google Scholar] [CrossRef]
- Thomas, G.; Siddharth, N.; Banerjee, S.; Ghosh, S. Thermodynamics of non-Markovian reservoirs and heat engines. Phys. Rev. E 2018, 97, 062108. [Google Scholar] [CrossRef]
- Kato, A.; Tanimura, Y. Quantum heat current under non-perturbative and non-Markovian conditions: Applications to heat machines. J. Chem. Phys. 2016, 145, 224105. [Google Scholar] [CrossRef]
- Feng, G.; Xu, G.; Long, G. Experimental realization of non-adiabatic holonomic quantum computation. Phys. Rev. Lett. 2013, 110, 190501. [Google Scholar] [CrossRef]
- Altowyan, A.S.; Berrada, K.; Abdel-Khalek, S.; Eleuch, H. Quantum coherence and total phase in semiconductor microcavities for multi-photon excitation. Nanomaterials 2022, 12, 2671. [Google Scholar] [CrossRef]
- Hu, M.L.; Hu, X.; Wang, J.; Peng, Y.; Zhang, Y.R.; Fan, H. Quantum coherence and geometric quantum discord. Phys. Rep. 2018, 762–764, 1–100. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [PubMed]
- Yu, T. Non-Markovian quantum trajectories versus master equations: Finite-temperature heat bath. Phys. Rev. A 2004, 69, 062107. [Google Scholar] [CrossRef]
- Sun, Y.J.; Zhang, W.M. Modeling neuronal systems as an open quantum system. Symmetry 2021, 13, 1603. [Google Scholar] [CrossRef]
- Ng, H. Decoherence of interacting Majorana modes. Sci. Rep. 2015, 5, 12530. [Google Scholar] [CrossRef] [PubMed]
- Moriya, T. New mechanism of anisotropic superexchange interaction. Phys. Rev. Lett. 1960, 4, 228–230. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Heide, M.; Bihlmayer, G.; Blügel, S. Dzyaloshinskii-Moriya interaction accounting for the orientation of magnetic domains in ultrathin films: Fe/W(110). Phys. Rev. B 2008, 78, 140403. [Google Scholar] [CrossRef]
- Emori, S.; Bauer, U.; Ahn, S.M.; Martinez, E.; Beach, G.S. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 2013, 12, 611–616. [Google Scholar] [CrossRef]
- Yu, X.; Kanazawa, N.; Zhang, W.; Nagai, T.; Hara, T.; Kimoto, K.; Matsui, Y.; Onose, Y.; Tokura, Y. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 2012, 3, 988. [Google Scholar] [CrossRef]
- Qaiumzadeh, A.; Ado, I.A.; Duine, R.A.; Titov, M.; Brataas, A. Theory of the interfacial Dzyaloshinskii-Moriya interaction in Rashba antiferromagnets. Phys. Rev. Lett. 2018, 120, 197202. [Google Scholar] [CrossRef]
- Liu, B.Q.; Shao, B.; Li, J.G.; Zou, J.; Wu, L.A. Quantum and classical correlations in the one-dimensional XY model with Dzyaloshinskii-Moriya interaction. Phys. Rev. A 2011, 83, 052112. [Google Scholar] [CrossRef]
- Kavokin, K.V. Anisotropic exchange interaction of localized conduction-band electrons in semiconductors. Phys. Rev. B 2001, 64, 075305. [Google Scholar] [CrossRef]
- Wang, Z.M.; Shao, B.; Zou, J. Anisotropy and magnetic field effects on the entanglement transfer in two parallel Heisenberg spin chains. Int. J. Mod. Phys. B 2001, 27, 4853–4861. [Google Scholar] [CrossRef]
- Abliz, A.; Gao, H.J.; Xie, X.C.; Wu, Y.S.; Liu, W.M. Entanglement control in an anisotropic two-qubit Heisenberg XYZ model with external magnetic fields. Phys. Rev. A 2006, 74, 052105. [Google Scholar] [CrossRef]
- Wang, Z.M.; Shao, B.; Chang, P.; Zou, J. Quantum state transfer in a Heisenberg XY chain with energy current. Physica A 2008, 387, 2197–2204. [Google Scholar] [CrossRef]
- Felcher, G.; Kleb, R.; Jaccarino, V. Observation of the spin-flop transition of MnF2 by neutron diffraction. J. Appl. Phys. 1979, 50, 1837. [Google Scholar] [CrossRef]
- Welp, U.; Berger, A.; Miller, D.J.; Vlasko-Vlasov, V.K.; Gray, K.E.; Mitchell, J.F. Direct imaging of the first-order spin-flop transition in the layered manganite La1.4Sr1.6Mn2O7. Phys. Rev. Lett. 1999, 83, 4180–4183. [Google Scholar] [CrossRef]
- Vega, I.D.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Pozzobom, M.B.; Maziero, J. Environment-induced quantum coherence spreading of a qubit. Ann. Phys. 2017, 377, 243–255. [Google Scholar] [CrossRef]
- Latune, C.L.; Sinayskiy, I.; Petruccione, F. Energetic and entropic effects of bath-induced coherences. Phys. Rev. A 2019, 99, 052105. [Google Scholar] [CrossRef]
- Eastham, P.R.; Kirton, P.; Cammack, H.M.; Lovett, B.W.; Keeling, J. Bath-induced coherence and the secular approximation. Phys. Rev. A 2016, 94, 012110. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ablimit, A.; He, R.-H.; Xie, Y.-Y.; Wu, L.-A.; Wang, Z.-M. Quantum Energy Current Induced Coherence in a Spin Chain under Non-Markovian Environments. Entropy 2022, 24, 1406. https://doi.org/10.3390/e24101406
Ablimit A, He R-H, Xie Y-Y, Wu L-A, Wang Z-M. Quantum Energy Current Induced Coherence in a Spin Chain under Non-Markovian Environments. Entropy. 2022; 24(10):1406. https://doi.org/10.3390/e24101406
Chicago/Turabian StyleAblimit, Arapat, Run-Hong He, Yang-Yang Xie, Lian-Ao Wu, and Zhao-Ming Wang. 2022. "Quantum Energy Current Induced Coherence in a Spin Chain under Non-Markovian Environments" Entropy 24, no. 10: 1406. https://doi.org/10.3390/e24101406
APA StyleAblimit, A., He, R.-H., Xie, Y.-Y., Wu, L.-A., & Wang, Z.-M. (2022). Quantum Energy Current Induced Coherence in a Spin Chain under Non-Markovian Environments. Entropy, 24(10), 1406. https://doi.org/10.3390/e24101406




