Multicriteria Group Decision Making Based on Intuitionistic Normal Cloud and Cloud Distance Entropy
Abstract
1. Introduction
2. Preliminaries
2.1. Intuitionistic Fuzzy Set
2.2. Cloud Model
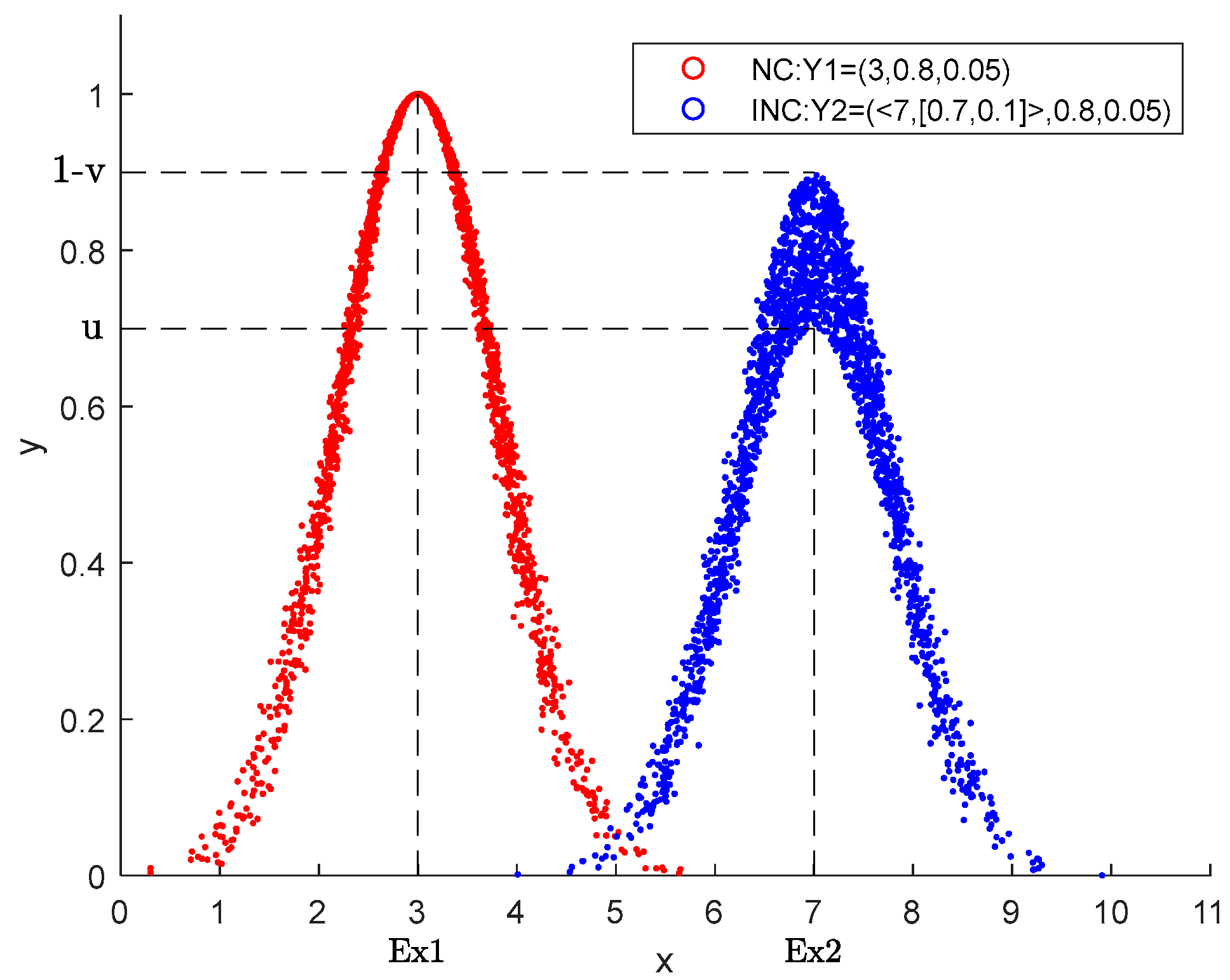
2.3. Intuitionistic Normal Cloud Model
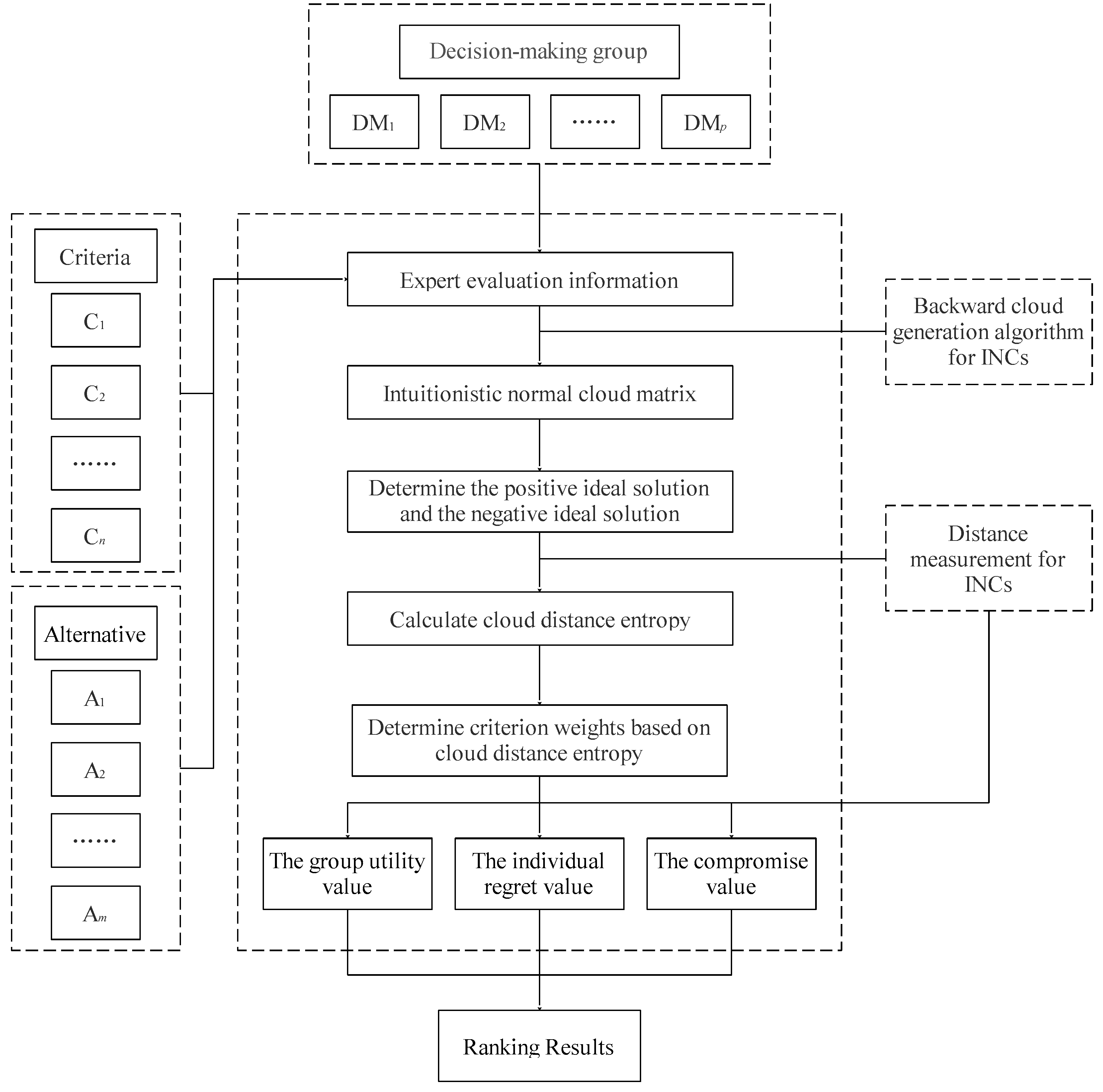
3. MCGDM Model Based on Intuitionistic Normal Cloud and Cloud Distance Entropy
3.1. Backward Cloud Generation Algorithm for INCs
3.2. Cloud Distance Entropy
3.3. Distance Measurement for INCs
- (1)
- ;
- (2)
- ;
- (3)
- If and only if , ;
- (4)
- Ifis an arbitrary INC, then.
3.4. VIKOR Method in Intuitionistic Normal Cloud Environment
4. Numerical Examples and Comparative Analysis
4.1. Numerical Example 1
4.2. Comparative Analysis
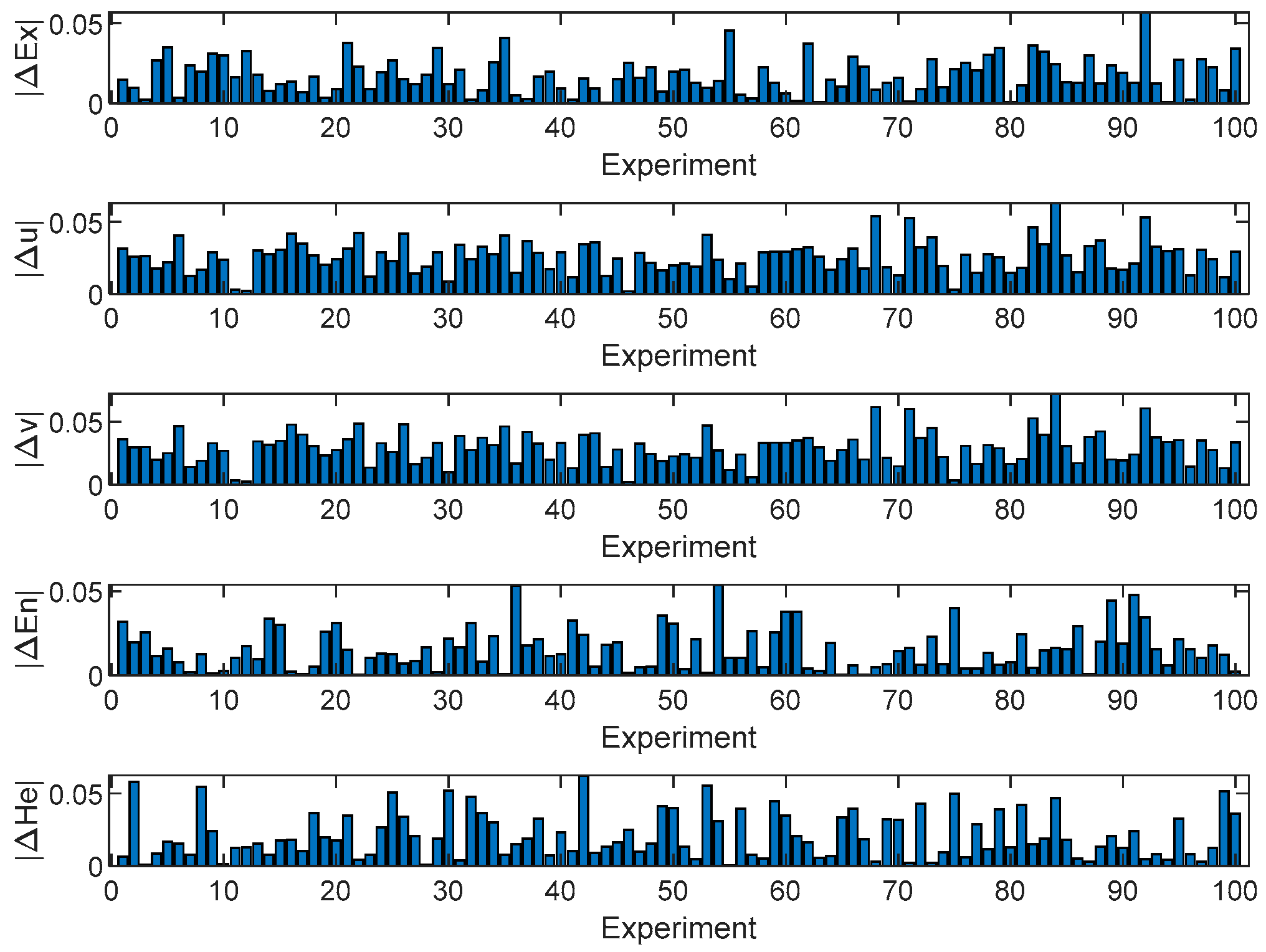
4.2.1. Error Analysis of Backward Cloud Generation Algorithm
- (1)
- Algorithm validity analysis
- (2)
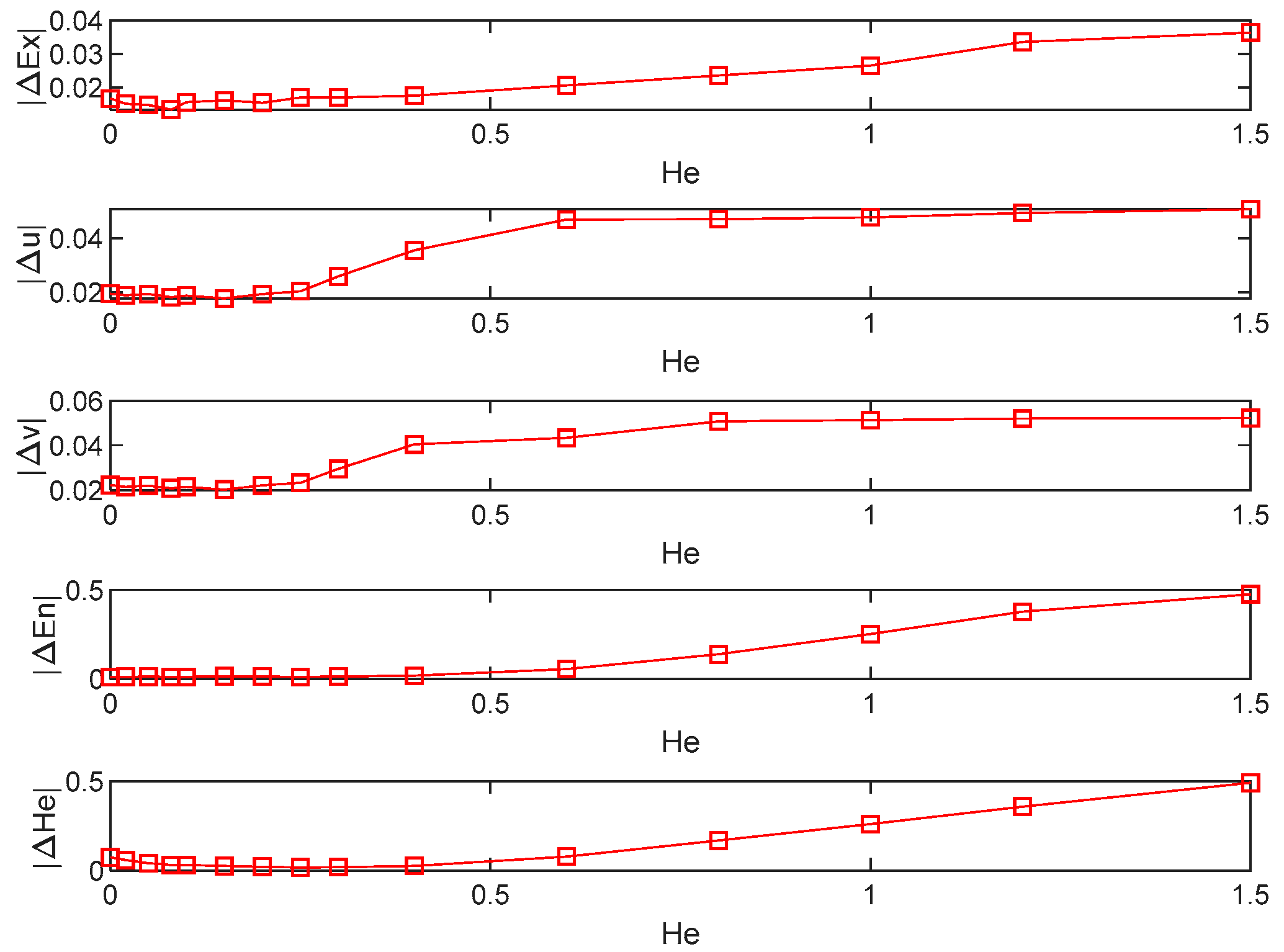
- Algorithm adaptability analysis
- (3)
- Effect of cloud droplet number on error
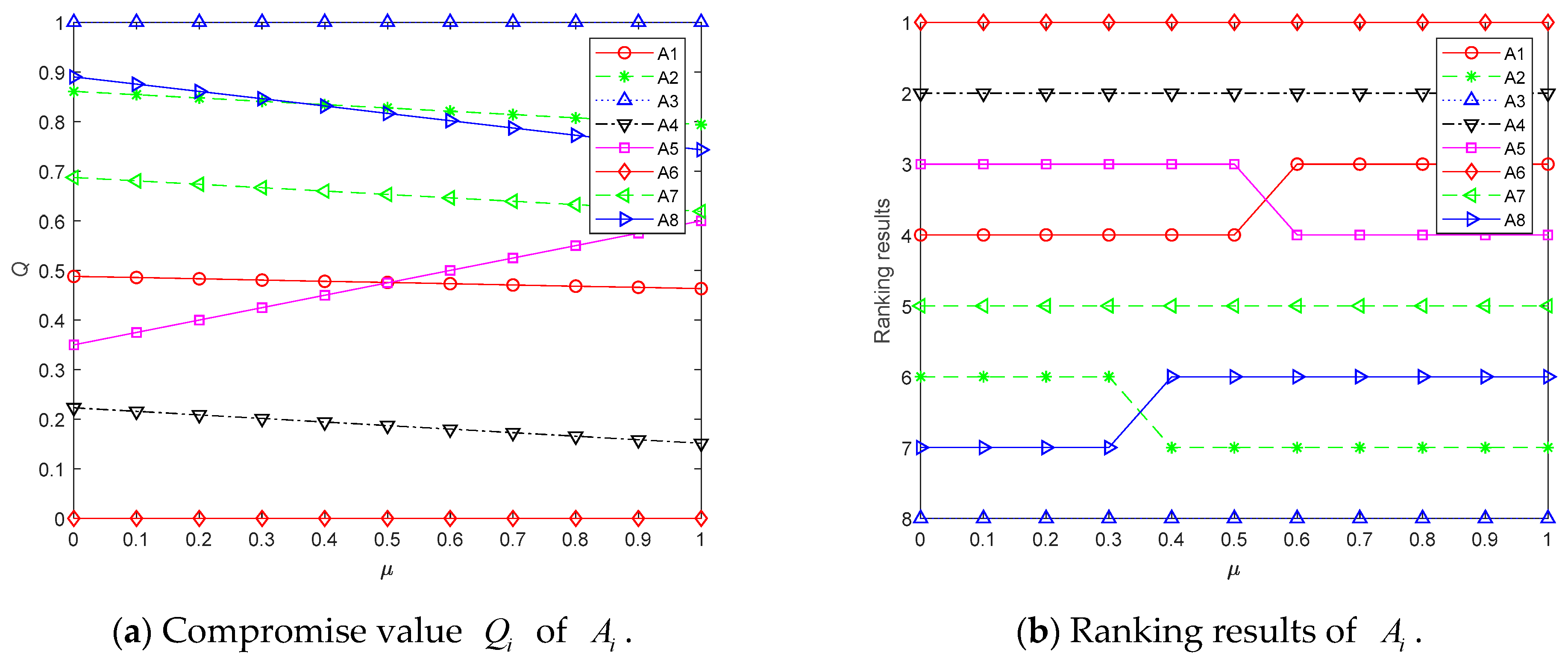
4.2.2. Sensitivity Analysis
4.2.3. Comparative Analysis
4.3. Numerical Example 2
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, M.W.; Xu, Z.S.; Zhai, Y.L.; Yao, Z.Q. Multi-attribute group decision-making under probabilistic uncertain linguistic environment. J. Oper. Res. Soc. 2018, 60, 157–170. [Google Scholar] [CrossRef]
- Hayat, K.; Shamim, R.A.; Alsalman, H.; Gumaei, A.; Yang, X.P.; Akbar, M.A. Group Generalized q-Rung Orthopair Fuzzy Soft Sets: New Aggregation Operators and Their Applications. Math. Probl. Eng. 2021, 2021, 5672097. [Google Scholar] [CrossRef]
- Akram, M.; Ali, G.; Alcantud, J.C.R.; Riaz, A. Group decision-making with Fermatean fuzzy soft expert knowledge. Artif. Intell. Rev. 2022, 55, 5349–5389. [Google Scholar] [CrossRef]
- Akram, M.; Ali, G.; Peng, X.D.; Ul Abidin, M.Z. Hybrid group decision-making technique under spherical fuzzy N-soft expert sets. Artif. Intell. Rev. 2022, 55, 4117–4163. [Google Scholar] [CrossRef]
- Hayat, K.; Tariq, Z.; Lughofer, E.; Aslam, M.F. New aggregation operators on group-based generalized intuitionistic fuzzy soft sets. Soft Comput. 2021, 25, 13353–13364. [Google Scholar] [CrossRef]
- Garcia-Zamora, D.; Labella, A.; Ding, W.P.; Rodriguez, R.M.; Martinez, L. Large-Scale Group Decision-making: A Systematic Review and a Critical Analysis. IEEE-CAA J. Automatic. 2022, 9, 949–966. [Google Scholar] [CrossRef]
- He, Y.; Wei, G.W.; Chen, X.D.; Wei, Y. Bidirectional projection method for multi-attribute group decision-making under probabilistic uncertain linguistic environment. J. Intell. Fuzzy Syst. 2021, 41, 1429–1443. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inform. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy set. Fuzzy Set. Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Gau, W.L.; Buehrer, D.J. Vague sets. IEEE T. Fuzzy Syst. 1993, 23, 610–614. [Google Scholar] [CrossRef]
- Bustince, H.; Burillo, P. Vague sets are Intuitionistic fuzzy set. Fuzzy Set. Syst. 1996, 79, 403–405. [Google Scholar] [CrossRef]
- Chang, Z.; Xiang, H.C.; Chen, Y.X.; Luo, C.K. Intuitionistic Fuzzy Group Decision-making Method Based on Evidence Theory. Fire. Contr. Comm. Contr. 2019, 44, 125–130. [Google Scholar]
- Shen, X.P.; Ding, Y.; Li, S.H. Air Defense Threat Assessment of Warship Formation Based on Dynamic Intuitionistic Fuzzy Group Decision-making. Comm. Contr. Simulat. 2017, 39, 19–26. [Google Scholar]
- Wang, C.; Chen, Y.X.; Cai, Z.Y.; Pan, T.F.; Luo, C.K. Method on Intuitionistic Fuzzy Multi-attribute Group Decision-making Based on TOPSIS. Fire. Contr. Comm. Contr. 2015, 40, 11–15. [Google Scholar]
- Cai, J.S.; Zhang, Z.G.; Shi, P.; He, Q. Method for Risk Ranking Based on Intuitionistic Fuzzy Multi-attribute Group Decision-making. Chin. J. Eng. Math. 2015, 32, 650–658. [Google Scholar]
- Garg, H.; Kumar, K. Some Aggregation Operators for Linguistic Intuitionistic Fuzzy Set and its Application to Group Decision-Making Process Using the Set Pair Analysis. Arab. J. Sci. Eng. 2018, 43, 3213–3227. [Google Scholar] [CrossRef]
- Garg, H.; Kumar, K. Linguistic Interval-Valued Atanassov Intuitionistic Fuzzy Sets and Their Applications to Group Decision Making Problems. IEEE Trans. Fuzzy Syst. 2019, 27, 2302–2311. [Google Scholar] [CrossRef]
- Tian, Y.; Guo, Z.X. A method based on cloud model and FCM clustering for risky large group decision-making. J. Intell. Fuzzy Syst. 2022, 43, 2647–2665. [Google Scholar] [CrossRef]
- Ji, C.L.; Lu, X.W.; Zhang, W.J. A Biobjective Optimization Model for Expert Opinions Aggregation and Its Application in Group Decision-making. IEEE. Syst. J. 2021, 15, 2834–2844. [Google Scholar] [CrossRef]
- Li, D.Y.; Meng, H.J.; Shi, X.M. Membership clouds and membership cloud generators. Comput. Res. Dev. 1995, 32, 16–21. [Google Scholar]
- Li, D.Y.; Liu, C.Y. Study on the universality of the normal cloud model. Eng. Sci. 2005, 3, 18–24. [Google Scholar]
- Su, W.H.; Zhou, J.M. Research on the Method of Quality Assessment with Statistical Information Based on Cloud Model. Stat. Res. 2018, 35, 86–93. [Google Scholar]
- Xiao, W.; Tian, W.P. Hazard assessment and zoning of collapse along highways in China based on backward cloud algorithm. Geomat. Nat. Hazards Risk 2019, 10, 1227–1241. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Ji, P.; Wang, J.Q.; Chen, X.H. A Neutrosophic Normal Cloud and Its Application in Decision-Making. Cogn. Comput. 2016, 8, 649–669. [Google Scholar] [CrossRef]
- Peng, K.K. Risk Evaluation for Bridge Engineering Based on Cloud-Clustering Group Decision Method. J. Perform. Constr. Facil. 2019, 33, 04018105. [Google Scholar] [CrossRef]
- Yu, S.W.; Shi, Z.K. New algorithm of backward cloud based on normal interval number. Syst. Eng. Theory. Pract. 2011, 31, 2021–2026. [Google Scholar]
- Wang, J.Q.; Yang, W.W. Multiple criteria group decision-making method based on intuitionistic normal cloud by Monte Carlo simulation. Syst. Eng. Theory Pract. 2013, 33, 2859–2865. [Google Scholar]
- He, D.Y.; Xu, J.Q.; Chen, X.L. Information-Theoretic-Entropy Based Weight Aggregation Method in Multiple-Attribute Group Decision-Making. Entropy 2016, 18, 171. [Google Scholar] [CrossRef]
- Yue, C. Entropy-based weights on decision makers in group decision-making setting with hybrid preference representations. Appl. Soft. Comput. 2017, 18, 737–749. [Google Scholar] [CrossRef]
- Chen, C.H. A Novel Multi-Criteria Decision-Making Model for Building Material Supplier Selection Based on Entropy-AHP Weighted TOPSIS. Entropy 2020, 22, 259. [Google Scholar] [CrossRef]
- Opricovic, S. Multi-criteria optimization of civil engineering systems. Electron. J. Fac. Civ. Eng. 1998, 2, 5–21. [Google Scholar]
- Li, J.Q.; Chen, W.; Yang, Z.L.; Li, C.Y. A time-preference and VIKOR-based dynamic intuitionistic fuzzy decision-making method. Filomat 2018, 32, 1523–1533. [Google Scholar] [CrossRef]
- Wu, J.; Jin, Y.T.; Zhou, M.; Cao, M.S.; Liu, Y.J. A group consensus decision-making based sustainable supplier selection method by combing DEMATEL and VIKOR. J. Intell. Fuzzy Syst. 2022, 42, 2595–2613. [Google Scholar] [CrossRef]
- Dong, J.Y.; Yuan, F.F.; Wan, S.P. Extended VIKOR method for multiple criteria decision-making with linguistic hesitant fuzzy information. Comput. Ind. Eng. 2017, 112, 305–319. [Google Scholar] [CrossRef]
- Xu, Z.S.; Zhao, N. Information fusion for intuitionistic fuzzy decision-making: An overview. Inform. Fusion 2015, 28, 10–23. [Google Scholar] [CrossRef]
- Li, D.Y.; Liu, C.Y.; Gan, W.Y. A new cognitive model: Cloud model. Int. J. Intell. Syst. 2009, 24, 357–375. [Google Scholar] [CrossRef]
- Lu, Z.M.; Sun, X.K.; Wang, Y.X.; Xu, C.B. Green supplier selection in straw biomass industry based on cloud model and possibility degree. J. Clean. Prod. 2019, 209, 995–1005. [Google Scholar] [CrossRef]
- Pele, D.T.; Lazar, E.; Dufour, A. Information Entropy and Measures of Market Risk. Entropy 2017, 19, 226. [Google Scholar] [CrossRef]
- Wang, H.D.; Yao, X. Objective reduction based on nonlinear correlation information entropy. Soft Comput. 2016, 20, 2393–2407. [Google Scholar] [CrossRef]
- Markechova, D.; Mosapour, B.; Ebrahimzadeh, A. Logical Divergence, Logical Entropy, and Logical Mutual Information in Product MV-Algebras. Entropy 2018, 20, 129. [Google Scholar] [CrossRef]
- Perez-Castrillo, D.; Sotomayor, M. On the manipulability of competitive equilibrium rules in many-to-many buyer-seller markets. Int. J. Game. Theory 2017, 46, 1137–1161. [Google Scholar] [CrossRef]
- Xu, S.D.; Geng, X.L.; Dong, X.Q. Improved FMEA approach for risk evaluation based on cloud model. Comput. Eng. Appl. 2018, 54, 228–233. [Google Scholar]
- Liu, P.D.; Liu, X. Multi-attribute Group Decision-Making Method Based on Cloud Distance Operators with Linguistic Information. Int. J. Fuzzy Syst. 2017, 19, 1011–1024. [Google Scholar] [CrossRef]
- Zhou, X.H.; Li, D.P.; Cheng, P.F.; Yu, W.G.; Fu, C.X. multi-source and heterogeneous VIKOR group decision-making method for cloud manufacturing collaborative innovation partner selection. Comput. Integra. Manuf. Sys. 2022, 28, 59–72. [Google Scholar]
- Li, M.D.; Li, S.B.; Xian, X.M.; He, C.J.; Zheng, L.K.; Wu, G.N. Insulation condition assessment for power transformer based on intuitionistic normal cloud model and optimal variable weights. Elec. Meas. Instrum. 2016, 53, 43–50. [Google Scholar]
- Gong, J.; Hu, T.; Zhao, J.; An, D.H. Research on Warship Construction Risk Method Based on Intuitionistic Normal Cloud and Image Map. Chinese. J. Ord. Eq. Eng. 2021, 42, 64–73. [Google Scholar]
- Faizi, S.; Rashid, T.; Salabun, W.; Zafar, S.; Watrobski, J. Decision Making with Uncertainty Using Hesitant Fuzzy Sets. Int. J. Fuzzy Syst. 2018, 20, 93–103. [Google Scholar] [CrossRef]
- Salabun, W.; Urbaniak, K. A New Coefficient of Rankings Similarity in Decision-Making Problems. In Proceedings of the International Conference on Computational Science–ICCS 2020, Amsterdam, The Netherlands, 3–5 June 2020; pp. 632–645. [Google Scholar]



| (<5.03, [0.71, 0.14]>, 0.78, 0.2) | (<7.35, [0.52, 0.21]>, 1.14, 0.33) | (<4.56, [0.74, 0.14]>, 0.46, 0.08) | |
| (<6.41, [0.67, 0.23]>, 0.47, 0.23) | (<7.38, [0.71, 0.13]>, 0.93, 0.41) | (<5.44, [0.79, 0.13]>, 0.55, 0.12) | |
| (<4.56, [0.79, 0.13]>, 0.81, 0.19) | (<8.12, [0.51, 0.36]>, 1.06, 0.29) | (<6.14, [0.53, 0.28]>, 0.59, 0.11) | |
| (<5.79, [0.62, 0.32]>, 0.66, 0.09) | (<6.71, [0.81, 0.11]>, 0.88, 0.38) | (<5.86, [0.68, 0.17]>, 0.35, 0.09) |
| 0.6739 | 0.2819 | 1.0000 | |
| 0.3165 | 0.1164 | 0.0000 | |
| 0.6441 | 0.2441 | 0.8585 | |
| 0.4376 | 0.1821 | 0.3621 |
| Algorithm | Parameters | |
|---|---|---|
| GRA | Grey correlation coefficient | 0.5 |
| Monte Carlo simulation | Number of cloud droplets | 5000 |
| Number of experiments | 10 | |
| VIKOR | Compromise coefficient | 0.6 |
| Method | Ranking Result | |||||
|---|---|---|---|---|---|---|
| INC-GRA | 0.6428 | 0.9069 | 0.6686 | 0.7947 | ||
| INC-TOPSIS | 1.6440 | 0.7830 | 1.5767 | 1.0559 | ||
| 1.4749 | 1.0426 | 1.3565 | 0.8703 | |||
| 0.4729 | 0.5711 | 0.4625 | 0.4518 | |||
| INC-Monte Carlo in [27] | 2.8729 | 3.5170 | 2.8854 | 3.2574 | ||
| 2.8898 | 3.4545 | 2.8960 | 3.2764 | |||
| 2.8521 | 3.4825 | 2.8611 | 3.2863 | |||
| 2.9062 | 3.4863 | 2.8659 | 3.2559 | |||
| 2.8685 | 3.4706 | 2.9048 | 3.2588 | |||
| 2.8785 | 3.4514 | 2.8924 | 3.2759 | |||
| 2.9033 | 3.4760 | 2.8589 | 3.2792 | |||
| 2.8625 | 3.4758 | 2.8887 | 3.2648 | |||
| 2.8712 | 3.5078 | 2.8914 | 3.2448 | |||
| 2.8836 | 3.4858 | 2.8649 | 3.2605 | |||
| 2.8789 | 3.4808 | 2.8849 | 3.2660 | |||
| The proposed method | 0.6739 | 0.3165 | 0.6441 | 0.4376 | ||
| 0.2819 | 0.1164 | 0.2441 | 0.1821 | |||
| 1.0000 | 0.0000 | 0.8585 | 0.3621 |
| (<5.84, [0.58, 0.32]>, 2.24, 0.39) | (<6.47, [0.65, 0.25]>, 2.35, 0.38) | (<4.28, [0.59, 0.24]>, 2.17, 0.39) | |
| (<4.91, [0.51, 0.39]>, 2.08, 0.43) | (<6.53, [0.63, 0.27]>, 2.28, 0.37) | (<5.33, [0.53, 0.37]>, 2.02, 0.45) | |
| (<3.83, [0.6, 0.3]>, 2.6, 0.29) | (<3.84, [0.64, 0.35]>, 2.26, 0.39) | (<3.25, [0.51, 0.43]>, 2.66, 0.23) | |
| (<7.95, [0.72, 0.18]>, 2.59, 0.28) | (<5.25, [0.6, 0.25]>, 2.66, 0.23) | (<5.56, [0.76, 0.21]>, 2.35, 0.37) | |
| (<4.19, [0.51, 0.38]>,2.39, 0.33) | (<4.3, [0.75, 0.1]>, 2.96, 0.13) | (<5.38, [0.58, 0.37]>, 2.41, 0.29) | |
| (<4.95, [0.8, 0.1]>, 2.96, 0.13) | (<8.65, [0.75, 0.15]>, 2.69, 0.27) | (<6.14, [0.81, 0.12]>, 2.44, 0.16) | |
| (<4.08, [0.7, 0.12]>, 2.37, 0.25) | (<5.14, [0.68, 0.21]>, 2.15, 0.34) | (<4.76, [0.73, 0.15]>, 2.16, 0.33) | |
| (<6.33, [0.68, 0.23]>, 2.14, 0.31) | (<7.14, [0.55, 0.34]>, 2.41, 0.33) | (<3.98, [0.61, 0.35]>, 2.31, 0.27) | |
| (<4.97, [0.72, 0.23]>, 1.97, 0.46) | (<6.19, [0.68, 0.22]>, 2.28, 0.51) | (<7.68, [0.71, 0.22]>, 2.65, 0.34) | |
| (<4.29, [0.56, 0.41]>, 2.09, 0.43) | (<4.28, [0.63, 0.27]>, 2.69, 0.48) | (<5.82, [0.59, 0.31]>, 1.99, 0.45) | |
| (<4.26, [0.6, 0.31]>, 2.46, 0.23) | (<4.56, [0.81, 0.12]>, 1.98, 0.39) | (<6.17, [0.72, 0.23]>, 1.94, 0.47) | |
| (<6.43, [0.7, 0.27]>, 2.16, 0.37) | (<4.97, [0.72, 0.18]>, 2.34, 0.42) | (<6.31, [0.68, 0.21]>, 2.38, 0.29) | |
| (<5.18, [0.67, 0.12]>, 2.36, 0.33) | (<5.41, [0.66, 0.3]>, 2.14, 0.46) | (<7.04, [0.66, 0.32]>, 2.09, 0.36) | |
| (<6.07, [0.8, 0.13]>, 2.28, 0.27) | (<6.74, [0.58, 0.34]>, 2.55, 0.37) | (<6.84, [0.58, 0.39]>, 2.46, 0.41) | |
| (<3.84, [0.74, 0.21]>, 2.66, 0.49) | (<4.97, [0.62, 0.21]>, 2.61, 0.53) | (<6.36, [0.73, 0.21]>, 2.17, 0.32) | |
| (<4.26, [0.55, 0.42]>, 2.04, 0.28) | (<5.31, [0.59, 0.24]>, 2.48, 0.32) | (<5.38, [0.67, 0.13]>, 2.27, 0.44) |
| Method | INC-GRA | INC-TOPSIS | INC-Monte Carlo | The Proposed Method |
|---|---|---|---|---|
| 0.6347 | 0.4754 | 2.7391 | 0.4732 | |
| 0.5452 | 0.3836 | 2.2320 | 0.8209 | |
| 0.5021 | 0.3940 | 1.8725 | 1.0000 | |
| 0.7774 | 0.6288 | 3.2142 | 0.1801 | |
| 0.5988 | 0.4355 | 2.4931 | 0.4999 | |
| 0.8650 | 0.6016 | 3.6403 | 0.0000 | |
| 0.5926 | 0.3920 | 2.5239 | 0.6463 | |
| 0.5586 | 0.4442 | 2.3559 | 0.8019 | |
| Ranking result |
| Method | Measure of Rank Correlation | ||
|---|---|---|---|
| INC-GRA | |||
| 0.9762 | 0.9762 | 0.9766 | |
| INC-TOPSIS | 0.7619 | 0.8095 | 0.8314 |
| The proposed method | 0.9762 | 0.9762 | 0.9766 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Lu, Y.; Fan, C.; Heng, Y.; Zhu, X. Multicriteria Group Decision Making Based on Intuitionistic Normal Cloud and Cloud Distance Entropy. Entropy 2022, 24, 1396. https://doi.org/10.3390/e24101396
Li W, Lu Y, Fan C, Heng Y, Zhu X. Multicriteria Group Decision Making Based on Intuitionistic Normal Cloud and Cloud Distance Entropy. Entropy. 2022; 24(10):1396. https://doi.org/10.3390/e24101396
Chicago/Turabian StyleLi, Wei, Yingqi Lu, Chengli Fan, Yong Heng, and Xiaowen Zhu. 2022. "Multicriteria Group Decision Making Based on Intuitionistic Normal Cloud and Cloud Distance Entropy" Entropy 24, no. 10: 1396. https://doi.org/10.3390/e24101396
APA StyleLi, W., Lu, Y., Fan, C., Heng, Y., & Zhu, X. (2022). Multicriteria Group Decision Making Based on Intuitionistic Normal Cloud and Cloud Distance Entropy. Entropy, 24(10), 1396. https://doi.org/10.3390/e24101396





