Velocity Multistability vs. Ergodicity Breaking in a Biased Periodic Potential
Abstract
1. Introduction
2. Methods
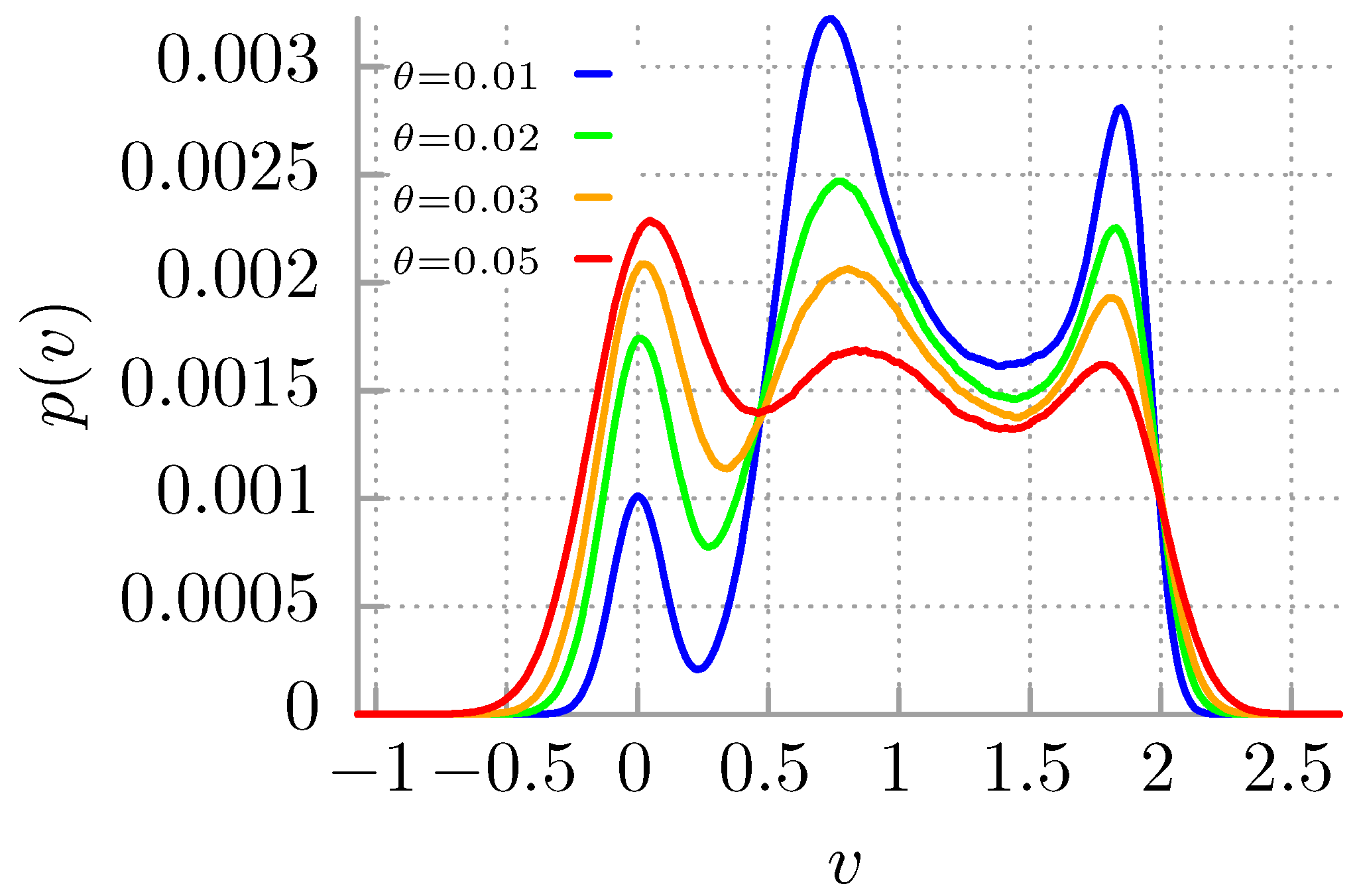
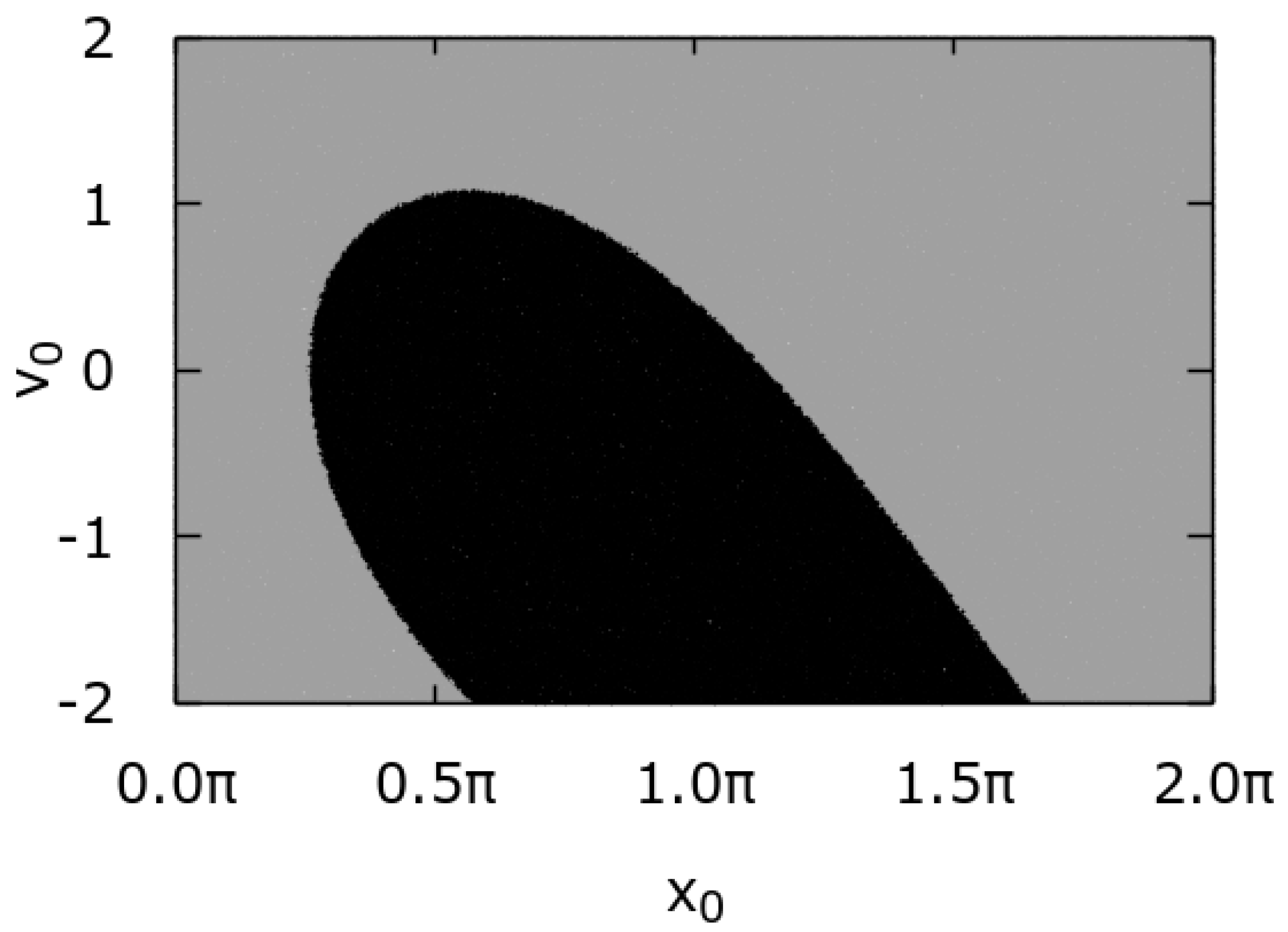
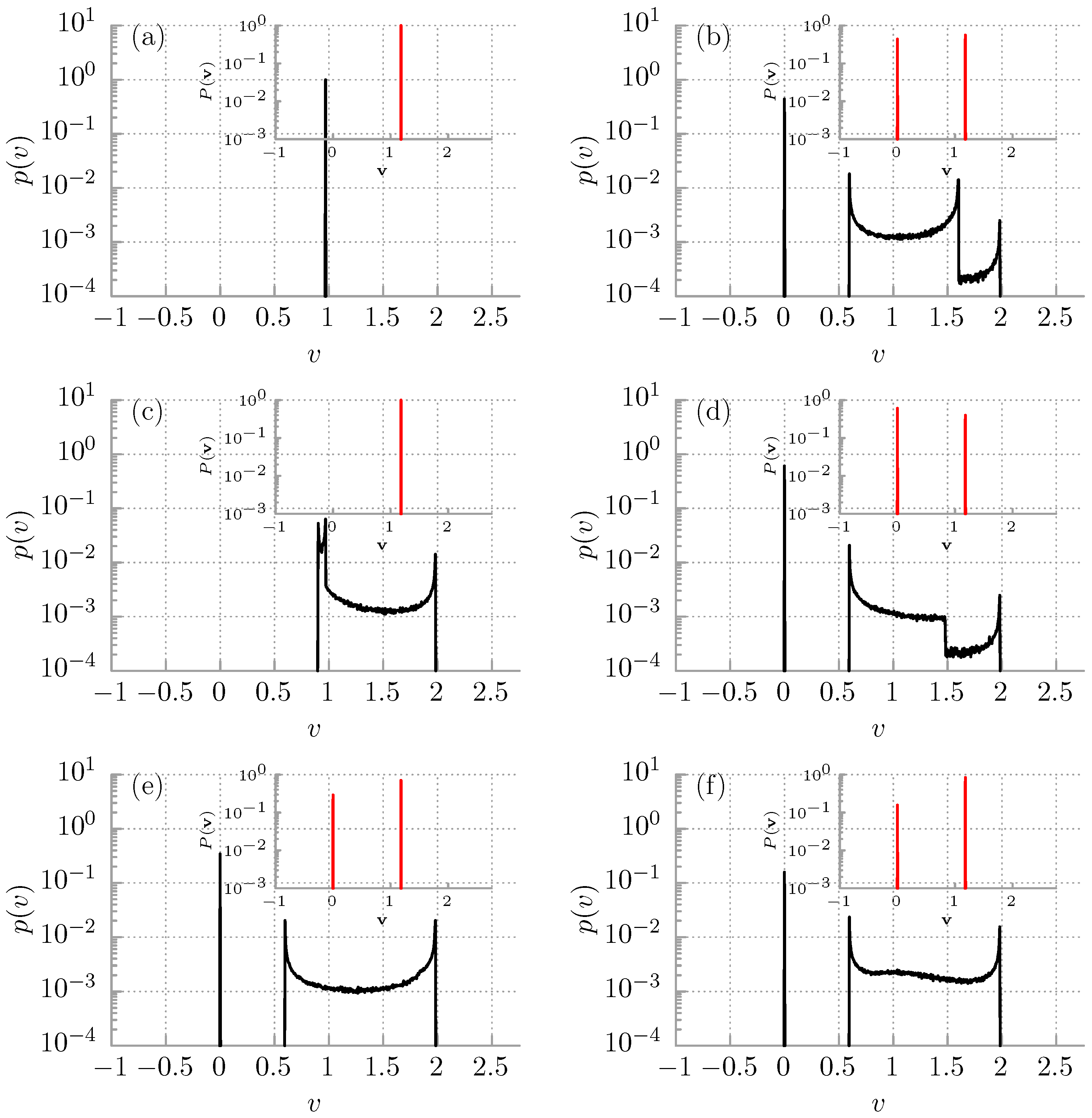
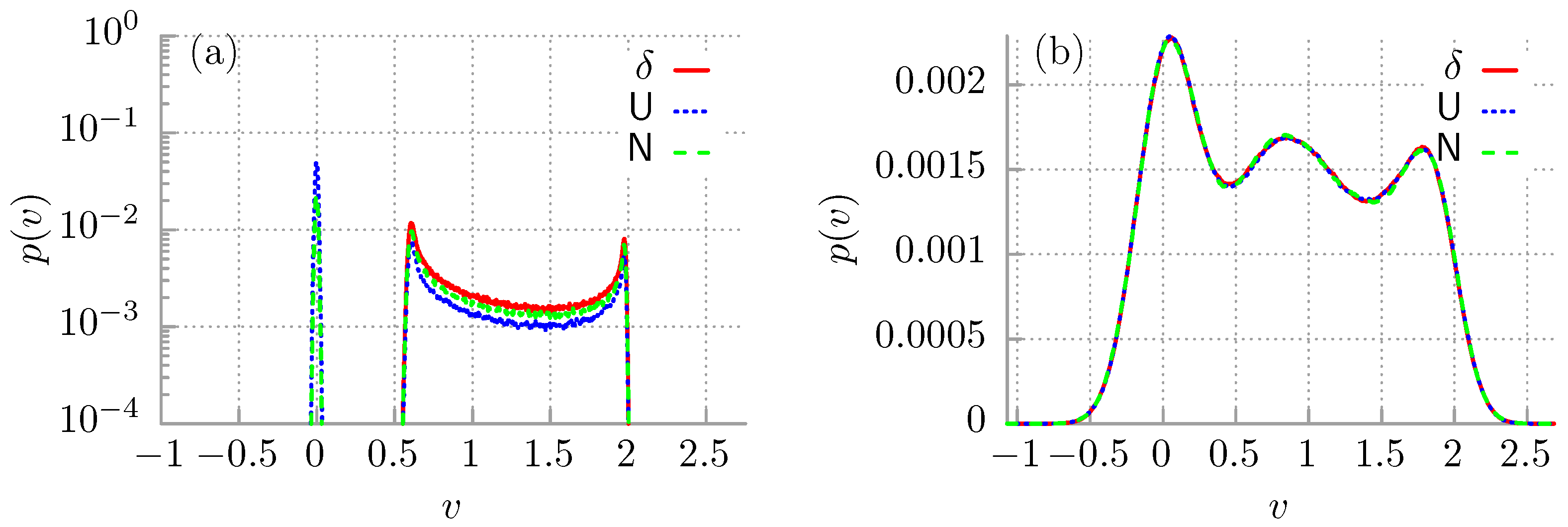
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128. [Google Scholar] [CrossRef]
- Spiechowicz, J.; Łuczka, J. Subdiffusion via dynamical localization induced by thermal equilibrium fluctuations. Sci. Rep. 2017, 7, 16451. [Google Scholar] [CrossRef]
- Spiechowicz, J.; Łuczka, J. SQUID ratchet: Statistics of transitions in dynamical localization. Chaos 2019, 29, 013105. [Google Scholar] [CrossRef] [PubMed]
- Spiechowicz, J.; Hänggi, P.; Łuczka, J. Coexistence of absolute negative mobility and anomalous diffusion. New J. Phys. 2019, 21, 083029. [Google Scholar] [CrossRef]
- Leptos, K.C.; Guasto, J.S.; Gollub, J.P.; Pesci, A.I.; Goldstein, R.E. Dynamics of Enhanced Tracer Diffusion in Suspensions of Swimming Eukaryotic Microorganisms. Phys. Rev. Lett. 2009, 103, 198103. [Google Scholar] [CrossRef]
- Wang, B.; Kuo, J.; Bae, S.C.; Granick, S. When Brownian diffusion is not Gaussian. Nat. Mater. 2012, 11, 481. [Google Scholar] [CrossRef] [PubMed]
- Chechkin, A.V.; Seno, F.; Metzler, R.; Sokolov, I.M. Brownian yet non-Gaussian diffusion: From superstatistics to subordination of diffusing diffusivities. Phys. Rev. X 2017, 7, 021002. [Google Scholar] [CrossRef]
- Białas, K.; Łuczka, J.; Hänggi, P.; Spiechowicz, J. Colossal Brownian yet non-Gaussian diffusion induced by nonequilibrium noise. Phys. Rev. E 2020, 102, 042121. [Google Scholar] [CrossRef] [PubMed]
- Barkai, E.; Burov, S. Packets of spreading particles exhibit universal exponential tails. Phys. Rev. Lett. 2020, 124, 060603. [Google Scholar] [CrossRef]
- Hänggi, P.; Marchesoni, F. Artificial Brownian motors: Controlling transport on the nanoscale. Rev. Mod. Phys. 2009, 81, 387. [Google Scholar] [CrossRef]
- Slapik, A.; Łuczka, J.; Spiechowicz, J. Temperature-induced tunable particle separation. Phys. Rev. Appl. 2019, 12, 054002. [Google Scholar] [CrossRef]
- Machura, Ł.; Kostur, M.; Talkner, P.; Łuczka, J.; Hänggi, P. Absolute negative mobility induced by thermal equilibrium fluctuations. Phys. Rev. Lett. 2007, 98, 040601. [Google Scholar] [CrossRef] [PubMed]
- Nagel, J.; Speer, D.; Gaber, T.; Sterck, A.; Eichhorn, R.; Reimann, P.; Ilin, K.; Siegel, M.; Koelle, D.; Kleiner, R. Observation of negative absolute resistance in a Josephson junction. Phys. Rev. Lett. 2008, 100, 217001. [Google Scholar] [CrossRef] [PubMed]
- Slapik, A.; Łuczka, J.; Hänggi, P.; Spiechowicz, J. Tunable mass separation via negative mobility. Phys. Rev. Lett. 2019, 122, 070602. [Google Scholar] [CrossRef] [PubMed]
- Slapik, A.; Spiechowicz, J. Tunable particle separation via deterministic absolute negative mobility. Sci. Rep. 2020, 10, 16639. [Google Scholar] [CrossRef] [PubMed]
- Pisarchik, A.; Feudel, U. Control of multistability. Phys. Rep. 2014, 540, 167. [Google Scholar] [CrossRef]
- Risken, H. The Fokker-Planck Equation: Methods of Solution and Applications; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Lindner, B.; Kostur, M.; Schimansky-Geier, L. Optimal diffusive transport in a tilted periodic potential. Fluct. Noise Lett. 2001, R25, 173. [Google Scholar] [CrossRef]
- Reimann, P.; Van den Broeck, C.; Linke, H.; Hänggi, P.; Rubi, J.M.; Perez-Madrid, A. Giant acceleration of free diffusion by use of tilted periodic potentials. Phys. Rev. Lett. 2001, 87, 010602. [Google Scholar] [CrossRef]
- Reimann, P.; Van den Broeck, C.; Linke, H.; Hänggi, P.; Rubi, J.M.; Perez-Madrid, A. Diffusion in tilted periodic potentials: Enhancement, universality, and scaling. Phys. Rev. E 2001, 65, 031104. [Google Scholar] [CrossRef]
- Constantini, G.; Marchesoni, F. Threshold diffusion in a tilted washboard potential. Europhys. Lett. 1999, 48, 491. [Google Scholar] [CrossRef]
- Lindenberg, K.; Lacasta, A.M.; Sancho, J.M.; Romero, A.H. Transport and diffusion on crystalline surfaces under external forces. New. J. Phys. 2005, 7, 29. [Google Scholar] [CrossRef]
- Marchenko, I.G.; Marchenko, I.I. Diffusion in the system with low dissipation: Exponential growth with temperature. Europhys. Lett. 2012, 100, 50005. [Google Scholar] [CrossRef]
- Latorre, J.C.; Pavliotis, G.A.; Kramer, P.R. Corrections to Einstein’s relation for Brownian motion in a tilted periodic potential. J. Stat. Phys. 2013, 150, 776. [Google Scholar] [CrossRef][Green Version]
- Lindner, B.; Sokolov, I.M. Giant diffusion of underdamped particles in a biased periodic potential. Phys. Rev. E 2016, 93, 042106. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.M.; Bao, J.D. Transition of multidiffusive states in a biased periodic potential. Phys. Rev. E 2017, 95, 032107. [Google Scholar] [CrossRef] [PubMed]
- Marchenko, I.G.; Marchenko, I.I.; Tkachenko, V.I. Temperature-Abnormal Diffusivity in Underdamped Spatially Periodic Systems. JETP Lett. 2017, 106, 242. [Google Scholar] [CrossRef]
- Cheng, C.; Cirillo, M.; Salina, G.; Gronbech-Jensen, N. Nonequilibrium transient phenomena in the washboard potential. Phys. Rev. E 2018, 98, 012140. [Google Scholar] [CrossRef]
- Goychuk, I. Fractional Hydrodynamic Memory and Superdiffusion in Tilted Washboard Potentials. Phys. Rev. Lett. 2019, 123, 180603. [Google Scholar] [CrossRef]
- Spiechowicz, J.; Łuczka, J. Diffusion in a biased washboard potential revisited. Phys. Rev. E 2020, 101, 032123. [Google Scholar] [CrossRef]
- Goychuk, I.; Pöschel, T. Nonequilibrium Phase Transition to Anomalous Diffusion and Transport in a Basic Model of Nonlinear Brownian Motion. Phys. Rev. Lett. 2021, 127, 110601. [Google Scholar] [CrossRef] [PubMed]
- Spiechowicz, J.; Łuczka, J. The conundrum of weak noise limit for diffusion in a tilted periodic potential. Phys. Rev. E 2021, 104, 034104. [Google Scholar] [CrossRef] [PubMed]
- Marchenko, I.G.; Marchenko, I.I.; Tkachenko, V.I. Temperature-Abnormal Diffusivity in Tilted Periodic Potentials. JETP Lett. 2019, 109, 671. [Google Scholar] [CrossRef]
- Vollmer, H.; Risken, H. Eigenvalues and their connection to transition rates for the Brownian motion in an inclined cosine potential. J. Phys. B. Cond. Mat. 1983, 52, 259. [Google Scholar] [CrossRef]
- Spiechowicz, J.; Łuczka, J. Arcsine law and multistable Brownian dynamics in a tilted periodic potential. Phys. Rev. E 2021, 104, 024132. [Google Scholar] [CrossRef] [PubMed]
- Meroz, Y.; Sokolov, I.M. A toolbox for determining subdiffusive mechanisms. Phys. Rep. 2015, 573, 1–29. [Google Scholar] [CrossRef]
- Bouchaud, J.P. Weak ergodicity breaking and aging in disordered systems. J. Phys. I France 1992, 2, 1705. [Google Scholar] [CrossRef]
- Barone, A.; Paternò, G. Physics and Application of the Josephson Effect; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Coffey, W.T.; Kalmykov, Y.P.; Waldron, J.T. The Langevin Equation; World Scientific: Singapore, 2004; See Sects. 5 and 7–10 therein. [Google Scholar]
- Grüner, G.; Zawadowski, A.; Chaikin, P.M. Nonlinear Conductivity and Noise due to Charge-Density-Wave Depinning in NbSe3. Phys. Rev. Lett. 1981, 46, 511. [Google Scholar] [CrossRef]
- Fulde, P.; Pietronero, L.; Schneider, W.R.; Strässler, S. Problem of Brownian Motion in a Periodic Potential. Phys. Rev. Lett. 1975, 35, 1776. [Google Scholar] [CrossRef]
- Denisov, S.; Flach, S.; Hänggi, P. Tunable transport with broken space–Time symmetries. Phys. Rep. 2014, 538, 77. [Google Scholar] [CrossRef]
- Kindermann, F.; Dechant, A.; Hohmann, M.; Lausch, T.; Mayer, D.; Schmidt, F.; Lutz, E.; Widera, A. Nonergodic diffusion of single atoms in a periodic potential. Nat. Phys. 2017, 13, 137. [Google Scholar] [CrossRef]
- Dechant, A.; Kindermann, F.; Widera, A.; Lutz, E. Continuous-Time Random Walk for a Particle in a Periodic Potential. Phys. Rev. Lett. 2019, 123, 070602. [Google Scholar] [CrossRef]
- Spiechowicz, J.; Kostur, M.; Machura, Ł. GPU accelerated Monte Carlo simulation of Brownian motors dynamics with CUDA. Comp. Phys. Commun. 2015, 191, 140. [Google Scholar] [CrossRef]
- Seibert, A.; Denisov, S.; Ponomarev, A.; Hänggi, P. Mapping the Arnold web with a GPU-supercomputer. Chaos 2011, 21, 043123. [Google Scholar] [CrossRef]
- Li, F.; Chen, X.S.; Liu, J. Anomalous correlated Lévy flight induced by coexistence of correlation and dissipative nonlinearity. J. Stat. Mech. 2020, 2020, 083209. [Google Scholar] [CrossRef]
- Li, F.; Zhu, P.; Bao, J.D.; Chen, X.S.; Liu, J. Nontrivial anomalous diffusions induced by the harmonic velocity Lévy noise. J. Stat. Mech. 2021, 2021, 043210. [Google Scholar] [CrossRef]
- Kheifets, S.; Simha, A.; Melin, K.; Li, T.; Raizen, M.G. Observation of Brownian Motion in Liquids at Short Times: Instantaneous Velocity and Memory Loss. Science 2014, 343, 1493. [Google Scholar] [CrossRef] [PubMed]
- Kraut, S.; Feudel, U.; Grebogi, C. Preference of attractors in noisy multistable systems. Phys. Rev. E 1999, 59, 5253. [Google Scholar] [CrossRef] [PubMed]
- Spiechowicz, J.; Łuczka, J.; Hänggi, P. Transient anomalous diffusion in periodic systems: Ergodicity, symmetry breaking and velocity relaxation. Sci. Rep. 2016, 6, 30948. [Google Scholar] [CrossRef]
- Kostur, M.; Machura, Ł.; Łuczka, J.; Talkner, P.; Hänggi, P. Negative conductance in driven Josephson junctions. Acta Phys. Polon. B 2008, 39, 1177. [Google Scholar]
- Cheng, L.; Yip, N.K. The long time behavior of Brownian motion in tilted periodic potentials. Phys. D 2015, 297, 1–32. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spiechowicz, J.; Hänggi, P.; Łuczka, J. Velocity Multistability vs. Ergodicity Breaking in a Biased Periodic Potential. Entropy 2022, 24, 98. https://doi.org/10.3390/e24010098
Spiechowicz J, Hänggi P, Łuczka J. Velocity Multistability vs. Ergodicity Breaking in a Biased Periodic Potential. Entropy. 2022; 24(1):98. https://doi.org/10.3390/e24010098
Chicago/Turabian StyleSpiechowicz, Jakub, Peter Hänggi, and Jerzy Łuczka. 2022. "Velocity Multistability vs. Ergodicity Breaking in a Biased Periodic Potential" Entropy 24, no. 1: 98. https://doi.org/10.3390/e24010098
APA StyleSpiechowicz, J., Hänggi, P., & Łuczka, J. (2022). Velocity Multistability vs. Ergodicity Breaking in a Biased Periodic Potential. Entropy, 24(1), 98. https://doi.org/10.3390/e24010098





