FPGA-Implemented Fractal Decoder with Forward Error Correction in Short-Reach Optical Interconnects
Abstract
:1. Introduction
2. Theoretical Aspects and Estimation of Indivisible Code Based on APM
2.1. Theoretical Aspects of Indivisible Code
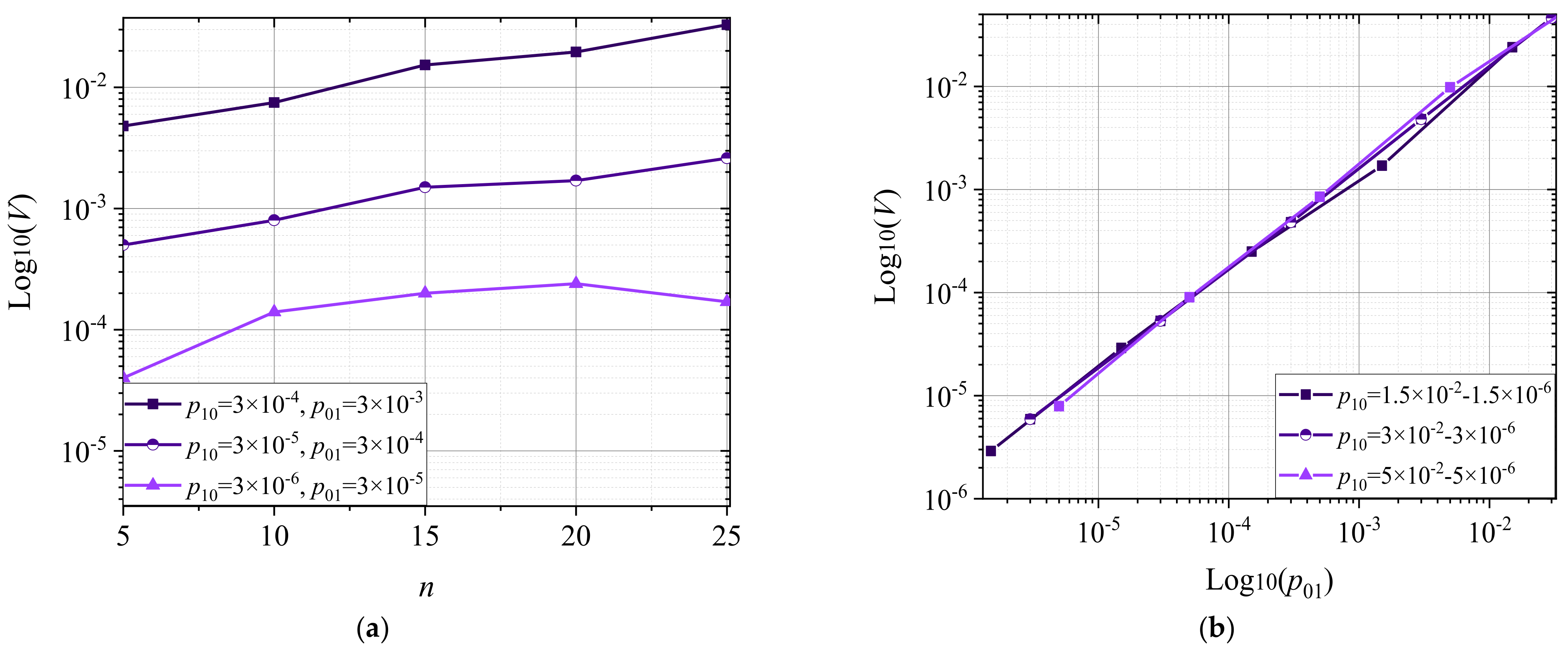
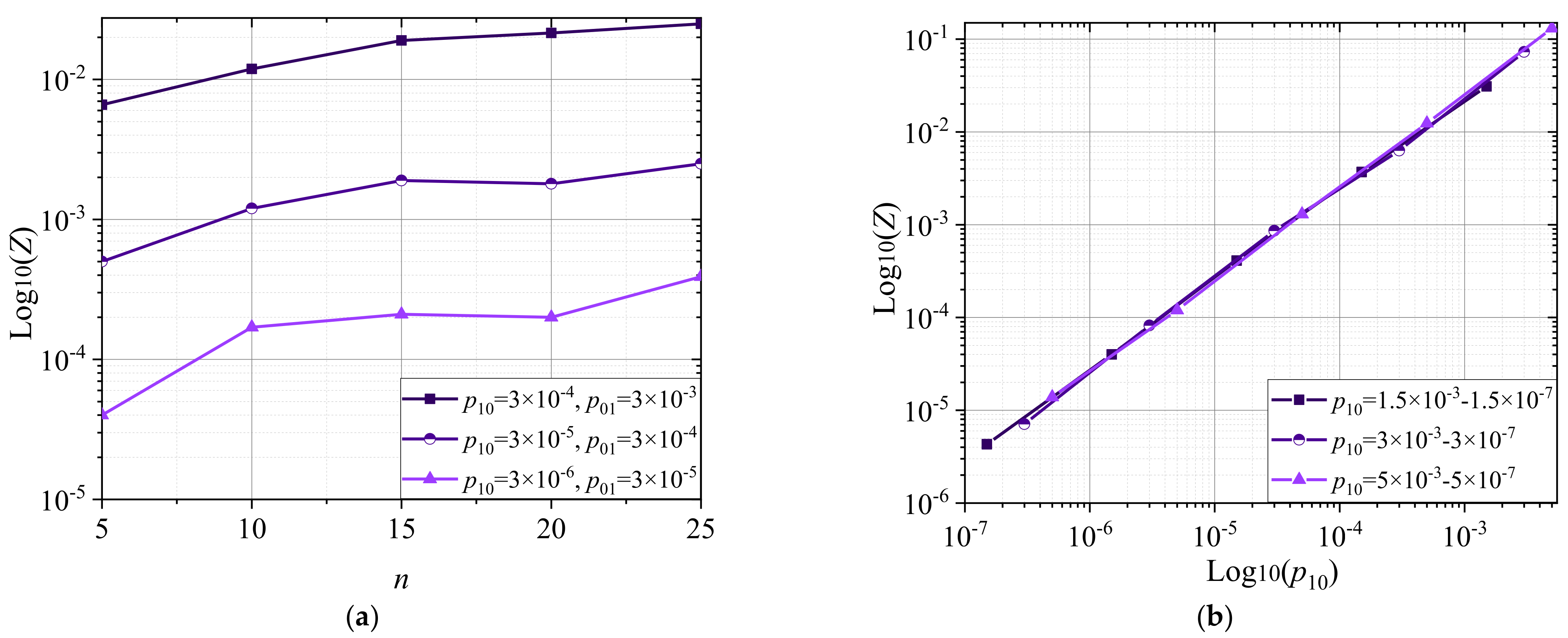
2.2. Estimation of Indivisible Code Based on Average Probability Method (APM)
3. System Model, Achievable Rates and Numerical Analysis of an Optical System
3.1. System Model and Achievable Rates
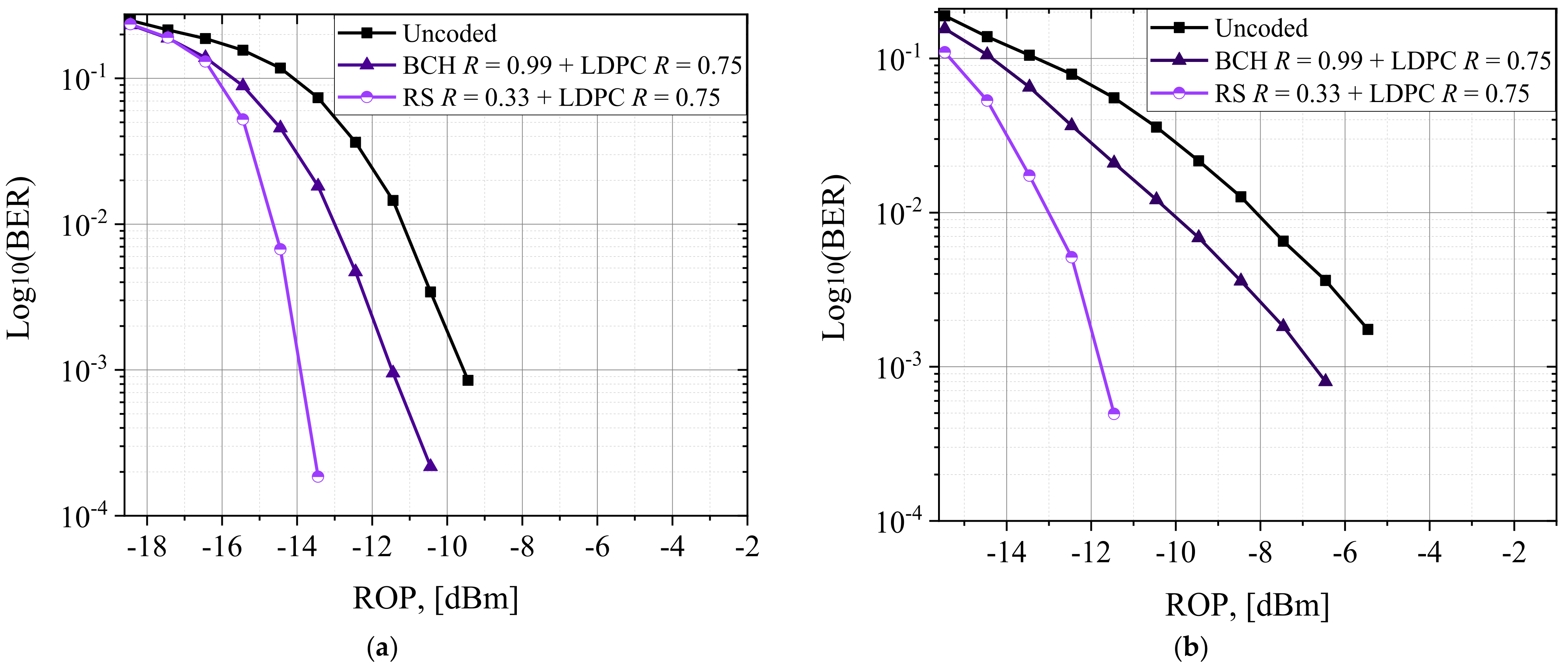
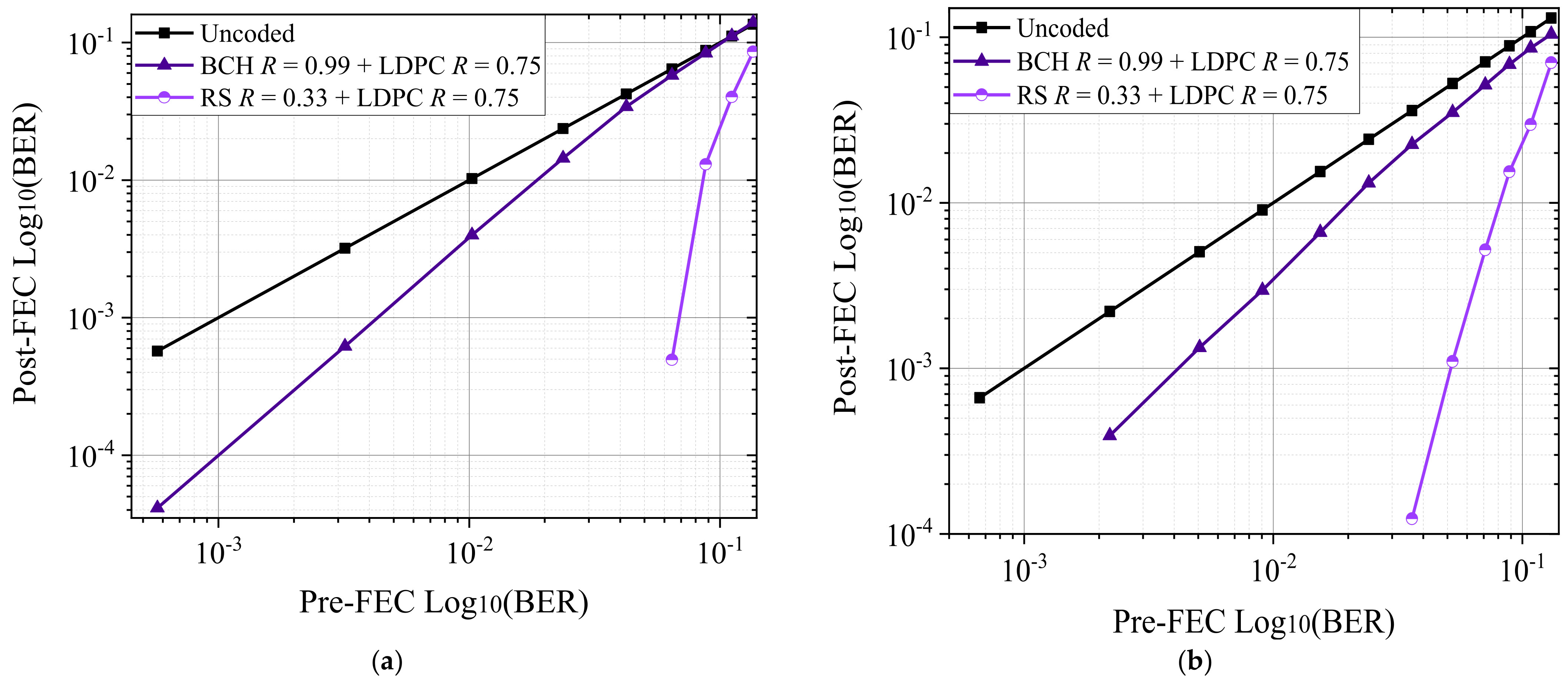
3.2. Numerical Analysis of an Optical System
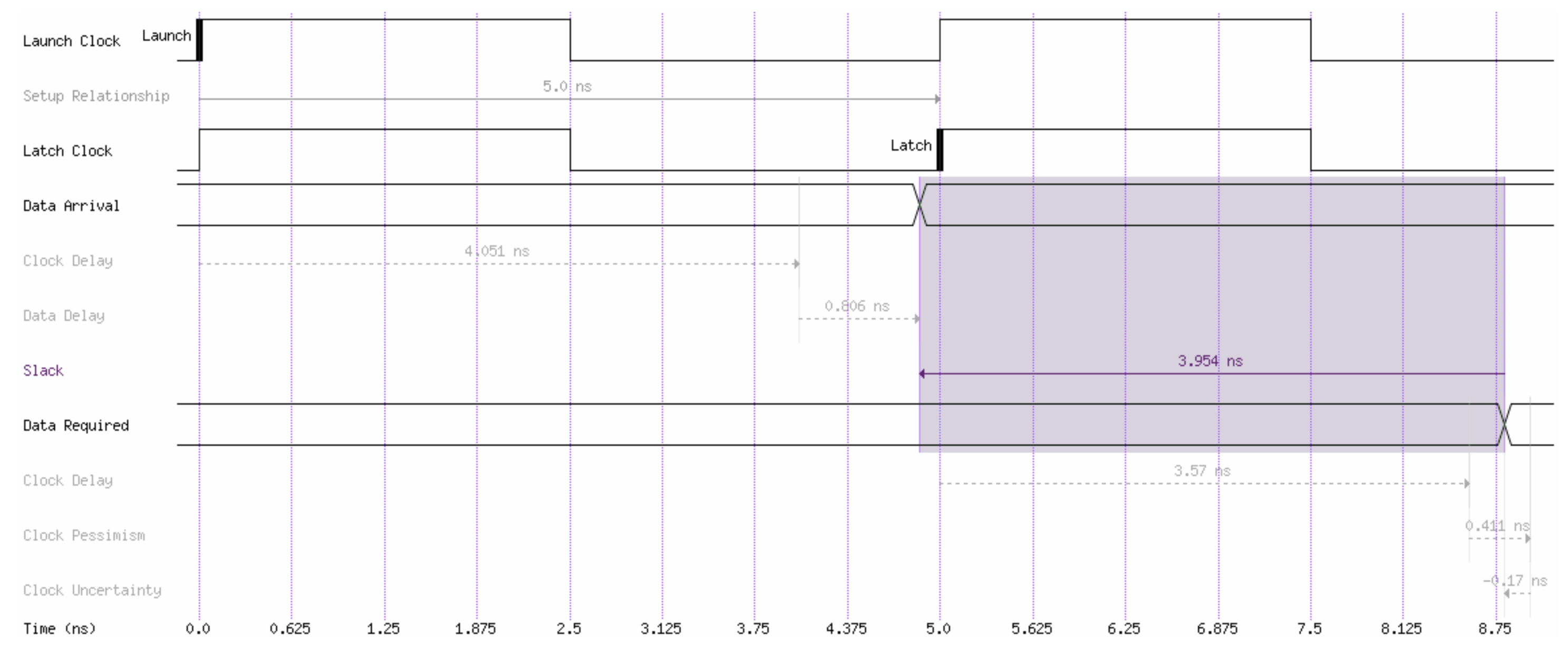
4. Design of the Fractal Decoder Device
- In a set of the indivisible code f = x1, x2, …, xj, …, xn, fractal parts are found that are distinguished by the presence of 0 or 1 in the MSB.
- The fractal part of the indivisible codes decodes by the line decoder (D 3.1).
- Depending on the signal of the MSB (0 or 1), the first (SW 1.1) or second switch (SW 1.2) is triggered, wherein its outputs correspond to the numbers of the first or second fractals.
- The codes are not included in the fractal part decoding by the line decoder (D 3.2).
- If an erroneous combination is received at the inputs of decoders DC 3.1 and DC 3.2, in which xj × x−-1 = 1, j = 1, 2, …, n, an error signal is detected.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Effenberger, F.J. Industrial Trends and Roadmap of Access. J. Lightwave Technol. 2017, 35, 1142–1146. [Google Scholar] [CrossRef]
- Huo, J.; Zhou, X.; Zhong, K.P.; Tu, J.; Yuan, J.; Guo, C.; Long, K.; Yu, C.; Lau, A.P.T.; Lu, C. Transmitter and receiver DSP for 112 Gbit/s PAM-4 amplifier-less transmissions using 25G-class EML and APD. Opt. Express 2018, 26, 22673. [Google Scholar] [CrossRef] [PubMed]
- Eiselt, N.; Wei, J.; Griesser, H.; Dochhan, A.; Eiselt, M.; Elbers, J.-P.; Olmos, J.J.V.; Monroy, I.T. First Real-Time 400G PAM-4 Demonstration for Inter-Data Center Transmission over 100 km of SSMF at 1550 nm. In Proceedings of the Optical Fiber Communication Conference (OFC), Anaheim, CA, USA, 20–24 March 2016. [Google Scholar]
- Lee, J.H.; Chang, S.H.; Huh, J.Y.; Kang, S.-K.; Kim, K.; Lee, J.K. EML based real-time 112 Gbit/s (2 × 56.25 Gbit/s) PAM-4 signal transmission in C-band over 80 km SSMF for inter DCI applications. Opt. Fiber Technol. 2018, 45, 141–145. [Google Scholar] [CrossRef]
- Li, H.; Hu, R.; Yang, Q.; Luo, M.; He, Z.; Jiang, P.; Liu, Y.; Li, X.; Yu, S. Improving the performance of mobile fronthaul architecture employing high order delta-sigma modulator with PAM-4 format. Opt. Express 2017, 25, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Li, Z.; Peng, J.; Tan, A.; Song, Y.; Li, Y.; Chen, J.; Wang, M. Decoding of 10-G Optics-Based 50-Gb/s PAM-4 Signal Using Simplified MLSE. IEEE Photonics J. 2018, 10, 7905508. [Google Scholar] [CrossRef]
- Zhong, K.; Zhou, X.; Huo, J.; Yu, C.; Lu, C.; Lau, A.P.T. Digital Signal Processing for Short-Reach Optical Communications: A Review of Current Technologies and Future Trends. J. Lightwave Technol. 2018, 36, 377–400. [Google Scholar] [CrossRef]
- Ungerboeck, G. Channel coding with multilevel/phase signals. IEEE Trans. Inf. Theory 1982, 28, 55–67. [Google Scholar] [CrossRef]
- Pillai, B.S.G.; Sedighi, B.; Guan, K.; Anthapadmanabhan, N.P.; Shieh, W.; Hinton, K.J.; Tucker, R.S. End-to-End Energy Modeling and Analysis of Long-Haul Coherent Transmission Systems. J. Lightwave Technol. 2014, 32, 3093–3111. [Google Scholar] [CrossRef]
- Chen, B.; Lei, Y.; Liga, G.; Okonkwo, C.; Alvarado, A. Hard-Decision Coded Modulation for High-Throughput Short-Reach Optical Interconnect. Entropy 2020, 22, 400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ITU-T. Forward Error Correction for High Bit-Rate DWDM Submarine Systems. 2013. Available online: https://www.itu.int/rec/T-REC-G.975.1/en (accessed on 20 November 2021).
- Scholten, M.; Coe, T.J.; Dillard, J. Continuously-interleaved BCH (CI-BCH) FEC delivers best-in-class NECG for 40 G and 100 G Metro applications. In Proceedings of the 2010 Conference on Optical Fiber Communication (OFC/NFOEC), Collocated National Fiber Optic Engineers Conference, San Diego, CA, USA, 21–25 March 2010; p. NTuB3. [Google Scholar]
- Scholten, M.; Coe, T.; Dillard, J.; Chang, F. Enhanced FEC for 40 G/100 G. Proc. ECOC 2009, 9, 1–12. [Google Scholar]
- Li, B.; Larsen, K.J.; Zibar, D.; Monroy, I.T. Over 10 dB net coding gain based on 20% overhead hard decision forward error correction in 100 G optical commnication systems. In Proceedings of the 2011 37th European Conference and Exhibition on Optical Communicatio, Geneva, Switzerland, 18–22 September 2011; pp. 1–3. [Google Scholar]
- Northcott, P. Swizzle, FEC for 40 G and 100 G Optical Transmission; PMC-Sierra, Inc.: Sunnyvale, CA, USA, 2011. [Google Scholar]
- Smith, B.; Farhood, A.; Hunt, A.; Kschischang, F.; Lodge, J. Staircase codes: FEC for 100 Gb/s OTN. J. Lightwave Technol. 2012, 30, 110–117. [Google Scholar] [CrossRef] [Green Version]
- Sugihara, K.; Miyata, Y.; Sugihara, T.; Kubo, K.; Yoshida, H.; Matsumoto, W.; Mizuochi, T. A spatially-coupled type LDPC Code with an NCG of 12 dB for optical transmission beyond 100 Gb/s. In Proceedings of the OFC/NFOEC, Anaheim, CA, USA, 17–21 March 2013; pp. 1–3. [Google Scholar]
- Chang, D.; Yu, F.; Xiao, Z.; Stojanovic, N.; Hauske, F.N.; Cai, Y.; Xie, C.; Li, L.; Xu, X.; Xiong, Q. LDPC convolutional codes using layered decoding algorithm for high speed coherent optical transmission. In Proceedings of the OFC/NFOEC, Los Angeles, CA, USA, 4–8 March 2012; pp. 1–3. [Google Scholar]
- Dave, D. Soft-decision forward error correction in a 40-nm ASIC for 100-Gbps OTN applications. In Proceedings of the National Fiber Optic Engineers Conference, Los Angeles, CA, USA, 6–10 March 2011; p. JWA014. [Google Scholar]
- FEC IP Cores; ECC66100 Series; Viasat: Cuyahoga Heights, OH, USA, 2017.
- Djordjevic, I.; Xu, L.; Wang, T.; Cvijetic, M. Large girth low-density parity-check codes for long-haul high-speed optical communictions. In Proceedings of the National Fiber Optic Engineers Conference, San Diego, CA, USA, 24–28 February 2008; pp. 1–3. [Google Scholar]
- Djordjevic, I.; Arabaci, M.; Minkov, L. Next generation FEC for high-capacity communication in optical transport networks. J. Lightwave Technol. 2009, 27, 3518–3530. [Google Scholar] [CrossRef] [Green Version]
- Arabaci, M.; Djordjevic, I.; Saunders, R.; Marcoccia, R. High-rate nonbinary regular quasi-cyclic LDPC codes for optical communications. J. Lightwave Technol. 2009, 27, 5261–5267. [Google Scholar] [CrossRef] [Green Version]
- Bergman, G. A number system with an irrational base. Math. Mag. 1957, 31, 98–110. [Google Scholar] [CrossRef]
- Hoggatt, V. Fibonacci and Lucas Numbers; Houghton Mifflin: Boston, MA, USA, 1969; 92p. [Google Scholar]
- Sergeev, I. On the Complexity of Fibonacci Coding. Probl. Inf. Transm. 2018, 54, 343–350. [Google Scholar] [CrossRef]
- Stakhov, A. Numeral Systems with Irrational Bases for Mission-Critical Applications; World Scientific: Singapore, 2017; 284p. [Google Scholar]
- Stakhov, A.; Aranson, S.; Olsen, S. The “Golden” Non-Euclidean Geometry; World Scientific: Singapore, 2016; 308p. [Google Scholar]
- Borysenko, A.A.; Horiachev, O.Y.; Matsenko, S.M.; Kobiakov, O.M. Noise-immune codes based on permutations. In Proceedings of the 2018 IEEE 9th International Conference on Dependable Systems, Services and Technologies, Kyiv, Ukraine, 24–27 May 2018; pp. 609–612. [Google Scholar]
- Borysenko, O.; Kalashnikov, V.; Kalashnikova, N. Description and applications of binomial numeral systems. Comput. Sci. Cyber Secur. 2016, 2, 13–21. [Google Scholar]
- Knuth, D.E. An imaginary number system. Commun. ACM 1960, 3, 245–247. [Google Scholar] [CrossRef]
- Lan, T.; Cai, Z.C. A Novel Image Representation Method under a Non-Standard Positional Numeral System. IEEE Trans. Multimed. 2021, 23, 1301–1315. [Google Scholar] [CrossRef]
- Chang, C.H.; Sousa, L. Modular Arithmetic based Circuits and Systems for Emerging Technologies and Applications: Deep Neural Networks and Cryptography. In Proceedings of the IEEE ISCAS 2018, Florence, Italy, 27–30 May 2018. [Google Scholar]
- Jenkins, W.K.; Soderstrand, M.A.; Radhakrishnan, C. Historical Patterns of Emerging Residue Number System Technologies During the Evolution of Computer Engineering and Digital Signal Processing. In Proceedings of the IEEE ISCAS 2018, Florence, Italy, 27–30 May 2018. [Google Scholar]
- Olsen, E. RNS Hardware Matrix Multiplier for High Precision Neural Network Acceleration. In Proceedings of the IEEE ISCAS 2018, Florence, Italy, 27–30 May 2018. [Google Scholar]
- Soderstrand, M.A. Contributions of Graham Jullien and William Miller to Modified Quadratic Number System Arithmetic. In Proceedings of the 2018 IEEE 61st International Midwest Symposium on Circuits and Systems (MWSCAS), Windsor, ON, Canada, 5–8 August 2018; pp. 161–164. [Google Scholar]
- Matsenko, S.; Borysenko, O.; Spolitis, S.; Bobrovs, V. Noise Immunity of the Fibonacci Counter with the Fractal Decoder Device for Telecommunication Systems. Latv. J. Phys. Tech. Sci. 2019, 56, 12–21. [Google Scholar] [CrossRef] [Green Version]
- Borysenko, A.A.; Matsenko, S.M.; Horiachev, O.Y.; Berezhna, O.V. Decoding device of Fibonacci codes in information systems. In Proceedings of the IEEE 9th International Conference on Dependable Systems, Services and Technologies (DESSERT), Kyiv, Ukraine, 24–27 May 2018; pp. 253–256. [Google Scholar]
- Borysenko, O.; Matsenko, S. Sumy State University. Device for Decoding Fibonacci Codes. Useful Model Patent No 99587U, MPK N03M 7/36, Nou201500089, 10 June 2015. (In Ukraine). [Google Scholar]
- Borysenko, O.; Matsenko, S.; Novhorodtsev, A.; Kobyakov, O.; Spolitis, S.; Bobrovs, V. Estimating the indivisible error detecting codes based on an average probability method. East.-Eur. J. Enterp. Technol. 2020, 6, 25–33. [Google Scholar] [CrossRef]
- ITU-T. Spectral Grids for WDM Applications: DWDM Frequency Grid. 2012. Available online: https://www.itu.int/rec/T-REC-G.694.1 (accessed on 20 November 2021).
- ITU-T. Characteristics of a Single-Mode Optical Fibre and Cable. 2016. Available online: https://www.itu.int/rec/T-REC-G.652 (accessed on 20 November 2021).
- ETSI. Digital Video Broadcasting (DVB); Second Generation Framing Structure, Channel Coding and Modulation Systems for Broadcasting, Interactive Services, Newsgathering and Other Broadband Satellite Applications (DVB-S2); ETSI: Valbonne, France, 2009. [Google Scholar]
- Matsenko, S. Synthesis of Components of Digital Devices Based on the Minimal Form of the Fibonacci Code. Ph.D. Thesis, Kharkiv National University of Radio Electronics, Kharkiv, Ukraine, 2016; 150p. [Google Scholar]




| Bit Number | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Bit Weight | 34 | 21 | 13 | 8 | 5 | 3 | 2 | 1 |
| N = 25 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| N = 54 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| N = 33 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| Code Combinations | Code Combinations | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fractal 1 | Fractal 2 | ||||||||||
| Bit Number | 5 | 4 | 3 | 2 | 1 | Bit Number | 5 | 4 | 3 | 2 | 1 |
| Bit Weight | 8 | 5 | 3 | 2 | 1 | Bit Weight | 8 | 5 | 3 | 2 | 1 |
 |  | ||||||||||
| № | x5 | x4 | x3 | x2 | x1 | № | x5 | x4 | x3 | x2 | x1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 8 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 9 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 1 | 0 | 10 | 1 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 | 11 | 1 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 1 | 12 | 1 | 0 | 1 | 0 | 1 |
 |  | ||||||||||
| 5 | 0 | 1 | 0 | 0 | 0 | ||||||
| 6 | 0 | 1 | 0 | 0 | 1 | ||||||
| 7 | 0 | 1 | 0 | 1 | 0 | ||||||
| Parameter Name | Value |
|---|---|
| WDM channels | 5 |
| Baud rate | 56 (PAM-4), 35 (PAM-8) Gbaud |
| Pulse shaping | Simple |
| Channel frequency spacing | 100 GHz |
| Attenuation | 0.2 dB/km |
| Dispersion parameter | 16 ps/(nm × km) |
| Nonlinear coefficient | 2.6 × 10−20 m2/W |
| EDFA noise figure | 3 dB |
| Coded modulation | PAM-M, Gray code mapping |
| n | Sn | n | Sn | n | Sn |
|---|---|---|---|---|---|
| 2 | 7 | 12 | 3.21 × 103 | 22 | 6.83 × 105 |
| 3 | 15 | 13 | 5.59 × 103 | 23 | 1.15 × 106 |
| 4 | 29 | 14 | 9.67 × 103 | 24 | 1.94 × 106 |
| 5 | 55 | 15 | 1.66 × 104 | 25 | 3.26 × 106 |
| 6 | 102 | 16 | 2.84 × 104 | 26 | 5.47 × 106 |
| 7 | 186 | 17 | 4.87 × 104 | 27 | 9.17 × 106 |
| 8 | 335 | 18 | 8.30 ×104 | 28 | 1.53 × 107 |
| 9 | 567 | 19 | 1.41 × 105 | 29 | 2.56 × 107 |
| 10 | 1.05 × 103 | 20 | 2.39 × 105 | 30 | 4.28 × 107 |
| 11 | 1.84 × 103 | 21 | 4.04 × 105 | 31 | 7.15 × 107 |
| n | Q/W × 100% | n | Q/W × 100% | n | Q/W × 100% | n | Q/W × 100% |
|---|---|---|---|---|---|---|---|
| 5 | 15.38 | 19 | 32.16 | 12 | 28.77 | 26 | 33.78 |
| 6 | 19.23 | 20 | 32.47 | 13 | 29.17 | 27 | 33.95 |
| 7 | 21.76 | 21 | 32.74 | 14 | 29.88 | 28 | 34.12 |
| 8 | 23.89 | 22 | 32.98 | 15 | 30.58 | 29 | 34.24 |
| 9 | 25.45 | 23 | 33.21 | 16 | 31.05 | 20 | 34.37 |
| 10 | 26.74 | 24 | 33.42 | 17 | 31.42 | 31 | 34.55 |
| 11 | 27.97 | 25 | 33.61 | 18 | 31.81 | 32 | 34.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsenko, S.; Borysenko, O.; Spolitis, S.; Udalcovs, A.; Gegere, L.; Krotov, A.; Ozolins, O.; Bobrovs, V. FPGA-Implemented Fractal Decoder with Forward Error Correction in Short-Reach Optical Interconnects. Entropy 2022, 24, 122. https://doi.org/10.3390/e24010122
Matsenko S, Borysenko O, Spolitis S, Udalcovs A, Gegere L, Krotov A, Ozolins O, Bobrovs V. FPGA-Implemented Fractal Decoder with Forward Error Correction in Short-Reach Optical Interconnects. Entropy. 2022; 24(1):122. https://doi.org/10.3390/e24010122
Chicago/Turabian StyleMatsenko, Svitlana, Oleksiy Borysenko, Sandis Spolitis, Aleksejs Udalcovs, Lilita Gegere, Aleksandr Krotov, Oskars Ozolins, and Vjaceslavs Bobrovs. 2022. "FPGA-Implemented Fractal Decoder with Forward Error Correction in Short-Reach Optical Interconnects" Entropy 24, no. 1: 122. https://doi.org/10.3390/e24010122
APA StyleMatsenko, S., Borysenko, O., Spolitis, S., Udalcovs, A., Gegere, L., Krotov, A., Ozolins, O., & Bobrovs, V. (2022). FPGA-Implemented Fractal Decoder with Forward Error Correction in Short-Reach Optical Interconnects. Entropy, 24(1), 122. https://doi.org/10.3390/e24010122










