Minimal Developmental Computation: A Causal Network Approach to Understand Morphogenetic Pattern Formation
Abstract
1. Introduction
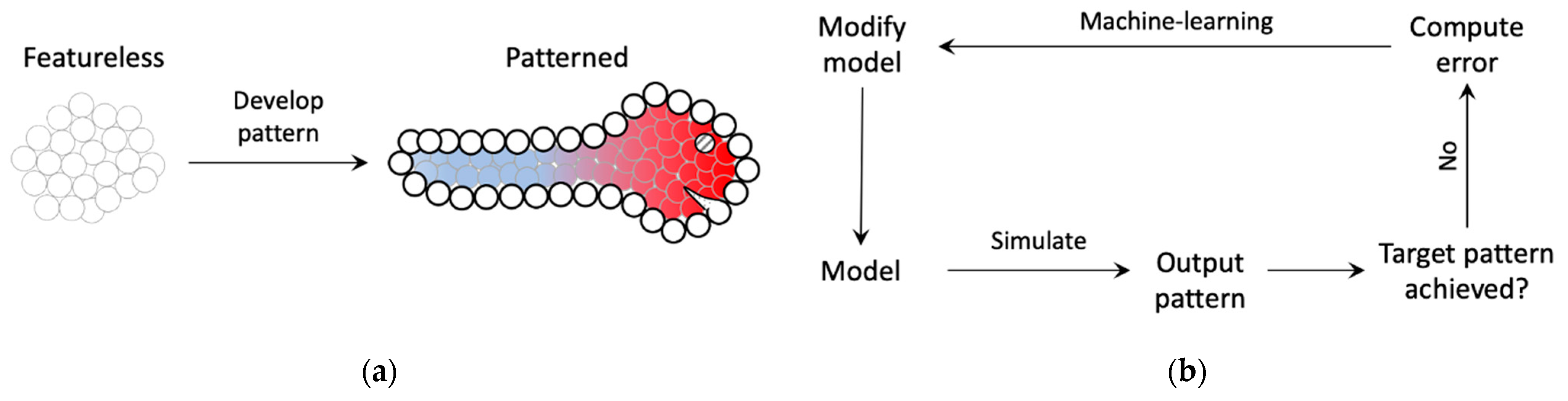
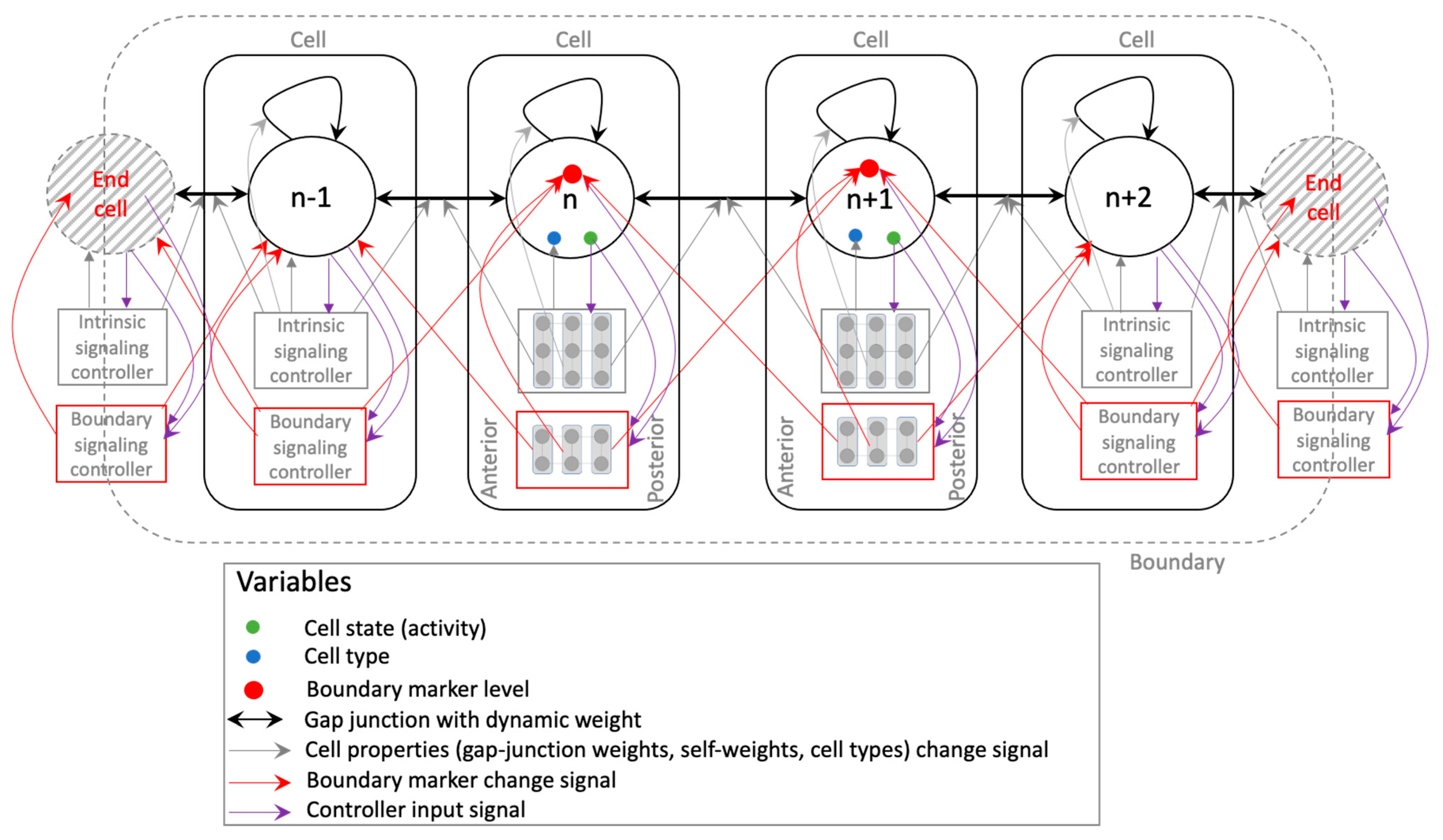
2. Model and Methods
3. Results
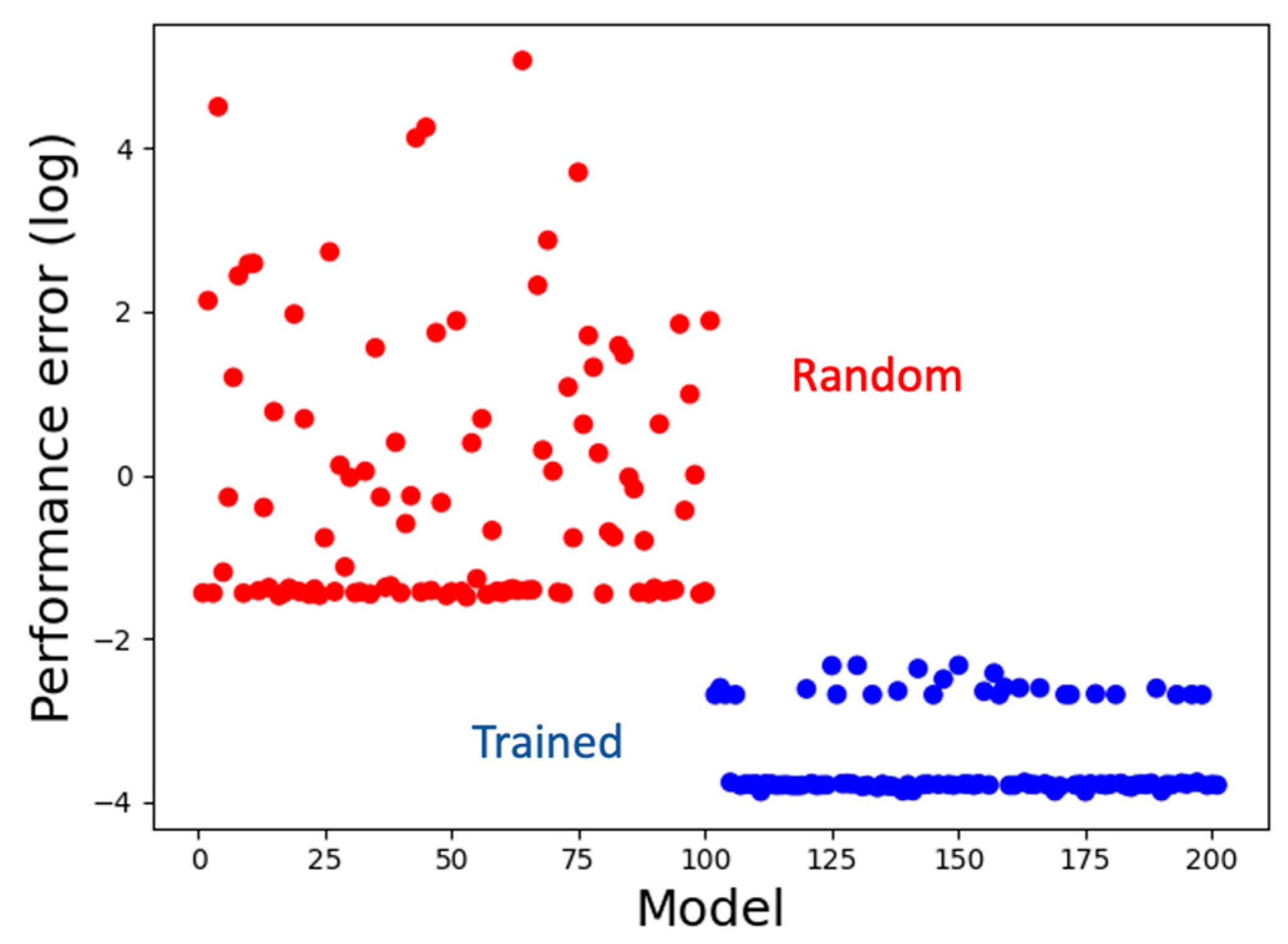
3.1. The Model Learns to Generate the Correct Activity Patterns and Mark Boundaries
3.2. Analysis of Cellular Activity and Structural Patterns
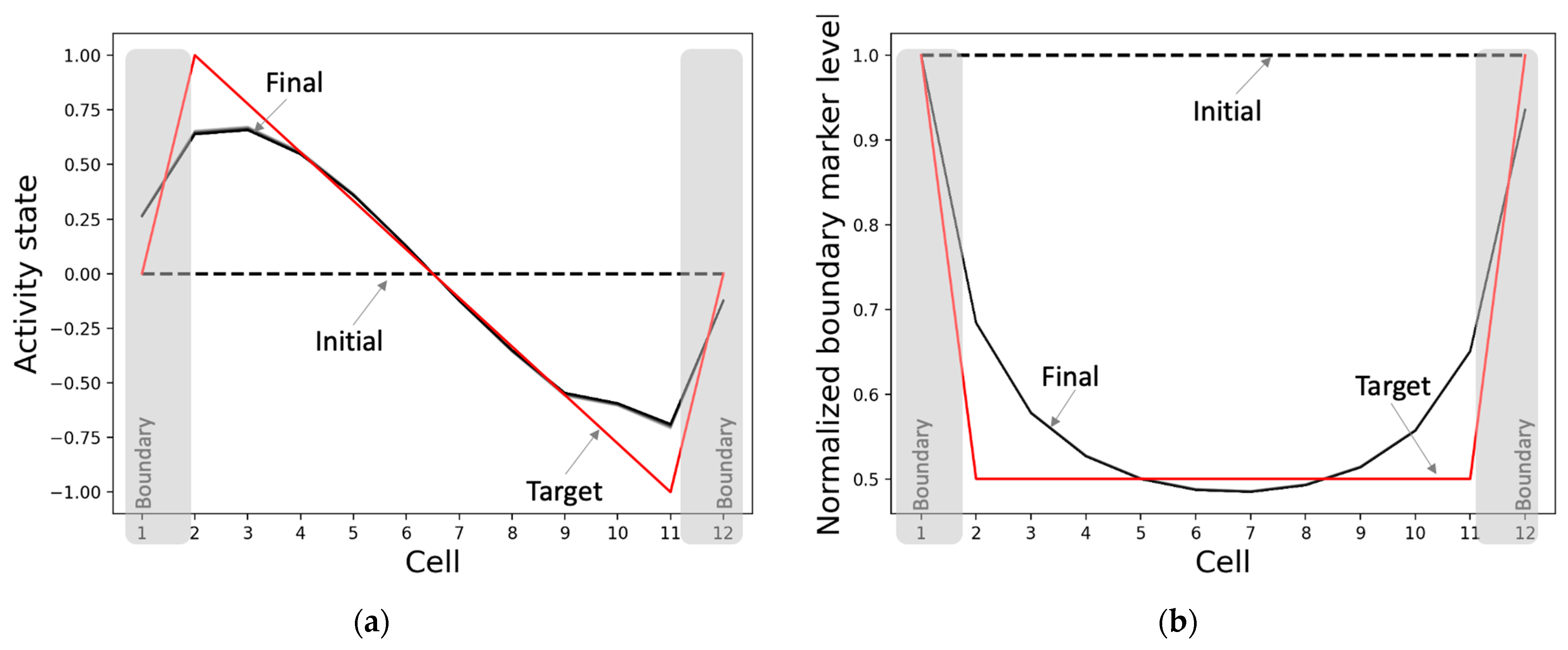
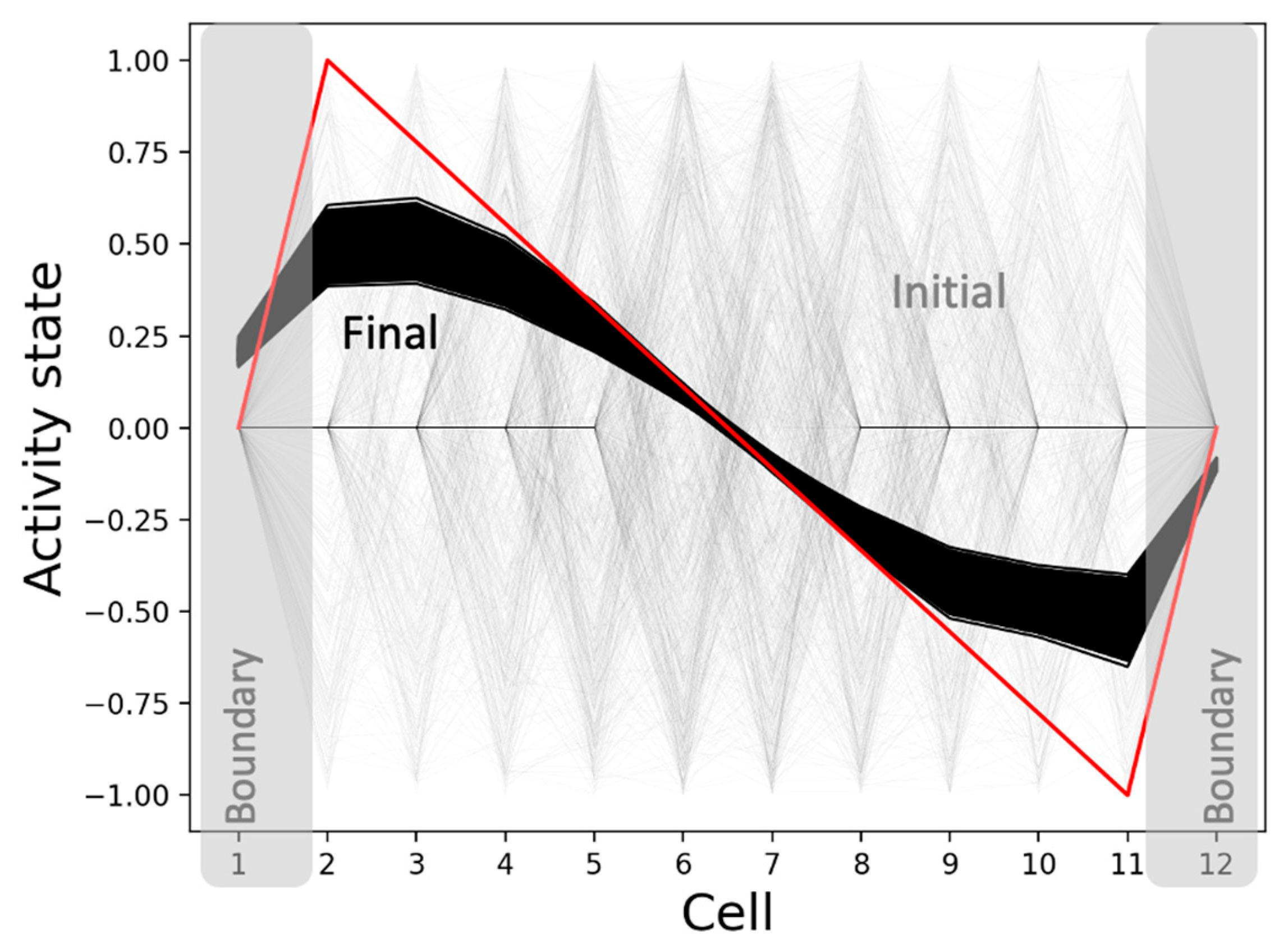
3.2.1. The Model Develops Network Activity and Boundary-Marker Patterns Establishing a Correct Axial Gradient Pattern within the Tissue
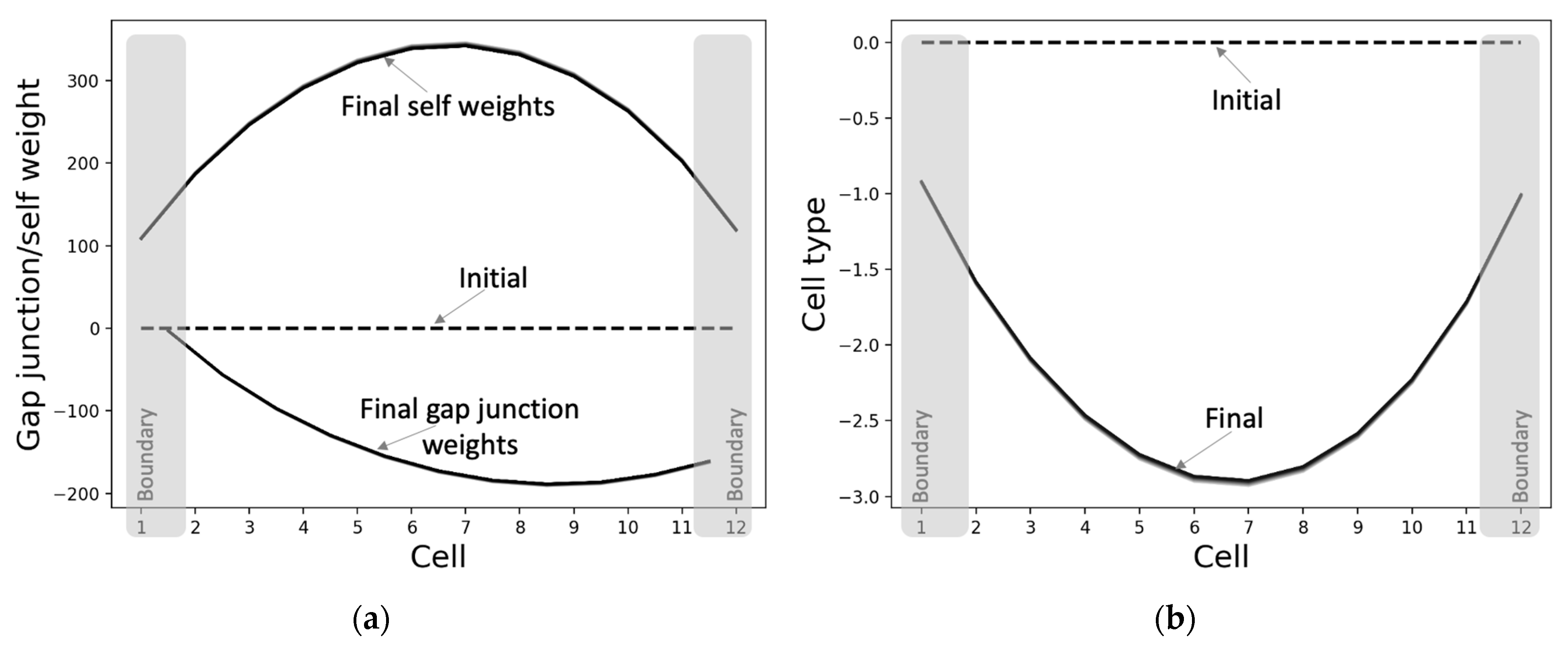
3.2.2. The Gap Junctions and Cell Types Also Self-Organize into Patterns Even Though They Were Not Specifically Selected for That Purpose
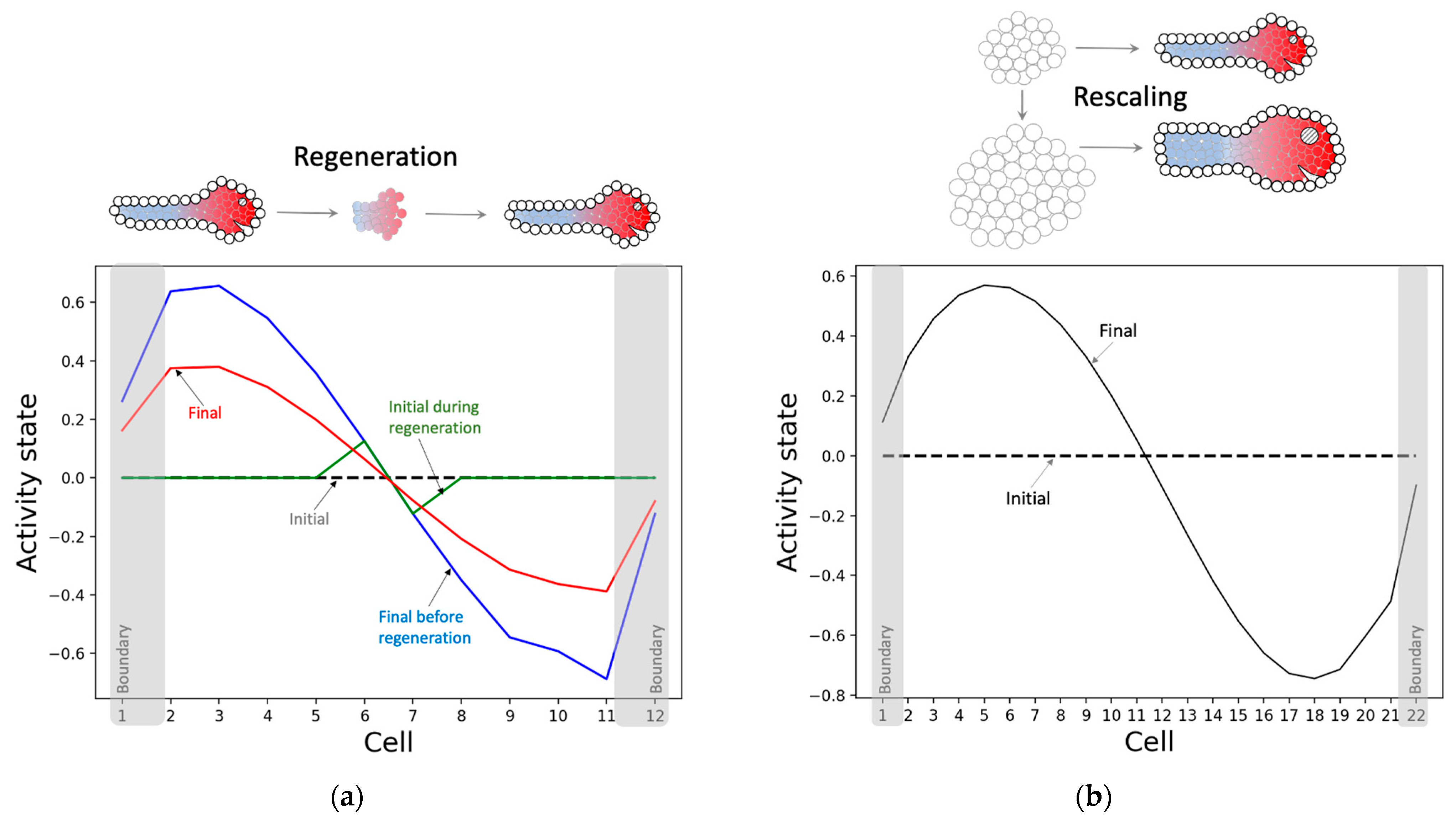
3.2.3. The Model Successfully Regenerates and Rescales the Pattern despite Not Being Selected for Those Abilities
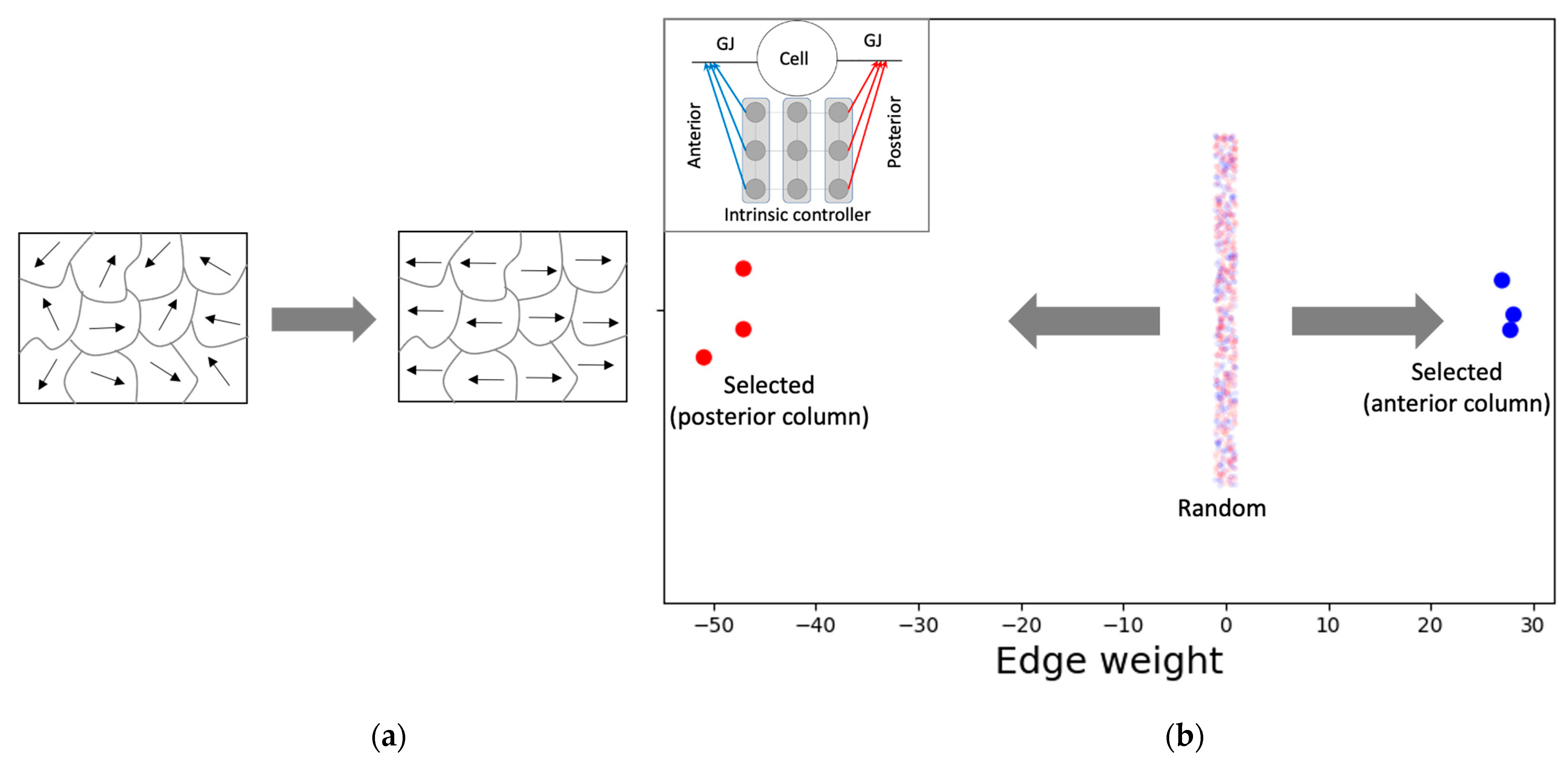
3.2.4. The Model Generates the Same Qualitative Patterns Regardless of the Initial Network Conditions: Robustness
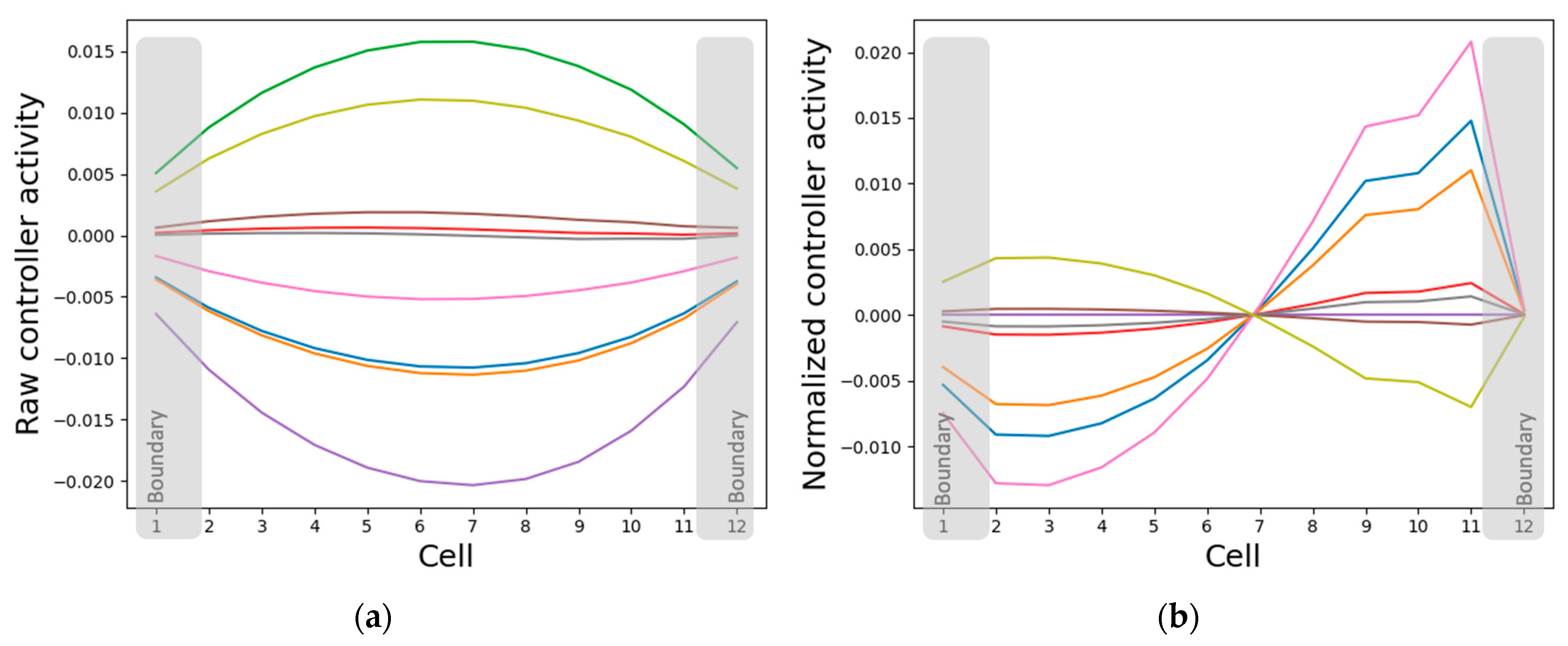
3.3. Analysis of Intracellular Controller Activity Patterns
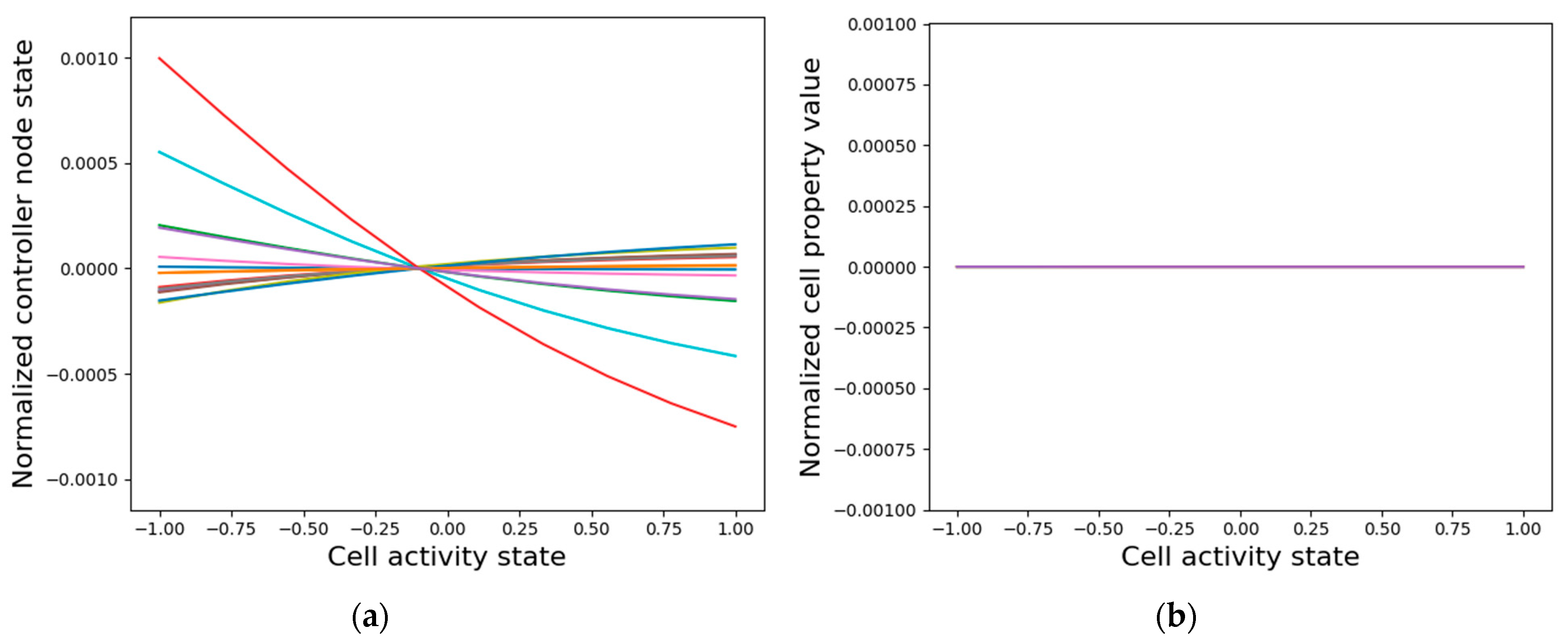
3.3.1. Internal Controller Activity Patterns Simultaneously Correlate with Cellular Properties and Network Activity Patterns
3.3.2. Isolated Cells Contain Relevant but Insufficient Information Required to Generate the Network-Level Patterns
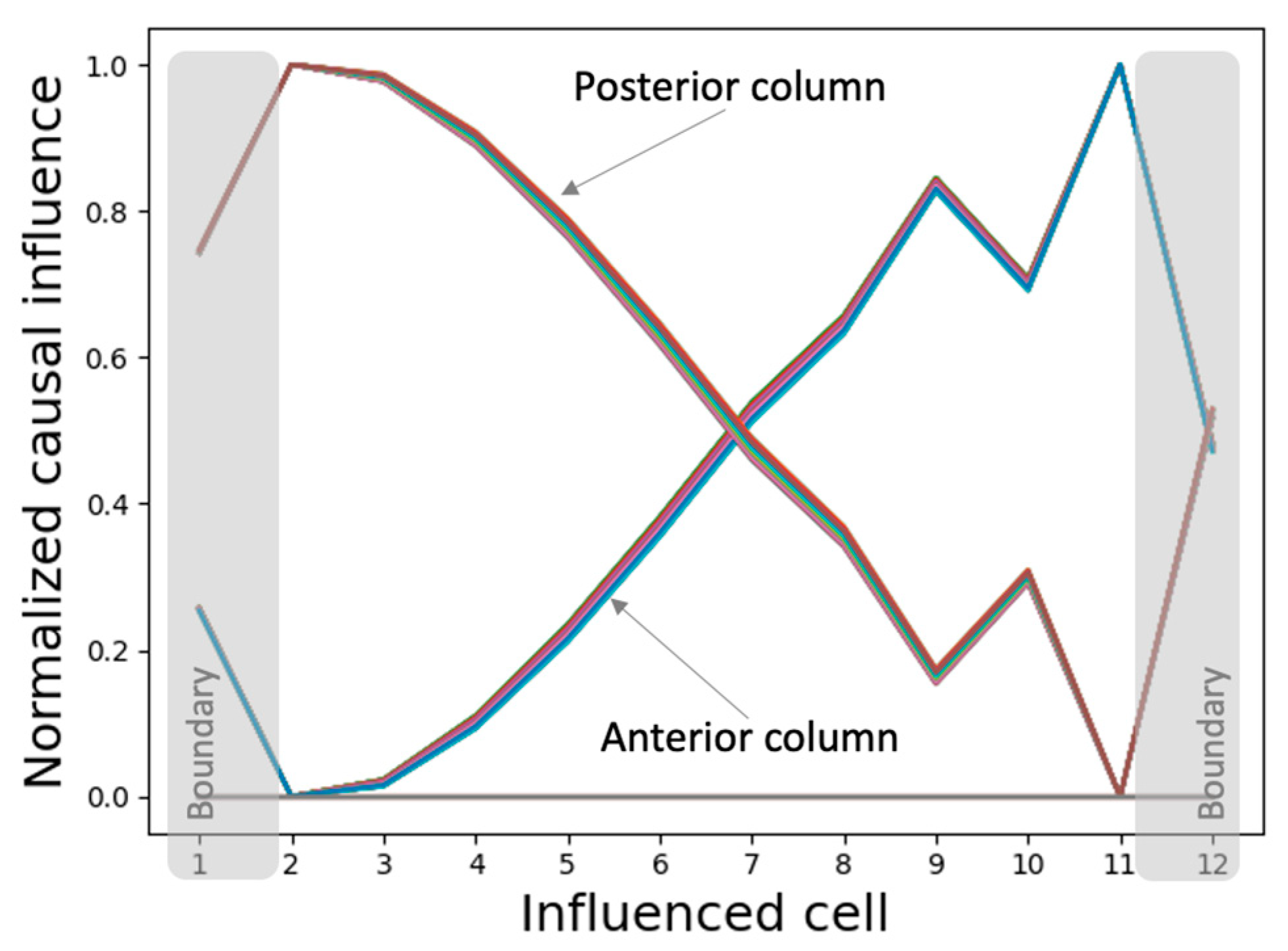
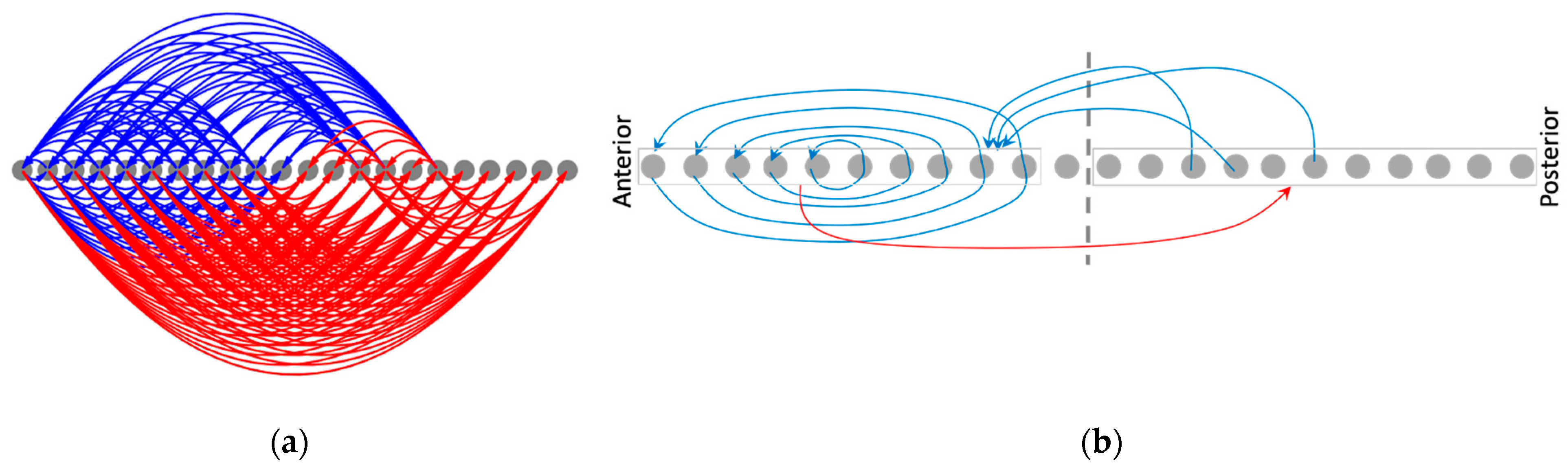
3.4. Analysis of Intercellular Causal Network Patterns
3.4.1. Every Cell in the Collective Contains the Full Causal Information about the Network-Level Patterns Explaining the Model’s High Degree of Robustness
3.4.2. The Network Dynamically Integrates into an Organization with Macro-Scale Modules Explaining the Overall Shape of the Functional Patterns
3.4.3. Rescaling the Model Rescales the Causal Networks, Explaining Why the Phenotypic Patterns Rescale
3.4.4. The Overall Structure of the Mean Causal Network Explains the Model’s Ability to Canalize Random Initial States into the Same Patterns
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Slack, J.M.W. From Egg to Embryo: Regional Specification in Early Development; Cambridge University Press: Cambridge UK, 1991. [Google Scholar]
- Child, C.M. Patterns and Problems of Development; The University of Chicago Press: Chicago, IL, USA, 1941. [Google Scholar]
- Siregar, P.; Julen, N.; Hufnagl, P.; Mutter, G. A general framework dedicated to computational morphogenesis Part I—Constitutive equations. Biosystems 2018, 173, 298–313. [Google Scholar] [CrossRef] [PubMed]
- Siregar, P.; Julen, N.; Hufnagl, P.; Mutter, G. A general framework dedicated to computational morphogenesis Part II—Knowledge representation and architecture. Biosystems 2018, 173, 314–334. [Google Scholar] [CrossRef]
- Morelli, L.G.; Uriu, K.; Ares, S.; Oates, A.C. Computational approaches to developmental patterning. Science 2012, 336, 187–191. [Google Scholar] [CrossRef] [PubMed]
- Hogeweg, P. Computing an organism: On the interface between informatic and dynamic processes. BioSystems 2002, 64, 97–109. [Google Scholar] [CrossRef]
- Wolpert, L.; Lewis, J.H. Towards a theory of development. Fed. Proc. 1975, 34, 14–20. [Google Scholar]
- Slack, J.M. A serial threshold theory of regeneration. J. Theor. Biol. 1980, 82, 105–140. [Google Scholar] [CrossRef]
- Slack, J.M.W. Serial Thresholds and Homeotic Variation. In Kinetic Logic: A Boolean Approach to the Analysis of Complex Regulatory Systems; Thomas, R., Ed.; Springer: Berlin/Heidelberg, Germany, 1979; Volume 29. [Google Scholar]
- Allen, M.; Friston, K.J. From cognitivism to autopoiesis: Towards a computational framework for the embodied mind. Synthese 2018, 195, 2459–2482. [Google Scholar] [CrossRef]
- Keijzer, F.A. Evolutionary convergence and biologically embodied cognition. Interface Focus 2017, 7, 20160123. [Google Scholar] [CrossRef] [PubMed]
- Ziemke, T. The body of knowledge: On the role of the living body in grounding embodied cognition. Biosystems 2016, 148, 4–11. [Google Scholar] [CrossRef]
- Pezzulo, G.; Levin, M. Top-down models in biology: Explanation and control of complex living systems above the molecular level. J. R. Soc. Interface 2016, 13, 20160555. [Google Scholar] [CrossRef]
- Pinet, K.; McLaughlin, K.A. Mechanisms of physiological tissue remodeling in animals: Manipulating tissue, organ, and organism morphology. Dev. Biol. 2019, 451, 134–145. [Google Scholar] [CrossRef]
- Harris, A.K. The need for a concept of shape homeostasis. Biosystems 2018, 173, 65–72. [Google Scholar] [CrossRef]
- Mustard, J.; Levin, M. Bioelectrical Mechanisms for Programming Growth and Form: Taming Physiological Networks for Soft Body Robotics. Soft Robot. 2014, 1, 169–191. [Google Scholar] [CrossRef]
- Sharpe, J. Computer modeling in developmental biology: Growing today, essential tomorrow. Development 2017, 144, 4214–4225. [Google Scholar] [CrossRef] [PubMed]
- Pastor-Escuredo, D.; del Álamo, J.C. How Computation Is Helping Unravel the Dynamics of Morphogenesis. Front. Phys. 2020, 8, 31. [Google Scholar] [CrossRef]
- Chara, O.; Tanaka, E.M.; Brusch, L. Mathematical modeling of regenerative processes. Curr. Top. Dev. Biol. 2014, 108, 283–317. [Google Scholar]
- Meinhardt, H. Pattern formation in biology: A comparison of models and experiments. Rep. Prog. Phys. 1992, 55, 797–849. [Google Scholar] [CrossRef]
- Umulis, D.M.; Othmer, H.G. The role of mathematical models in understanding pattern formation in developmental biology. Bull. Math. Biol. 2015, 77, 817–845. [Google Scholar] [CrossRef]
- Gierer, A.; Meinhardt, H. A theory of biological pattern formation. Kybernetik 1972, 12, 30–39. [Google Scholar] [CrossRef]
- Briscoe, J. Understanding Pattern Formation in Embryos: Experiment, Theory, and Simulation. J. Comput. Biol. 2019, 26, 696–702. [Google Scholar] [CrossRef]
- Maini, P.K. Using mathematical models to help understand biological pattern formation. Comptes Rendus Biol. 2004, 327, 225–234. [Google Scholar] [CrossRef]
- Wolpert, L. Positional information and the spatial pattern of cellular differentiation. J. Theor. Biol. 1969, 25, 1–47. [Google Scholar] [CrossRef]
- Wolpert, L. The French Flag Problem: A Contribution to the Discussion on Pattern Deve Lopment and Regulation, towards a Theoretical Biology; Waddington, C.H., Ed.; Edinburgh University Press: Edinburgh, UK, 1968; Volume 1. [Google Scholar]
- Sharpe, J. Wolpert’s French Flag: What’s the problem? Development 2019, 146, dev185967. [Google Scholar] [CrossRef]
- Bryant, P.J.; Bryant, S.V.; French, V. Biological regeneration and pattern formation. Sci. Am. 1977, 237, 66–81. [Google Scholar] [CrossRef] [PubMed]
- Agata, K.; Saito, Y.; Nakajima, E. Unifying principles of regeneration I: Epimorphosis versus morphallaxis. Dev. Growth Differ. 2007, 49, 73–78. [Google Scholar] [CrossRef] [PubMed]
- Martinez Arias, A.; Steventon, B. On the nature and function of organizers. Development 2018, 145, dev159525. [Google Scholar] [CrossRef] [PubMed]
- Cooke, J.; Zeeman, E.C. A Clock and Wavefront Model for Control of the Number of Repeated Structures during Animal Morphogenesis. J. Theor. Biol. 1976, 58, 455–476. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Bull. Math. Biol. 1990, 52, 153–197. [Google Scholar] [CrossRef]
- Azuaje, F. Computational discrete models of tissue growth and regeneration. Brief. Bioinform. 2011, 12, 64–77. [Google Scholar] [CrossRef]
- Minh-Thai, T.N.; Aryal, J.; Samarasinghe, S.; Levin, M. A Computational Framework for Autonomous Self-repair Systems. In AI 2018: Advances in Artificial Intelligence; Springer: New York, NY, USA, 2018; pp. 153–159. [Google Scholar]
- De, A.; Chakravarthy, V.S.; Levin, M. A computational model of planarian regeneration. Int. J. Parallel Emergent Distrib. Syst. 2016, 32, 331–347. [Google Scholar] [CrossRef]
- Tosenberger, A.; Bessonov, N.; Levin, M.; Reinberg, N.; Volpert, V.; Morozova, N. A conceptual model of morphogenesis and regeneration. Acta Biotheor. 2015, 63, 283–294. [Google Scholar] [CrossRef] [PubMed]
- Bessonov, N.; Levin, M.; Morozova, N.; Reinberg, N.; Tosenberger, A.; Volpert, V. On a Model of Pattern Regeneration Based on Cell Memory. PLoS ONE 2015, 10, e0118091. [Google Scholar] [CrossRef] [PubMed]
- Bessonov, N.; Levin, M.; Morozova, N.; Reinberg, N.; Tosenberger, A.; Volpert, V. Target morphology and cell memory: A model of regenerative pattern formation. Neural Regen. Res. 2015, 10, 1901–1905. [Google Scholar] [PubMed]
- Lobo, D.; Solano, M.; Bubenik, G.A.; Levin, M. A linear-encoding model explains the variability of the target morphology in regeneration. J. R. Soc. Interface 2014, 11, 20130918. [Google Scholar] [CrossRef]
- Harrington, K.I.S. A circuit basis for morphogenesis. Theor. Comput. Sci. 2016, 633, 28–36. [Google Scholar] [CrossRef]
- Voosen, P. The AI Detectives. Science 2017, 357, 22–27. [Google Scholar] [CrossRef]
- Beer, R.D.; Williams, P.L. Information processing and dynamics in minimally cognitive agents. Cogn. Sci. 2015, 39, 1–38. [Google Scholar] [CrossRef]
- Tkačik, G.; Bialek, W. Information processing in living systems. Annu. Rev. Condens. Matter Phys. 2016, 7, 89–117. [Google Scholar] [CrossRef]
- Gatenby, R.A.; Frieden, B.R. Information theory in living systems, methods, applications, and challenges. Bull. Math. Biol. 2007, 69, 635–657. [Google Scholar] [CrossRef]
- Mannino, M.; Bressler, S.L. Foundational perspectives on causality in large-scale brain networks. Phys. Life Rev. 2015, 15, 107–123. [Google Scholar] [CrossRef]
- Chicharro, D.; Ledberg, A. When two become one: The limits of causality analysis of brain dynamics. PLoS ONE 2012, 7, e32466. [Google Scholar] [CrossRef]
- Friston, K.J.; Harrison, L.; Penny, W. Dynamic causal modelling. Neuroimage 2003, 19, 1273–1302. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable ai: A review of machine learning interpretability methods. Entropy 2021, 23, 18. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Fong, R.; Patrick, M.; Vedaldi, A. Understanding Deep Networks Via Extremal Perturbations and Smooth Masks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 2950–2958. [Google Scholar]
- Hernández, A.; Amigó, J.M. Differentiable programming and its applications to dynamical systems. arXiv 2019, arXiv:1912.08168. [Google Scholar]
- Durston, A.J.; Zhu, K. A time space translation hypothesis for vertebrate axial patterning. Semin. Cell Dev. Biol. 2015, 42, 86–93. [Google Scholar] [CrossRef]
- Durston, A.J.; Jansen, H.J.; Wacker, S.A. Review: Time-space translation regulates trunk axial patterning in the early vertebrate embryo. Genomics 2010, 95, 250–255. [Google Scholar] [CrossRef][Green Version]
- Houston, D.W. Vertebrate Axial Patterning: From Egg to Asymmetry. Adv. Exp. Med. Biol. 2017, 953, 209–306. [Google Scholar]
- Delgado, I.; Torres, M. Coordination of limb development by crosstalk among axial patterning pathways. Dev. Biol. 2017, 429, 382–386. [Google Scholar] [CrossRef]
- Bode, H.R. Axial patterning in hydra. Cold Spring Harb. Perspect. Biol. 2009, 1, a000463. [Google Scholar] [CrossRef]
- Whitfield, T.T.; Hammond, K.L. Axial patterning in the developing vertebrate inner ear. Int. J. Dev. Biol. 2007, 51, 507–520. [Google Scholar] [CrossRef]
- Wellik, D.M. Hox patterning of the vertebrate axial skeleton. Dev. Dyn. 2007, 236, 2454–2463. [Google Scholar] [CrossRef]
- Bowman, J.L. Axial patterning in leaves and other lateral organs. Curr. Opin. Genet. Dev. 2000, 10, 399–404. [Google Scholar] [CrossRef]
- Stocum, D.L. A conceptual framework for analyzing axial patterning in regenerating urodele limbs. Int. J. Dev. Biol. 1996, 40, 773–783. [Google Scholar] [PubMed]
- Mathews, J.; Levin, M. Gap junctional signaling in pattern regulation: Physiological network connectivity instructs growth and form. Dev. Neurobiol. 2017, 77, 643–673. [Google Scholar] [CrossRef]
- Pandit, N.K. Introduction to the Pharmaceutical Sciences; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2007. [Google Scholar]
- Palacios-Prado, N.; Bukauskas, F.F. Heterotypic gap junction channels as voltage-sensitive valves for intercellular signaling. Proc. Natl. Acad. Sci. USA 2009, 106, 14855–14860. [Google Scholar] [CrossRef]
- Roberts, K.; Alberts, B.; Johnson, A.; Walter, P.; Hunt, T. Molecular Biology of the Cell; Garland Science: New York, NY, USA, 2002. [Google Scholar]
- Bischof, J.; Day, M.E.; Miller, K.A.; LaPalme, J.V.; Levin, M. Nervous system and tissue polarity dynamically adapt to new morphologies in planaria. Dev. Biol. 2020, 467, 51–65. [Google Scholar] [CrossRef]
- Pietak, A.; Bischof, J.; LaPalme, J.; Morokuma, J.; Levin, M. Neural control of body-plan axis in regenerating planaria. PLoS Comput. Biol. 2019, 15, e1006904. [Google Scholar] [CrossRef] [PubMed]
- Levin, M. Bioelectric signaling: Reprogrammable circuits underlying embryogenesis, regeneration, and cancer. Cell 2021, 184, 1971–1989. [Google Scholar] [CrossRef] [PubMed]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Processing Syst. 2019, 32, 8026–8037. [Google Scholar]
- Liu, Y.-Y.; Slotine, J.-J.; Barabási, A.-L. Controllability of complex networks. Nature 2011, 473, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Brush, E.R.; Krakauer, D.C.; Flack, J.C. A family of algorithms for computing consensus about node state from network data. PLoS Comput. Biol. 2013, 9, e1003109. [Google Scholar] [CrossRef] [PubMed]
- Manicka, S.V.S. The Role of Canalization in the Spreading of Perturbations in Boolean Networks; Indiana University: Bloomington, IN, USA, 2017. [Google Scholar]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. A framework for the local information dynamics of distributed computation in complex systems. In Guided Self-Organization: Inception; Springer: New York, NY, USA, 2014; pp. 115–158. [Google Scholar]
- Wang, Y.; Nathans, J. Tissue/planar cell polarity in vertebrates: New insights and new questions. Development 2007, 134, 647–658. [Google Scholar] [CrossRef] [PubMed]
- Aranda-Anzaldo, A.; Dent, M.A. Developmental noise, ageing and cancer. Mech. Ageing Dev. 2003, 124, 711–720. [Google Scholar] [CrossRef]
- Woods, H.A. Mosaic physiology from developmental noise: Within-organism physiological diversity as an alternative to phenotypic plasticity and phenotypic flexibility. J. Exp. Biol. 2014, 217 Pt 1, 35–45. [Google Scholar] [CrossRef]
- Cooke, J. Scale of body pattern adjusts to available cell number in amphibian embryos. Nature 1981, 290, 775–778. [Google Scholar] [CrossRef]
- Fankhauser, G. Maintenance of normal structure in heteroploid salamander larvae, through compensation of changes in cell size by adjustment of cell number and cell shape. J. Exp. Zool. 1945, 100, 445–455. [Google Scholar] [CrossRef]
- Kriegman, S.; Blackiston, D.; Levin, M.; Bongard, J. Kinematic self-replication in reconfigurable organisms. Proc. Natl. Acad. Sci. USA 2021, 118, e2112672118. [Google Scholar] [CrossRef]
- Blackiston, D.; Lederer, E.; Kriegman, S.; Garnier, S.; Bongard, J.; Levin, M. A cellular platform for the development of synthetic living machines. Sci. Robot. 2021, 6, eabf1571. [Google Scholar] [CrossRef]
- Watson, R.A.; Wagner, G.P.; Pavlicev, M.; Weinreich, D.M.; Mills, R. The evolution of phenotypic correlations and “developmental memory”. Evolution 2014, 68, 1124–1138. [Google Scholar] [CrossRef]
- Parter, M.; Kashtan, N.; Alon, U. Facilitated variation: How evolution learns from past environments to generalize to new environments. PLoS Comput. Biol. 2008, 4, e1000206. [Google Scholar] [CrossRef]
- Gerhart, J.; Kirschner, M. The theory of facilitated variation. Proc. Natl. Acad. Sci. USA 2007, 104 (Suppl. S1), 8582–8589. [Google Scholar] [CrossRef] [PubMed]
- Melo, D.; Porto, A.; Cheverud, J.M.; Marroig, G. Modularity: Genes, development, and evolution. Annu. Rev. Ecol. Evol. Syst. 2016, 47, 463–486. [Google Scholar] [CrossRef]
- Mitchell, M. Ubiquity symposium: Biological computation. Ubiquity 2011, 2011, 1–7. [Google Scholar] [CrossRef]
- Tung, A.; Levin, M. Extra-genomic instructive influences in morphogenesis: A review of external signals that regulate growth and form. Dev. Biol. 2020, 461, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Hartwell, L.H.; Hopfield, J.J.; Leibler, S.; Murray, A.W. From molecular to modular cell biology. Nature 1999, 402, C47–C52. [Google Scholar] [CrossRef]
- Kolchinsky, A.; Rocha, L.M. Prediction and modularity in dynamical systems. arXiv 2011, arXiv:1106.3703. [Google Scholar]
- Marques-Pita, M.; Rocha, L.M. Canalization and control in automata networks: Body segmentation in Drosophila melanogaster. PLoS ONE 2013, 8, e55946. [Google Scholar] [CrossRef]
- Jaeger, J.; Monk, N. Dynamical modules in metabolism, cell and developmental biology. Interface Focus 2021, 11, 20210011. [Google Scholar] [CrossRef]
- Biswas, S.; Manicka, S.; Hoel, E.; Levin, M. Gene regulatory networks exhibit several kinds of memory: Quantification of memory in biological and random transcriptional networks. Iscience 2021, 24, 102131. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.I. Top-down causation and the rise of information in the emergence of life. Information 2014, 5, 424–439. [Google Scholar] [CrossRef]
- Gates, A.J.; Correia, R.B.; Wang, X.; Rocha, L.M. The effective graph reveals redundancy, canalization, and control pathways in biochemical regulation and signaling. Proc. Natl. Acad. Sci. USA 2021, 118, e2022598118. [Google Scholar] [CrossRef]
- Daniels, B.C.; Ellison, C.J.; Krakauer, D.C.; Flack, J.C. Quantifying collectivity. Curr. Opin. Neurobiol. 2016, 37, 106–113. [Google Scholar] [CrossRef]
- Flack, J.C. Coarse-graining as a downward causation mechanism. Philos. Trans. A Math. Phys. Eng. Sci. 2017, 375, 20160338. [Google Scholar] [CrossRef] [PubMed]
- Hoel, E. When the Map Is Better Than the Territory. Entropy 2017, 19, 188. [Google Scholar] [CrossRef]
- Klein, B.; Hoel, E. The Emergence of Informative Higher Scales in Complex Networks. Complexity 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Kim, H.; Sayama, H. The role of criticality of gene regulatory networks in morphogenesis. IEEE Trans. Cogn. Dev. Syst. 2018, 12, 390–400. [Google Scholar] [CrossRef]
- Daniels, B.C.; Kim, H.; Moore, D.; Zhou, S.; Smith, H.B.; Karas, B.; Kauffman, S.A.; Walker, S.I. Criticality Distinguishes the Ensemble of Biological Regulatory Networks. Phys. Rev. Lett. 2018, 121, 138102. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manicka, S.; Levin, M. Minimal Developmental Computation: A Causal Network Approach to Understand Morphogenetic Pattern Formation. Entropy 2022, 24, 107. https://doi.org/10.3390/e24010107
Manicka S, Levin M. Minimal Developmental Computation: A Causal Network Approach to Understand Morphogenetic Pattern Formation. Entropy. 2022; 24(1):107. https://doi.org/10.3390/e24010107
Chicago/Turabian StyleManicka, Santosh, and Michael Levin. 2022. "Minimal Developmental Computation: A Causal Network Approach to Understand Morphogenetic Pattern Formation" Entropy 24, no. 1: 107. https://doi.org/10.3390/e24010107
APA StyleManicka, S., & Levin, M. (2022). Minimal Developmental Computation: A Causal Network Approach to Understand Morphogenetic Pattern Formation. Entropy, 24(1), 107. https://doi.org/10.3390/e24010107






