Introduction and Analysis of a Method for the Investigation of QCD-like Tree Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Physical System
2.2. Particle Generator
2.3. Introduction to the Algorithm
2.4. A Simple Example
2.5. Extension to Jets
2.6. The 2 Neural Networks (2NN) Algorithm
2.6.1. Generating the Test Dataset
2.6.2. Optimizing the Classifier
2.6.3. Optimizing the Neural Network f
2.7. Evaluation of the 2NN Algorithm
3. Results
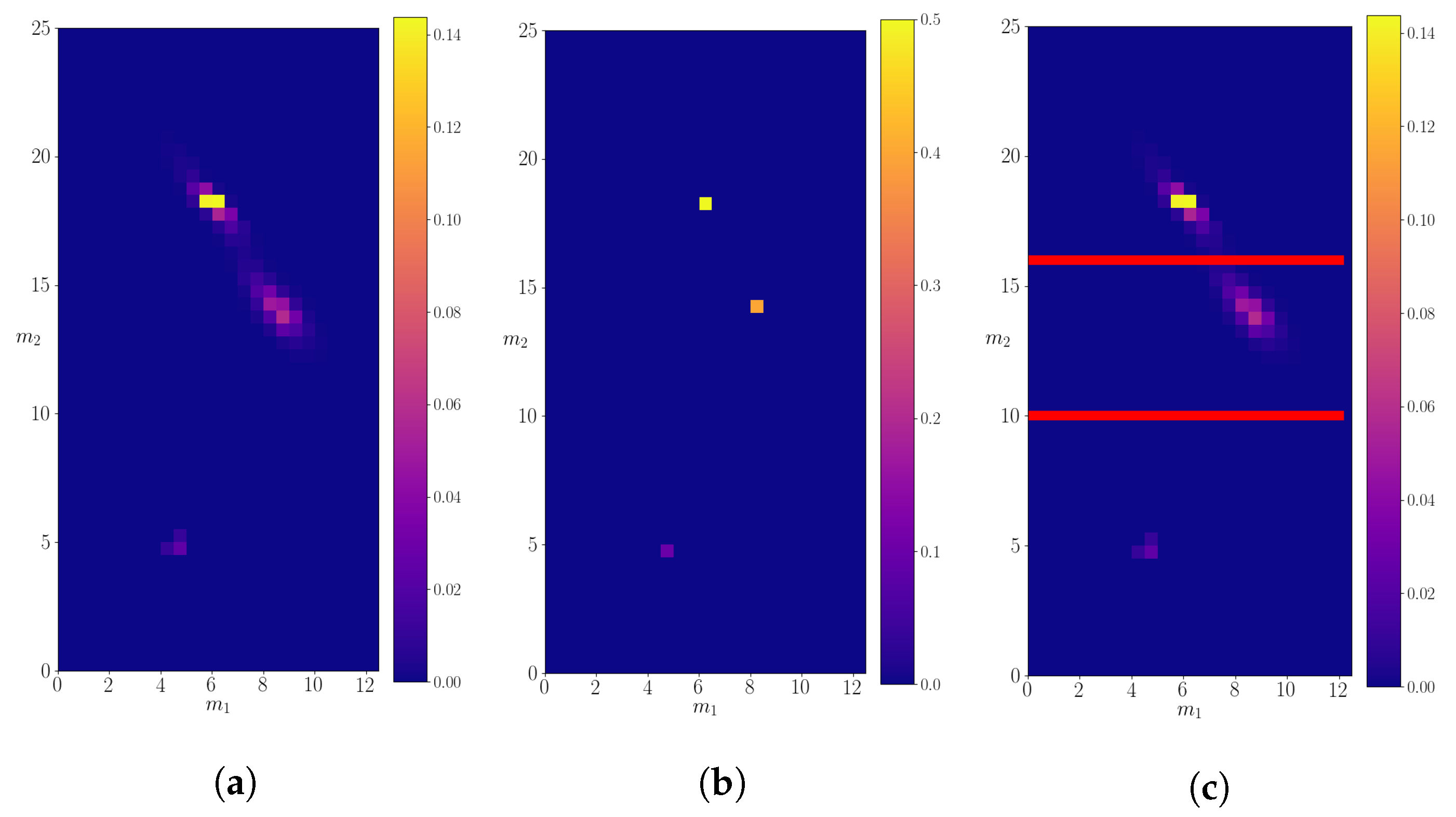
3.1. Mother Particle with Mass M = 25.0
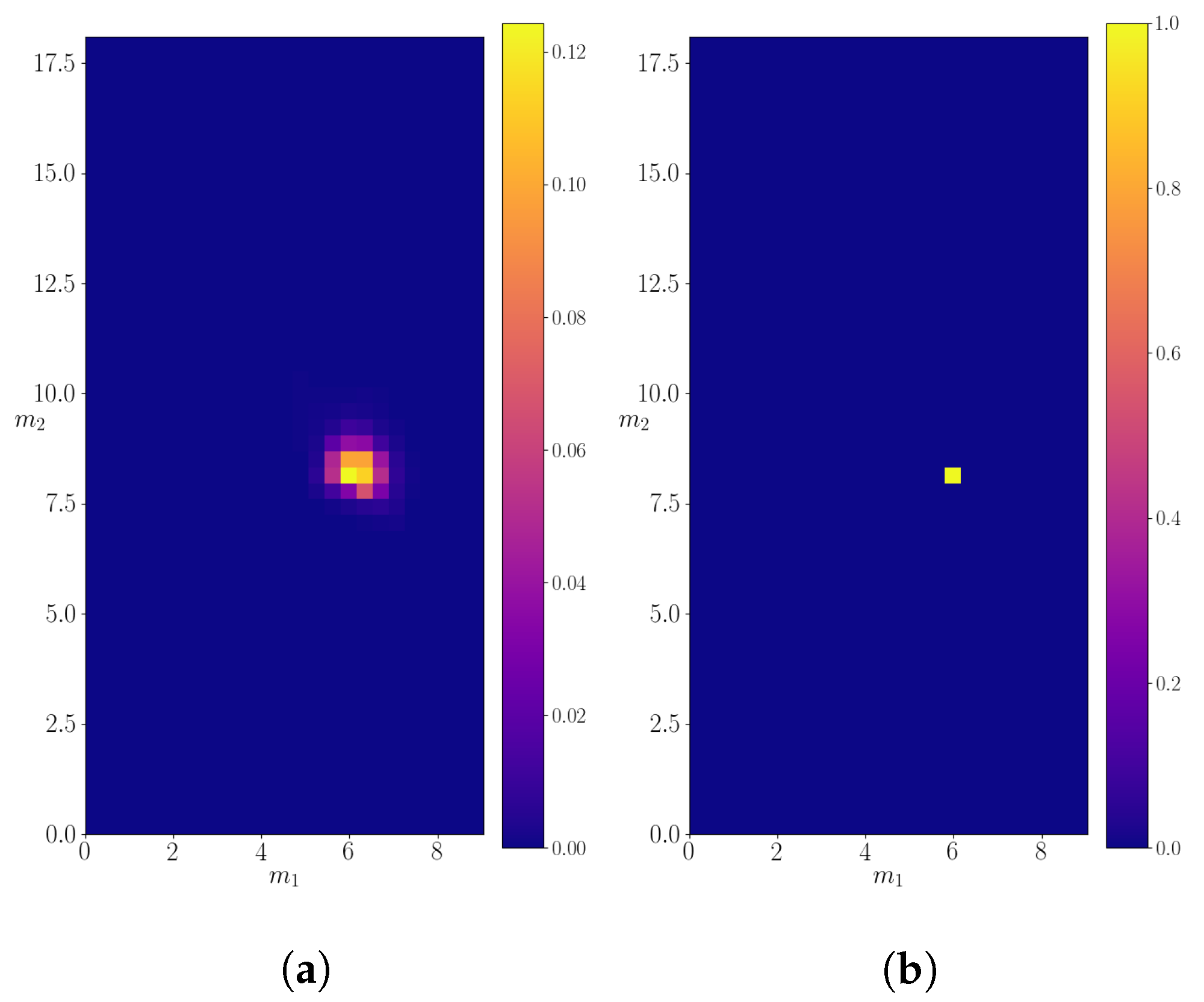
3.2. Mother Particle with Mass M = 18.1
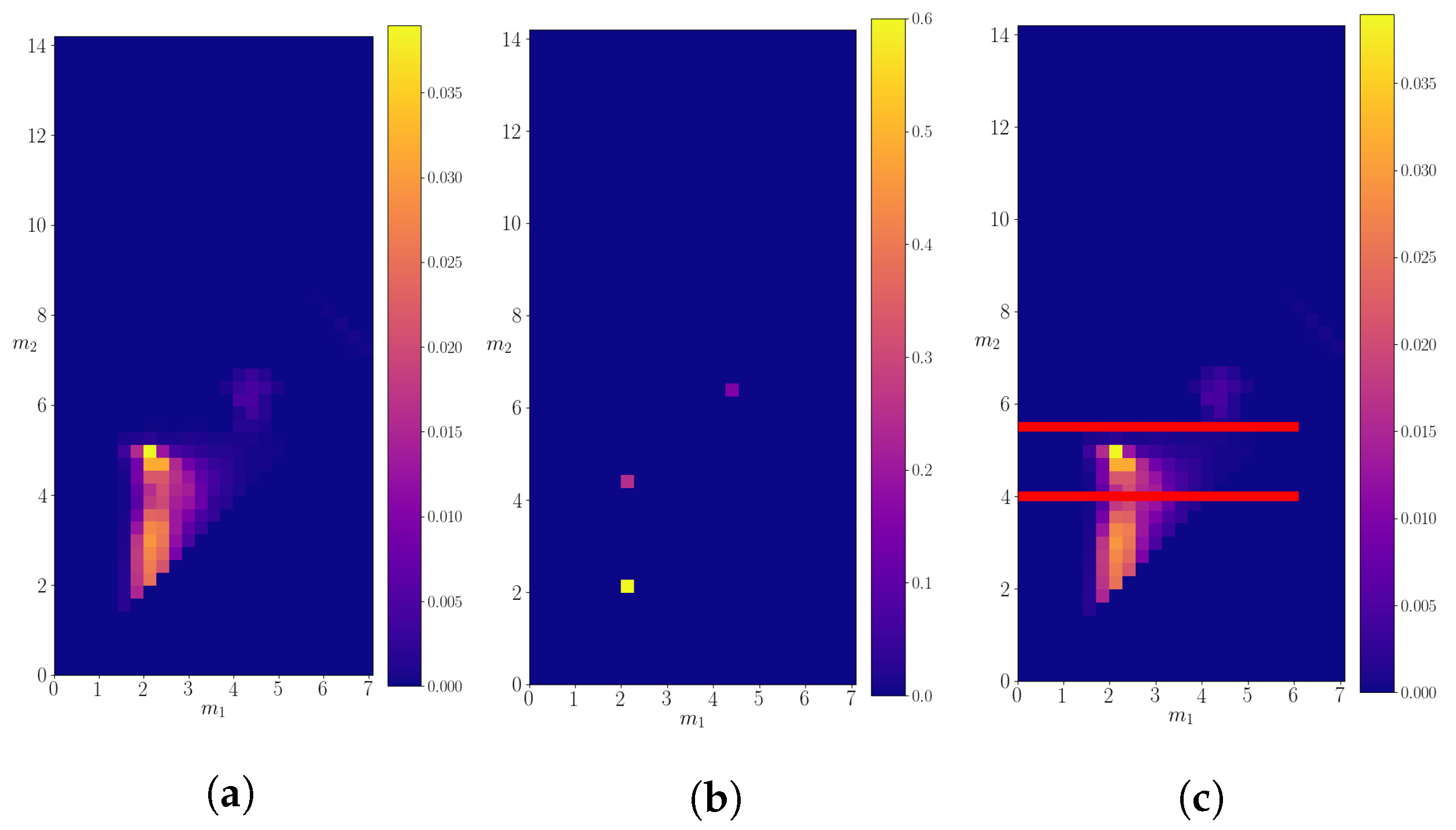
3.3. Mother Particle with Mass M = 14.2
3.4. Mother Particle with Mass M = 1.9
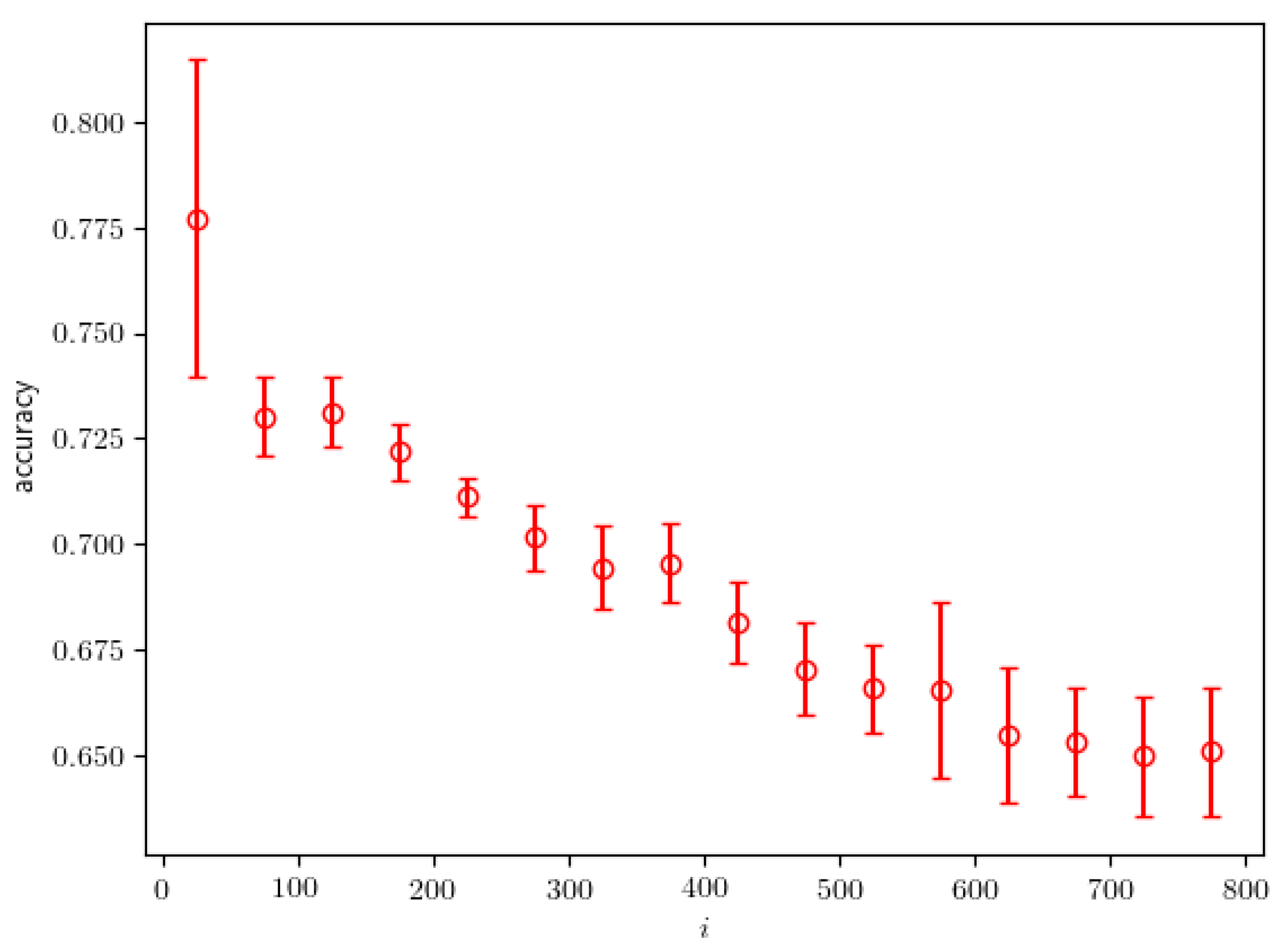
3.5. The Accuracy of the Classifier
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QCD | Quantum Chromodynamics |
| LHC | Large Hadron Collider |
| CERN | Conseil Européen pour la Recherche Nucléaire |
| 2NN | 2 Neural Networks |
| ROC | Receiver Operating Characteristic |
| GAN | Generative Adversarial Network |
| CNN | Convolutional Neural Network |
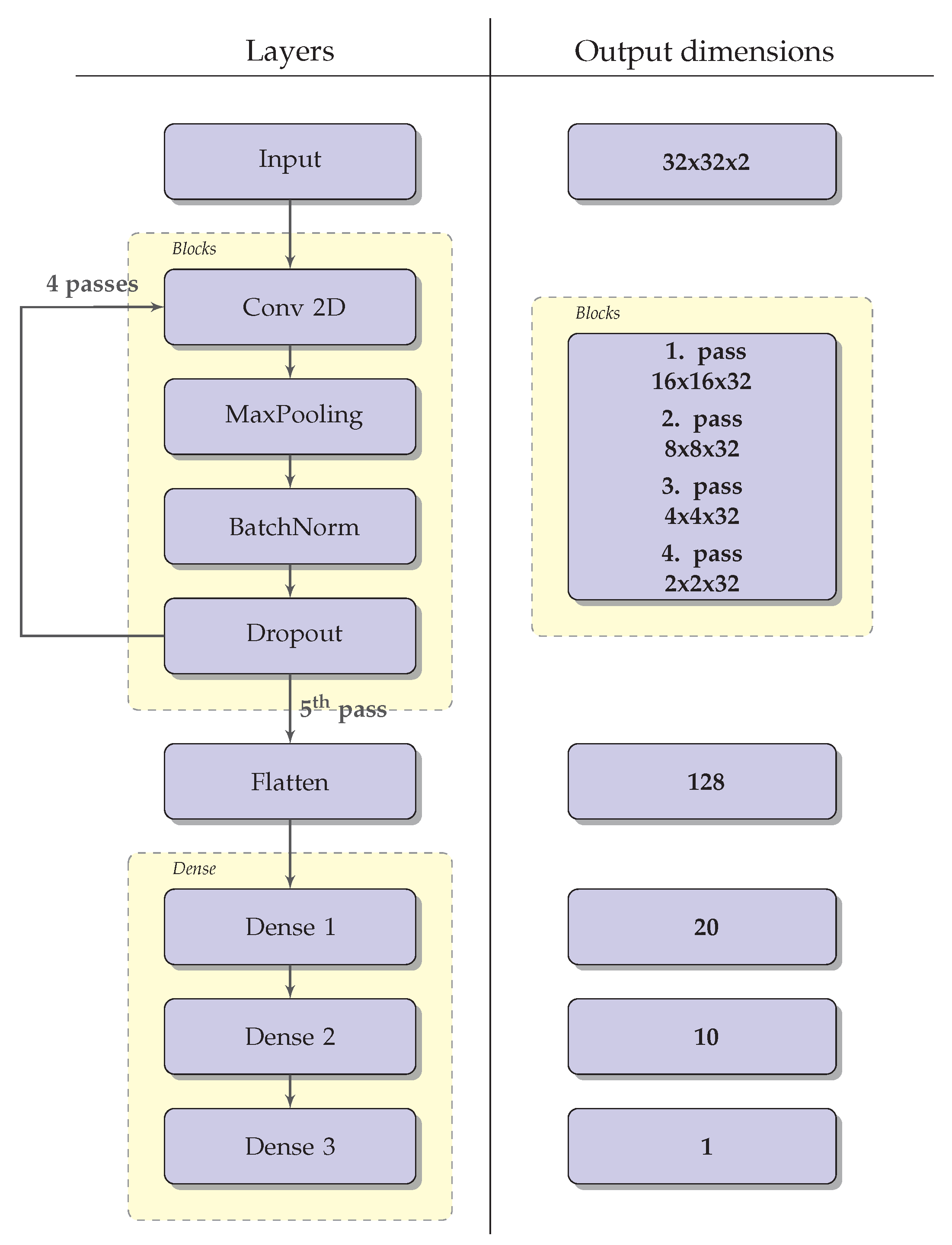
Appendix A. Description of the Neural Networks
References
- Cacciari, M.; Salam, G.P.; Soyez, G. The anti-kt jet clustering algorithm. J. High Energy Phys. 2008, 4, 63. [Google Scholar] [CrossRef] [Green Version]
- Sjostrand, T.; Mrenna, S.; Skands, P. PYTHIA 6.4 Physics and Manual. arXiv 2006, arXiv:hep-ph/0603175. [Google Scholar] [CrossRef]
- Guest, D.; Cranmer, K.; Whiteson, D. Deep Learning and Its Application to LHC Physics. Annu. Rev. Nucl. Part. Sci. 2018, 68, 161–181. [Google Scholar] [CrossRef] [Green Version]
- Andreassen, A.; Feige, I.; Frye, C.; Schwartz, M.D. Junipr: A framework for unsupervised machine learning in particle physics. Eur. Phys. J. C 2019, 79, 1–24. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 1 January 2021).
- Streit, R.L. A neural network for optimum Neyman-Pearson classification. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; Volume 1, pp. 685–690. [Google Scholar]
- Tong, X.; Feng, Y.; Li, J.J. Neyman-Pearson classification algorithms and NP receiver operating characteristics. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jercic, M.; Poljak, N. Exploring the Possibility of a Recovery of Physics Process Properties from a Neural Network Model. Entropy 2020, 22, 994. [Google Scholar] [CrossRef] [PubMed]
- Neyman, J.; Pearson, E.S. On the problem of the most efficient tests of statistical hypotheses. Phil. Trans. R. Soc. Lond. A. 1933, 231, 694–706. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Kingma, D.; Ba, J. A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Nielsen, M.A. Neural Networks and Deep Learning. 2015. Available online: http://neuralnetworksanddeeplearning.com/ (accessed on 1 January 2021).



| Particle | A | B | C | D | E | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| mass | 0.1 | 0.6 | 1.3 | 1.9 | 4.4 | |||||
| p/channel | 1 | A | 0.7 | B | 1 | C | 0.3 | A + C | 0.6 | C + C |
| 0.3 | A + A | 0.3 | A + A | 0.4 | E | |||||
| 0.4 | D | |||||||||
| particle | F | G | H | I | J | |||||
| mass | 6.1 | 8.4 | 14.2 | 18.1 | 25 | |||||
| p/channel | 0.5 | A + A | 0.9 | B + B | 0.6 | D + D | 1 | F + G | 0.5 | F + I |
| 0.5 | B + C | 0.1 | A + F | 0.25 | D + E | 0.4 | G + H | |||
| 0.15 | E + F | 0.1 | E + E | |||||||
| particle mass | 25 | 25 | 25 | |||
| decay masses | 18.1 | 6.1 | 14.2 | 8.4 | 4.4 | 4.4 |
| reconstructed masses | ||||||
| channel probability | 0.5 | 0.4 | 0.1 | |||
| reconstructed probability | 0.48 | 0.47 | 0.05 | |||
| particle mass | 18.1 | 14.2 | 14.2 | |||
| decay masses | 8.4 | 6.1 | 6.1 | 4.4 | 4.4 | 1.9 |
| reconstructed masses | ||||||
| channel probability | 1 | 0.15 | 0.25 | |||
| reconstructed probability | 1 | 0.05 | 0.06 | |||
| particle mass | 14.2 | 1.9 | 1.9 | |||
| decay masses | 1.9 | 1.9 | 1.3 | 0.1 | no decay | |
| reconstructed masses | no decay | |||||
| channel probability | 0.6 | 0.3 | 0.4 | |||
| reconstructed probability | 0.89 | 0.29 | 0.71 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jercic, M.; Jercic, I.; Poljak, N. Introduction and Analysis of a Method for the Investigation of QCD-like Tree Data. Entropy 2022, 24, 104. https://doi.org/10.3390/e24010104
Jercic M, Jercic I, Poljak N. Introduction and Analysis of a Method for the Investigation of QCD-like Tree Data. Entropy. 2022; 24(1):104. https://doi.org/10.3390/e24010104
Chicago/Turabian StyleJercic, Marko, Ivan Jercic, and Nikola Poljak. 2022. "Introduction and Analysis of a Method for the Investigation of QCD-like Tree Data" Entropy 24, no. 1: 104. https://doi.org/10.3390/e24010104
APA StyleJercic, M., Jercic, I., & Poljak, N. (2022). Introduction and Analysis of a Method for the Investigation of QCD-like Tree Data. Entropy, 24(1), 104. https://doi.org/10.3390/e24010104







