Unitarity and Page Curve for Evaporation of 2D AdS Black Holes
Abstract
1. Introduction
2. 2D AdS Black Holes
2.1. Classical Solutions in Absence of Matter
2.2. Coupling to Matter, Conformal Anomaly and Evaporation
3. Black Hole Evaporation
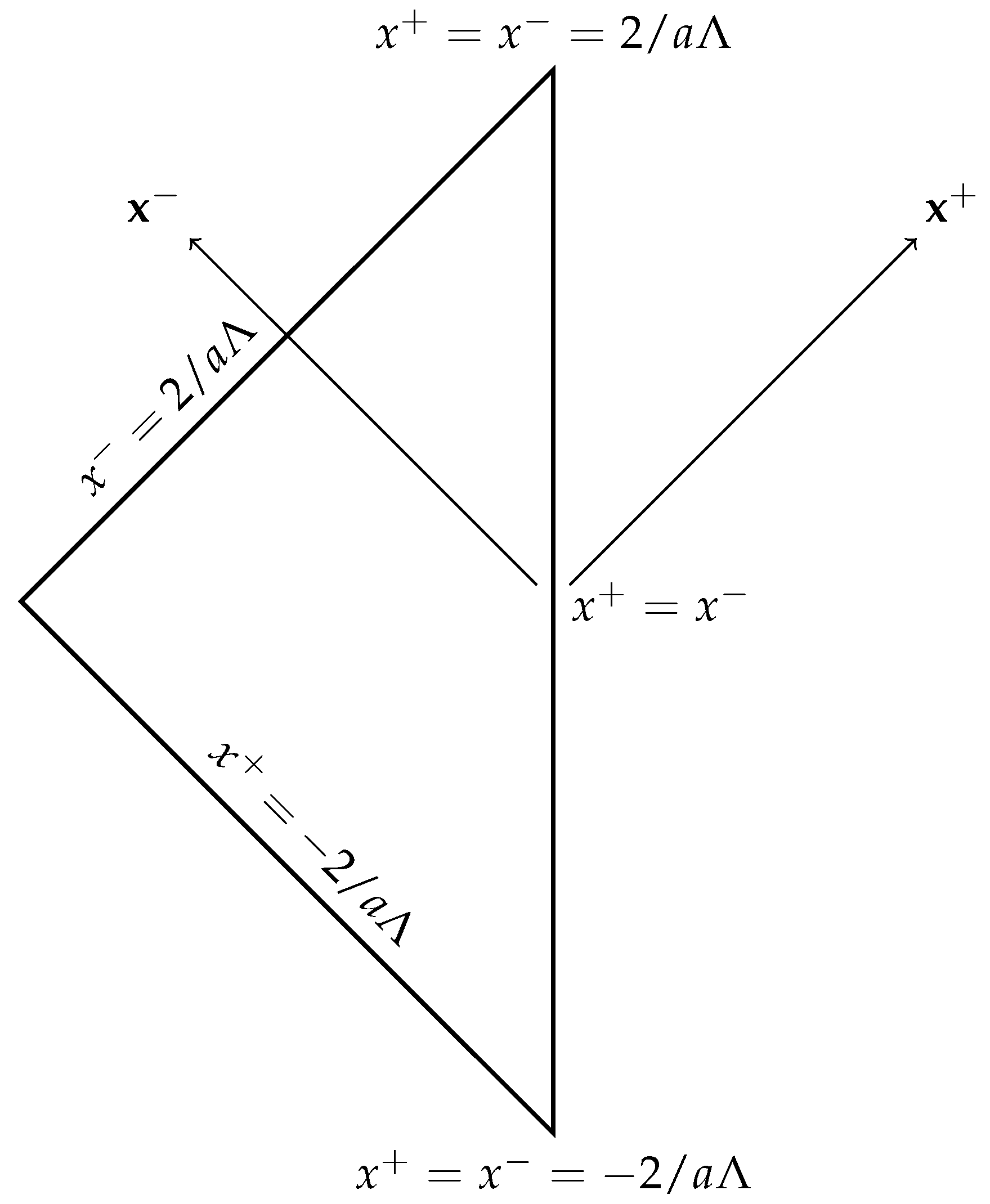
3.1. Black Hole Evaporation in the Static Patch
3.2. Boundary Dynamics
4. Entanglement Entropy of 2D AdS Black Holes
- The BH entropy has its origin in the entanglement entropy of the two edges of maximally extended AdS space-time when the degrees of freedom (DOF) in one edge are traced out [69]. The result (51) is a slightly different realization of the idea proposed in [69], where the entanglement entropy is generated by two copies of a CFT in an initial entangled state and by using a thermo-field double. Equation (51) is instead obtained using a single CFT defined in the maximally extended space-time by tracing the degrees of freedom (DOF) in half of it;
5. Information Flow and the Page Curve for Evaporating JT Black Holes
5.1. Hawking Radiation
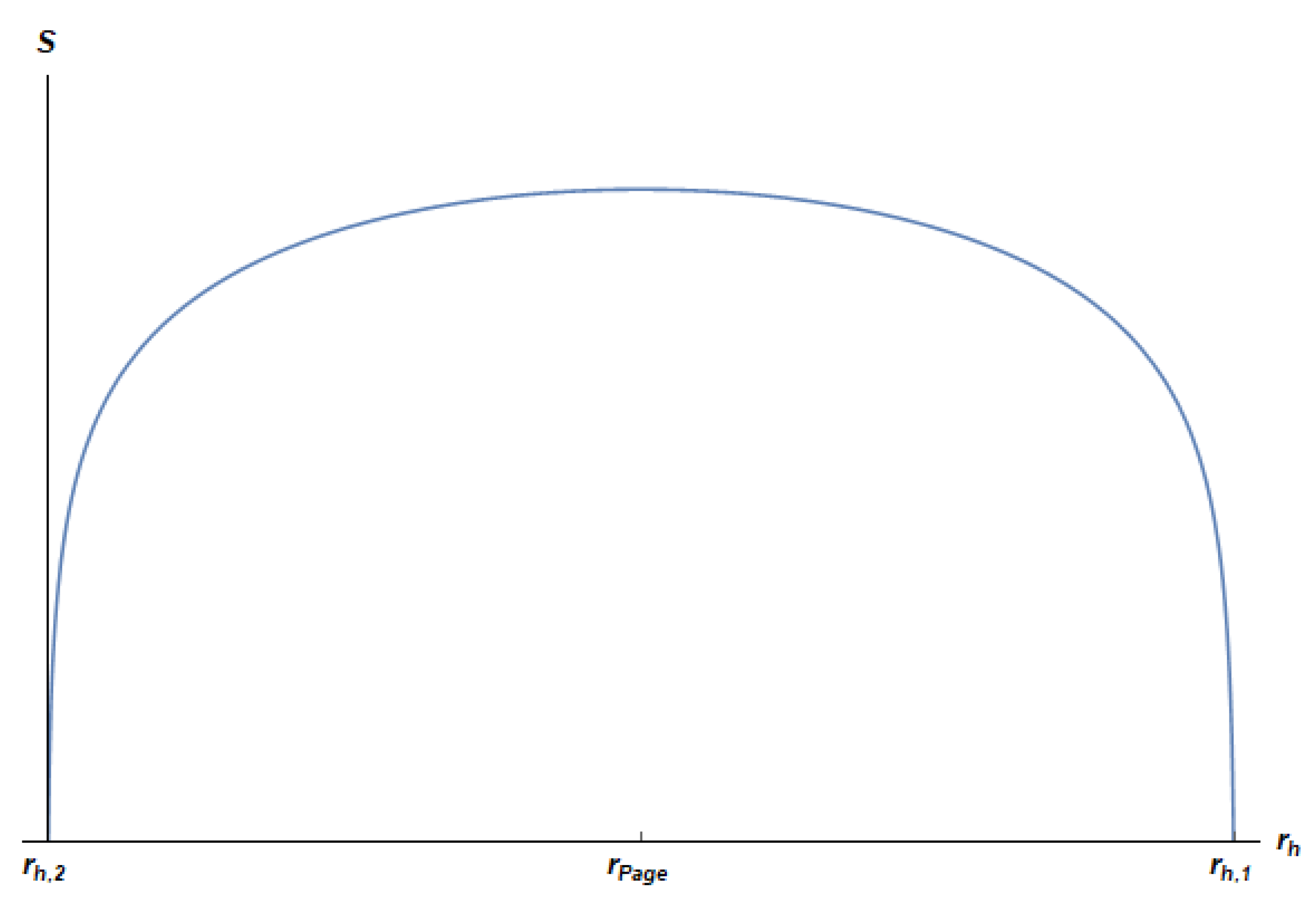
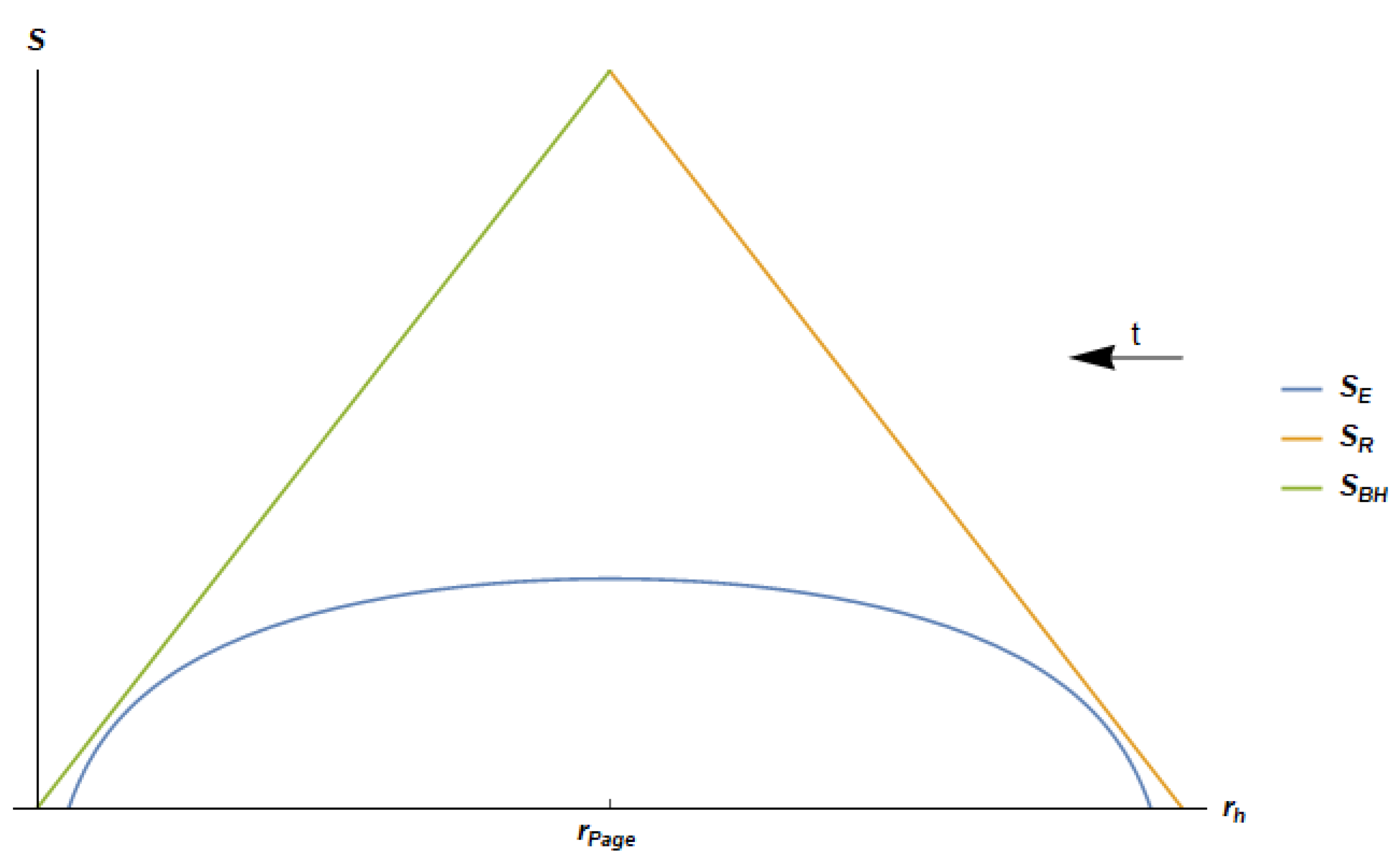
5.2. The Page Curve
5.3. Black Hole Information
5.4. Entanglement Entropy of Hawking Radiation
5.4.1. Thermal Entropy of Hawking Radiation and Relation between N and c
5.4.2. Entanglement Entropy and Page Curve for the JT Black Hole
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220, Erratum in Commun. Math. Phys. 1976, 46, 206. [Google Scholar] [CrossRef]
- Hawking, S.W. Black hole explosions. Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Hawking, S.W. Breakdown of Predictability in Gravitational Collapse. Phys. Rev. D 1976, 14, 2460–2473. [Google Scholar] [CrossRef]
- Polchinski, J. The Black Hole Information Problem. arXiv 2016, arXiv:1609.04036. [Google Scholar]
- Harlow, D. Jerusalem Lectures on Black Holes and Quantum Information. Rev. Mod. Phys. 2016, 88, 015002. [Google Scholar] [CrossRef]
- Mathur, S.D. The Information paradox: A Pedagogical introduction. Class. Quant. Grav. 2009, 26, 224001. [Google Scholar] [CrossRef]
- Unruh, W.G.; Wald, R.M. On evolution laws taking pure states to mixed states in quantum field theory. Phys. Rev. D 1995, 52, 2176–2182. [Google Scholar] [CrossRef] [PubMed]
- Unruh, W.G.; Wald, R.M. Information Loss. Rept. Prog. Phys. 2017, 80, 092002. [Google Scholar] [CrossRef]
- Banks, T.; Susskind, L.; Peskin, M.E. Difficulties for the Evolution of Pure States Into Mixed States. Nucl. Phys. B 1984, 244, 125–134. [Google Scholar] [CrossRef]
- Chen, P.; Ong, Y.C.; Yeom, D.H. Black Hole Remnants and the Information Loss Paradox. Phys. Rept. 2015, 603, 1–45. [Google Scholar] [CrossRef]
- Mathur, S.D. The Fuzzball proposal for black holes: An Elementary review. Fortsch. Phys. 2005, 53, 793–827. [Google Scholar] [CrossRef]
- Susskind, L. The World as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from noncritical string theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Aharony, O.; Gubser, S.S.; Maldacena, J.M.; Ooguri, H.; Oz, Y. Large N field theories, string theory and gravity. Phys. Rept. 2000, 323, 183–386. [Google Scholar] [CrossRef]
- Almheiri, A.; Marolf, D.; Polchinski, J.; Sully, J. Black Holes: Complementarity or Firewalls? J. Energy Phys. 2013, 2, 062. [Google Scholar] [CrossRef]
- Almheiri, A.; Marolf, D.; Polchinski, J.; Stanford, D.; Sully, J. An Apologia for Firewalls. J. Energy Phys. 2013, 9, 018. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space, thermal phase transition, and confinement in gauge theories. Adv. Theor. Math. Phys. 1998, 2, 505–532. [Google Scholar] [CrossRef]
- Strominger, A. Black hole entropy from near horizon microstates. J. Energy Phys. 1998, 2, 009. [Google Scholar] [CrossRef]
- Cadoni, M.; Mignemi, S. Entropy of 2-D black holes from counting microstates. Phys. Rev. D 1999, 59, 081501. [Google Scholar] [CrossRef]
- Almheiri, A.; Hartman, T.; Maldacena, J.; Shaghoulian, E.; Tajdini, A. The entropy of Hawking radiation. arXiv 2020, arXiv:2006.06872. [Google Scholar] [CrossRef]
- Giddings, S.B. Models for unitary black hole disintegration. Phys. Rev. D 2012, 85, 044038. [Google Scholar] [CrossRef]
- Giddings, S.B.; Shi, Y. Quantum information transfer and models for black hole mechanics. Phys. Rev. D 2013, 87, 064031. [Google Scholar] [CrossRef]
- Giddings, S.B. Nonviolent nonlocality. Phys. Rev. D 2013, 88, 064023. [Google Scholar] [CrossRef]
- Giddings, S.B. A ”black hole theorem”, and its implications. arXiv 2021, arXiv:2110.10690. [Google Scholar]
- Zhang, B.; Cai, Q.Y.; Zhan, M.S.; You, L. Information conservation is fundamental: Recovering the lost information in Hawking radiation. Int. J. Mod. Phys. D 2013, 22, 1341014. [Google Scholar] [CrossRef]
- Corda, C. Time dependent Schrödinger equation for black hole evaporation: No information loss. Ann. Phys. 2015, 353, 71–82. [Google Scholar] [CrossRef]
- Page, D.N. Information in black hole radiation. Phys. Rev. Lett. 1993, 71, 3743–3746. [Google Scholar] [CrossRef]
- Page, D.N. Time Dependence of Hawking Radiation Entropy. JCAP 2013, 9, 28. [Google Scholar] [CrossRef]
- Penington, G.; Shenker, S.H.; Stanford, D.; Yang, Z. Replica wormholes and the black hole interior. arXiv 2019, arXiv:1911.11977. [Google Scholar]
- Almheiri, A.; Hartman, T.; Maldacena, J.; Shaghoulian, E.; Tajdini, A. Replica Wormholes and the Entropy of Hawking Radiation. J. Energy Phys. 2020, 5, 13. [Google Scholar] [CrossRef]
- Ryu, S.; Takayanagi, T. Holographic derivation of entanglement entropy from AdS/CFT. Phys. Rev. Lett. 2006, 96, 181602. [Google Scholar] [CrossRef] [PubMed]
- Engelhardt, N.; Wall, A.C. Quantum Extremal Surfaces: Holographic Entanglement Entropy beyond the Classical Regime. J. Energy Phys. 2015, 1, 73. [Google Scholar] [CrossRef]
- Penington, G. Entanglement Wedge Reconstruction and the Information Paradox. J. Energy Phys. 2020, 9, 2. [Google Scholar] [CrossRef]
- Almheiri, A.; Engelhardt, N.; Marolf, D.; Maxfield, H. The entropy of bulk quantum fields and the entanglement wedge of an evaporating black hole. J. Energy Phys. 2019, 12, 63. [Google Scholar] [CrossRef]
- Almheiri, A.; Mahajan, R.; Maldacena, J.; Zhao, Y. The Page curve of Hawking radiation from semiclassical geometry. J. Energy Phys. 2020, 3, 149. [Google Scholar] [CrossRef]
- Almheiri, A.; Mahajan, R.; Maldacena, J. Islands outside the horizon. arXiv 2019, arXiv:1910.11077. [Google Scholar]
- Jackiw, R. Lower Dimensional Gravity. Nucl. Phys. B 1985, 252, 343–356. [Google Scholar] [CrossRef]
- Teitelboim, C. Gravitation and Hamiltonian Structure in Two Space-Time Dimensions. Phys. Lett. B 1983, 126, 41–45. [Google Scholar] [CrossRef]
- Grumiller, D.; Kummer, W.; Vassilevich, D.V. Dilaton gravity in two-dimensions. Phys. Rept. 2002, 369, 327–430. [Google Scholar] [CrossRef]
- Cadoni, M.; Mignemi, S. Classical and semiclassical properties of extremal black holes with dilaton and modulus fields. Nucl. Phys. B 1994, 427, 669–696. [Google Scholar] [CrossRef]
- Cadoni, M.; Mignemi, S. Nonsingular four-dimensional black holes and the Jackiw-Teitelboim theory. Phys. Rev. D 1995, 51, 4319–4329. [Google Scholar] [CrossRef]
- Cadoni, M.; Ciulu, M.; Tuveri, M. Symmetries, Holography and Quantum Phase Transition in Two-dimensional Dilaton AdS Gravity. Phys. Rev. D 2018, 97, 103527. [Google Scholar] [CrossRef]
- Cadoni, M. Entanglement entropy of two-dimensional Anti-de Sitter black holes. Phys. Lett. B 2007, 653, 434–438. [Google Scholar] [CrossRef]
- Hubeny, V.E.; Rangamani, M.; Takayanagi, T. A Covariant holographic entanglement entropy proposal. J. Energy Phys. 2007, 7, 62. [Google Scholar] [CrossRef]
- Giataganas, D.; Tetradis, N. Entanglement entropy, horizons and holography. Phys. Lett. B 2019, 796, 88–92. [Google Scholar] [CrossRef]
- Van Raamsdonk, M. Building up spacetime with quantum entanglement. Gen. Rel. Grav. 2010, 42, 2323–2329. [Google Scholar] [CrossRef]
- Maldacena, J.; Susskind, L. Cool horizons for entangled black holes. Fortsch. Phys. 2013, 61, 781–811. [Google Scholar] [CrossRef]
- Van Raamsdonk, M. Comments on quantum gravity and entanglement. arXiv 2009, arXiv:0907.2939. [Google Scholar]
- Gautason, F.F.; Schneiderbauer, L.; Sybesma, W.; Thorlacius, L. Page Curve for an Evaporating Black Hole. J. Energy Phys. 2020, 5, 91. [Google Scholar] [CrossRef]
- Callan, C.G., Jr.; Giddings, S.B.; Harvey, J.A.; Strominger, A. Evanescent black holes. Phys. Rev. D 1992, 45, 1005. [Google Scholar] [CrossRef] [PubMed]
- Russo, J.G.; Susskind, L.; Thorlacius, L. The Endpoint of Hawking radiation. Phys. Rev. D 1992, 46, 3444–3449. [Google Scholar] [CrossRef] [PubMed]
- Verheijden, E.; Verlinde, E. From the BTZ black hole to JT gravity: Geometrizing the island. arXiv 2021, arXiv:2102.00922. [Google Scholar] [CrossRef]
- Goto, K.; Hartman, T.; Tajdini, A. Replica wormholes for an evaporating 2D black hole. arXiv 2020, arXiv:2011.09043. [Google Scholar] [CrossRef]
- Marolf, D.; Maxfield, H. Observations of Hawking radiation: The Page curve and baby universes. arXiv 2020, arXiv:2010.06602. [Google Scholar] [CrossRef]
- Kim, W.; Nam, M. Entanglement entropy of asymptotically flat non-extremal and extremal black holes with an island. arXiv 2020, arXiv:2103.16163. [Google Scholar] [CrossRef]
- Hollowood, T.J.; Kumar, S.P. Islands and Page Curves for Evaporating Black Holes in JT Gravity. J. Energy Phys. 2020, 8, 94. [Google Scholar] [CrossRef]
- Anegawa, T.; Iizuka, N. Notes on islands in asymptotically flat 2d dilaton black holes. J. Energy Phys. 2020, 7, 36. [Google Scholar] [CrossRef]
- Bousso, R.; Shahbazi-Moghaddam, A. Island Finder and Entropy Bound. Phys. Rev. D 2021, 103, 106005. [Google Scholar] [CrossRef]
- Almheiri, A.; Polchinski, J. Models of AdS2 backreaction and holography. J. Energy Phys. 2015, 11, 14. [Google Scholar] [CrossRef]
- Achucarro, A.; Ortiz, M.E. Relating black holes in two-dimensions and three-dimensions. Phys. Rev. D 1993, 48, 3600–3605. [Google Scholar] [CrossRef]
- Maldacena, J.M.; Michelson, J.; Strominger, A. Anti-de Sitter fragmentation. J. Energy Phys. 1999, 2, 11. [Google Scholar] [CrossRef]
- Christensen, S.M.; Fulling, S.A. Trace Anomalies and the Hawking Effect. Phys. Rev. D 1977, 15, 2088–2104. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black hole evaporation. Phys. Rev. D 1976, 14, 870. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Cadoni, M.; Cavaglia, M. Open strings, 2-D gravity and AdS / CFT correspondence. Phys. Rev. D 2001, 63, 084024. [Google Scholar] [CrossRef]
- Cadoni, M.; Cavaglia, M. Two-dimensional black holes as open strings: A New realization of the AdS / CFT duality. Phys. Lett. B 2001, 499, 315–320. [Google Scholar] [CrossRef]
- Maldacena, J.M. Eternal black holes in anti-de Sitter. J. Energy Phys. 2003, 4, 21. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar] [CrossRef]
- Horowitz, G.T.; Maldacena, J.M. The Black hole final state. J. Energy Phys. 2004, 2, 8. [Google Scholar] [CrossRef]
- Papadodimas, K.; Raju, S. An Infalling Observer in AdS/CFT. J. Energy Phys. 2013, 10, 212. [Google Scholar] [CrossRef]
- Avery, S.G.; Chowdhury, B.D.; Puhm, A. Unitarity and fuzzball complementarity: ‘Alice fuzzes but may not even know it!’. J. Energy Phys. 2013, 9, 12. [Google Scholar] [CrossRef]
- Verlinde, E.; Verlinde, H. Passing through the Firewall. arXiv 2013, arXiv:1306.0515. [Google Scholar]
- ‘t Hooft, G. Black hole unitarity and antipodal entanglement. Found. Phys. 2016, 46, 1185–1198. [Google Scholar] [CrossRef]
- Liu, H.; Vardhan, S. A dynamical mechanism for the Page curve from quantum chaos. J. Energy Phys. 2021, 3, 088. [Google Scholar] [CrossRef]
- Fiola, T.M.; Preskill, J.; Strominger, A.; Trivedi, S.P. Black hole thermodynamics and information loss in two-dimensions. Phys. Rev. D 1994, 50, 3987–4014. [Google Scholar] [CrossRef] [PubMed]
- Cadoni, M.; Tuveri, M.; Sanna, A.P. Long-Range Quantum Gravity. Symmetry 2020, 12, 1396. [Google Scholar] [CrossRef]
- Tuveri, M.; Cadoni, M. Galactic dynamics and long-range quantum gravity. Phys. Rev. D 2019, 100, 024029. [Google Scholar] [CrossRef]
- Susskind, L.; Witten, E. The Holographic bound in anti-de Sitter space. arXiv 1998, arXiv:hep-th/9805114. [Google Scholar]
- Alonso-Serrano, A.; Visser, M. Entropy/information flux in Hawking radiation. Phys. Lett. B 2018, 776, 10–16. [Google Scholar] [CrossRef]
- Mück, W. Hawking radiation is corpuscular. Eur. Phys. J. C 2016, 76, 374. [Google Scholar] [CrossRef][Green Version]
- Giddings, S.B.; Strominger, A. Dynamics of extremal black holes. Phys. Rev. D 1992, 46, 627–637. [Google Scholar] [CrossRef] [PubMed]
- Trivedi, S.P. Semiclassical extremal black holes. Phys. Rev. D 1993, 47, 4233–4238. [Google Scholar] [CrossRef]
- Almheiri, A.; Kang, B. Conformal Symmetry Breaking and Thermodynamics of Near-Extremal Black Holes. J. Energy Phys. 2016, 10, 52. [Google Scholar] [CrossRef]
- Nayak, P.; Shukla, A.; Soni, R.M.; Trivedi, S.P.; Vishal, V. On the Dynamics of Near-Extremal Black Holes. J. Energy Phys. 2018, 9, 48. [Google Scholar] [CrossRef]
- Moitra, U.; Trivedi, S.P.; Vishal, V. Extremal and near-extremal black holes and near-CFT1. J. Energy Phys. 2019, 7, 55. [Google Scholar] [CrossRef]
- Moitra, U.; Sake, S.K.; Trivedi, S.P.; Vishal, V. Jackiw-Teitelboim Gravity and Rotating Black Holes. J. Energy Phys. 2019, 11, 47. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cadoni, M.; Sanna, A.P. Unitarity and Page Curve for Evaporation of 2D AdS Black Holes. Entropy 2022, 24, 101. https://doi.org/10.3390/e24010101
Cadoni M, Sanna AP. Unitarity and Page Curve for Evaporation of 2D AdS Black Holes. Entropy. 2022; 24(1):101. https://doi.org/10.3390/e24010101
Chicago/Turabian StyleCadoni, Mariano, and Andrea P. Sanna. 2022. "Unitarity and Page Curve for Evaporation of 2D AdS Black Holes" Entropy 24, no. 1: 101. https://doi.org/10.3390/e24010101
APA StyleCadoni, M., & Sanna, A. P. (2022). Unitarity and Page Curve for Evaporation of 2D AdS Black Holes. Entropy, 24(1), 101. https://doi.org/10.3390/e24010101





