2. Background: Operads and Their Representations
In an introduction to operads, it is helpful to first think about algebras. An algebra
A is a vector space
V equipped with a bilinear map
thought of as multiplication. Depending on whether
satisfies a particular relation, the algebra will usually be described by an approriate qualifier. For instance, if
for all
, then
A is called a
commutative algebra; if
for all
, then
A is a called an
associative algebra, and so on. Behind each of these algebras is a particular operad that encodes the behavior of the multiplication map
. To motivate the formal definition, it is helpful to visualize
as a planar binary rooted tree and more generally to imagine an arbitrary
n-ary operation as a planar rooted tree with
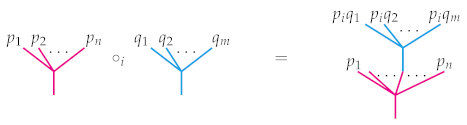
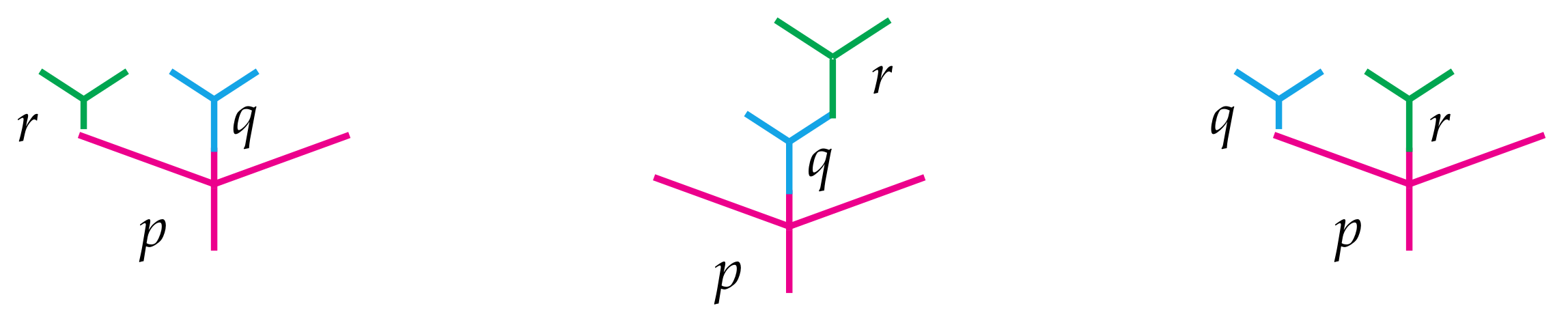
n leaves. There is a natural way to compose such operations. For instance, when
f is a 3-ary operation and
g is a 4-ary operation, they may be composed to obtain a 6-ary operation by using the output of
g as one of the inputs of
f as illustrated in
Figure 1. There
g has been grafted into the
second leaf of the tree associated to
f, and so we denote that choice with the subscript “
” in the figure. There are two other composites
and
, which are not shown but are obtained similarly.
In general, there are
n ways to compose an
m-ary operation with an
n-ary operation, and the resulting operation will always have arity
. This composition should further satisfy some sensible associativity and unital axioms, and the collection of all such operations with their compositions is called an
operad. The concept has origins in category theory [
9] and has been used extensively in algebraic topology and homotopy theory [
10,
11,
12,
13,
14] with applications in physics as well [
15,
16]. Operads may be defined in any symmetric monoidal category, and for ease of exposition below, we will assume all categories
are concrete (that is, all objects have underlying sets) so that we may refer to
elements in a given object of
. Indeed, the main example to have in mind is the category of topological spaces.
Definition 1. Let be a symmetric monoidal category with monoidal product . Anoperad
in consists of a sequence of objects together with morphismsin for all and and an operation satisfying the following: - (i)
[associativity] For all and and , - (ii)
[identity] The operation acts as an identity in the sense that for all and
The definition is conceptually simple despite its cumbersome appearance. For instance,
Figure 2 illustrates the associativity requirements listed in item (i).
As mentioned above, one often thinks of the elements as abstract n-to-1 operations, and the morphisms specify a way to compose them. It is common to begin indexing the sequence of objects at to account for 0-ary operations, but as we will soon see, our main example of an operad in Example 2 will have no 0-ary operations, and so our definition starts with . We do not consider an action of the symmetric group and so is sometimes called a non-symmetric operad, but we will simply call it an operad. In the special case when is the category of vector spaces with linear maps and ⊗ is the tensor product, is often called a linear operad. When it is the category of topological spaces with continuous maps and ⊗ is the Cartesian product, is often called a topological operad.
Example 1. Given a set X, theendomorphism operad
is where denotes the set of all functions from the n-fold Cartesian product to X. The unit operation in is the identity function If and are a pair of functions, then for each the composition is obtained by using the output of g as the ith input of Explicitly, given , The simultaneous composition of several functions may also be considered. That is, given n functions where they may be composed with f simultaneously to obtain a new function , which is again defined by using the outputs of the as the inputs of Explicitly, given , we have Example 2. The simplices give rise to a topological operad calledthe operad of topological simplices
where . The unit operation in is the unique probability distribution on a one-point set. If and are probability distributions, then the composition is obtained by multiplying each of the m coordinates of q by and then replacing the coordinate of p with the resulting m-tuple. Explicitly, Equivalently, the distribution p may be visualized as a planar tree with n leaves labeled by the probabilities and similarly for q. Then the composition is obtained by “painting” each of the leaves of q with the probability and grafting the resulting tree into the leaf of p as below. Notice the sum of the probabilities on the leaves on the composite tree is 1.![Entropy 23 01195 i001]()
As an example, if represents the probability distribution of rolling a six-sided die and is that of a fair coin toss, then is a point in , whose picture is shown on the left of Figure 3. Further recall that if we have n different distributions where , then we may compose them with p simultaneously to obtain the following point in This simultaneous composition is illustrated by the tree on the right in Figure 3. Just as groups come to life when considering representations of them, so operads come to life when each abstract n-ary operation is mapped to a concrete n-ary operation on a particular object. This assignment is traditionally called an algebra of the operad, but we prefer the more descriptive name representation.
Definition 2. Let be an operad in the category of sets. Arepresentation of
, or an-representation
, is set X together with functionsthat respect the operad unit and compositions. That is, and for all and .
Importantly, one may also wish to define a representation of an operad in any symmetric monoidal category whenever “” is in fact an object in It must consist of an object X together with a family of morphisms in that are compatible with the operad unit and compositions. This holds, for instance, when the monoidal category is also closed—that is, when it is equipped with an internal hom functor that is compatible with the monoidal product. Monoidal closure, however, will not be required in our work, which primarily concerns the category of topological spaces. Indeed, the main example to have in mind is when is the operad of simplices and is the real line in . In this case, we define to be the space of continuous functions equipped with the product topology. Now, consider the continuous maps given by where whenever . Then, it is simple to check that for all and i and that for all n, and so is a representation of
3. Derivations of the Operad of Simplices
With these basic definitions in hand, the present goal is to define a mapping
d out of the topological operad
that satisfies an appropriate version of the Leibniz rule,
for all
and
and for all
. This desired equation suggests the codomain of
d should be a (bi)module over
that is, moreover, an abelian monoid. This motivates the following two definitions, the first of which is a slight generalization of that given by Markl in [
15].
Definition 3. Let be an operad in a symmetric monoidal category . Abimodule over
, or simply an-bimodule
, is a collection of objects in together with morphismsin for each such that wheneverthe following holds: The associativity requirements displayed in Equation (
4)—and hence the intuition behind them—are completely analogous to those defining operads as illustrated in
Figure 2. The only difference here is that one of the three operations may come from the bimodule rather than the operad. Here is the main example to have in mind.
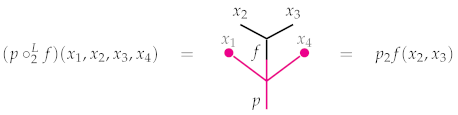
Example 3. As every algebra is a bimodule over itself, so every representation of is an -bimodule in a straightforward way. Indeed, in the case of the topological operad of simplices, the maps comprising the Δ-representation structure on induce a Δ-bimodule structure on . However, we will make use of a slight variant of this bimodule structure. Right composition will be defined in the expected way, though left composition will not. Explicitly, we define the left and right composition mapsas follows. Given a probability distribution and a continuous function, define left composition by , where the composition on the right-hand side is defined as in the simultaneous composition in the endomorphism operad of illustrated in Example 1, and where each 0 denotes the zero function . Here, recall that maps a point x to the standard inner product as introduced in Section 1. Unwinding this, left composition thus evaluates explicitly as . In words, the value of the left composite at a point x is computed by evaluating f at the m-subtuple of x beginning at the coordinate and scaling that output by . All other coordinates of x are ignored. The picture to have in mind is that below, where the bold dots are imagined to be “plugs” that prevent the surplus coordinates from playing a role. In this picture,and.
![Entropy 23 01195 i002]()
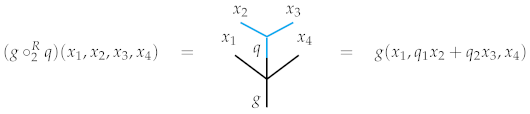
Given a probability distribution and a continuous function , define right composition by This may be understood visually as well. The value of the right composite at a point x is computed by taking the inner product of q with the m-tuple of x beginning at the coordinate and using that number as the input of g with all other coordinates of x falling into place as in the picture below. There are no “plugs” in this instance since all coordinates of x play a role.![Entropy 23 01195 i003]()
These examples suggest the inner product notation is a convenient choice. Given and and a point , let denote the k-subtuple of x beginning at the coordinate: Then given any point , the left and right composition maps may be written more succinctly as We will use this notation below and will always write in lieu of since the context will make it clear that must be an m-tuple. The boldface font is used to distinguish a tuple from a real number . Finally, note that the maps and are continuous since f and g are continuous, and moreover that the associativity requirements in Equation (4) are analogous to those illustrated in Figure 2, so it is straightforward to verify they are satisfied. In particular, the zero functions appearing in the definition of simplify the situation greatly. For instance, several of associativity requirements follow from the simple fact that multiplying an input by a probability and then mapping the result to zero is the same as first mapping the input to zero and then multiplying that zero by a probability. So is indeed a Δ-bimodule. Next, recall that the desired Leibniz rule in Equation (
3) suggests the bimodule should be equipped with a notion of addition. This motivates the following definition.
Definition 4. Let be an operad in a symmetric monoidal category . An -bimodule M is anabelian -bimoduleif each is an abelian monoid in ; that is, if for each the following hold:
- (i)
[associativity, commutativity] there is a morphism in such that and for all ,
- (ii)
[identity] there is an element such that for all .
As the primary example, consider viewed as a -bimodule as described in Example 3. For each define by pointwise addition, meaning that for each we have where for all . The identity element in is the constant map at zero. Moreover each is continuous and inherits associativity and commutativity from In this way, is an abelian -bimodule.
Remark 1. Notice that the Δ-bimodule composition maps and distribute over sums in the abelian Δ-bimodule . In other words, for all continuous functions and for all probability distributions ,and similarly for left composition . This follows directly from pointwise addition. With this setup in mind, our desideratum in Equation (
3) is now realized in the following definition.
Definition 5. Let be an operad in a category and let M be an abelian -bimodule. Aderivation of
valued in
M is sequence of morphisms in satisfyingfor all and for all In the special case when
is a linear operad, this definition coincides with that given by Markl in [
15]. In what follows, we omit the subscripts and simply write
d instead of
. Now, suppose
is the operad of topological simplices and
is equipped with the structure of an abelian
-bimodule given above. Here is the picture to have in mind for Equation (
5):
![Entropy 23 01195 i004]()
On the right-hand side we have used the “plug” notation introduced in Example 3, which can also be understood explicitly by evaluating
d at a point
,
Of particular interest is the behavior of a derivation
when it is applied to a simultaneous composition of probability distributions. A derivation applied to the composite
for probability distributions
, and
can be understood in a convenient picture when
q and
r are composed onto different leaves of
p; that is, when
or
. This follows straightforwardly from a repeated application of
d. Indeed, by definition we have
and by applying the Leibniz rule again to the first summand, this is equal to
which we can expand to obtain
since composition distributes over sums as noted in Remark 1. We will identify this function with the picture below in lieu of the cumbersome notation.
![Entropy 23 01195 i005]()
Importantly, the obvious generalization of the formula holds for any simultaneous composition
for any
and
where
. This again follows directly from repeated applications of Equation (
5), as illustrated below.
![Entropy 23 01195 i006]()
This is summarized in the following proposition.
Proposition 1. Let and for and let be a derivation of the operad of topological simplices. Then for any point , Finally, the main result follows.
Theorem 3. Shannon entropy defines a derivation of the operad of topological simplices, and for every derivation of this operad there exists a point at which it is given by a constant multiple of Shannon entropy.
Proof. For each
define
by
where
is constant for all
. Then,
d is continuous since
H is continuous. Moreover, if
and
are probability distributions, then for any
and
, we have
where the last line follows since
is computed by evaluating the function
at some point, and this function is assumed to be constant at
Conversely, suppose
is a derivation. For each
define a function
by
where
. Then
F is continuous since
d is continuous, and Proposition 1 further implies that
From the Faddeev–Leinster result in Theorem 1, it follows that for some . □
Notice that the important Equation (
2) mentioned in the introduction is obtained as a corollary. Indeed, if for each
the map
is defined to be constant at entropy
, then
d is a derivation by Theorem 3 and so Proposition 1 yields the following by evaluating
at any point.
Corollary 1. Let and with Then As a closing remark, Faddeev’s characterization of entropy in Theorem 1 can be reexpressed using the language of category theory and operads as in [
1], (Theorem 12.3.1). We have omitted this language here but invite the reader to explore the full category theoretical story in Chapter 12 of Leinster’s book.