Adaptive Fixed-Time Neural Network Tracking Control of Nonlinear Interconnected Systems
Abstract
:1. Introduction
- (1)
- The combination of fixed-time control and neural network adaptive control for nonlinear interconnected systems.
- (2)
- A fixed-time low pass filter is designed to solve the “explosion of complexity” based on backstepping control technology.
- (3)
- A fixed-time controller is designed, which contains the convergence time of the error system, weights of neural networks, and a low pass filter system.
2. Problem Formation and Preliminaries
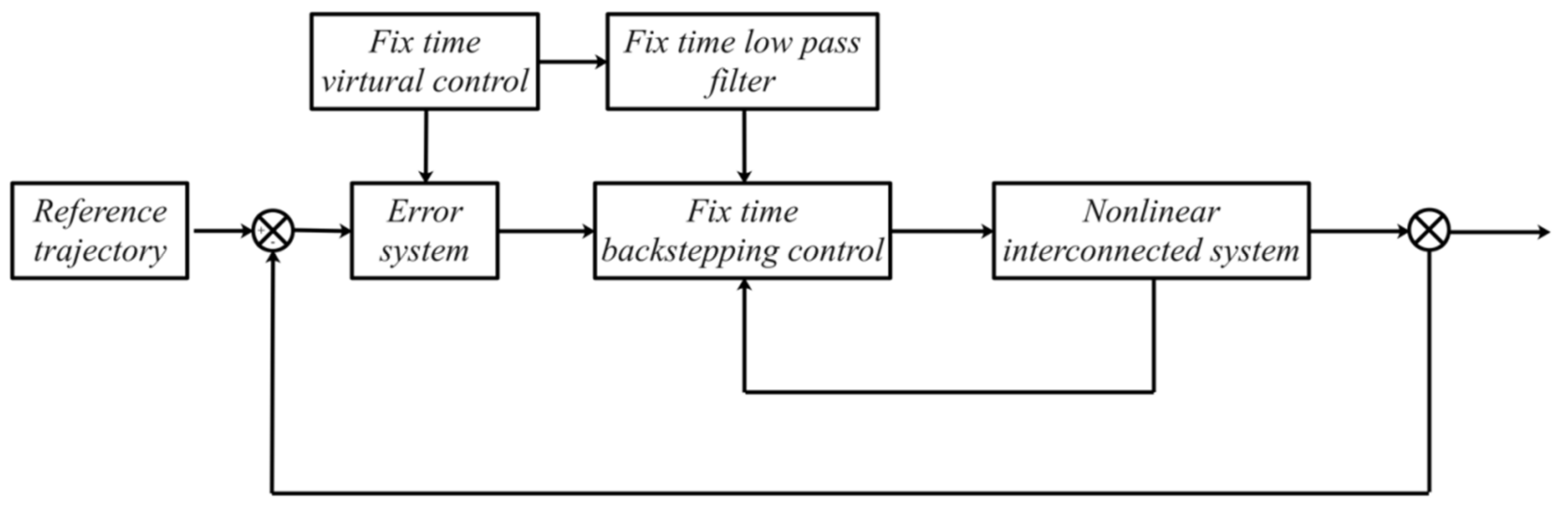
3. Adaptive Fixed-Time Tracking Control System Design
3.1. Control System Design
3.2. Control System Analysis
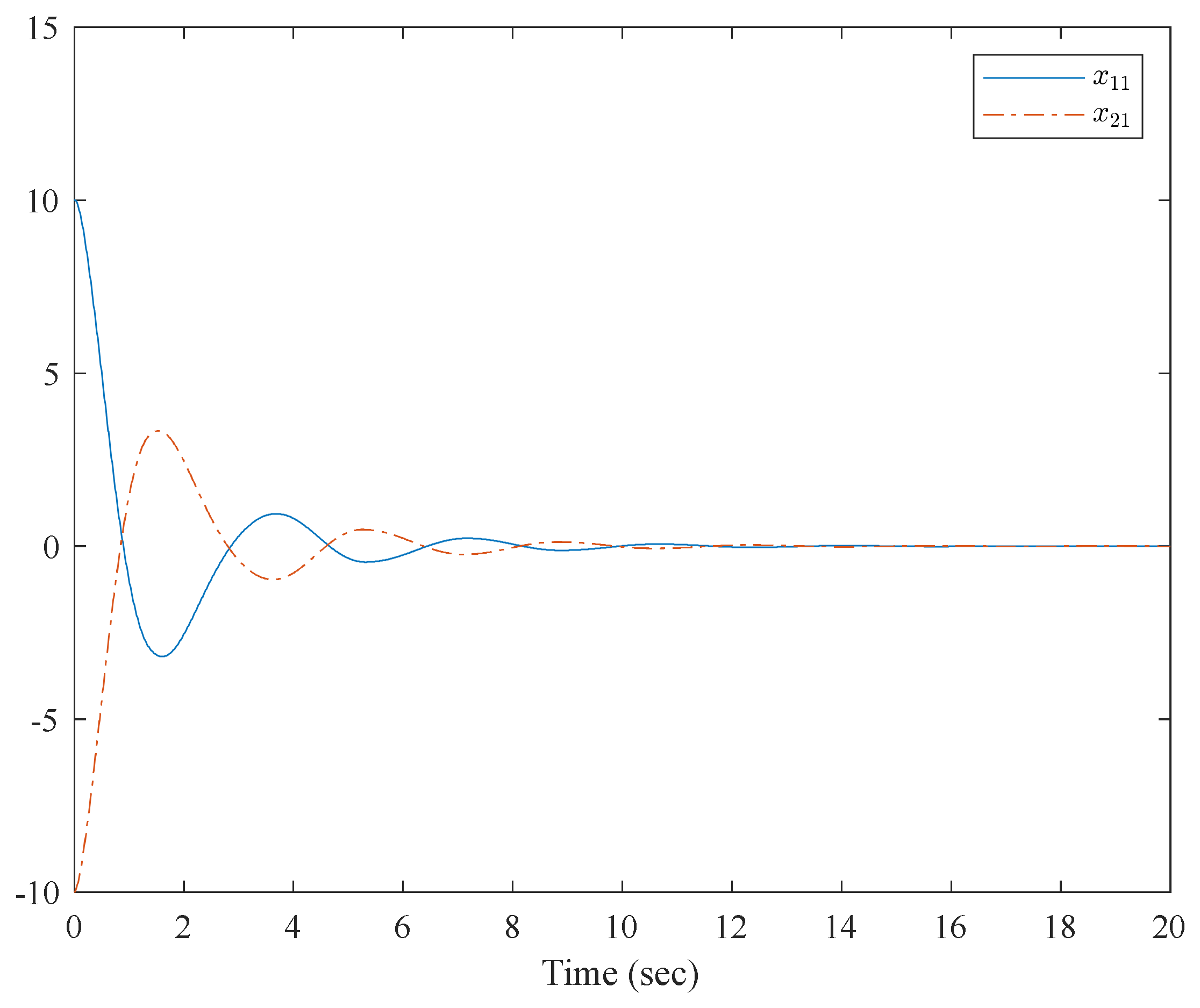
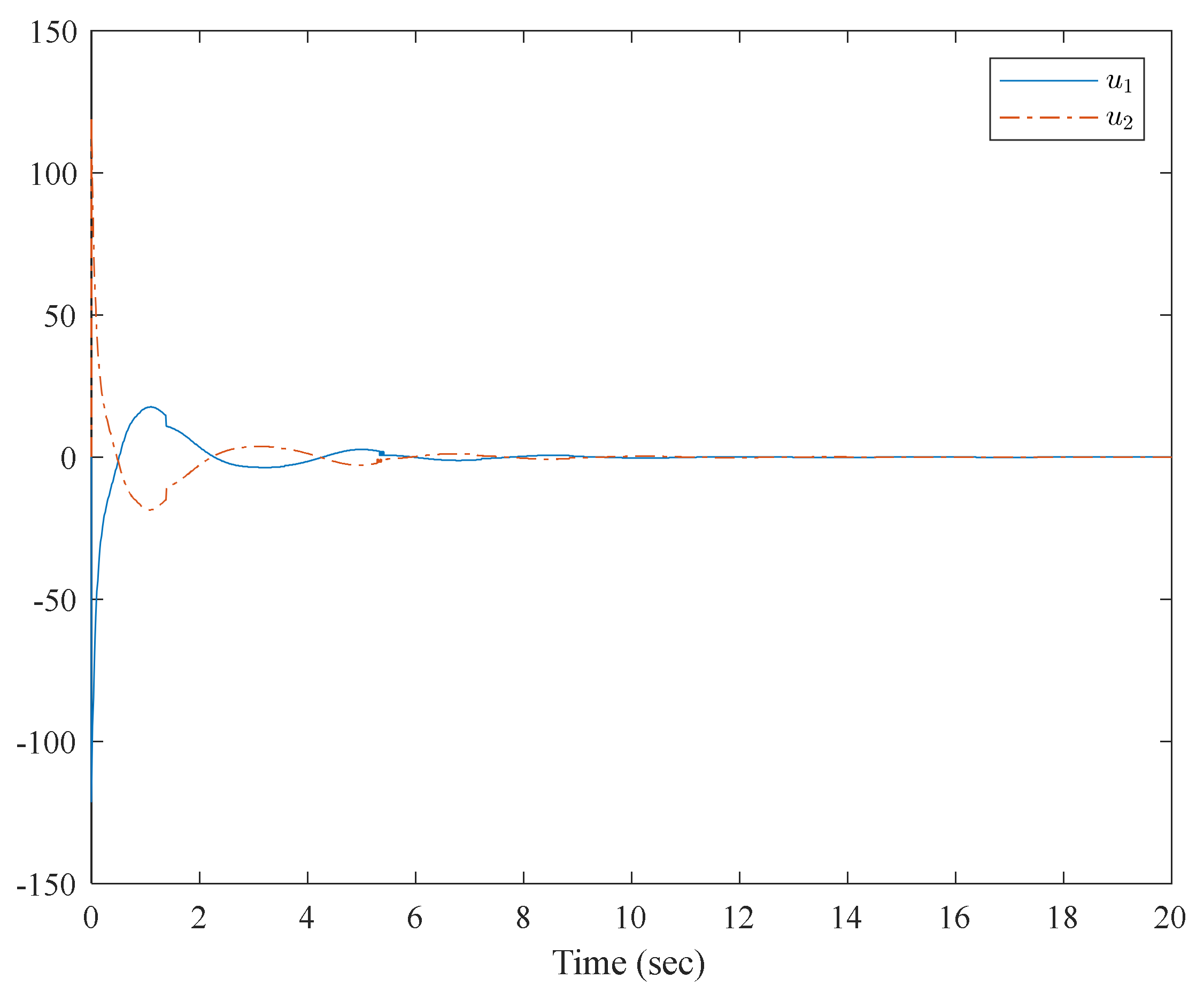
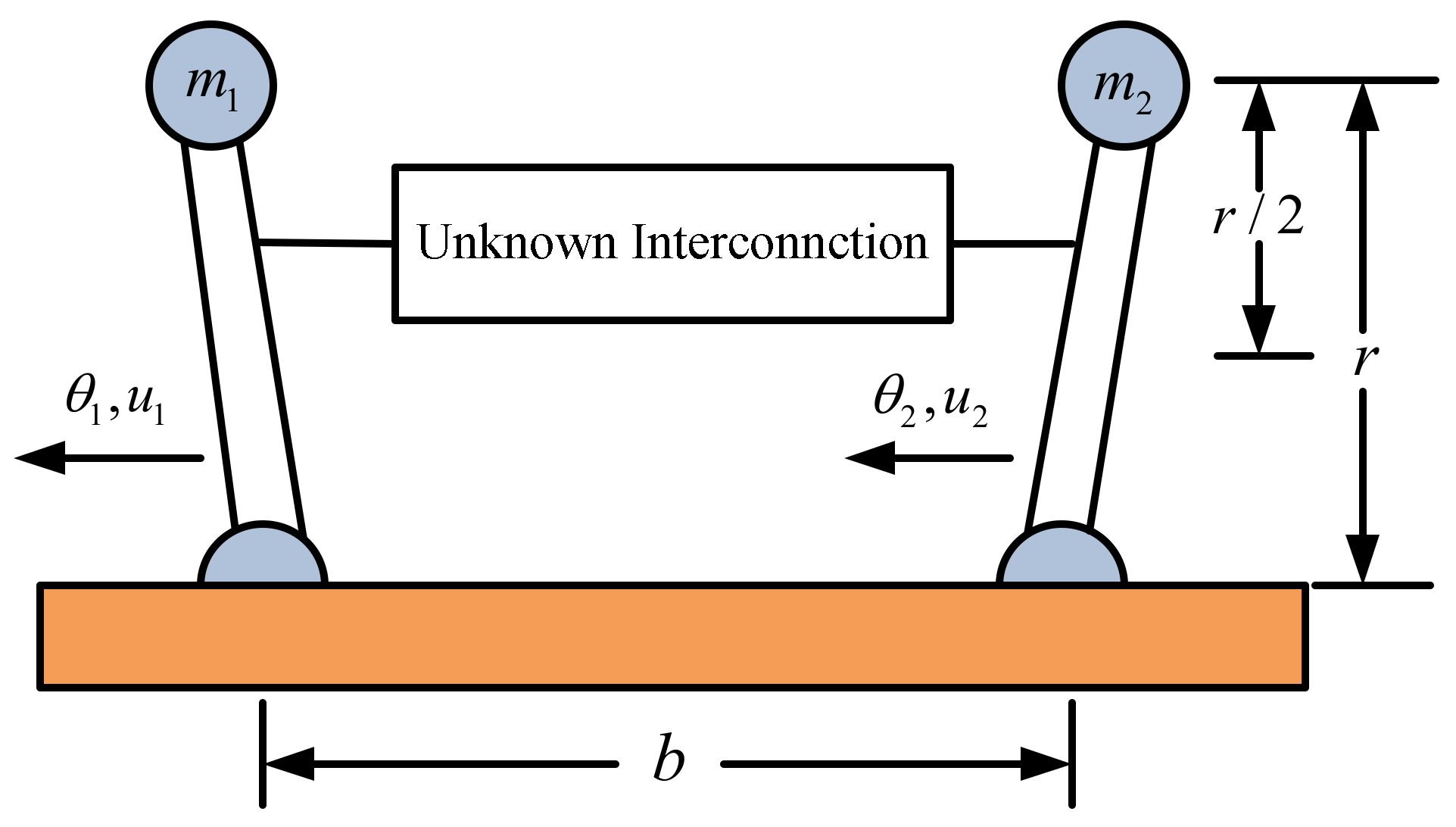
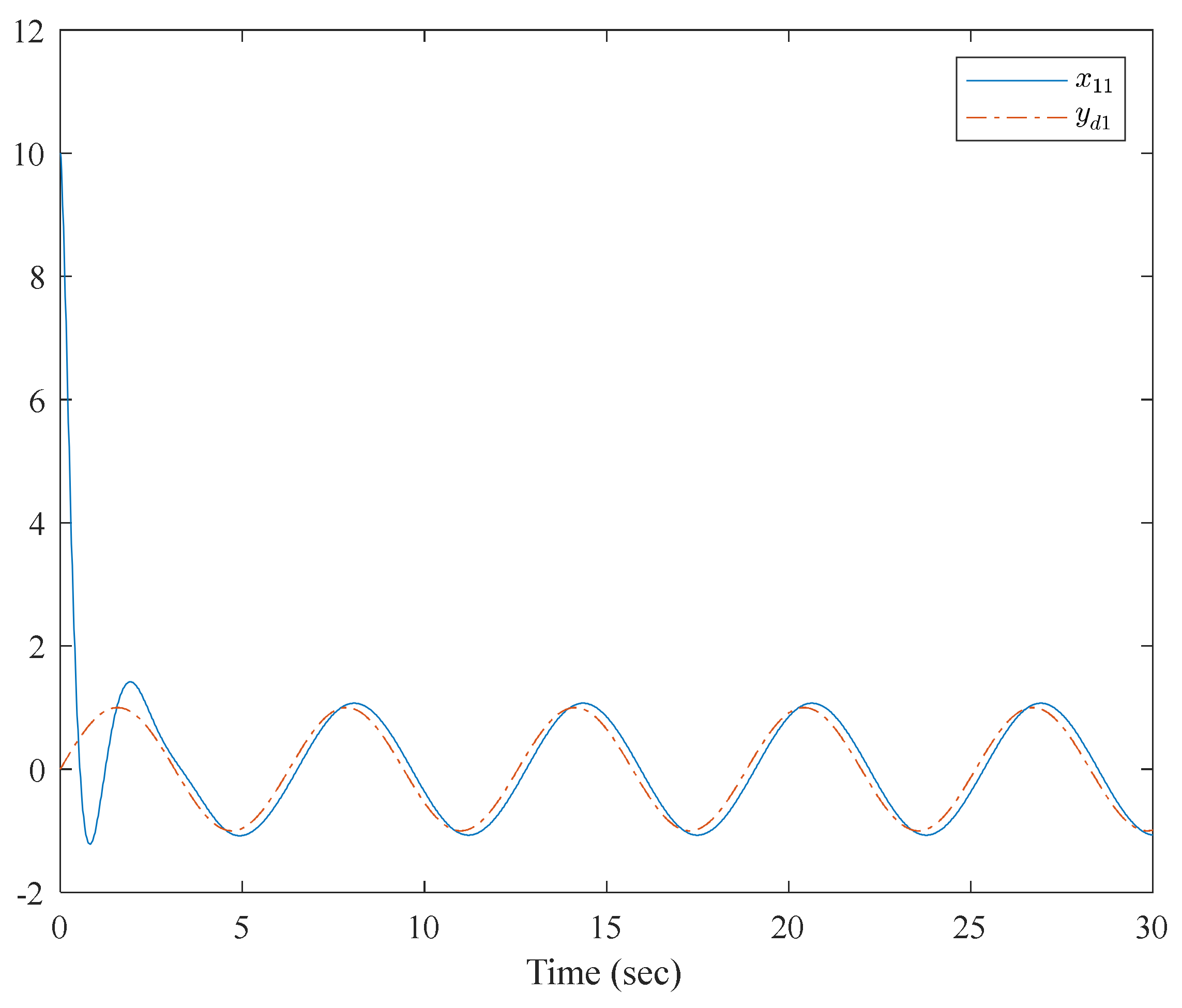
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, W.; Jiang, Y.; Jiang, Z.P.; Chai, T. Output-Feedback Adaptive Optimal Control of Interconnected Systems Based on Robust Adaptive Dynamic Programming; Automatica Oxford: Oxford, UK, 2016. [Google Scholar]
- Gao, W.; Jiang, Z.P. Adaptive Dynamic Programming and Adaptive Optimal Output Regulation of Linear Systems. IEEE Trans. Autom. Control. 2016, 61, 4164–4169. [Google Scholar] [CrossRef]
- Yan, X.G.; Edwards, C.; Spurgeon, S.K. Decentralised robust sliding mode control for a class of nonlinear interconnected systems by static output feedback. Automatica 2004, 40, 613–620. [Google Scholar] [CrossRef]
- Zhang, J.H.; Li, Y.; Fei, W.B. Neural Network-Based Nonlinear Fixed-Time Adaptive Practical Tracking Control. for Quadrotor Unmanned Aerial Vehicles. Complexity 2020, 2020, 13. [Google Scholar] [CrossRef]
- Tong, S.C.; Min, X.; Li, Y.X. Observer-Based Adaptive Fuzzy Tracking Control. for Strict-Feedback Nonlinear Systems with Unknown Control. Gain Functions. IEEE Trans. Cybern. 2020, 50, 3903–3913. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Q.; Li, Y.; Wu, X. Homeomorphism Mapping Based Neural Networks for Finite Time Constraint Control of a Class of Nonaffine Pure-Feedback Nonlinear Systems. Complexity 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Fei, W.; Wu, X. U-Model Based Adaptive Neural Networks Fixed-Time Backstepping Control for Uncertain Nonlinear System. Math. Probl. Eng. 2020, 2020, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.M.; Zhao, D.; Zhang, J. A general U-block model-based design procedure for nonlinear polynomial control systems. Int. J. Syst. Sci. 2016, 47, 3465–3475. [Google Scholar] [CrossRef]
- Li, R.; Zhu, Q.; Narayan, P.; Yue, A.; Yao, Y.; Deng, M. U-Model-Based Two-Degree-of-Freedom Internal Model Control of Nonlinear Dynamic Systems. Entropy 2021, 23, 169. [Google Scholar] [CrossRef]
- Yu, X.; Man, Z. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2009, 49, 261–264. [Google Scholar]
- Muñoz, D.; Sbarbaro, D. An adaptive sliding-mode controller for discrete nonlinear systems. IEEE Trans. Ind. Electron. 2000, 47, 574–581. [Google Scholar] [CrossRef]
- Da, F. Decentralized sliding mode adaptive controller design based on fuzzy neural networks for interconnected uncertain nonlinear systems. IEEE Trans. Neural Netw. 2000, 11, 1471–1480. [Google Scholar]
- Moreno, J.A.; Osorio, M. Strict Lyapunov Functions for the Super-Twisting Algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Q.; Li, Y. Convergence Time Calculation for Supertwisting Algorithm and Application for Nonaffine Nonlinear Systems. Complexity 2019, 2019, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Ge, S.S.; Cong, W. Adaptive neural control of uncertain MIMO nonlinear systems. IEEE Trans. Neural Netw. 2004, 15, 674–692. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Q.; Wu, X.; Li, Y. A generalized indirect adaptive neural networks backstepping control procedure for a class of non-affine nonlinear systems with pure-feedback prototype. Neurocomputing 2013, 121, 131–139. [Google Scholar] [CrossRef]
- Pan, J.; Qu, L.; Peng, K. Sensor and Actuator Fault Diagnosis for Robot Joint Based on Deep CNN. Entropy 2021, 23, 751. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Huang, H.; Ge, S.S. Adaptive Neural Network Control of a Robotic Manipulator With Time-Varying Output Constraints. IEEE Trans. Cybern. 2017, 47, 3136–3147. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Huang, R.; Li, X.; Liu, S. Adaptive neural network control of uncertain robotic manipulators with external disturbance and time-varying output constraints. Neurocomputing 2019, 323, 108–116. [Google Scholar] [CrossRef]
- Ge, S.S.; Hang, C.C.; Lee, T.H.; Zhang, T. Stable Adaptive Neural Network Control; Springer: New York, NY, USA, 2002. [Google Scholar]
- Polyakov, A.; Fridman, L. Stability notions and Lyapunov functions for sliding mode control systems. J. Frankl. Inst. 2014, 351, 1831–1865. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Ji, H. A three-dimensional robust nonlinear terminal guidance law with ISS finite-time convergence. Int. J. Control 2016, 89, 938–949. [Google Scholar] [CrossRef]
- Du, P.; Liang, H.; Zhao, S.; Ahn, C.K. Neural-Based Decentralized Adaptive Finite-Time Control for Nonlinear Large-Scale Systems With Time-Varying Output Constraints. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3136–3147. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Ye, X.; Chin, C. Adaptive Fixed-Time Control of Strict-Feedback High-Order Nonlinear Systems. Entropy 2021, 23, 963. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liu, W.; Qiu, J.; Liu, P.X. Adaptive Fuzzy Decentralized Control for a Class of Strong Interconnected Nonlinear Systems with Unmodeled Dynamics. IEEE Trans. Fuzzy Syst. 2018, 26, 836–846. [Google Scholar] [CrossRef]
- Li, X.; Yang, G. Neural-Network-Based Adaptive Decentralized Fault-Tolerant Control for a Class of Interconnected Nonlinear Systems. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 144–155. [Google Scholar] [CrossRef] [PubMed]
- Si, W.; Dong, X.; Yang, F. Decentralized adaptive neural control for high-order interconnected stochastic nonlinear time-delay systems with unknown system dynamics. Neural Netw. 2018, 99, 123–133. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, J.; Xu, X.; Chin, C.S. Adaptive Fixed-Time Neural Network Tracking Control of Nonlinear Interconnected Systems. Entropy 2021, 23, 1152. https://doi.org/10.3390/e23091152
Li Y, Zhang J, Xu X, Chin CS. Adaptive Fixed-Time Neural Network Tracking Control of Nonlinear Interconnected Systems. Entropy. 2021; 23(9):1152. https://doi.org/10.3390/e23091152
Chicago/Turabian StyleLi, Yang, Jianhua Zhang, Xinli Xu, and Cheng Siong Chin. 2021. "Adaptive Fixed-Time Neural Network Tracking Control of Nonlinear Interconnected Systems" Entropy 23, no. 9: 1152. https://doi.org/10.3390/e23091152
APA StyleLi, Y., Zhang, J., Xu, X., & Chin, C. S. (2021). Adaptive Fixed-Time Neural Network Tracking Control of Nonlinear Interconnected Systems. Entropy, 23(9), 1152. https://doi.org/10.3390/e23091152








