Structural Complexity and Informational Transfer in Spatial Log-Gaussian Cox Processes
Abstract
:1. Introduction
2. Preliminaries
2.1. Log-Gaussian Cox Processes
2.2. Information and Complexity
3. Methodology
- ‘Mean Intra SD’—The average of the internal standard deviations of the entropy and divergence values obtained within each of the M sets of R point patterns:
- ‘Inter-Mean SD’—The standard deviation of the internal average entropy and divergence values obtained within each of the M sets of point patterns:
- ‘Total SD’—The standard deviation of the entropy and divergence values obtained for the patterns:
- ‘Inter-Single SD’—The standard deviation of entropy and divergence values based on only one single pattern being generated from each of the M replicates of the intensity field:
4. Analysis
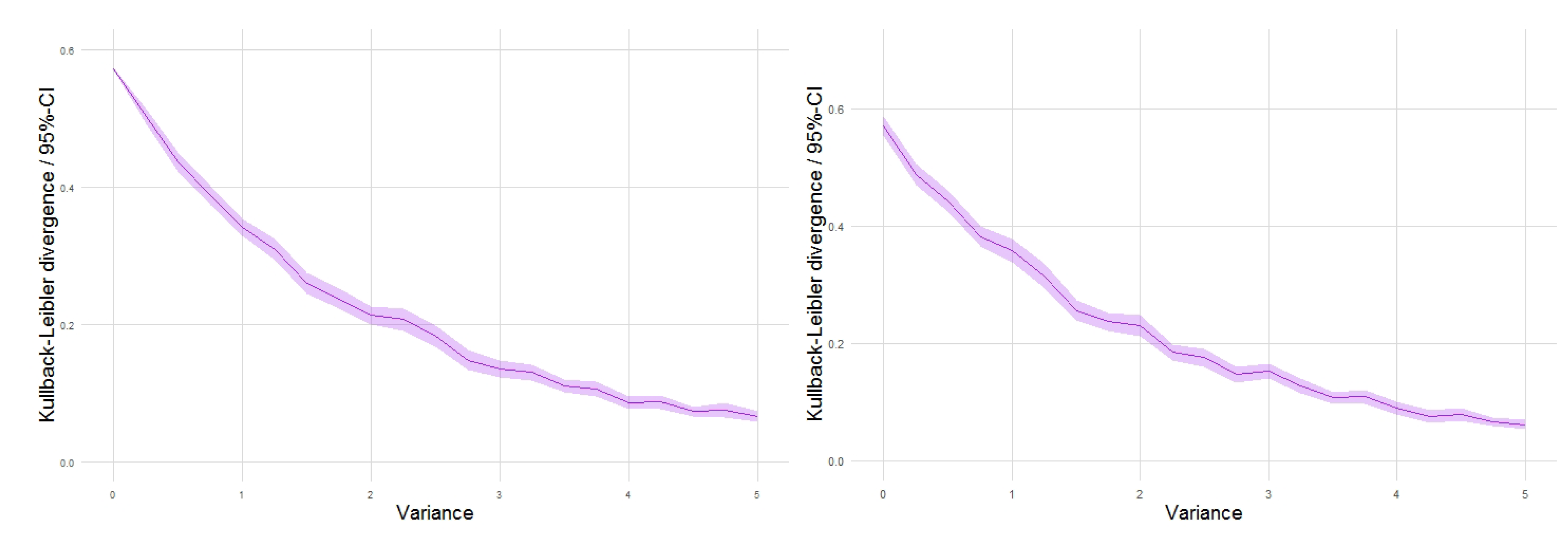
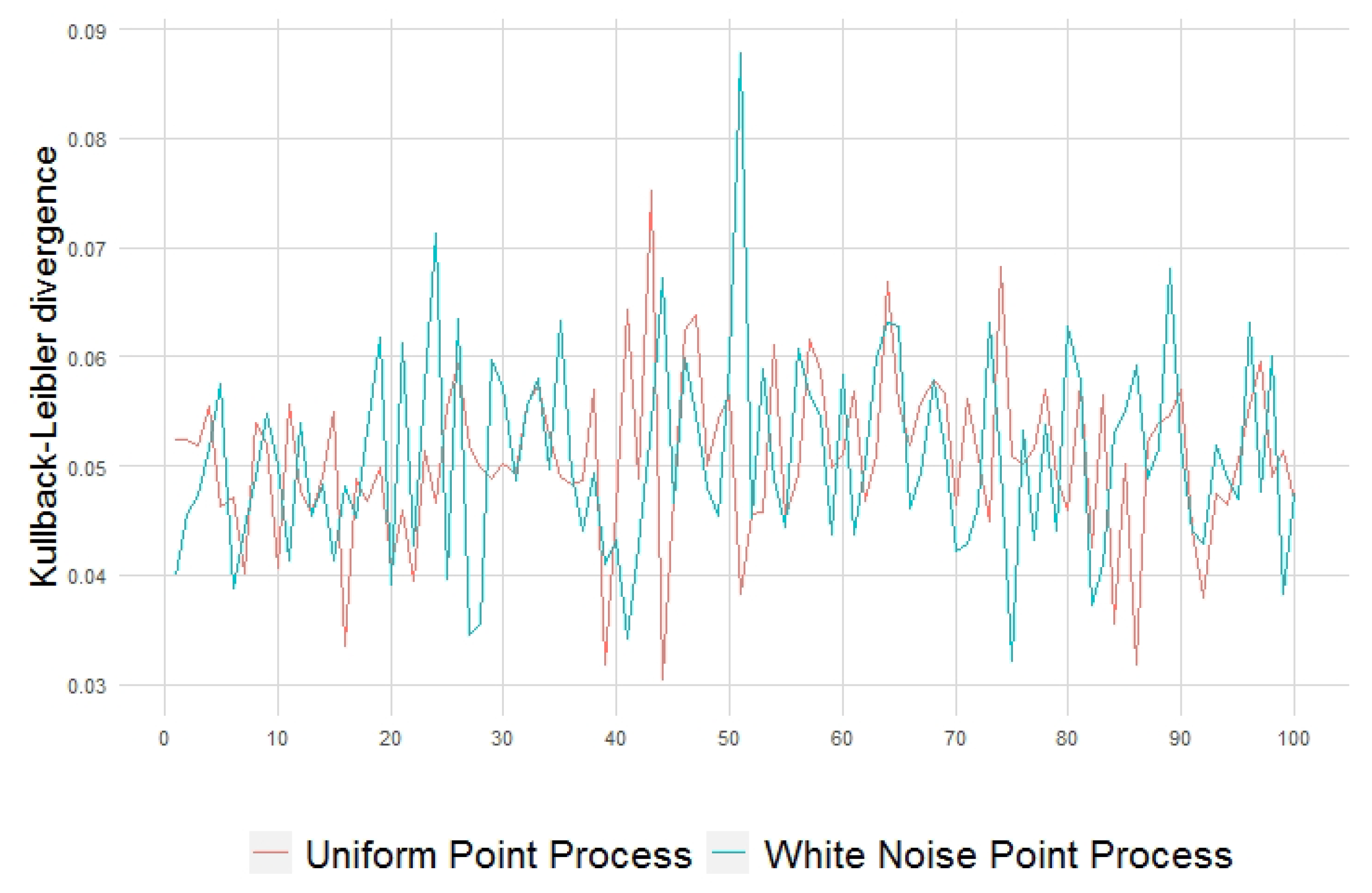
4.1. Weak Structure Reference Processes
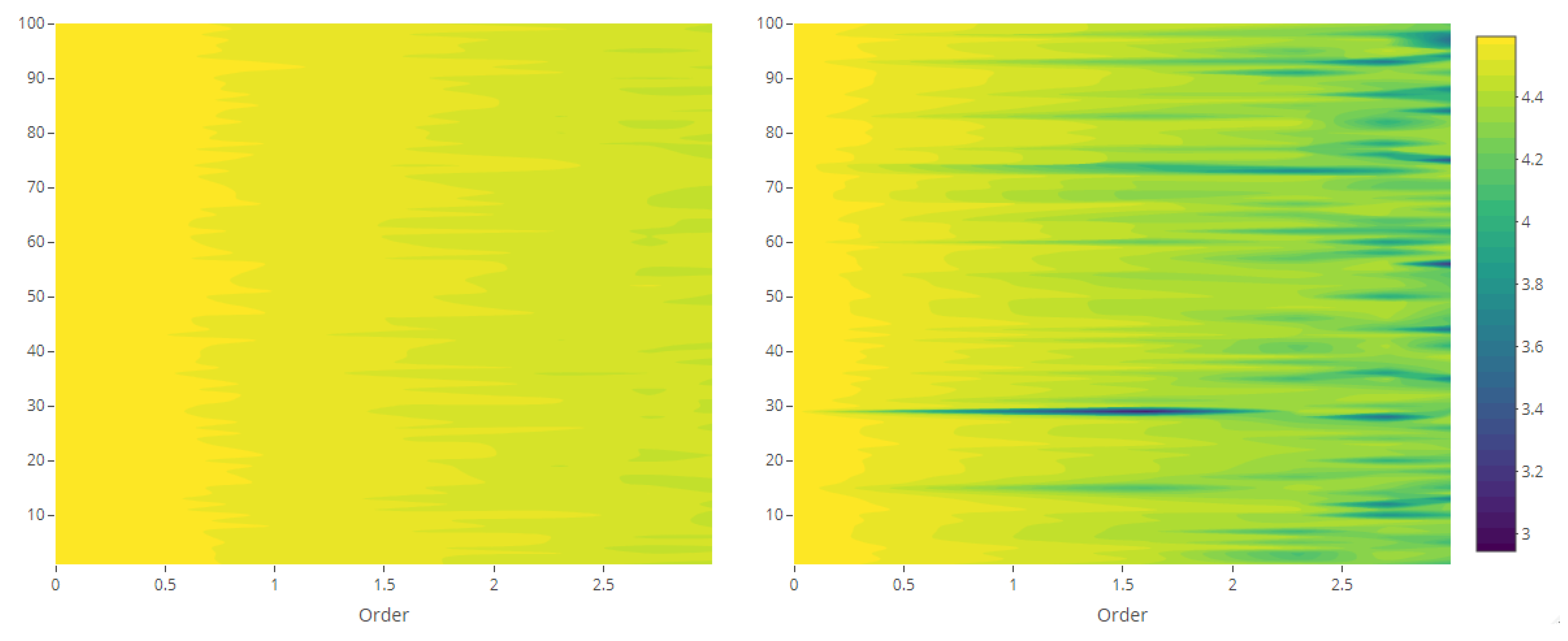
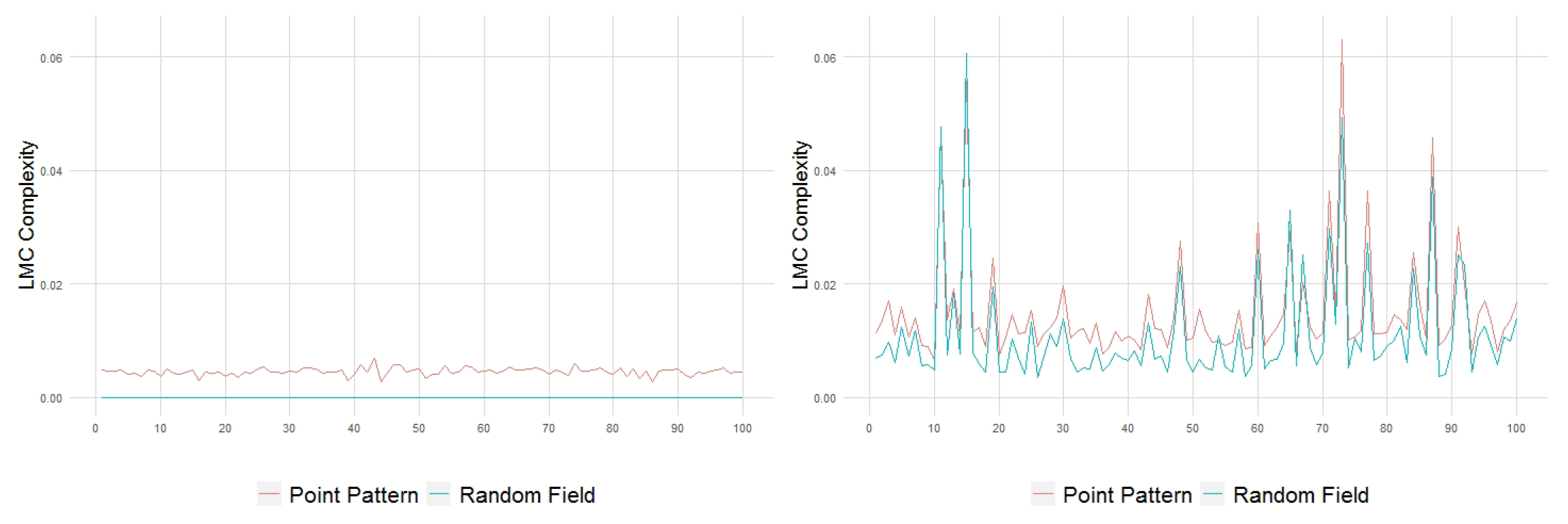
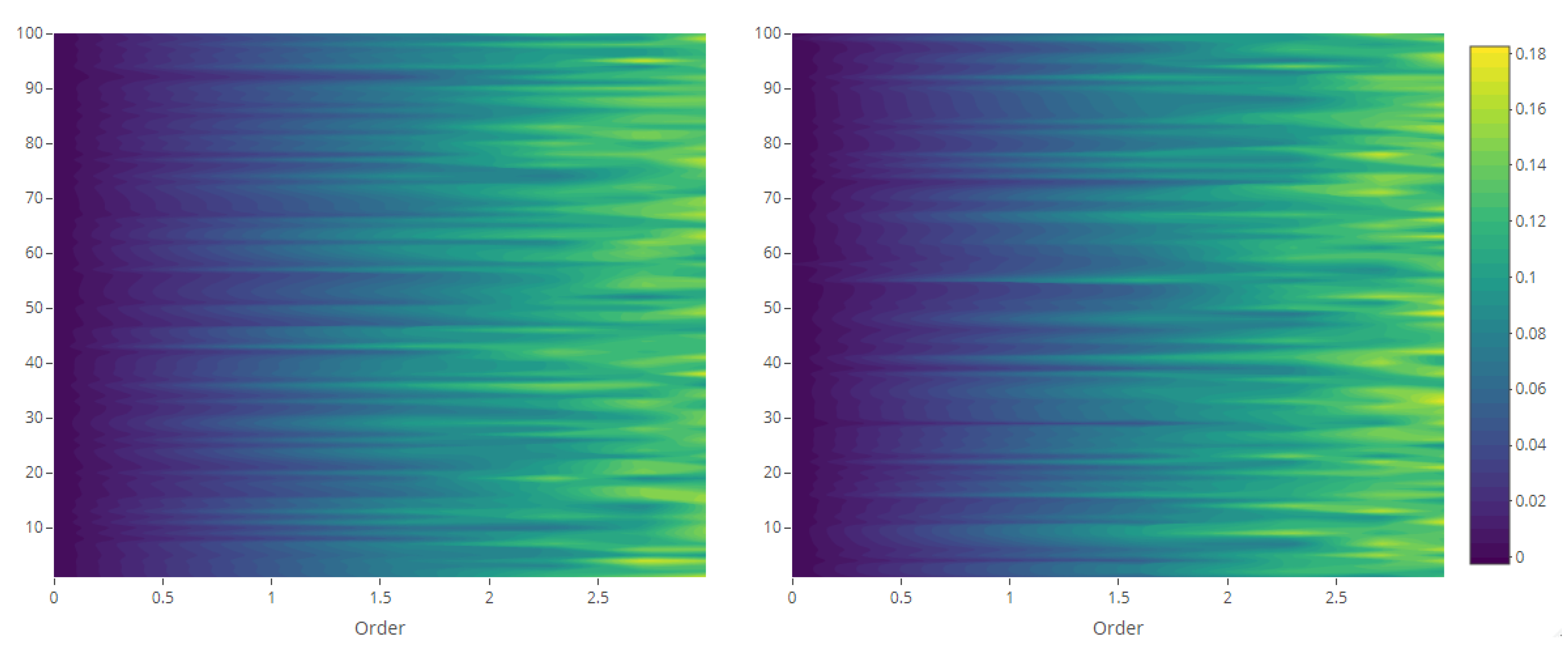
4.2. Marginal Analysis
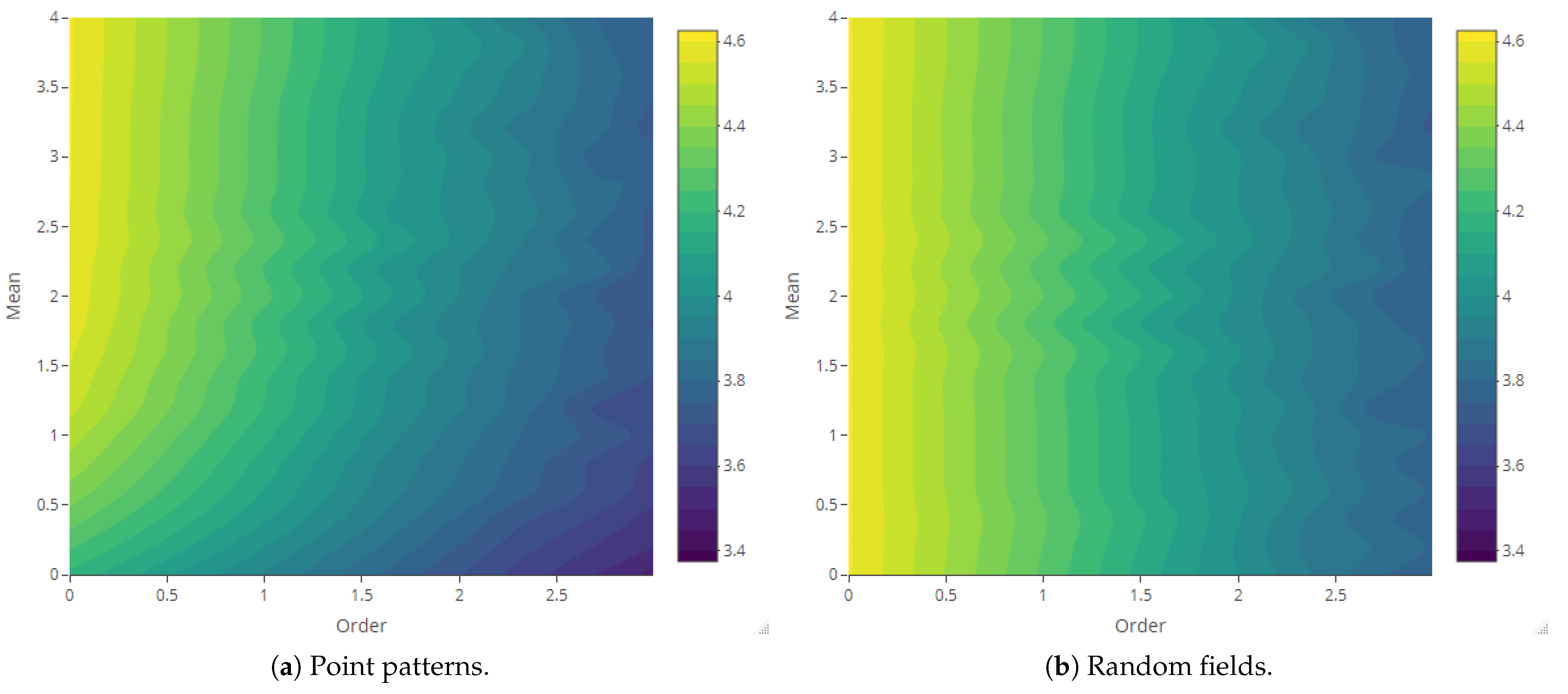
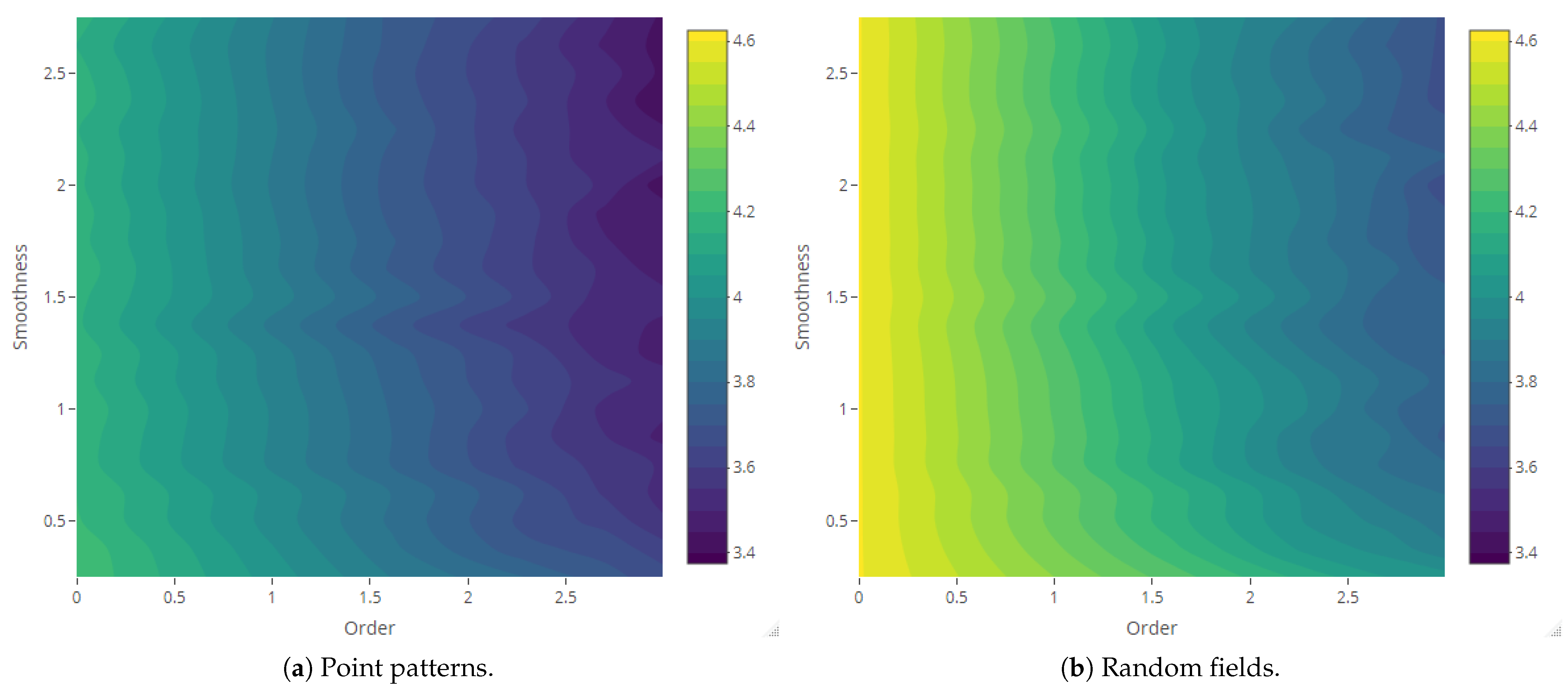
4.3. Joint Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Cox, D.R. Some statistical methods connected with series of events. J. R. Stat. Soc. Ser. B (Methodol.) 1955, 17, 129–157. [Google Scholar] [CrossRef]
- Møller, J.; Syversveen, A.R.; Waagepetersen, R.P. Log Gaussian Cox processes. Scand. J. Stat. 2001, 25, 451–482. [Google Scholar] [CrossRef]
- Coles, P.; Jones, B. A lognormal model for the cosmological mass distribution. Mon. Not. R. Astron. Soc. 1991, 248, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Rathbun, S.L. Estimation of Poisson intensity using partially observed concomitant variables. Biometrics 1996, 52, 226–242. [Google Scholar] [CrossRef]
- Illian, J.B.; Martino, S.; Sørbye, S.H.; Gallego-Fernández, J.B.; Zunzunegui, M.; Esquivias, M.P.; Travis, J.M.J. Fitting complex ecological point process models with integrated nested Laplace approximation. Methods Ecol. Evol. 2013, 4, 305–315. [Google Scholar] [CrossRef] [Green Version]
- Diggle, P.; Zheng, P.; Durr, P. Nonparametric estimation of spatial segregation in a multivariate point process: Bovine tuberculosis in Cornwall, UK. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2005, 54, 645–658. [Google Scholar] [CrossRef]
- Illian, J.B.; Møller, J.; Waagepetersen, R.P. Hierarchical spatial point process analysis for a plant community with high biodiversity. Environ. Ecol. Stat. 2009, 16, 389–405. [Google Scholar] [CrossRef]
- Waagepetersen, R.; Schweder, T. Likelihood-based inference for clustered line transect data. J. Agric. Biol. Environ. Stat. 2006, 11, 264–279. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, A.; Diggle, P.J. Bayesian estimation and prediction for inhomogeneous spatiotemporal log-Gaussian Cox processes using low-rank models, with application to criminal surveillance. J. Am. Stat. Assoc. 2012, 107, 93–101. [Google Scholar] [CrossRef]
- Siino, M.; Adelfio, G.; Mateu, J.; Chiodi, M.; D’Alessando, A. Spatial pattern analysis using hybrid models: An application to the Hellenic seismicity. Stoch. Environ. Res. Risk Assess. 2017, 31, 1633–1648. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability. Volume 1: Contributions to the Theory of Statistics; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef] [Green Version]
- Catalán, R.G.; Garay, J.; López-Ruiz, R. Features of the extension of a statistical measure of complexity to continuous systems. Phys. Rev. E 2002, 66, 011102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Angulo, J.M.; Esquivel, F.J.; Madrid, A.E.; Alonso, F.J. Information and complexity analysis of spatial data. Spat. Stat. 2021, 42, 100462. [Google Scholar] [CrossRef]
- Campbell, L.L. Exponential entropy as a measure of extent of a distribution. Z. Wahrscheinlichkeitstheorie Verw Geb. 1966, 5, 217–225. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Nagy, A.; Romera, E.; Sañudo, J. A generalized statistical complexity measure: Applications to quantum systems. J. Math. Phys. 2009, 50, 123528. [Google Scholar] [CrossRef] [Green Version]
- Romera, E.; Sen, K.D.; Nagy, A. A generalized relative complexity measure. J. Stat. Mech. Theory Exp. 2011, 2011, 9–16. [Google Scholar] [CrossRef]
- Papangelou, F. On the entropy rate of stationary point processes and its discrete approximation. Z. Wahrscheinlichkeitstheorie Verw Geb. 1978, 44, 191–211. [Google Scholar] [CrossRef]
- Baratpour, S.; Ahmadi, J.; Arghami, N.R. Some characterizations based on entropy of order statistics and record values. Commun. Stat. Theory Methods 2007, 36, 47–57. [Google Scholar] [CrossRef]
- Daley, D.; Vere-Jones, D. Scoring probability forecasts for point processes: The entropy score and information gain. J. Appl. Probab. 2004, 41, 297–312. [Google Scholar] [CrossRef]
- Matérn, B. Spatial Variation, 2nd ed.; Springer: Berlin, Germany, 1986. [Google Scholar]
- Handcock, M.S.; Stein, M.L. A Bayesian analysis of kriging. Technometrics 1993, 35, 403–410. [Google Scholar] [CrossRef]
- Guttorp, P.; Gneiting, T. On the Whittle-Matérn Correlation Family; Technical Report 80; NRCSE: London, UK, 2005. [Google Scholar]
- Guttorp, P.; Gneiting, T. Studies in the history of probability and statistics XLIX. On the Matérn correlation family. Biometrika 2006, 93, 989–995. [Google Scholar] [CrossRef]
- Hartley, R.V.L. Transmission of information. Bell Syst. Tech. J. 1928, 7, 535–563. [Google Scholar] [CrossRef]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Baïle, R.; Muzy, J.F.; Silvani, X. Multifractal point processes and the spatial distribution of wildfires in French Mediterranean regions. Phys. A Stat. Mech. Its Appl. 2021, 568, 125697. [Google Scholar] [CrossRef]
- Romero, J.L.; Madrid, A.E.; Angulo, J.M. Quantile-based spatiotemporal risk assessment of exceedances. Stoch. Environ. Res. Risk Assess. 2018, 32, 2275–2291. [Google Scholar] [CrossRef]


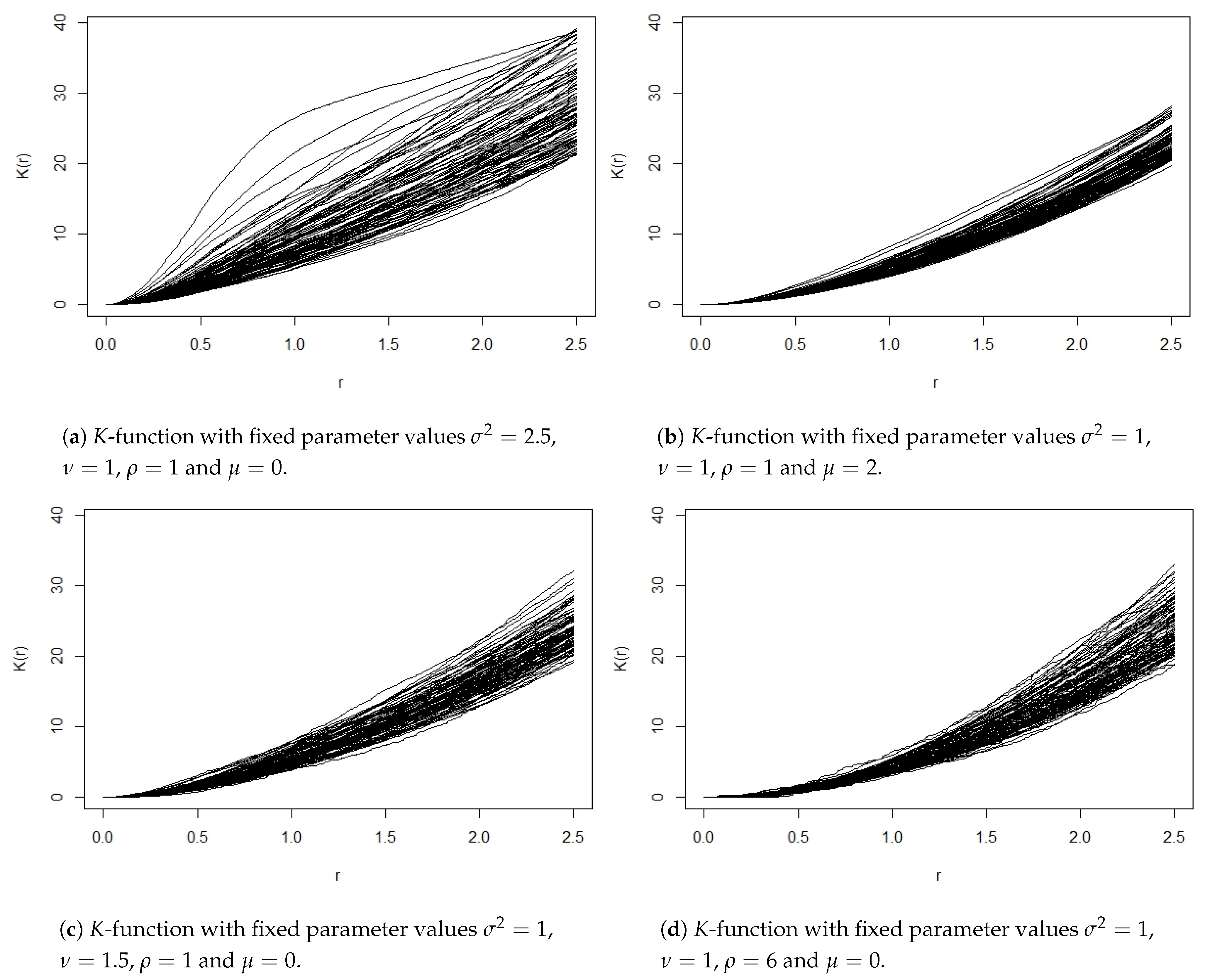





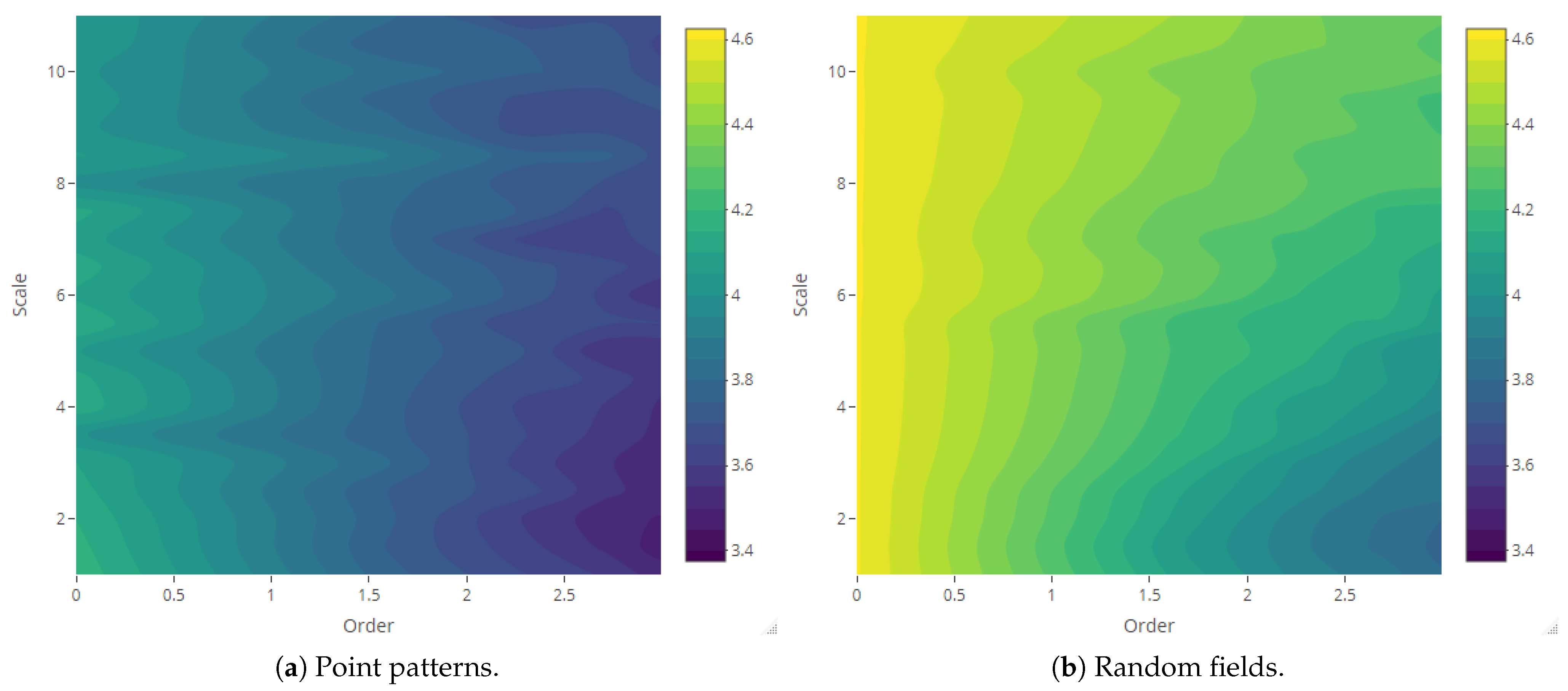

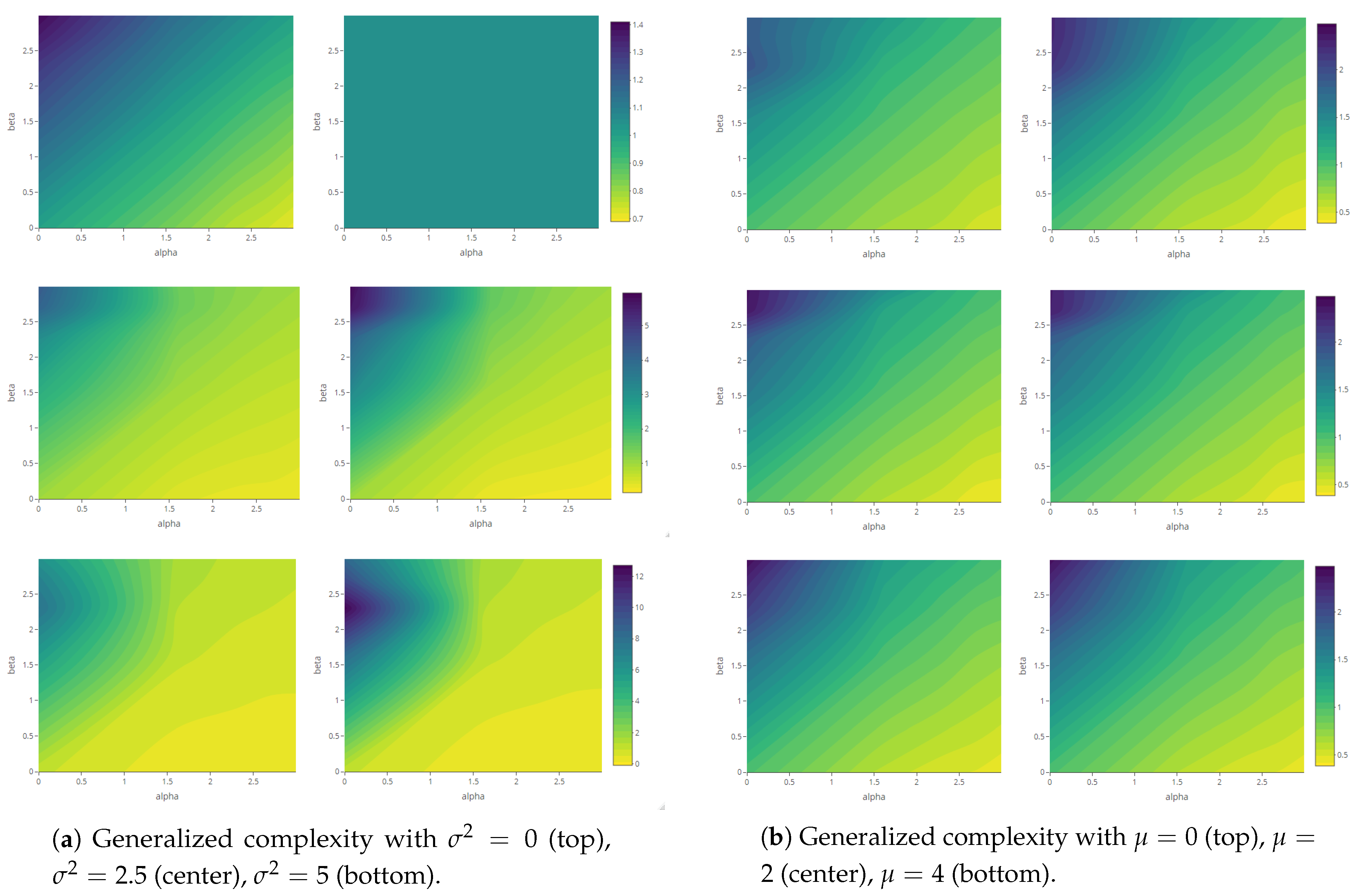

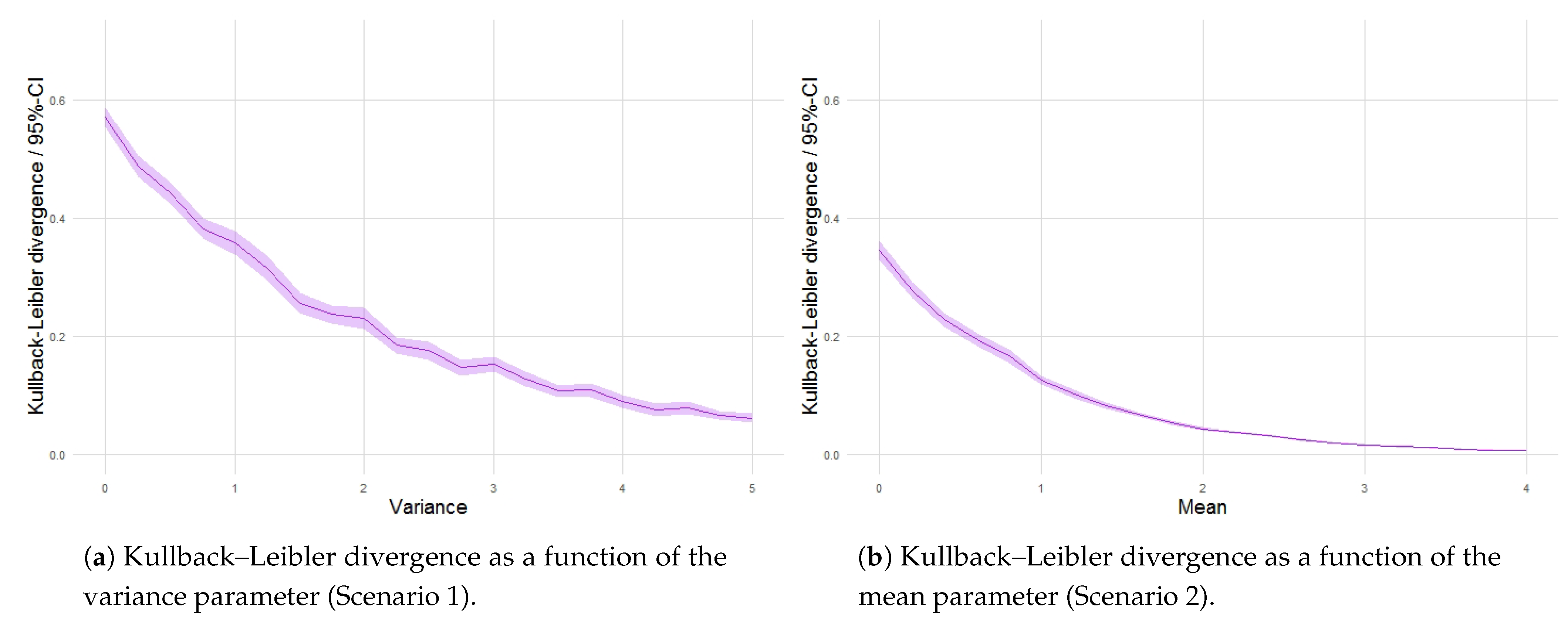

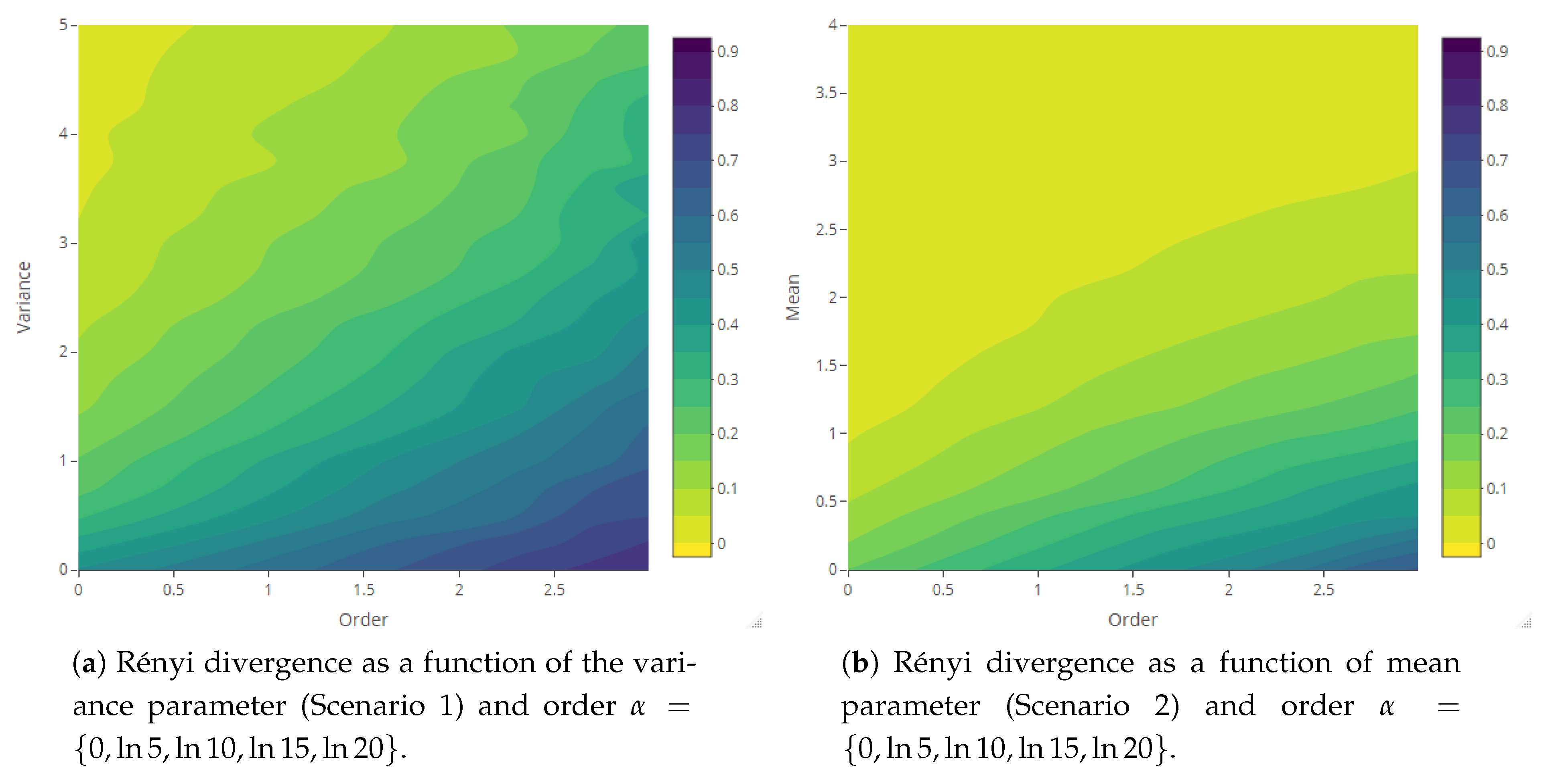

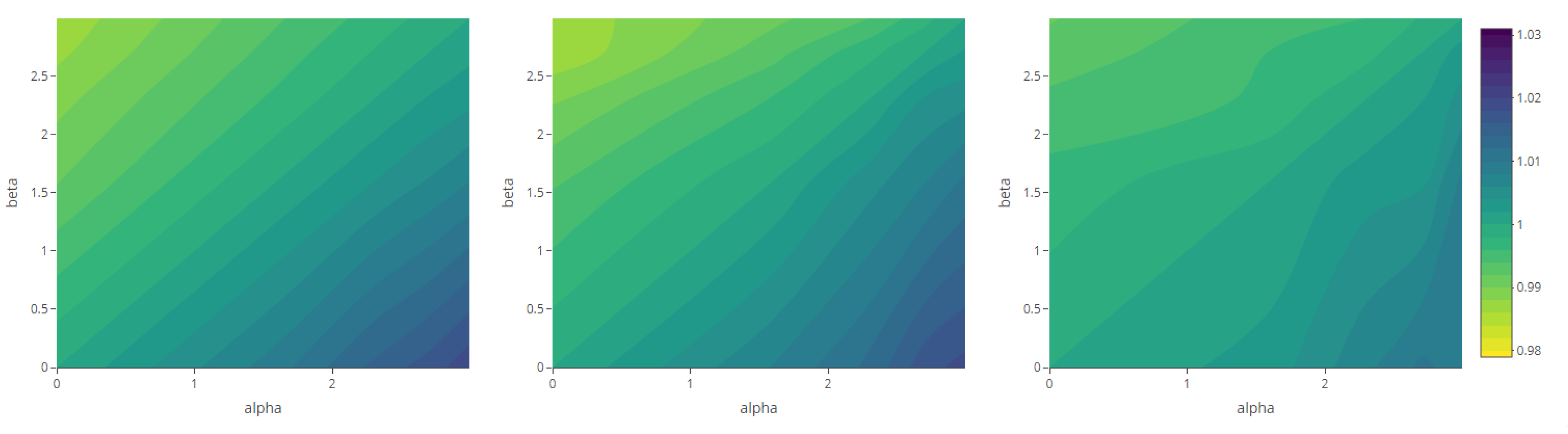
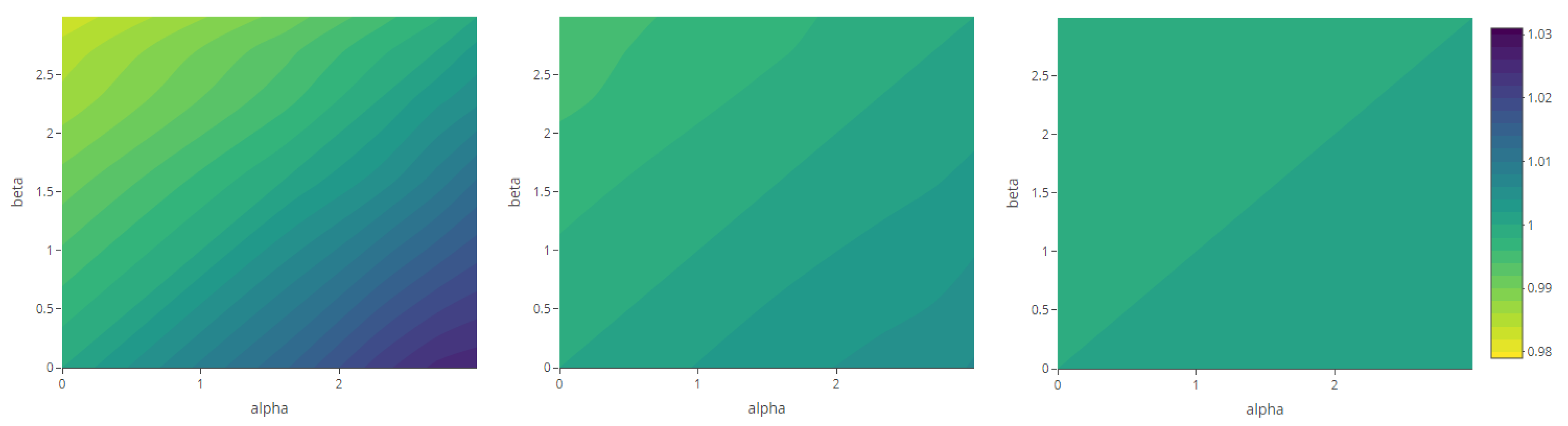

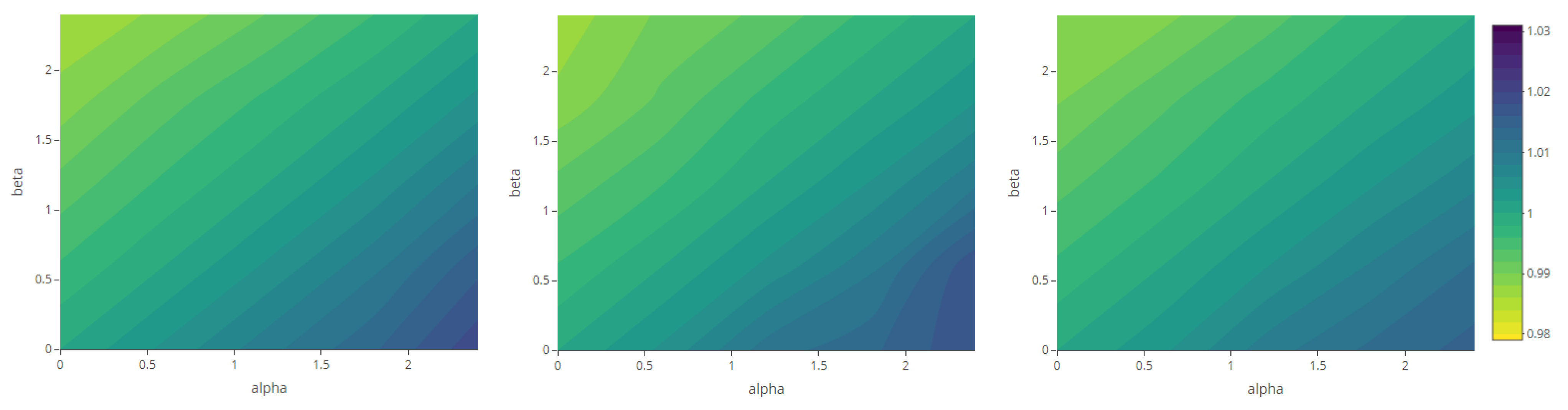
| Variable Parameters | Fixed Parameters | |||
|---|---|---|---|---|
| Scenario 1 | ||||
| Scenario 2 | ||||
| Scenario 3 | ||||
| Scenario 4 | ||||
| Parameter Value | Shannon Entropy SD | |||
|---|---|---|---|---|
| Multiple Patterns | Single Pattern | |||
| Mean Intra SD | Inter-Mean SD | Total SD | Inter-Single SD | |
| 0.0782 | 0.0076 | 0.0784 | 0.0820 | |
| 0.0765 | 0.0552 | 0.0943 | 0.0914 | |
| 0.0737 | 0.0607 | 0.0954 | 0.0911 | |
| 0.0749 | 0.0849 | 0.1133 | 0.1245 | |
| 0.0733 | 0.0966 | 0.1211 | 0.1279 | |
| 0.0743 | 0.1127 | 0.1349 | 0.1364 | |
| 0.0709 | 0.1497 | 0.1654 | 0.2081 | |
| 0.0702 | 0.1590 | 0.1734 | 0.1767 | |
| 0.0685 | 0.1432 | 0.1584 | 0.2025 | |
| 0.0695 | 0.1856 | 0.1977 | 0.2141 | |
| 0.0650 | 0.2227 | 0.2312 | 0.2758 | |
| 0.0619 | 0.2187 | 0.2266 | 0.3048 | |
| 0.0607 | 0.3478 | 0.3516 | 0.2188 | |
| 0.0625 | 0.2711 | 0.2774 | 0.2982 | |
| 0.0574 | 0.3561 | 0.3591 | 0.2585 | |
| 0.0560 | 0.2575 | 0.2627 | 0.2949 | |
| 0.0516 | 0.3702 | 0.3722 | 0.3422 | |
| 0.0519 | 0.3046 | 0.3079 | 0.4179 | |
| 0.0495 | 0.4012 | 0.4025 | 0.3855 | |
| 0.0493 | 0.3999 | 0.4013 | 0.3825 | |
| 0.0471 | 0.3920 | 0.3131 | 0.4212 | |
| Parameter Value | Kullback–Leibler Divergence SD | |||
|---|---|---|---|---|
| Multiple Patterns | Single Pattern | |||
| Mean Intra SD | Inter-Mean SD | Total SD | Inter-Single SD | |
| 0.0782 | 0.0076 | 0.0784 | 0.0820 | |
| 0.0698 | 0.0561 | 0.0895 | 0.0911 | |
| 0.0600 | 0.0707 | 0.0927 | 0.0912 | |
| 0.0532 | 0.0717 | 0.0894 | 0.0892 | |
| 0.0469 | 0.0655 | 0.0807 | 0.1051 | |
| 0.0429 | 0.0806 | 0.0917 | 0.1064 | |
| 0.0358 | 0.0778 | 0.0860 | 0.0865 | |
| 0.0326 | 0.0749 | 0.0820 | 0.0767 | |
| 0.0290 | 0.0666 | 0.0729 | 0.0914 | |
| 0.0282 | 0.0812 | 0.0863 | 0.0686 | |
| 0.0249 | 0.0788 | 0.0830 | 0.0759 | |
| 0.0201 | 0.0716 | 0.0746 | 0.0696 | |
| 0.0184 | 0.0632 | 0.0661 | 0.0649 | |
| 0.0177 | 0.0598 | 0.0626 | 0.0638 | |
| 0.0150 | 0.0491 | 0.0516 | 0.0512 | |
| 0.0143 | 0.0530 | 0.0551 | 0.0574 | |
| 0.0117 | 0.0493 | 0.0510 | 0.0572 | |
| 0.0116 | 0.0490 | 0.0505 | 0.0575 | |
| 0.0100 | 0.0370 | 0.0384 | 0.0567 | |
| 0.0103 | 0.0543 | 0.0556 | 0.0387 | |
| 0.0088 | 0.0384 | 0.0396 | 0.0428 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medialdea, A.; Angulo, J.M.; Mateu, J. Structural Complexity and Informational Transfer in Spatial Log-Gaussian Cox Processes. Entropy 2021, 23, 1135. https://doi.org/10.3390/e23091135
Medialdea A, Angulo JM, Mateu J. Structural Complexity and Informational Transfer in Spatial Log-Gaussian Cox Processes. Entropy. 2021; 23(9):1135. https://doi.org/10.3390/e23091135
Chicago/Turabian StyleMedialdea, Adriana, José Miguel Angulo, and Jorge Mateu. 2021. "Structural Complexity and Informational Transfer in Spatial Log-Gaussian Cox Processes" Entropy 23, no. 9: 1135. https://doi.org/10.3390/e23091135
APA StyleMedialdea, A., Angulo, J. M., & Mateu, J. (2021). Structural Complexity and Informational Transfer in Spatial Log-Gaussian Cox Processes. Entropy, 23(9), 1135. https://doi.org/10.3390/e23091135






